# Wahrscheinlichkeitsdichte für x=2
# in der Standardnormalverteilung
dnorm(2)## [1] 0.05399097In R sind zahlreiche Verteilungsfunktionen implementiert. Wir beschränken uns in diesem Buch auf die für uns wichtigen Wahrscheinlichkeisverteilungen.
Eine vollständige Liste aller implementierten Verteilungen findet sich unter https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Distributions.html
Der Funktionsumfang folgt dabei einer gewissen Logik, für jede Verteilung existiert je eine d, p, q und r-Funktion. Für die Normalverteilung (siehe Näheres in Abschnitt 18.1) sind das dnorm(), pnorm(), qnorm() und rnorm(). Für die t-Verteilung (siehe Abschnitt 18.2) heißen die Equivalente dt(), pt(), qt() und rt(), für \(\chi^2\) entsprechend dchisq(), pchisq(), qchisq() und rchisq().
d: ist jeweils die Dichtefunktion der Verteilung
p: berechnet die Werte der Verteilungsfunktion (kumulierte Dichte)
q: bestimmt die Quantile der Verteilung
r: erzeugt Zufallswerte aus der Verteilung
Dies möchten wir am Beispiel der Normalverteilung verdeutlichen.
Die Normalverteilung ist mit den oben beschriebenen Funktionen in R implementiert.
Mit der Funktion dnorm() berechnet man die Werte der Wahrscheinlichkeitsdichte. Möchte man beispielsweise die Wahrscheinlichkeitsdichte für \(x=2\) aus der Standardnormalverteilung berechnen lautet der Befehl:
# Wahrscheinlichkeitsdichte für x=2
# in der Standardnormalverteilung
dnorm(2)## [1] 0.05399097Standardmäßig stammen diese Werte aus der Standardnormalverteilung, sie streuen also mit einer Standardabweichung von \(s=1\) um den Mittelwert \(\bar{x}=0\).
Möchte man dies ändern, können der Funktion entsprechende Werte für Mittelwert und Standardabweichung übergeben werden:
# Wahrscheinlichkeitsdichte für x=4
# aus einer Verteilung mit Mittelwert 8 und Standardabweichung 2
dnorm(4, mean=8, sd=2)## [1] 0.02699548Die Werte der Verteilungsfunktion lassen sich mit pnorm() berechnen. Die Funktion gibt die Wahrscheinlichkeit an, dass ein Zufallsvariable einen Wert von \(\le x\) (= “höchstens” \(x\)) annimmt.
# Wahrscheinlichkeit dass Wert kleiner-gleich 2
# in Standardnormalverteilung
pnorm(2)## [1] 0.9772499Für andere Normalverteilungen ändert sich der Befehl entsprechend:
# Wahrscheinlichkeit dass Wert kleiner-gleich 8
# in Normalverteilung mit xquer=12 und s=3
pnorm(8, mean=12, s=3)## [1] 0.09121122Quantile lassen sich mit der Funktion qnorm() berechnen. Quantile stellen Grenzen dar, die ein zufälliger Wert mit einer vorgegebenen Wahrscheinlichkeit nicht überschreiten wird. Wenn das 95%-Quantil beispielsweise den Wert \(5\) hat, wird eine zufällig gezogene Zahl mit 95% Sicherheit kleiner als \(5\) sein.
# Grenze des 95% Quantils
# in Standardnormalverteilung
qnorm(p=0.95)## [1] 1.644854Auch qnorm() können Werte für andere Normalverteilungen übergeben werden.
# Grenze des 95% Quantils
# in Normalverteilung mit xquer=9 und sd=5
qnorm(p=0.95, mean=9, sd=5)## [1] 17.22427Mit rnorm() lassen sich normalverteilte Zufallswerte erzeugen:
# erzeuge "zufällig" 10 Werte # aus der Standardnormalverteilung
rnorm(10)## [1] -1.400043517 0.255317055 -2.437263611 -0.005571287 0.621552721
## [6] 1.148411606 -1.821817661 -0.247325302 -0.244199607 -0.282705449Auch mit rnorm() können wir andere Normalverteilungen für unsere Zufallszahlen angeben:
# erzeuge "zufällig" 10 normalverteilte Werte
# mit Mittelwert 8 und Standardabweichung 2
rnorm(10, mean=8, sd=2)## [1] 6.892601 9.257964 12.130050 4.738021 9.024854 4.273977 6.955975
## [8] 7.894796 9.085993 6.171850Plot-Beispiel mit der plot()-Funktion (siehe Kapitel 34).
# Erzeuge Werte von -3 bis 6
x <- seq(-3, 6, by = 0.005)
# Plot erstellen
plot(x, dnorm(x, mean = 0, sd = 1),
type = "l", xlim = c(-3, 6), ylim = c(0, 0.8),
xlab = "x", ylab = "Dichtefunktion", main = "Normalverteilungen")
lines(x, dnorm(x, mean = 2, sd = 0.5), col = "blue")
lines(x, dnorm(x, mean = 2, sd = 2), col = "darkorchid")
# Annotationen hinzufügen
text(0, 0.42, "N(0;1)", col = "black")
text(3, 0.6, "N(2;0.5)", col = "blue")
text(5, 0.1, "N(2;2)", col = "darkorchid")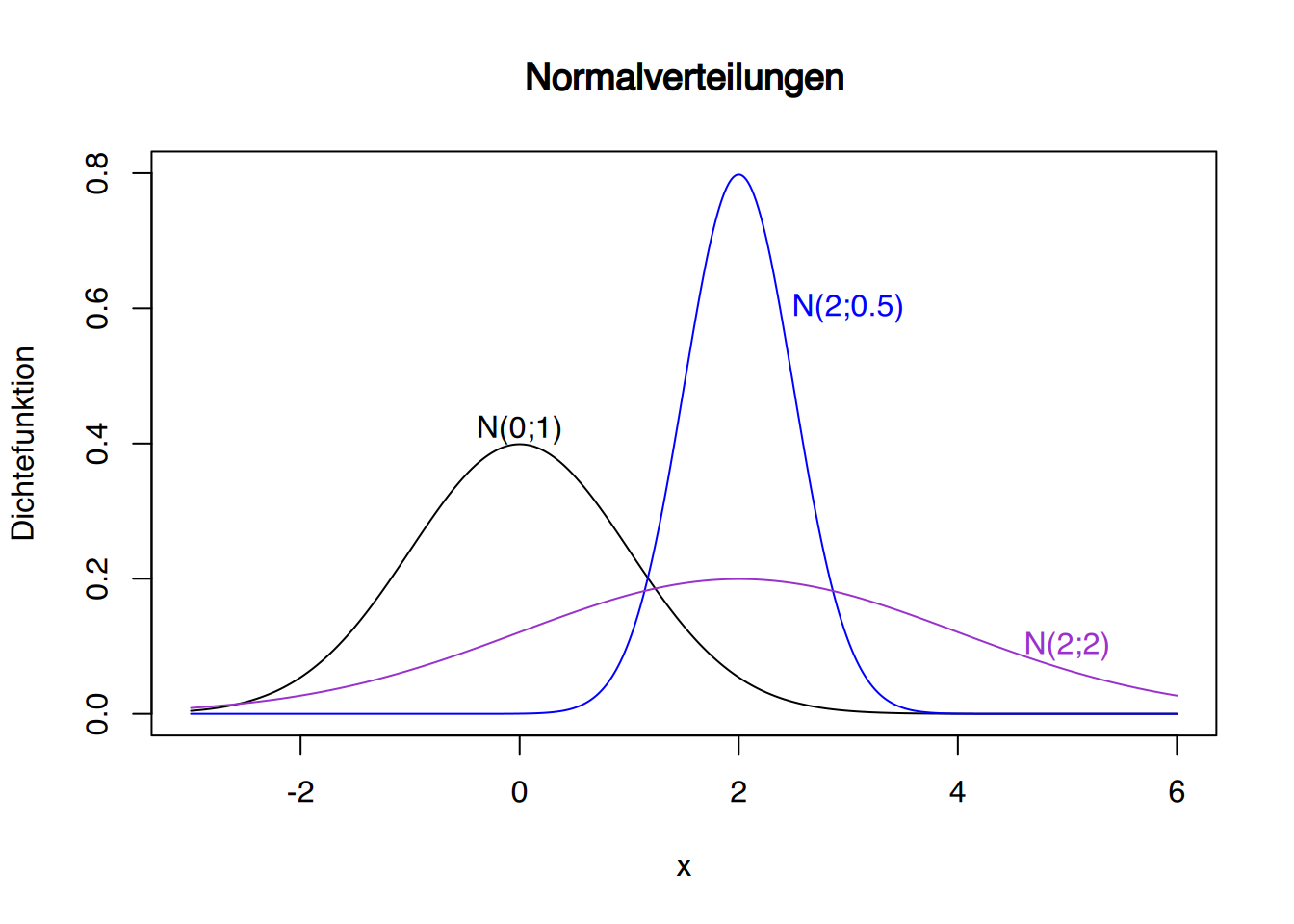
Beispiel mit ggplot() (siehe Kapitel 35).
# erzeuge Werte von -3 bis 6
x <- seq(-3,6, by=0.005)
# übergebe in ein data.frame
df <- data.frame(x)
# ggplot erstellen
library(ggplot2)
p <- ggplot(data=df, aes(x)) + xlim(-3,6) + ylim(0, 0.8) + xlab("x") +
ylab("Dichtefunktion") + ggtitle("Normalverteilungen")
p +
stat_function(fun=dnorm, args=(c(mean=0,sd=1)), colour="black")+
annotate(geom="text", x=0, y=0.42, label="N(0;1)", color="black")+
stat_function(fun=dnorm, args=(c(mean=2,sd=0.5)), colour="blue") +
annotate(geom="text", x=3, y=0.6, label="N(2;0.5)", color="blue")+
stat_function(fun=dnorm, args=(c(mean=2,sd=2)), colour="darkorchid") +
annotate(geom="text", x=5, y=0.1, label="N(2;2)",
color="darkorchid")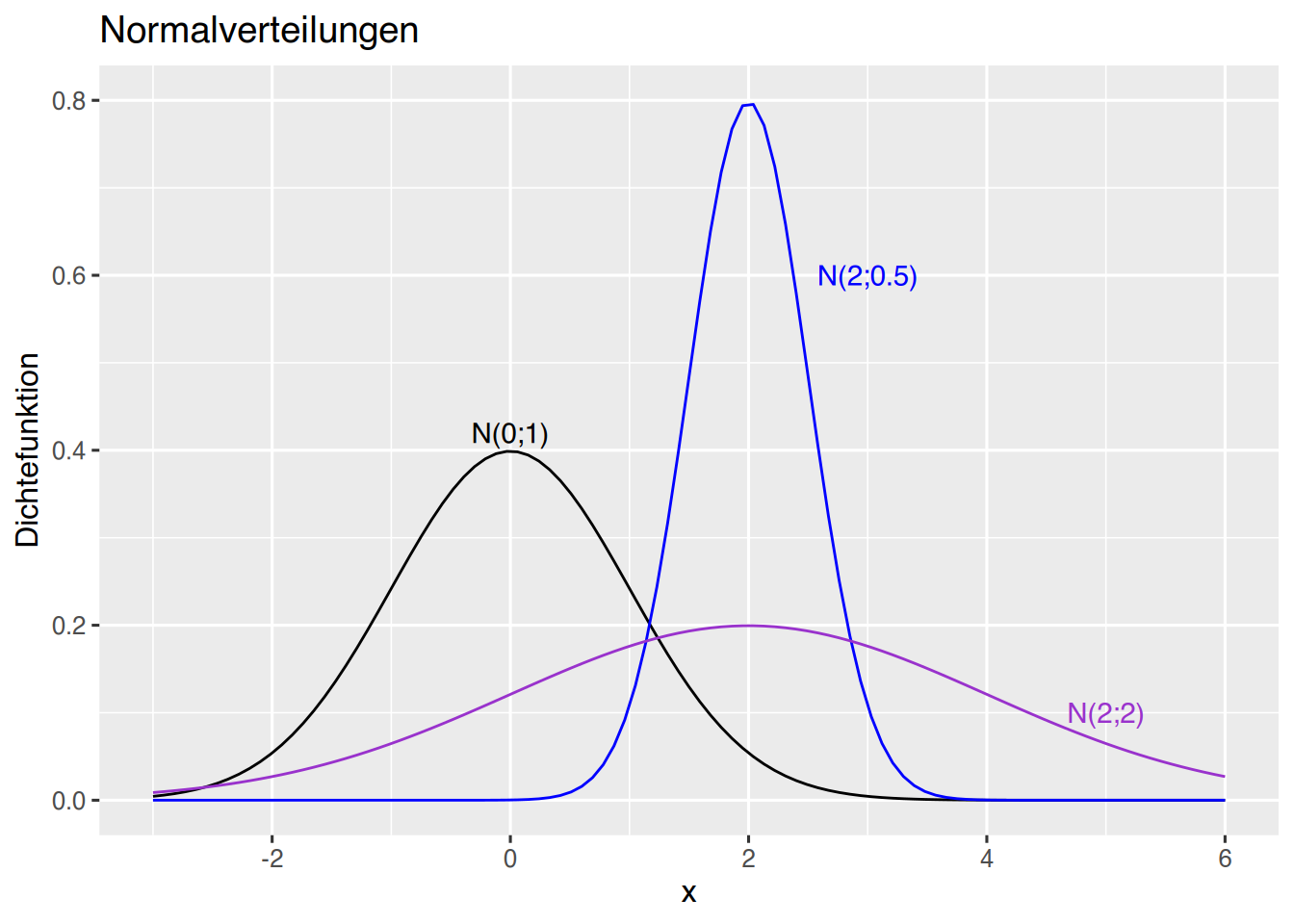
Für weitere Plot-Beispiele zur Normalverteilung siehe Abschnitt 37.2.
Die “kleine Schwester” der Standardnormalverteilung ist die Student-t-Verteilung (oder einfach kurz t-Verteilung). Für sie stehen die selben Funktionstypen zur Verfügung wie für die Normalverteilung (siehe Abschnitt 18.1). Diese heissen entsprechend dt(), pt(), qt() und rt() und funktionieren genau wie ihre Pendants der Standardnormalverteilung. Jedoch muss ihnen noch die Anzahl der Freiheitsgrade (\(df\)) übergeben werden:
# Wahrscheinlichkeitsdichte für x=2
# in der t-Verteilung mit 4 Freiheitsgraden
dt(2, df=4)## [1] 0.06629126# Wahrscheinlichkeit dass Wert kleiner-gleich 2
# in der t-Verteilung mit 3 Freiheitsgraden
pt(2, df=3)## [1] 0.930337# Grenze des 95% Quantils # in der t-Verteilung mit 3 Freiheitsgraden
qt(p=0.95, df=3)## [1] 2.353363# erzeuge "zufällig" 10 Werte
# aus der t-Verteilung mit 13 Freiheitsgraden
rt(10, df=13)## [1] 0.45366019 -1.18009245 2.00550964 0.07126229 0.63480028 0.17499076
## [7] 1.65206115 -0.22859755 -2.07243796 -0.28974980Möchte man die t-Verteilung plotten, kann das mittels plot() (siehe Kapitel 34) beispielsweise so geschehen:
# Erzeuge x-Werte
x <- seq(-3, 3, by = 0.005)
# Plot erstellen
plot(x, dt(x, df = 1), type = "l",
xlim = c(-3, 3), ylim = c(0, 0.4),
xlab = "x", ylab = "Dichtefunktion",
main = "t-Verteilungen nach Freiheitsgraden")
# Text hinzufügen
text(0, 0.25, "df=1", col = "black")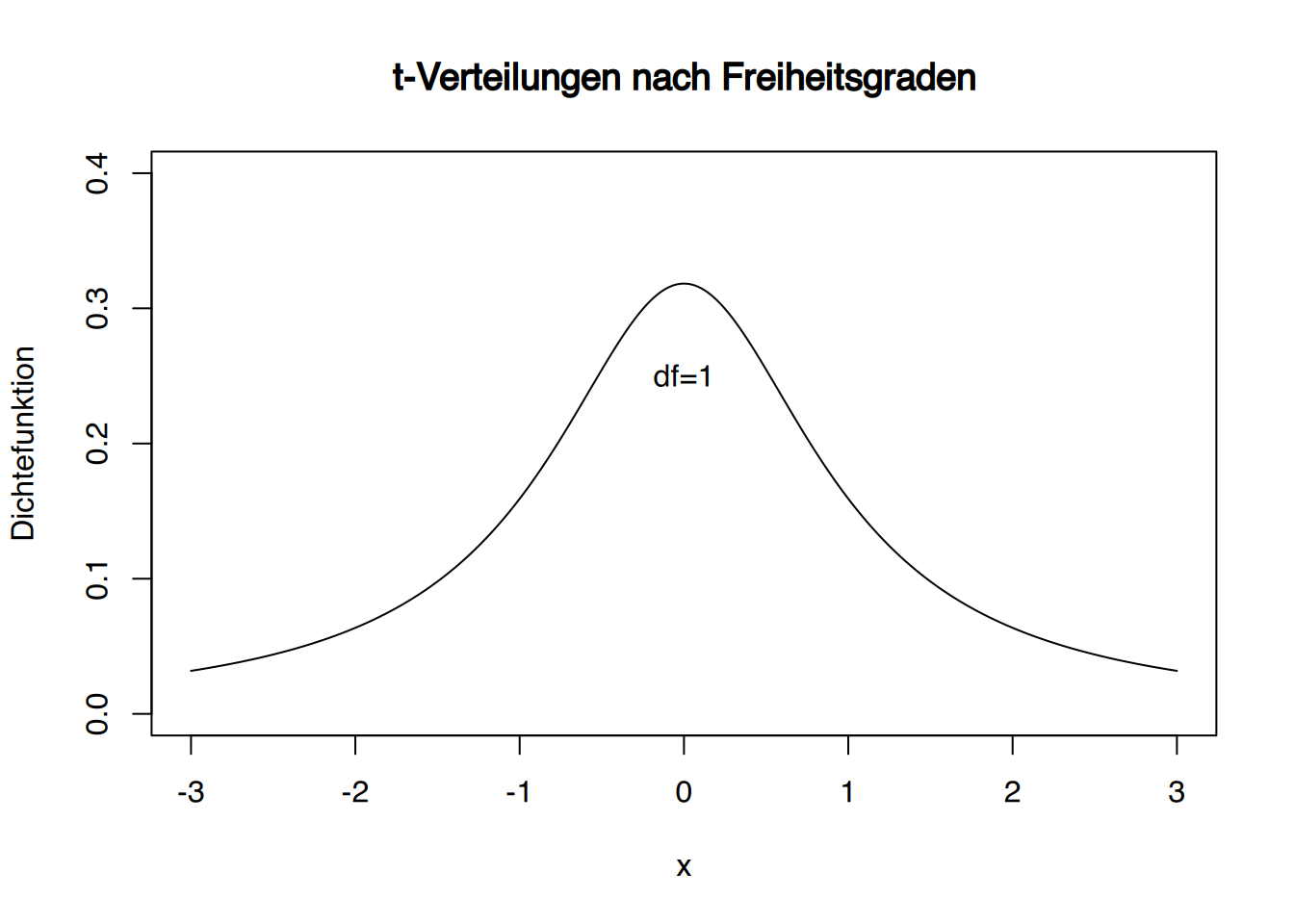
…oder mittels mit ggplot (siehe Kapitel 35) wie folgt.
# Erzeuge x-werte
df <- data.frame(x=seq(-3,3, by=0.005))
# Grundlegene Plotangaben
p <- ggplot(data=df, aes(x)) +
# begrenze die Achsen
xlim(-3,3) + ylim(0, 0.4) +
# Achsen-Titel
xlab("x") + ylab("Dichtefunktion") +
# Plot-Titel
ggtitle("t-Verteilungen", subtitle = "nach Freiheitsgraden")
# t-Verteilung plotten
p + stat_function(fun=dt, args=list(df=1), col="black") +
# Textfeld hinzufügen
annotate(geom="text", x=0, y=0.25, label="df=1", color="black")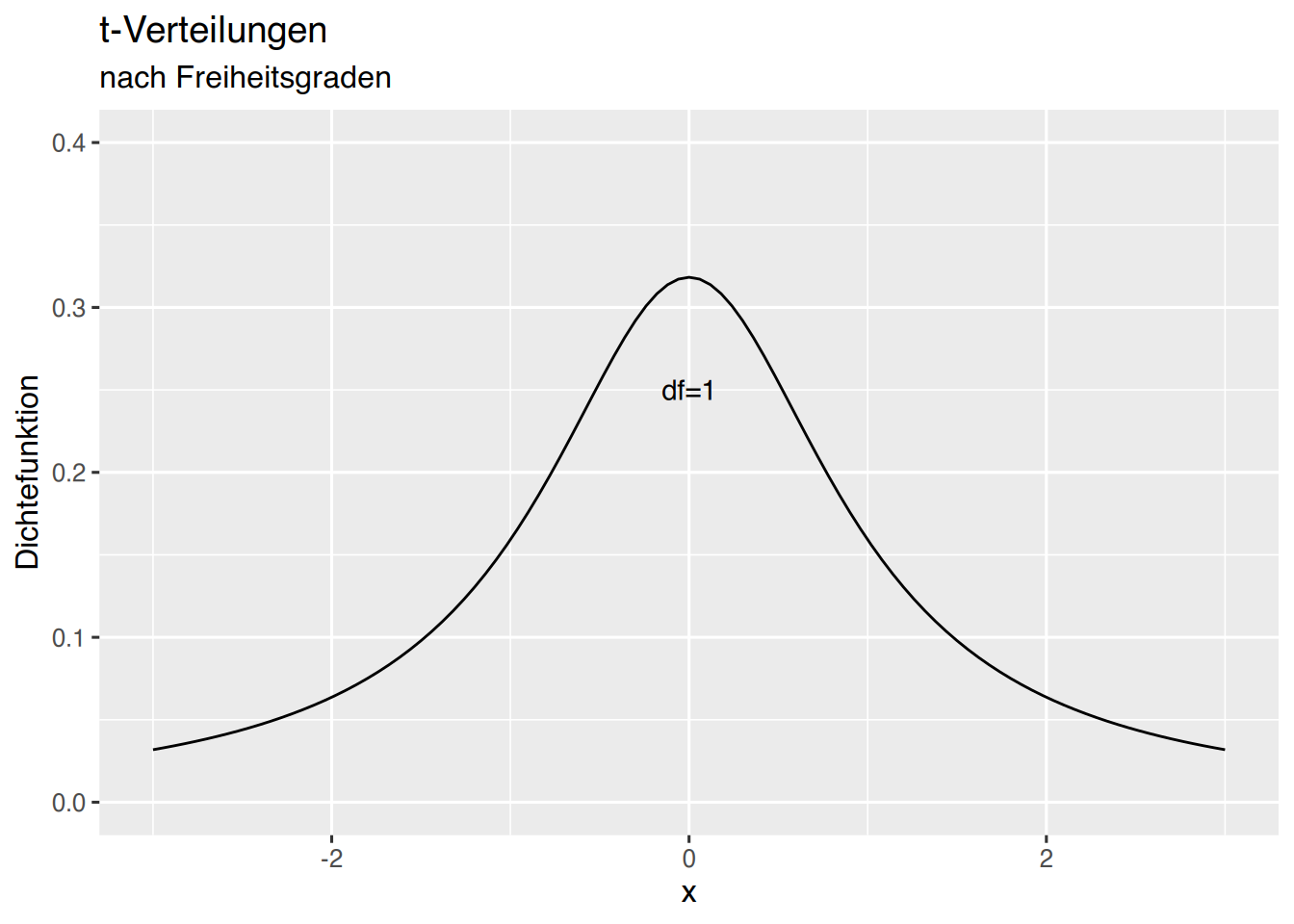
Für weitere Plot-Beispiele zur Normalverteilung siehe Abschnitt 37.3.
Die \(\chi^2\)-Verteilung ist mit den oben beschriebenen Funktionen in R implementiert. Diese heissen entsprechend dchisq(), pchisq(), qchisq() und rchisq() und funktionieren genau wie ihre Pendants der Standardnormalverteilung. Jedoch muss ihnen (wie bei der t-Verteilung) noch die Anzahl der Freiheitsgrade (\(df\)) übergeben werden:
# Wahrscheinlichkeitsdichte für x=2
# in der Chi^2-Verteilung mit 4 Freiheitsgraden
dchisq(2, df=4)## [1] 0.1839397Möchte man die \(\chi^2\)-Verteilung plotten, kann das mit der plot()-Funktion (siehe Kapitel 34) so umgesetzt werden:
# Erzeuge x-Werte
x <- seq(0, 25, by = 0.005)
# Dichte-Funktionen berechnen
df01 <- dchisq(x, df = 1)
df05 <- dchisq(x, df = 5)
df10 <- dchisq(x, df = 10)
df15 <- dchisq(x, df = 15)
# Plot erstellen
plot(x, df01, type = "l",
xlim = c(0, 25), ylim = c(0, 0.2),
xlab = "x", ylab = "Dichtefunktion",
main = "Chi^2-Verteilungen nach Freiheitsgraden")
# Linien für andere Freiheitsgrade hinzufügen
lines(x, df05, col = "blue")
lines(x, df10, col = "darkgreen")
lines(x, df15, col = "darkred")
# Legende hinzufügen
legend("topright", legend = c("df=1", "df=5", "df=10", "df=15"),
col = c("black", "blue", "darkgreen", "darkred"),
lty = 1, cex = 0.8)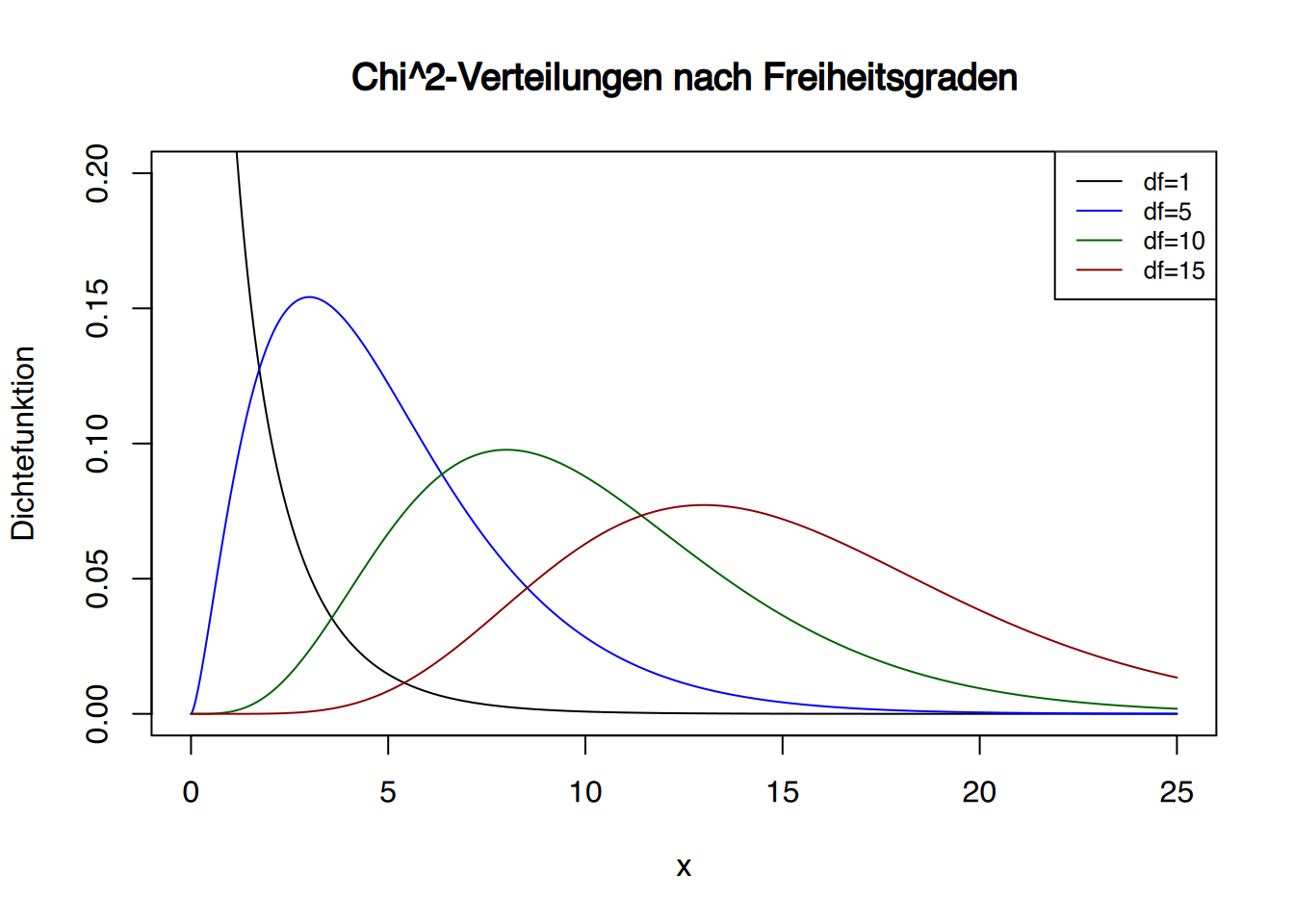
… oder mittels ggplot (siehe Kapitel 35) wie folgt.
# Erzeuge x-werte
x=seq(0,25, by=0.005)
df <- data.frame( x,
df01 = dchisq(x, df=1),
df05 = dchisq(x, df=5),
df10 = dchisq(x, df=10),
df15 = dchisq(x, df=15)
)
# erzeuge long-table
df <- pivot_longer(df, cols=c(df01, df05, df10, df15))
p <- ggplot(data=df, aes(x, value, fill=name)) +
xlim(0,25) + ylim(0, 0.2) +
xlab("x") + ylab("Dichtefunktion") +
ggtitle("Chi^2-Verteilungen", subtitle = "nach Freiheitsgraden")
p + geom_line(aes(col=name,linetype=name))+
labs(col="Freiheitsgrade",linetype="")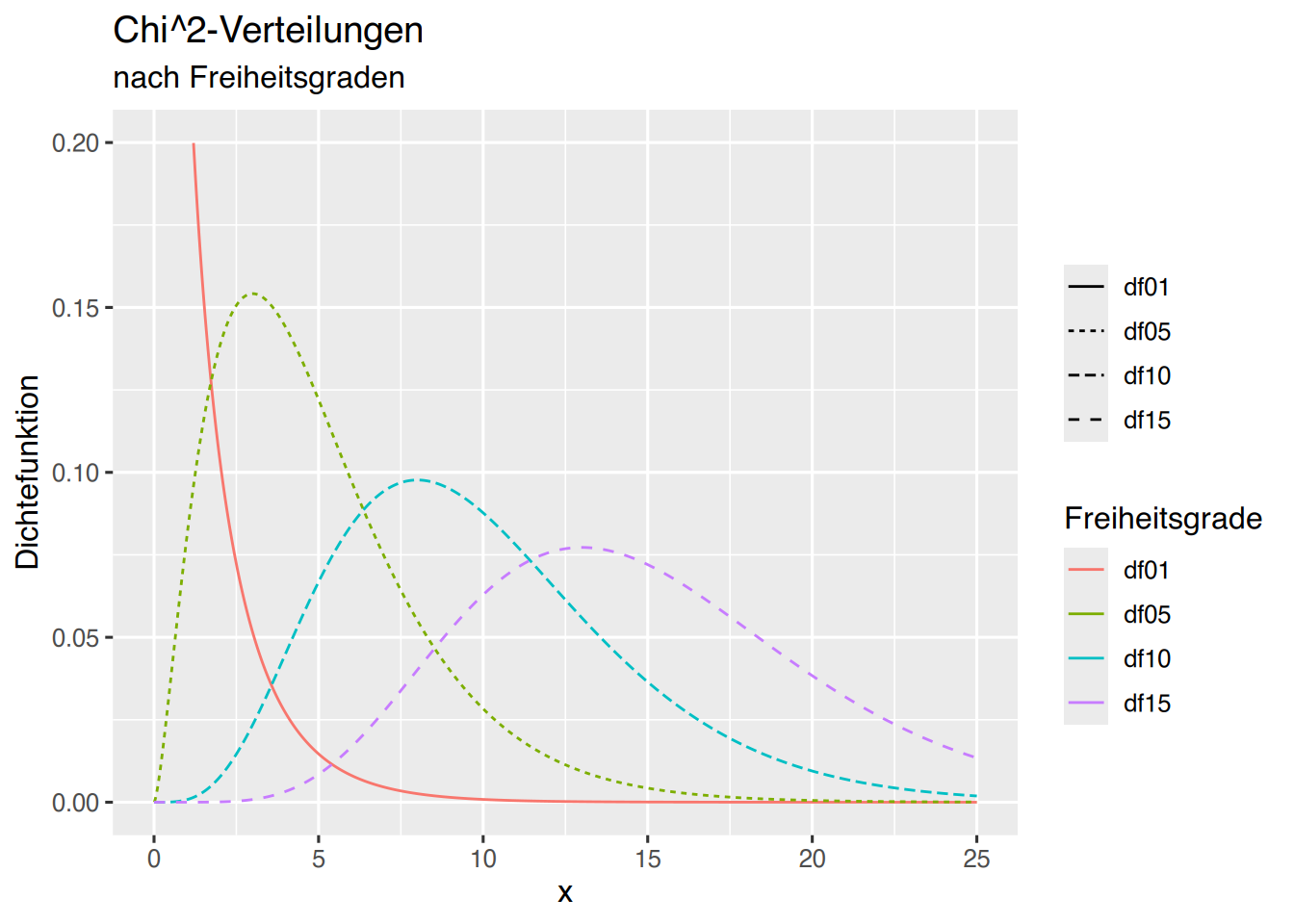
Für weitere Plot-Beispiele zur \(\chi^2\)-Verteilung siehe Abschnitt 37.4.
Die Poisson-Verteilung ist mit den oben beschriebenen Funktionen in R implementiert. Diese heissen entsprechend dpois(), ppois(), qpois() und rpois() und funktionieren genau wie ihre Pendants der Standardnormalverteilung. Jedoch muss ihnen der Wert für \(\lambda\) übergeben werden.
# Wahrscheinlichkeitsdichte für x=2
# in der Poisson-Verteilung mit Lambda=4
dpois(2, lambda=4)## [1] 0.1465251Möchte man die Poisson-Verteilung plotten, kann dies mittels plot() (siehe Kapitel 34) z.B. so erfolgen:
# Erzeuge x-Werte
x <- seq(0, 25)
# Dichtefunktionen berechnen
l1 <- dpois(x, lambda = 1)
l2 <- dpois(x, lambda = 2)
l4 <- dpois(x, lambda = 4)
l9 <- dpois(x, lambda = 9)
# Plot erstellen
plot(x, l1, type = "l",
xlim = c(0, 17), ylim = c(0, 0.4),
xlab = "x", ylab = "Dichtefunktion",
main = "Poisson-Verteilungen nach Lambda")
# Linien für andere Lambdas hinzufügen
lines(x, l2, col = "blue")
lines(x, l4, col = "darkgreen")
lines(x, l9, col = "darkred")
# Legende hinzufügen
legend("topright", legend = c("lambda=1", "lambda=2", "lambda=4", "lambda=9"),
col = c("black", "blue", "darkgreen", "darkred"),
lty = 1, cex = 0.8)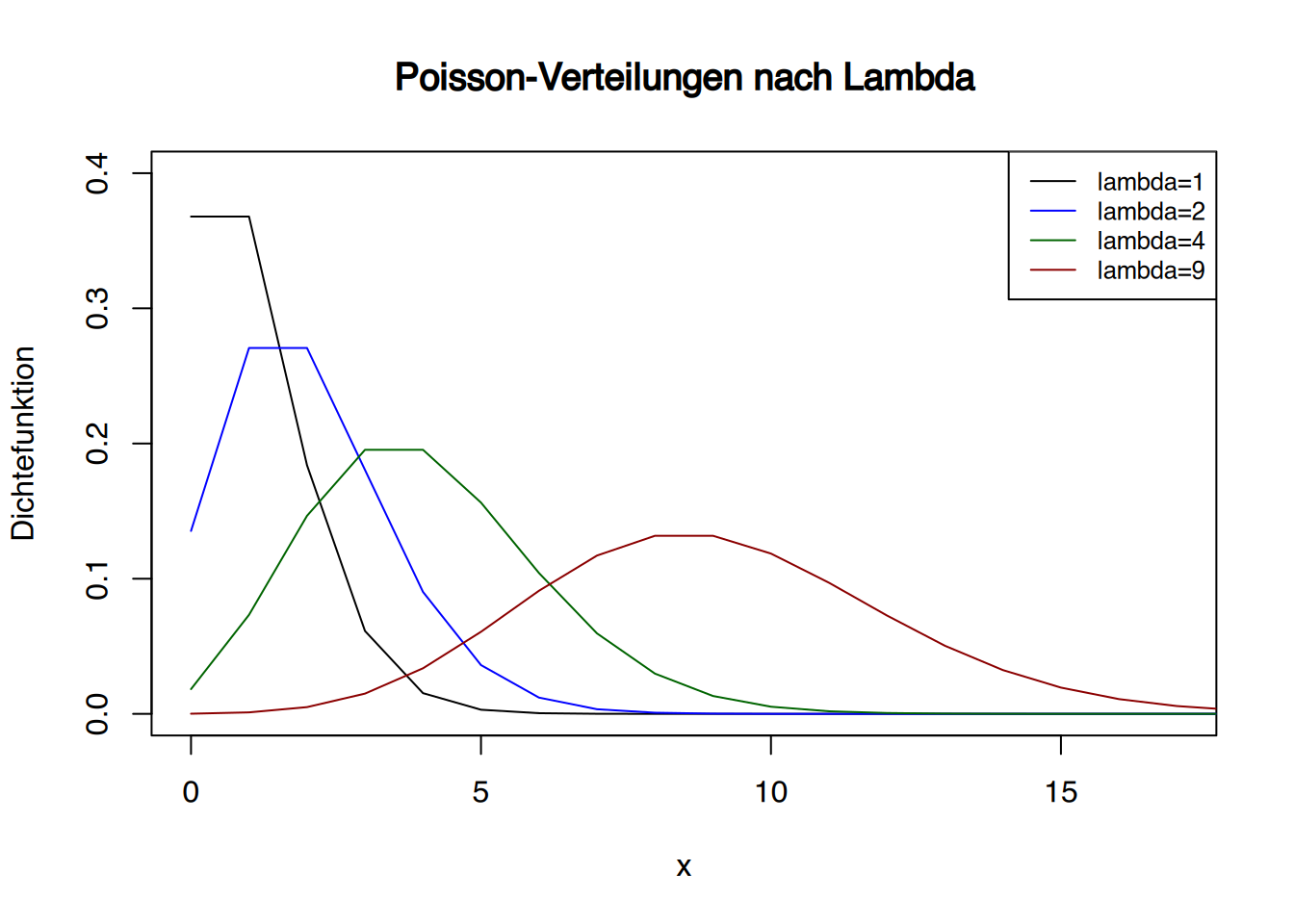
oder mittels ggplot (siehe Kapitel 35) wie folgt.
# Erzeuge x-Werte
x=seq(0,25)
df <- data.frame( x,
l1 = dpois(x, 1),
l2 = dpois(x, 2),
l4 = dpois(x, 4),
l9 = dpois(x, 9)
)
# erzeuge eine long-table
df <- pivot_longer(df, cols=c(l1, l2, l4, l9))
# plot vorbereiten
p <- ggplot(data=df, aes(x, value, fill=name)) +
xlim(0,17) + ylim(0, 0.4) +
xlab("x") + ylab("Dichtefunktion") +
ggtitle("Poisson-Verteilungen", subtitle = "nach Lambda")
p + geom_line(aes(col=name,linetype=name))+
labs(col="Lambda",linetype="")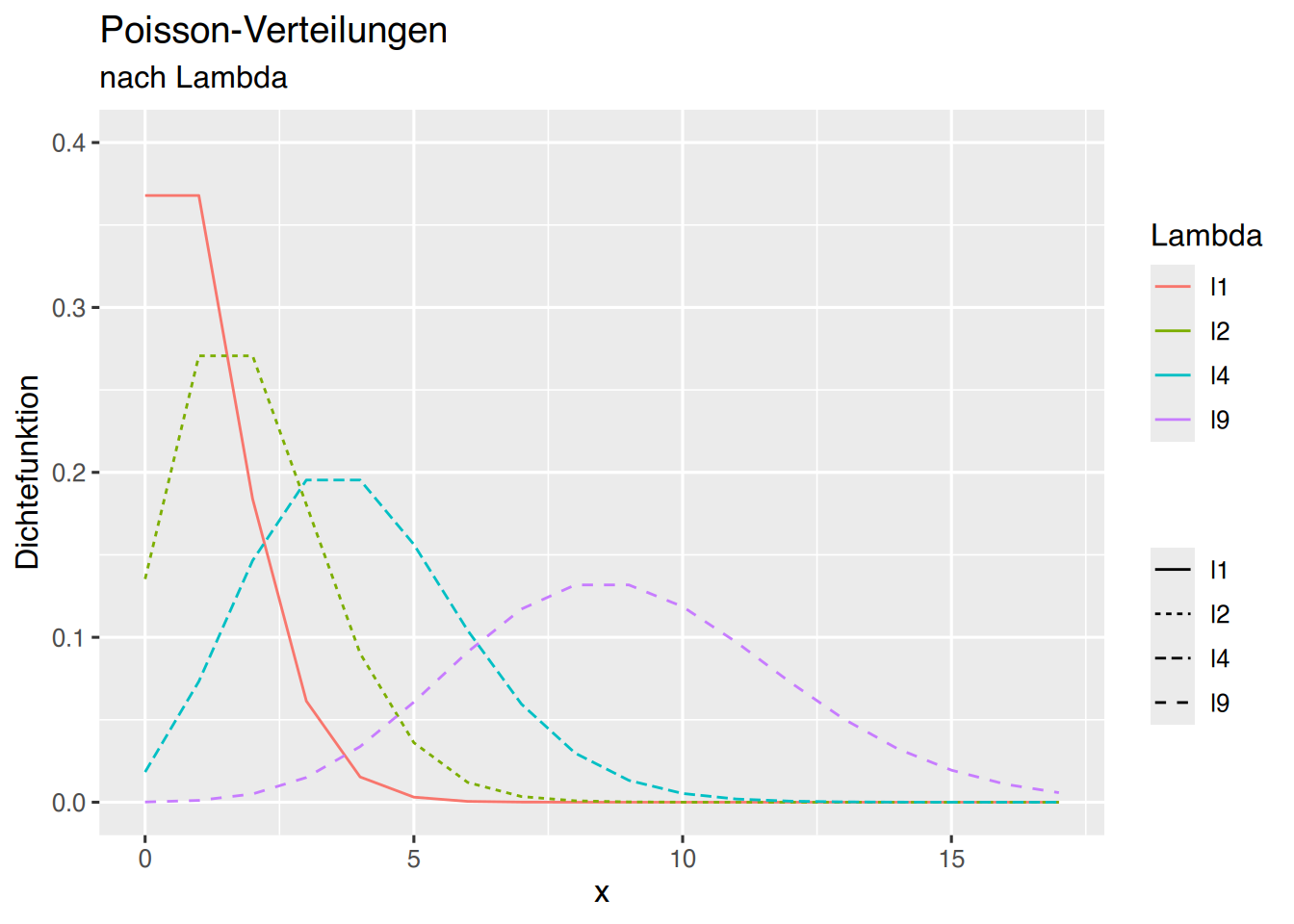
Für weitere Plot-Beispiele zur Poisson-Verteilung siehe Abschnitt 37.5.
Die Binomial-Verteilung ist mit den oben beschriebenen Funktionen in R implementiert. Diese heissen entsprechend dbinom(), pbinom(), qbinom() und rbinom() und funktionieren genau wie ihre Pendants der Standardnormalverteilung.
Als Parameter werden übergeben:
x = günstige Werten = Anzahl der Beobachtungenprob = Wahrscheinleichkeit des EreignissesDie Wahrscheinlichkeit, dass ich in einem 4-tägigen Seminar mit insgesamt 10 Teilnehmern 2mal das Tagesprotokoll schreiben muss1 errechnet sich wie folgt:
# Wahrscheinlichkeit, insgesamt 2mal das Tagesprotokoll
# schreiben zu müssen,
# bei 10 Teilnehmern und 4 Seminartagen
dbinom(x=2, size=4, prob=0.1)## [1] 0.0486Die Wahrscheinlichkeitswerte können für jedes Ereignis “Protokoll schreiben” errechnet und geplottet werden:
# Erzeuge Ereignisraum
protokoll <- c(0:4)
# überführe in Datenframe und berechne alle
# Wahrscheinlichkeiten, das Tagesprotokoll schreiben zu müssen,
# bei 10 Teilnehmern an 4 Seminartagen
df <- data.frame(protokoll, y=dbinom(x=protokoll, size=4, prob=0.1)*100)
# plotten
ggplot(df, aes(x=protokoll, y=y)) + geom_bar(stat="identity", col="black",fill="skyblue3")+
geom_text(aes(label = y),size = 5,vjust = -0.5)+
xlab("Anzahl Protokolle")+
ylab("Wahrscheinlichkeit")+ ylim(0,100)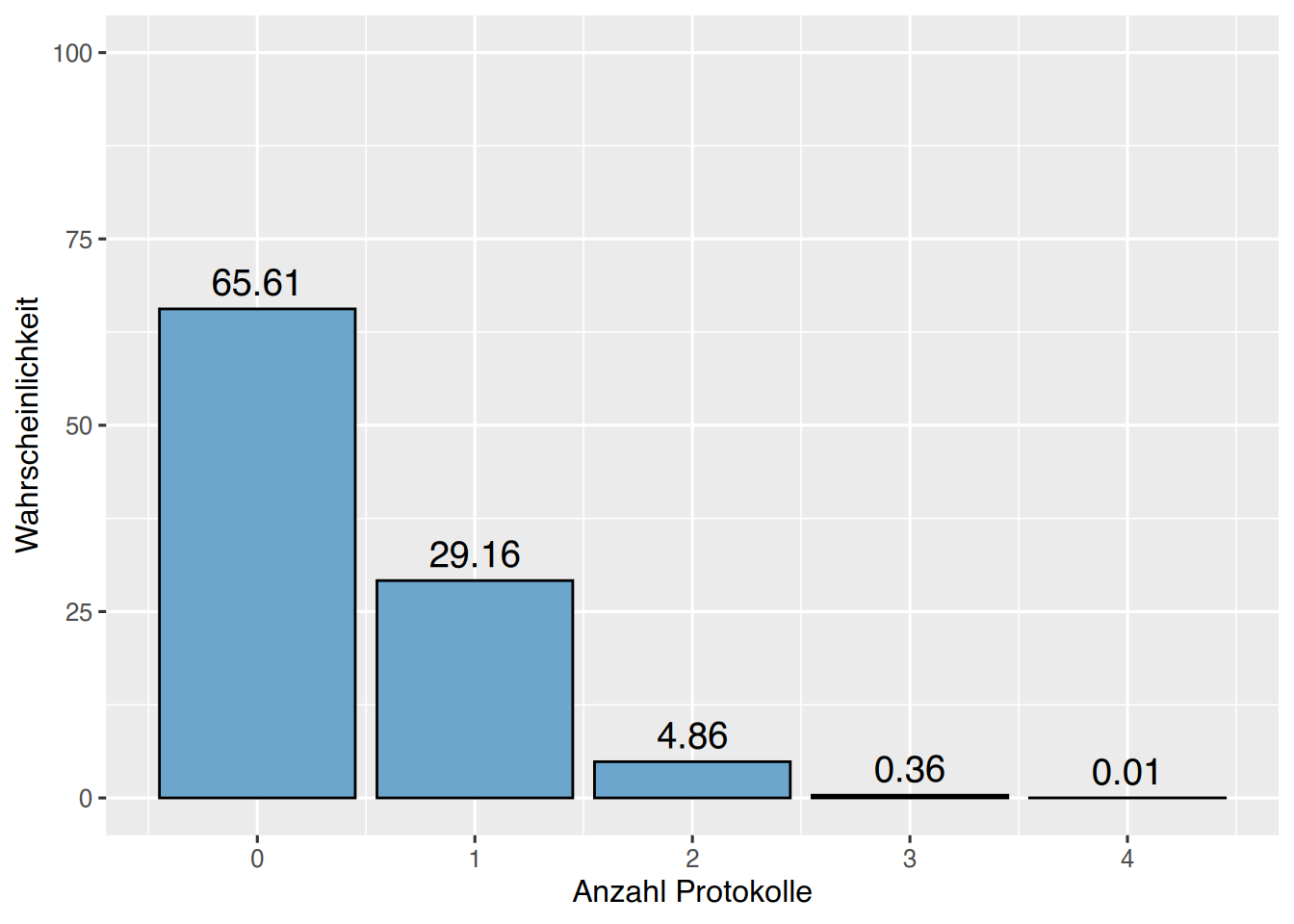
Die Wahrscheinlichkeit, bei 10 Münzwürfen k-mal Kopf zu werfen, errechnet sich wie folgt:
# Ereignisraum erzeugen
münze <- c(1:10)
# überführe in Datenframe und berechne
# alle Wahrscheinlichkeiten, k-mal "Kopf" zu werfen
df <- data.frame(münze, y=round(dbinom(x=münze, size=10, prob=0.5)*100,1))
# plotten
ggplot(df, aes(x=münze, y=y)) +
geom_bar(stat="identity", col="black",fill="skyblue3")+
geom_text(aes(label = y),size = 5,vjust = -0.5)+
xlab("Anzahl 'Kopf'")+
ylab("Wahrscheinlichkeit")+ ylim(0,33) +
scale_x_continuous(breaks = 0:10) 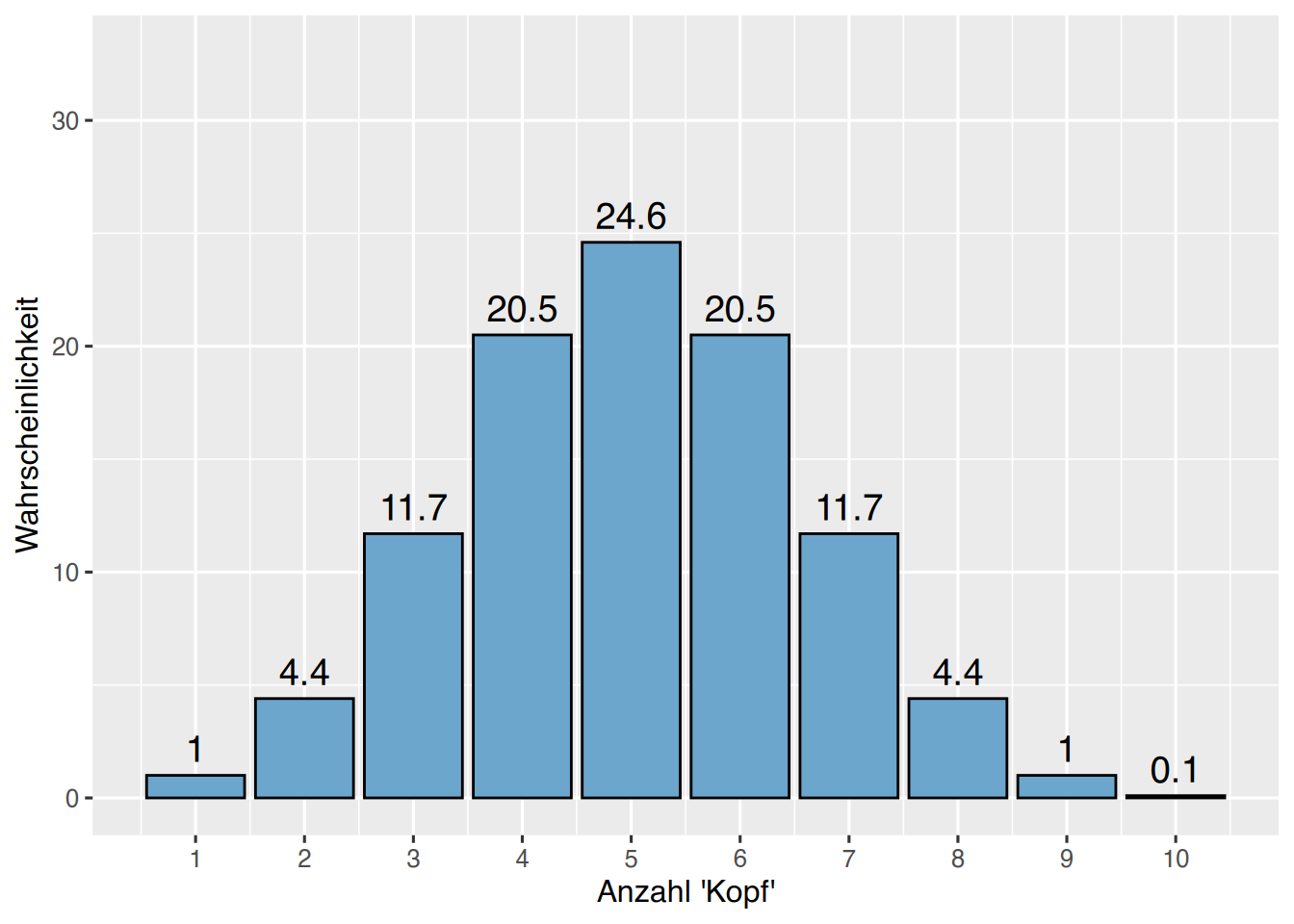
Kuckartz, U; Rädiker, S; Ebert, T. Schehl, J (2013): Statistik - Eine verständliche Einführung, Springer, ISBN 978-3-531-19889-7, S.125↩︎