# erzeuge Datenframe
df <- data.frame(x = c( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ),
y = c( 2, 5, 8, 11, 14, 17, 20, 23, 26, 29))47 Lösungen Lineare Regression
Hier finden Sie die Lösungen zu den Übungsaufgaben von Abschnitt 44.3.
Die hier vorgestellten Lösungen stellen immer nur eine mögliche Vorgehensweisen dar und sind sicherlich nicht der Weisheit letzter Schluss. In R führen viele Wege nach Rom, und wenn Sie mit anderem Code zu den richtigen Ergebnissen kommen, dann ist das völlig in Ordnung.
47.1 Lösung zur Aufgabe 44.3.1
a) Erstellen Sie ein Datenframe mit den Variablen
x und y.
b) Erzeugen Sie ein Scatterplot von
x und y. Bestimmen Sie anhand des Plots, welche Regressionsfunktion die Daten am besten erklären würde.
# plot()
plot(df$x, df$y)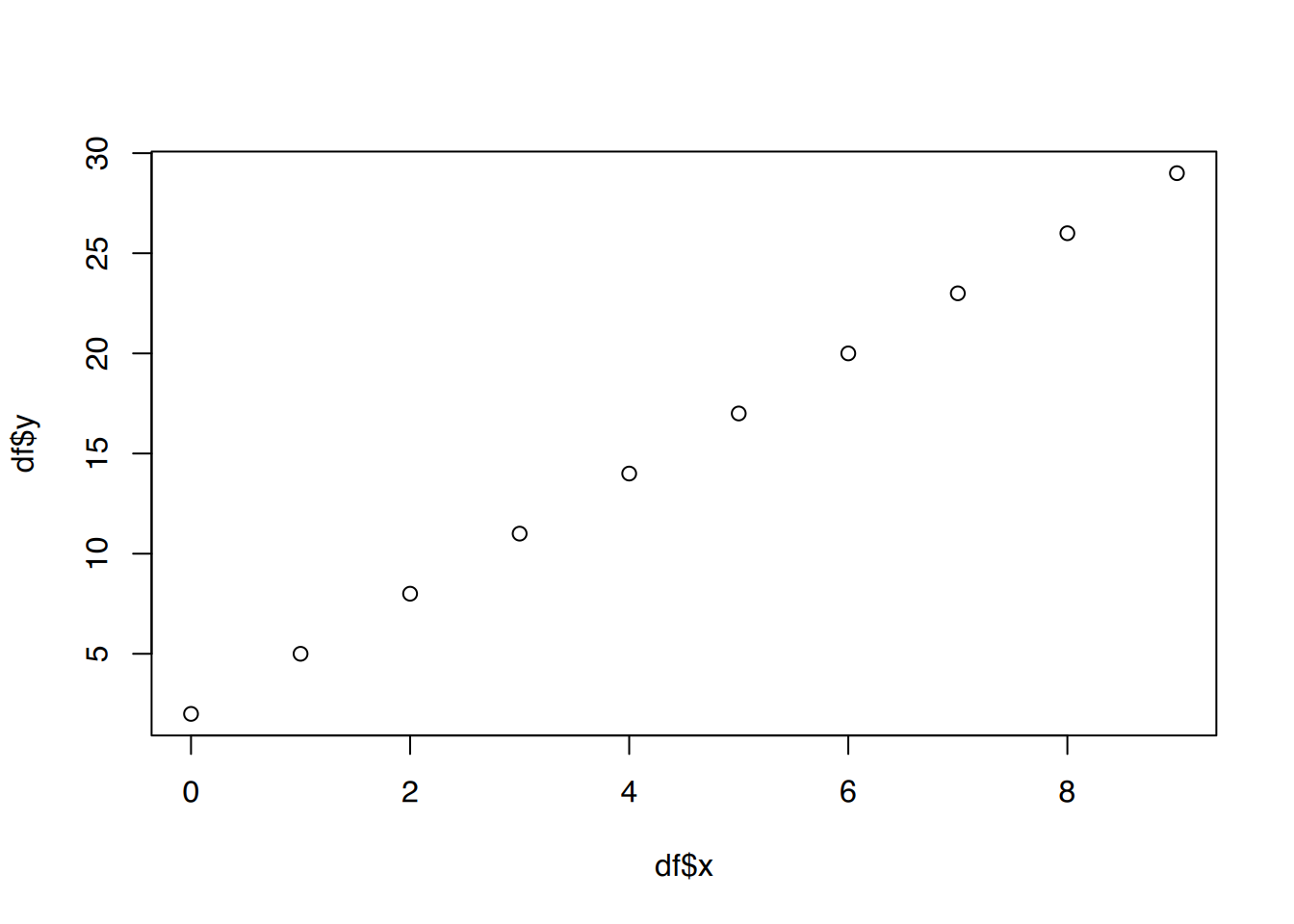
# ggplot()
ggplot(df, aes(x=x, y=y)) +
geom_point()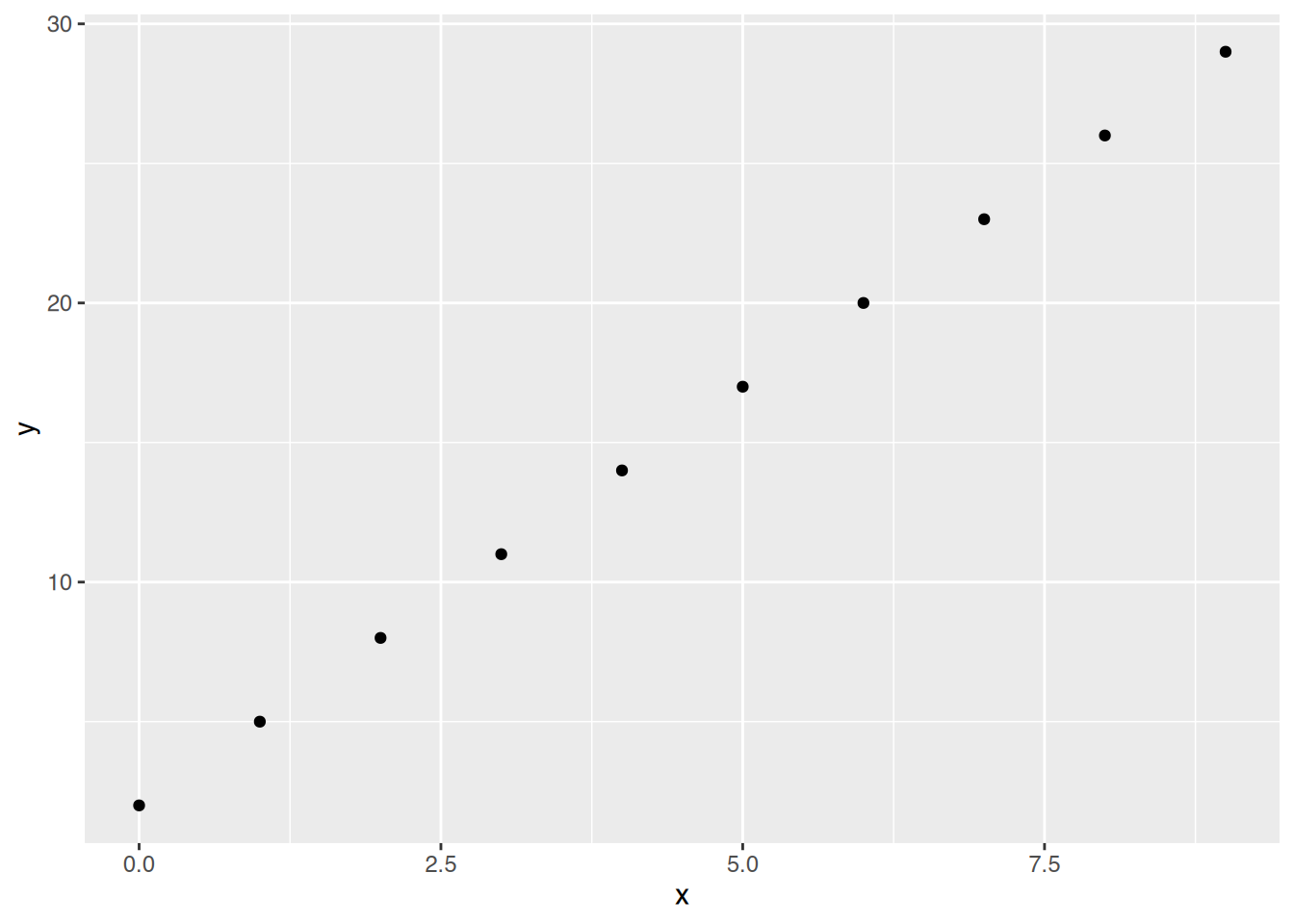
Es ist ein deutlicher linearer Zusammenhang erkennbar.
c) Führen Sie die Regression durch.
# lineares Modell
fit <- lm(y ~ x, data=df)
# anschauen
summary(fit)Warning in summary.lm(fit): im Wesentlichen ein perfekter Fit: summary kann
unzuverlässig sein
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.675e-15 -8.783e-16 5.168e-16 9.646e-16 1.944e-15
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.000e+00 1.049e-15 1.906e+15 <2e-16 ***
x 3.000e+00 1.965e-16 1.527e+16 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.785e-15 on 8 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 2.33e+32 on 1 and 8 DF, p-value: < 2.2e-16
d) Fügen Sie die Regressionsfunktion
y erklärt durch x dem Plot hinzu.
# plot()
plot(df$x, df$y)
# Regressionsgerade
abline(lm(y~x, data=df), col="skyblue2")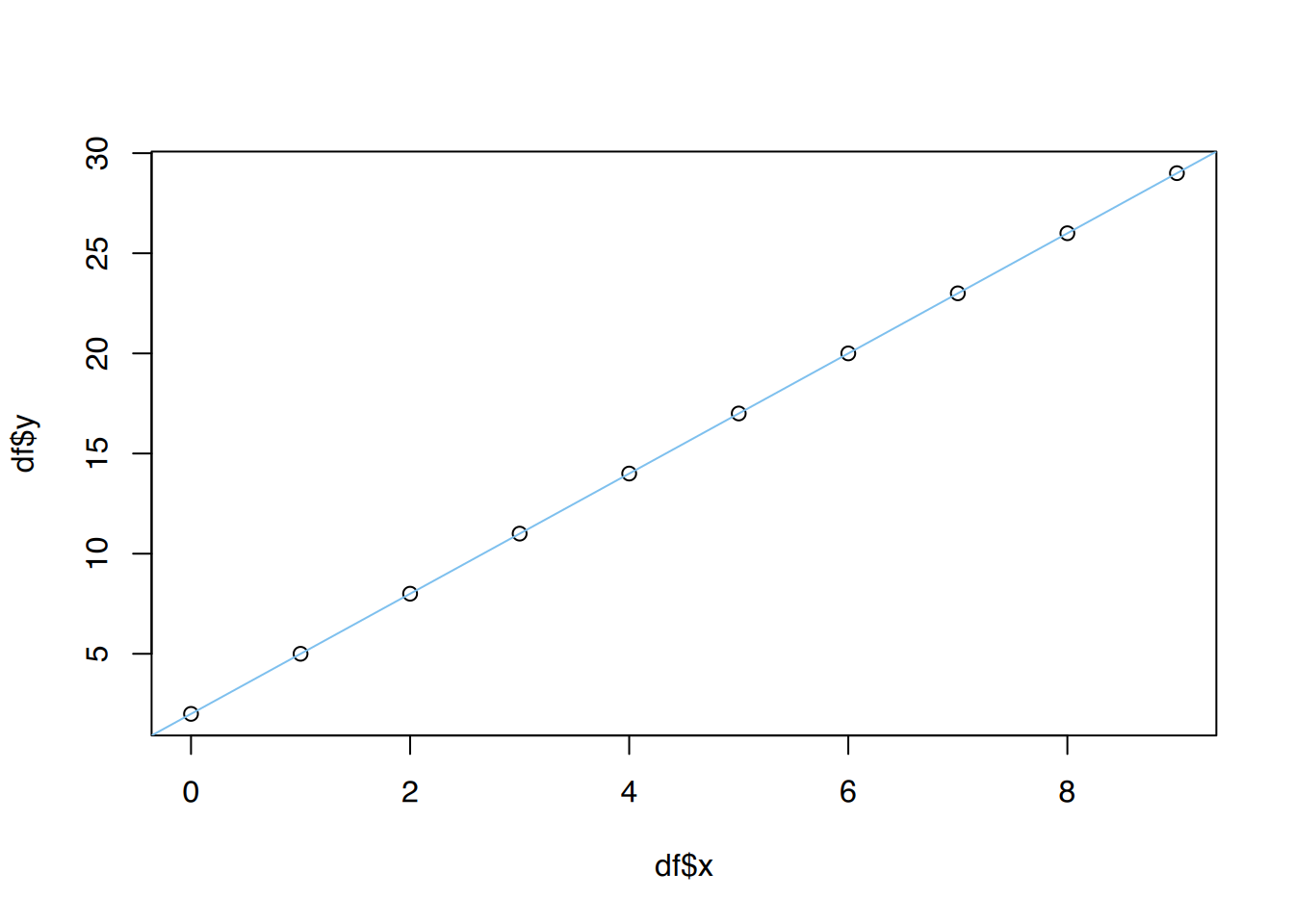
# ggplot()
ggplot(df, aes(x=x, y=y)) +
geom_point() +
geom_smooth(method="lm", color="skyblue2") `geom_smooth()` using formula = 'y ~ x'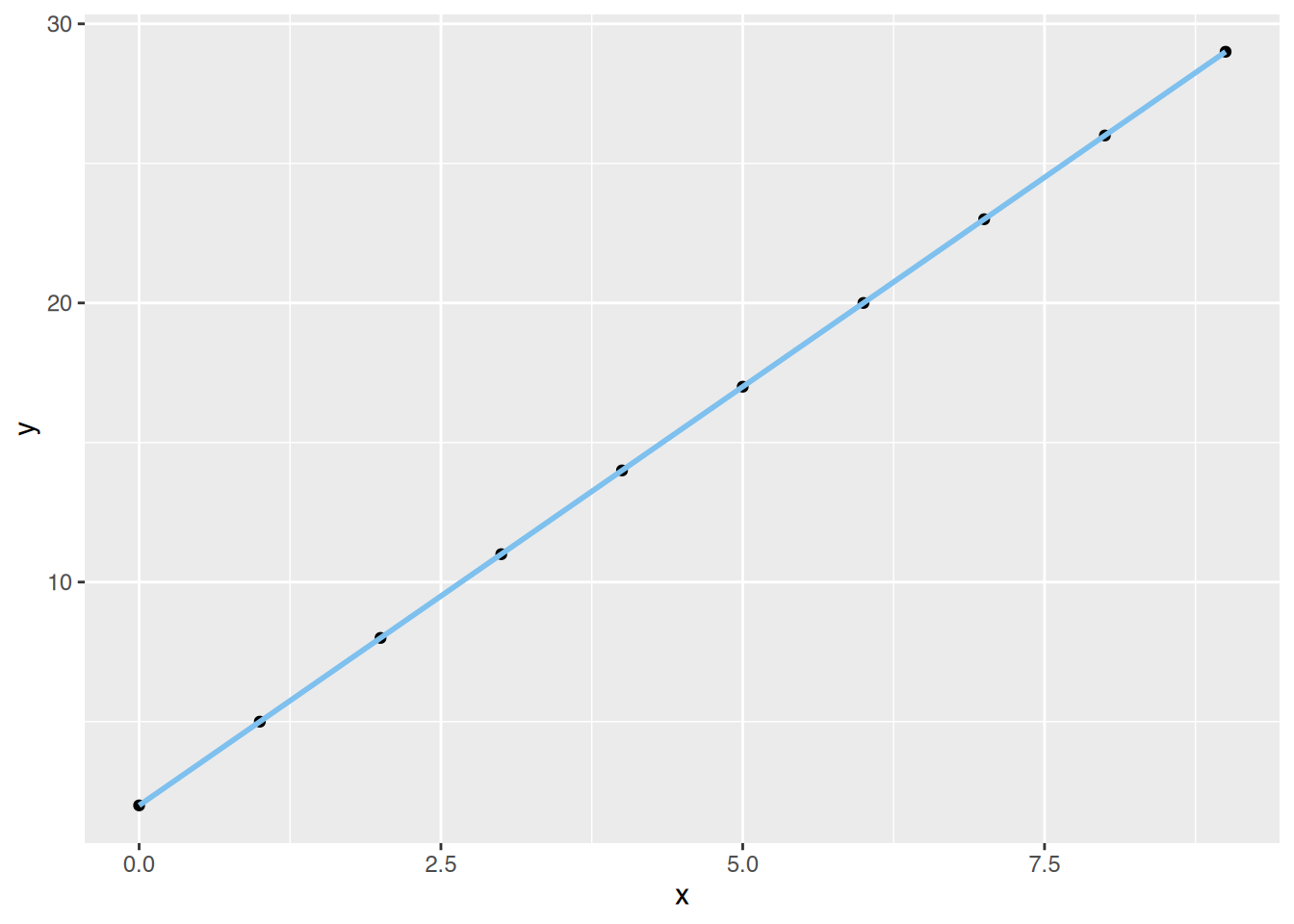
e) Fügen Sie die Regressionsfunktion
x erklärt durch y ebenfalls dem Plot hinzu, aber in roter Farbe.
# plot()
plot(df$x, df$y)
# Regressionsgeraden
abline(lm(y~x, data=df), col="skyblue2")
abline(lm(x~y, data=df), col="red")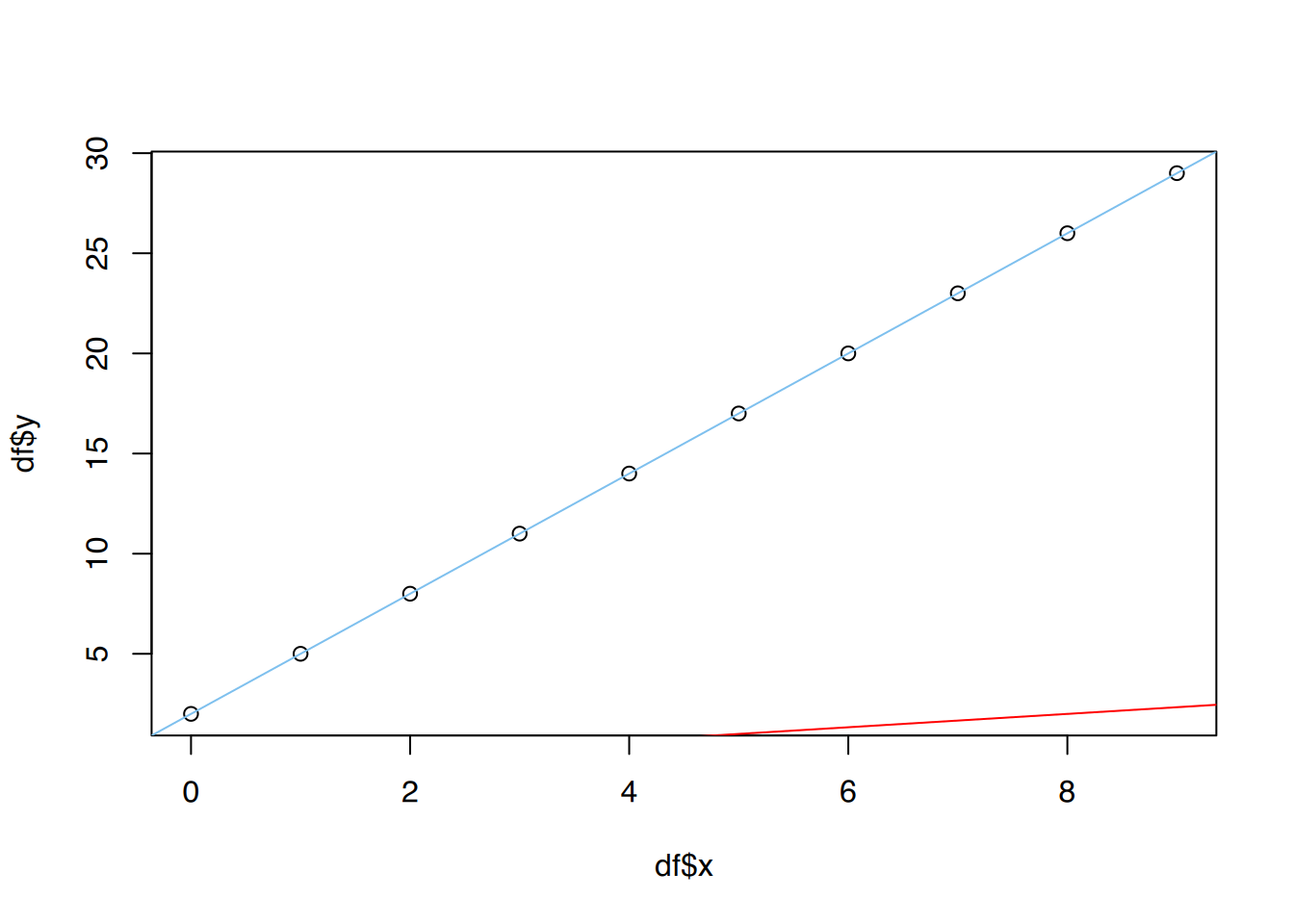
# ggplot()
ggplot(df, aes(x=x, y=y)) +
geom_point() +
geom_smooth(method="lm", color="skyblue2") +
geom_smooth(aes(x=y, y=x), method="lm", color="red") `geom_smooth()` using formula = 'y ~ x'
`geom_smooth()` using formula = 'y ~ x'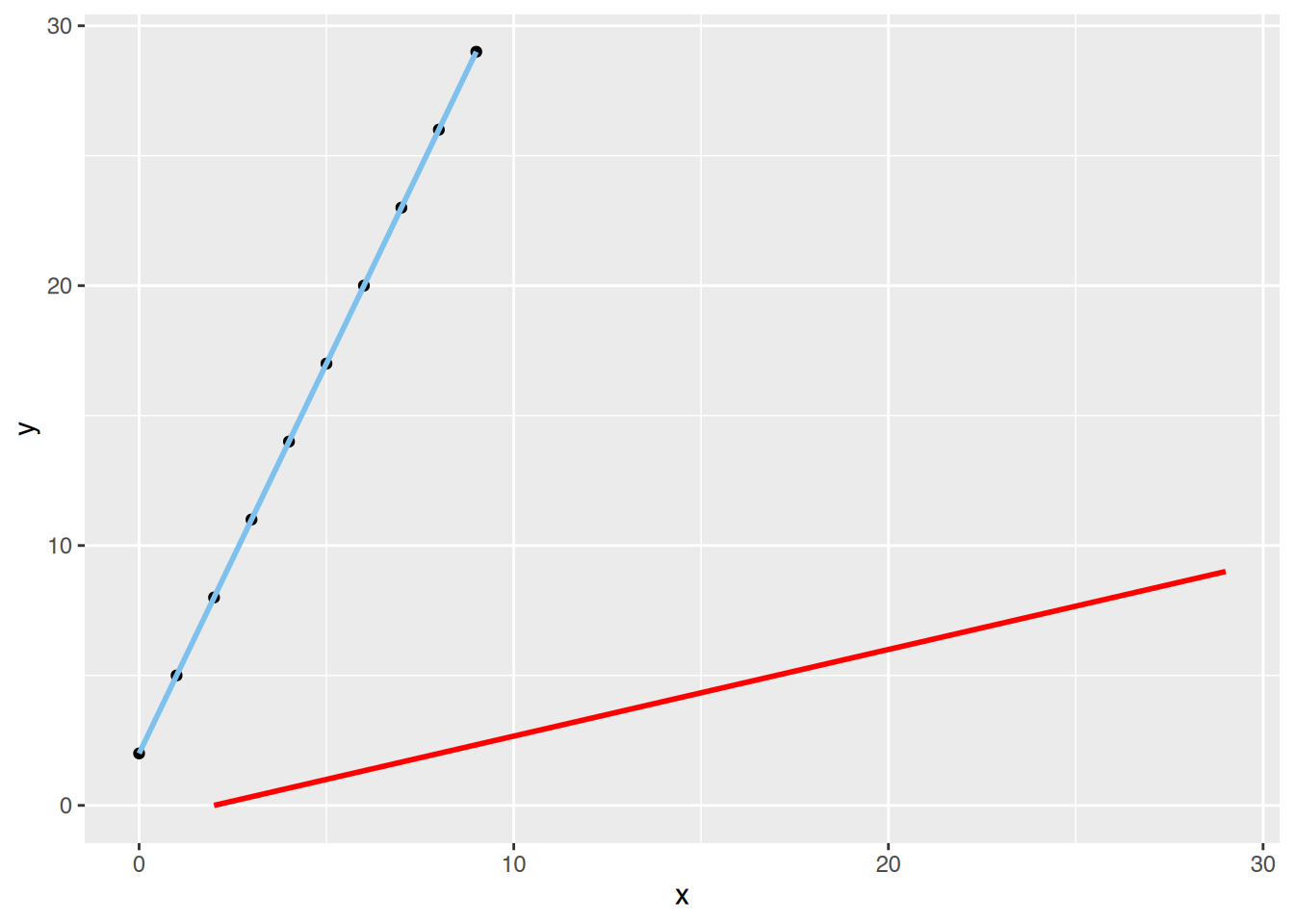
Achten Sie darauf, die Variablen nicht zu vertauschen!
f) Wie große sind die Residuen?
fit <- lm(y ~ x, data=df)
# Residuen
fit$residuals 1 2 3 4 5
-3.675227e-15 4.362024e-16 1.944285e-15 1.385502e-15 1.048764e-15
6 7 8 9 10
7.120252e-16 5.973314e-16 -1.293719e-15 3.679437e-16 -1.523107e-15 Die Residuen sind sehr klein. Die Regressionsgerade scheint sehr gut zu passen.
47.2 Lösung zur Aufgabe 44.3.2
a) Erstellen Sie ein Datenframe mit den Variablen
Lernen und Durchgefallen.
# erzeuge Datenframe
df <- data.frame(Lernen = c( 3.5, 0.6, 2.8, 2.5, 2.6, 3.9, 1.5, 0.7, 3.6, 3.7,
2.2, 3.3, 1.7, 1.1, 2.0, 3.5, 2.1, 1.8, 1.1, 0.7,
1.3, 3.1, 2.3, 3.2, 0.9, 1.7, 0.2, 2.9, 1.0, 2.3),
Durchgefallen = c( 1, 5, 1, 3, 1, 0, 3, 3, 1, 1,
2, 0, 3, 3, 3, 0, 2, 2, 4, 4,
4, 0, 2, 2, 4, 2, 5, 1, 3, 2))
b) Erzeugen Sie eine Kreuztabelle der Variablen
Lernen und Durchgefallen.
# entweder
table(df$Lernen, df$Durchgefallen)
0 1 2 3 4 5
0.2 0 0 0 0 0 1
0.6 0 0 0 0 0 1
0.7 0 0 0 1 1 0
0.9 0 0 0 0 1 0
1 0 0 0 1 0 0
1.1 0 0 0 1 1 0
1.3 0 0 0 0 1 0
1.5 0 0 0 1 0 0
1.7 0 0 1 1 0 0
1.8 0 0 1 0 0 0
2 0 0 0 1 0 0
2.1 0 0 1 0 0 0
2.2 0 0 1 0 0 0
2.3 0 0 2 0 0 0
2.5 0 0 0 1 0 0
2.6 0 1 0 0 0 0
2.8 0 1 0 0 0 0
2.9 0 1 0 0 0 0
3.1 1 0 0 0 0 0
3.2 0 0 1 0 0 0
3.3 1 0 0 0 0 0
3.5 1 1 0 0 0 0
3.6 0 1 0 0 0 0
3.7 0 1 0 0 0 0
3.9 1 0 0 0 0 0# oder
xtabs(~ Lernen + Durchgefallen, data=df) Durchgefallen
Lernen 0 1 2 3 4 5
0.2 0 0 0 0 0 1
0.6 0 0 0 0 0 1
0.7 0 0 0 1 1 0
0.9 0 0 0 0 1 0
1 0 0 0 1 0 0
1.1 0 0 0 1 1 0
1.3 0 0 0 0 1 0
1.5 0 0 0 1 0 0
1.7 0 0 1 1 0 0
1.8 0 0 1 0 0 0
2 0 0 0 1 0 0
2.1 0 0 1 0 0 0
2.2 0 0 1 0 0 0
2.3 0 0 2 0 0 0
2.5 0 0 0 1 0 0
2.6 0 1 0 0 0 0
2.8 0 1 0 0 0 0
2.9 0 1 0 0 0 0
3.1 1 0 0 0 0 0
3.2 0 0 1 0 0 0
3.3 1 0 0 0 0 0
3.5 1 1 0 0 0 0
3.6 0 1 0 0 0 0
3.7 0 1 0 0 0 0
3.9 1 0 0 0 0 0
c) Führen Sie eine lineare Regression
Durchgefallen erklärt durch Lernen durch und plotten Sie Ihr Ergebnis.
# lineare Regression
fit <- lm(Durchgefallen ~ Lernen , data=df)
summary(fit)
Call:
lm(formula = Durchgefallen ~ Lernen, data = df)
Residuals:
Min 1Q Median 3Q Max
-1.03614 -0.53214 -0.02013 0.49187 1.22587
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.8491 0.2622 18.49 < 2e-16 ***
Lernen -1.2300 0.1106 -11.12 8.7e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6359 on 28 degrees of freedom
Multiple R-squared: 0.8155, Adjusted R-squared: 0.8089
F-statistic: 123.8 on 1 and 28 DF, p-value: 8.7e-12# plot()
plot(df$Lernen, df$Durchgefallen)
# Regressionsgerade
abline(lm(Durchgefallen ~ Lernen, data=df), col="skyblue2")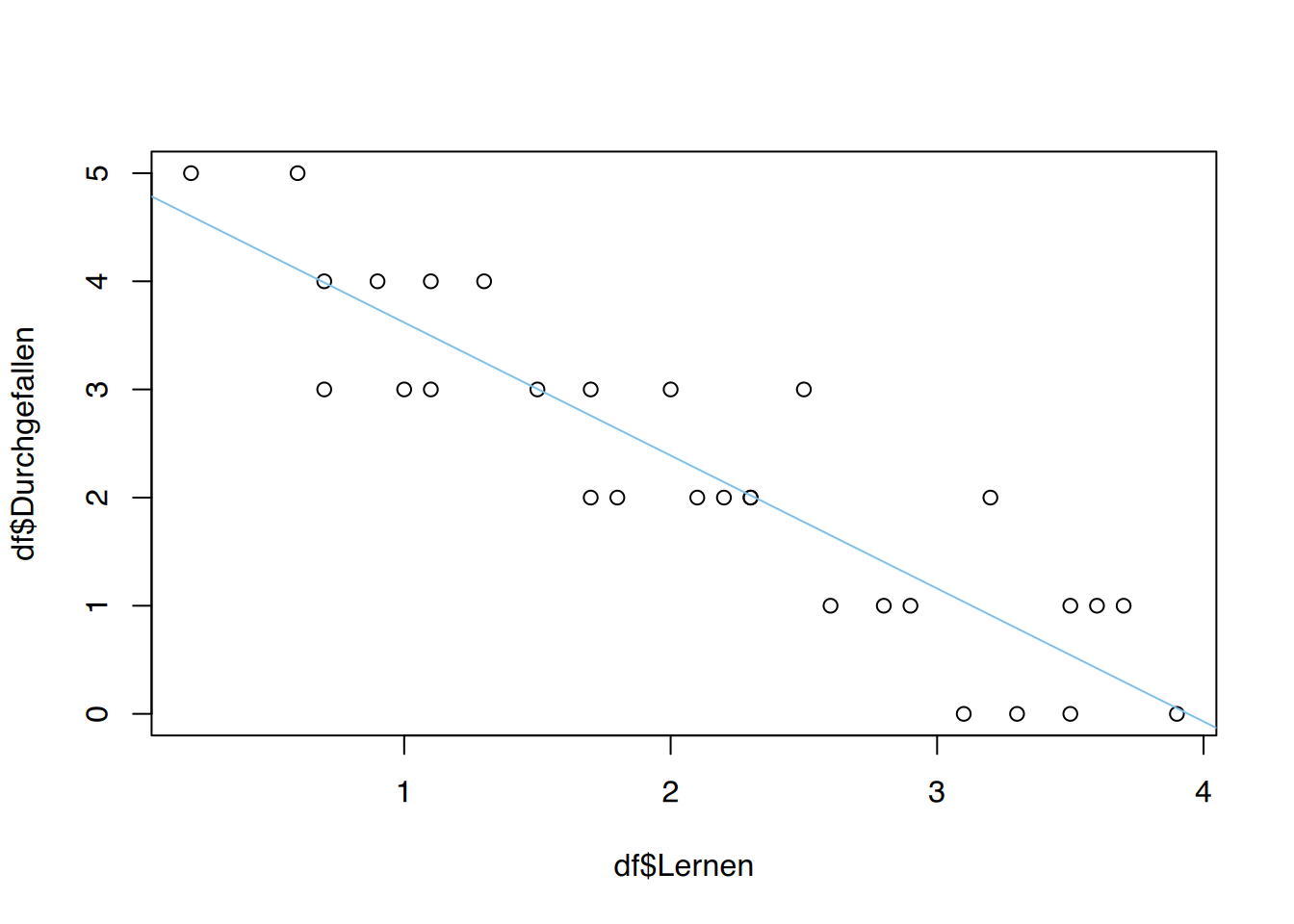
# ggplot()
ggplot(df, aes(x=Lernen, y=Durchgefallen)) +
geom_point() +
geom_smooth(method="lm", color="skyblue2") `geom_smooth()` using formula = 'y ~ x'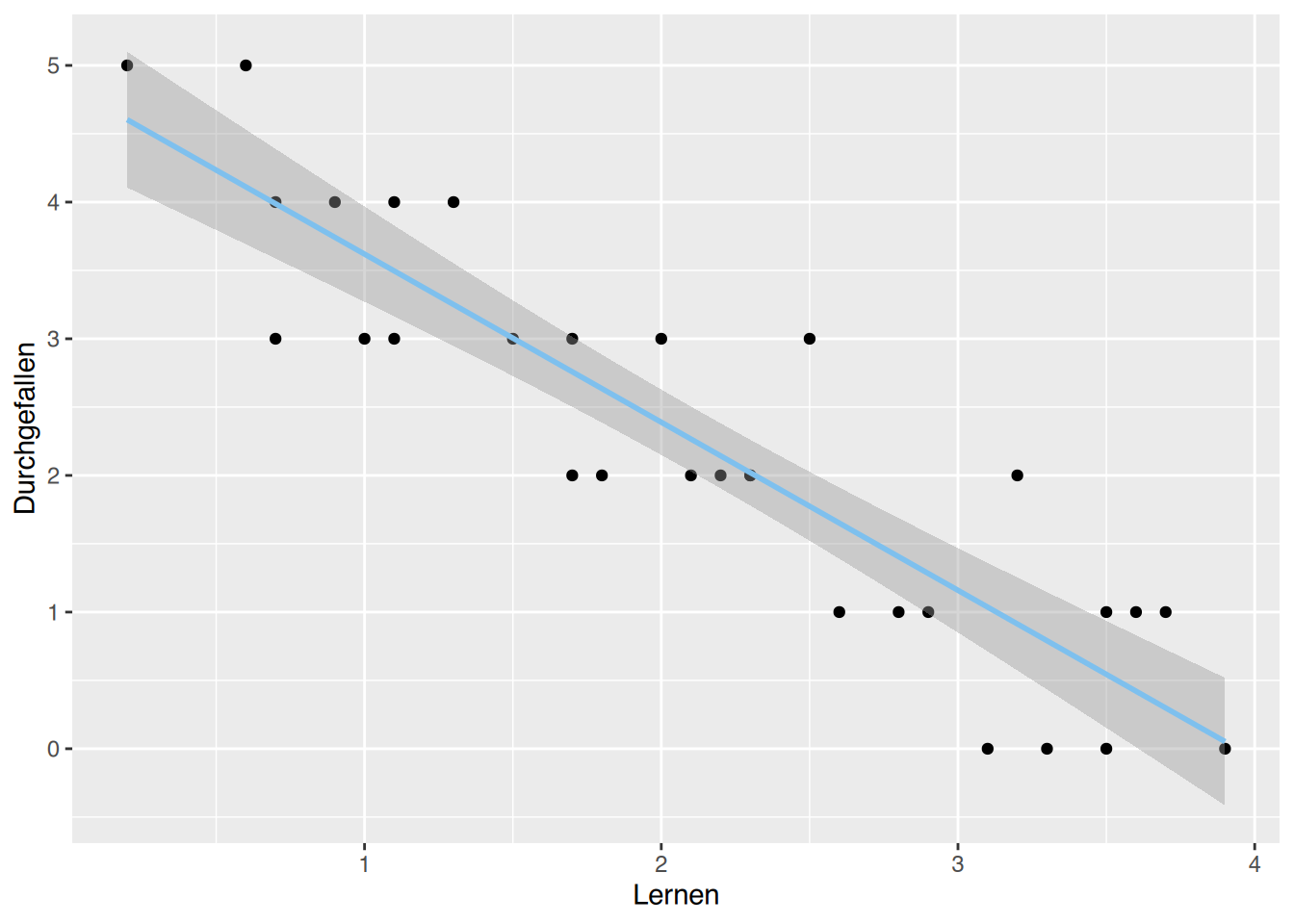
d) Wie lauten die Regressionskoeffizient des Modells, und wie ist er zu interpretieren?
# Koeffizienten anzeigen
fit$coefficients(Intercept) Lernen
4.849127 -1.229997 Der Regressionskoeffizient für Lernen beträgt -1.2299972. Das bedeutet, dass mit ungefähr jeder Stunde Lernen ein Kurs weniger nicht bestanden wird.
e) Ist das soeben erstellte Modell besser als das in Abschnitt 47.1 berechnete? Vergleichen Sie zur Beantwortung die Residuen beider Modelle.
# aktuelles Modell
# Residuen anschauen
fit$residuals 1 2 3 4 5 6
0.455862792 0.888870974 -0.405135233 1.225865613 -0.651134669 -0.052138337
7 8 9 10 11 12
-0.004131565 -0.988129308 0.578862510 0.701862227 -0.143133540 -0.790136644
13 14 15 16 17 18
0.241867871 -0.496130437 0.610867024 -0.544137208 -0.266133258 -0.635132412
19 20 21 22 23 24
0.503869563 0.011870692 0.749868999 -1.036136080 -0.020133822 1.086863638
25 26 27 28 29 30
0.257870128 -0.758132129 0.396872103 -0.282135515 -0.619130154 -0.020133822 # Modell aus anderer Aufgabe
df2 <- data.frame(x = c( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ),
y = c( 2, 5, 8, 11, 14, 17, 20, 23, 26, 29))
fit2 <- lm(y~x, data=df2)
fit2$residuals 1 2 3 4 5
-3.675227e-15 4.362024e-16 1.944285e-15 1.385502e-15 1.048764e-15
6 7 8 9 10
7.120252e-16 5.973314e-16 -1.293719e-15 3.679437e-16 -1.523107e-15 Im aktuellen Modell sind die Residuen größer als im vorherigen Modell. Somit ist das vorherige Modell besser.
f) Berechnen Sie den linearen Bestimmungskoeffizient und den Korrelationskoeffizient. Ist das lineare Modell ein gutes Modell, um die Beziehung zwischen den gescheiterten Prüfungen und den täglichen Studienzeiten zu erklären? Wie viel Prozent der Variabilität der durchgefallenen Prüfungen wird durch das lineare Modell erklärt?
# aktuelles Modell
lernen <- summary(fit)
# R^2 anschauen
lernen$r.squared[1] 0.8154995# Korrelationskoeffizient
cor.test(df$Lernen, df$Durchgefallen)
Pearson's product-moment correlation
data: df$Lernen and df$Durchgefallen
t = -11.125, df = 28, p-value = 8.7e-12
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9532031 -0.8045264
sample estimates:
cor
-0.9030501 Das Bestimmtheitsmaß \(R^{2}\) beträgt 0.8154995. Somit können 81.55% des Rauschens im aktuellen Modell erklärt werden.
Der Korrelationskoeffizient von -0.9030501 ist nahe an -1. Dies spricht für einen starken negativen Zusammenhang.
g) Benutzen Sie das lineare Modell, um die Anzahl an durchgefallenen Prüfungen für einen Studenten zu bestimmen, der 3 Stunden Lernzeit investiert hat. Wie glaubwürdig ist die Vorhersage?
# aktuelles Modell
predict(fit, list(Lernen=3)) 1
1.159136 Wenn der Student 3 Stunden lernt, wird er wahrscheinlich “nur” durch 1 Kurs durchfallen.
h) Wie viele Stunden Lernzeit wird benötigt, um alle Kurse zu bestehen?
# neues Modell
fit <- lm(Lernen ~ Durchgefallen, data = df)
# Wieviel lernen für Durchgefallen=0?
predict(fit, list(Durchgefallen=0)) 1
3.607387 Wenn der Student 3 Stunden lernt, wird er wahrscheinlich “nur” durch 1 Kurs durchfallen.
47.3 Lösung zur Aufgabe 44.3.3
a) Erstellen Sie ein Datenframe mit den Variablen
Minuten und Alkohol.
# erzeuge Datenframe
df <- data.frame(Alkohol = c(1.6, 1.7, 1.5, 1.1, 0.7, 0.2, 2.1),
Minuten = c(30, 60, 90, 120, 150, 180, 210))
b) Bestimmen Sie den passenden Korrelationskoeffizienten. Werden die Daten ausreichend gut durch das Modell beschrieben?
# Korrelation
cor(df$Minuten, df$Alkohol)[1] -0.2730367Der Korrelationskoeffizient ist eher gering. Das spricht für keinen starken Zusammenhang.
c) Plotten Sie das lineare Regressionsmodell
Alkohol erklärt durch Minuten. Gibt es Punkte mit großen Residuen? Wenn ja, entfernen Sie diese und führen die Berechnungen erneut durch. Hat sich der Korrelationskoeffizient verbessert?
# plot()
plot(df$Minuten, df$Alkohol)
abline(lm(Alkohol ~ Minuten, data=df))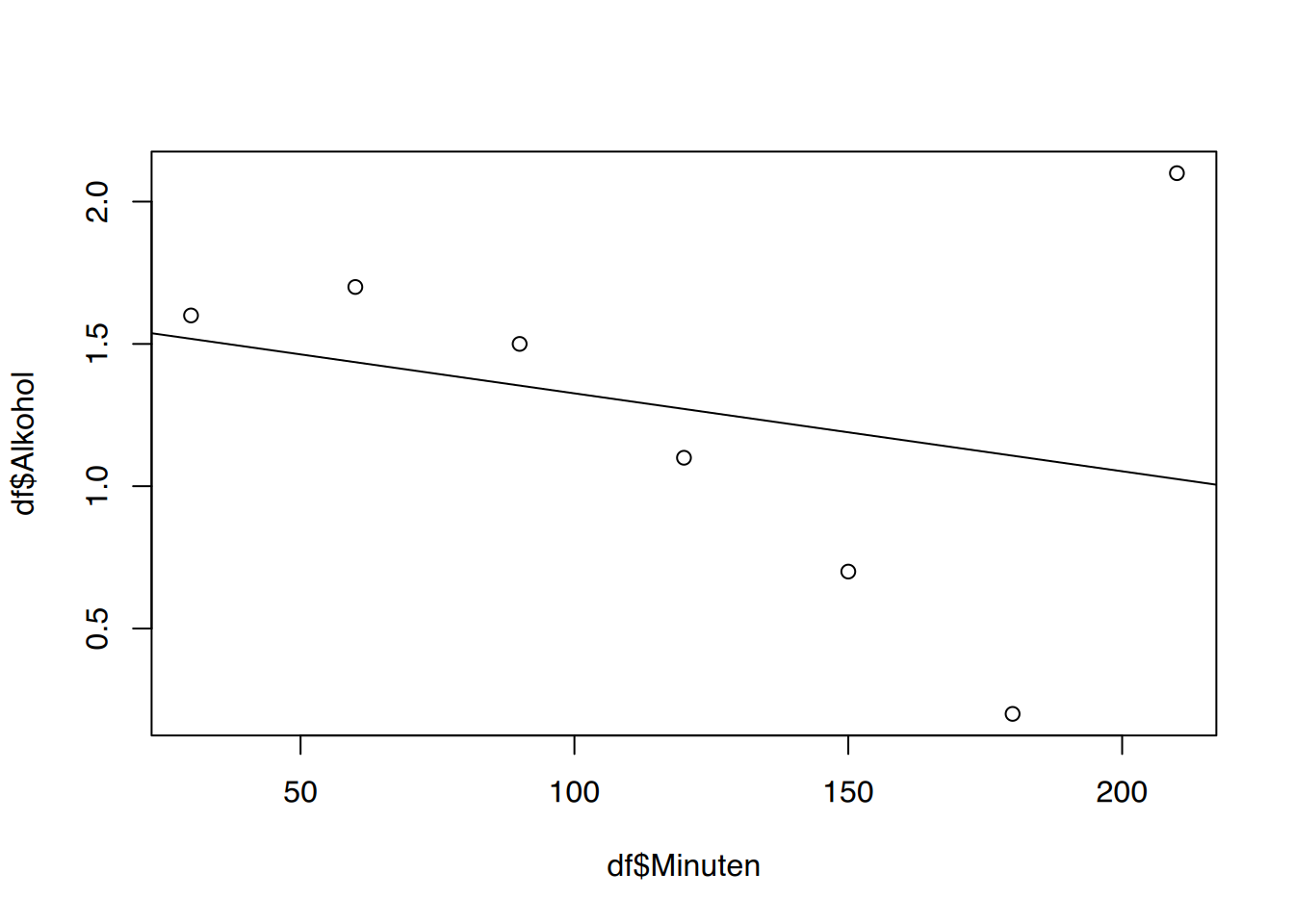
# ggplot()
ggplot(df, aes(x=Minuten, y=Alkohol)) +
geom_point()+
geom_smooth(method="lm", color="skyblue2") `geom_smooth()` using formula = 'y ~ x'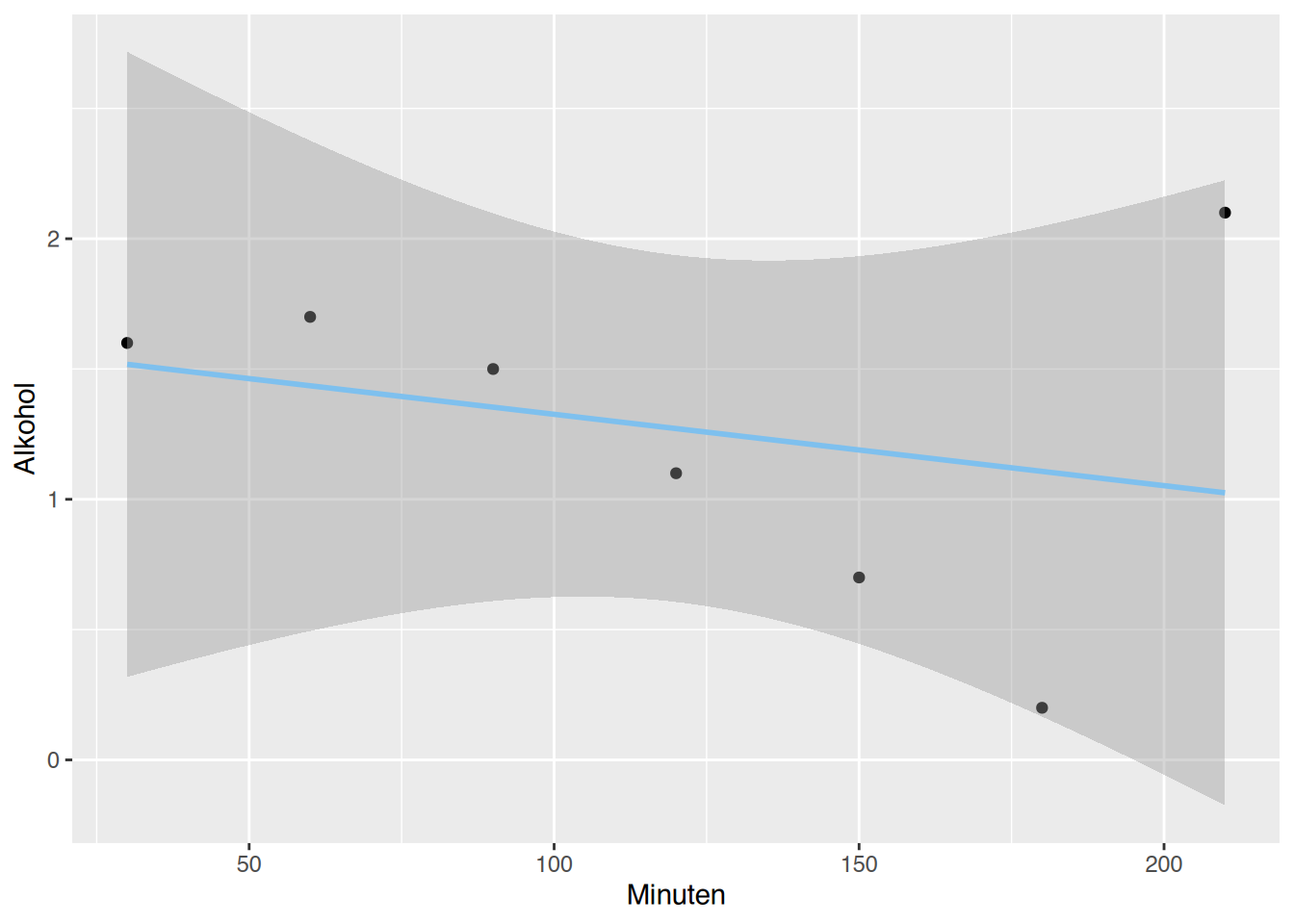
Der letzte Wert ist ein deutlicher Ausreißer, wahrscheinlich ein Tippfehler bei der Dateneingabe.
# entferne letzten Wert
df <- df[-7,]
# Korrelation
cor(df$Minuten, df$Alkohol)[1] -0.944155Der Korrelationskoeffizient ist nun sehr nah an -1. Das spricht für einen starken Zusammenhang.
# Modell
# plot()
plot(df$Minuten, df$Alkohol)
abline(lm(Alkohol ~ Minuten, data=df))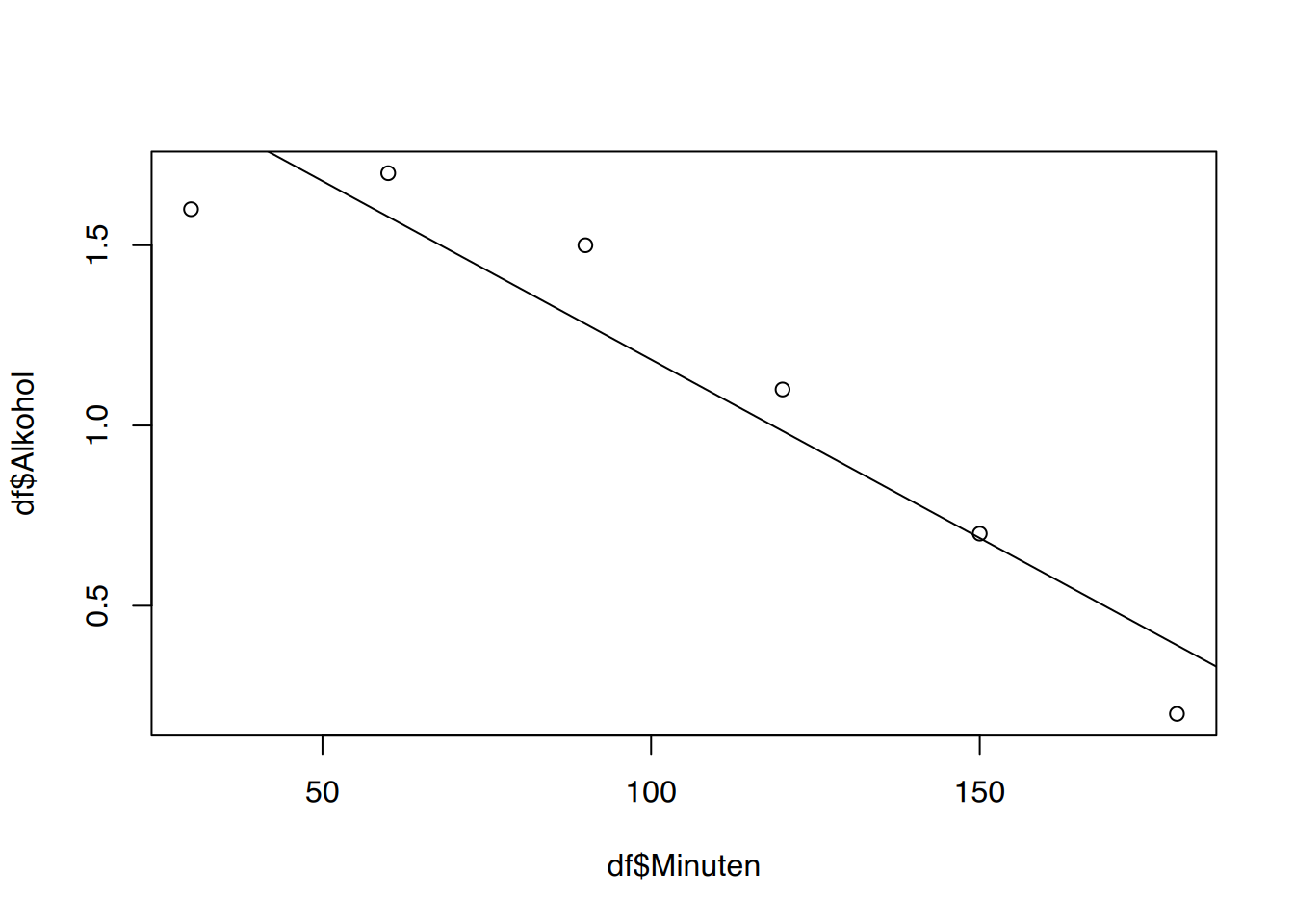
# ggplot()
ggplot(df, aes(x=Minuten, y=Alkohol)) +
geom_point()+
geom_smooth(method="lm", color="skyblue2") `geom_smooth()` using formula = 'y ~ x'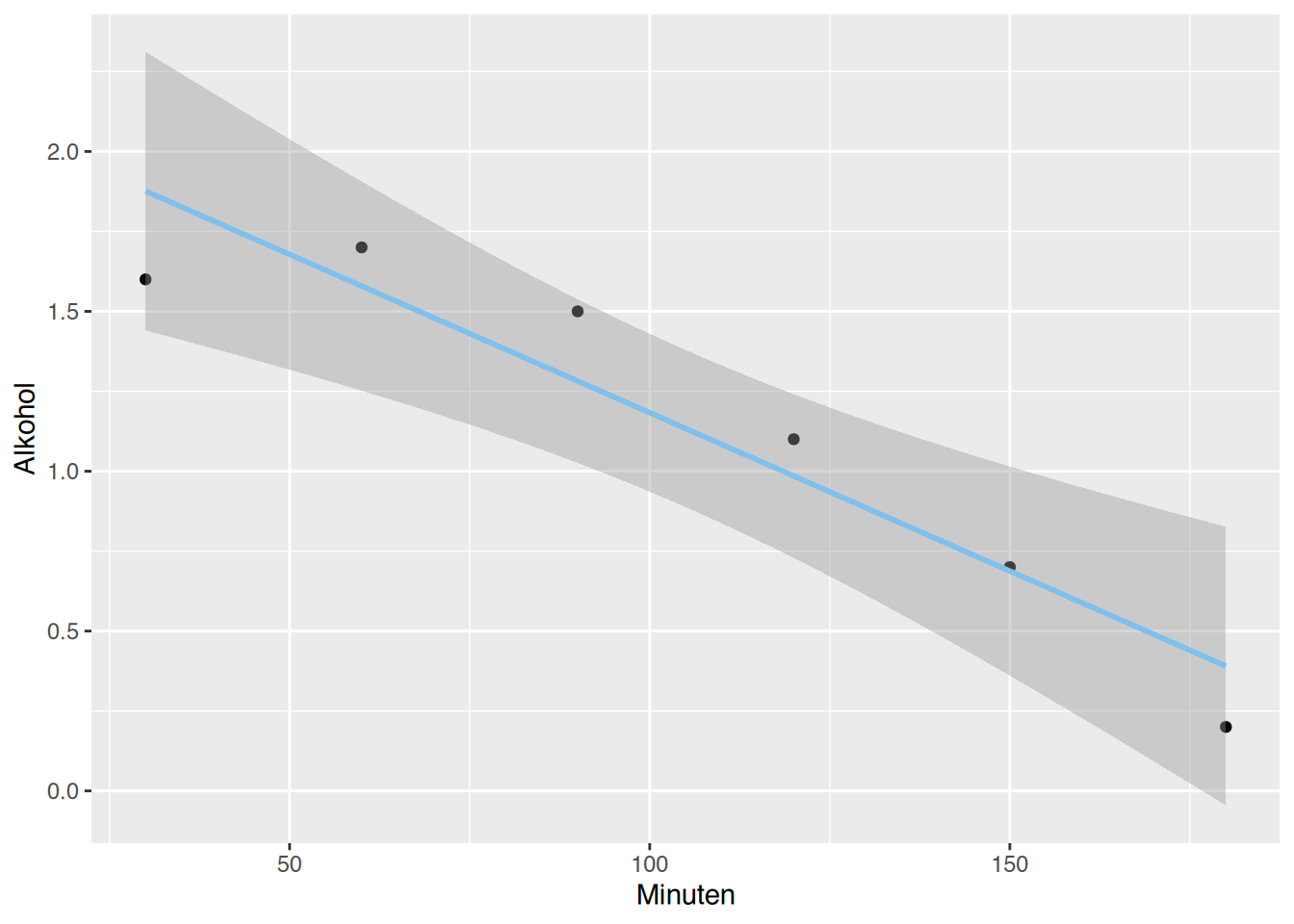
d) Mit welcher Geschwindigkeit wird der Alkohol pro Minute verstoffwechselt?
# Koeffizienten
fit <- lm(Alkohol ~ Minuten, data=df)
fit$coefficient (Intercept) Minuten
2.173333333 -0.009904762 Der Alkoholspiegel sinkt pro Minute um -0.0099048 g/l.
e) Wenn es gesetzlich erlaubt wäre, mit einem Blutalkoholwert von \(0,3\) g/l Auto zu fahren, wie lange muss die Person warten, nachdem sie \(1\) Liter Weingetrunken hat, um wieder fahrtüchtig zu sein? Wie zuverlässig ist diese Vorhersage?
# Koeffizienten
fit <- lm(Minuten ~ Alkohol, data=df)
predict(fit, list(Alkohol=0.3)) 1
180 Der Alkoholspiegel wird nach 180 Minuten auf \(0,3\) g/l fallen.
47.4 Lösung zur Aufgabe 44.3.4
a) Laden Sie den Datensatz
age.height in Ihre R-Session.
# lade Datensatz
load(url("https://www.produnis.de/R/data/age.height.RData"))
b) Berechnen Sie die Regressionsgerade
Größe erklärt durch Alter. Ist das lineare Modell geeignet, den Zusammenhang zwischen Alter und Körpergröße zu erklären?
# Regression
fit <- lm(height ~ age, data=age.height)
summary(fit)
Call:
lm(formula = height ~ age, data = age.height)
Residuals:
Min 1Q Median 3Q Max
-0.9137 -0.1018 0.0449 0.1644 0.4202
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.413724 0.091080 15.522 2.77e-15 ***
age 0.004612 0.002036 2.265 0.0314 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2852 on 28 degrees of freedom
Multiple R-squared: 0.1549, Adjusted R-squared: 0.1247
F-statistic: 5.131 on 1 and 28 DF, p-value: 0.03142R2 ist eher gering, es können nur 15.49% des Rauschens mit dem Modell erklärt werden.
c) Erstellen Sie eine Punktwolke inklusive der Regressionsgeraden. Ab welchem Alter ändert sich die Punktetendenz?
# plot()
plot(age.height$age, age.height$height)
abline(fit)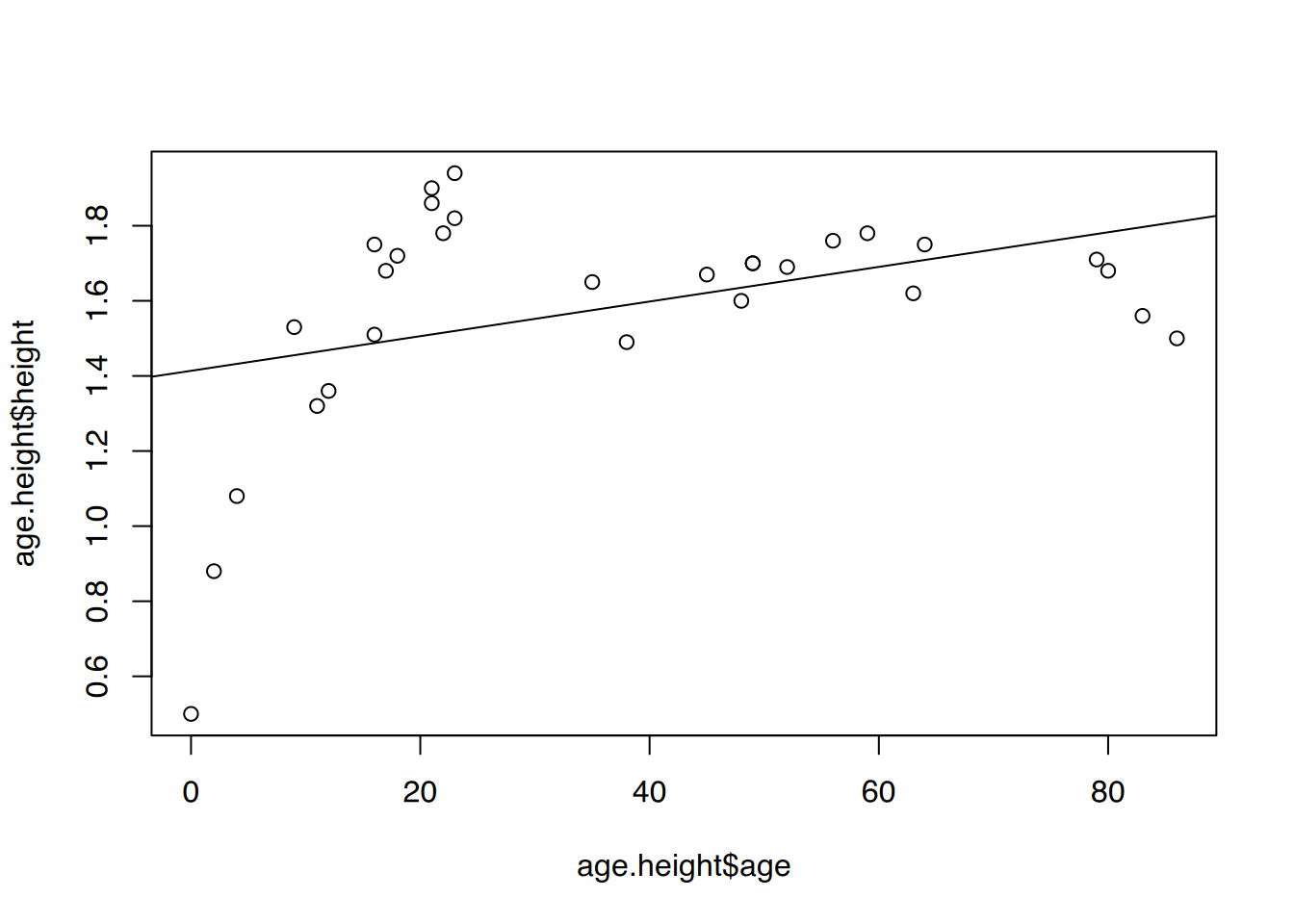
# ggplot()
ggplot(age.height, aes(x=age, y=height)) +
geom_point()+
geom_smooth(method="lm", color="skyblue2") `geom_smooth()` using formula = 'y ~ x'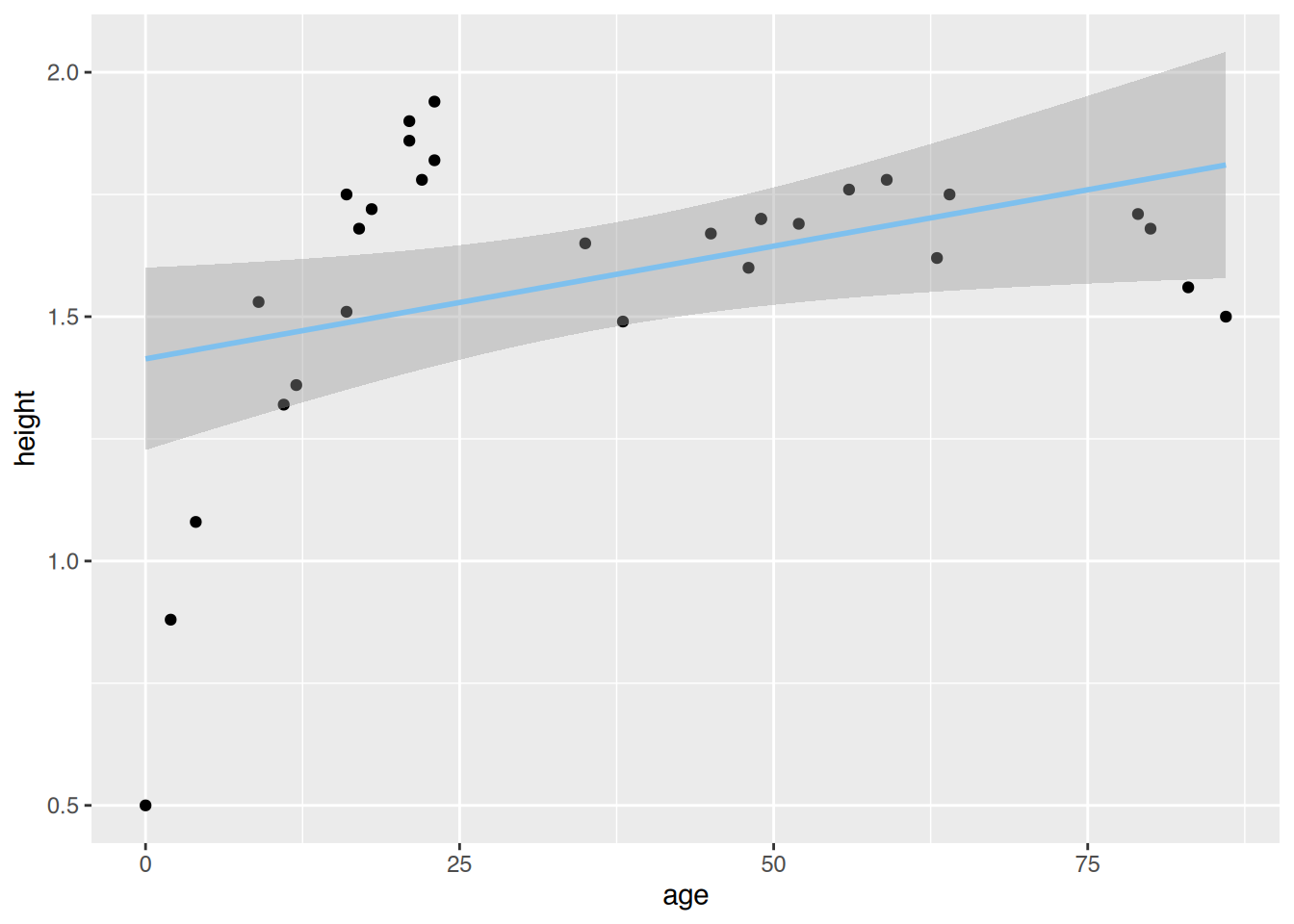
Ab etwa 20 Jahren ändert sich die Punktetendenz.
d) Erstellen Sie eine Gruppierungsvariable, welche
Alter in einen ordinalen Faktor mit den Ausprägungen “jünger als 20” und “20 und älter” einteilt.
# klassieren
age.height$ageK <- cut(age.height$age,
breaks = c(0,20, Inf),
right=FALSE,
labels = c("jünger als 20",
"20 und älter"))
# anschauen
head(age.height) age height ageK
1 18 1.72 jünger als 20
2 21 1.90 20 und älter
3 45 1.67 20 und älter
4 59 1.78 20 und älter
5 21 1.86 20 und älter
6 22 1.78 20 und älter
e) Führen Sie die lineare Regressionsanalyse für beide Gruppen erneut durch. In welcher Gruppe wird der Zusammenhang zwischen
Alter und Körpergröße am besten erklärt?
# Gruppen
df1 <- subset(age.height, ageK=="jünger als 20")
# Regression
fit1 <- lm(height ~ age, data=df1)
summary(fit1)
Call:
lm(formula = height ~ age, data = df1)
Residuals:
Min 1Q Median 3Q Max
-0.22746 -0.05601 -0.03485 0.08416 0.28351
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.727459 0.094487 7.699 5.75e-05 ***
age 0.057671 0.007738 7.453 7.25e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1525 on 8 degrees of freedom
Multiple R-squared: 0.8741, Adjusted R-squared: 0.8584
F-statistic: 55.54 on 1 and 8 DF, p-value: 7.245e-05Das Bestimmtheitsmaß in der Gruppe “jünger als 20” liegt bei 0.8741033, d.h. es werden 87.41% des Rauschens erklärt.
# Gruppen
df2 <- subset(age.height, ageK=="20 und älter")
# Regression
fit2 <- lm(height ~ age, data=df2)
summary(fit2)
Call:
lm(formula = height ~ age, data = df2)
Residuals:
Min 1Q Median 3Q Max
-0.25783 -0.04614 -0.01064 0.07793 0.14155
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.876084 0.056839 33.007 < 2e-16 ***
age -0.003375 0.001051 -3.213 0.00483 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.09931 on 18 degrees of freedom
Multiple R-squared: 0.3644, Adjusted R-squared: 0.3291
F-statistic: 10.32 on 1 and 18 DF, p-value: 0.004827Das Bestimmtheitsmaß in der Gruppe “20 und älter” liegt bei 0.3644171, d.h. es werden 36.44% des Rauschens erklärt.
f) Plotten Sie Ihre Modelle
# < 20 Jahre
plot(df1$age, df1$height)
abline(fit1)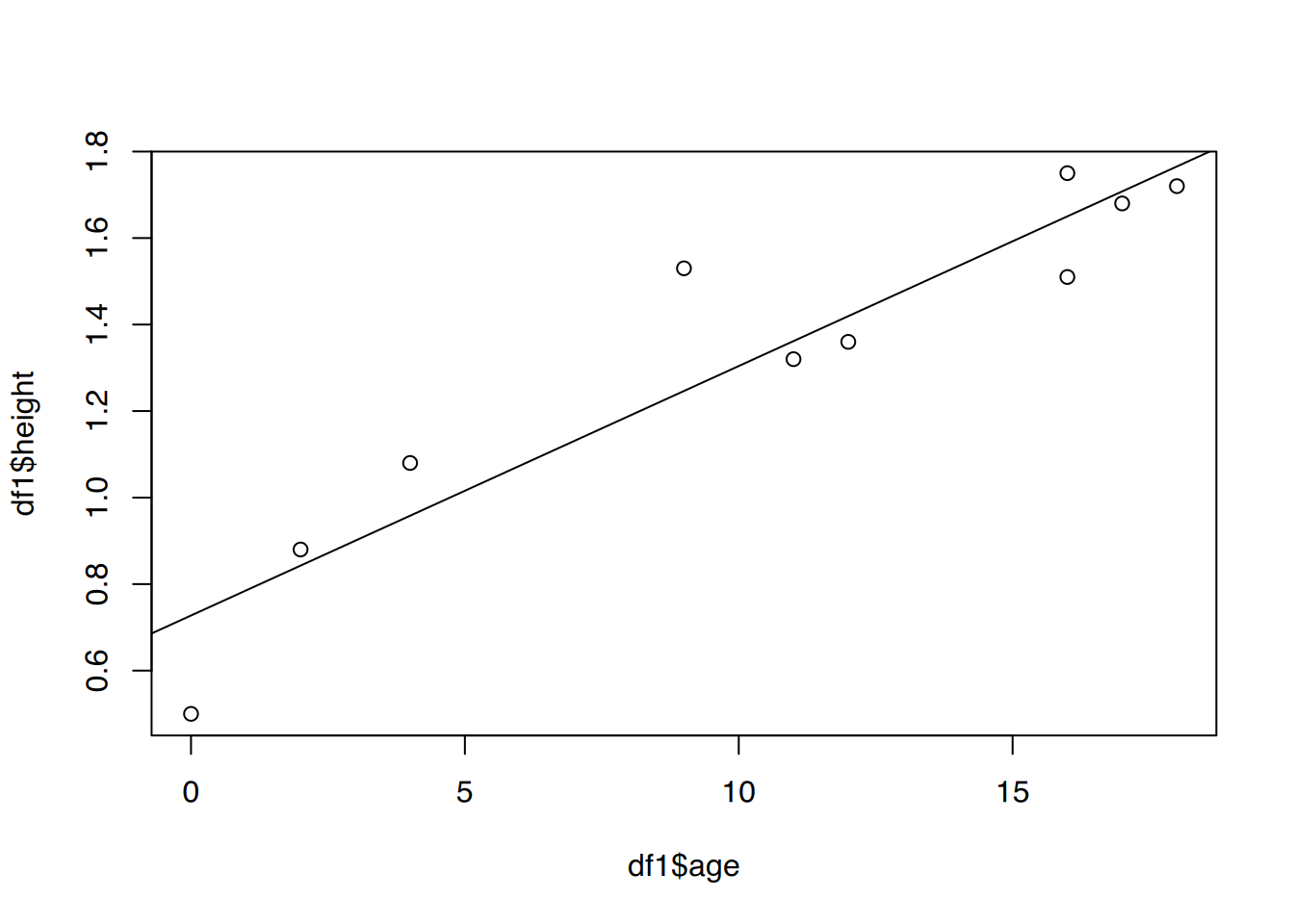
# >= 20 Jahre
plot(df2$age, df2$height)
abline(fit2)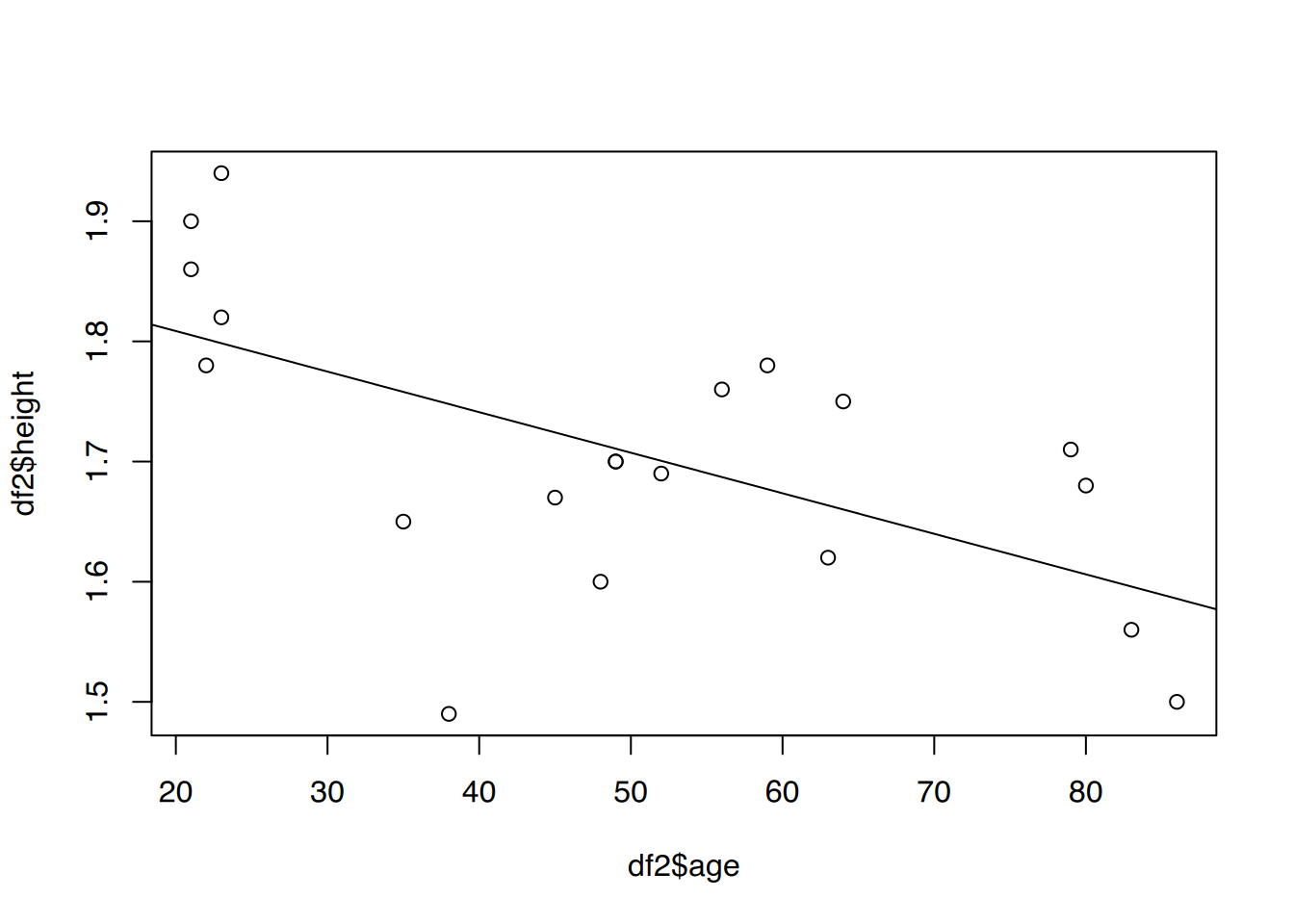
## ggplot()
# < 20 Jahre
ggplot(df1, aes(x=age, y=height)) +
geom_point() +
geom_smooth(method="lm")`geom_smooth()` using formula = 'y ~ x'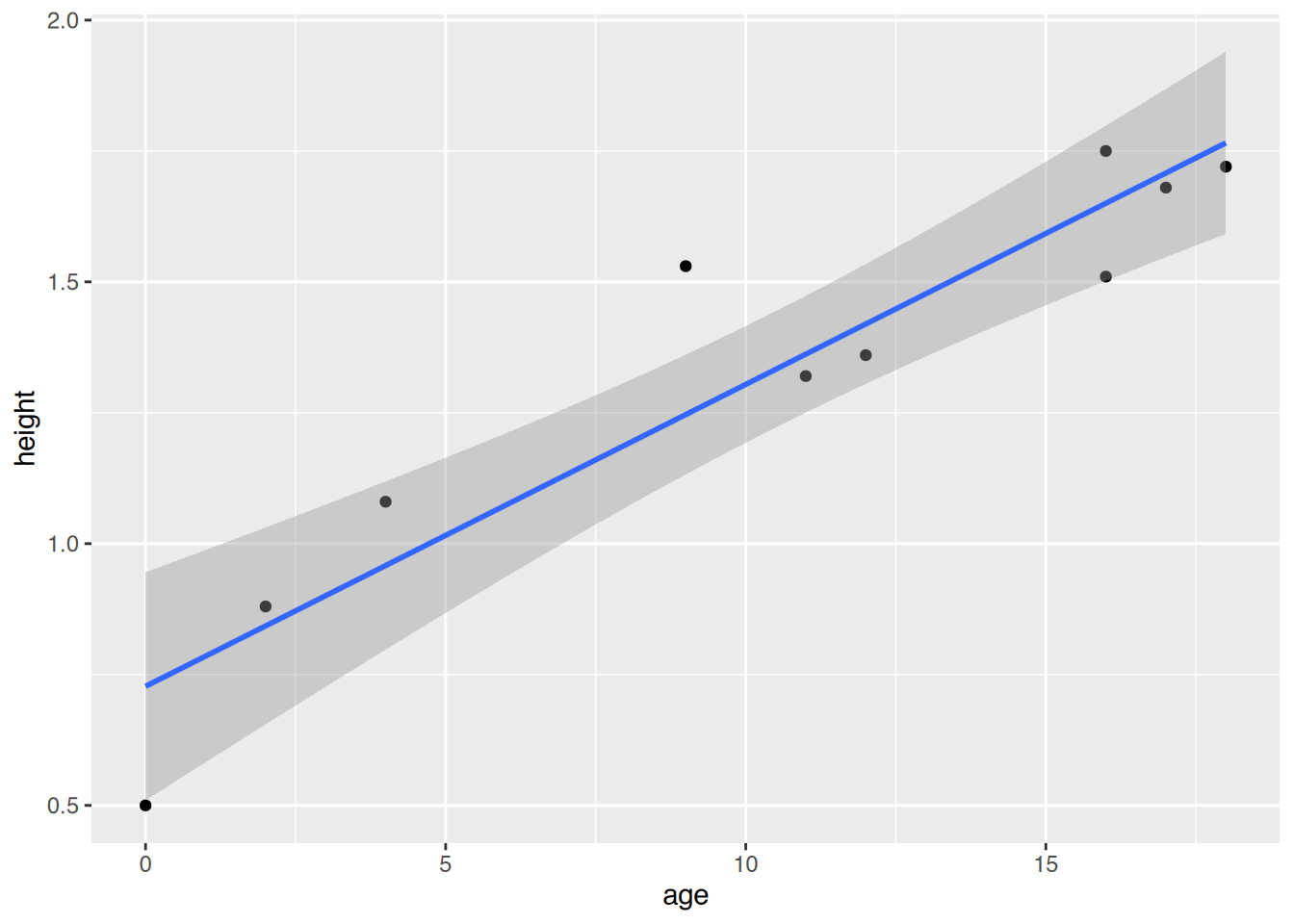
# >= 20 Jahre
ggplot(df2, aes(x=age, y=height)) +
geom_point() +
geom_smooth(method="lm")`geom_smooth()` using formula = 'y ~ x'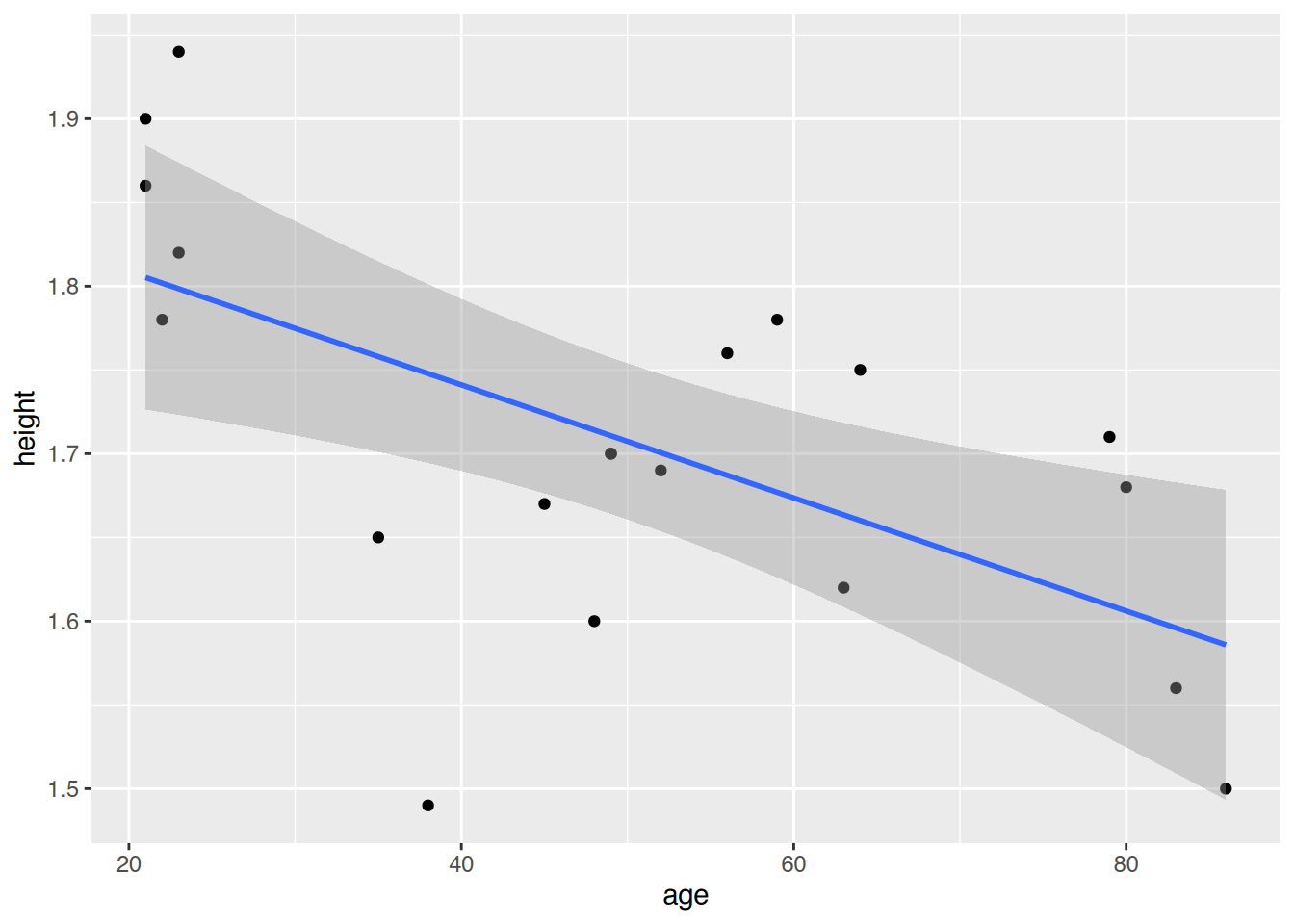
g) Welche Körpergröße sagt Ihr Modell für eine 14jährige Person vorher, und welche für eine 38jährige Person?
# 14 jährige Person
predict(fit1, list(age=14)) 1
1.534847 # 38 jährige Person
predict(fit2, list(age=38)) 1
1.747827 47.5 Lösung zur Aufgabe 44.3.5
df <- data.frame(Jahr=c(1:5),
Wirksamkeit=c(96, 84, 70, 58, 52)
)
a) Führen Sie eine lineare Regression
Wirksamkeit erklärt durch Jahr durch und plotten Sie Ihr Ergebnis.
# Regression
fit <- lm(Wirksamkeit~Jahr, data=df)
summary(fit)
Call:
lm(formula = Wirksamkeit ~ Jahr, data = df)
Residuals:
1 2 3 4 5
1.2 0.6 -2.0 -2.6 2.8
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 106.2000 2.7350 38.83 3.76e-05 ***
Jahr -11.4000 0.8246 -13.82 0.000819 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.608 on 3 degrees of freedom
Multiple R-squared: 0.9845, Adjusted R-squared: 0.9794
F-statistic: 191.1 on 1 and 3 DF, p-value: 0.0008192# plot()
plot(df$Jahr, df$Wirksamkeit)
abline(fit)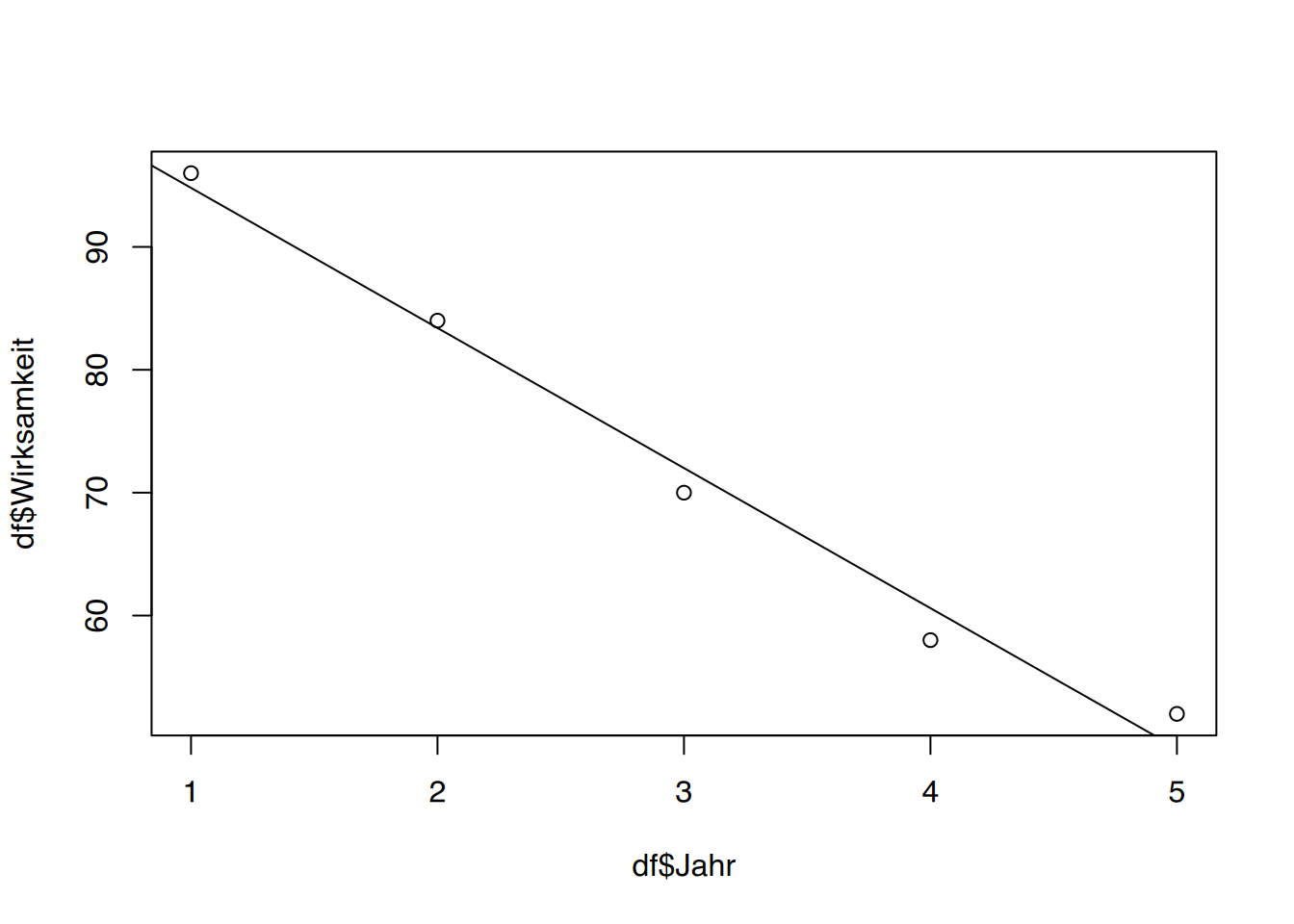
# ggplot()
ggplot(df, aes(x=Jahr, y=Wirksamkeit)) +
geom_point() +
geom_smooth(method="lm")`geom_smooth()` using formula = 'y ~ x'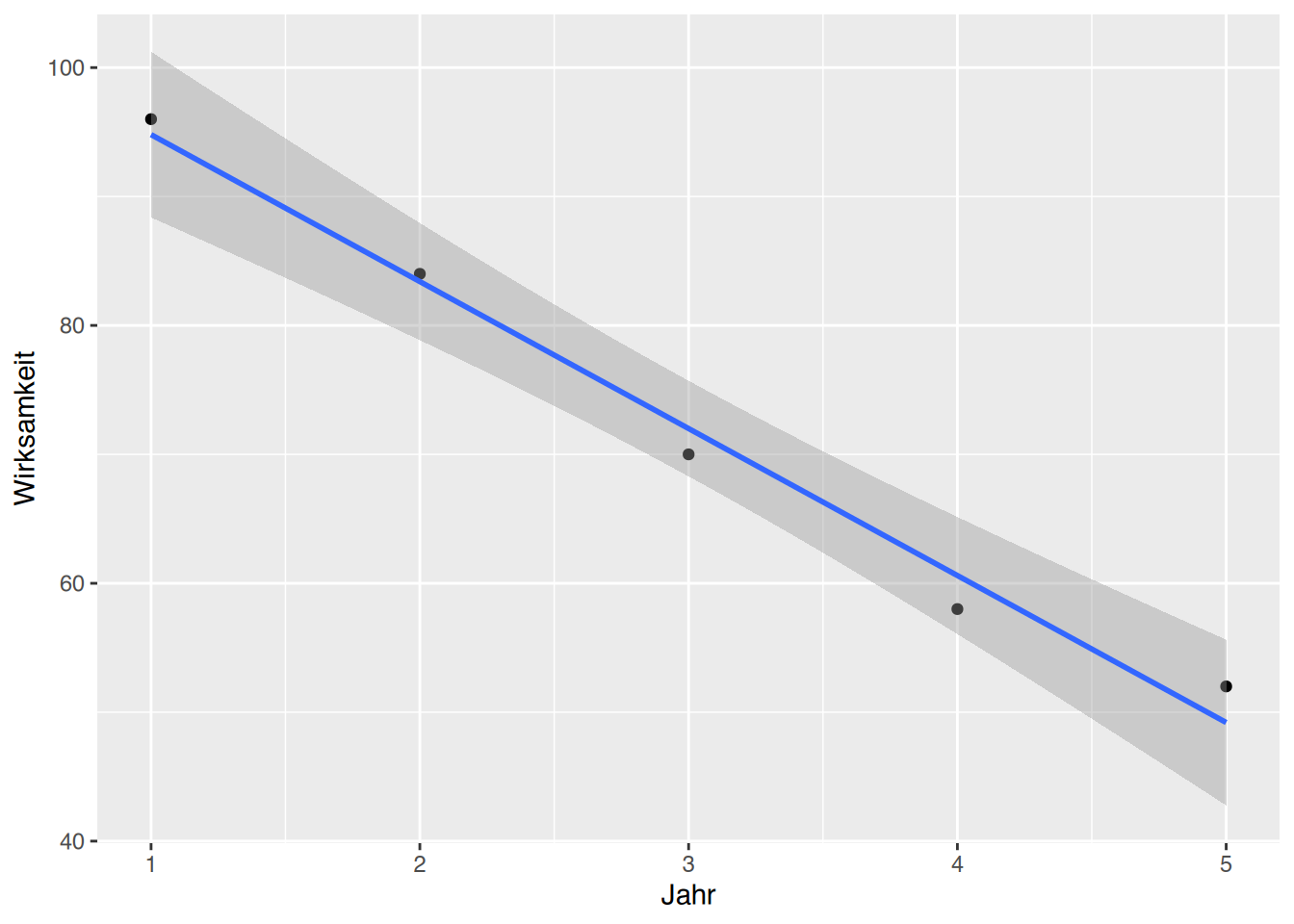
b) Wie große ist der jährliche Wirksamkeitsverlust in %?
# Regression
fit$coefficients(Intercept) Jahr
106.2 -11.4 Der Wirksamkeitsverlust beträgt 11.4% pro Jahr.
c) Nach wie vielen Jahren ist die Wirksamkeit bei 80%, und nach wie vielen bei 0%? Sind beide Werte gleich zuverlässig?
# anderes Modell
fit2 <- lm(Jahr ~ Wirksamkeit, data=df)
# 80% und 0%
predict(fit2, list(Wirksamkeit=c(80,0))) 1 2
2.309091 9.218182 Nach 2.31 Jahren ist die Wirksamkeit bei 80%, nach 9.22 Jahren bei 0%.
47.6 Lösung zur Aufgabe 44.3.6
df <- data.frame(Dosis=c(2,2, 2,2,2,2,
3,3, 3,3,3,3,
3, 4,4,4,4,4, 4,4),
Tage =c(5,5, 6,6,6,6,
3,3, 5,5,5,5,
6, 3,3,3,3,3, 5,5))
a) Berechnen Sie die Regressionsgerade der Heilungstage in Abhängigkeit von der Dosis.
# Regression
fit <- lm(Tage~Dosis, data=df)
summary(fit)
Call:
lm(formula = Tage ~ Dosis, data = df)
Residuals:
Min 1Q Median 3Q Max
-1.6023 -0.5560 0.3513 0.3977 1.4440
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.7413 0.7941 9.749 1.32e-08 ***
Dosis -1.0463 0.2517 -4.156 0.000593 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9059 on 18 degrees of freedom
Multiple R-squared: 0.4897, Adjusted R-squared: 0.4614
F-statistic: 17.28 on 1 and 18 DF, p-value: 0.000593
b) Berechnen Sie den Regressionskoeffizienten der Heilungstage in Abhängigkeit von der Dosis und interpretieren Sie ihn.
# Regression
fit$coefficients(Intercept) Dosis
7.741313 -1.046332 Mit jeder Dosiserhöhung um 1 verkürzt sich die Heilungsdauer um ca. 1 Tag.
c) Berechnen Sie den Korrelationskoeffizienten und interpretieren Sie ihn.
# Regression
cor(df$Dosis, df$Tage)[1] -0.69981Der Korrelationskoeffizient ist größer als 0,5. Es liegt ein mittelstarker Zusammenhang vor.
d) Bestimmen Sie die erwartete Zeit, die für die Heilung mit einer Dosis von 5 mg benötigt wird. Ist diese Vorhersage zuverlässig? Begründen Sie die Antwort.
# Vorhersage
predict(fit, list(Dosis=5)) 1
2.509653
e) Welche Dosis muss angewendet werden, um in 4 Tagen zu heilen? Ist diese Vorhersage zuverlässig? Begründen Sie die Antwort.
# neues Modell
fit2 <- lm(Dosis~Tage, data=df)
# Vorhersage
predict(fit2, list(Tage=4)) 1
3.307427 47.7 Lösung zur Aufgabe 44.3.7
a) Laden Sie den Datensatz
heigths.weights.students in Ihre R-Session.
# lade Datensatz
load(url("https://www.produnis.de/R/data/heights.weights.students.RData"))
b) Führen Sie eine lineare Regression
Gewicht erklärt durch Größe durch und plotten Sie Ihr Modell.
# Regression
fit <- lm(weight ~ height, data=heights.weights.students)
summary(fit)
Call:
lm(formula = weight ~ height, data = heights.weights.students)
Residuals:
Min 1Q Median 3Q Max
-16.6372 -4.8272 0.9568 4.8008 16.6542
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -91.15252 13.28198 -6.863 6.16e-10 ***
height 0.96724 0.08009 12.077 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.356 on 98 degrees of freedom
Multiple R-squared: 0.5981, Adjusted R-squared: 0.594
F-statistic: 145.9 on 1 and 98 DF, p-value: < 2.2e-16# plot()
plot(heights.weights.students$height, heights.weights.students$weight)
abline(fit)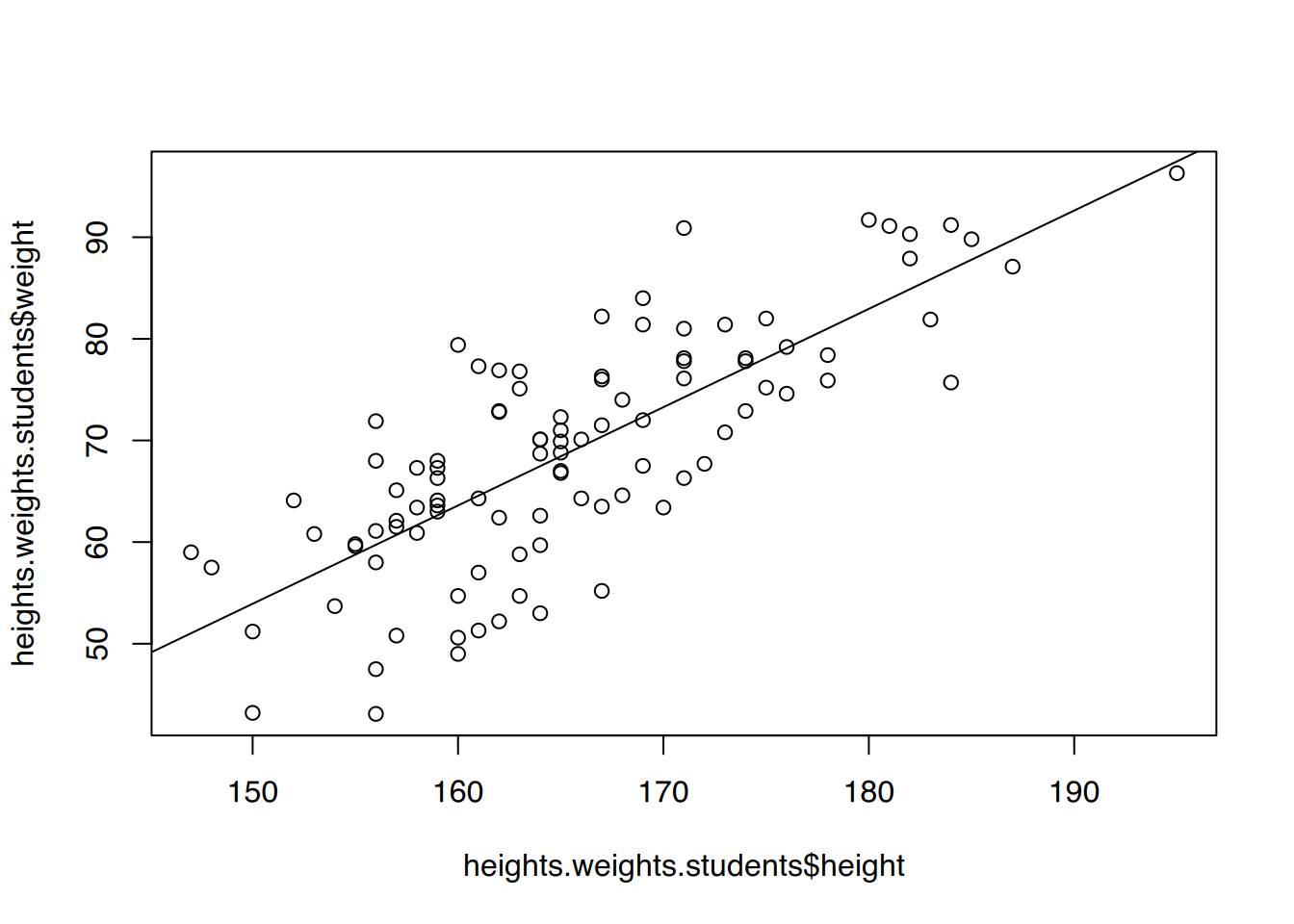
# ggplot()
ggplot(heights.weights.students, aes(x=height, y=weight)) +
geom_point() +
geom_smooth(method="lm")`geom_smooth()` using formula = 'y ~ x'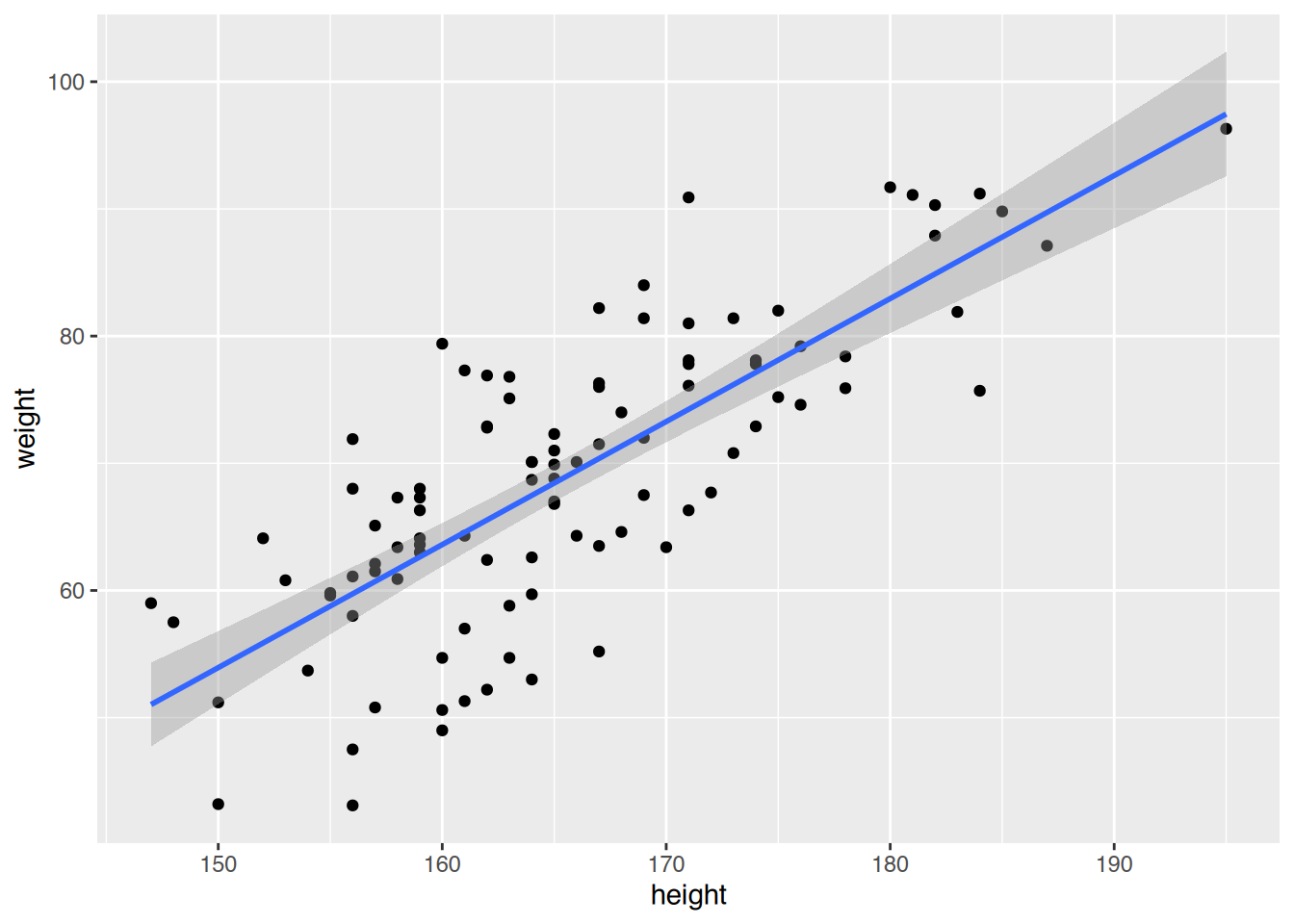
c) Erstellen Sie eine Punktwolke inklusive Regressionsgeraden jeweils für Männer und Frauen getrennt.
m <- subset(heights.weights.students, sex=="male")
w <- subset(heights.weights.students, sex=="female")
fit1 <- lm(weight ~ height, data=m)
fit2 <- lm(weight ~ height, data=w)
## plot()
# männlich
plot(m$height, m$weight)
abline(fit1, col="royalblue")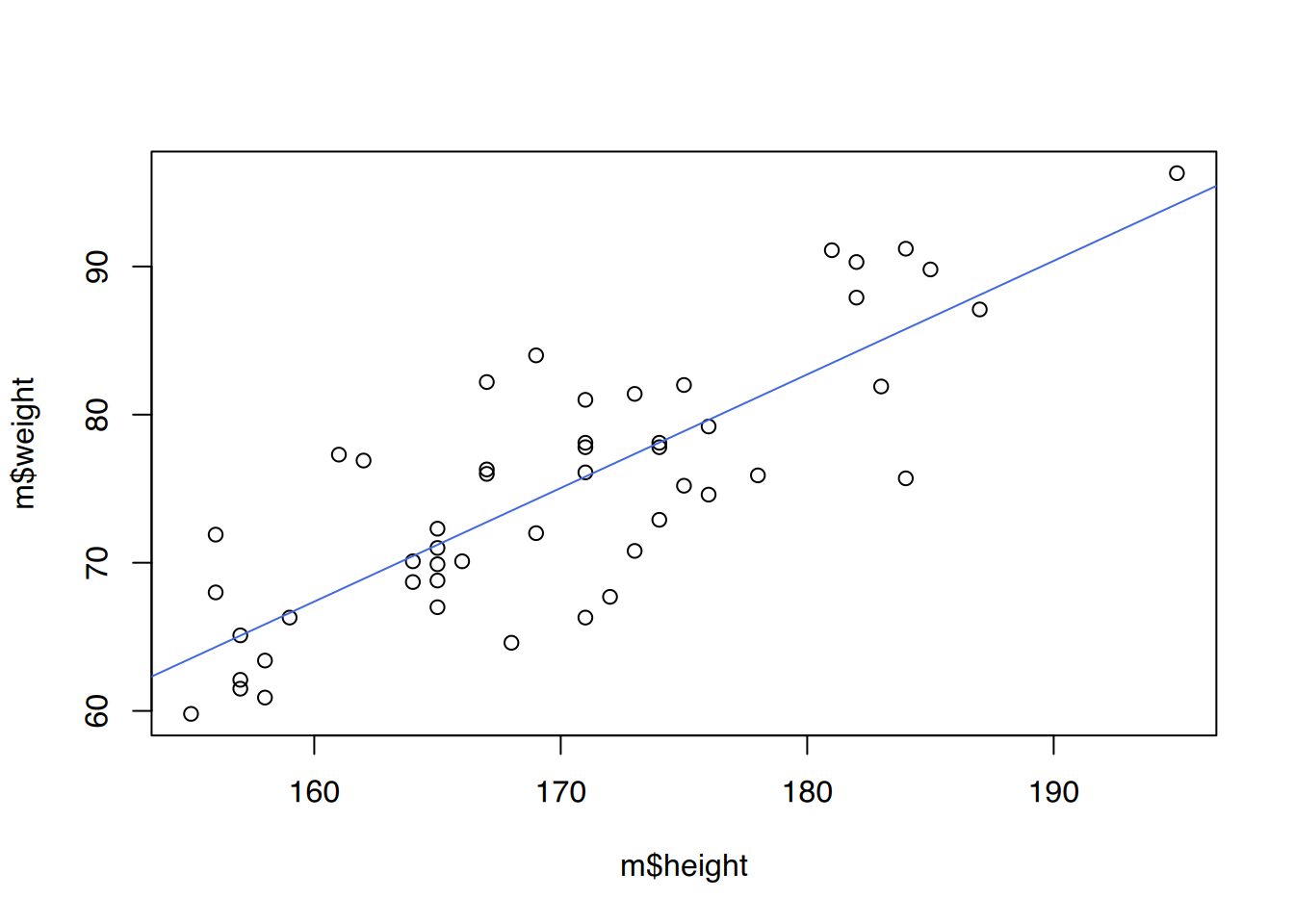
# weiblich
plot(w$height, w$weight)
abline(fit2, col="pink")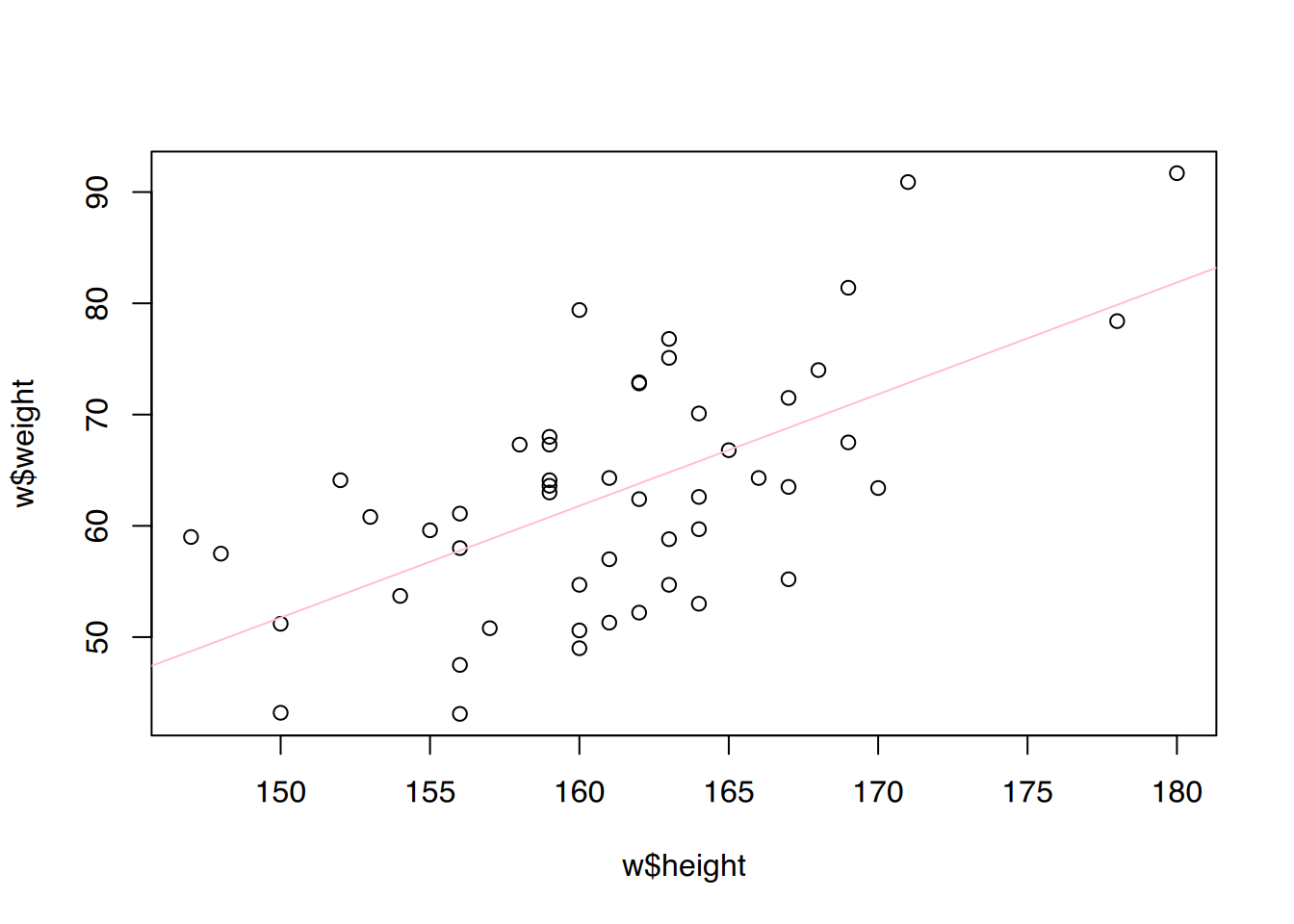
## ggplot()
# männlich
ggplot(m, aes(x=height, y=weight)) +
geom_point() +
geom_smooth(method="lm", color="royalblue")`geom_smooth()` using formula = 'y ~ x'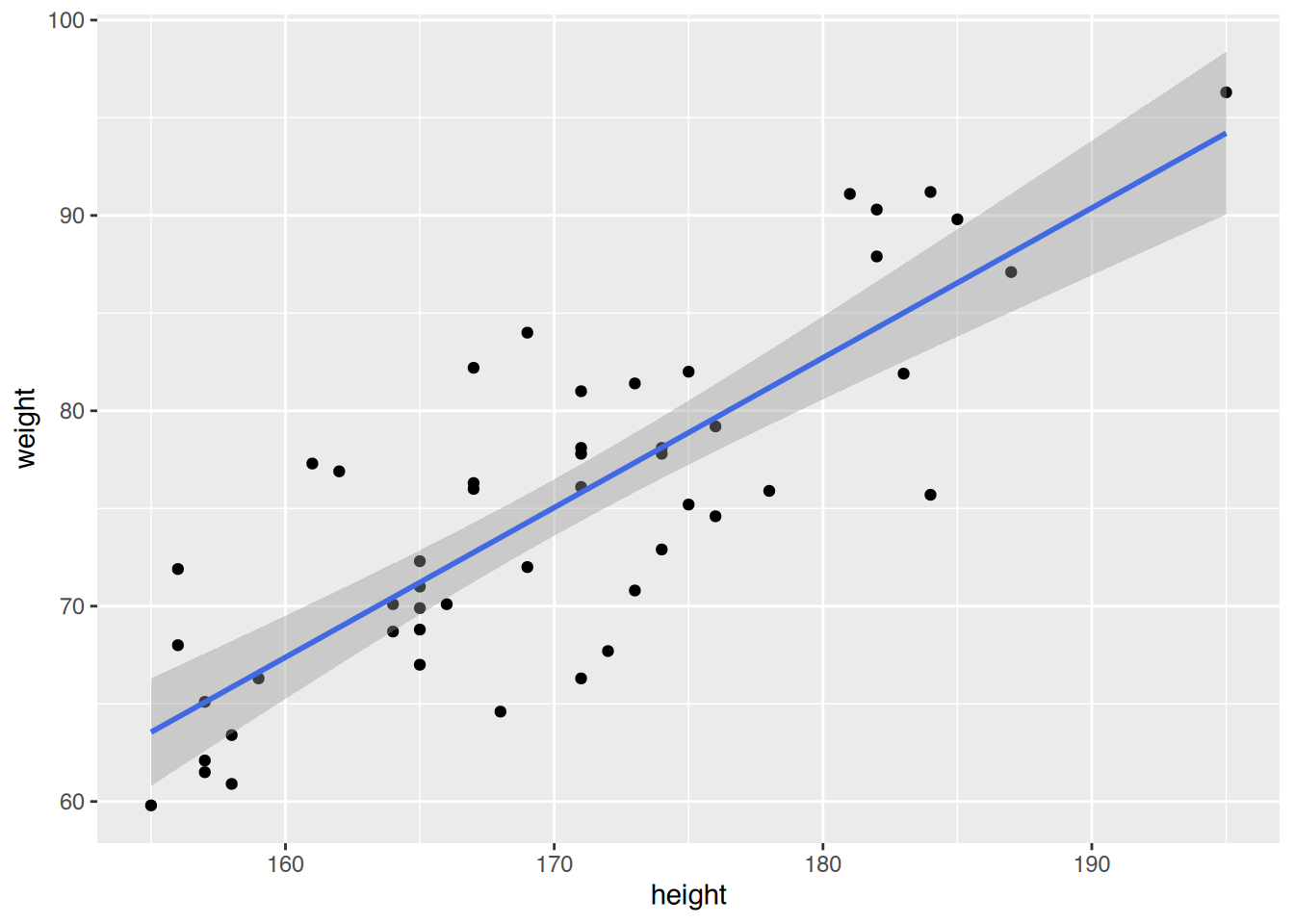
# weiblich
ggplot(w, aes(x=height, y=weight)) +
geom_point() +
geom_smooth(method="lm", color="pink")`geom_smooth()` using formula = 'y ~ x'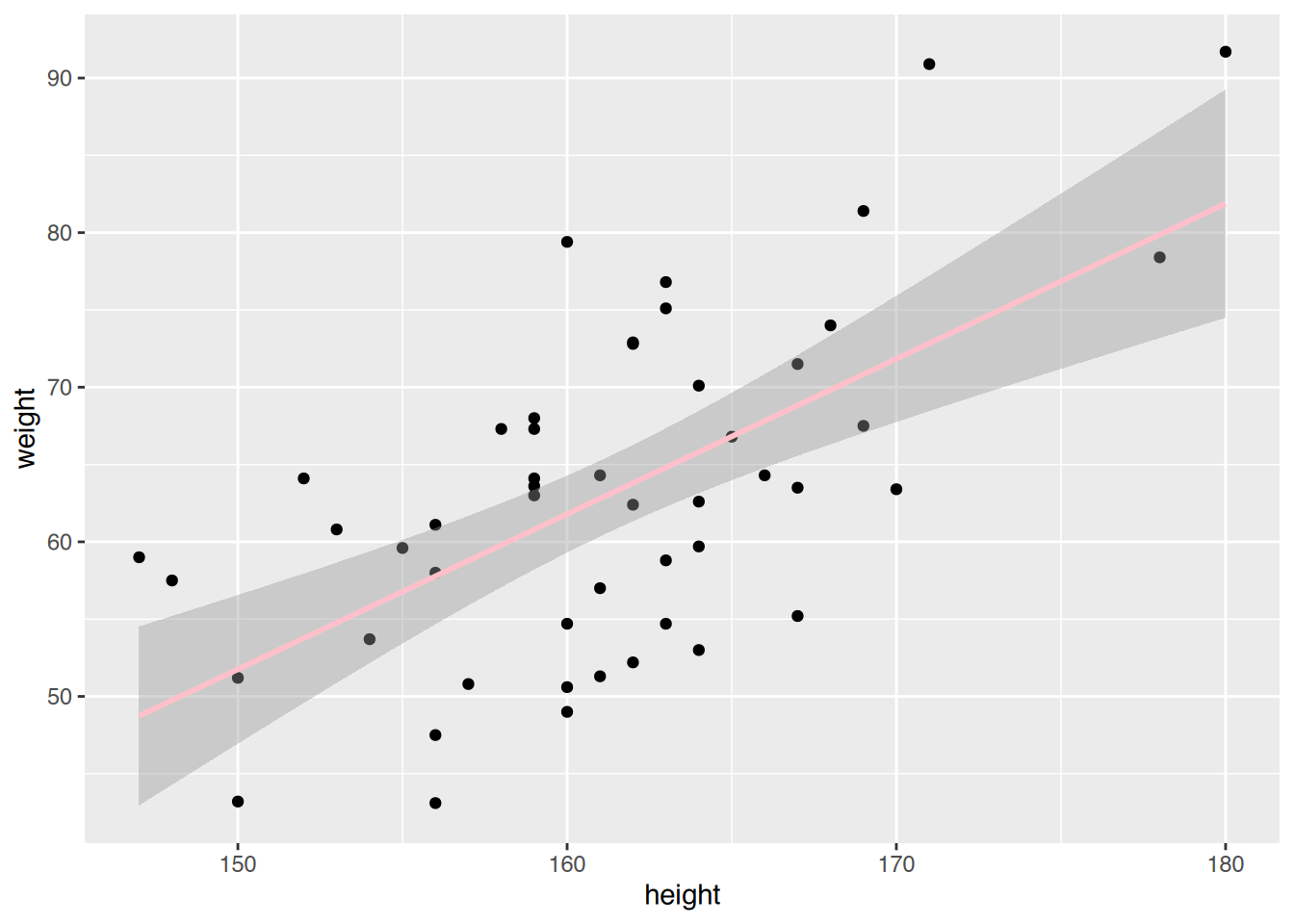
d) Berechnen Sie die Bestimmtheitskoeffizienten (R2) für beide Modelle. Welches Modell erklärt besser die Beziehung zwischen Gewicht und Größe, das der Männer oder das der Frauen? Begründen Sie die Antwort.
# Männer
summary(fit1)$r.squared[1] 0.6699418# Frauen
summary(fit2)$r.squared[1] 0.3828876Das Modell der Männer erklärt 0.67% der Streuung, und das der Frauen “nur” 0.38%. Somit ist das Modell für Männer besser als das der Frauen.
e) Was ist das zu erwartende Gewicht für einen Mann mit 170cm Körpergröße? Und für eine Frau der selben Größe?
# Männer
predict(fit1, list(height=170)) 1
75.048 # Frauen
predict(fit2, list(height=170)) 1
71.8338 47.8 Lösung zur Aufgabe 44.3.8
# lade Datensatz
load(url("https://www.produnis.de/R/data/neonates.RData"))
a) Erstellen Sie eine Kreuztabelle vom APGAR-Wert nach 1 Minute und dem Rauchverhalten der Mütter während der Schwangerschaft. Welche Schlüsse lassen sich ziehen?
# entweder
table(neonates$smoke, neonates$apgar1)
2 3 4 5 6 7 8 9
No 1 6 18 50 77 40 23 5
Yes 3 15 20 31 20 6 5 0# oder
xtabs(~ smoke + apgar1, data=neonates) apgar1
smoke 2 3 4 5 6 7 8 9
No 1 6 18 50 77 40 23 5
Yes 3 15 20 31 20 6 5 0Kinder von Frauen, die nicht während der Schangerschaft rauchen, haben höhere APGAR1-Werte als Kinder von Raucherinnen.
b) Erstellen Sie eine Kreuztabelle vom APGAR-Wert nach 1 Minute und der Alterskategorie der Mütter. Welche Schlüsse lassen sich ziehen?
# entweder
table(neonates$age, neonates$apgar1)
2 3 4 5 6 7 8 9
greater than 20 2 10 22 53 69 34 24 4
less than 20 2 11 16 28 28 12 4 1# oder
xtabs(~ age + apgar1, data=neonates) apgar1
age 2 3 4 5 6 7 8 9
greater than 20 2 10 22 53 69 34 24 4
less than 20 2 11 16 28 28 12 4 1Kinder von Frauen, die älter als 20 Jahre sind, haben höhere APGAR1-Werte als Kinder von jüngeren Müttern.
c) Führen Sie eine lineare Regression für
Geburtsgewicht erklärt durch Anzahl täglich gerauchter Zigaretten durch. Gibt es einen starken linearen Zusammenhang?
# Regression
fit <- lm(weight ~ cigarettes, data=neonates)
summary(fit)
Call:
lm(formula = weight ~ cigarettes, data = neonates)
Residuals:
Min 1Q Median 3Q Max
-0.98756 -0.16656 -0.00649 0.18769 1.03544
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.146557 0.018604 169.13 <2e-16 ***
cigarettes -0.031067 0.002512 -12.37 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2832 on 318 degrees of freedom
Multiple R-squared: 0.3248, Adjusted R-squared: 0.3227
F-statistic: 153 on 1 and 318 DF, p-value: < 2.2e-16Der Zusammenhang ist eher gering.
d) Plotten Sie Ihre Regression. Passt die Regressionsgerade gut zur Punktwolke?
# plot()
plot(neonates$cigarettes, neonates$weight)
abline(fit)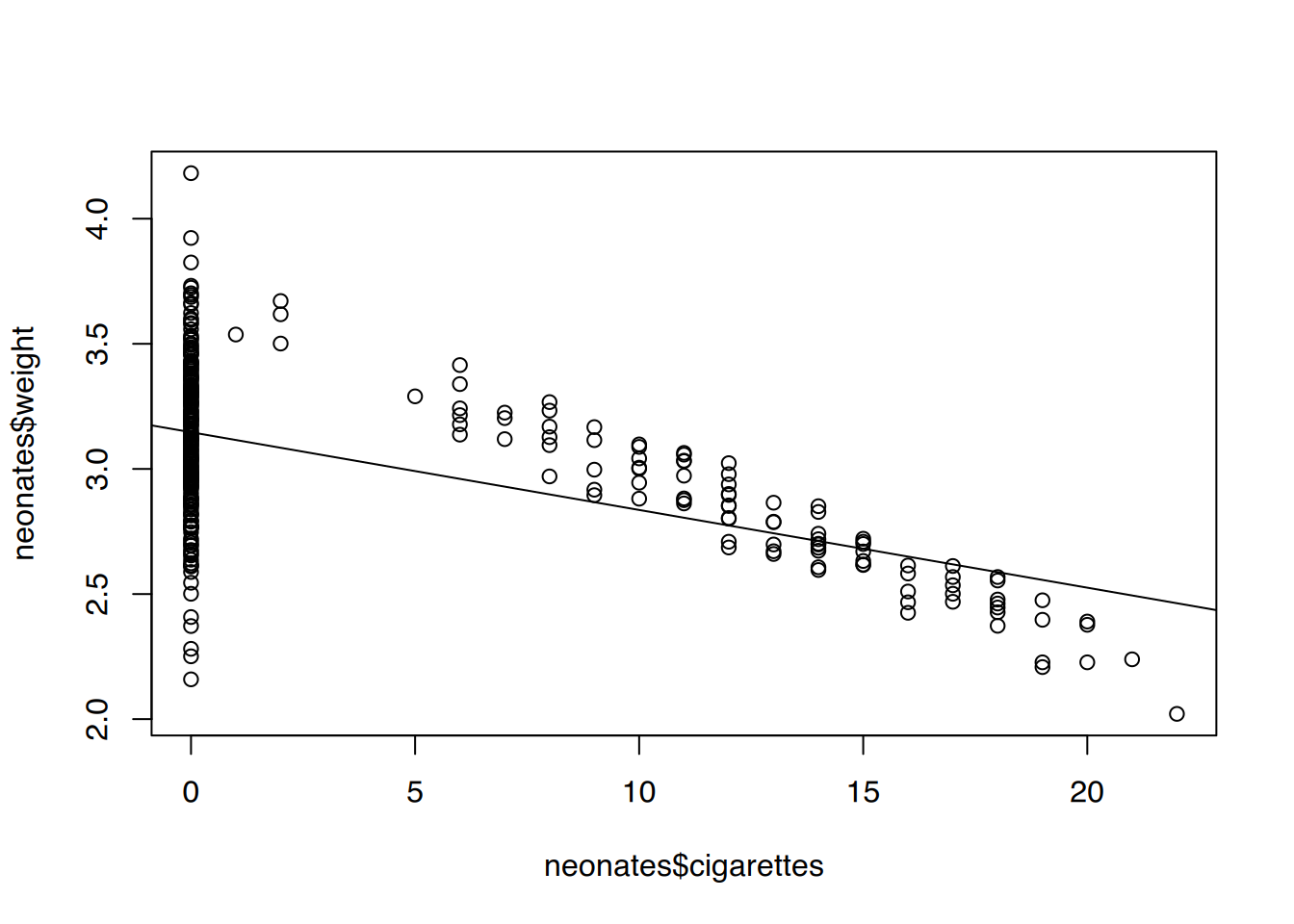
# ggplot()
ggplot(neonates, aes(x=cigarettes, y=weight)) +
geom_point() +
geom_smooth(method="lm", color="pink")`geom_smooth()` using formula = 'y ~ x'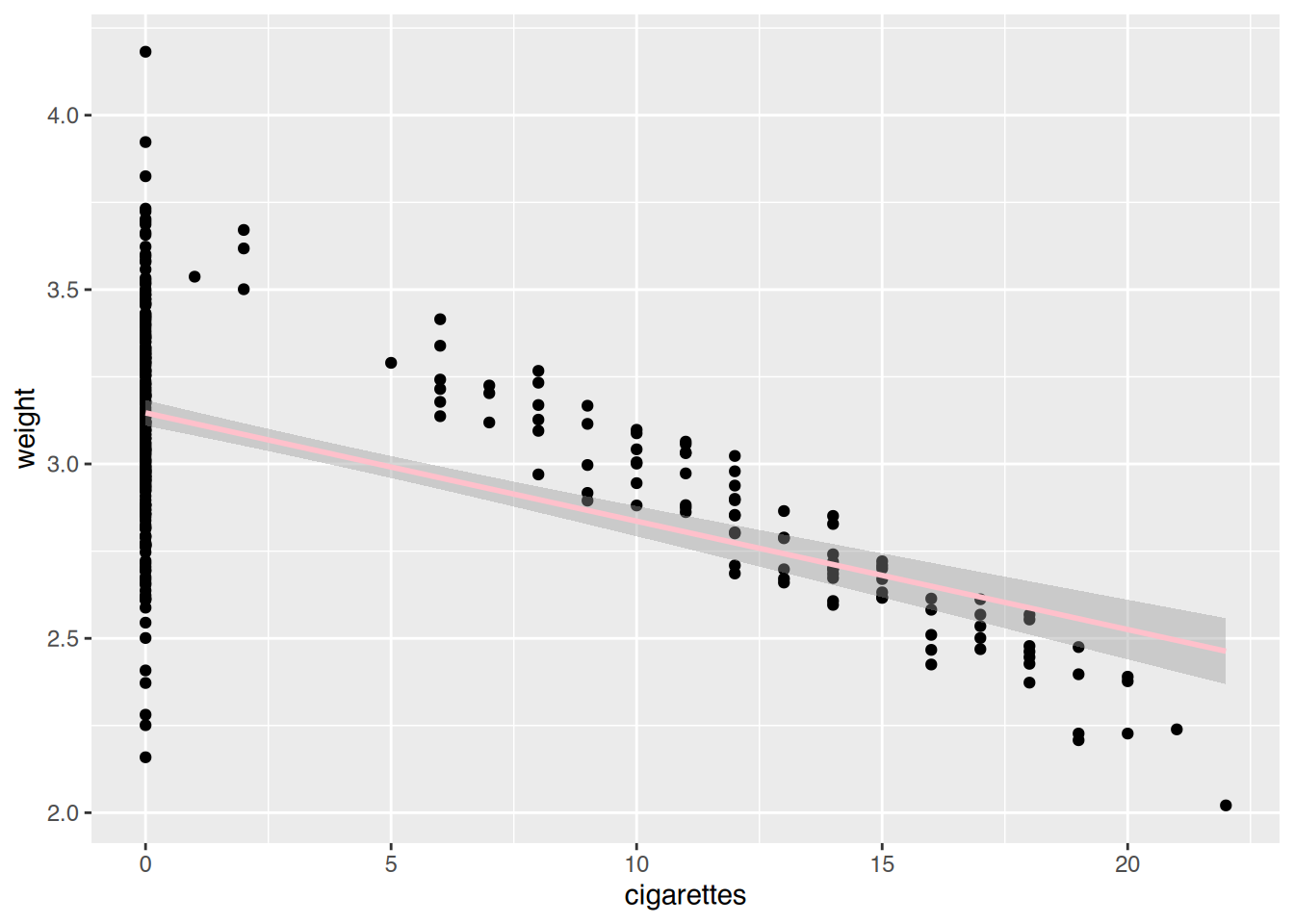
Der Zusammenhang wird durch die Nichtraucherinnen (0 Zigaretten) verzerrt.
e) Wiederholen Sie die Regression, aber nutzen Sie dieses Mal nur Daten von Raucherinnen. Ist dieses Modell besser oder schlechter als das vorherige? Wieviel Gewicht verliert ein Neugeborenes nach diesem Modell pro täglich gerauchter Zigarette?
# Subset erzeugen
smoke <- subset(neonates, smoke=="Yes")
# Regression
fit2 <- lm(weight ~ cigarettes, data=smoke)
summary(fit2)
Call:
lm(formula = weight ~ cigarettes, data = smoke)
Residuals:
Min 1Q Median 3Q Max
-0.168338 -0.057531 0.002855 0.068180 0.168662
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.687879 0.025542 144.38 <2e-16 ***
cigarettes -0.069462 0.001928 -36.03 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08735 on 98 degrees of freedom
Multiple R-squared: 0.9298, Adjusted R-squared: 0.9291
F-statistic: 1298 on 1 and 98 DF, p-value: < 2.2e-16# plot()
plot(smoke$cigarettes, smoke$weight)
abline(fit2)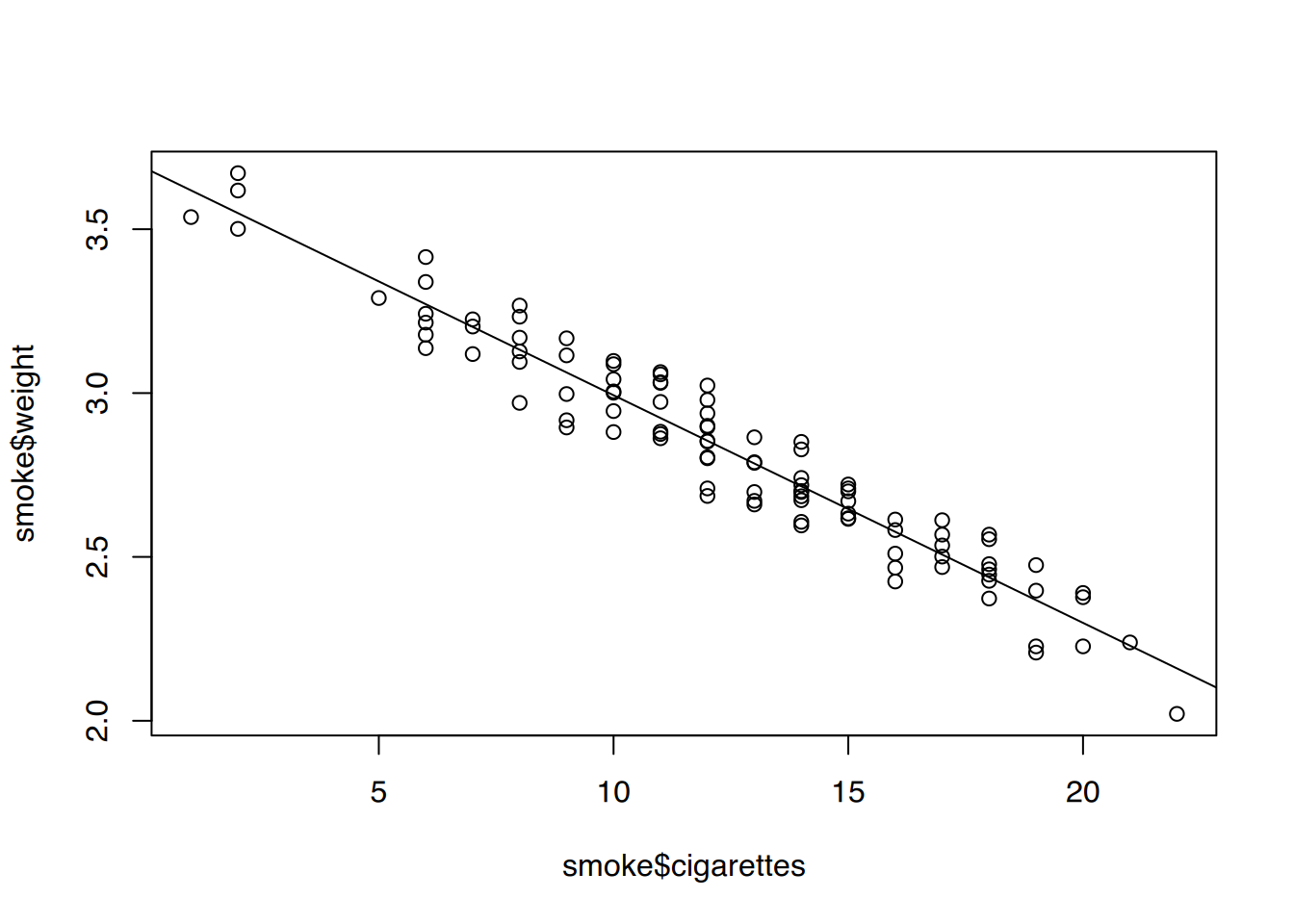
# ggplot()
ggplot(smoke, aes(x=cigarettes, y=weight)) +
geom_point() +
geom_smooth(method="lm", color="pink")`geom_smooth()` using formula = 'y ~ x'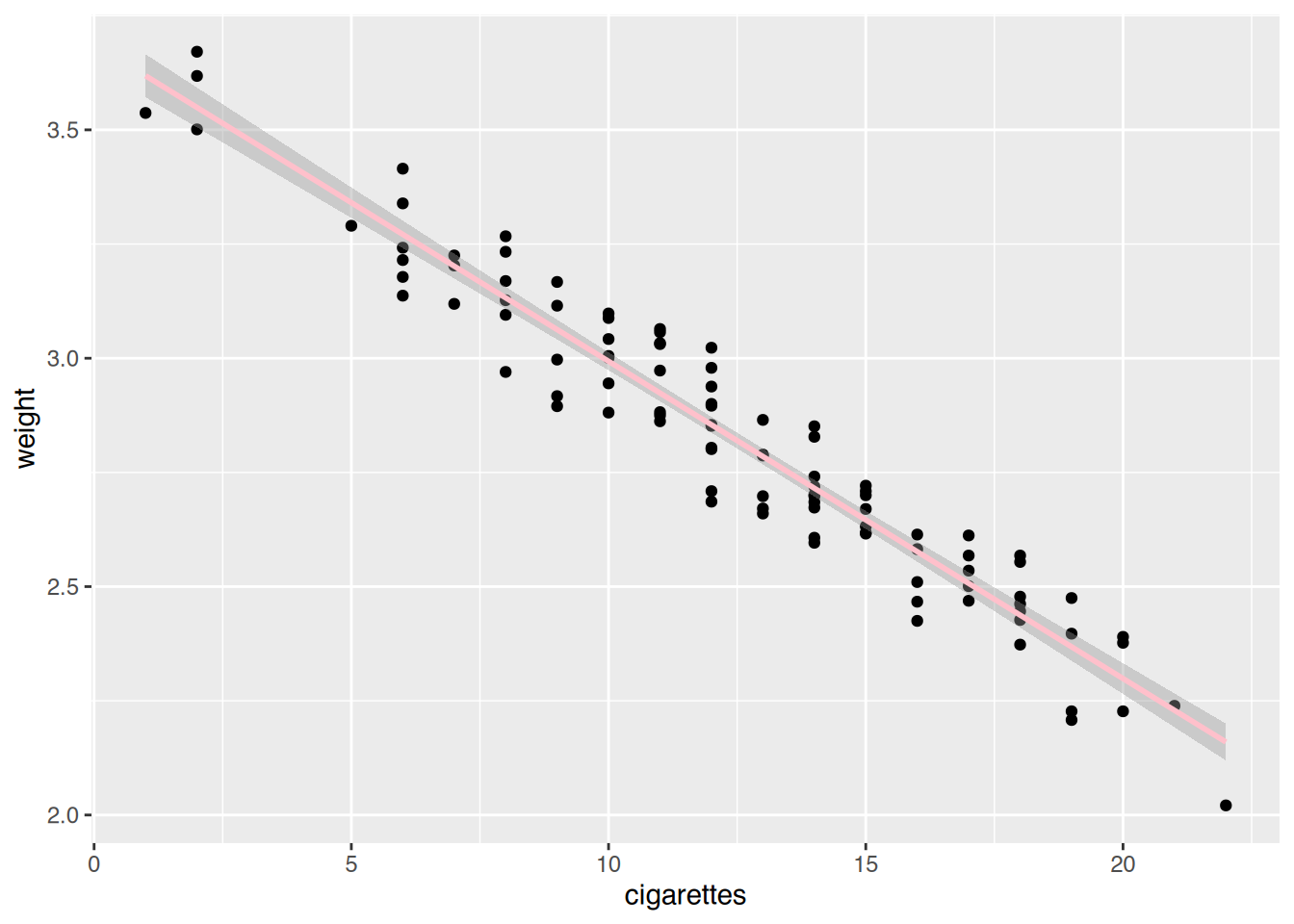
Der Zusammenhang ist nun sehr stark.
f) Welches Geburtsgewicht sagt dieses Modell für ein Neugeborenes vorher, dessen Mutter 5 Zigaretten täglich während der Schwangerschaft geraucht hat? Wieviel für eine Mutter, die 30 Zigaretten täglich raucht. Wie zuverlässich sind diese Ergebnisse?
# Vorhersage
predict(fit2, list(cigarettes=c(5, 30))) 1 2
3.340570 1.604026
g) Ändert sich der lineare Zusammenhang, wenn die Daten nach Altersgruppen getrennt untersucht werden?
# Subset
s1 <- subset(smoke, age=="greater than 20")
s2 <- subset(smoke, age=="less than 20")
# neue Modelle
fit1 <- lm(weight ~ cigarettes, data=s1)
fit1 <- lm(weight ~ cigarettes, data=s2)
# vergleichen
summary(fit1)
Call:
lm(formula = weight ~ cigarettes, data = s2)
Residuals:
Min 1Q Median 3Q Max
-0.151567 -0.049334 -0.001749 0.062936 0.127103
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.65752 0.05636 64.90 < 2e-16 ***
cigarettes -0.06833 0.00375 -18.22 6.33e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08286 on 20 degrees of freedom
Multiple R-squared: 0.9432, Adjusted R-squared: 0.9404
F-statistic: 332.1 on 1 and 20 DF, p-value: 6.333e-14summary(fit2)
Call:
lm(formula = weight ~ cigarettes, data = smoke)
Residuals:
Min 1Q Median 3Q Max
-0.168338 -0.057531 0.002855 0.068180 0.168662
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.687879 0.025542 144.38 <2e-16 ***
cigarettes -0.069462 0.001928 -36.03 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08735 on 98 degrees of freedom
Multiple R-squared: 0.9298, Adjusted R-squared: 0.9291
F-statistic: 1298 on 1 and 98 DF, p-value: < 2.2e-16Der Zusammenhang bleibt unabhängig von der Altersgruppe bestehen.