# Daten erzeugen
df <- data.frame(Stunden=c(1:9),
Bakterien=c(25, 28, 47, 65, 86, 121, 190, 290, 362))48 Lösungen Nicht-Lineare Regression
Hier finden Sie die Lösungen zu den Übungsaufgaben von Abschnitt 44.4.
Die hier vorgestellten Lösungen stellen immer nur eine mögliche Vorgehensweisen dar und sind sicherlich nicht der Weisheit letzter Schluss. In R führen viele Wege nach Rom, und wenn Sie mit anderem Code zu den richtigen Ergebnissen kommen, dann ist das völlig in Ordnung.
48.1 Lösung zur Aufgabe 44.4.1
a) Erstellen Sie ein Datenframe mit den Variablen
Stunden und Bakterien.
b) Erzeugen Sie ein Scatterplot. Welche Regression würden Sie auf Grundlage des Plots vorschlagen?
# plot()
plot(df$Stunden, df$Bakterien)
# ggplot()
ggplot(df, aes(x=Stunden, y=Bakterien)) +
geom_point()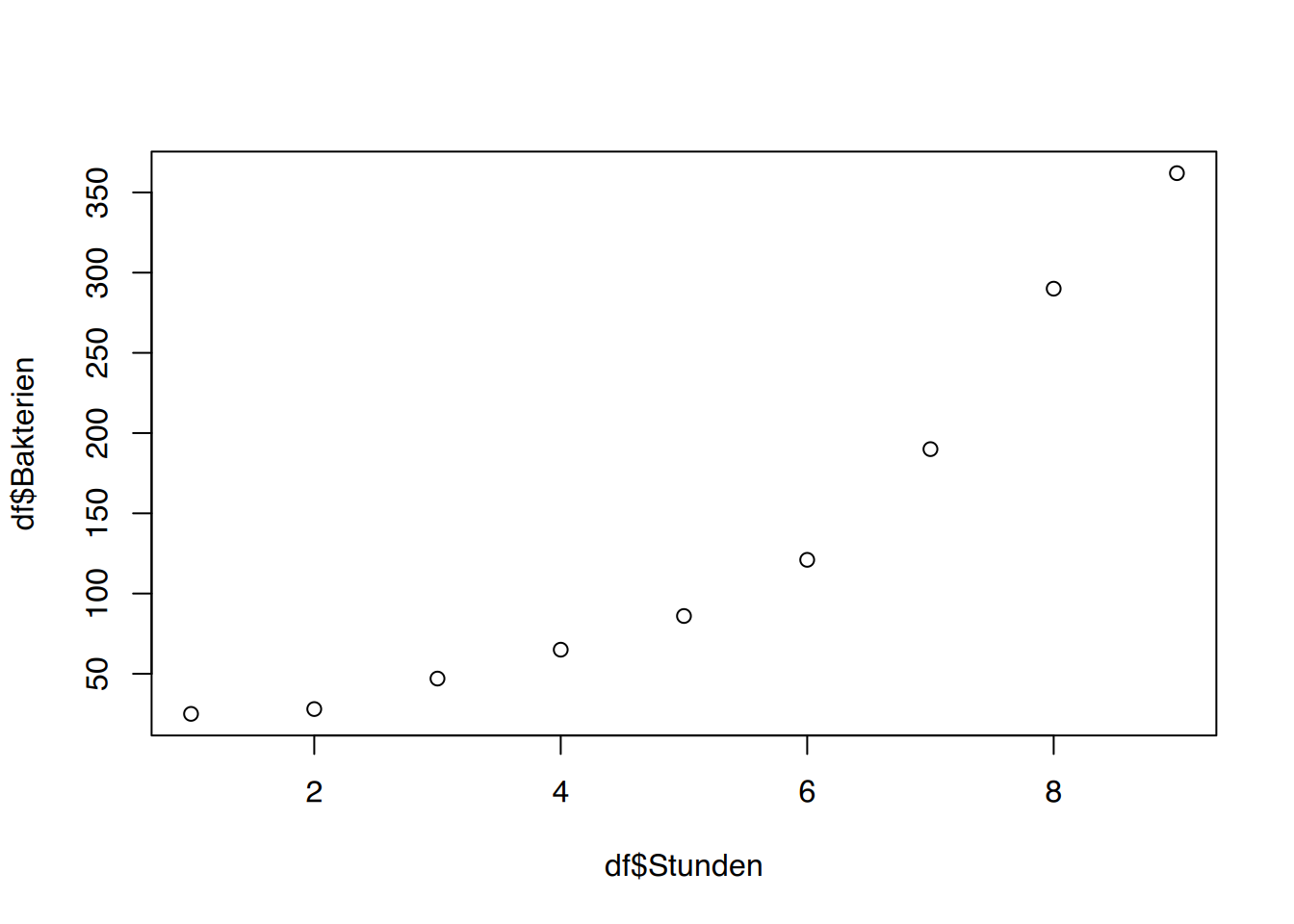
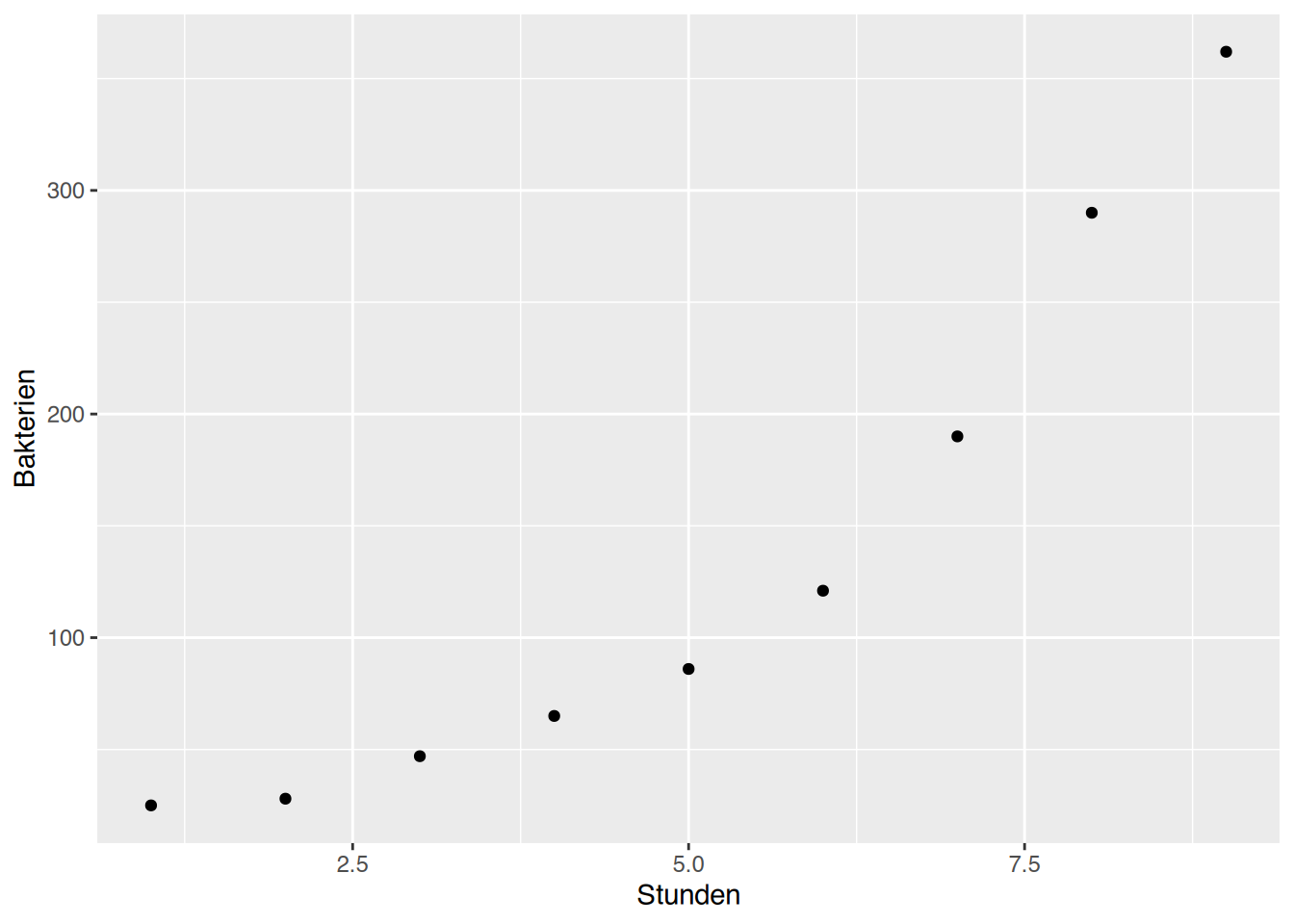
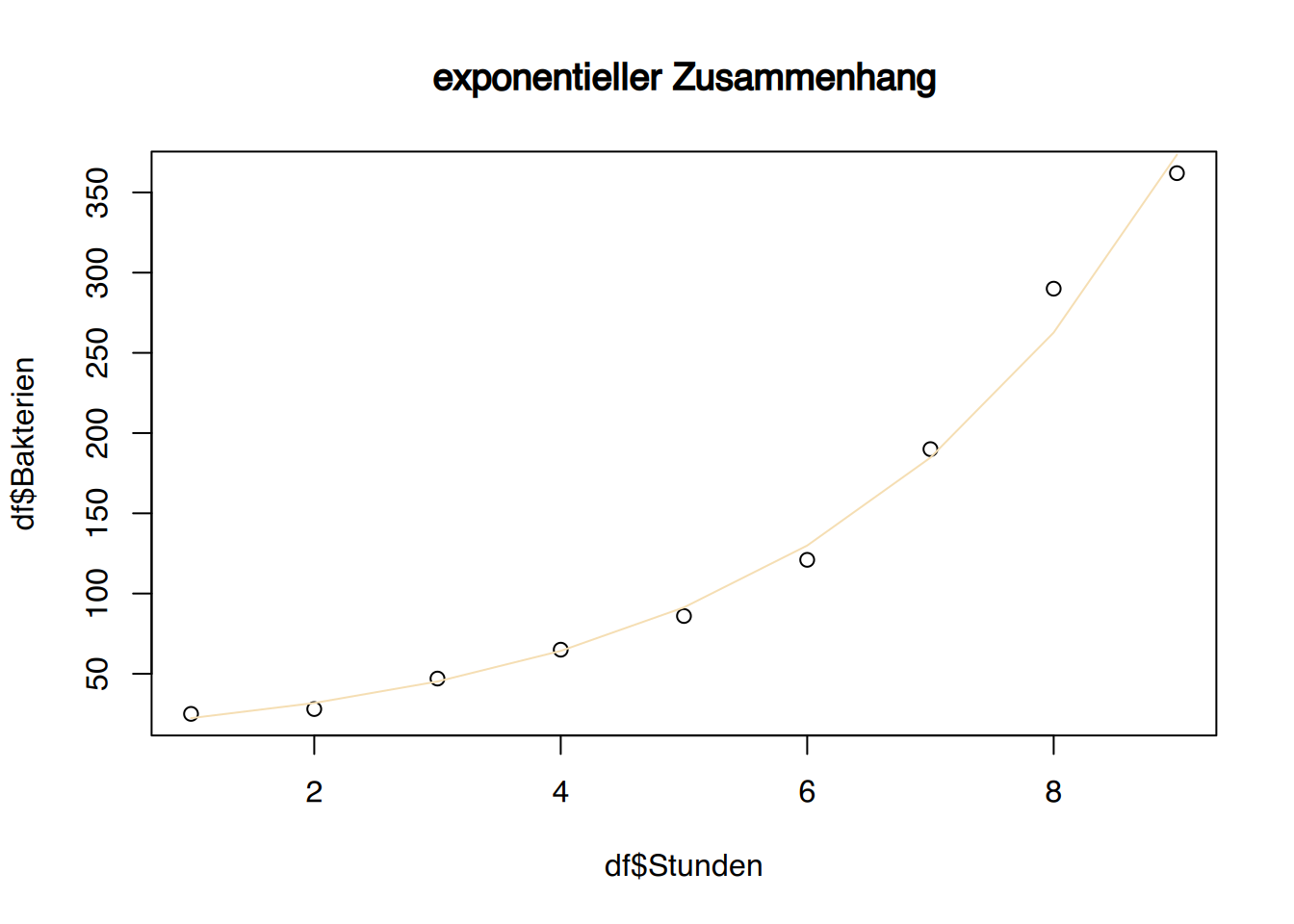
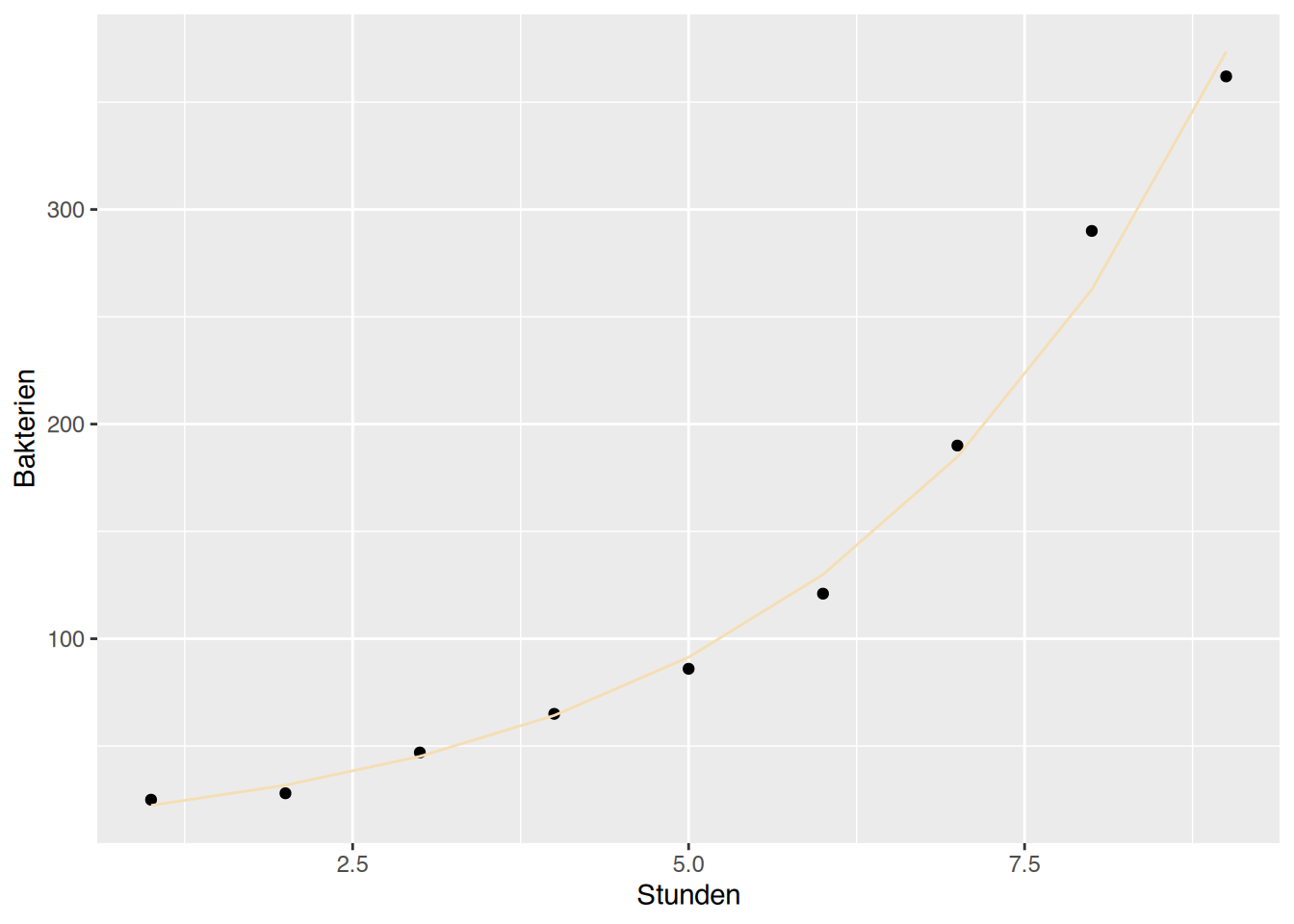
Die Punktwolken sprechen für einen exponentiellen Anstieg.
c) Berechnen Sie die quadratischen und exponentiellen Modelle für die Bakterienvermehrung über die Zeit.
# quadratisch
q <- lm(Bakterien ~ Stunden + I(Stunden^2), data=df)
summary(q)
Call:
lm(formula = Bakterien ~ Stunden + I(Stunden^2), data = df)
Residuals:
Min 1Q Median 3Q Max
-16.617 -8.297 -1.430 9.916 15.442
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 53.2381 15.9862 3.330 0.0158 *
Stunden -26.7420 7.3403 -3.643 0.0108 *
I(Stunden^2) 6.8009 0.7159 9.500 7.75e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.56 on 6 degrees of freedom
Multiple R-squared: 0.9919, Adjusted R-squared: 0.9892
F-statistic: 368.8 on 2 and 6 DF, p-value: 5.254e-07# exponentiell
e <- lm(log(Bakterien) ~ Stunden, data=df)
summary(e)
Call:
lm(formula = log(Bakterien) ~ Stunden, data = df)
Residuals:
Min 1Q Median 3Q Max
-0.12676 -0.06057 0.01145 0.03920 0.11190
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.75498 0.06174 44.62 7.41e-10 ***
Stunden 0.35199 0.01097 32.08 7.39e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08498 on 7 degrees of freedom
Multiple R-squared: 0.9932, Adjusted R-squared: 0.9923
F-statistic: 1029 on 1 and 7 DF, p-value: 7.389e-09
d) Plotten Sie das bessere Modell in die Punktwolke.
# Vorbereitung quadratisch
vorhersageQ <- predict(q, list(Stunden=df$Stunden))
# plot() quadratisch
plot(df$Stunden, df$Bakterien,
main="quadratischer Zusammenhang")
lines(df$Stunden, vorhersageQ, col="tan4")
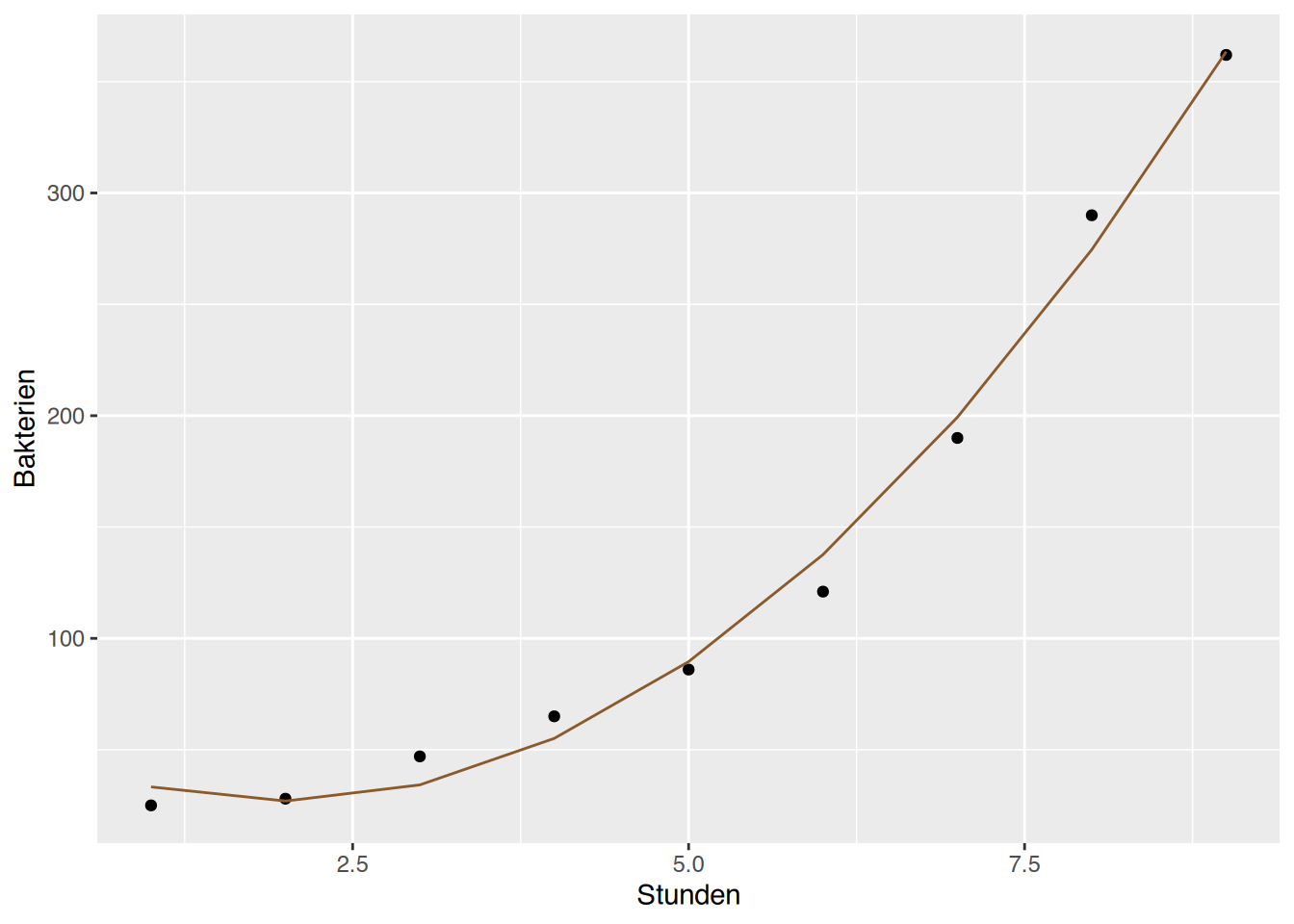
# ggplot() quadratisch
ggplot(df, aes(x=Stunden, y=Bakterien)) +
geom_point() +
geom_line(aes(y=vorhersageQ), col="tan4")
# Vorbereitung exponentiell
vorhersageE <- exp(predict(e, list(Stunden=df$Stunden)))
# plot() exponentiell
plot(df$Stunden, df$Bakterien,
main="exponentieller Zusammenhang")
lines(df$Stunden, vorhersageE, col="wheat")
# ggplot() exponentiell
ggplot(df, aes(x=Stunden, y=Bakterien)) +
geom_point() +
geom_line(aes(y=vorhersageE), col="wheat")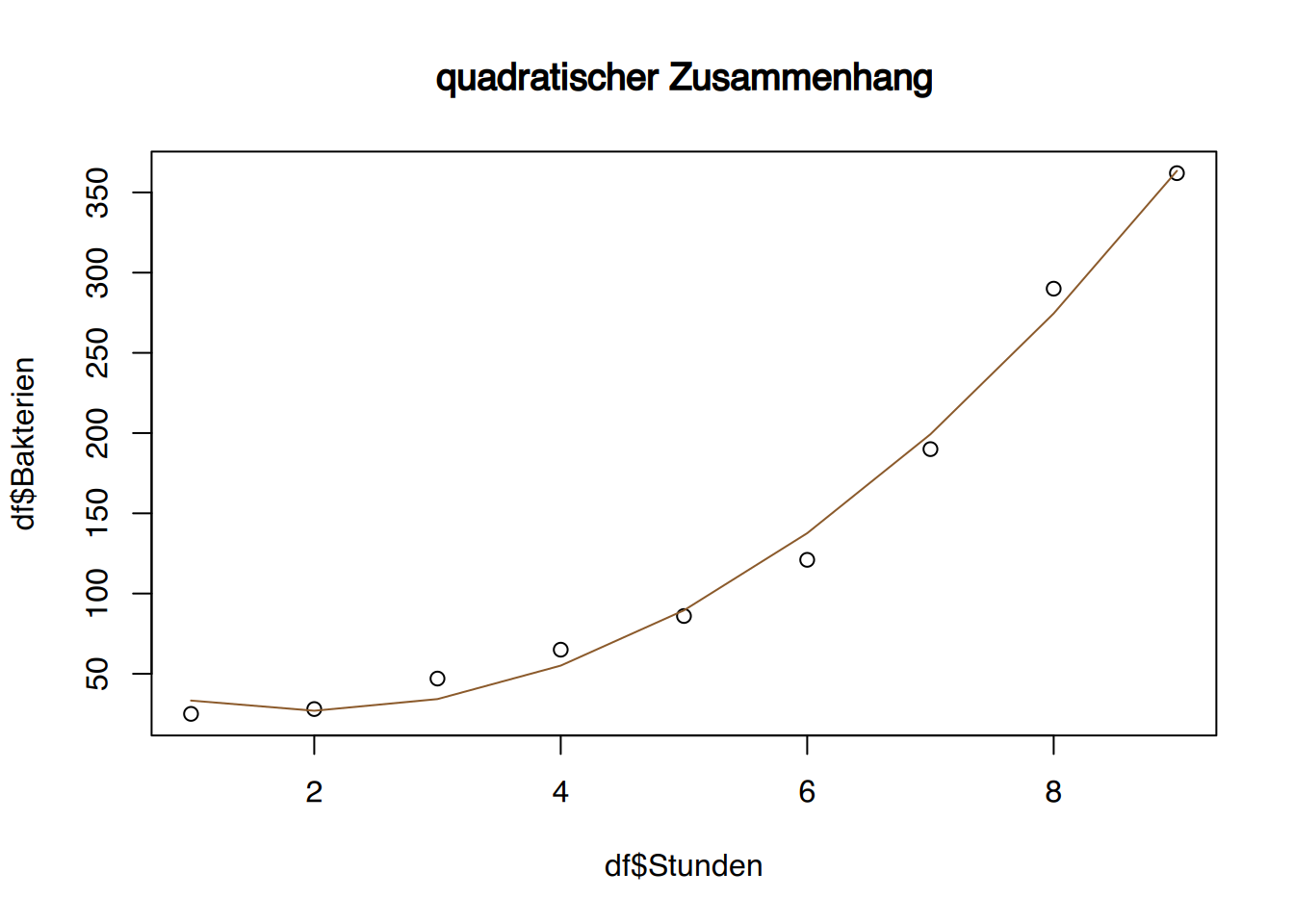
e) Wie viele Bakterien werden nach dem besten Modell 3 Stunden nach Anlegen der Kultur vorhanden sein? Und nach 10 Stunden? Sind diese Vorhersagen zuverlässig?
# Vorhersage
exp(predict(e, list(Stunden=c(3, 10)))) 1 2
45.19322 531.05241 Nach 3 Stunden können wir 46 Bakterien erwarten, nach 10 Stunden 532.
f) Machen Sie eine möglichst zuverlässige Vorhersage über die Zeit, die benötigt wird, um 100 Bakterien in der Kultur zu haben.
# neues Modell
df$BakterienLog <- log(df$Bakterien)
fit <- lm(BakterienLog ~ Stunden, data=df)
a <- exp(fit$coefficients[1])
b <- fit$coefficients[2]
# Vorhersage für 100 Bakterien
(log(100) - log(a)) / b(Intercept)
5.256395 Nach ca 5.3 Stunden sind 100 Bakterien zu erwarten.
48.2 Lösung zur Aufgabe 44.4.2
a) Laden Sie den Datensatz
diet in Ihre R-Session.
# lade Datensatz
load(url("https://www.produnis.de/R/data/diet.RData"))
b) Erstellen Sie eine Punktwolke. Welche Art von Modell erklärt auf Grundlage der Punktwolke den Gewichtsverlust pro Diättag besser?
# plot()
plot(diet$days, diet$weight.loss)
# ggplot()
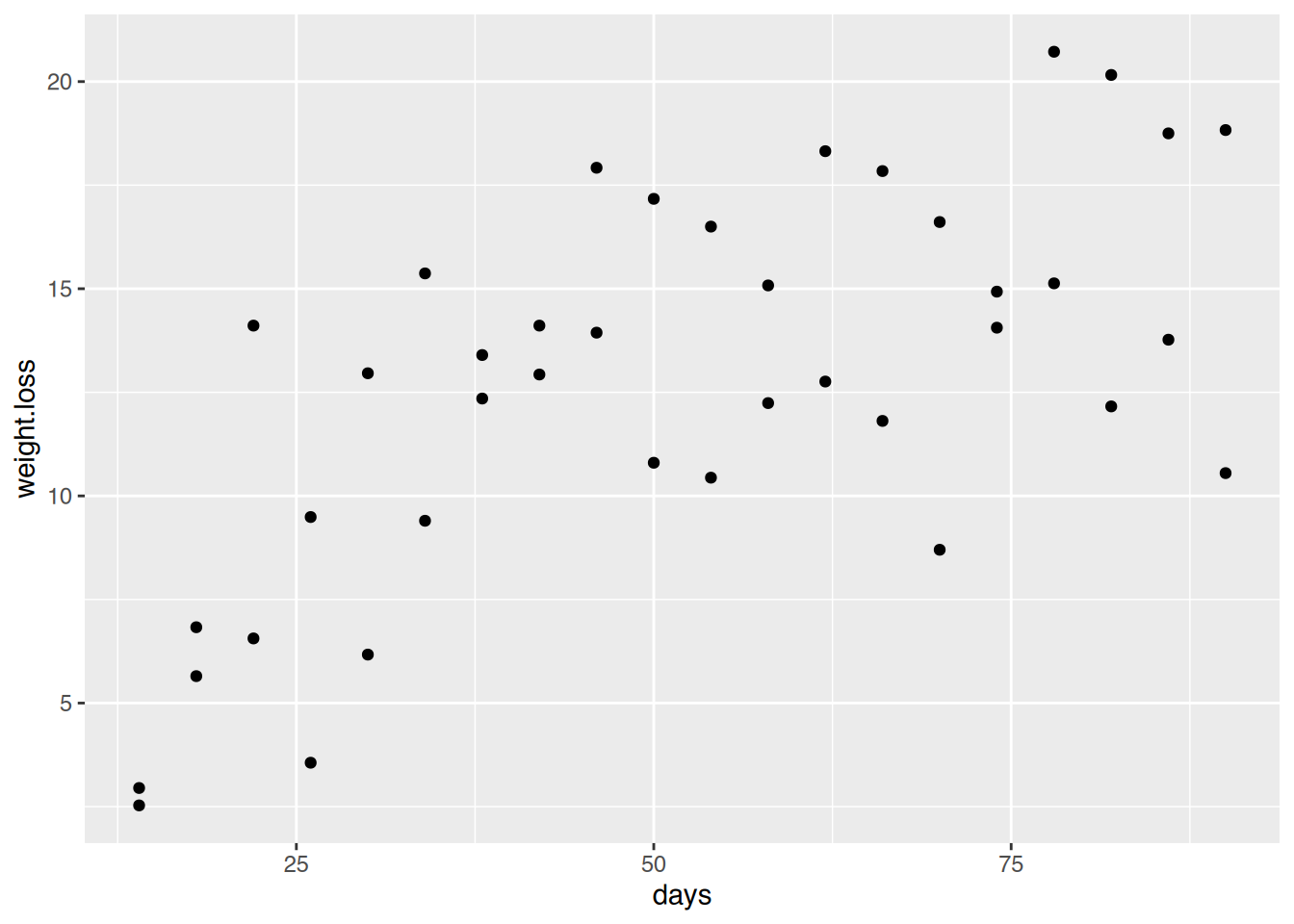
ggplot(diet, aes(x=days, y=weight.loss)) +
geom_point()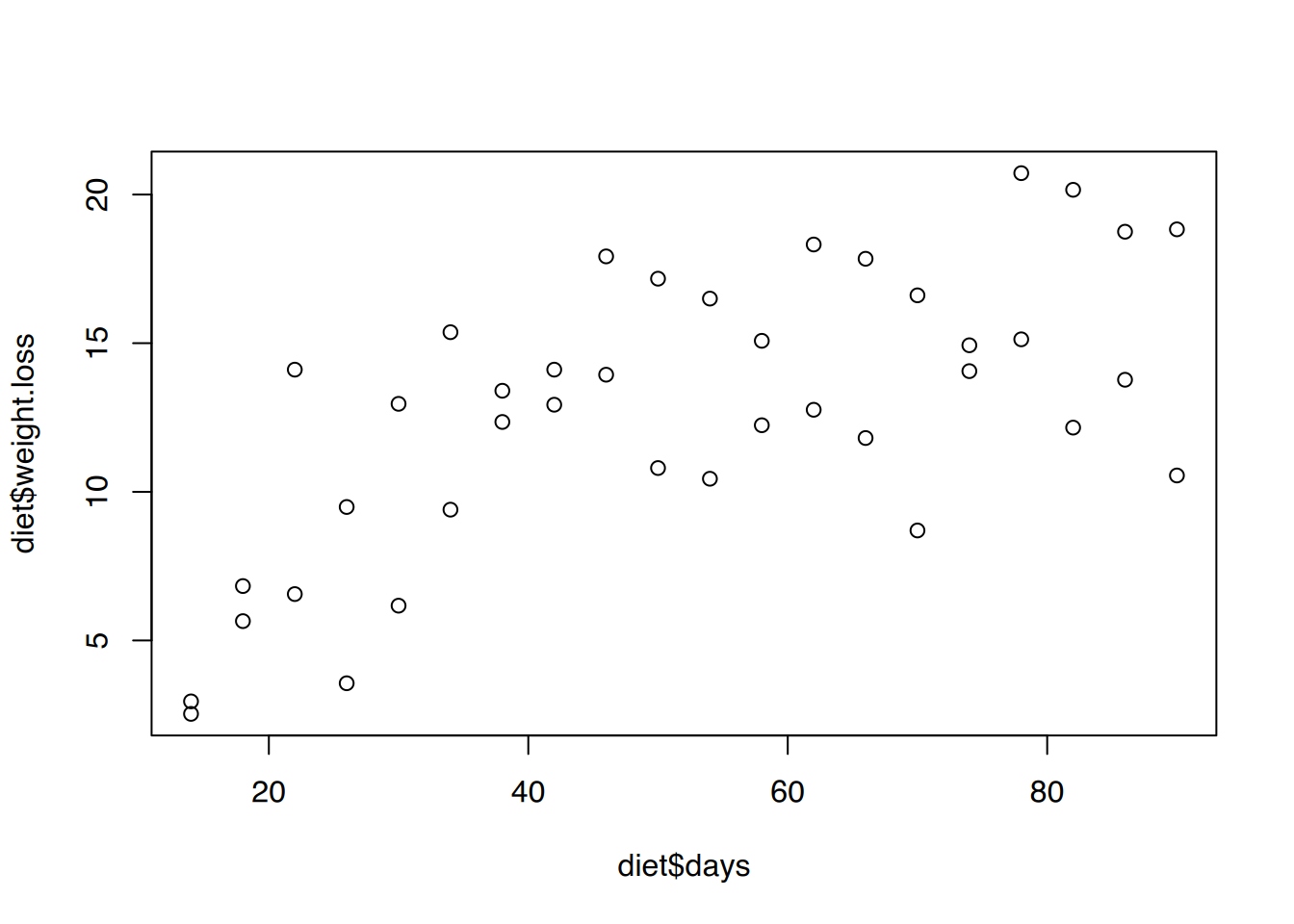
c) Berechnen Sie das Regressionsmodell, welches den Gewichtsverlust mit der Anzahl an Diättagen am besten (im Vergleich zu anderen) erklären kann. Wird das Modell zuverlässige Vorhersagen machen?
# Vergleiche Bestimmheitsmaße verschiedener Modelle
# quadratisches Modell
q <- lm(weight.loss ~ days + I(days^2), data=diet)
# exponentielles Modell
e <- lm (log(weight.loss) ~ days, data=diet)
# logarithmisches Modell
l <- lm(weight.loss ~ log(days), data=diet)
# sigmoidales Modell
s <- lm(log(weight.loss) ~ I(1/days), data=diet)
result <- data.frame(Modell = c("quadratisch", "exponentiell",
"logarithmisch", "sigmoidal"),
R.square = c(summary(q)$r.square,
summary(e)$r.square,
summary(l)$r.square,
summary(s)$r.square))
# Anzeigen
result[order(result$R.square, decreasing = TRUE),] Modell R.square
4 sigmoidal 0.6662170
1 quadratisch 0.5397848
3 logarithmisch 0.5254856
2 exponentiell 0.4308936## oder mit der compare.lm()-Funktion
jgsbook::compare.lm(diet$weight.loss, diet$days) Modell R.square
6 sigmoidal 0.6662170
7 potenz 0.5684490
3 kubisch 0.5584355
2 quadratisch 0.5397848
5 logarithmisch 0.5254856
1 linear 0.4356390
4 exponentiell 0.4308936Das sigmoidale Modell kann die Daten am besten erklären, da in diesem Modell das Bestimmtheitsmaß am größten ist.
d) Plotten Sie Ihr Modell.
# sigmoidales Modell
s <- lm(log(weight.loss) ~ I(1/days), data=diet)
# vorhersage vorbereiten
tage <- seq(min(diet$days), max(diet$days))
# alle "tage" vorhersagen
vorhersage <- predict(s, list(days=tage))
vorhersage[-1]=exp(vorhersage[-1])
# plot()
plot(diet$days, diet$weight.loss)
lines(tage, vorhersage, col="purple")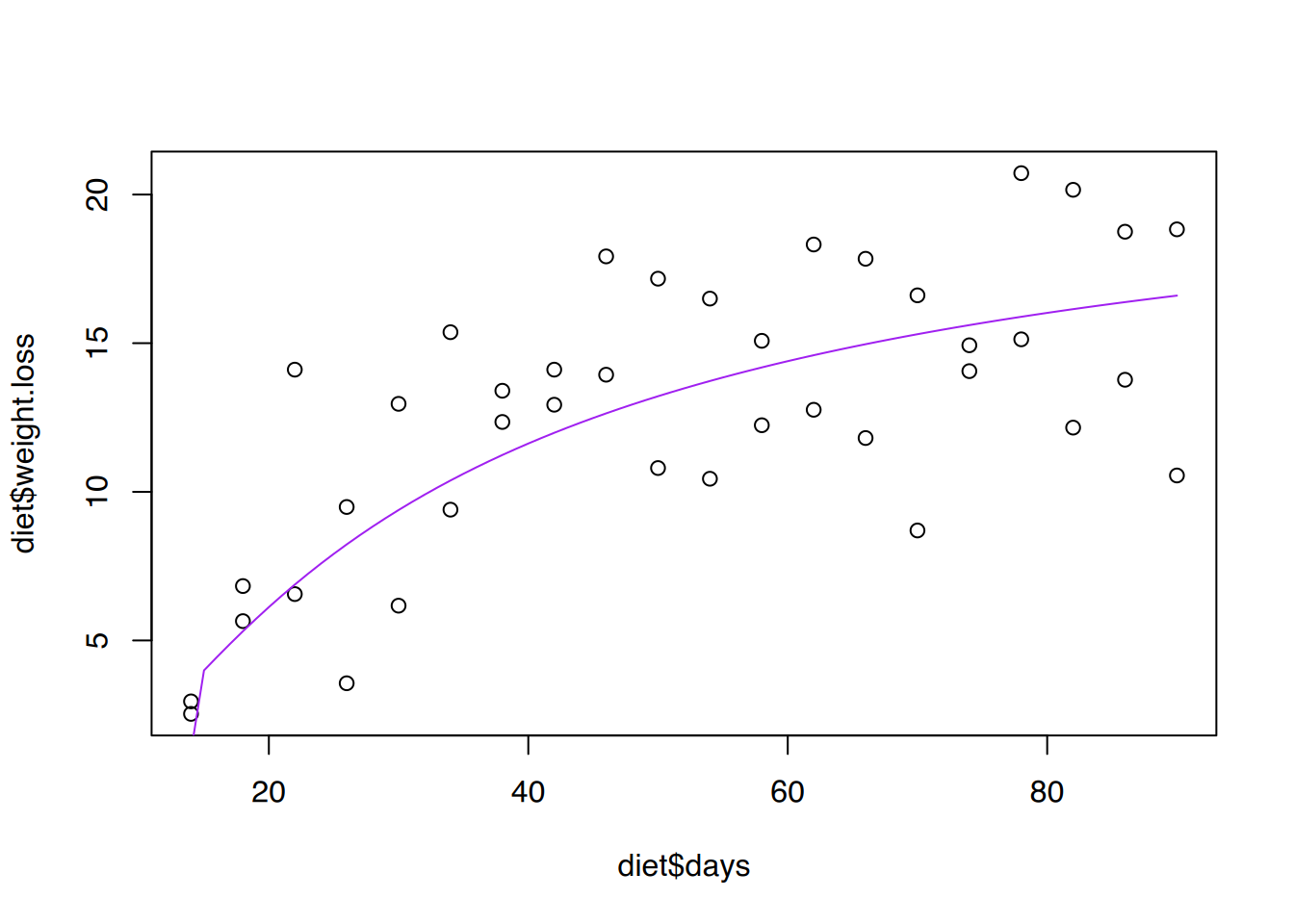
# ggplot()
# in Datenframe für ggplot speichern
helper <- data.frame(tage, vorhersage)
ggplot(diet, aes(x=days, y=weight.loss)) +
geom_point(color="#FF9999", size=3) +
# Legend
scale_linetype("Regression model") +
# Sigmoidal model
geom_line(data=helper, aes(x=tage, y=vorhersage, linetype="Sigmoidal"))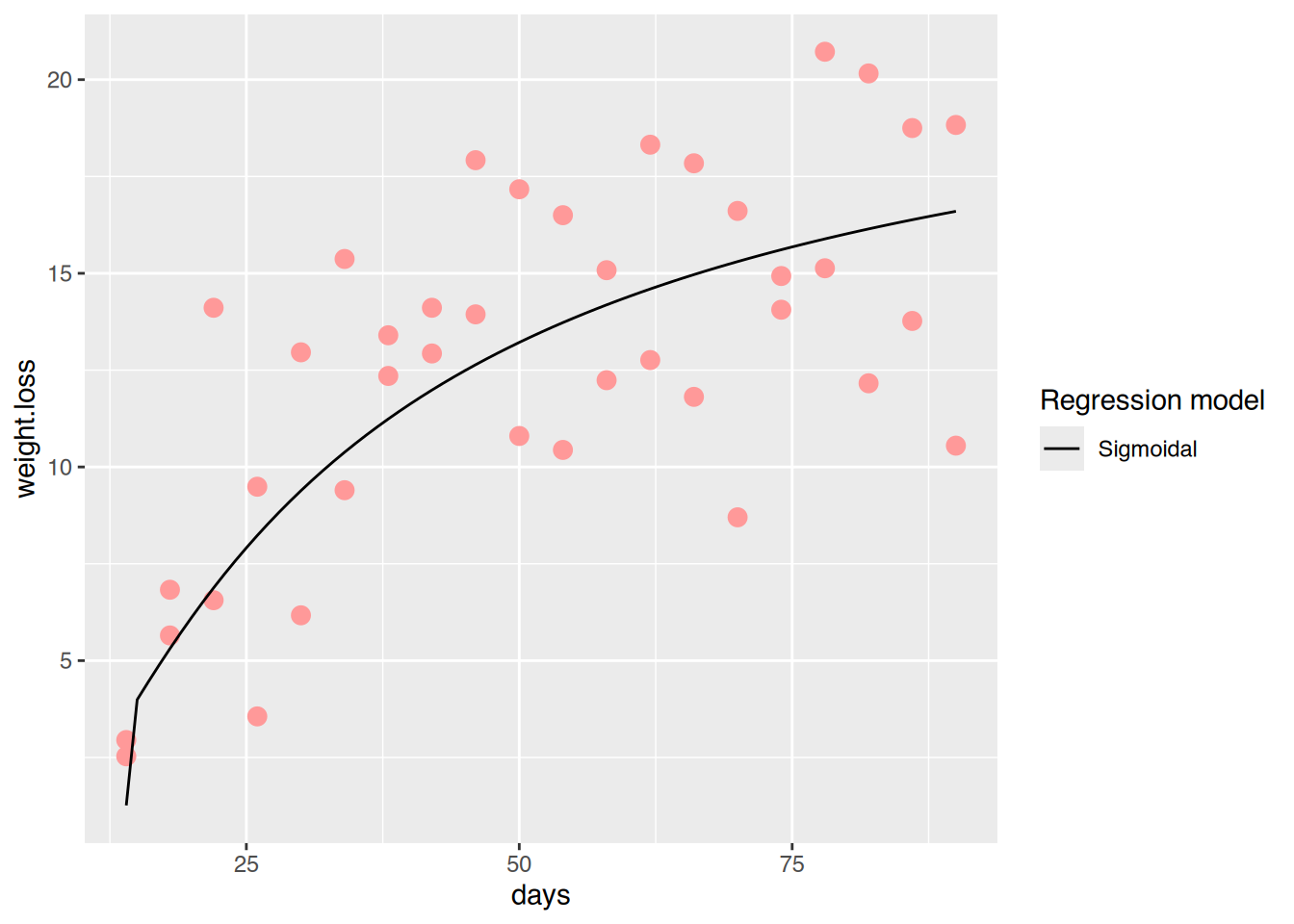
Auch die Vorhersagewerte für die Idealkurve können mittels compare.lm() und dem Parameter predict=TRUE erzeugt werden.
help <- jgsbook::compare.lm(diet$weight.loss, diet$days,
predict=TRUE)
# anschauen
head(help) pred.x line quad cube expo loga sigm power
1 14.00 7.645786 4.766305 3.526750 6.714088 5.166988 1.262199 4.966500
2 14.01 7.647113 4.770032 3.532726 6.715040 5.171506 3.537806 4.969006
3 14.02 7.648440 4.773757 3.538700 6.715992 5.176020 3.542430 4.971512
4 14.03 7.649767 4.777483 3.544671 6.716944 5.180531 3.547052 4.974018
5 14.04 7.651094 4.781207 3.550641 6.717896 5.185040 3.551675 4.976523
6 14.05 7.652422 4.784931 3.556608 6.718848 5.189544 3.556296 4.979027
logistic
1 4.261378
2 4.264669
3 4.267962
4 4.271256
5 4.274552
6 4.277850# plot()
plot(diet$days, diet$weight.loss)
lines(help$pred.x, help$sigm, col="purple")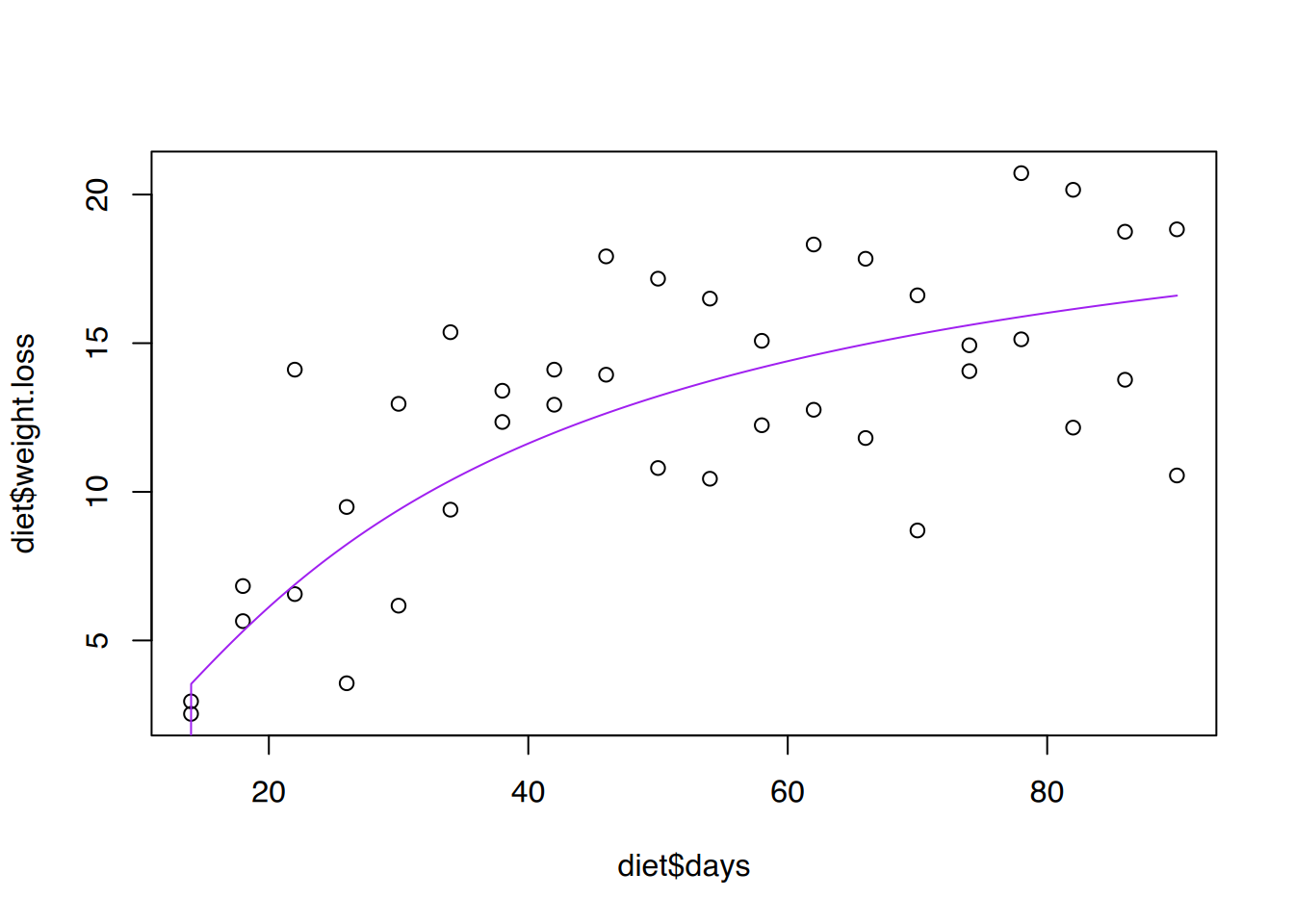
# ggplot()
ggplot(diet, aes(x=days, y=weight.loss)) +
geom_point(color="#FF9999", size=3) +
# Legend
scale_linetype("Regression model") +
# Sigmoidal model
geom_line(data=help, aes(x=pred.x, y=sigm, linetype="Sigmoidal"))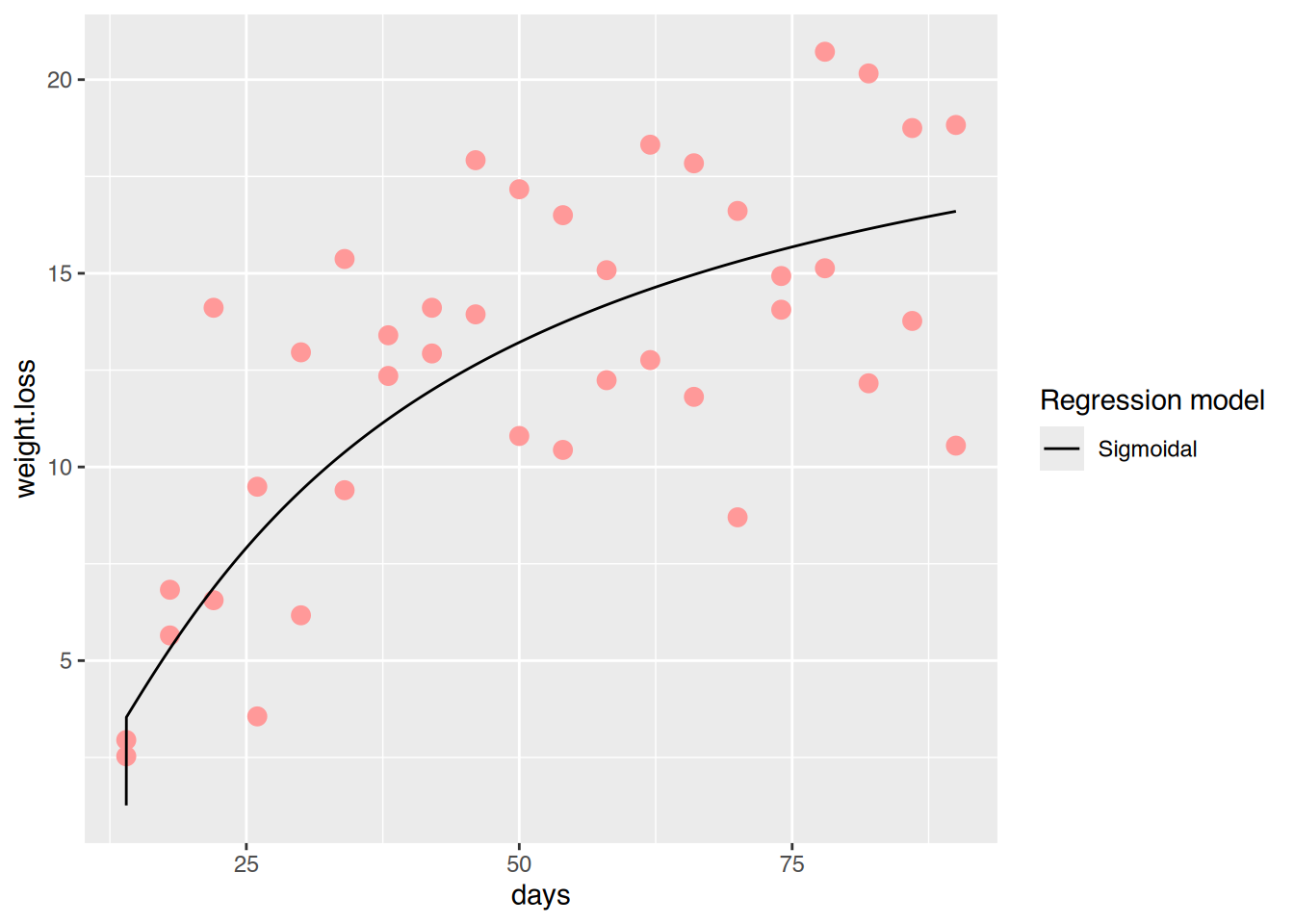
e) Berechnen Sie das Regressionsmodell, das den Gewichtsverlust anhand der Tage der Diät für die Gruppe der Personen, die sich nicht regelmäßig körperlich betätigen, am besten erklärt.
# Subset bilden
df1 <- subset(diet, exercise=="no")
# Vergleiche Bestimmheitsmaße verschiedener Modelle
# quadratisches Modell
q1 <- lm(weight.loss ~ days + I(days^2), data=df1)
# exponentielles Modell
e1 <- lm (log(weight.loss) ~ days, data=df1)
# logarithmisches Modell
l1 <- lm(weight.loss ~ log(days), data=df1)
# sigmoidales Modell
s1 <- lm(log(weight.loss) ~ I(1/days), data=df1)
result1 <- data.frame(Modell = c("quadratisch", "exponentiell",
"logarithmisch", "sigmoidal"),
R.square = c(summary(q1)$r.square,
summary(e1)$r.square,
summary(l1)$r.square,
summary(s1)$r.square))
result1[order(result1$R.square, decreasing = TRUE),] Modell R.square
4 sigmoidal 0.7401212
1 quadratisch 0.7100610
3 logarithmisch 0.6494521
2 exponentiell 0.5222832# oder mittels compare.lm()
jgsbook::compare.lm(df1$weight.loss, df1$days) Modell R.square
6 sigmoidal 0.7401212
3 kubisch 0.7151929
2 quadratisch 0.7100610
7 potenz 0.6700051
5 logarithmisch 0.6494521
1 linear 0.5286338
4 exponentiell 0.5222832Das sigmoidale Modell liefert wieder die beste Erklärung der Daten.
f) Wiederholen Sie die Analyse für die Gruppe, die sich regelmäßig körperlich betätigt.
# Subset bilden
df2 <- subset(diet, exercise=="yes")
# Vergleiche Bestimmheitsmaße verschiedener Modelle
# quadratisches Modell
q2 <- lm(weight.loss ~ days + I(days^2), data=df2)
# exponentielles Modell
e2 <- lm (log(weight.loss) ~ days, data=df2)
# logarithmisches Modell
l2 <- lm(weight.loss ~ log(days), data=df2)
# sigmoidales Modell
s2 <- lm(log(weight.loss) ~ I(1/days), data=df2)
result2 <- data.frame(Modell = c("quadratisch", "exponentiell",
"logarithmisch", "sigmoidal"),
R.square = c(summary(q2)$r.square,
summary(e2)$r.square,
summary(l2)$r.square,
summary(s2)$r.square))
result2[order(result1$R.square, decreasing = TRUE),] Modell R.square
4 sigmoidal 0.8305013
1 quadratisch 0.7791671
3 logarithmisch 0.7885173
2 exponentiell 0.4945564# oder mittels compare.lm()
jgsbook::compare.lm(df2$weight.loss, df2$days) Modell R.square
3 kubisch 0.8326179
6 sigmoidal 0.8305013
5 logarithmisch 0.7885173
2 quadratisch 0.7791671
7 potenz 0.6704843
1 linear 0.6623502
4 exponentiell 0.4945564Das kubische Modell liefert hier die beste Erklärung der Daten.
g) Benutzen Sie die erstellen Modelle, um den Gewichtsverlust nach 30 und nach 100 Tagen Diät für Personen, die sich körperlich betätigen, und für solche, die dies nicht tun, vorherzusagen. Sind diese Vorhersagen zuverlässig?
# Vorhersage Kein Sport
exp(predict(s1, list(days=c(30,100)))) 1 2
7.808926 13.806339 # Vorhersage Sport
exp(predict(s2, list(days=c(30,100)))) 1 2
11.28578 21.13143 48.3 Lösung zur Aufgabe 44.4.3
df <- data.frame(Stunden = c(2:8),
Konzentration = c(25, 36, 48, 64, 86, 114, 168))
a) Benutzen Sie ein exponentielles Modell, um die Konzentration nach 10 Stunden vorherzusagen. Ist die Vorhersage zuverlässig?
# exponentielles Modell
fit <- lm(log(Konzentration) ~ Stunden, data=df)
summary(fit)
Call:
lm(formula = log(Konzentration) ~ Stunden, data = df)
Residuals:
1 2 3 4 5 6 7
-0.023147 0.034218 0.014623 -0.004972 -0.016786 -0.042212 0.038276
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.627468 0.033673 78.03 6.55e-09 ***
Stunden 0.307277 0.006253 49.14 6.59e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.03309 on 5 degrees of freedom
Multiple R-squared: 0.9979, Adjusted R-squared: 0.9975
F-statistic: 2415 on 1 and 5 DF, p-value: 6.594e-08# Vorhersage 10 Stunden
exp(predict(fit, list(Stunden=10))) 1
298.94 Nach 10 Stunden beträgt die Konzentration 298,94 mg/dl.
Das Bestimmtheitsmaß R2 des Modells ist mit 0,9979 sehr groß. Die Daten werden sehr gut durch das Modell erklärt.
b) Benutzen Sie ein logarithmisches Modell um zu bestimmen, nach wie vielen Stunden eine Konzentration von 100 mg/dl erreicht sein wird.
# exponentielles Modell
fit <- lm(log(Konzentration) ~ Stunden, data=df)
# coefficienten
a <- fit$coefficient[1]
b <- fit$coefficient[2]
# Vorhersage 100 mg/dl
( log(100) - a ) / b(Intercept)
6.436209 Nach 6,436209 Stunden sind 100 mg/dl erreicht.