function(Parameter1, Parameter2, ...) {
FUNKTIONSWEISE
}19 Eigene Funktionen programmieren
In R lassen sich auch eigene Funktionen integrieren. Die wohl “einfachste” Methode hierbei ist, die Funktionen in der R-Sprache selber zu schreiben. Es besteht aber auch die Möglichkeit, neue Funktionen in Programmiersprachen wie z.B. C++ zu programmieren.
Zum Erstellen einer eigenen Funktion steht der Befehl function() zur Verfügung. Dieser ist wie folgt aufzurufen:
In den Klammern direkt nach function können Parameter benannt werden, welche dann beim Funktionsaufruf der Funktion zur Verfügung stehen. Innerhalb der geschweiften Klammern wird die eigentliche Funktionsweise geschrieben.
Um eine neue Funktion in R aufrufen zu können, wird die Funktionsweise einem neuen Objekt (z.b. myfunc) zugeordnet.
myfunc <- function(x,y){ # Neue Funktion mit den Parametern x und y
z <- x+y # Die Summe von x und y wird in z gespeichert
return(z) # z wird zurückgemeldet
}Der obigen Dummy-Funktion werden im Funktionsaufruf die Parameter x und y übergeben. Innerhalb der Funktion wird die Summe aus x und y gebildet, und per return() an die R-Konsole zurückgemeldet. Jetzt können wir diese Funktion aufrufen:
myfunc(4,6)## [1] 10Es besteht ferner die Möglichkeit, Standardwerte für die Parameter zu setzen, welche verwendet werden, falls der Funktionsaufruf ohne Parameter erfolgt.
myfunc <- function(x=3,y=7){ # Neue Funktion mit Standardwerten für die Parameter x und y
z <- x+y # Die Summe von x und y wird in z gespeichert
return(z) # z wird zurückgemeldet
}Rufen wird die Funktion ohne Parameter auf, so werden die Standardwerte genutzt.
# Funktionsaufruf OHNE Parameter
myfunc()## [1] 10Rufen wir die Funktion mit Parametern auf, werden diese verwendet.
myfunc(12,4)## [1] 1619.1 Beispiele
Alle Funktionen (und Datensätze) dieses Lehrbuches sind auch im Zusatzpaket jgsbook enthalten (siehe Abschnitt 16.1).
19.1.1 z-Transformation
Zwar ist in R bereits die Funktion scale() integriert, aber zu edukativen Zwecken programmieren wir unsere eigene Funktion ztrans().
Mit dieser Funktion wird die z-Transformation für gegebene Werte errechnet. Die Funktion folgt der Formel
\(z_{i} = \frac{x_{i}-\mu}{\sigma}\)
Als Standardparameter werden die Werte der Standardnormalverteilung gesetzt.
ztrans <- function(x, mu=0, sd=1){
z = (x-mu)/sd
return(z)
}# x ist 120, aus einer normalverteilten Reihe mit
# Mittelwert 118 und Standardabweichung 20
ztrans(120,mu=118,sd=20)## [1] 0.119.1.2 Sensitivität
Die folgende Funktion errechnet Sensitivität, Spezifität sowie positiv- und negativ-prädiktive Werte für gegebene Werte.
sens.spec <- function(rp, rn, fp, fn){
x <- data.frame(
sens=round(rp/(rp+fn)*100, 2),
spec=round(rn/(rn+fp)*100, 2),
ppw =round(rp/(rp+fp)*100, 2),
npw =round(rn/(rn+fn)*100, 2)
)
return(x)
}Die zu übergebenden Parameter sind
rp= Anzahl richtig positivern= Anzahl richtig negativefp= Anzahl falsch positivefn= Anzahl falsch negative
sens.spec(40, 17, 85, 4)## sens spec ppw npw
## 1 90.91 16.67 32 80.9519.1.3 Kenngrößen
Die folgende Funktion gibt die gebräuchlichsten Kenngrößen einer Wertereihe zurück:
kenngroessen <- function(werte){
bla <- data.frame(0)
bla$modus=paste(as.character(statip::mfv(werte)), collapse="|")
bla$mean=mean(werte, na.rm=T)
bla$median=median(werte, na.rm=T)
bla$p25=quantile(werte,0.25,type=6)
bla$p75=quantile(werte,0.75,type=6)
bla$iqr=IQR(werte,type=6)
bla$sd=sd(werte, na.rm=T)
bla$var=var(werte, na.rm=T)
bla$VK= (sd(werte, na.rm=T)/mean(werte,na.rm=T))
return(bla[-1])
}# erzeuge zufällige Werte
x <- ceiling(rnorm(100, 10,5))
# Kenngrößen anzeigen
kenngroessen(x)## modus mean median p25 p75 iqr sd var VK
## 1 9 10.84 11 9 14 5 5.304315 28.13576 0.48932819.1.4 Häufigkeitstabellen
Die folgende Funktion gibt eine vollständige Häufigkeitstabelle mit absoluten und relativen Häufigkeiten sowie kummulierten Werten zurück.
freqTable <- function(werte){
x <- table(werte)
tabelle <- data.frame(x)
tabelle$freqcum <- cumsum(x)
tabelle$relfreq <- round(x/length(werte)*100,2)
tabelle$relcum <- cumsum(round(x/length(werte)*100,2))
colnames(tabelle) <- c("Wert", "Häufig", "Hkum", "Relativ", "Rkum")
tabelle$Wert <- as.numeric(as.vector(tabelle$Wert))
return(tabelle)
}x <- ceiling(rnorm(13, 10,2))
freqTable(x)## Wert Häufig Hkum Relativ Rkum
## 1 7 1 1 7.69 7.69
## 2 8 2 3 15.38 23.07
## 3 9 5 8 38.46 61.53
## 4 10 2 10 15.38 76.91
## 5 11 2 12 15.38 92.29
## 6 12 1 13 7.69 99.9819.2 Bedingungen
Innerhalb der Funktion können Variablenbedingungen mit dem if()-Befehl abgefragt werden. Der Aufruf erfolgt etwa so:
if(VARIABLENBEDINGUNG) {FUNKTIONSWEISE}Innerhalb der Klammern des if()-Befehls werden die Variablenbedingungen gesetzt. Falls diese Bedingungen erfüllt sind, wird der Code innerhalb der geschweiften Klammern ausgeführt. Folgende Bedingungen können abgefragt werden
| Zeichen | Bedingung |
|---|---|
| == | gleich |
| != | ungleich |
| < | kleiner |
| <= | kleiner-gleich |
| > | größer |
| >= | größer-gleich |
| & | UND |
| | | ODER |
Innerhalb von Funktionen kann man dies wie folgt anwenden
myfunc <- function(x=3,y=7){
z <- x+y # Die Summe von x und y wird in z gespeichert
if(z>20) { # Abfrage, ob die Summer größer als 20 ist
z <- "wow, bist du gross" # wenn ja, dann schreibe einen Text in das Objekt z
}
return(z) # z wird zurückgemeldet
}Mehrere Bedingungen können verknüpft werden, z.B. so:
myfunc <- function(x=3,y=7){
if(x<0 & y<0) { # Abfrage, ob x und y negativ sind
x <- x*(-1) # wenn ja, dann mache beide positiv
y <- y*(-1)
}
z <- x+y # Die Summe von x und y wird in z gespeichert
if(z==0 | z>50) { # Abfrage, ob z gleich 0 oder größer 50 ist
z <- "Summe ist 0 oder größer 50" # wenn ja, schreibe einen Text...
}
return(z) # z wird zurückgemeldet
}19.2.1 Beispiel Zusatzpakete
Die folgende Funktion installiert die vorgegebenen Pakete, sofern sie noch nicht installiert sind. Dies ist hilfreich, wenn z.B. auf eine höhere R-Version geupdatet wurde, und alle Zusatzpakete neu installiert werden müssen.
install.my.packages <- function(){
# Liste meiner favorisierten Pakete
my_packages <- c("blogdown", "bookdown",
"car",
"foreign",
"gghighlight", "ggplot2",
"haven",
"likert",
"prettyR", "psych",
"reshape", "reshape2",
"samplingbook", "scales", "statip",
"tidyverse",
"VGAM",
"xtable"
)
#--------------
# Überprüfe, ob die Pakete bereits installiert sind
not_installed <- my_packages[!(my_packages %in% installed.packages()[ , "Package"])]
# installiere solche, die noch nicht installiert sind
if(length(not_installed)) install.packages(not_installed, dependencies = TRUE)
return(paste(length(not_installed), "Pakete wurden installiert (plus dependencies)."))
}Die Funktion kann dann wie folgt aufgerufen werden:
install.my.packages()Bei mir ist alles up-to-date, so dass kein Paket installiert werden muss.
Mit einer leichten Änderung können weitere Pakete an den Parameter p übergeben werden:
install.my.packages <- function(p=""){
# Liste meiner favorisierten Pakete
my_packages <- c("blogdown", "bookdown",
"car",
"foreign",
"gghighlight", "ggplot2",
"haven",
"likert",
"prettyR", "psych",
"reshape", "reshape2",
"samplingbook", "scales", "statip",
"tidyverse",
"VGAM",
"xtable"
)
# Falls Pakete über den Parameter "p" übergeben wurden,
# füge sie der Liste hinzu
if(p!=""){
my_packages <- c(p, my_packages)
}
#--------------
# Überprüfe, ob die Pakete bereits installiert sind
not_installed <- my_packages[!(my_packages %in% installed.packages()[ , "Package"])]
# installiere solche, die noch nicht installiert sind
if(length(not_installed)) install.packages(not_installed, dependencies = TRUE)
return(paste(length(not_installed), "Pakete wurden installiert (plus dependencies)."))
}Der Funktion kann so ein Vektor weiterer Pakete übergeben werden, die zusätzlich zur vorgegebenen Liste installiert werden, falls sie noch nicht installiert sind:
install.my.packages(c("ggpubr", "qqplotr"))[1] "2 Pakete wurden installiert (plus dependencies)."19.2.2 Beispiel verschiedene lineare Modelle vergleichen
Wir programmieren eine Funktion, welche verschiedene lineare Modelle vergleicht. Hierbei sollen die Modelle mittels Bestimmtheitsmaß (R2) verglichen werden, und auf Wunsch können Vorhersagewerte erzeugt werden.
compare.lm <- function(dep, ind, predict=FALSE, steps=0.01){
# erzeuge lineares Modell
lin <- lm(dep ~ ind)
# erzeuge quadratisches Modell
q <- lm(dep ~ ind + I(ind^2))
# erzeuge kubisches Modell
c <- lm(dep ~ ind + I(ind^2) + I(ind^3))
# erzeuge exponentielles Modell
e <- lm(log(dep) ~ ind)
# erzeuge logarithmisches Modell
l <- lm(dep ~ log(ind))
# erzeuge sigmoidales Modell
s <- lm(log(dep) ~ I(1/ind))
# erzeuge Potenzmodell
p <- lm(log(dep) ~ log(ind))
# Speichere die R²-Ergebnisse in einem Datenframe
result <- data.frame(Modell = c("linear", "quadratisch", "kubisch", "exponentiell",
"logarithmisch", "sigmoidal", "potenz"),
R.square = c(summary(lin)$r.squared,
summary(q)$r.squared,
summary(c)$r.squared,
summary(e)$r.squared,
summary(l)$r.squared,
summary(s)$r.squared,
summary(p)$r.squared))
# Sollen Vorhersagewerte erzeugt werden?
if(predict==TRUE){
# x-Werte
pred.x <- seq(min(ind), max(ind), steps)
# lineare Vorhersagewerte
pred.lin <- predict(lin, list(ind=pred.x))
# quadratische Vorhersagewerte
pred.q <- predict(q, list(ind=pred.x))
# kubische Vorhersagewerte
pred.c <- predict(c, list(ind=pred.x))
# exponentielle Vorhersagewerte
pred.e <- exp(predict(e, list(ind=pred.x)))
# logarithmische Vorhersagewerte
pred.l <- predict(l, list(ind=pred.x))
# sigmoidale Vorhersagewerte
pred.s <- predict(s, list(ind=pred.x))
pred.s[-1] <- exp(pred.s[-1])
# potenzvorhersagewerte
pred.p <- exp(predict(p, list(ind=pred.x)))
# Vorhersagewerte zurückgeben
return(data.frame(x = pred.x,
line = pred.lin,
quad = pred.q,
cube = pred.c,
expo = pred.e,
loga = pred.l,
sigm = pred.s,
power = pred.p))
} else {
return(result[order(result$R.square, decreasing = TRUE),])
}
}Probieren wir die Funktion aus:
# Dummy-Daten
x <- c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60)
y <- c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27)
# Modellvergleich
compare.lm(y, x)## Modell R.square
## 3 kubisch 0.97480010
## 2 quadratisch 0.96019615
## 6 sigmoidal 0.47930323
## 7 potenz 0.26118539
## 5 logarithmisch 0.18835564
## 4 exponentiell 0.08309738
## 1 linear 0.04459826# Vorhersagewerte
head(compare.lm(y, x, predict=TRUE))## x line quad cube expo loga sigm power
## 1 6.00 50.24169 18.56932 13.44564 39.81109 36.63143 2.949079 28.94804
## 2 6.01 50.24467 18.62461 13.51854 39.81464 36.65621 19.134154 28.96656
## 3 6.02 50.24765 18.67988 13.59140 39.81820 36.68095 19.179906 28.98506
## 4 6.03 50.25063 18.73513 13.66423 39.82175 36.70564 19.225615 29.00354
## 5 6.04 50.25361 18.79036 13.73702 39.82530 36.73029 19.271282 29.02200
## 6 6.05 50.25660 18.84557 13.80977 39.82885 36.75491 19.316905 29.04044Mit den Vorhersagedaten können alle Modelle in eine Punktwolke geplottet werden.
df <- compare.lm(y, x, predict=TRUE)
ggplot(df) +
scale_linetype("Regression model") +
geom_line(aes(x=x, y=line, linetype="lineal"), col="blue") +
geom_line(aes(x=x, y=quad, linetype="quadratisch"), col="skyblue") +
geom_line(aes(x=x, y=expo, linetype="exponential"), col="seagreen") +
geom_line(aes(x=x, y=loga, linetype="logarithmisch"), col="coral") +
geom_line(aes(x=x, y=sigm, linetype="sigmoidal"), col="violet") +
geom_line(aes(x=x, y=cube, linetype="kubisch"), col="burlywood") +
geom_line(aes(x=x, y=power, linetype="potenz"), col="maroon") 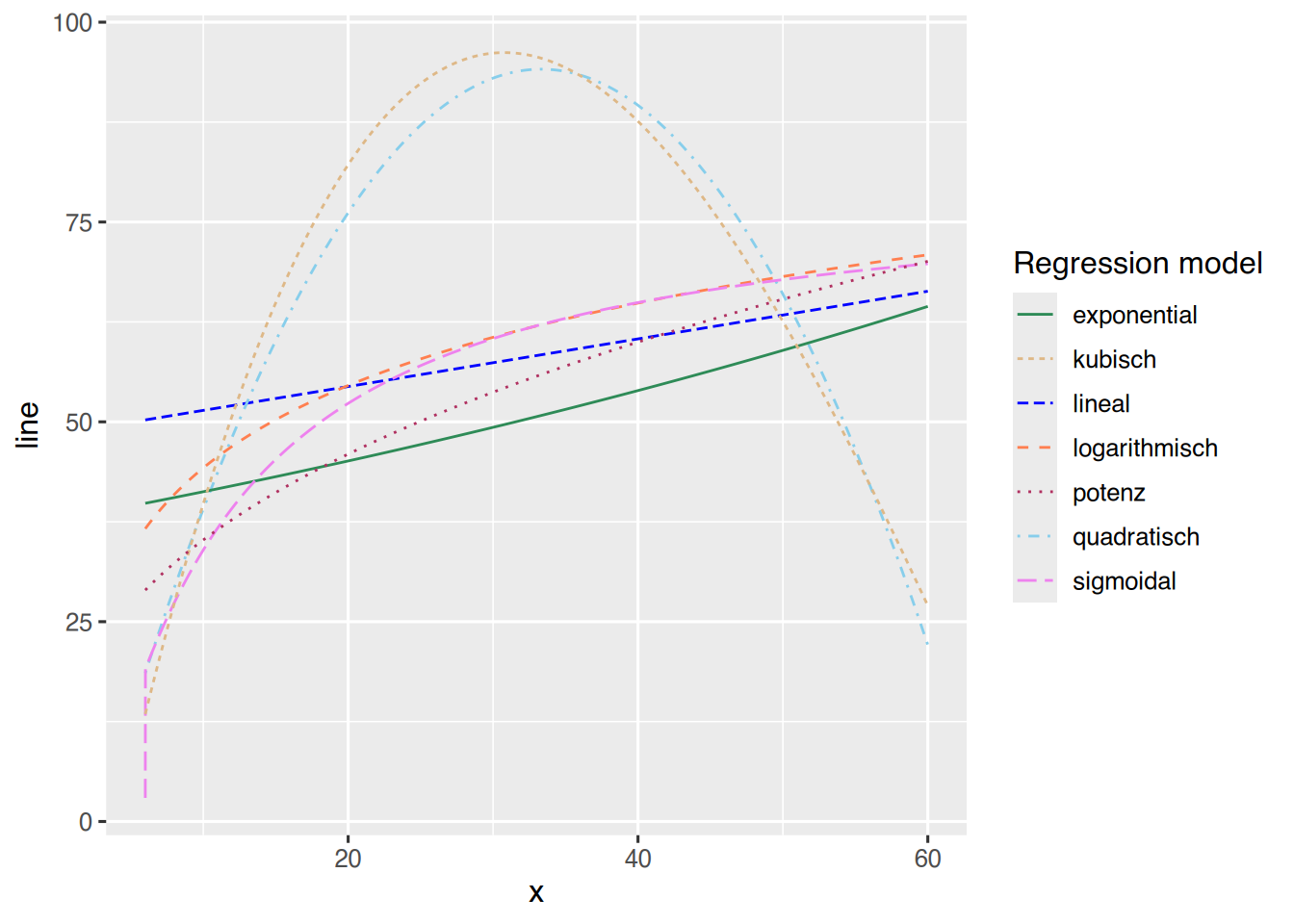
Die Funktion ist auch im jgsbook Zusatzpaket enthalten.
19.3 Funktionen in Dateien speichern
Eigene Funktionen sind Objekte wie alle anderen Variablen im Workspace. Wenn sie nicht abgespeichert werden, stehen Sie u.U. nach einem Neustart (oder wenn der Workspace überschrieben oder geleert wird) nicht mehr zur Verfügung.
Es bietet sich an, die eigenen Funktionen in einer .R-Datei zu speichern. Mit dem source()-Befehl kann die Datei dann in neuen Projekten eingelesen werden, und die Funktionen stehen zur Verfügung.
source("/Pfad/zu/MeineFunktionen.R")