# erzeuge Datenframe
df <- data.frame(Kinder = c(1, 2, 4, 2, 2, 2, 3, 2, 1, 1, 0, 2, 2, 0,
2, 2, 1, 2, 2, 3, 1, 2, 2, 1, 2))45 Lösungen Häufigkeitsverteilungen
Hier finden Sie die Lösungen zu den Übungsaufgaben von Kapitel 44.
Die hier vorgestellten Lösungen stellen immer nur eine mögliche Vorgehensweisen dar und sind sicherlich nicht der Weisheit letzter Schluss. In R führen viele Wege nach Rom, und wenn Sie mit anderem Code zu den richtigen Ergebnissen kommen, dann ist das völlig in Ordnung.
45.1 Lösung zur Aufgabe 44.1.1
a) Erstellen Sie ein Datenframe mit der Variable
Kinder und übertragen Sie die Daten.
b) Erzeugen Sie eine einfache Häufigkeitstabelle
# erzeuge Datenframe
table(df$Kinder)
0 1 2 3 4
2 6 14 2 1 # oder
xtabs(~Kinder, data=df)Kinder
0 1 2 3 4
2 6 14 2 1
c) Erzeugen Sie ein Balkendiagramm der Häufigkeiten
# Balkendiagramm mit R-Base
barplot(table(df$Kinder), col="skyblue", xlab="Anzahl Kinder")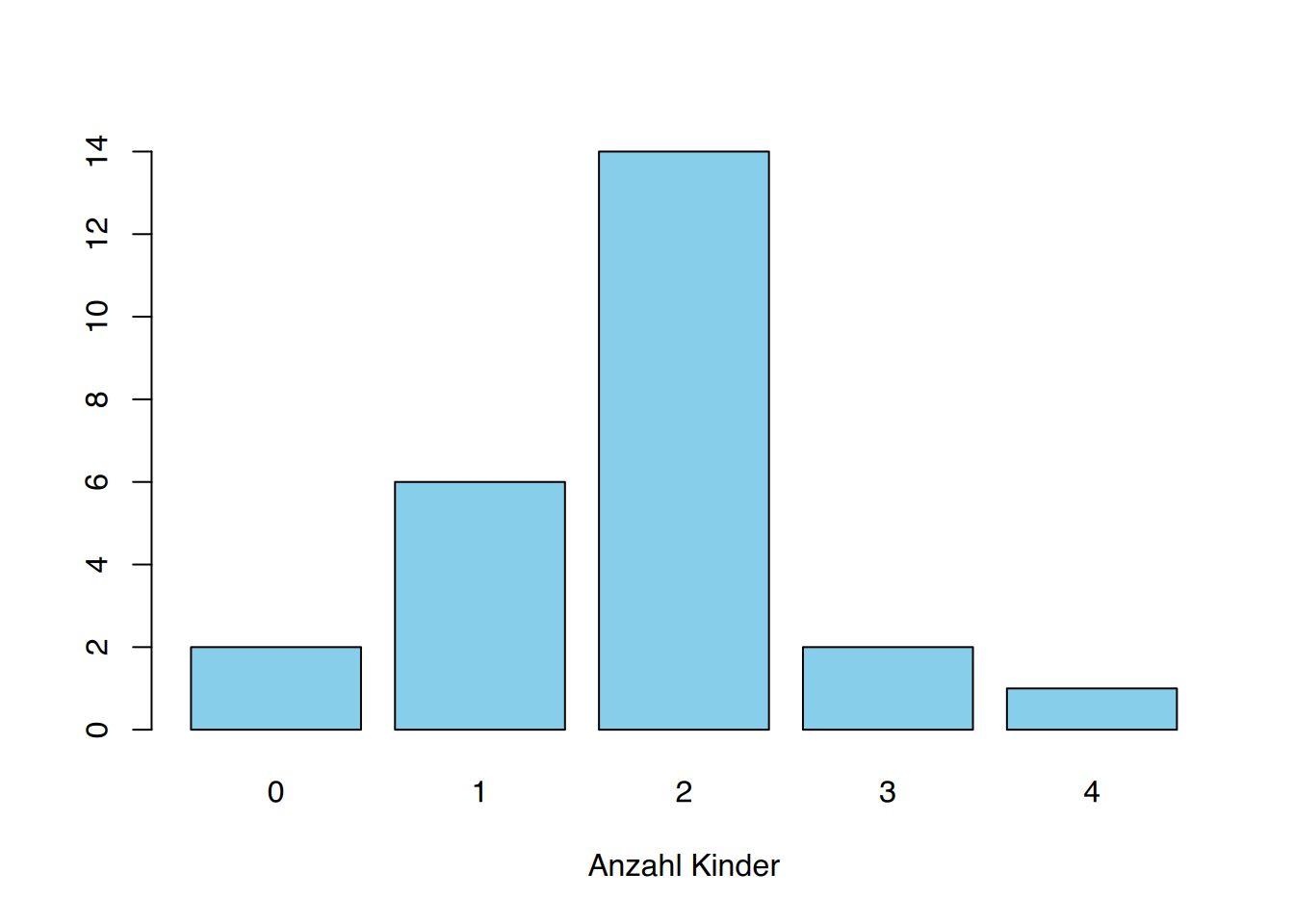
# mit ggplot
ggplot(df, aes(x=Kinder)) +
geom_bar(fill="skyblue", color="black")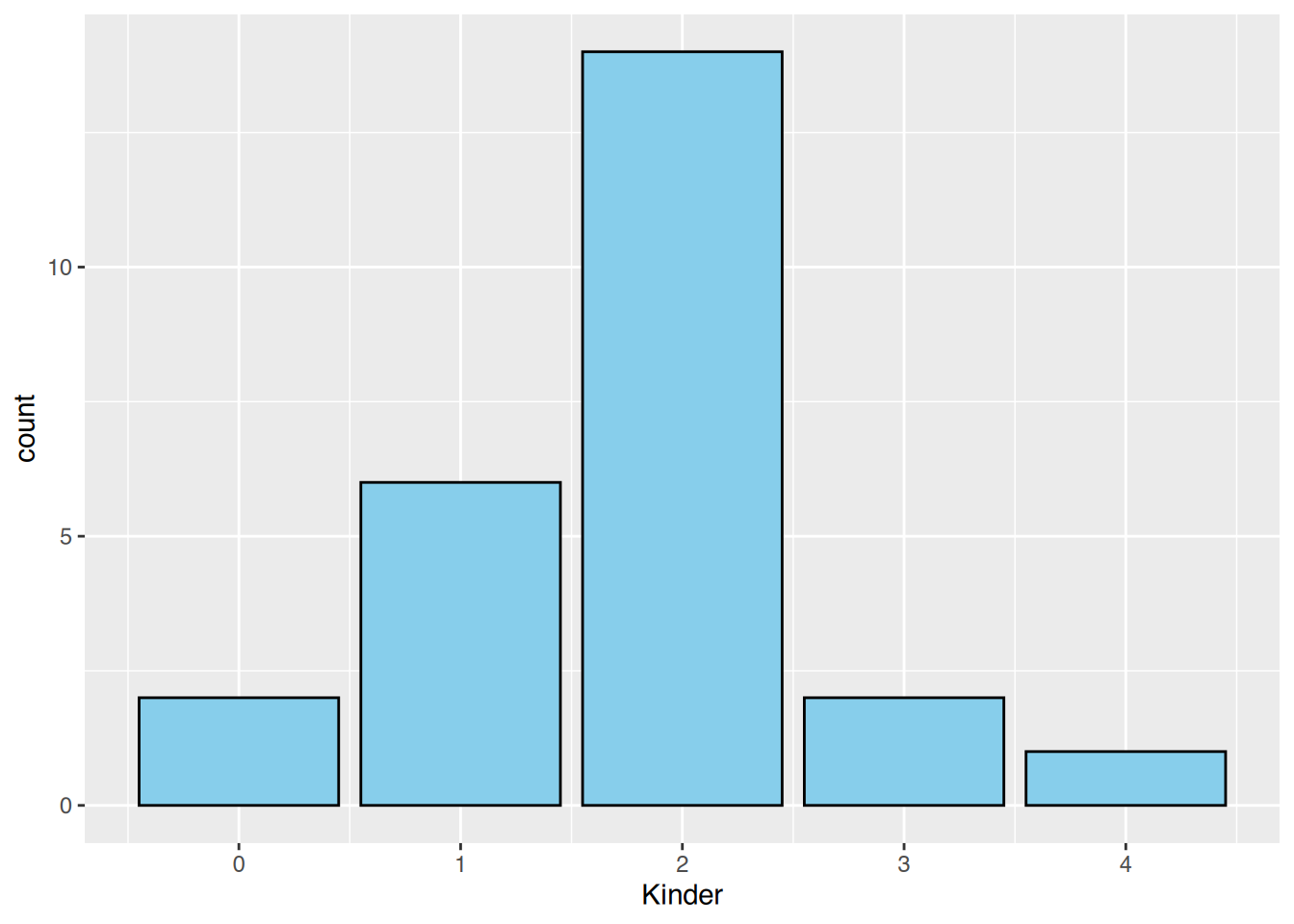
d) Erzeugen Sie eine vollständige Häufigkeitstabelle, inklusive absoluter, relativer und jeweils kumulativer Häufigkeiten
## zu Fuß
# kumulierte absoulte Häufigkeiten
cumsum(table(df$Kinder)) 0 1 2 3 4
2 8 22 24 25 # relative Häufigkeiten
(table(df$Kinder)/length(df$Kinder))*100
0 1 2 3 4
8 24 56 8 4 # kumulierterelative Häufigkeiten
cumsum(table(df$Kinder)/length(df$Kinder))*100 0 1 2 3 4
8 32 88 96 100 ## einfacher
# erzeuge vollständige Häufigkeitstabelle
jgsbook::freqTable(df$Kinder) Wert Haeufig Hkum Relativ Rkum
1 0 2 2 8 8
2 1 6 8 24 32
3 2 14 22 56 88
4 3 2 24 8 96
5 4 1 25 4 10045.2 Lösung zur Aufgabe 44.1.2
a) Erstellen Sie ein Datenframe mit der Variable
Patienten und übertragen Sie die Daten.
# erzeuge Datenframe
df <- data.frame(Patienten = c(15, 23, 12, 10, 28, 50, 12, 17, 20,
21, 18, 13, 11, 12, 26, 30, 6, 16,
19, 22, 14, 17, 21, 28, 9, 16, 13,
11, 16, 20))
b) Erzeugen Sie ein Boxplot und entfernen Sie etwaige Ausreißer.
# Boxplot mit Rbase
boxplot(df$Patienten, col="seagreen3", ylab="Anzahl Patienten")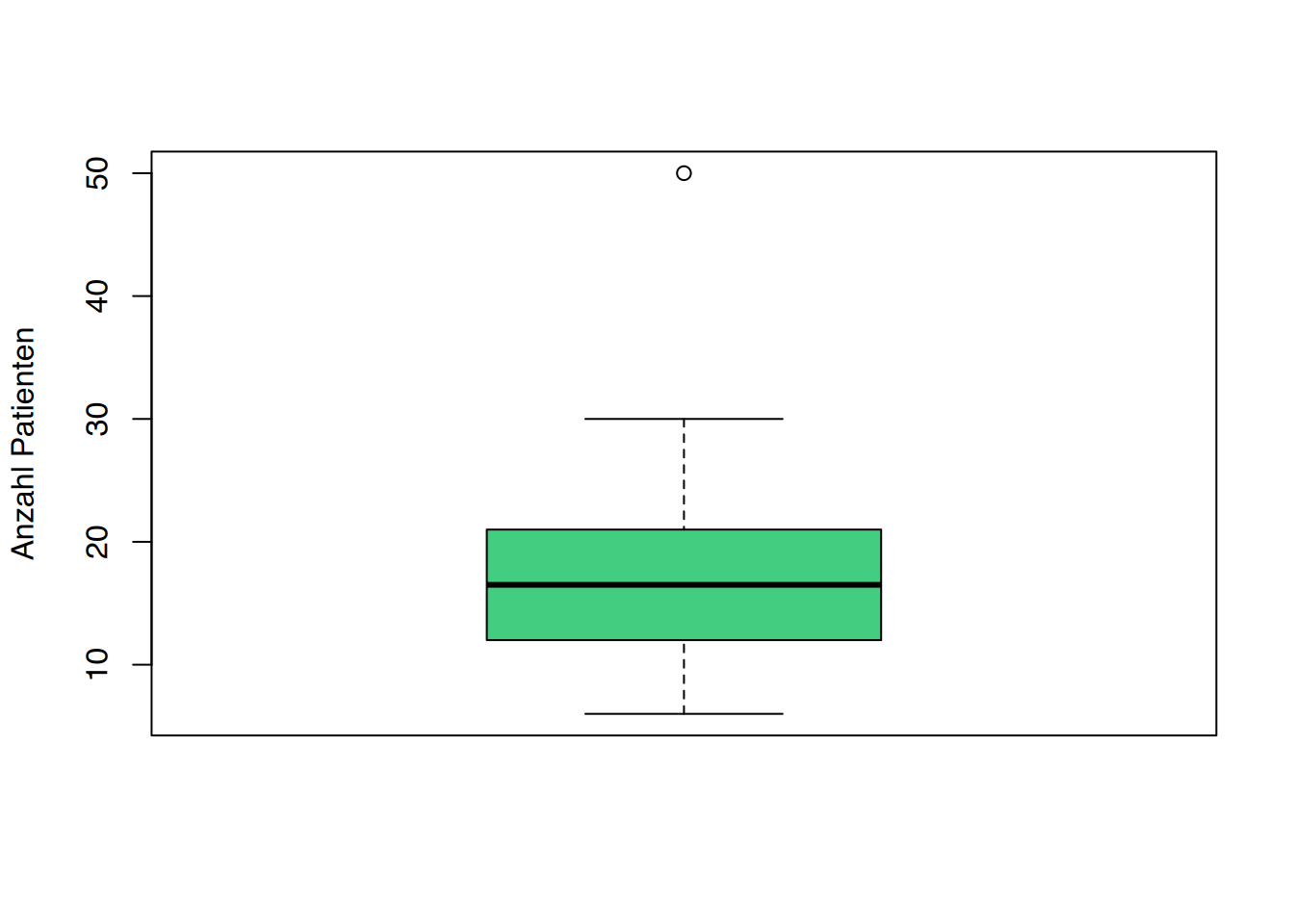
# Boxplot mit ggplot
ggplot(df, aes(y=Patienten)) +
geom_boxplot(fill="seagreen3") +
# whiskers
stat_boxplot(geom="errorbar") +
theme(axis.ticks.x=element_blank(),
axis.text.x=element_blank())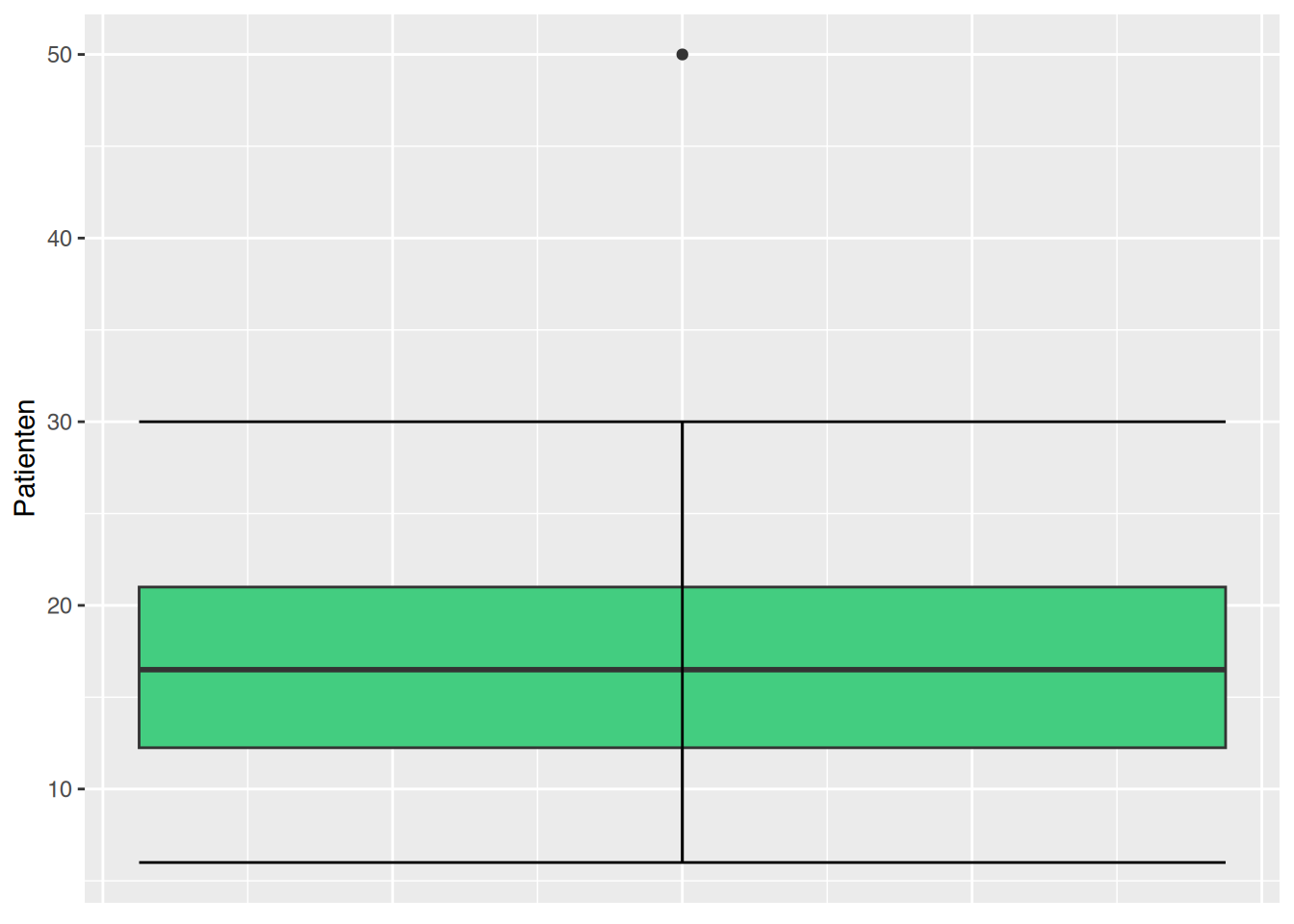
Es ist ein Ausreißer enthalten.
# entferne Ausreißer für weiteres Vorgehen
df <- subset(df, Patienten < 50)
c) Erzeugen Sie eine Häufigkeitstabelle, welche die Daten in 5 Klassen gruppiert.
# klassiere in 5 Gruppen
gruppen <- cut(df$Patienten, breaks = 5, ordered_result = TRUE)
# Häufigkeitstabelle
table(gruppen)gruppen
(5.98,10.8] (10.8,15.6] (15.6,20.4] (20.4,25.2] (25.2,30]
3 9 9 4 4
d) Erzeugen Sie ein Histogram der klassierten absoluten Häufigkeiten.
# Histogram mit Rbase
hist(df$Patienten, col="pink")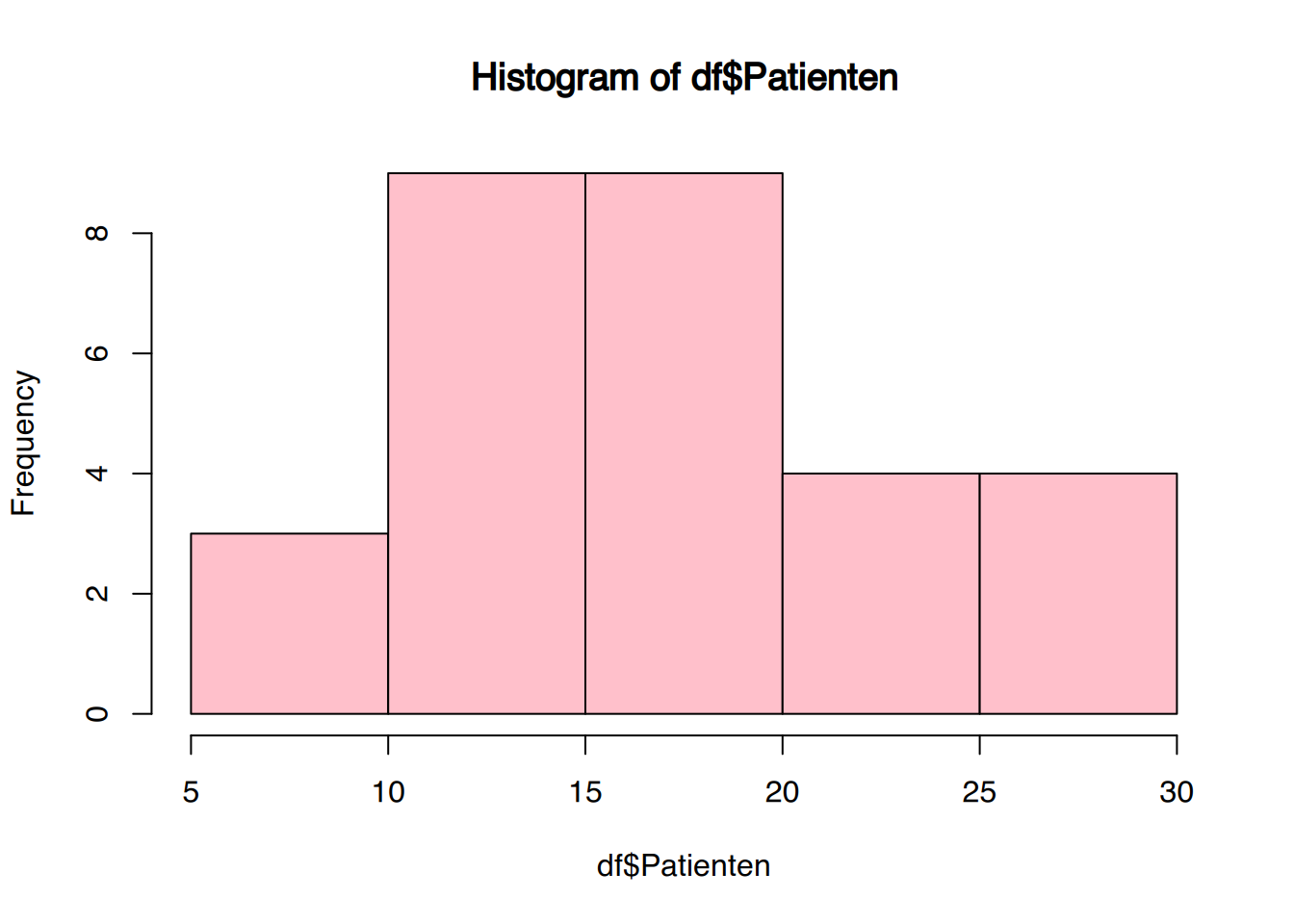
# mit ggplot werden andere Breaks erzeugt
ggplot(df, aes(x=Patienten)) +
geom_histogram(fill="pink", color="black",
bins=5)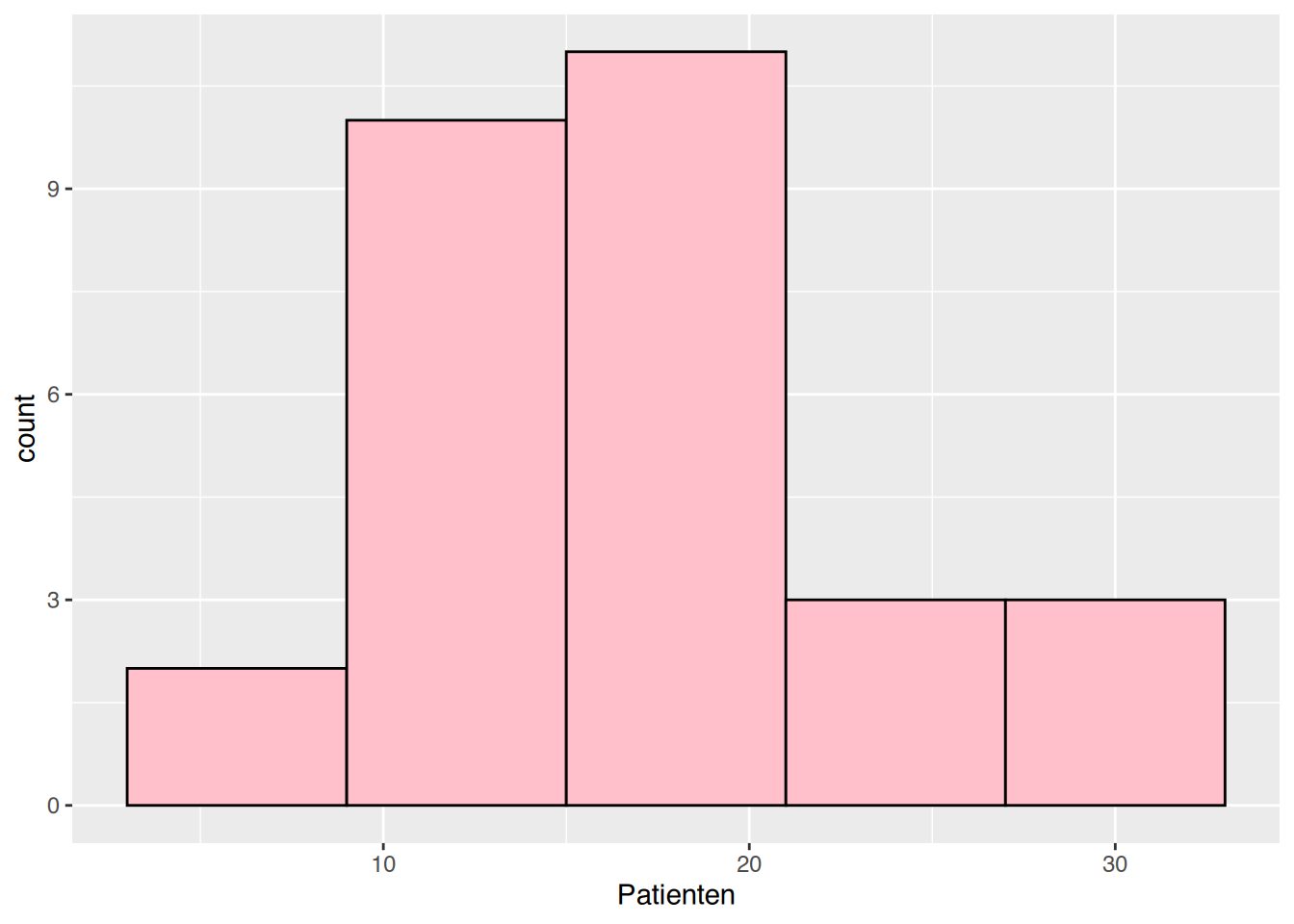
# also die Klassengrenzen manuell festlegen
ggplot(df, aes(x=Patienten)) +
geom_histogram(fill="pink", color="black",
breaks=c(5, 10, 15, 20, 25, 30))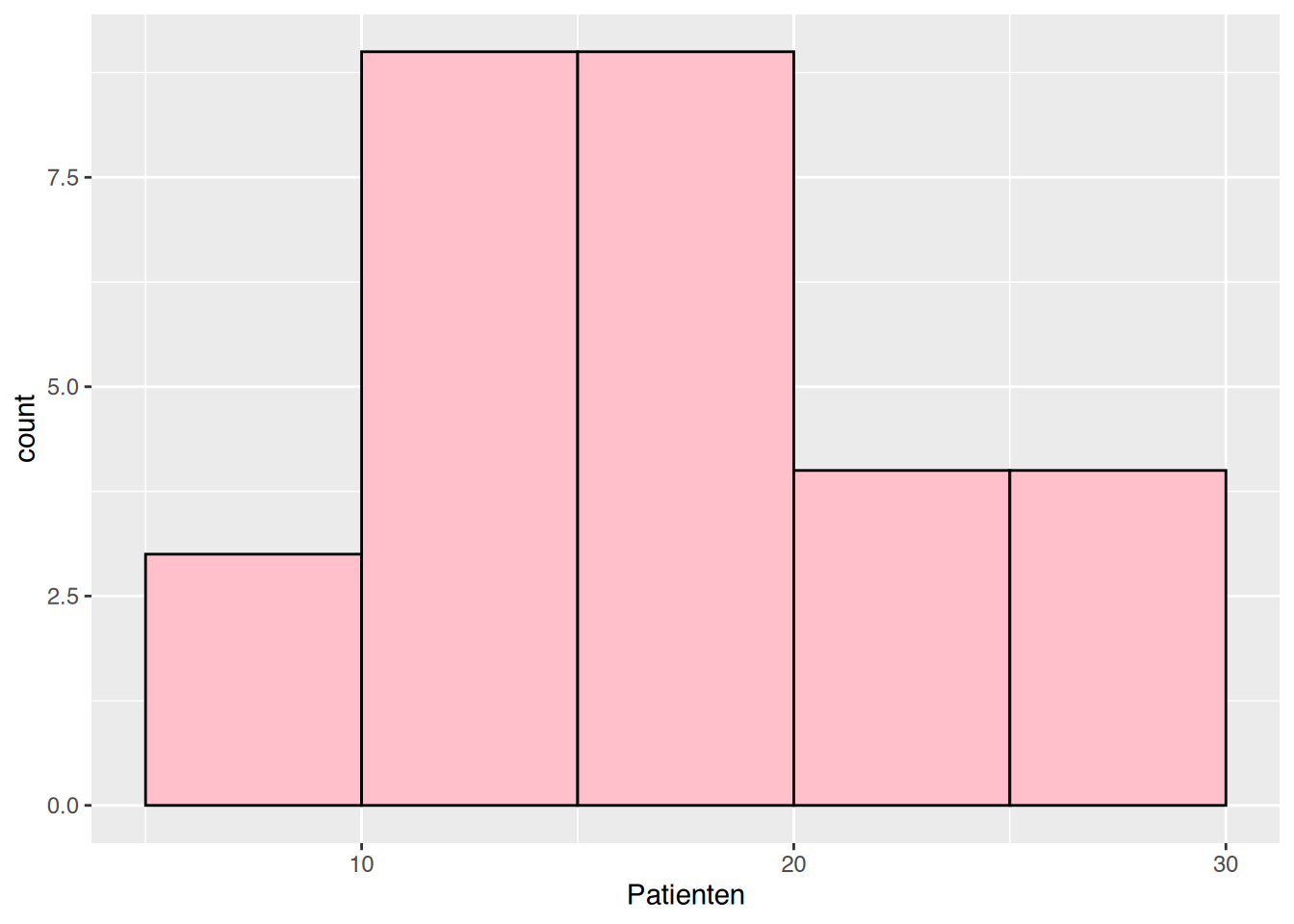
e) Erzeugen Sie ebenso Histogramme der relativen und jeweils kumulativen Häufigkeiten, inklusive Polygonzügen.
Mit R base können wir wie folgt vorgehen.
# 1. kumulierte absolute Häufigkeiten
#------------------------------------
# speichere Histogramm in Objekt h
h <- hist(df$Patienten, plot=FALSE)
# ersetze die Zellen durch kumulierte Häufigkeiten
h$counts <- cumsum(h$counts)
# plotte das kumulative Histogram
plot(h, col="hotpink", main = "kumulierte Häufigkeiten")
# füge Polygonzug hinzu
lines(c(0, h$mids),c(0,h$counts), col="blue") # type="s"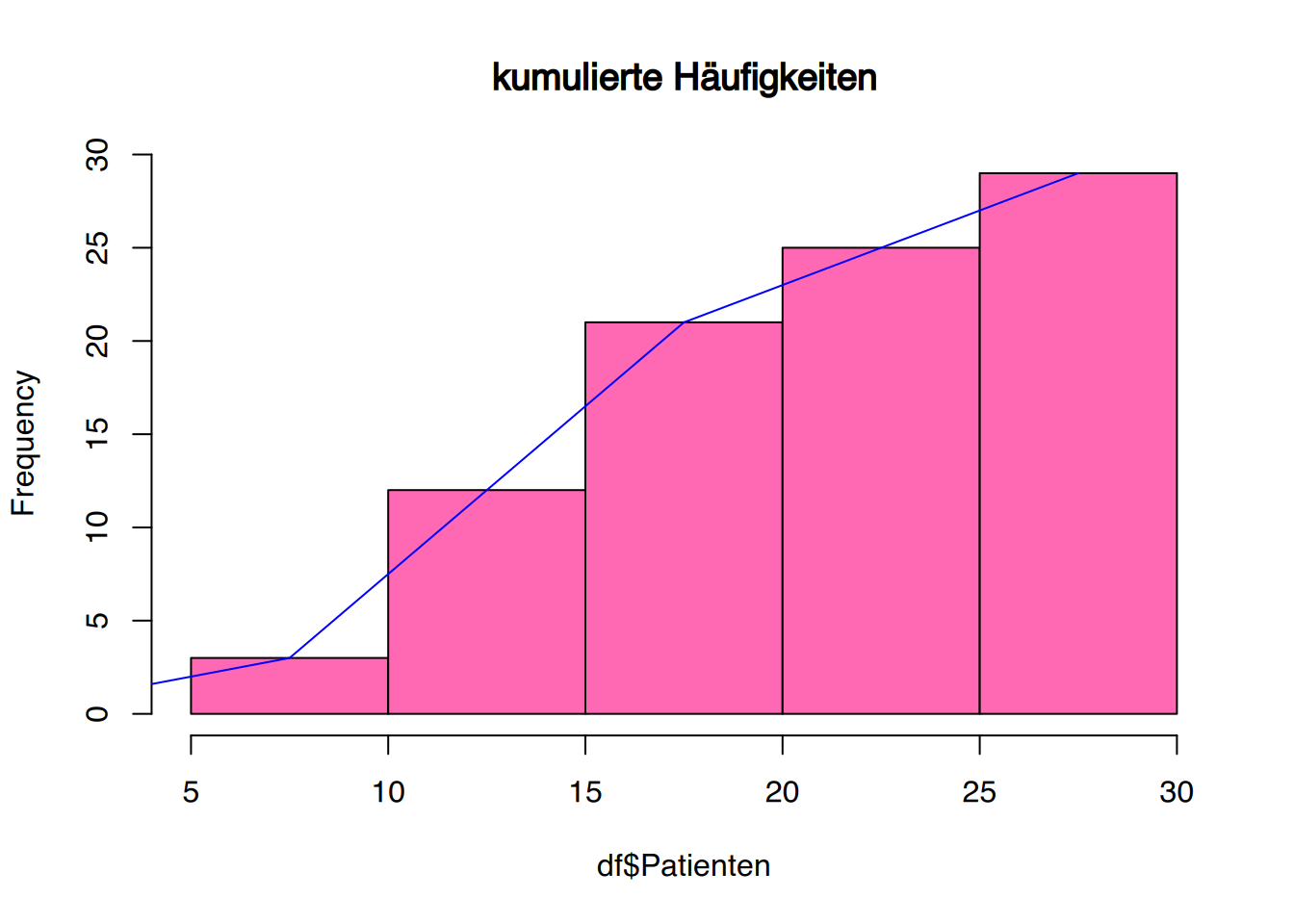
# 2. Histogram der relativen Häufigkeiten #
##----------------------------------------#
# speichere Histogramm in Objekt h
h <- hist(df$Patienten, plot=FALSE)
# relative Häufigkeiten
h$counts <- h$counts/sum(h$counts)
### plot
plot(h, col="hotpink", main = "Relative Häufigkeiten",
ylab = "Relative Häufigkeit" )
# Polygon hinzufügen
lines(h$breaks, c(0, h$counts), col = "blue") # add type="s" if you like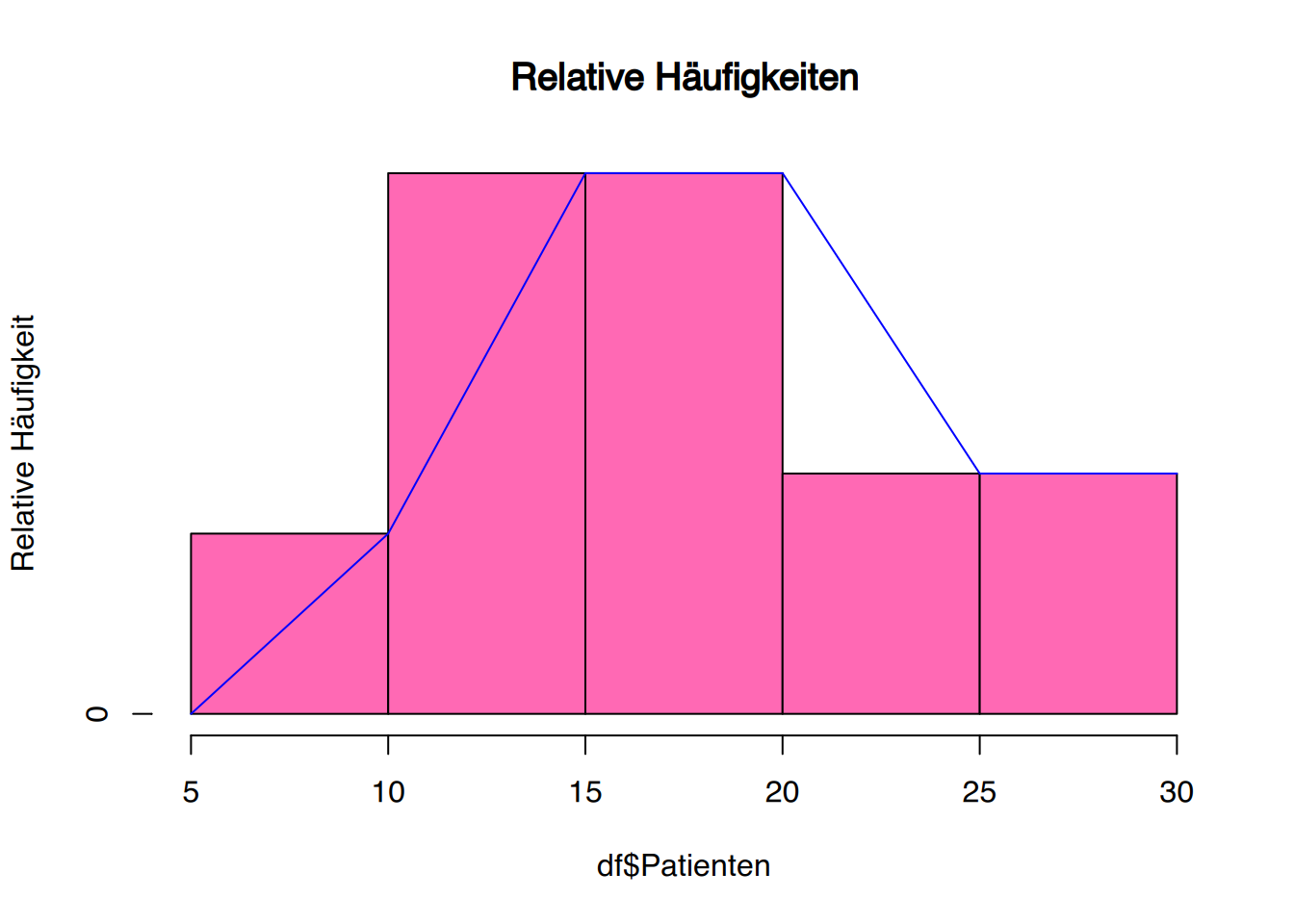
# 3. Histogram der kumulierten relativen Häufigkeiten #
##----------------------------------------------------#
# speichere Histogramm in Objekt h
h <- hist(df$Patienten, plot=FALSE)
# kumulative relative Häufigkeiten
h$counts <- cumsum(h$counts)/sum(h$counts)
### plot
plot(h, col="hotpink", main = "Kumulierte relative Häufigkeiten",
ylab = "Relative Häufigkeit" )
# Polygon hinzufügen
lines(h$breaks, c(0, h$counts), col = "blue") # add type="s" if you like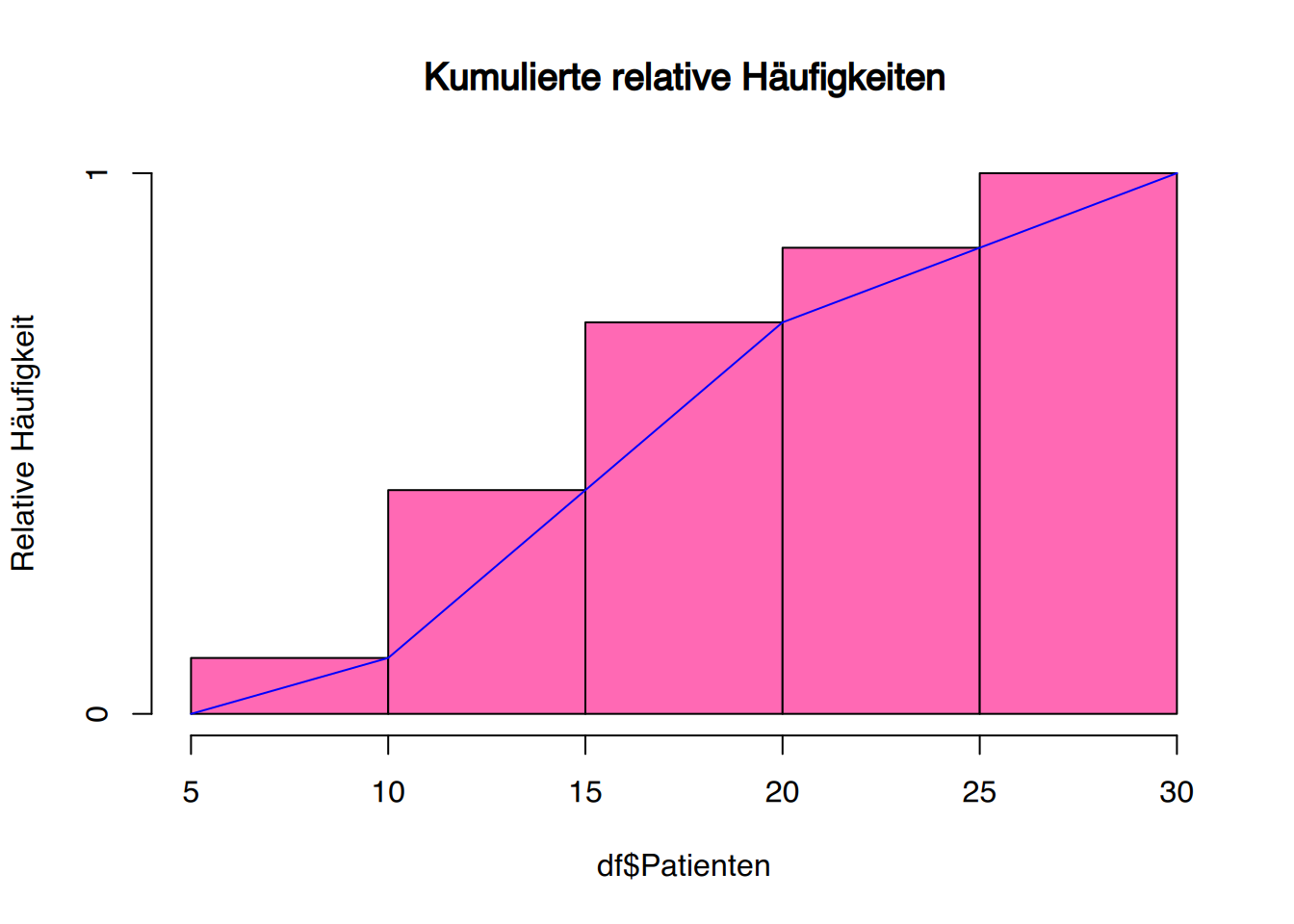
Im Tidyverse können wir so vorgehen.
### Mittels ggplot()
# Klassengrenzen festlegen
breaks = c(5, 10, 15, 20, 25, 30)
# kumulierte Häufigkeiten
ggplot(df, aes(x=Patienten)) +
ylab("Häufigkeiten")+
geom_histogram(aes(y=cumsum(after_stat(count))),
fill="hotpink", color="black",
breaks=breaks) +
stat_bin(aes(y=cumsum(after_stat(count))),
breaks=breaks,
geom="line", color="blue", linewidth=1.5) # oder geom="step"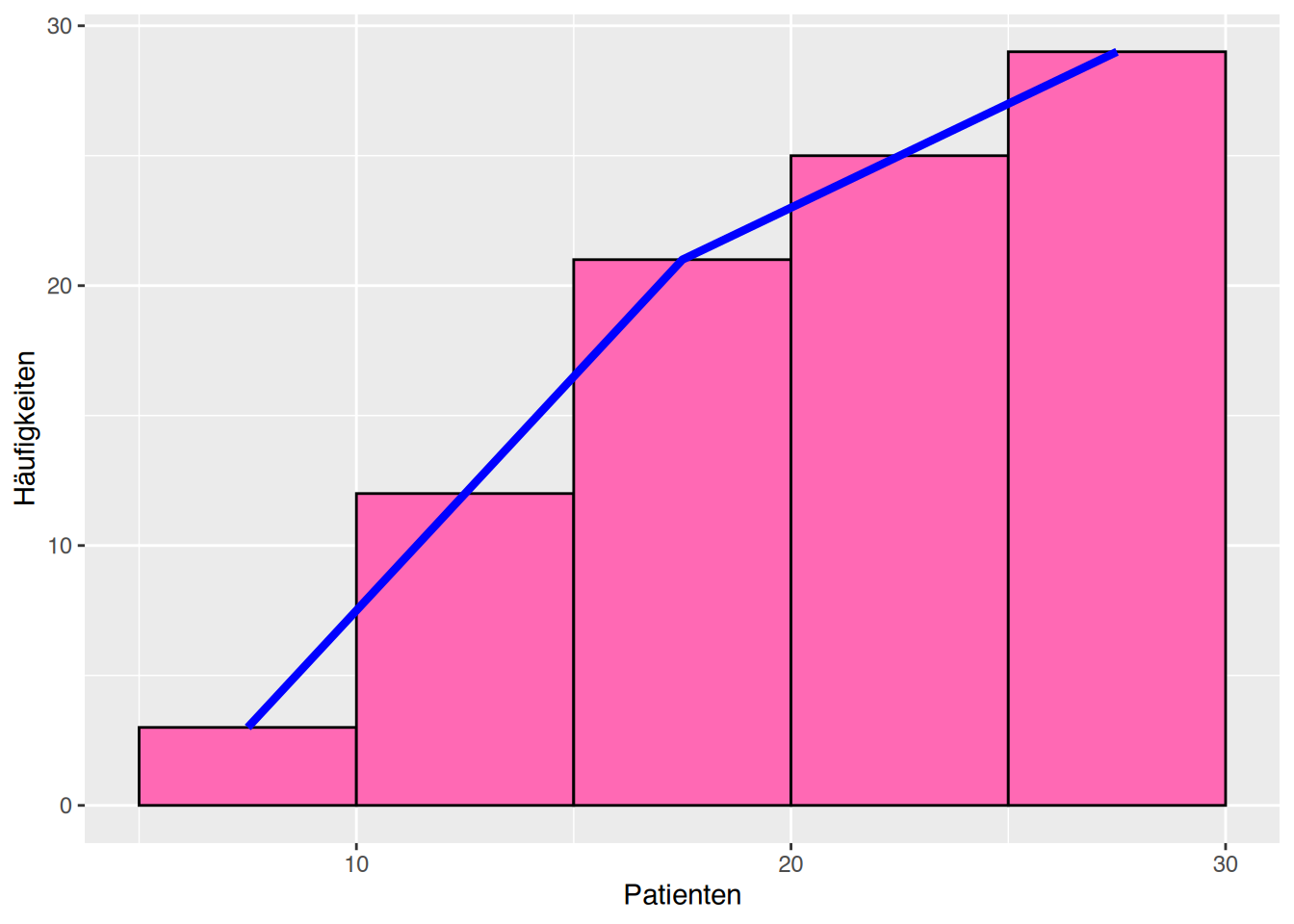
# relative Häufigkeiten
ggplot(df, aes(x=Patienten))+
ylab("relative Häufigkeiten")+
geom_histogram(aes(y=after_stat(count)/sum(after_stat(count))),
breaks=breaks, fill="hotpink2", color="black") +
geom_freqpoly(aes(y=after_stat(count)/sum(after_stat(count))),
breaks=breaks, color="blue", linewidth=1.5)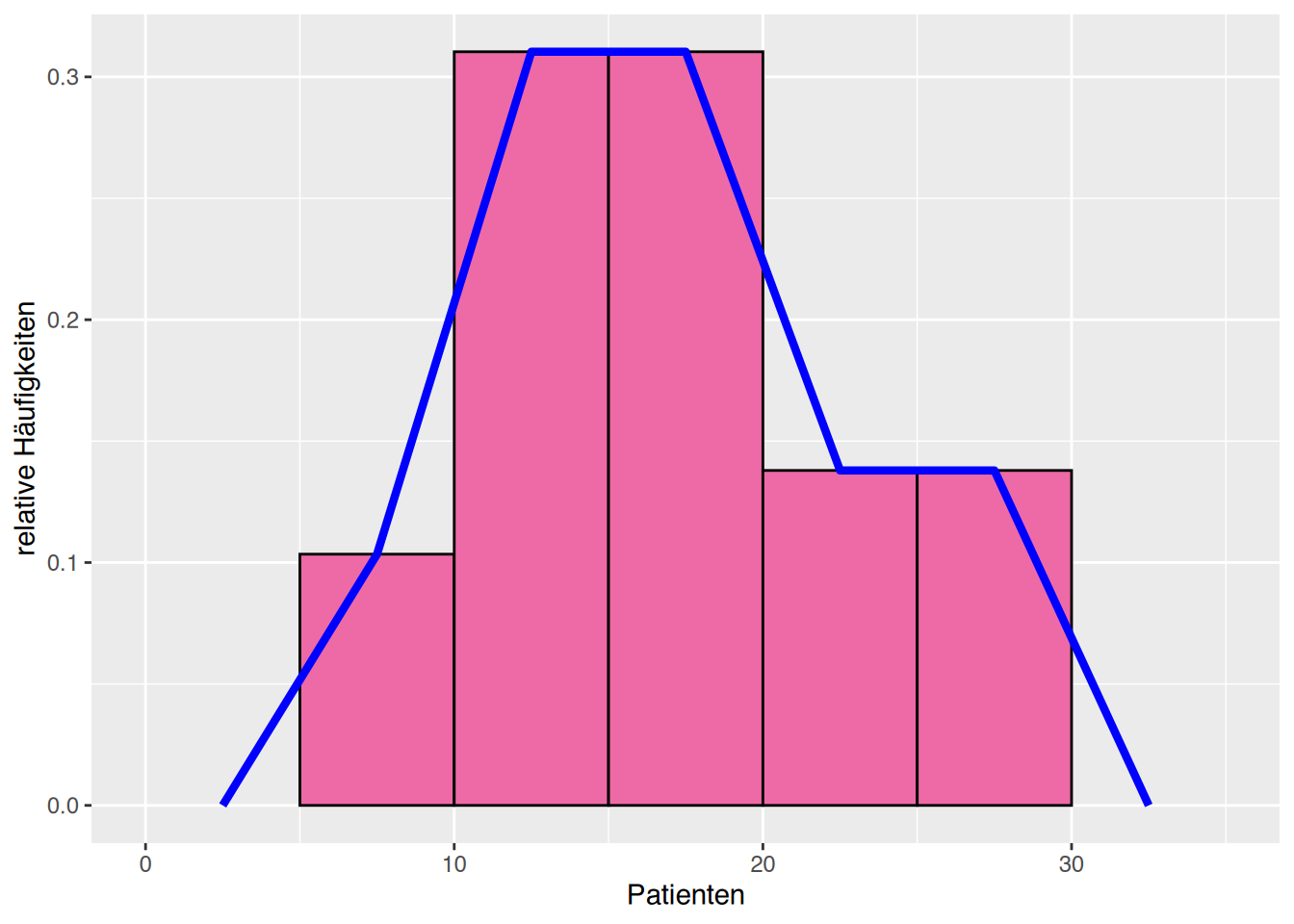
# kumulierte relative Häufigkeiten
ggplot(df, aes(x=Patienten)) +
ylab("relative Häufigkeiten")+
geom_histogram(aes(y=cumsum(after_stat(count)/sum(after_stat(count)))),
breaks=breaks, fill="hotpink3", color="black") +
stat_bin(aes(y=cumsum(after_stat(count)/sum(after_stat(count)))),
breaks=breaks,
geom="step", color="blue", linewidth=1.5) # oder geom="line"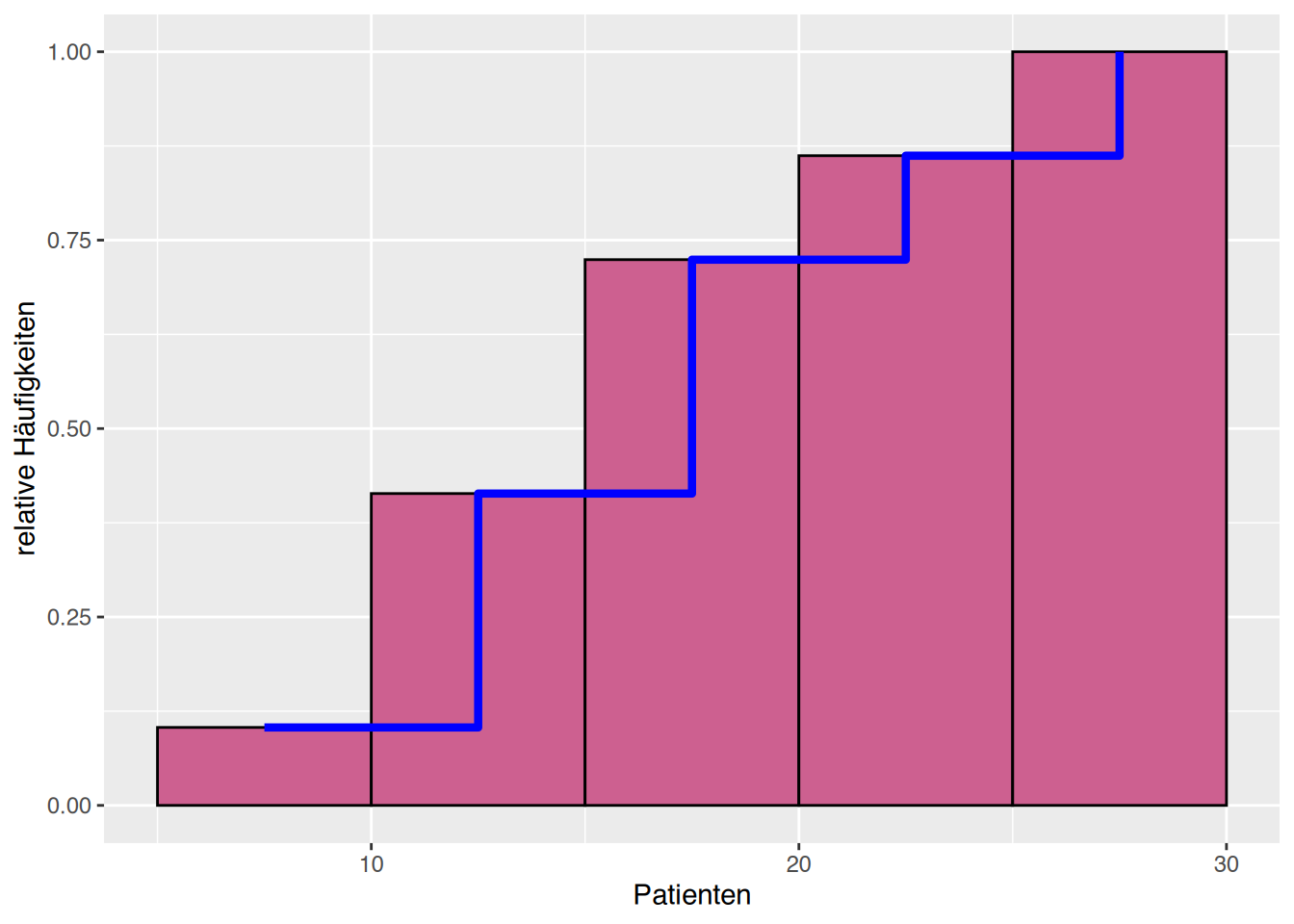
45.3 Lösung zur Aufgabe 44.1.3
a) Erstellen Sie ein Datenframe mit der Variable
Blutgruppe und übertragen Sie die Daten.
# Übertrage Daten
df <- data.frame(Blutgruppe = factor(c("A", "B", "B", "A", "AB", "0", "0", "A",
"B", "B", "A", "A", "A", "A", "AB", "A",
"A", "A", "B", "0", "B", "B", "B", "A",
"A", "A", "0", "A", "AB", "0")))
b) Erzeugen Sie eine Häufigkeitstabelle
table(df$Blutgruppe)
0 A AB B
5 14 3 8
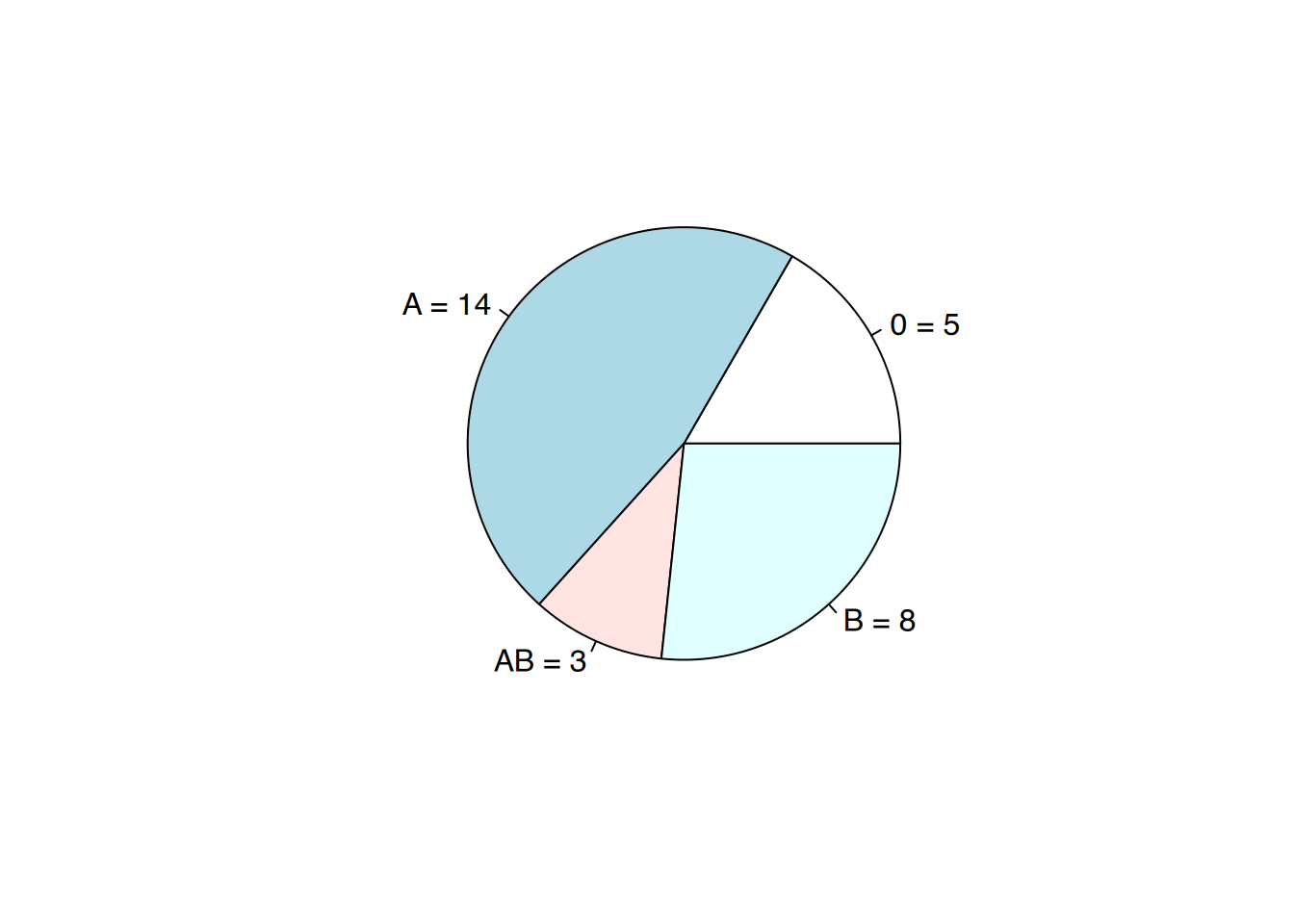
c) Erzeugen Sie ein Kreisdiagramm
# mit R base
pie(table(df$Blutgruppe),
labels = paste(levels(df$Blutgruppe),"=",
as.numeric(table(df$Blutgruppe))
)
)
# für ggplot benötigen wir ein Hilfsdatenframe
df2 <- as.data.frame(table(df$Blutgruppe))
colnames(df2) <- c("Blutgruppe", "Wert")
ggplot(df2, aes(x="", y=Wert, fill=Blutgruppe)) +
geom_col(color="black") +
# Werte schreiben
geom_text(aes(label = Wert),
position = position_stack(vjust = 0.5)) +
# verbiege zu Kreisdiagramm
coord_polar(theta="y") +
# entferne Achsen und Ticks
theme_void()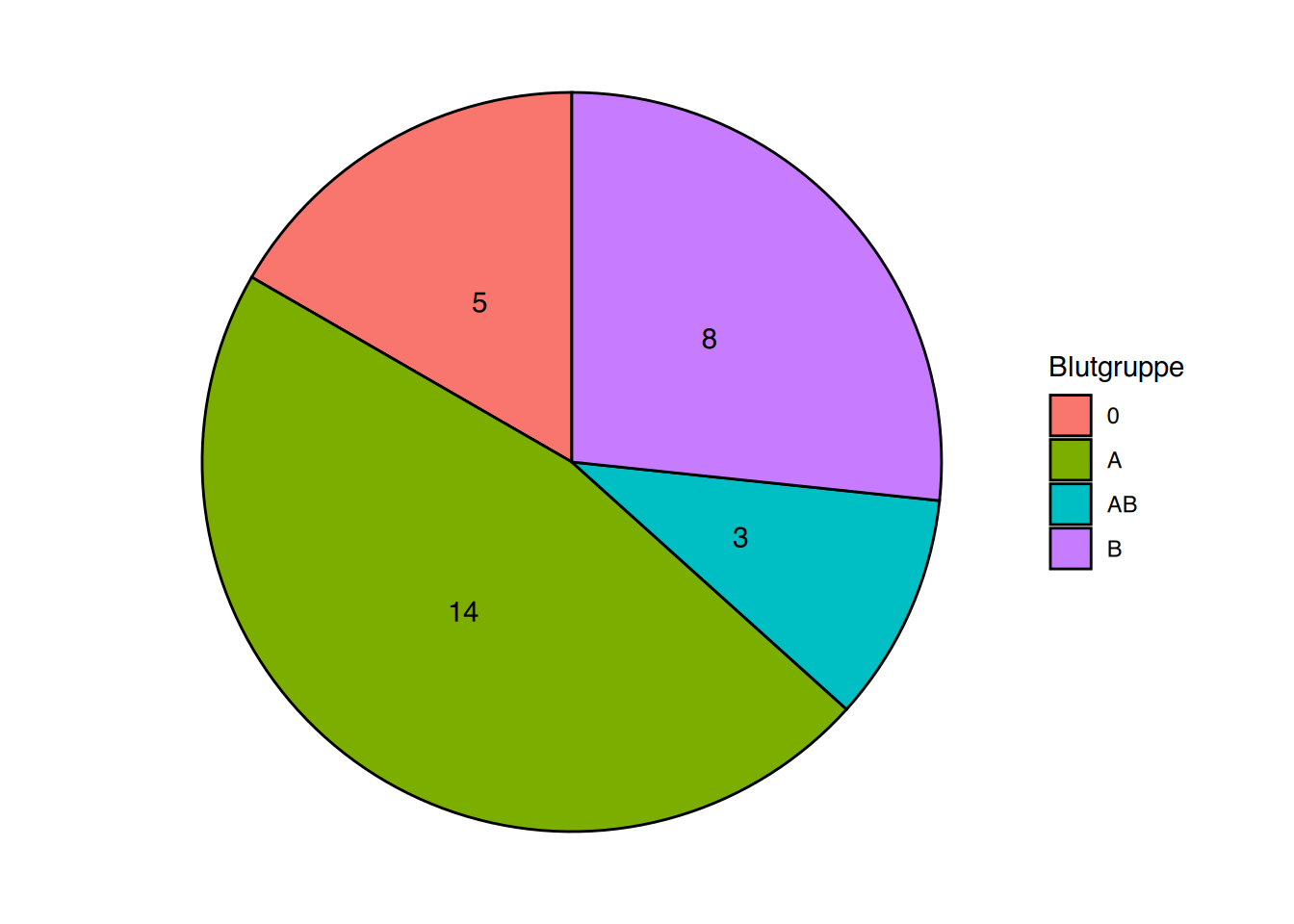
45.4 Lösung zur Aufgabe 44.1.4
a) Erstellen Sie ein Datenframe mit den Variablen
Alter und Familienstand und übertragen Sie die Daten.
df <- data.frame(Alter = c(31, 45, 35, 65, 21, 38, 62, 22, 31,
72, 39, 62, 59, 25, 44, 54,
80, 68, 65, 40, 78, 69, 75,
31, 65, 59, 58, 50),
Familienstand = c( rep("Single", 9),
rep("Verheiratet", 7),
rep("Verwitwet", 7),
rep("Geschieden", 5)
)
)
b) Erzeugen Sie für jeden
Familienstand eine Häufigkeitstabelle des Alters.
# Singles
df2 <- subset(df, Familienstand=="Single")
table(df2$Alter)
21 22 31 35 38 45 62 65
1 1 2 1 1 1 1 1 # Verheiratet
df2 <- subset(df, Familienstand=="Verheiratet")
table(df2$Alter)
25 39 44 54 59 62 72
1 1 1 1 1 1 1 # Verwitwet
df2 <- subset(df, Familienstand=="Verwitwet")
table(df2$Alter)
40 65 68 69 75 78 80
1 1 1 1 1 1 1 # Geschieden
df2 <- subset(df, Familienstand=="Geschieden")
table(df2$Alter)
31 50 58 59 65
1 1 1 1 1
c) Erzeugen Sie für jeden
Familienstand eine Boxplot des Alters. Gibt es Ausreißer? In welcher Gruppe streut das Alter am meisten?
Mit R base können wir so vorgehen.
# Singles
df2 <- subset(df, Familienstand=="Single")
boxplot(df2$Alter, main="Alter der Singles", col="seagreen")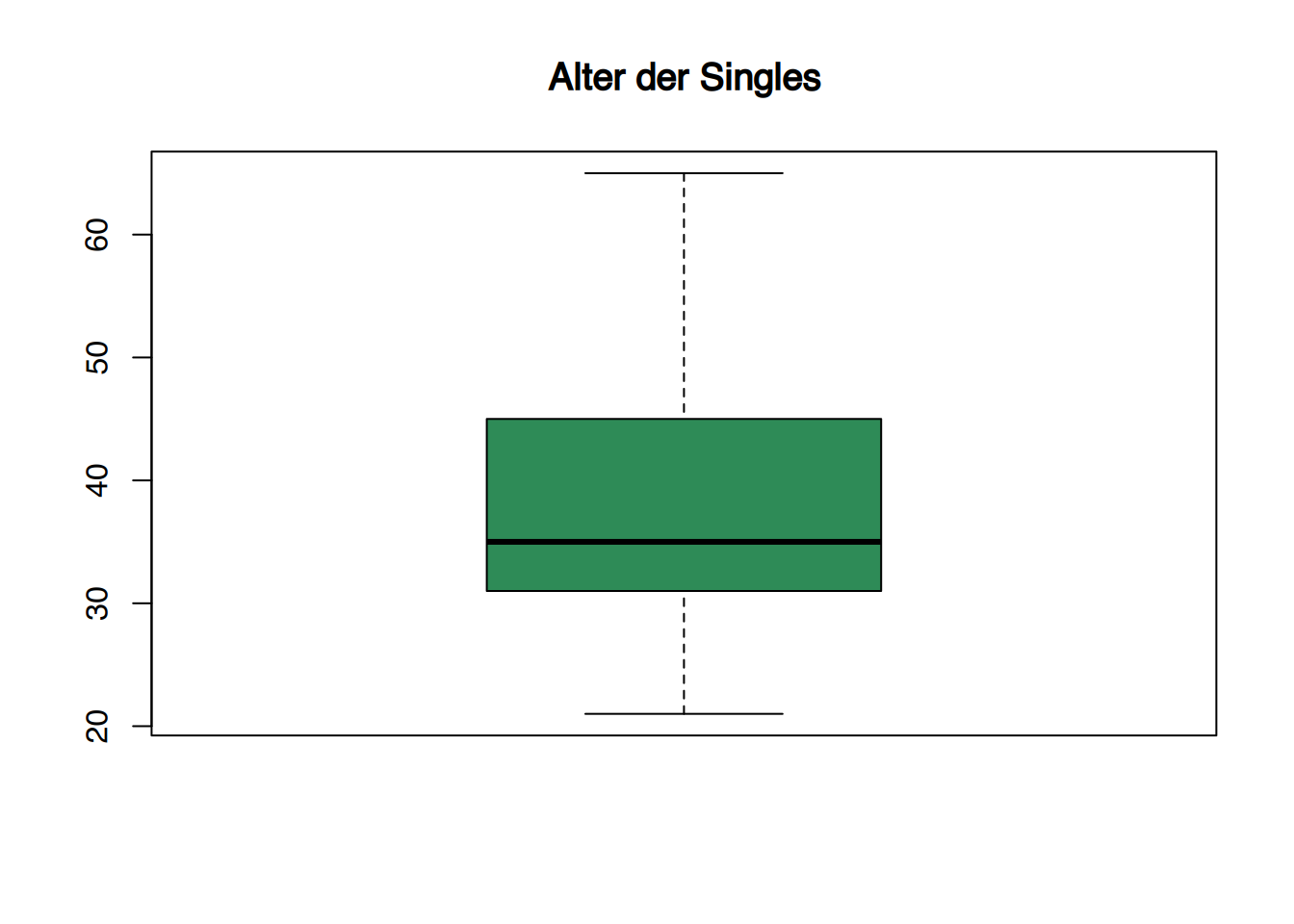
# Verheiratet
df2 <- subset(df, Familienstand=="Verheiratet")
boxplot(df2$Alter, main="Alter der Verheirateten", col="skyblue2")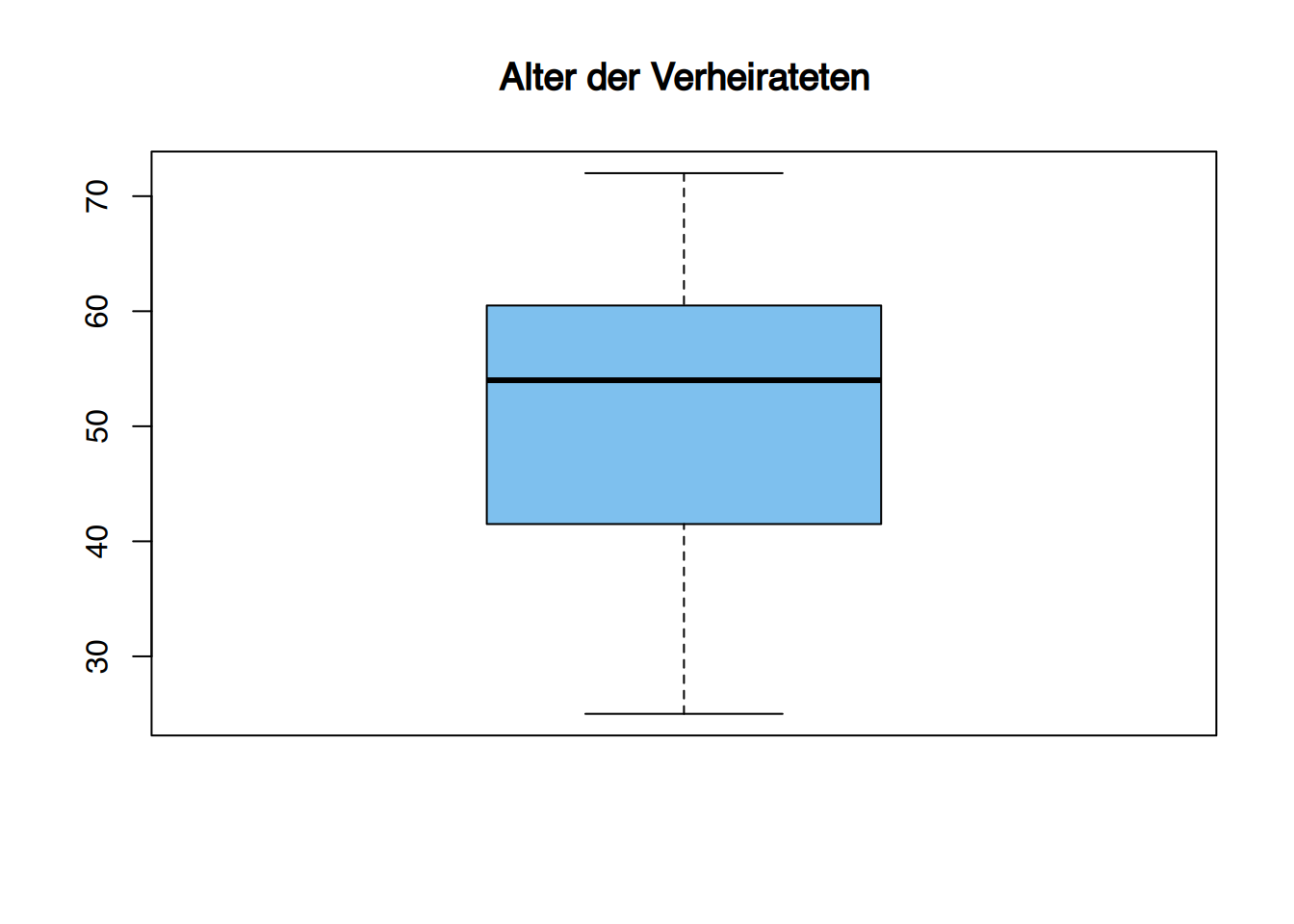
# Verwitwet
df2 <- subset(df, Familienstand=="Verwitwet")
boxplot(df2$Alter, main="Alter der Verwitweten", col="lightsalmon4")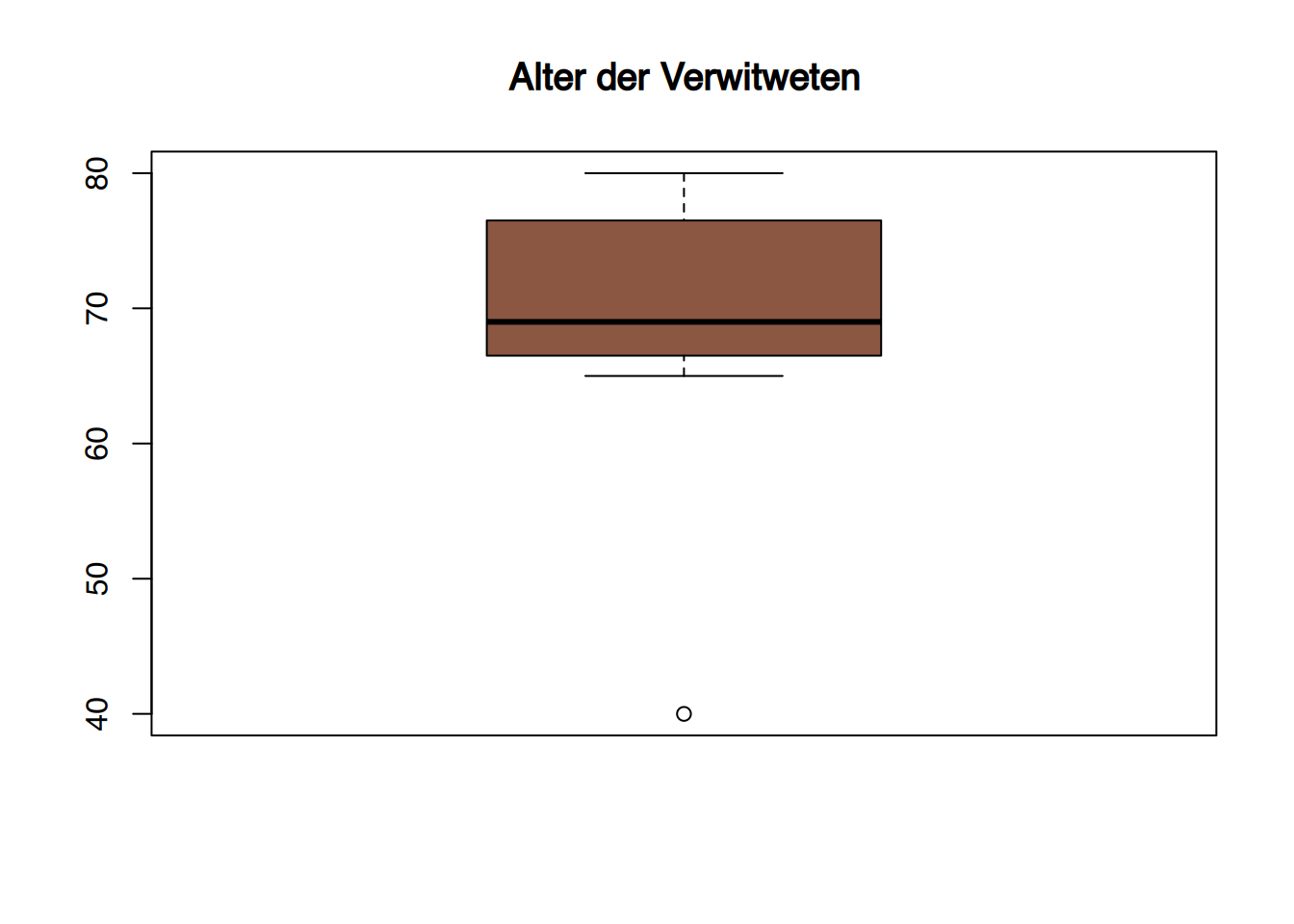
# Geschieden
df2 <- subset(df, Familienstand=="Geschieden")
boxplot(df2$Alter, main="Alter der Geschiedenen", col="maroon3")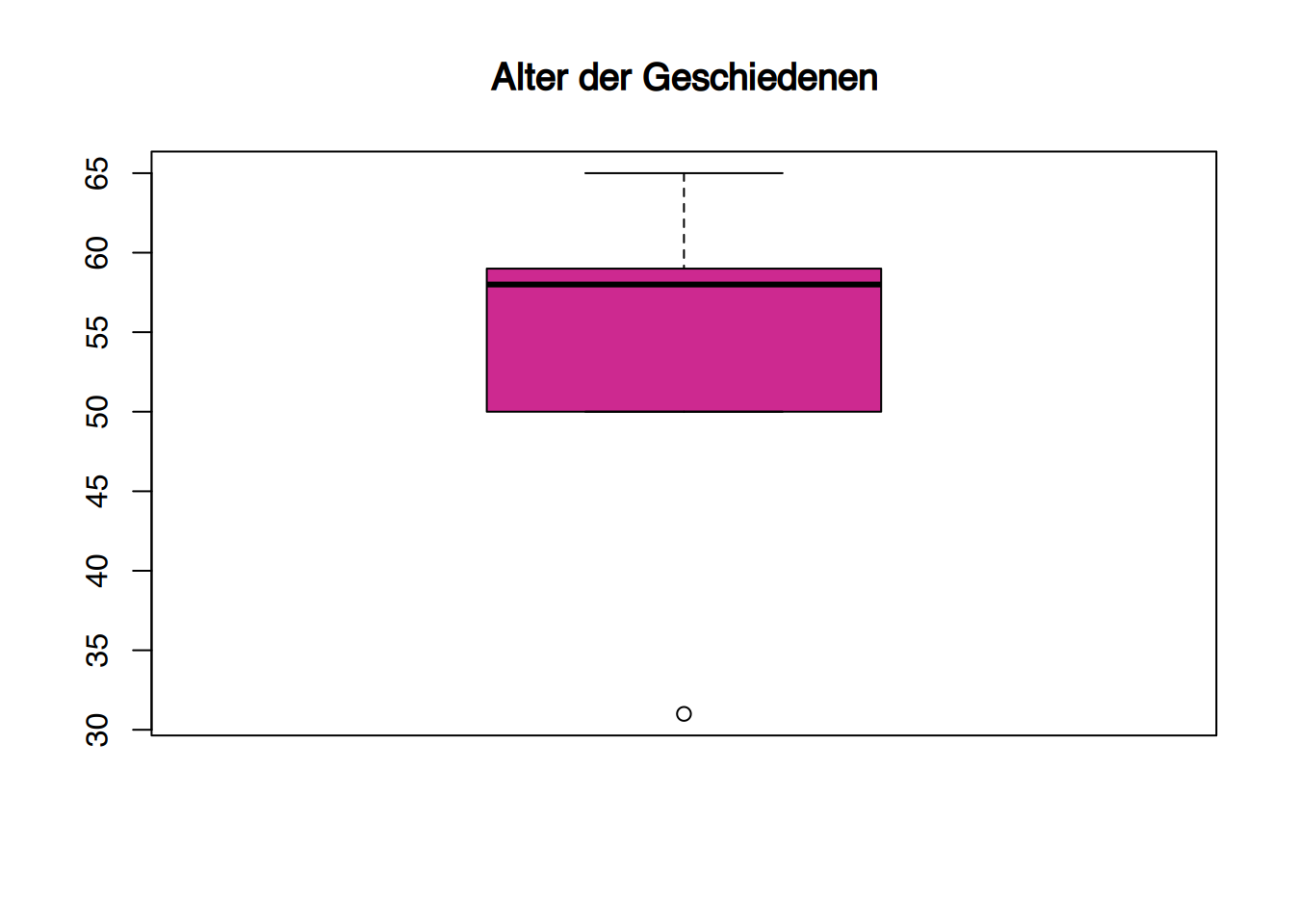
Oder alle auf einmal:
boxplot(Alter ~ Familienstand , data=df,
col=c("maroon3", "seagreen", "skyblue2", "lightsalmon4"))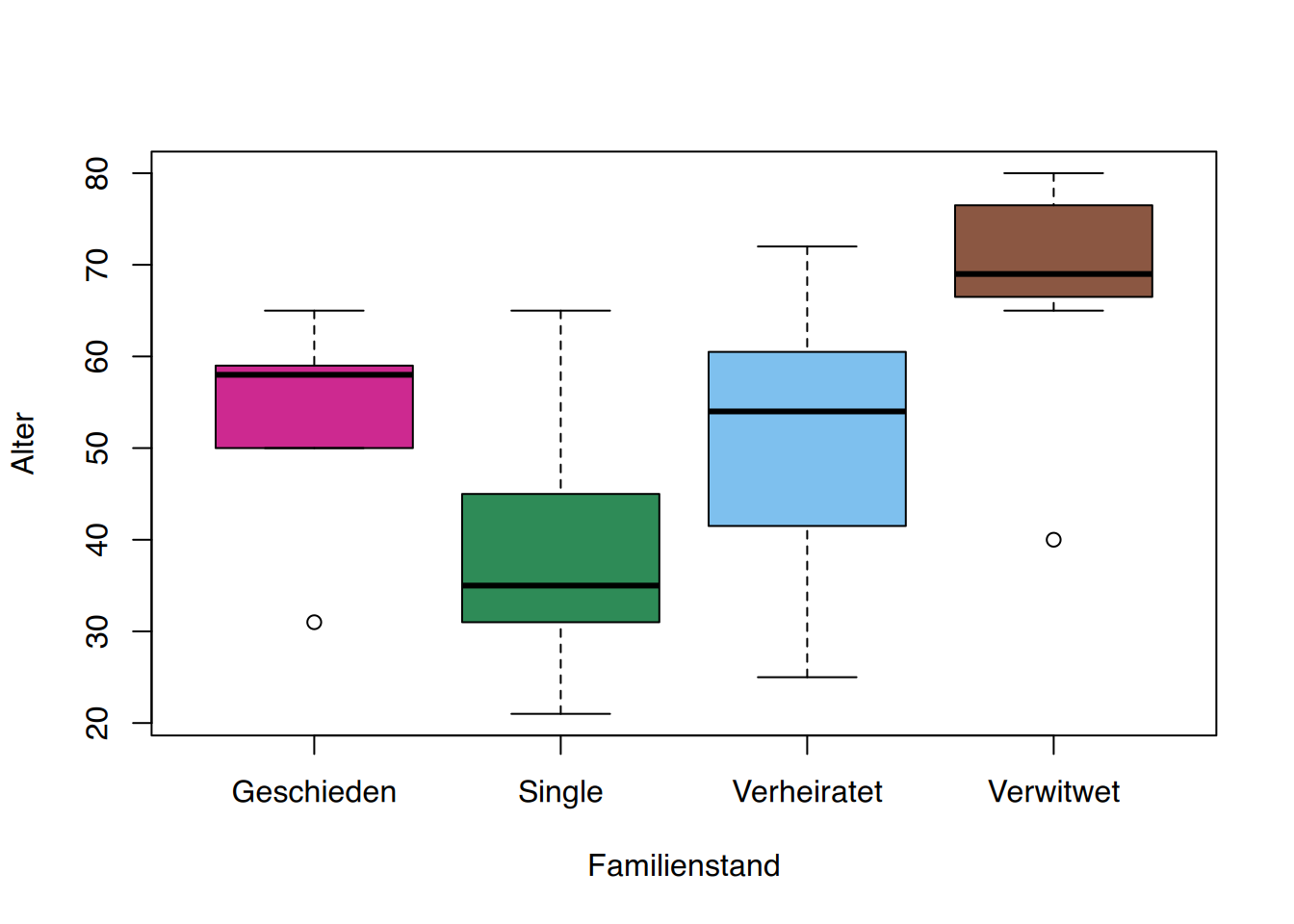
Es sind Ausreißer erkennbar in der Gruppe der Verwitweten und der Geschiedenen.
Im Tidyverse können wir so vorgehen:
ggplot(df, aes(y=Alter, x=Familienstand)) +
geom_boxplot(aes(fill=Familienstand)) +
stat_boxplot(geom="errorbar")+
scale_fill_manual(values=c("seagreen", "skyblue2",
"lightsalmon4", "maroon3"),
breaks=c("Single", "Verheiratet",
"Verwitwet", "Geschieden"))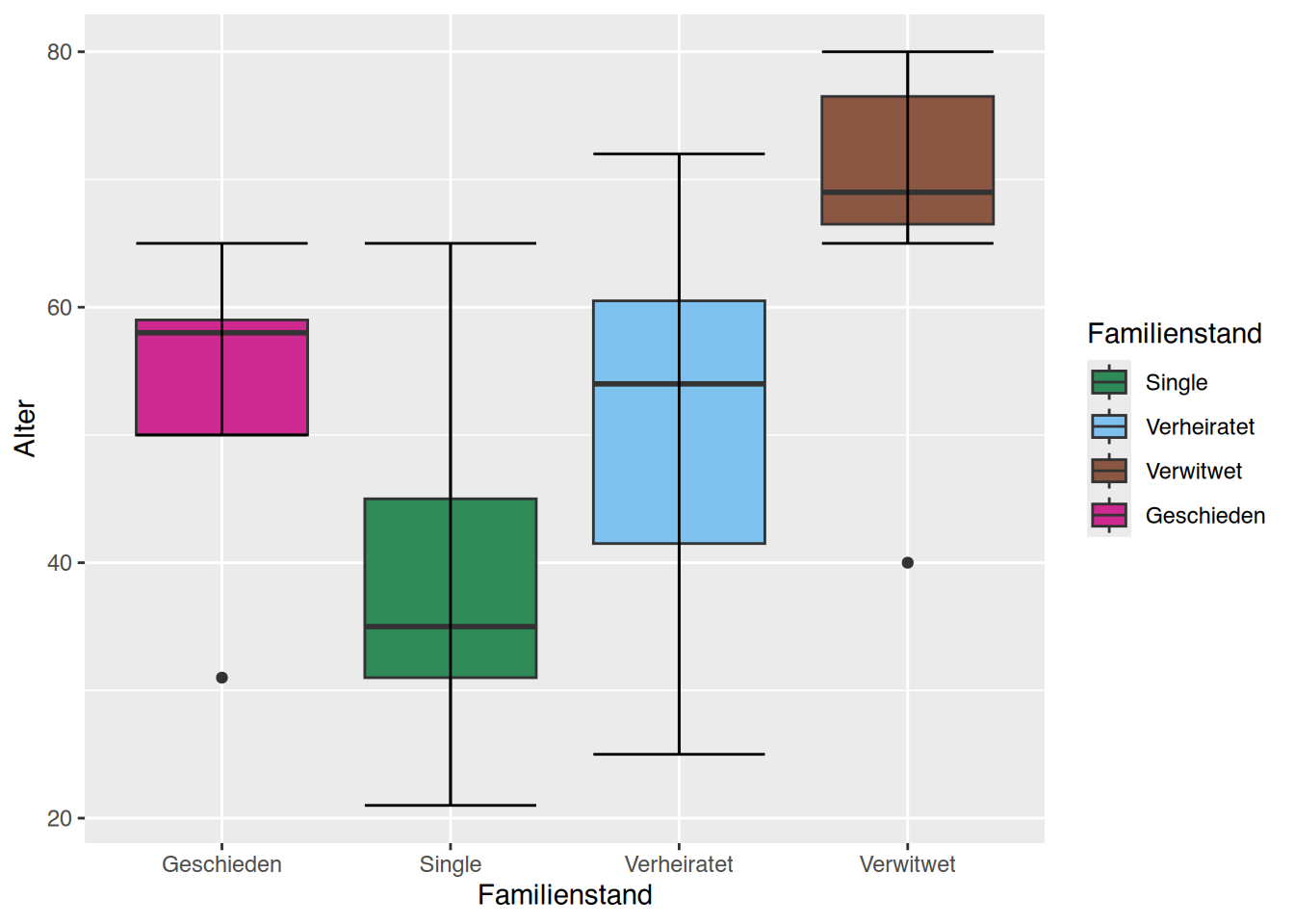
Auch hier sind die Ausreißer in den Gruppen der Verwitweten und der Geschiedenen erkennbar.
d) Erzeugen Sie für jeden
Familienstand eine Histogram des Alters. Wie unterscheiden sich die Histogramme?
Mit R base können wir so vorgehen
# Singles
df2 <- subset(df, Familienstand=="Single")
hist(df2$Alter, main="Alter der Singles", col="seagreen")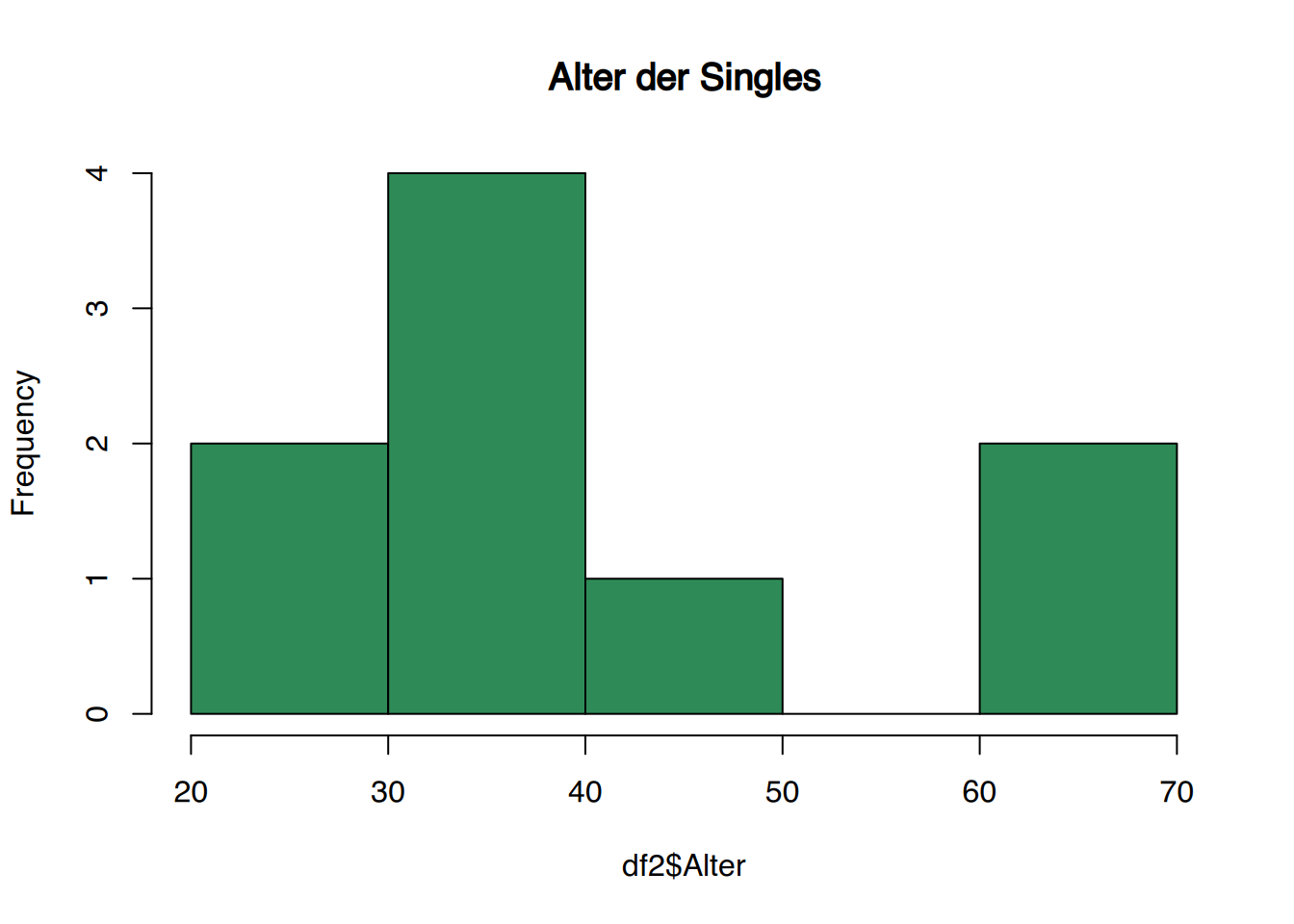
# Verheiratet
df2 <- subset(df, Familienstand=="Verheiratet")
hist(df2$Alter, main="Alter der Verheirateten", col="skyblue2")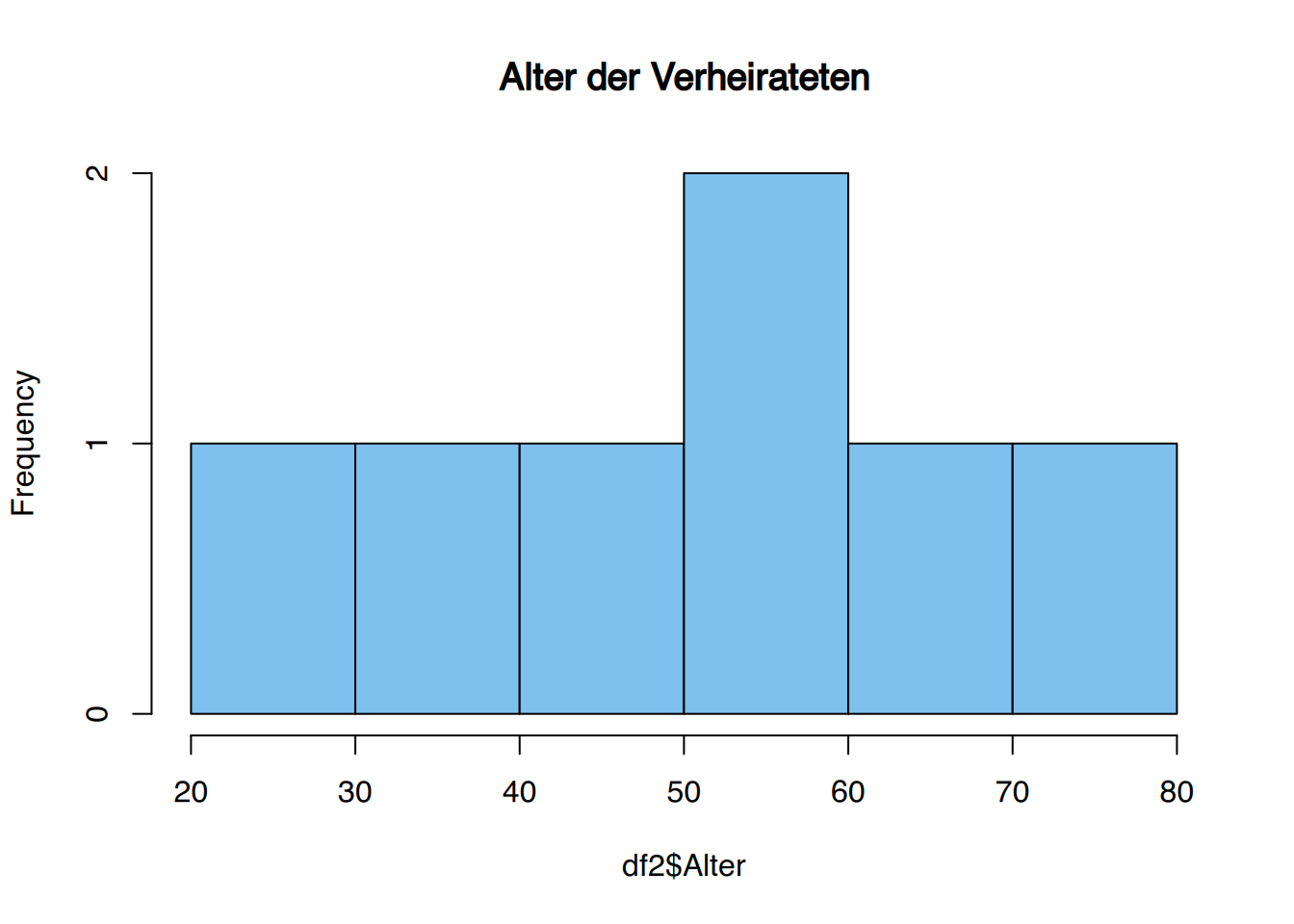
# Verwitwet
df2 <- subset(df, Familienstand=="Verwitwet")
hist(df2$Alter, main="Alter der Verwitweten", col="lightsalmon4")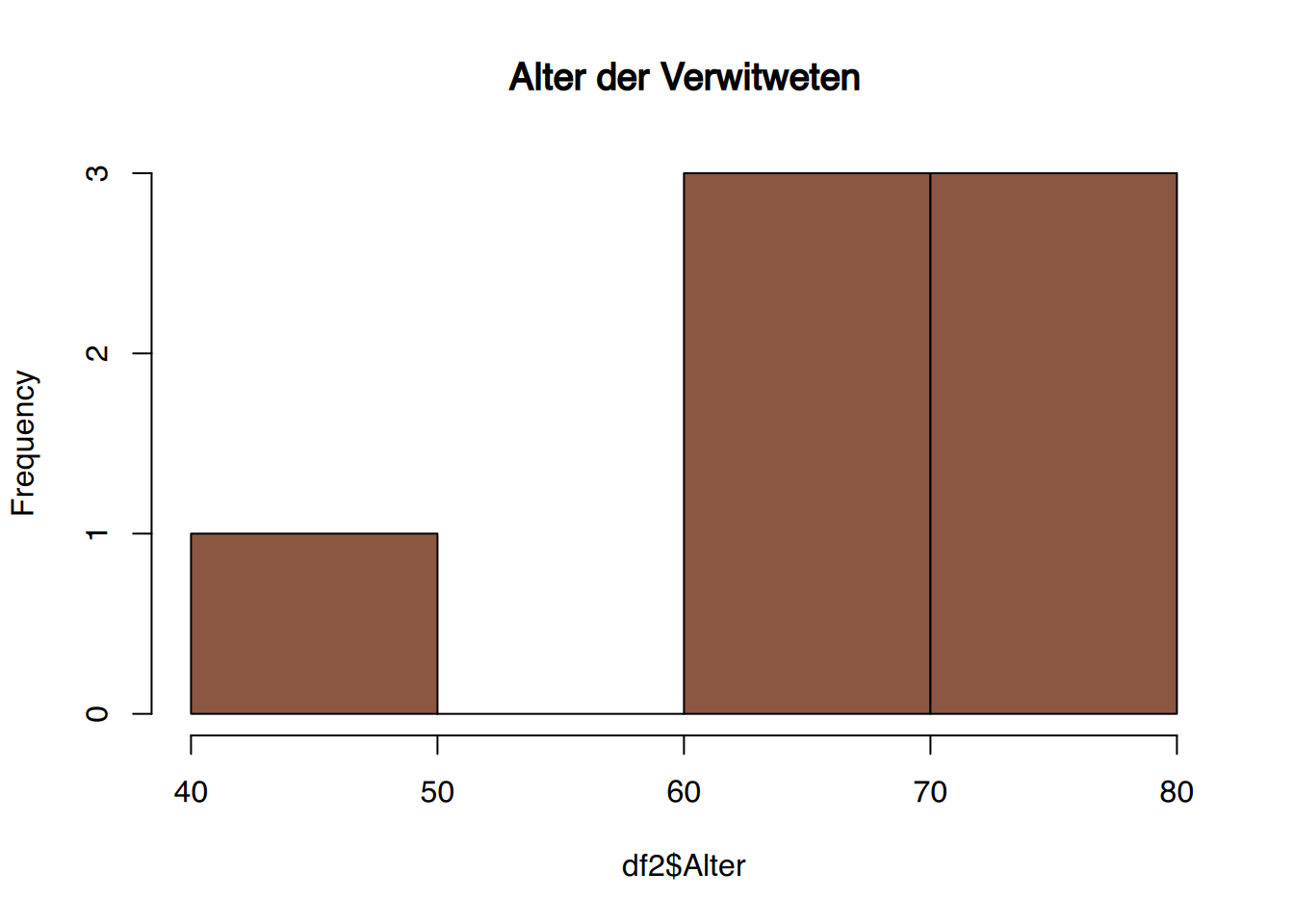
# Geschieden
df2 <- subset(df, Familienstand=="Geschieden")
hist(df2$Alter, main="Alter der Geschiedenen", col="maroon3")
Im Tidyverse können wir so vorgehen:
breaks = c(seq(10,80,10))
ggplot(df, aes(x=Alter, fill=Familienstand)) +
geom_histogram(breaks=breaks, color="black")+
scale_fill_manual(values=c("seagreen", "skyblue2",
"lightsalmon4", "maroon3"),
breaks=c("Single", "Verheiratet",
"Verwitwet", "Geschieden"))+
facet_wrap(~Familienstand)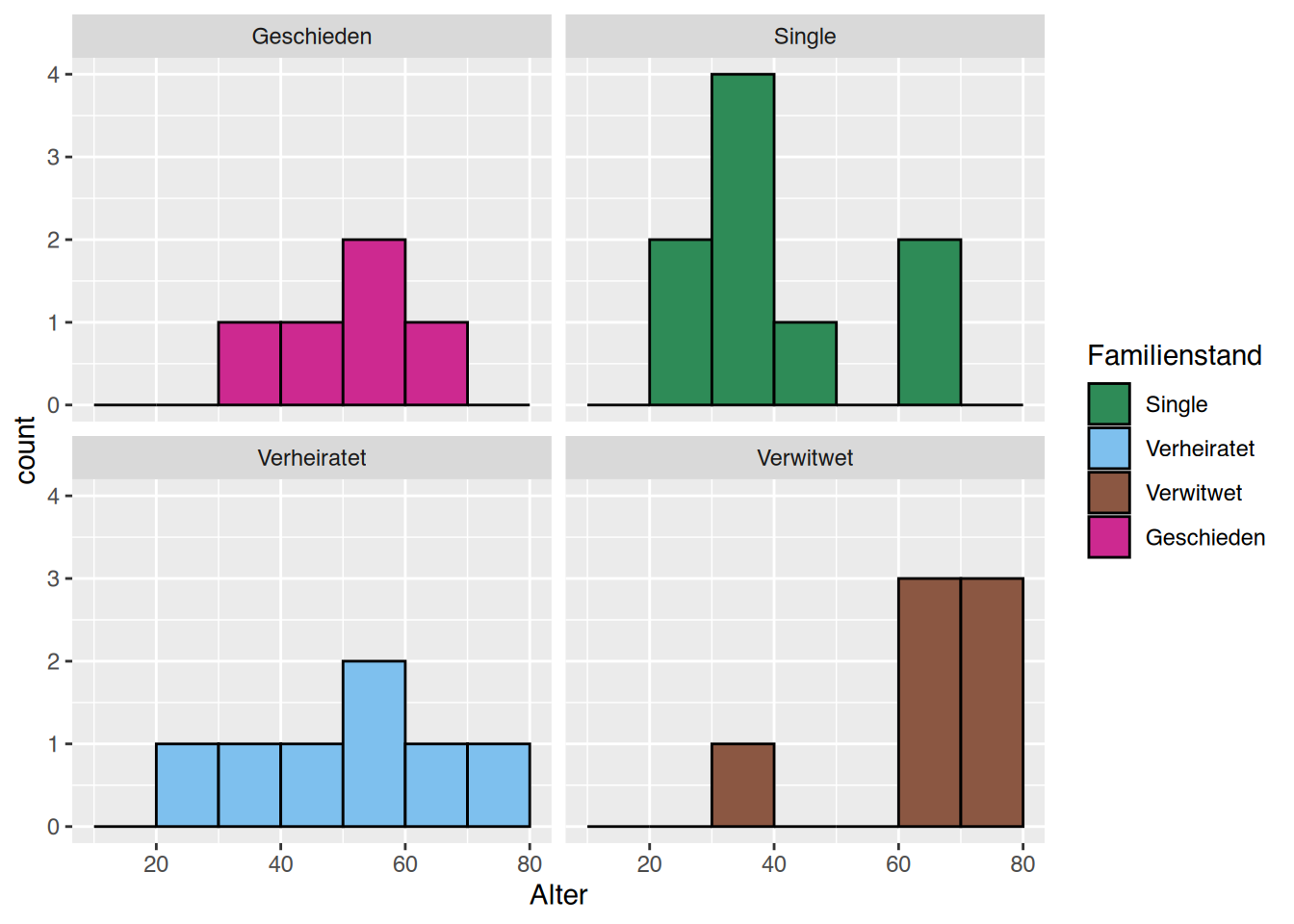
45.5 Lösung zur Aufgabe 44.1.5
a) Erstellen Sie eine Häufigkeitstabelle
# erzeuge Daten
Verletzung <- c(0, 1, 2, 1, 3, 0, 1, 0, 1, 2, 0, 1, 1, 1, 2, 0,
1, 3, 2, 1, 2, 1, 0, 1)
# Häufigkeitstabelle
xtabs(~Verletzung)Verletzung
0 1 2 3
6 11 5 2
b) Erzeugen Sie ein Säulendiagramm der relativen und kumulativen relativen Häufigkeiten.
# relative Häufigkeiten als Barplot
barplot( table(Verletzung) / length(Verletzung)*100,
col="blanchedalmond", main="relative Häufigkeiten",
ylab="relative Häufigkeit in %", xlab="Verletzungen")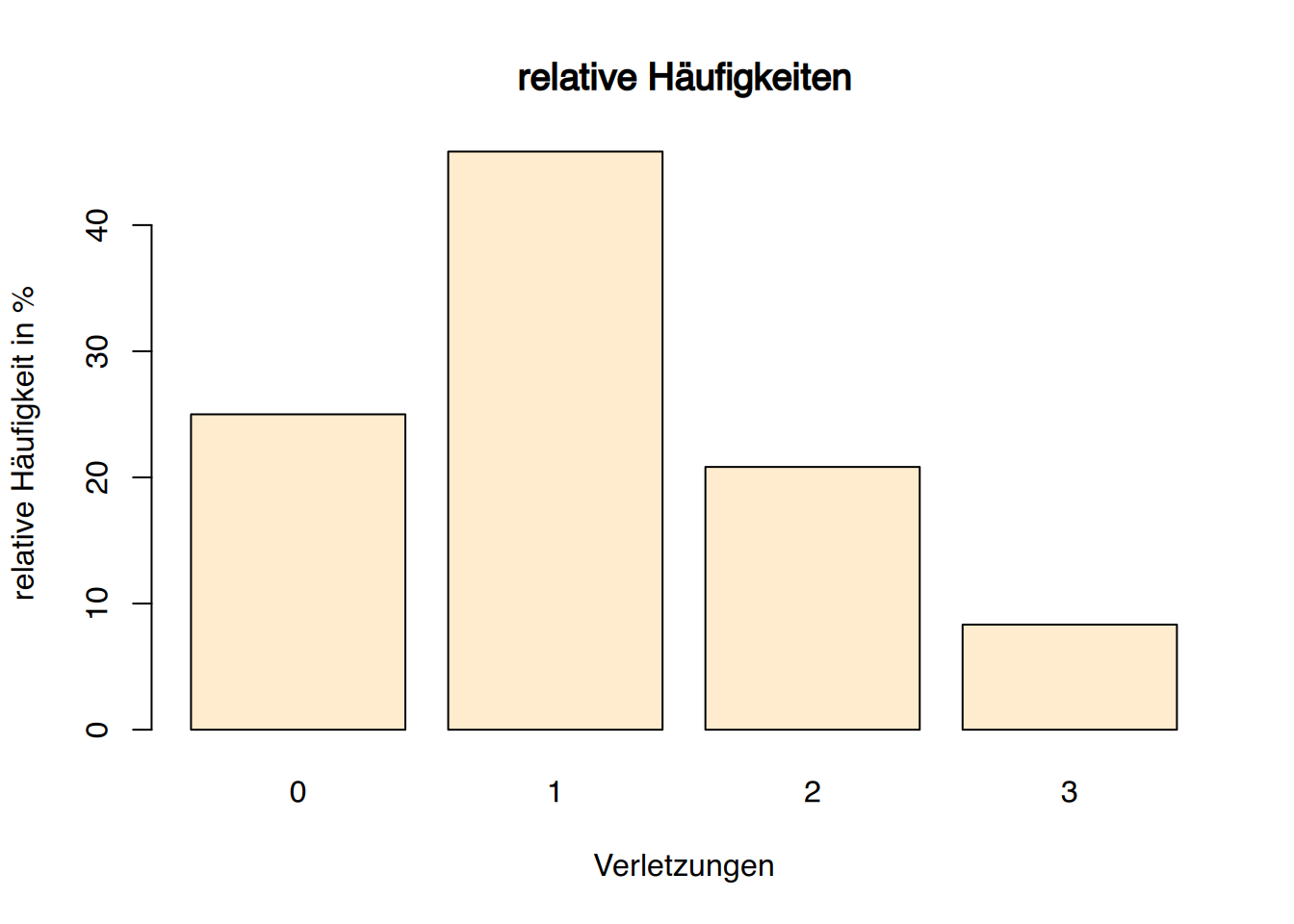
# relative kumulierte Häufigkeiten als Barplot
barplot( cumsum(table(Verletzung)) / sum(table(Verletzung))*100,
col="goldenrod1", main="kumulierte relative Häufigkeiten",
ylab="relative Häufigkeit in %", xlab="Verletzungen")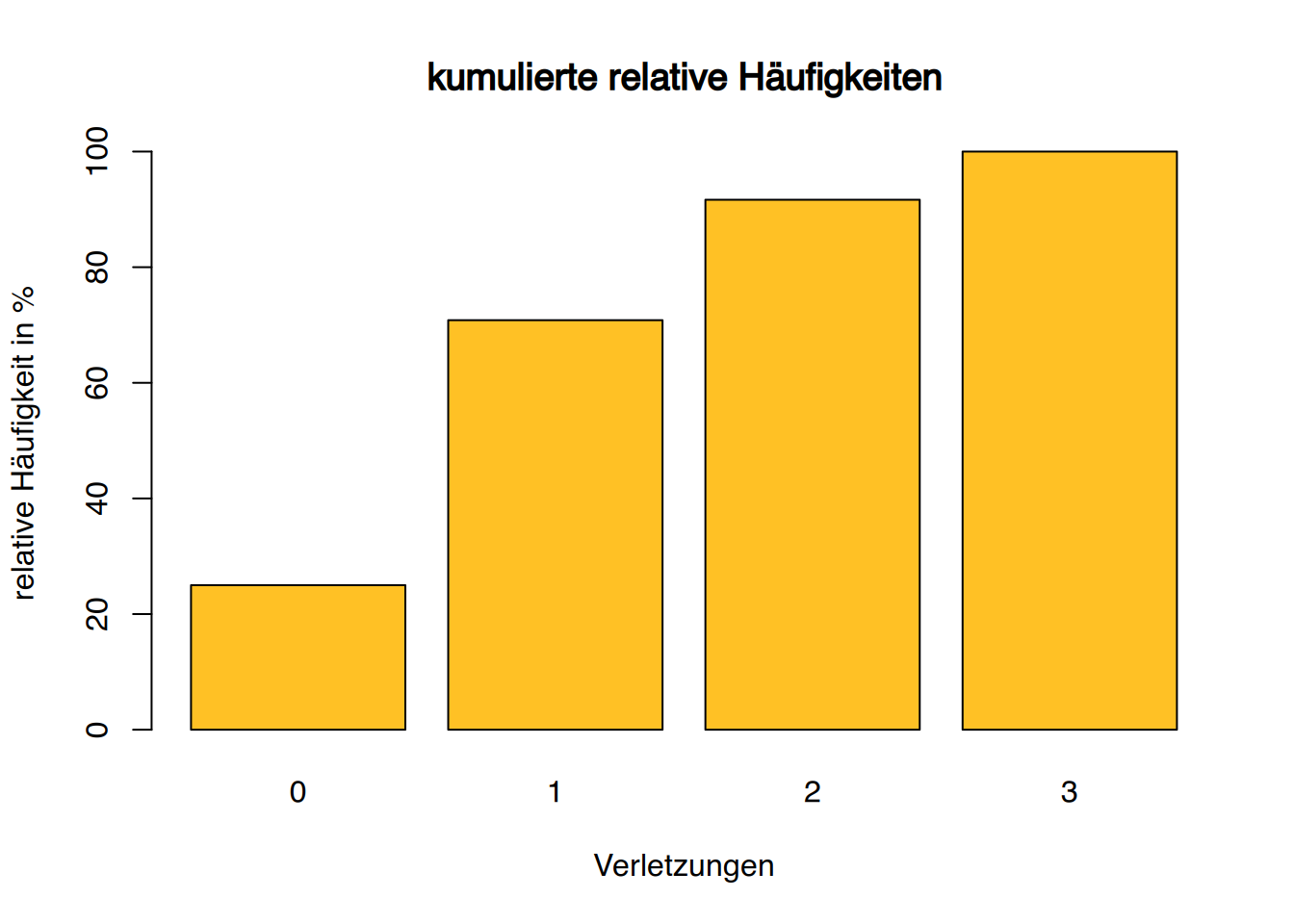
Mit ggplot
df <- data.frame(Verletzung)
ggplot(df, aes(x=Verletzung))+
geom_bar(aes(y=after_stat(count)/sum(after_stat(count))*100),
fill="blanchedalmond", color="black") +
ylab("relative Häufigkeiten in %")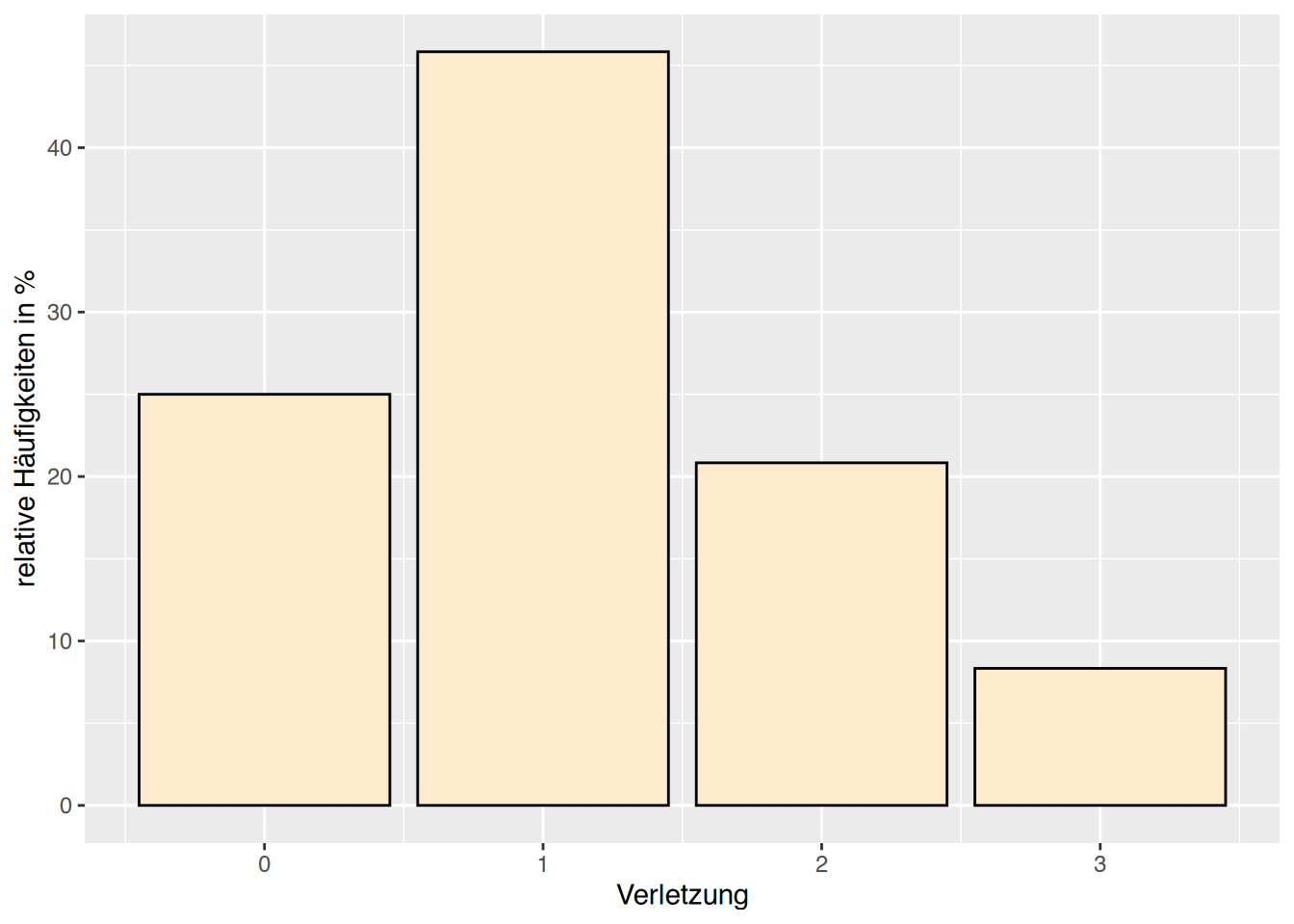
# kumulierte relative Häufigkeiten
ggplot(df, aes(x=Verletzung))+
ylab("relative Häufigkeiten in %")+
geom_bar(aes(y=cumsum(after_stat(count)/sum(after_stat(count)))*100),
fill="goldenrod1", color="black")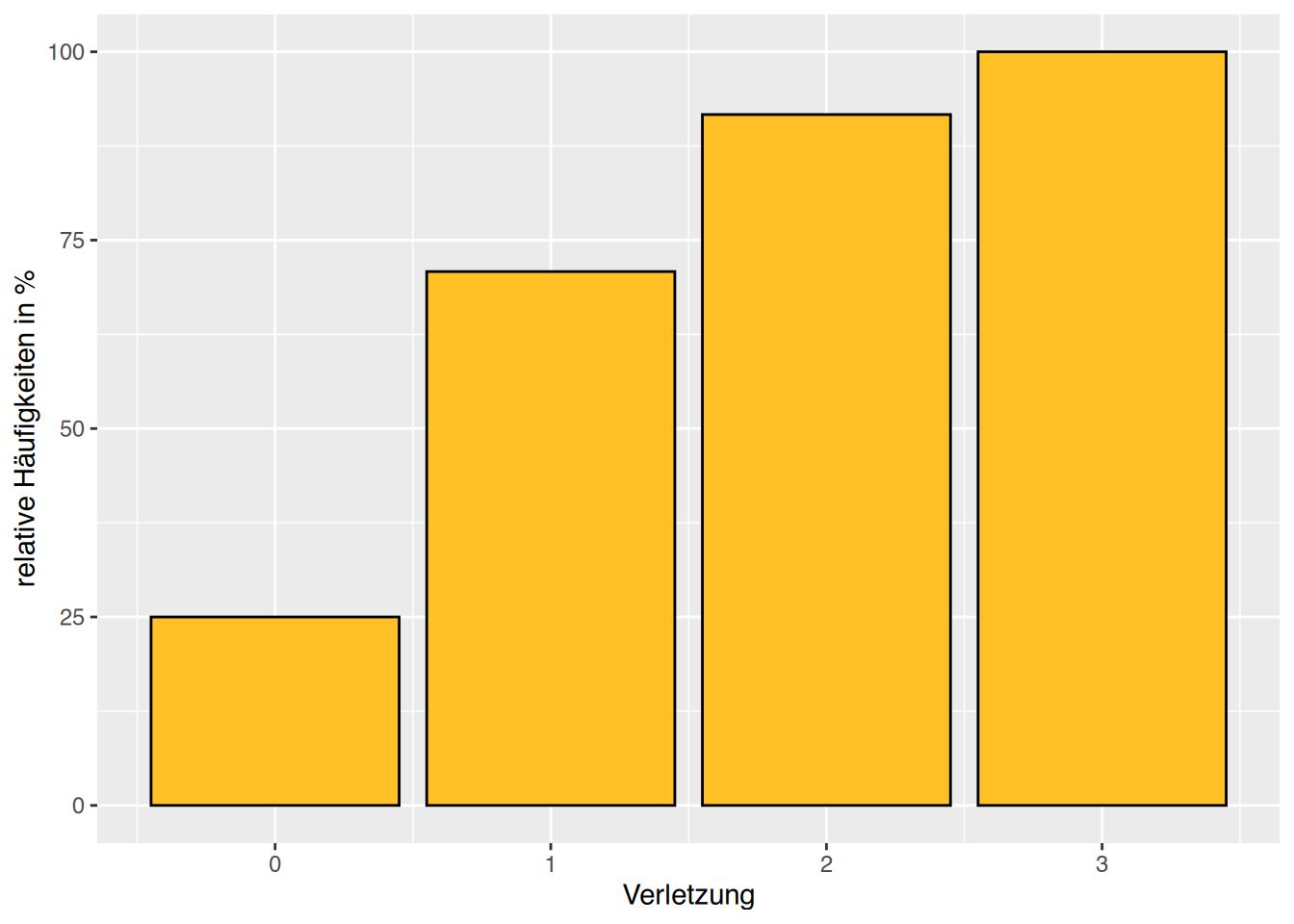
c) Erzeugen Sie ein Boxplot
boxplot(Verletzung, col="lightcoral", ylab="Anzahl der Verletzungen")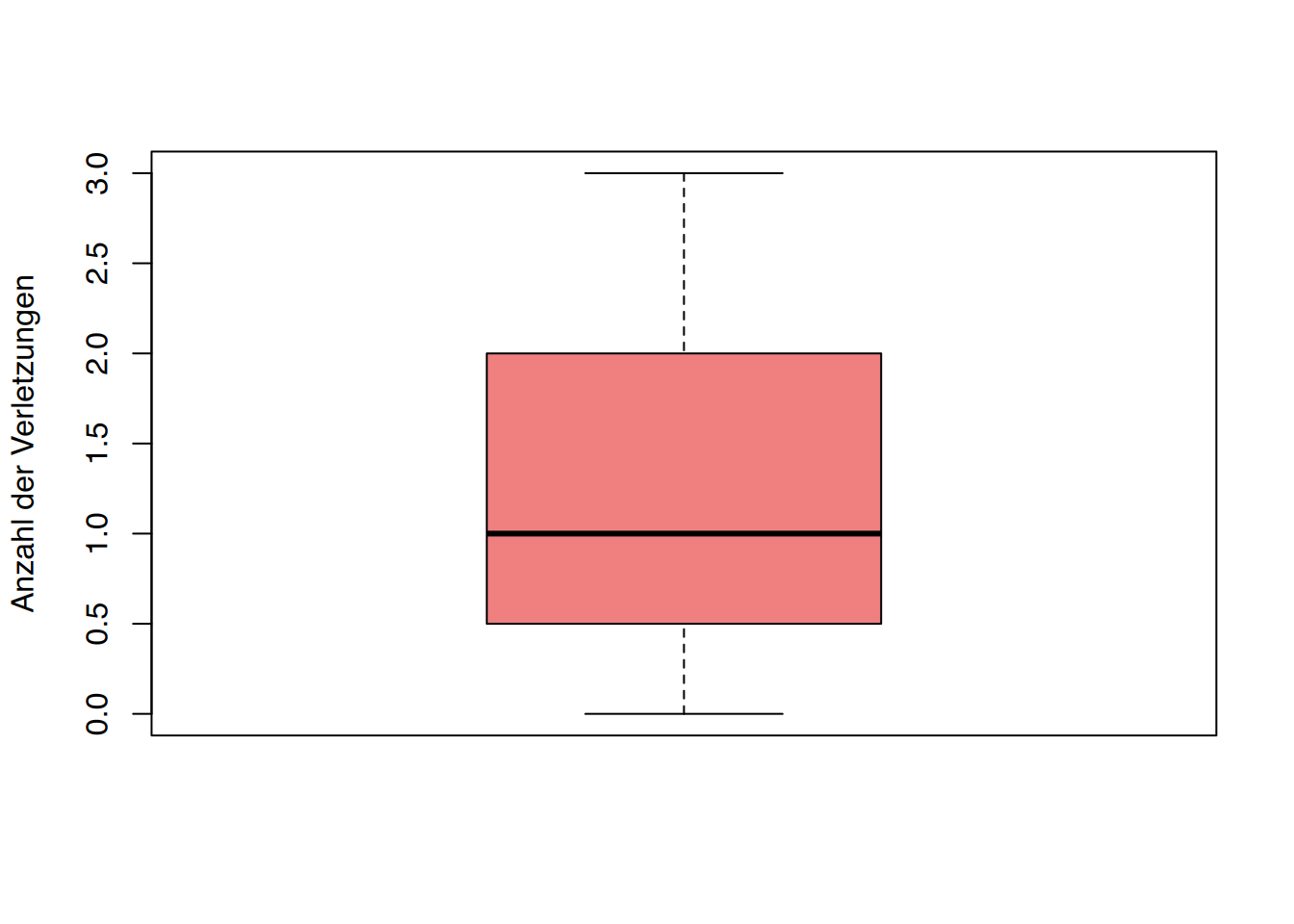
# mit ggplot
ggplot(df, aes(y=Verletzung)) +
geom_boxplot(fill="lightcoral") +
stat_boxplot(geom="errorbar") +
theme(axis.ticks.x=element_blank(),
axis.text.x=element_blank())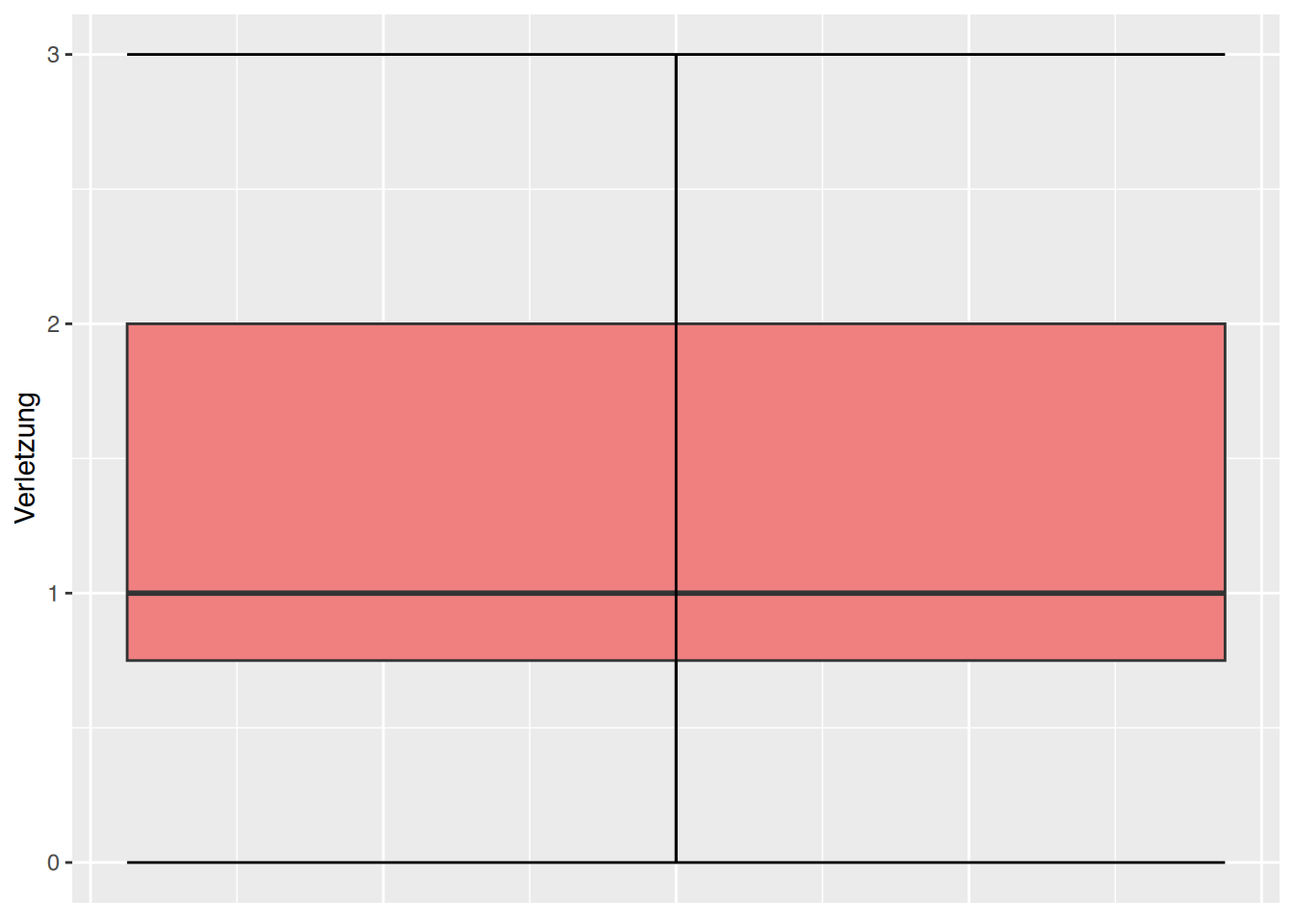
45.6 Lösung zur Aufgabe 44.1.6
a) Erstellen Sie ein Histogram der Körpergröße mit Klassen von 150cm bis 200cm, die jeweils 10cm breit sind.
Koerpergroesse <- c(179, 173, 181, 170, 158, 174, 172, 166, 194, 185,
162, 187, 198, 177, 178, 165, 154, 188, 166, 171,
175, 182, 167, 169, 172, 186, 172, 176, 168, 187)
hist(Koerpergroesse, breaks=seq(150, 200, 10),
col="aliceblue")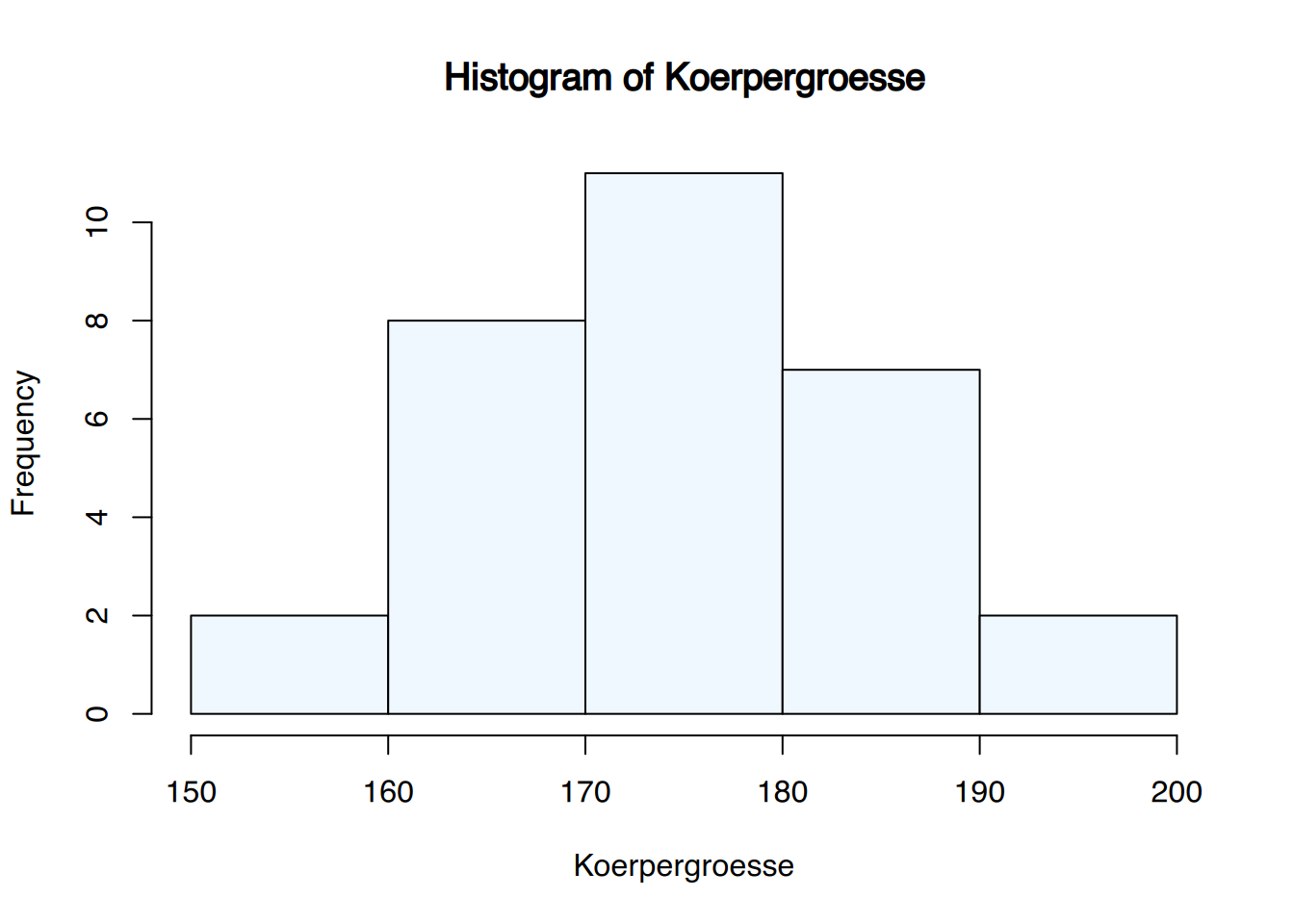
# mit ggplot
as.data.frame(Koerpergroesse) %>%
ggplot(aes(x=Koerpergroesse)) +
geom_histogram(breaks=seq(150, 200, 10),
fill="aliceblue", color="black")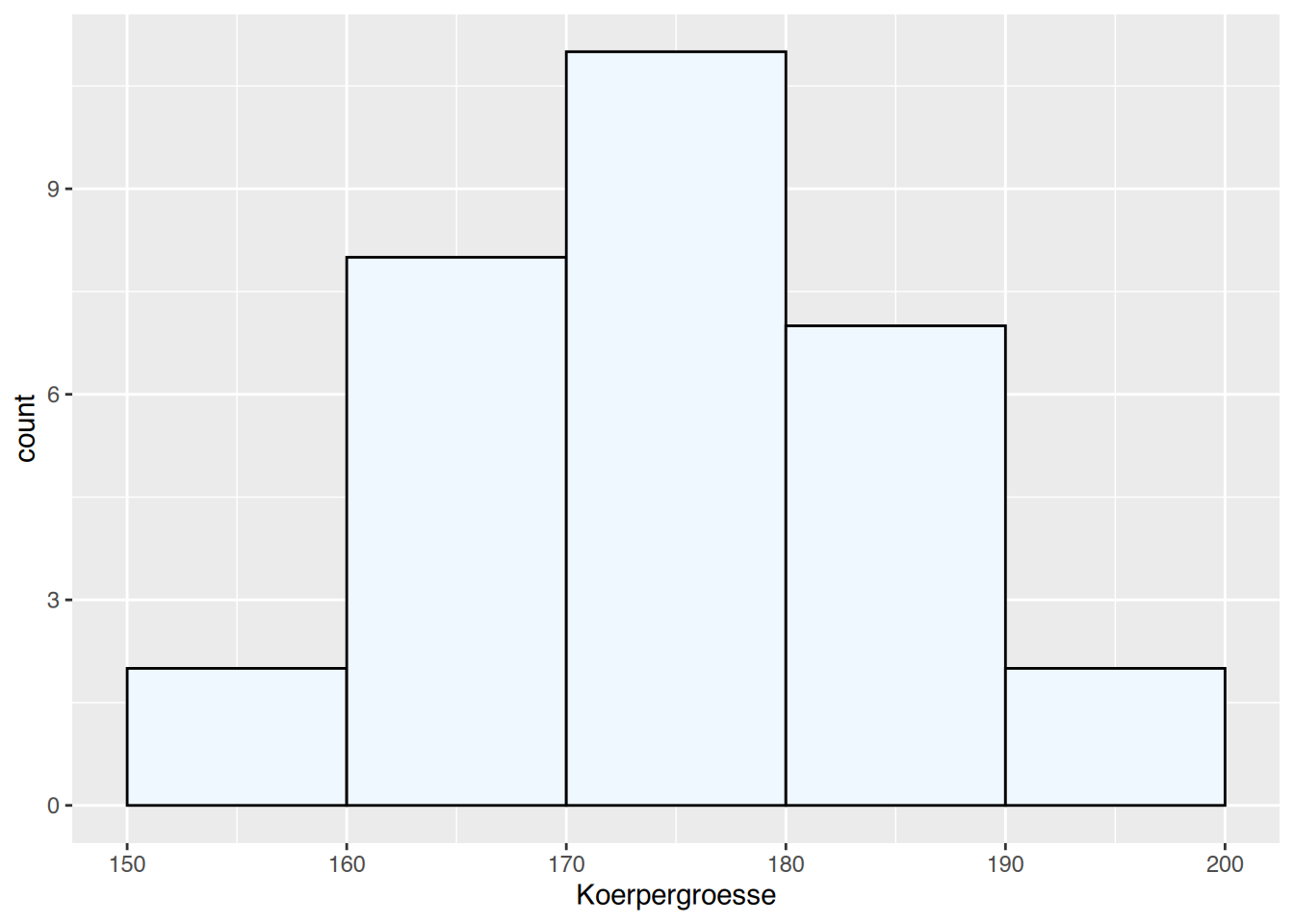
b) Gibt es Ausreißer?
boxplot(Koerpergroesse, col="dodgerblue1")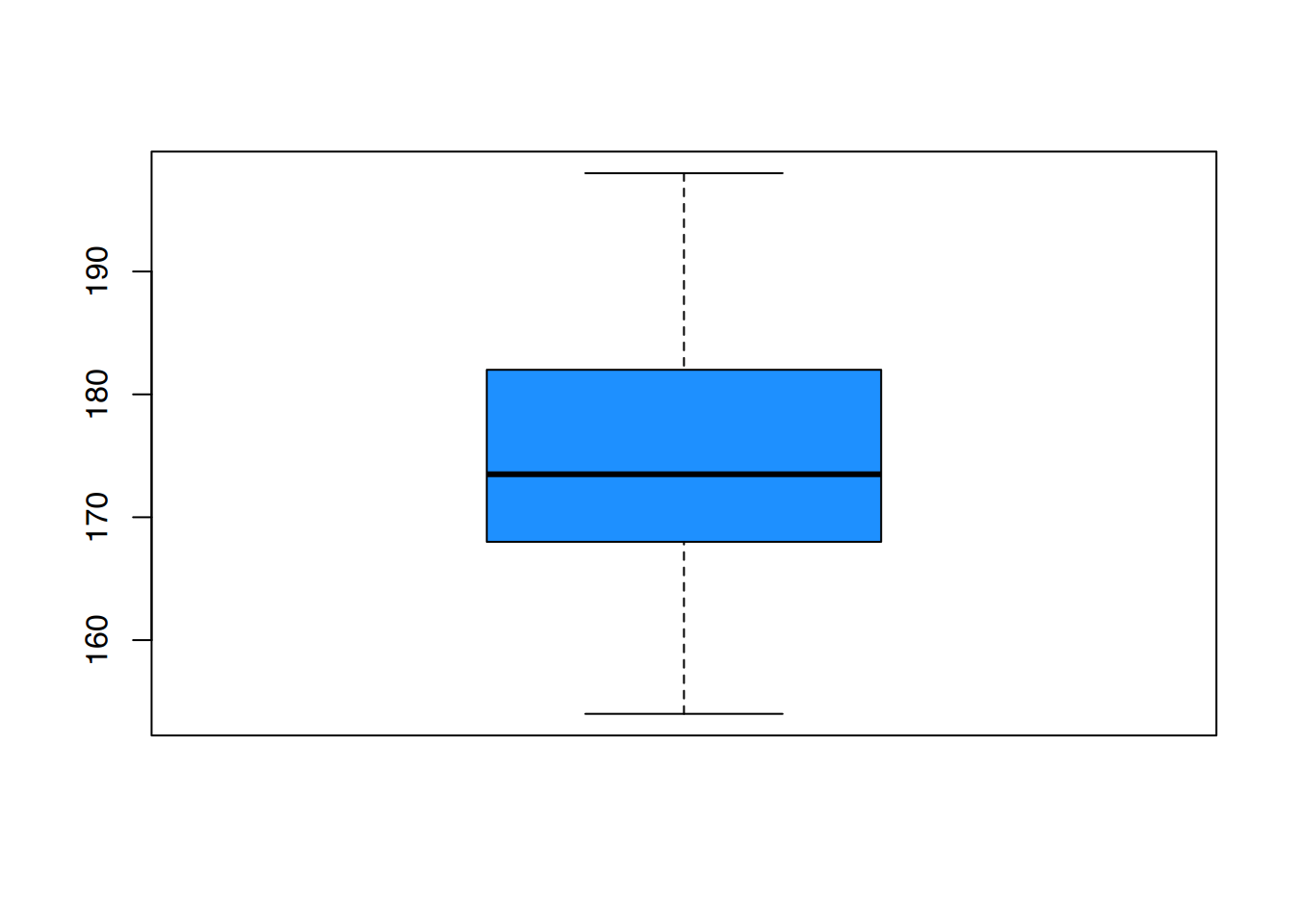
Es sind keine Ausreißer erkennbar.
45.7 Lösung zur Aufgabe 44.1.7
# lade Daten
load("https://www.produnis.de/R/data/neonates.RData")# Datensatz anschauen
summary(neonates) weight gender age smoke cigarettes
Min. :2.021 male :157 greater than 20:218 No :220 Min. : 0.000
1st Qu.:2.794 female:163 less than 20 :102 Yes:100 1st Qu.: 0.000
Median :3.030 Median : 0.000
Mean :3.026 Mean : 3.891
3rd Qu.:3.267 3rd Qu.: 8.250
Max. :4.182 Max. :22.000
smoke.before apgar1 apgar5
No :185 Min. :2.000 Min. : 2.000
Yes:135 1st Qu.:5.000 1st Qu.: 5.000
Median :6.000 Median : 6.000
Mean :5.628 Mean : 6.213
3rd Qu.:6.000 3rd Qu.: 7.000
Max. :9.000 Max. :10.000
a) Erstellen Sie die Häufigkeitstabelle des APGAR-Scores nach 1 Minute. Wenn ein Score von 3 oder weniger anzeigt, dass das Neugeborene in einem kritischen Zusatand ist, wie viel Prozent der Neugeborenen in der Stichprobe sind dann in einem kritischen Zustand?
# neue Variable "kritisch"
neonates$kritisch <- FALSE
# nur solche mit APGAR <4 sind kritisch
neonates$kritisch[neonates$apgar1 < 4] <- TRUE
# relative Häufigkeiten
table(neonates$kritisch) / length(neonates$kritisch) * 100
FALSE TRUE
92.1875 7.8125 7,81% der Neugeborenen sind in einem kritischen Zustand.
b) Erstellen Sie die Häufigkeitstabelle des Geburtsgewichts der Neugeborenen, indem Sie die Daten in Klassen mit einer Breite von 0,5 kg von 2 bis 4,5 kg einteilen. Welches Intervall enthält die meisten Neugeborenen?
# neue Variable für die Gewichtsklassifikation
neonates$gewiKat <- cut(neonates$weight,
breaks=seq(2, 4.5, 0.5),
ordered_results=TRUE)
# einfache Häufigkeitstabelle
table(neonates$gewiKat)
(2,2.5] (2.5,3] (3,3.5] (3.5,4] (4,4.5]
22 127 146 24 1 # oder vollständige
jgsbook::freqTable(neonates$gewiKat) Wert Haeufig Hkum Relativ Rkum
1 (2,2.5] 22 22 6.88 6.88
2 (2.5,3] 127 149 39.69 46.57
3 (3,3.5] 146 295 45.62 92.19
4 (3.5,4] 24 319 7.50 99.69
5 (4,4.5] 1 320 0.31 100.00Das Intervall von 3-3,5kg enthält die meisten Neugeborenen.
c) Vergleichen Sie die Häufigkeitsverteilung des APGAR-Scores nach 1 Minute für Mütter unter 20 Jahren und für Mütter über 20 Jahren. Welche Gruppe hat mehr Neugeborene in kritischem Zustand?
# gruppieren
gruppe1 <- neonates$apgar1[neonates$age=="less than 20"]
gruppe2 <- neonates$apgar1[neonates$age=="greater than 20"]
# Jünger als 20
jgsbook::freqTable(gruppe1) Wert Haeufig Hkum Relativ Rkum
1 2 2 2 1.96 1.96
2 3 11 13 10.78 12.74
3 4 16 29 15.69 28.43
4 5 28 57 27.45 55.88
5 6 28 85 27.45 83.33
6 7 12 97 11.76 95.09
7 8 4 101 3.92 99.01
8 9 1 102 0.98 99.99# Älter als 20
jgsbook::freqTable(gruppe2) Wert Haeufig Hkum Relativ Rkum
1 2 2 2 0.92 0.92
2 3 10 12 4.59 5.51
3 4 22 34 10.09 15.60
4 5 53 87 24.31 39.91
5 6 69 156 31.65 71.56
6 7 34 190 15.60 87.16
7 8 24 214 11.01 98.17
8 9 4 218 1.83 100.00In der Gruppe der unter-20-jährigen liegt der Prozentsatz an Neugeborenen mit APGAR-Werten kleinergleich 3 bei 12,74%. In der Gruppe der über-20-jährigen liegt der Prozentwert bei 5,51%. Es tritt also in der Gruppe der jüngeren Mütter häufiger auf.
d) Vergleichen Sie die relative Häufigkeitsverteilung des Geburtsgewichts der Neugeborenen, je nachdem, ob die Mutter während der Schwangerschaft geraucht hat oder nicht. Wenn ein Gewicht unter 2,5 kg als niedriges Gewicht gilt, welche Gruppe hat einen höheren Prozentsatz an Neugeborenen mit niedrigem Gewicht?
# wir müssen neu klassieren, damit weight KLEINER 2,5kg ist
# Gewichtsklassifikation mit "rigth=FALSE"
neonates$gewiKat <- cut(neonates$weight,
breaks=seq(2, 4.5, 0.5),
right=FALSE, ordered_results=TRUE)
gruppe1 <- neonates$gewiKat[neonates$smoke=="No"]
gruppe2 <- neonates$gewiKat[neonates$smoke=="Yes"]
# Nichtraucherinnen
jgsbook::freqTable(gruppe1) Wert Haeufig Hkum Relativ Rkum
1 [2,2.5) 5 5 2.27 2.27
2 [2.5,3) 75 80 34.09 36.36
3 [3,3.5) 119 199 54.09 90.45
4 [3.5,4) 20 219 9.09 99.54
5 [4,4.5) 1 220 0.45 99.99# Raucherinnen
jgsbook::freqTable(gruppe2) Wert Haeufig Hkum Relativ Rkum
1 [2,2.5) 17 17 17 17
2 [2.5,3) 52 69 52 69
3 [3,3.5) 27 96 27 96
4 [3.5,4) 4 100 4 100
5 [4,4.5) 0 100 0 100In der Gruppe der Nichtraucherinnen trat ein Geburtsgewicht kleiner 2,5kg in 2,27% der Fälle auf. Bei den Raucherinnen waren es 17%.
e) Berechnen Sie die Prävalenz von Neugeborenen mit niedrigem Gewicht für Mütter, die vor der Schwangerschaft geraucht haben, und den Nichtraucherinnen.
gruppe1 <- neonates$gewiKat[neonates$smoke.before=="No"]
gruppe2 <- neonates$gewiKat[neonates$smoke.before=="Yes"]
# Nichtraucherinnen
jgsbook::freqTable(gruppe1) Wert Haeufig Hkum Relativ Rkum
1 [2,2.5) 2 2 1.08 1.08
2 [2.5,3) 60 62 32.43 33.51
3 [3,3.5) 105 167 56.76 90.27
4 [3.5,4) 18 185 9.73 100.00
5 [4,4.5) 0 185 0.00 100.00# Raucherinnen
jgsbook::freqTable(gruppe2) Wert Haeufig Hkum Relativ Rkum
1 [2,2.5) 20 20 14.81 14.81
2 [2.5,3) 67 87 49.63 64.44
3 [3,3.5) 41 128 30.37 94.81
4 [3.5,4) 6 134 4.44 99.25
5 [4,4.5) 1 135 0.74 99.99Die Prävalenz beträgt unter den Nichtraucherinnen 1,08% und unter den Raucherinnen 14,81%.
f) Berechnen Sie das relative Risiko eines niedrigen Geburtsgewichts des Neugeborenen, wenn die Mutter während der Schwangerschaft raucht, im Vergleich dazu, wenn die Mutter nicht raucht.
# neue binäre Variable, ob Gewicht niedrig ist
neonates$gewiLow <- FALSE
neonates$gewiLow[neonates$gewiKat=="[2,2.5)"] <- TRUE
# Kreuztabelle
table(neonates$smoke, neonates$gewiLow)
FALSE TRUE
No 215 5
Yes 83 17Die Formel für das relative Risiko lautet:
\(\text{relatives Risiko} = \frac{a\cdot(c+d)}{c\cdot(a+b)}\)
# Kreuztabelle als numerische Werte
tab <- as.numeric(table(neonates$smoke, neonates$gewiLow))
# rechne das relative Risiko nach der obigen Formel
( tab[1] * (tab[2]+tab[4]) ) / ( tab[2] * (tab[1]+tab[3]) )[1] 1.177437Raucherinnen haben ein 1,177437-fach höheres Risiko ein Kind mit niedrigem Gewicht zugebären als Nichtraucherinnen. Die Wahrscheinlichkeit ist in der Raucherinnengruppe also 17,74% höher als bei den Nichtraucherinnen.
g) Erstellen Sie ein Balkendiagramm des APGAR-Scores nach 1 Minute. Welcher Score ist am häufigsten?
# mit R base
barplot(table(neonates$apgar1), col="mistyrose")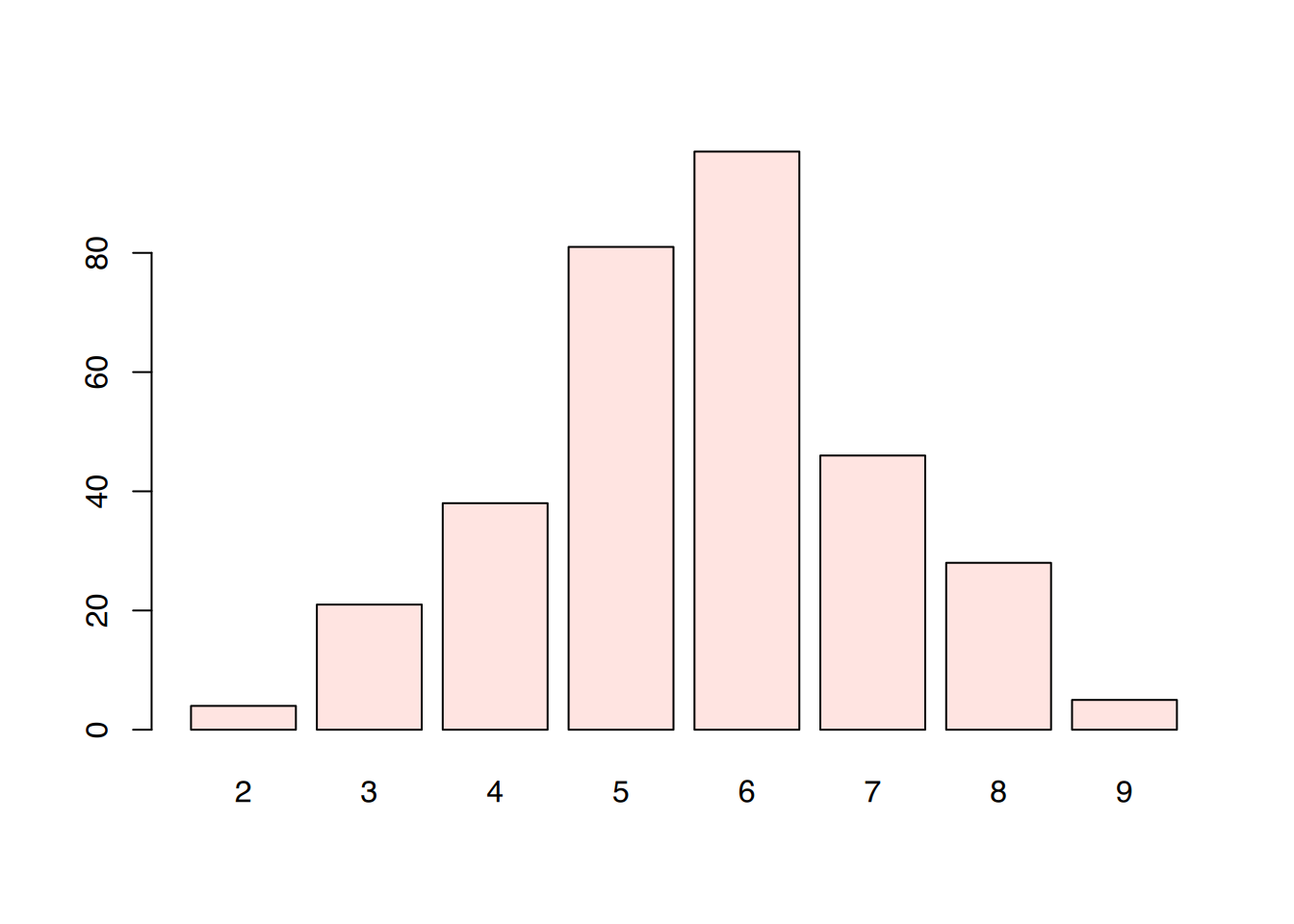
# mit ggplot
ggplot(neonates, aes(x=apgar1)) +
geom_bar(color="black", fill="mistyrose")+
scale_x_continuous(breaks=seq(2, 9, 1))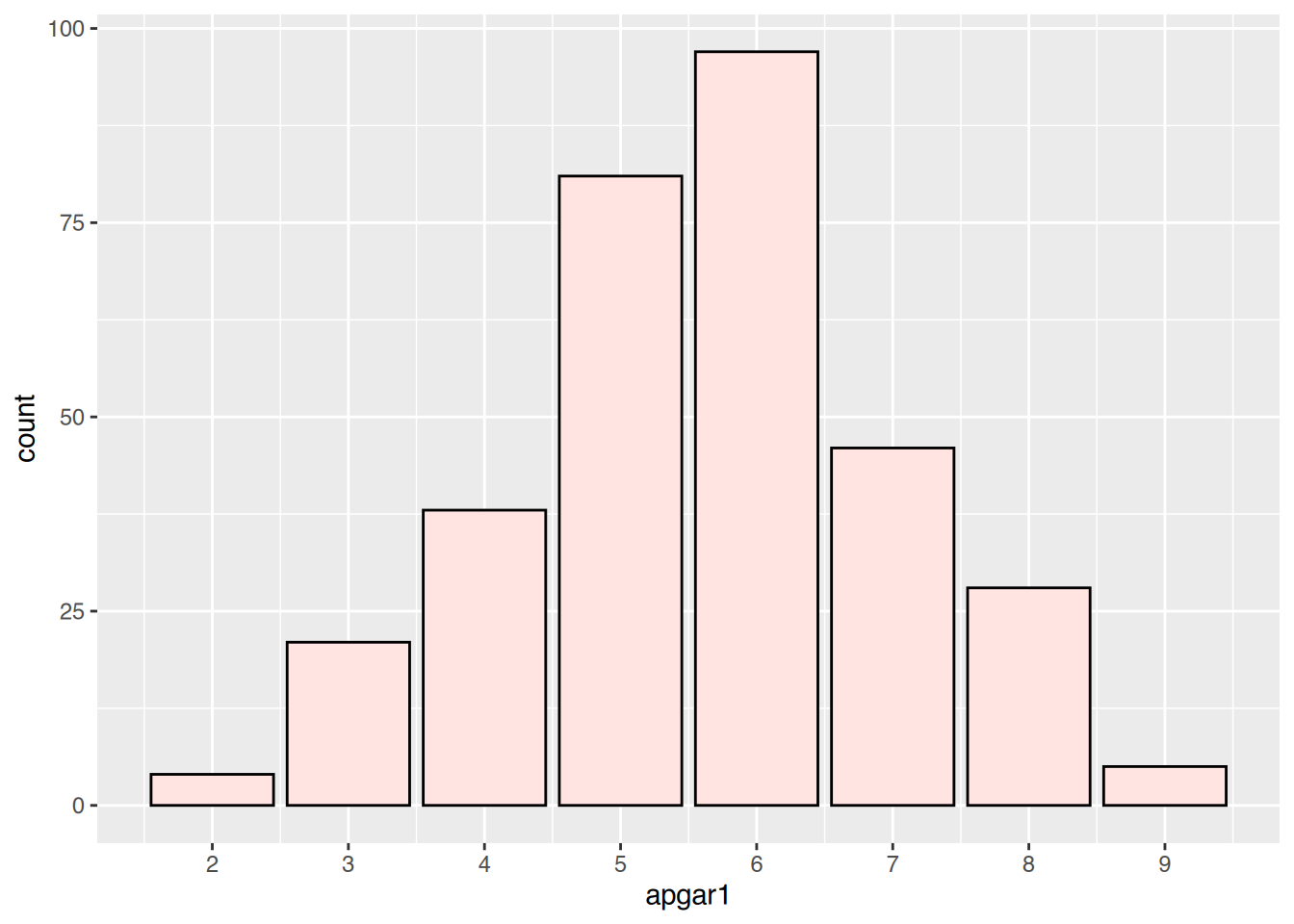
Am häufigsten tritt Wert \(6\) auf.
h) Erstellen Sie das Balkendiagramm der kumulierten relativen Häufigkeit des APGAR-Scores nach 1 Minute. Unter welchem Wert liegen die Hälfte der Neugeborenen?
# mit R base
# plotte das kumulative Balkendiagramm
barplot(cumsum(table(neonates$apgar1))/sum(table(neonates$apgar1)),
col="olivedrab1", main = "kumulierte relative Häufigkeiten")
# Linie bei 50% ziehen
abline(h=0.5, col="blue")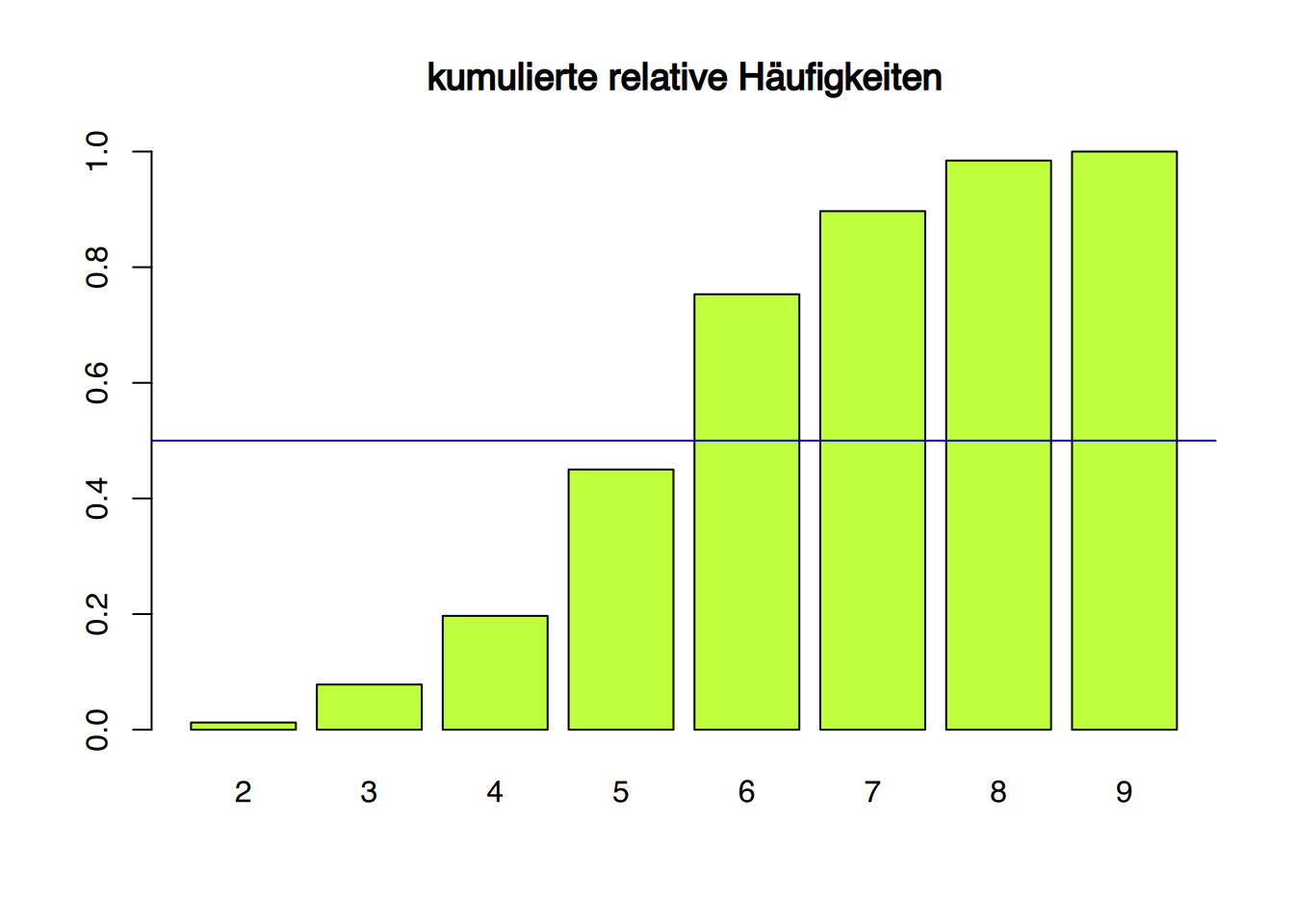
# mit ggplot()
ggplot(neonates, aes(x=apgar1)) +
geom_bar(aes(y=cumsum(after_stat(count)/sum(after_stat(count)))),
fill="olivedrab1", color="black") +
ylab("relative Häufigkeit") +
geom_hline(yintercept= 0.5, color="blue", linewidth=1) +
scale_x_continuous(breaks=seq(2, 9, 1))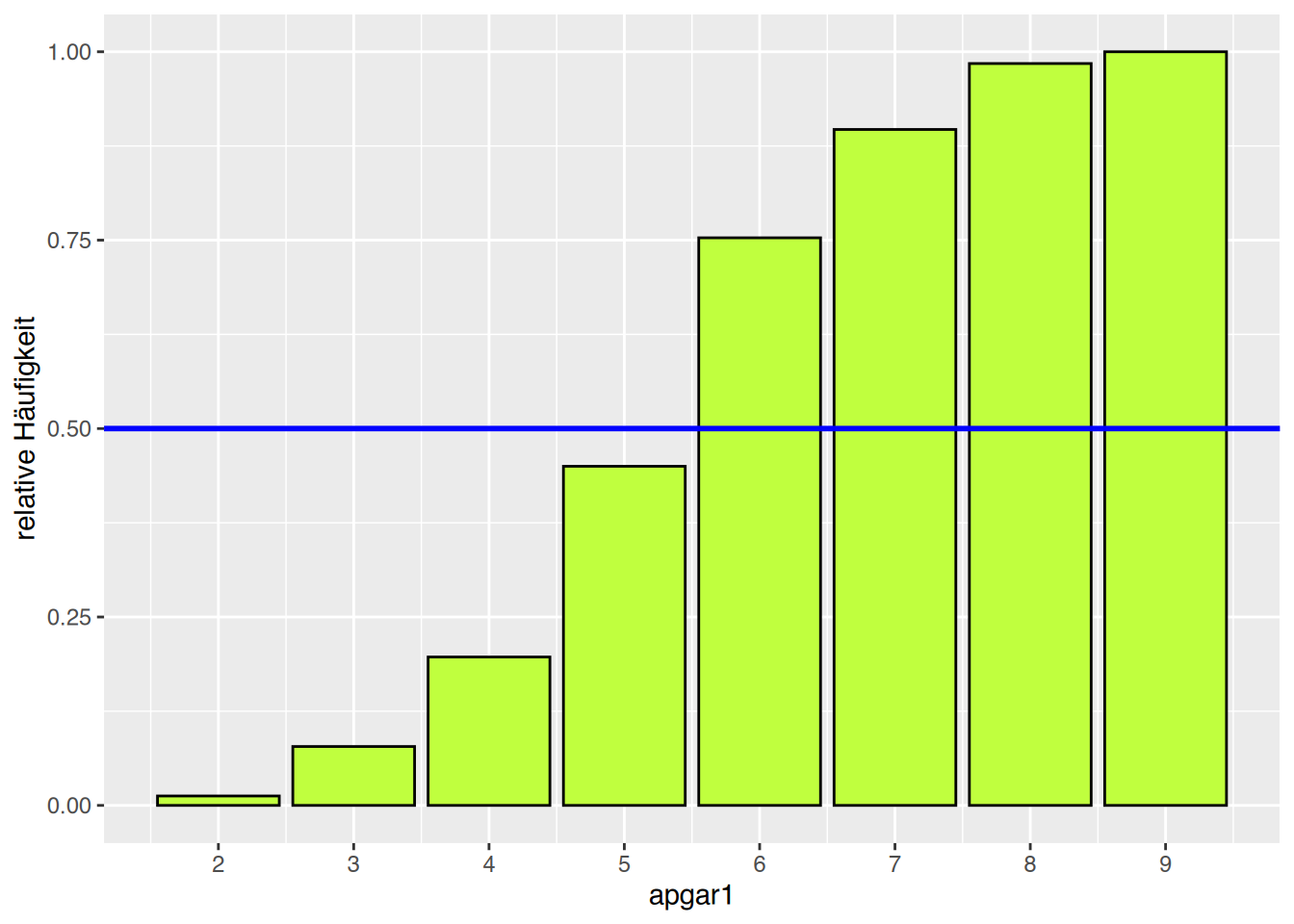
Der Median liegt bei \(6\).
i) Vergleichen Sie die Balkendiagramme der relativen Häufigkeitsverteilungen des APGAR-Scores nach 1 Minute, je nachdem, ob die Mutter während der Schwangerschaft geraucht hat oder nicht. Welche Schlussfolgerungen können gezogen werden?
# mit R base
gruppe1 <- neonates$apgar1[neonates$smoke=="No"]
gruppe2 <- neonates$apgar1[neonates$smoke=="Yes"]
barplot( table(gruppe1)/sum(table(gruppe1)) *100,
ylab="relative Häufigkeit in %", main="Nichtraucherinnen",
ylim=c(0,35), col="paleturquoise1")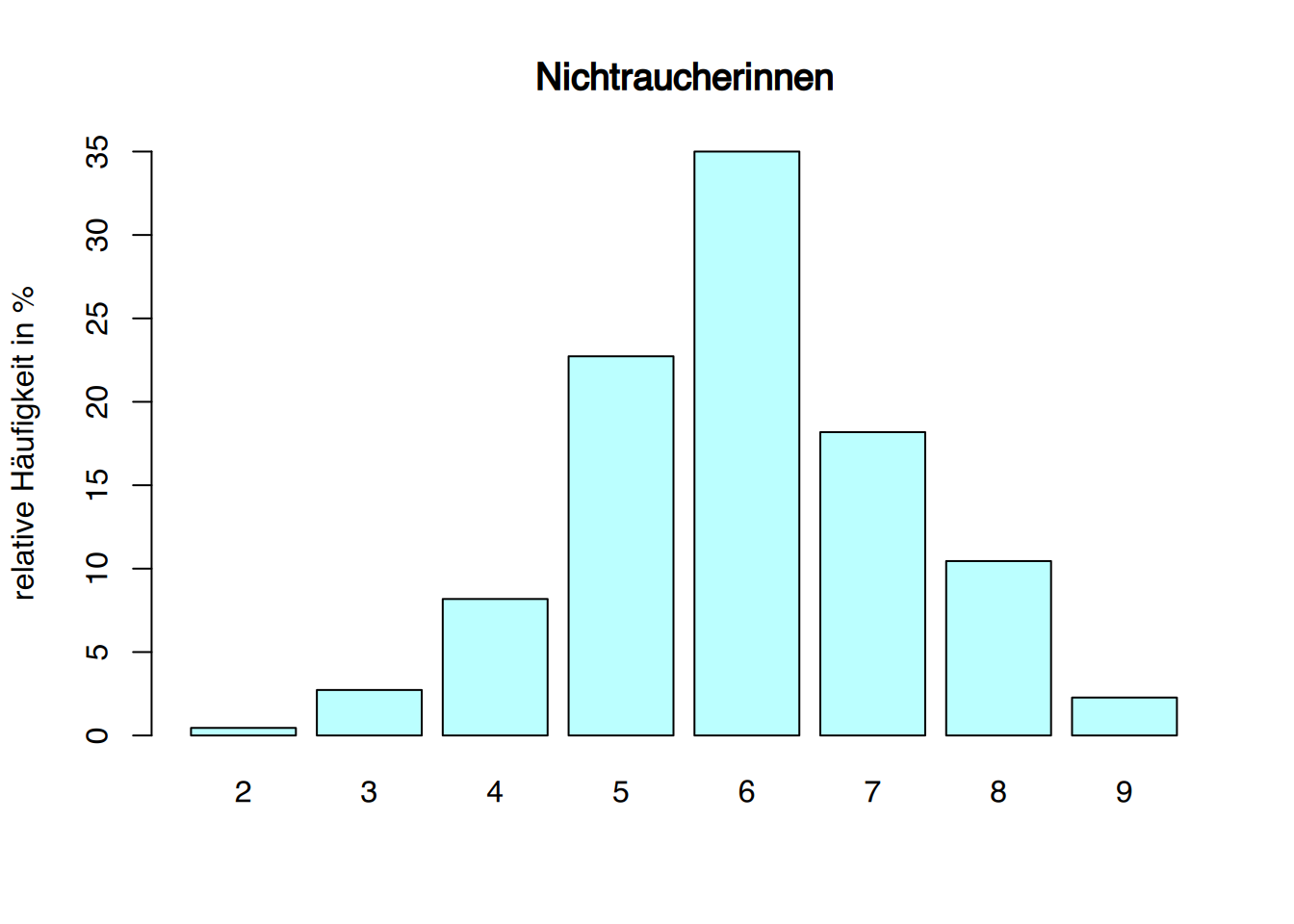
barplot( table(gruppe2)/sum(table(gruppe2)) *100,
ylab="relative Häufigkeit in %", main="Raucherinnen",
ylim=c(0,35), col="paleturquoise4")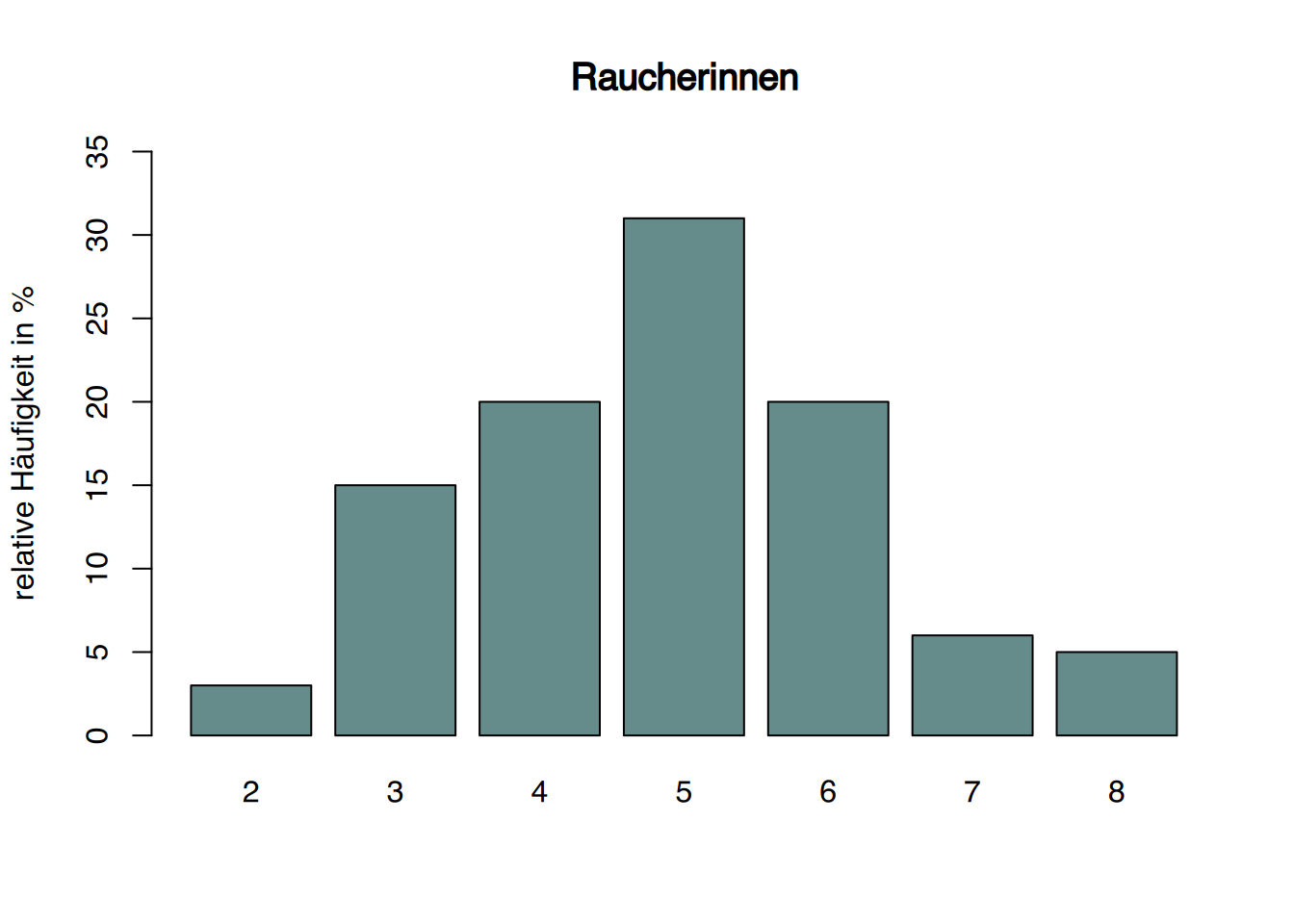
# mit ggplot
# Nichtraucherinnen
neonates %>%
filter(smoke=="No") %>%
ggplot(aes(x=apgar1))+
geom_bar(aes(y=after_stat(count)/sum(after_stat(count))*100),
color="black", fill="paleturquoise1")+
scale_x_continuous(breaks=seq(2, 9, 1)) +
ylab("relative Häufigkeit in %") +
ylim(0,35)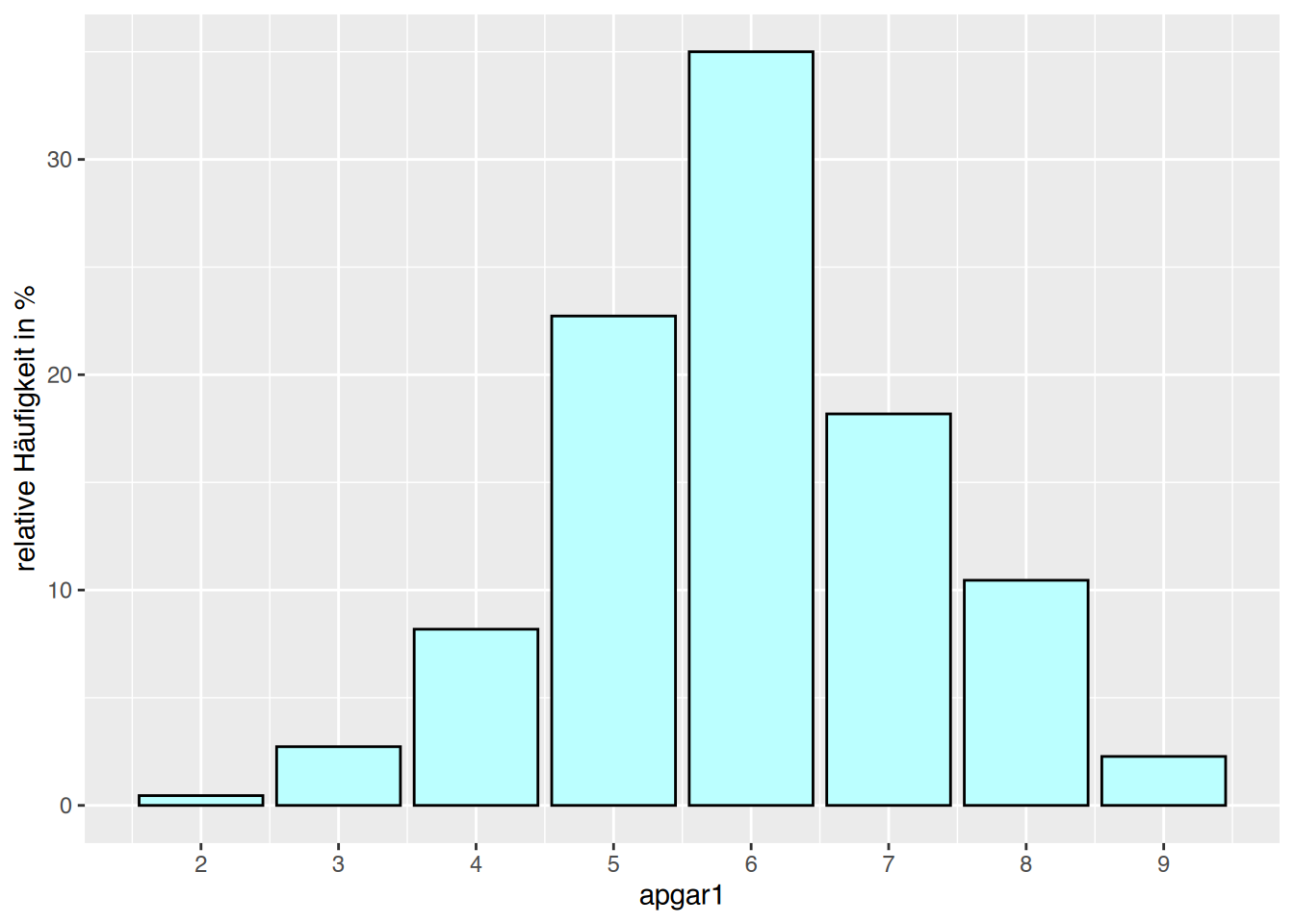
# Raucherinnen
neonates %>%
filter(smoke=="Yes") %>%
ggplot(aes(x=apgar1))+
geom_bar(aes(y=after_stat(count)/sum(after_stat(count))*100),
color="black", fill="paleturquoise4") +
scale_x_continuous(breaks=seq(2, 9, 1)) +
ylab("relative Häufigkeit in %") +
ylim(0,35)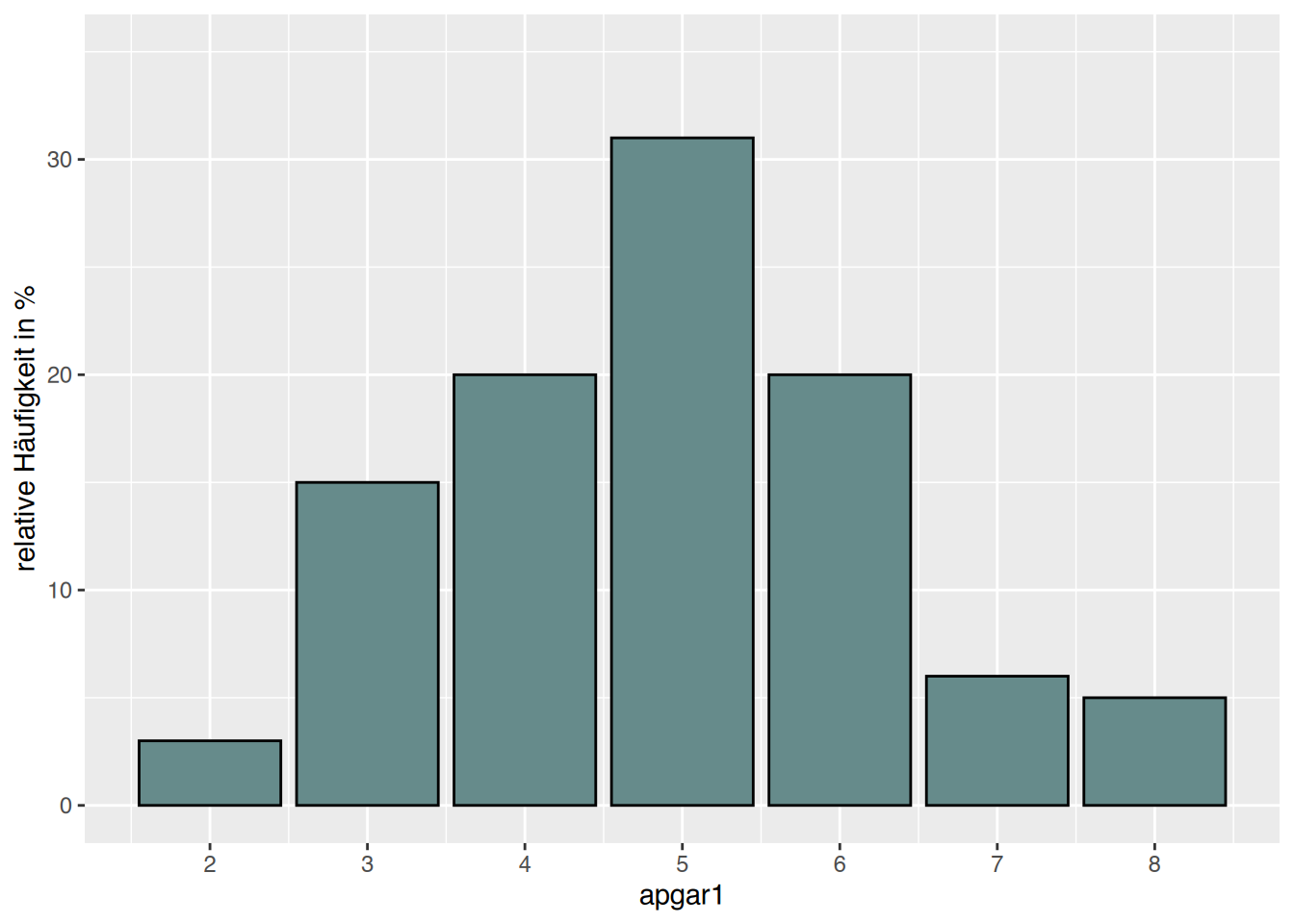
Die Kinder der Raucherinnen haben geringere APGAR-Werte.
j) Erstellen Sie ein Histogramm der Geburtsgewichte der Neugeborenen mit Klassenbreiten von 0,5 kg von 2 bis 4,5 kg. Welche Klasse enthält die meisten Neugeborenen?
# mit R base
hist(neonates$weight,
breaks = seq(2, 4.5, 0.5),
col="peachpuff3")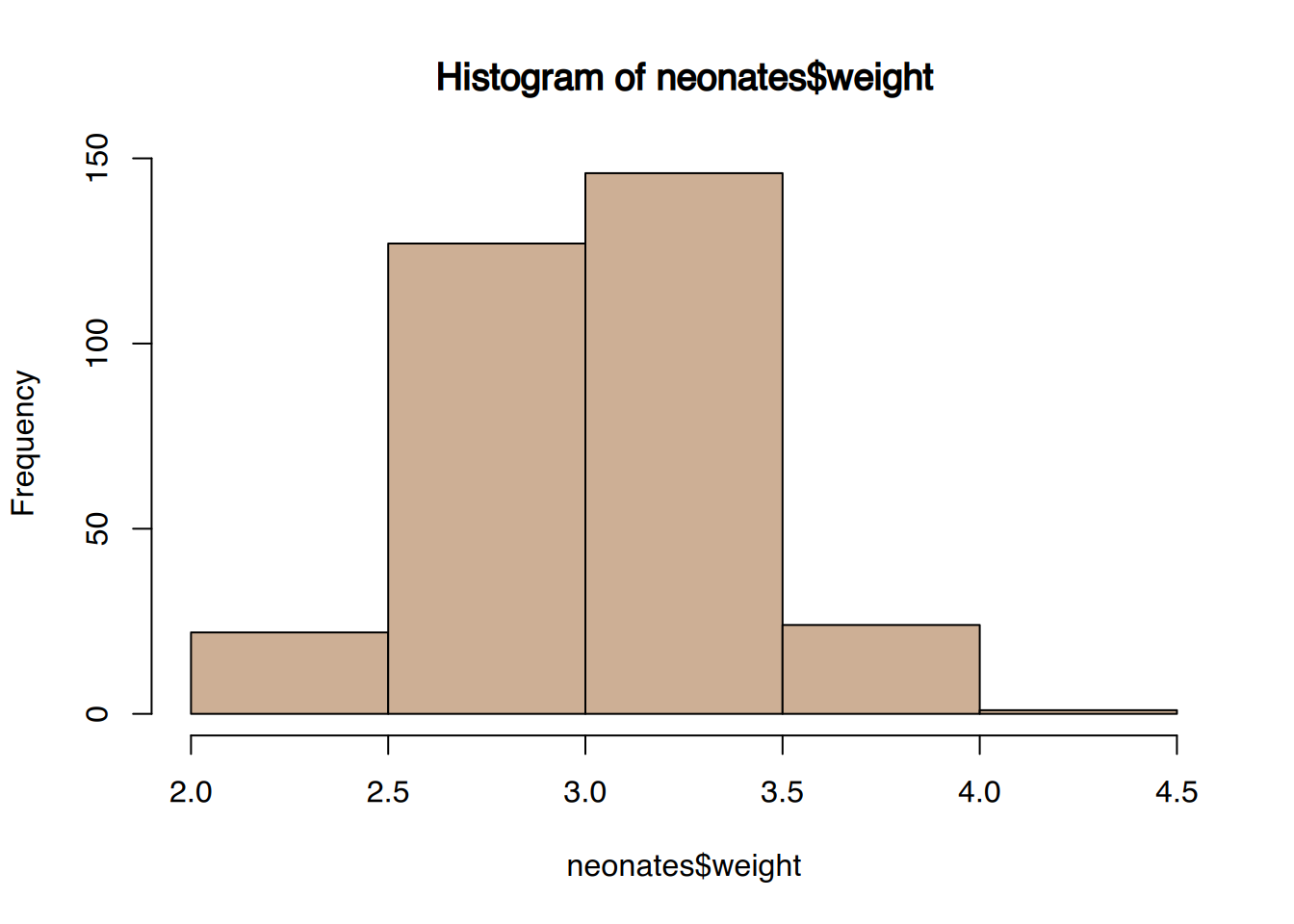
# mit ggplot
ggplot(neonates, aes(x=weight)) +
geom_histogram( breaks = seq(2, 4.5, 0.5),
fill="peachpuff3", color="black")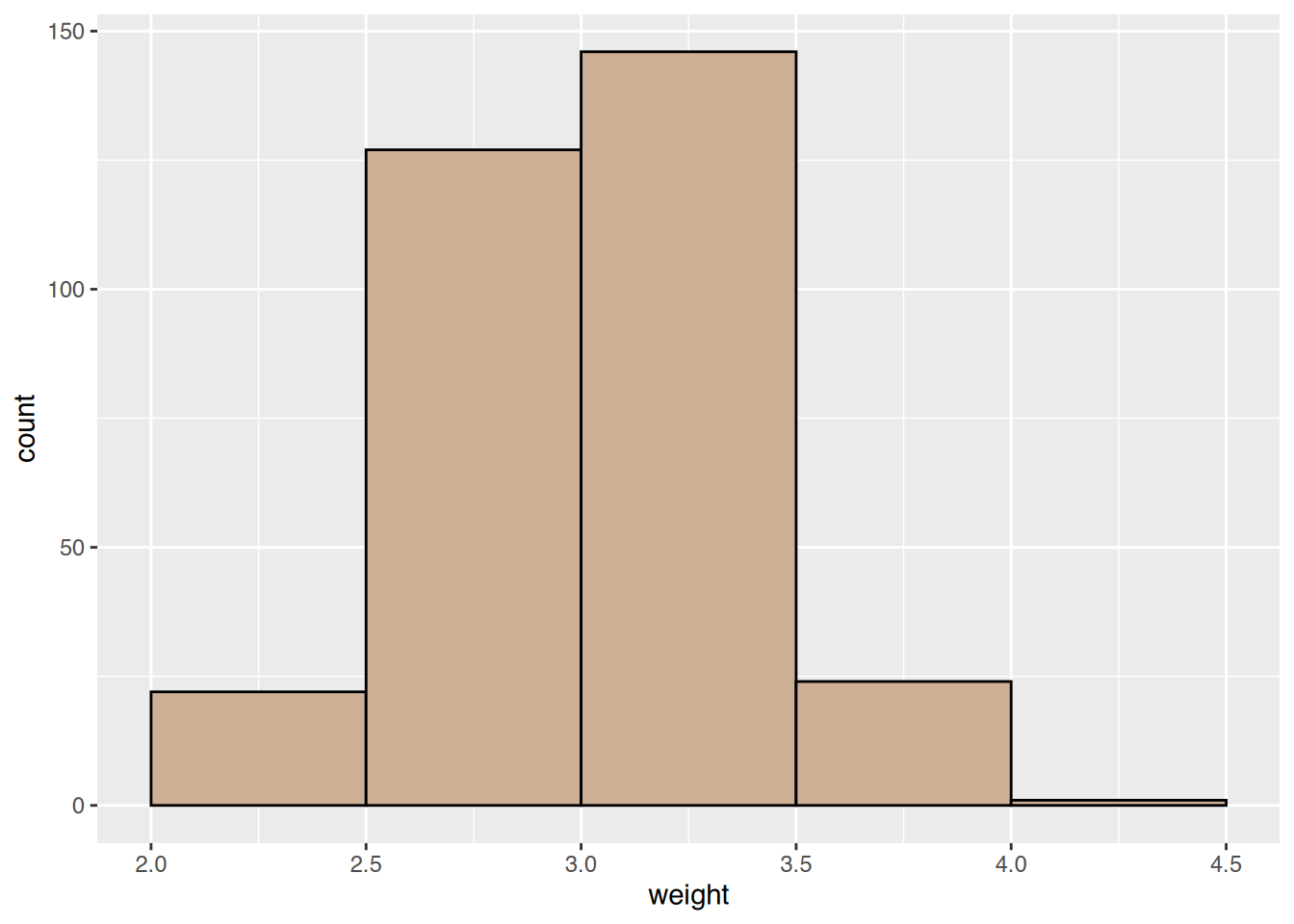
Die Gewichtsklasse \(3\)kg-\(3,5\)kg enthält die meisten Neugeborenen.
k) Vergleichen Sie die relativen Häufigkeitshistogramme der Geburtsgewichte der Neugeborenen, mit Klassenbreiten von 0,5 kg von 2 bis 4,5 kg, je nachdem, ob die Mutter während der Schwangerschaft geraucht hat oder nicht. Welche Gruppe hat Neugeborene mit geringeren Gewichten?
# mit R base
hist(neonates$weight[neonates$smoke=="No"],
breaks=seq(2, 4.5, 0.5), col="springgreen1",
main="Nichtraucherinnen", xlab="Gewichtskategorien",
ylab="relative Häufigkeiten", freq=FALSE)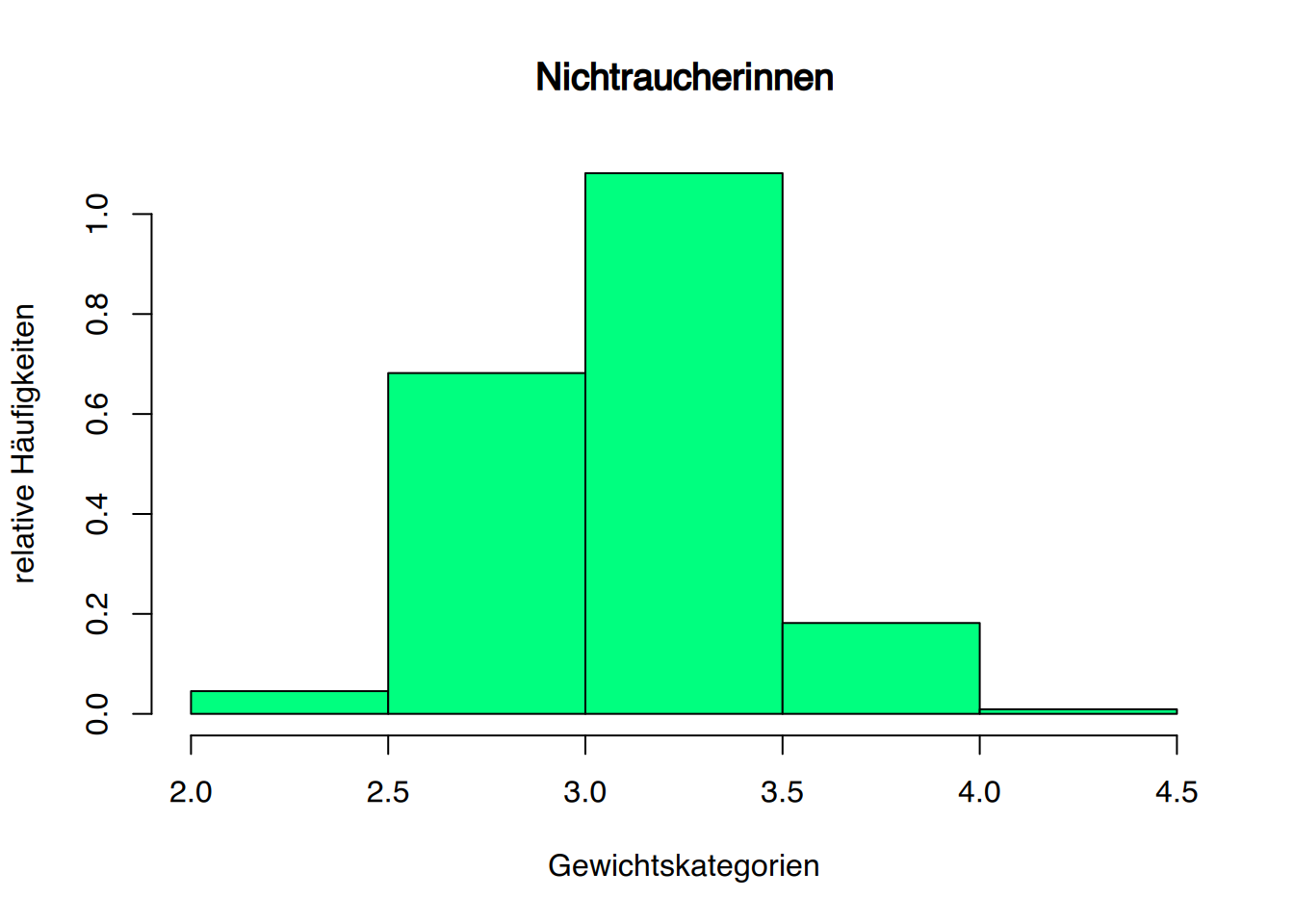
# Raucherinnen
hist(neonates$weight[neonates$smoke=="Yes"],
breaks=seq(2, 4.5, 0.5), col="springgreen4",
main="Raucherinnen", xlab="Gewichtskategorien",
ylab="relative Häufigkeiten", freq=FALSE)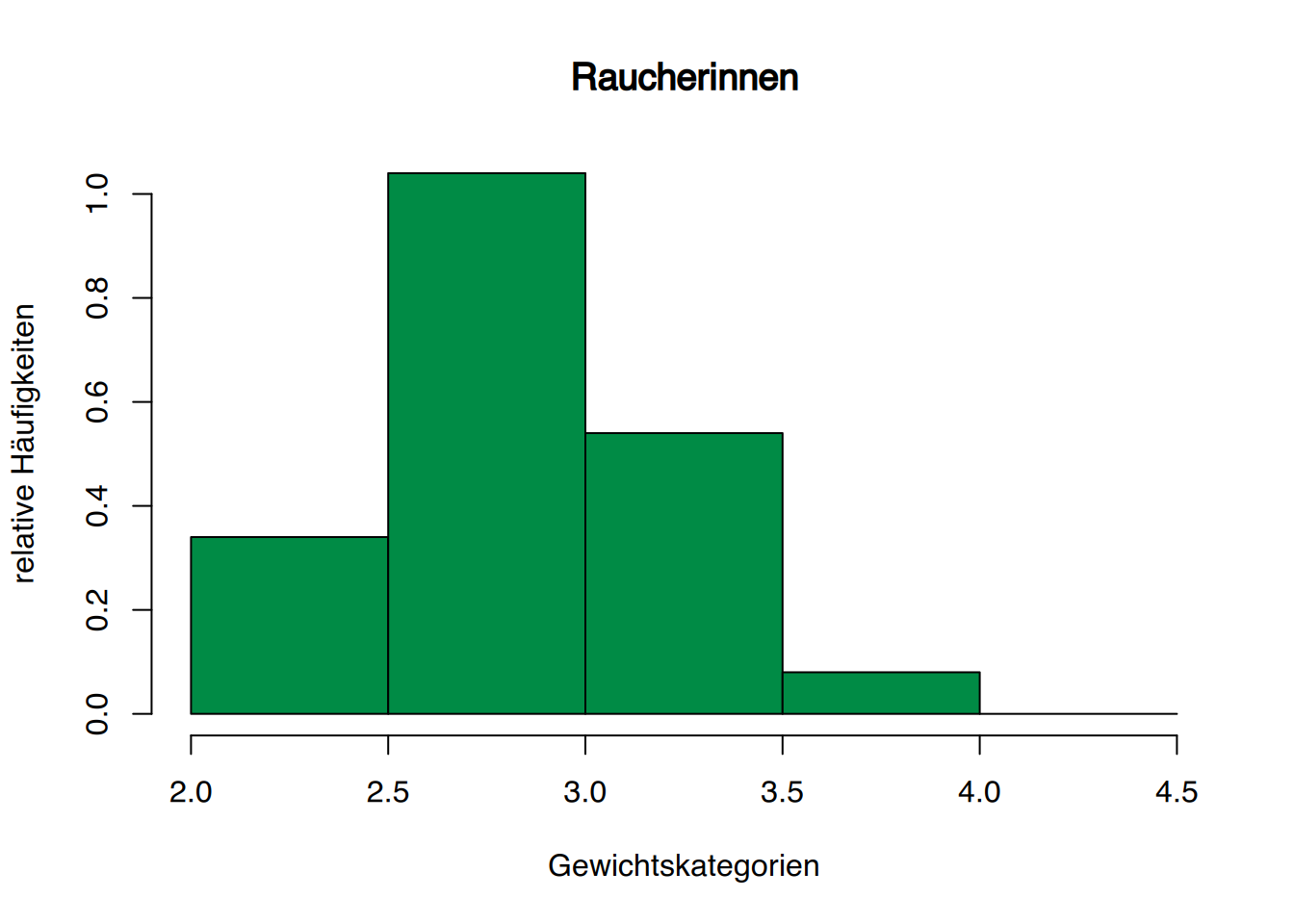
# mit ggplot
neonates %>%
filter(smoke=="No") %>%
ggplot(aes(x=weight)) +
geom_histogram(aes(y=after_stat(count)/sum(after_stat(count))),
breaks=seq(2, 4.5, 0.5),
fill="springgreen1", color="black") +
ylab("relative Häufigkeiten") + xlab("Geburtsgewicht")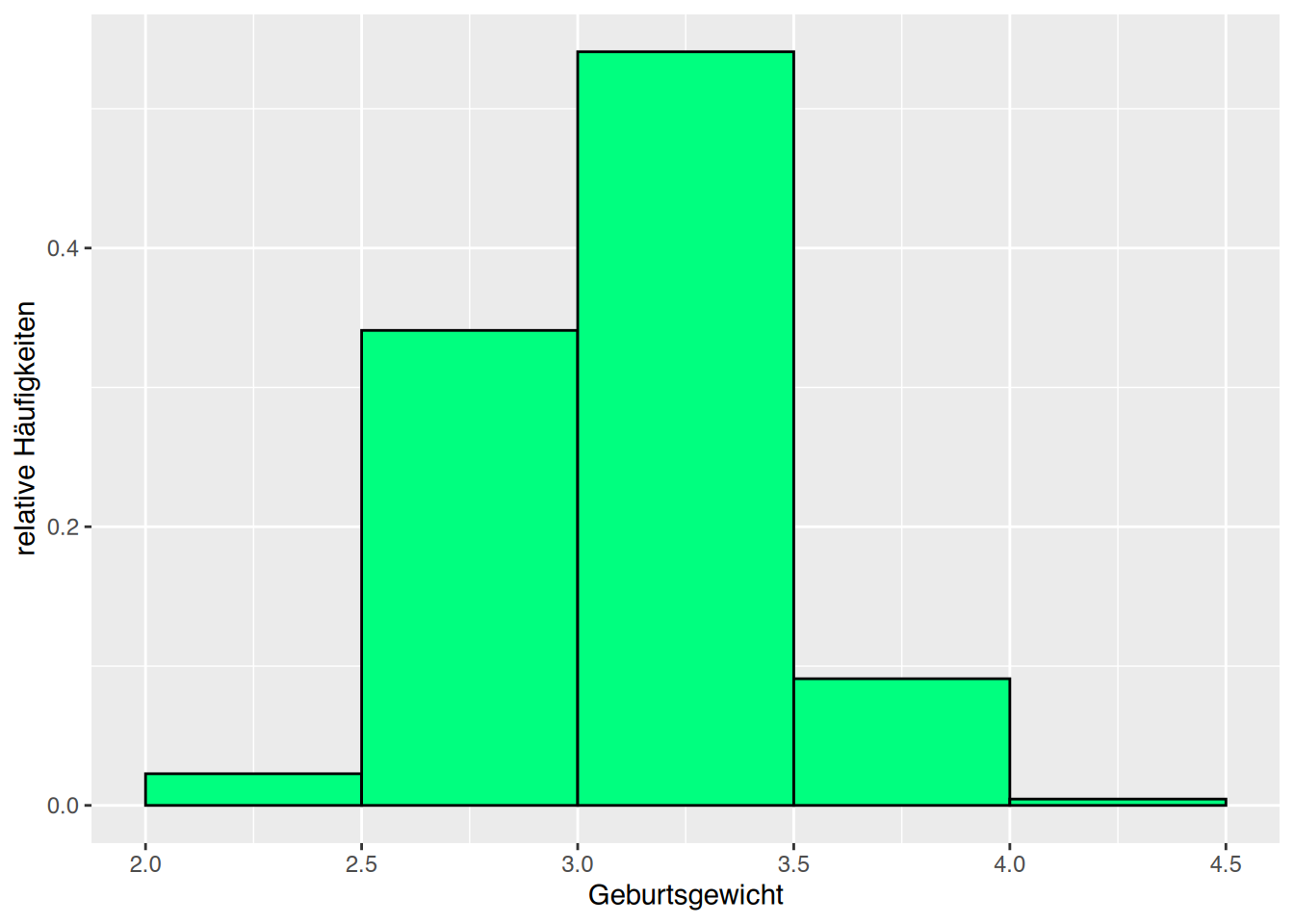
# Raucherinnen
neonates %>%
filter(smoke=="Yes") %>%
ggplot(aes(x=weight)) +
geom_histogram(aes(y=after_stat(count)/sum(after_stat(count))),
breaks=seq(2, 4.5, 0.5),
fill="springgreen4", color="black") +
ylab("relative Häufigkeiten") + xlab("Geburtsgewicht")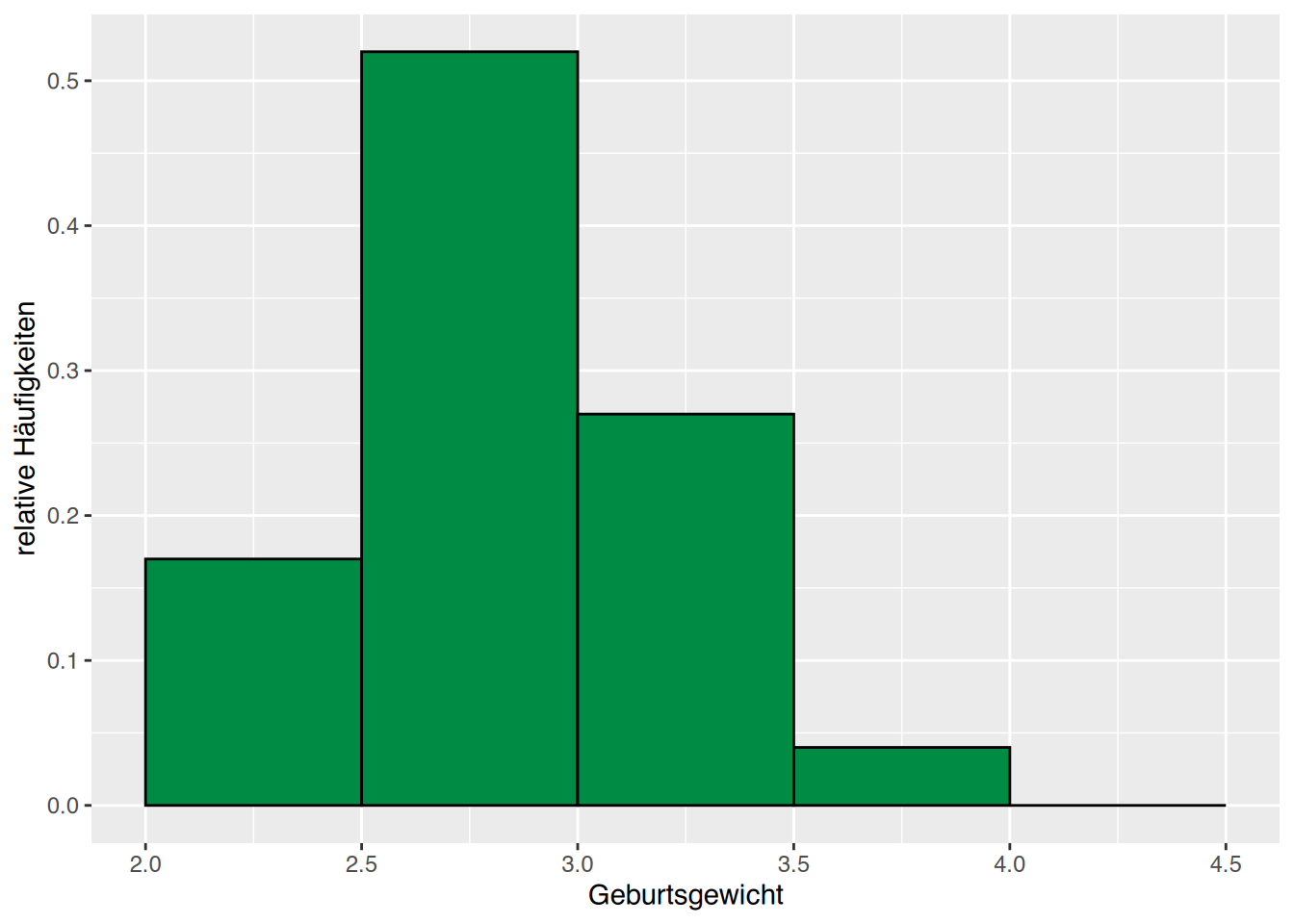
Kinder von Raucherinnen haben durchschnittlich weniger Geburtsgewicht.
l) Vergleichen Sie die relativen Häufigkeitshistogramme der Geburtsgewichte der Neugeborenen, mit Klassenbreiten von 0,5 kg von 2 bis 4,5 kg, je nachdem, ob die Mutter vor der Schwangerschaft geraucht hat oder nicht. Welche Schlussfolgerungen können gezogen werden?
# mit R base
hist(neonates$weight[neonates$smoke.before=="No"],
breaks=seq(2, 4.5, 0.5), col="steelblue1",
main="Nichtraucherinnen", xlab="Gewichtskategorien",
ylab="relative Häufigkeiten", freq=FALSE)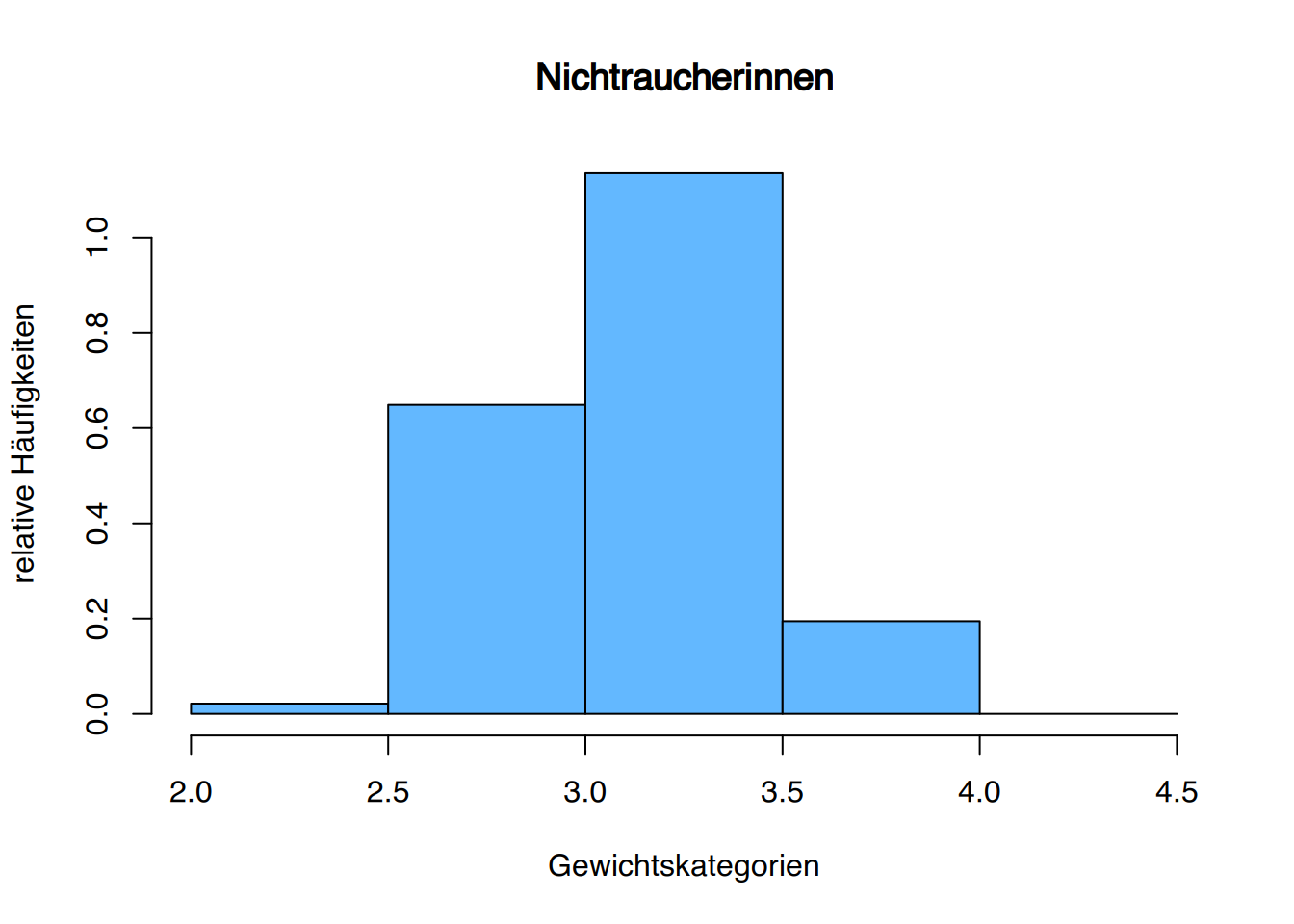
# Raucherinnen
hist(neonates$weight[neonates$smoke.before=="Yes"],
breaks=seq(2, 4.5, 0.5), col="steelblue4",
main="Raucherinnen", xlab="Gewichtskategorien",
ylab="relative Häufigkeiten", freq=FALSE)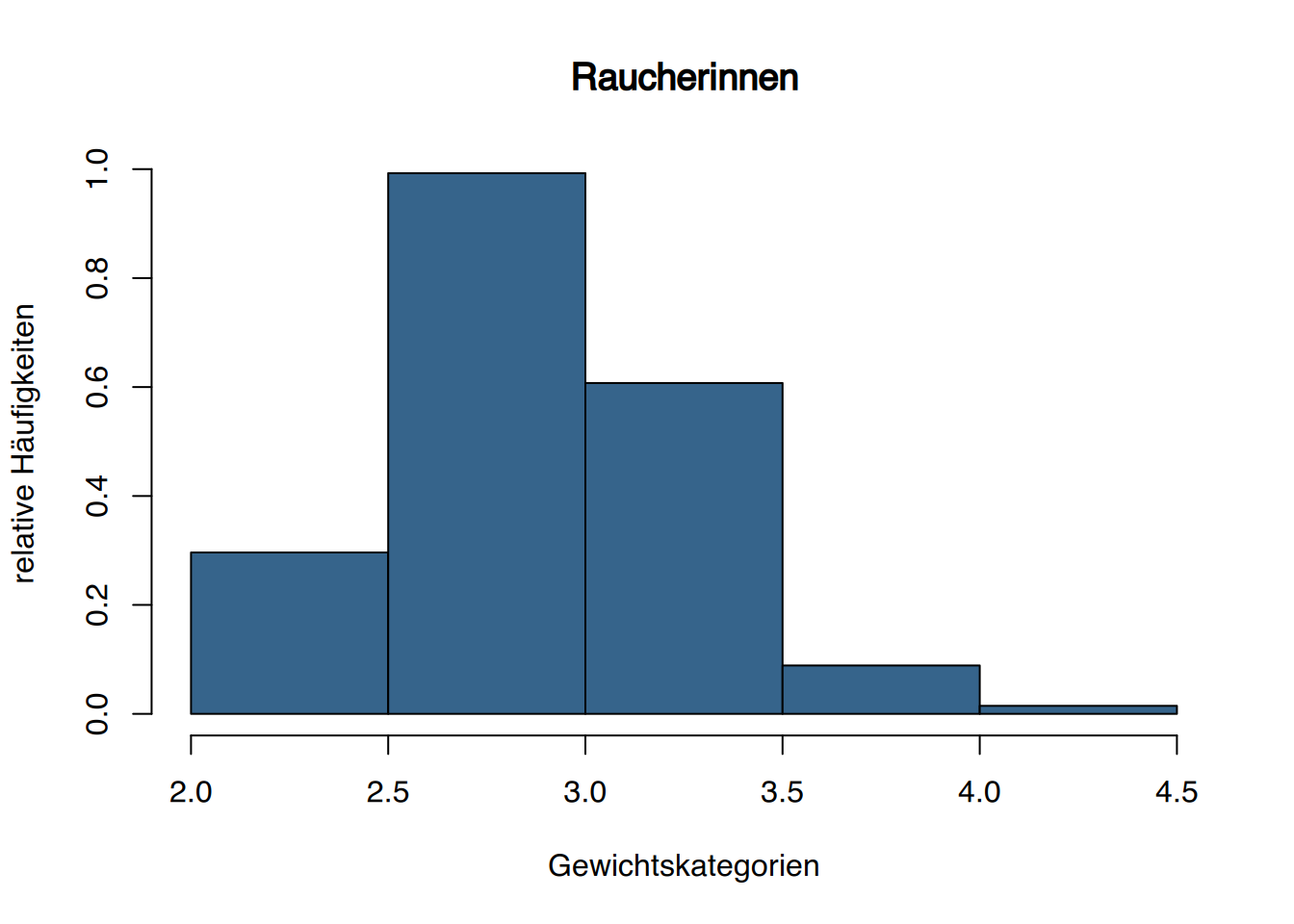
# mit ggplot
neonates %>%
filter(smoke.before=="No") %>%
ggplot(aes(x=weight)) +
geom_histogram(aes(y=after_stat(count)/sum(after_stat(count))),
breaks=seq(2, 4.5, 0.5),
fill="steelblue1", color="black") +
ylab("relative Häufigkeiten") + xlab("Geburtsgewicht")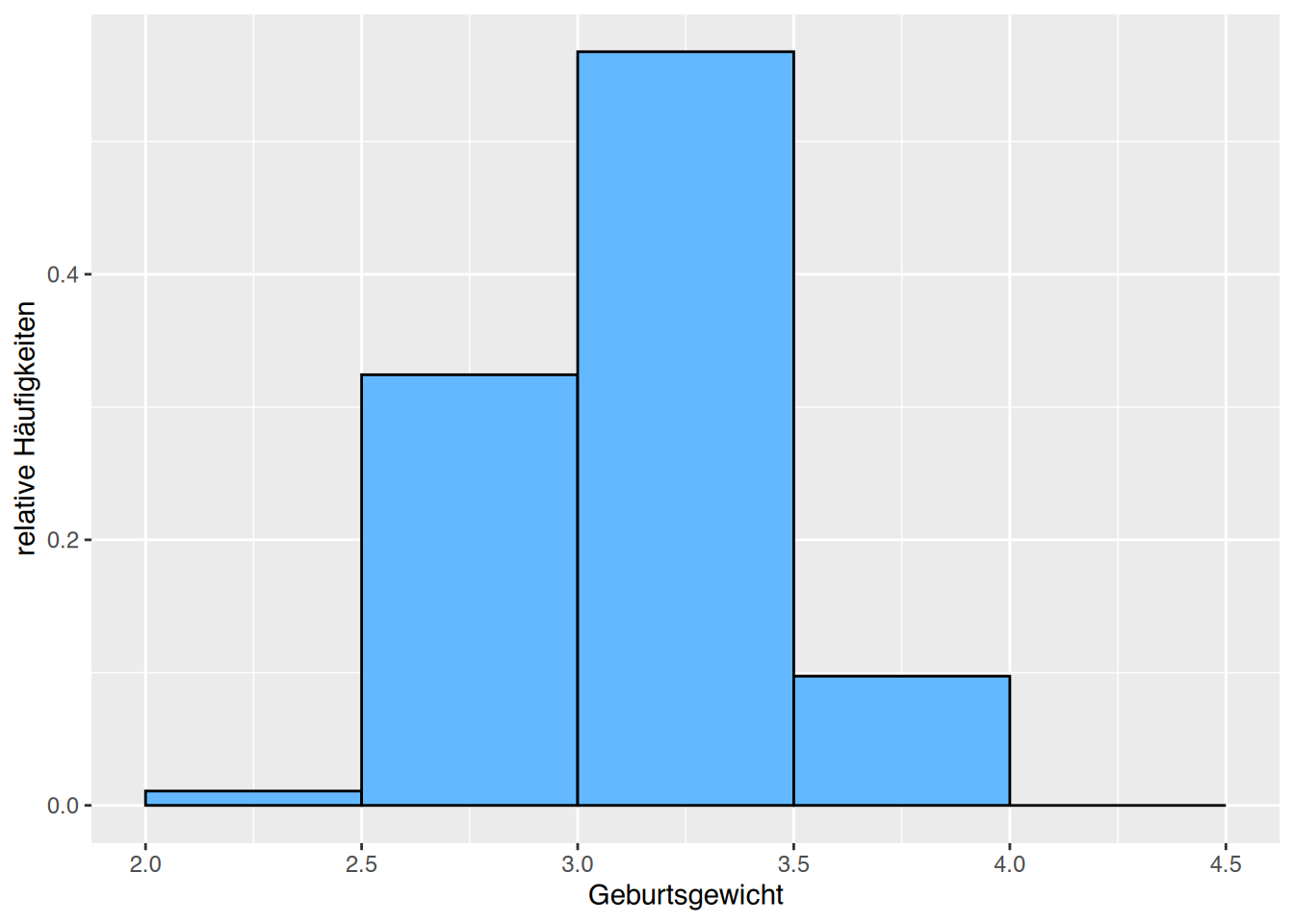
# Raucherinnen
neonates %>%
filter(smoke.before=="Yes") %>%
ggplot(aes(x=weight)) +
geom_histogram(aes(y=after_stat(count)/sum(after_stat(count))),
breaks=seq(2, 4.5, 0.5),
fill="steelblue4", color="black") +
ylab("relative Häufigkeiten") + xlab("Geburtsgewicht")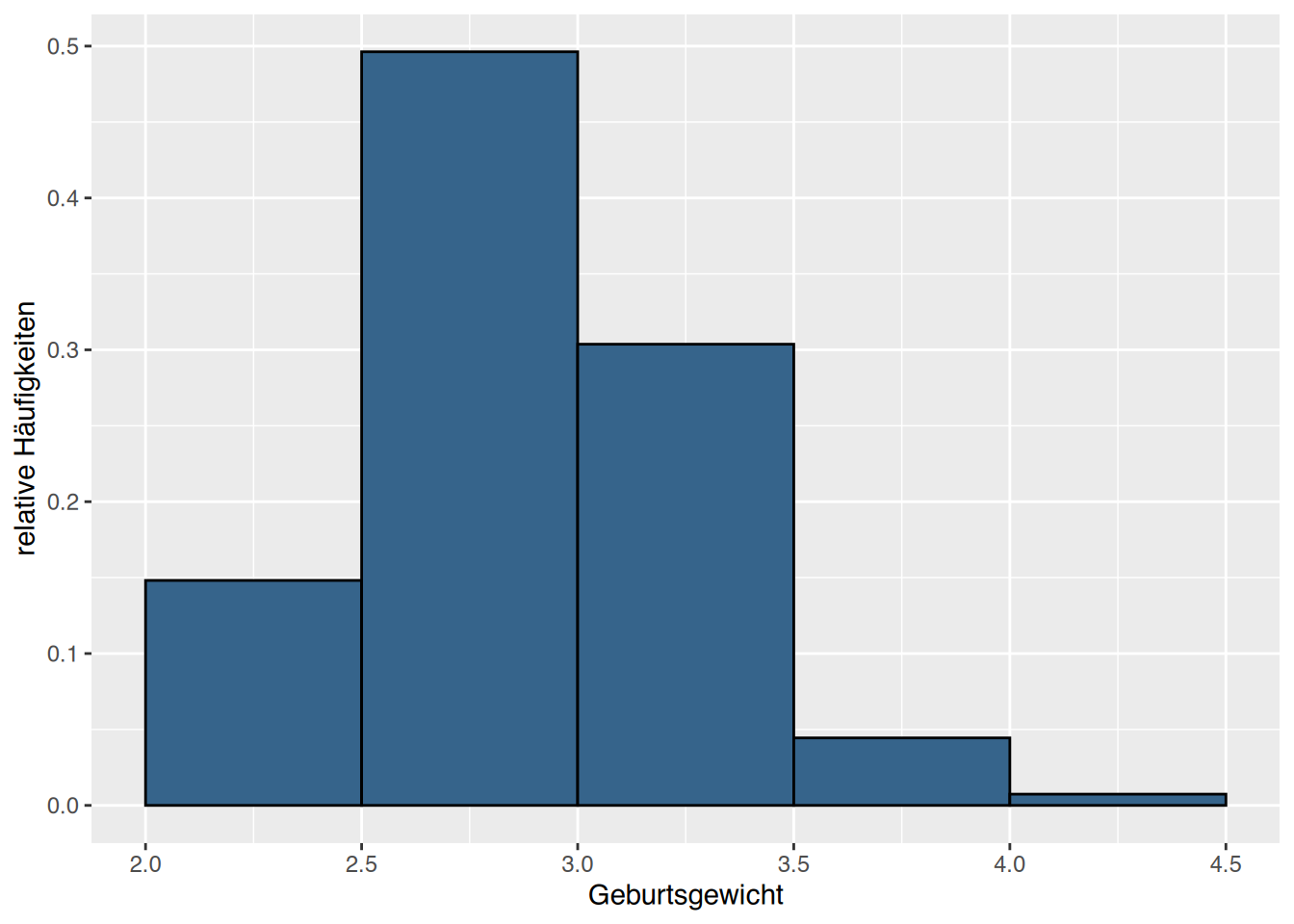
Kinder von Müttern, die vor der Schwangerschaft geraucht haben, haben durchschnittlich weniger Geburtsgewicht.
m) Erstellen Sie ein Boxplot der Geburtsgewichte der Neugeborenen. Welcher Gewichtsbereich kann in der Stichprobe als normal angesehen werden? Gibt es Ausreißer in der Stichprobe?
# mit R base
boxplot(neonates$weight, col="thistle")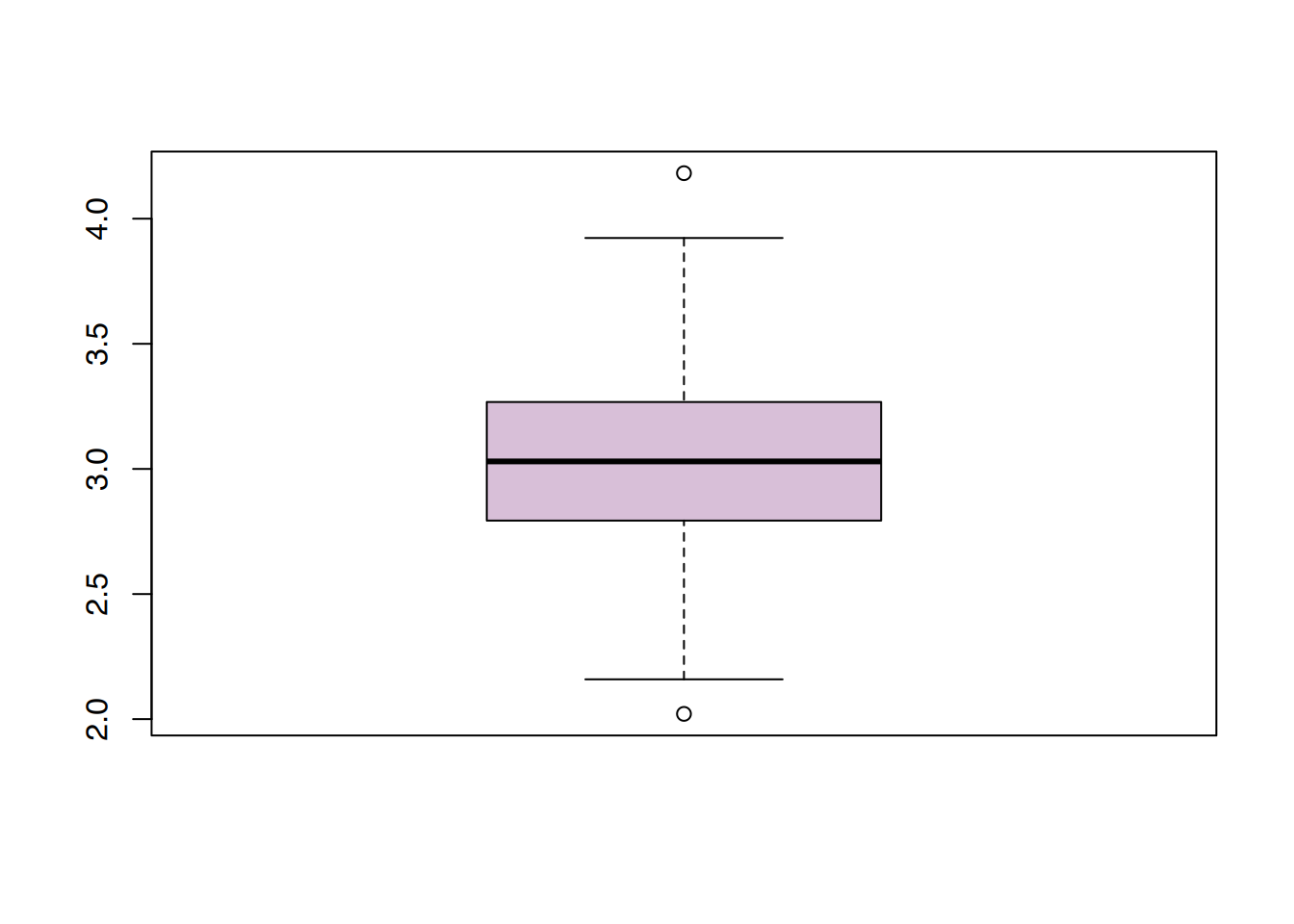
# mit ggplot()
ggplot(neonates, aes(y=weight)) +
geom_boxplot(fill="thistle") +
stat_boxplot(geom="errorbar") +
theme(axis.ticks.x=element_blank(),
axis.text.x=element_blank())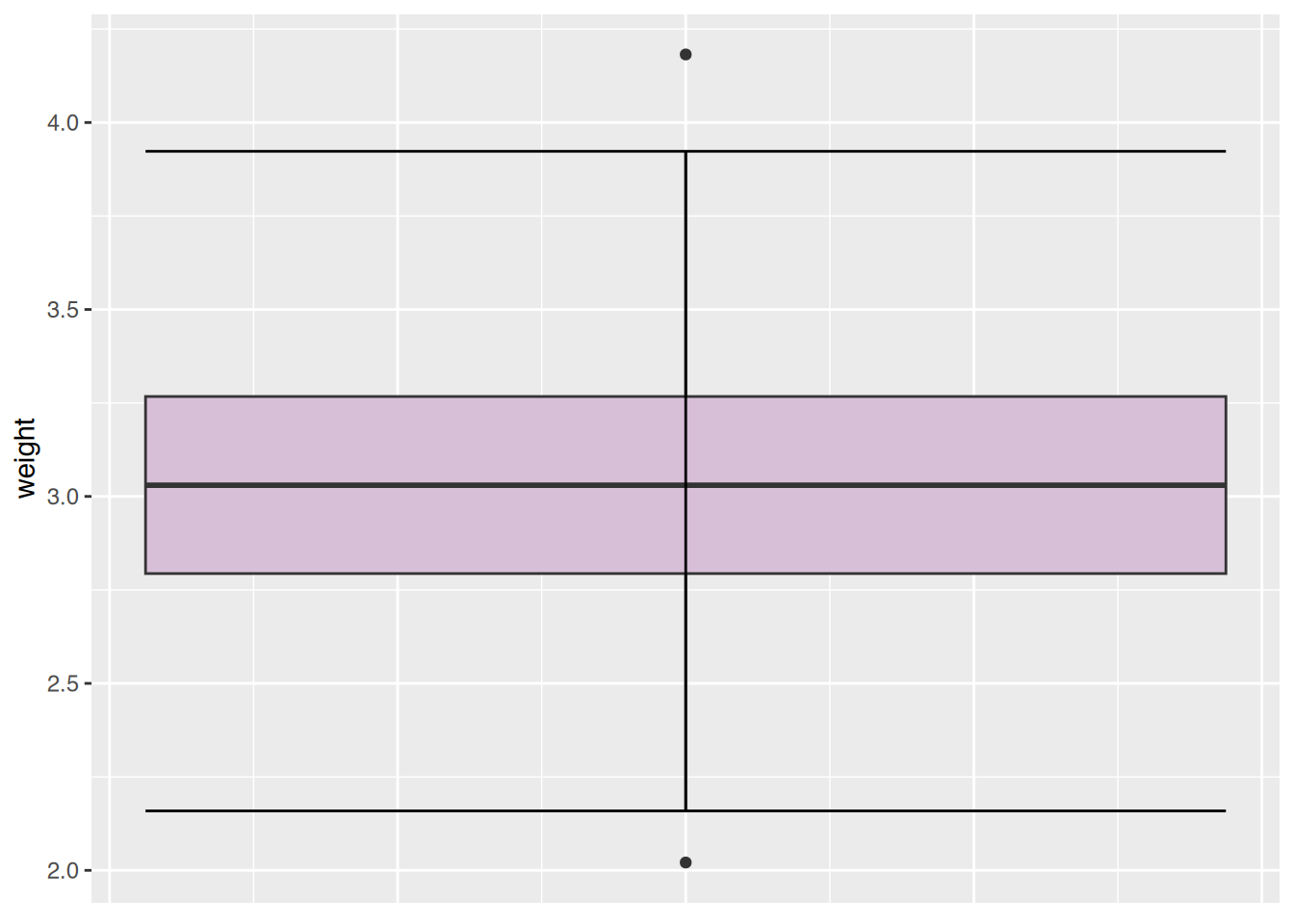
# Zusammenfassung
summary(neonates$weight) Min. 1st Qu. Median Mean 3rd Qu. Max.
2.021 2.794 3.030 3.026 3.267 4.182 Gewichte zwischen \(2,794\)kg und \(3,267\)kg können als normal angesehen werden. Es gibt je einen Ausreißer nach oben und nach unten.
n) Vergleichen Sie die Boxplots der Geburtsgewichte der Neugeborenen je nachdem, ob die Mutter während der Schwangerschaft geraucht hat oder nicht und ob die Mutter unter 20 oder über 20 Jahre alt war. Welche Gruppe hat eine größere zentrale Streuung? Welche Gruppe hat Neugeborene mit geringerem Gewicht?
# R base
boxplot(weight ~ smoke, data=neonates)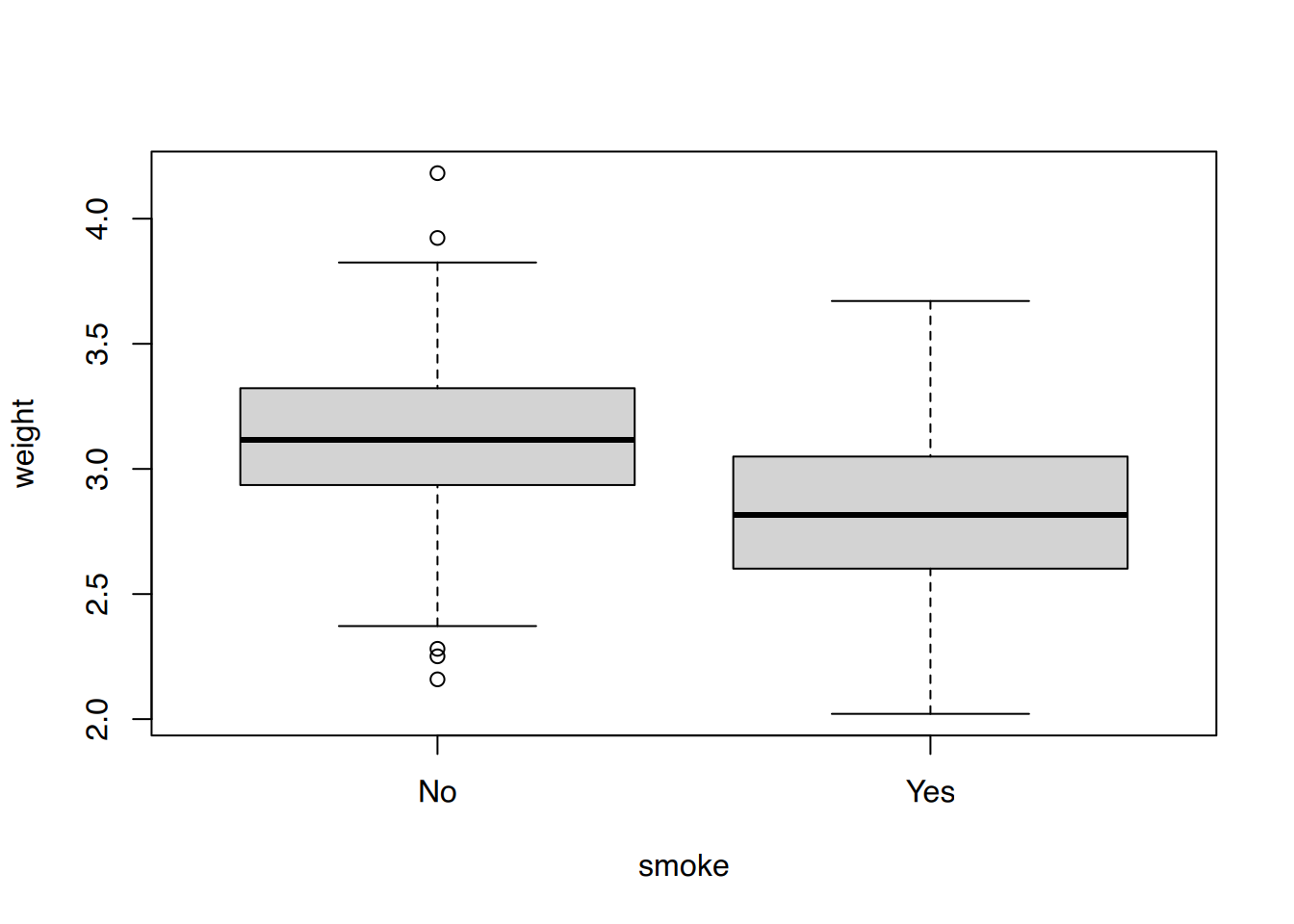
# Alterkategorie
boxplot(weight ~ age, data=neonates)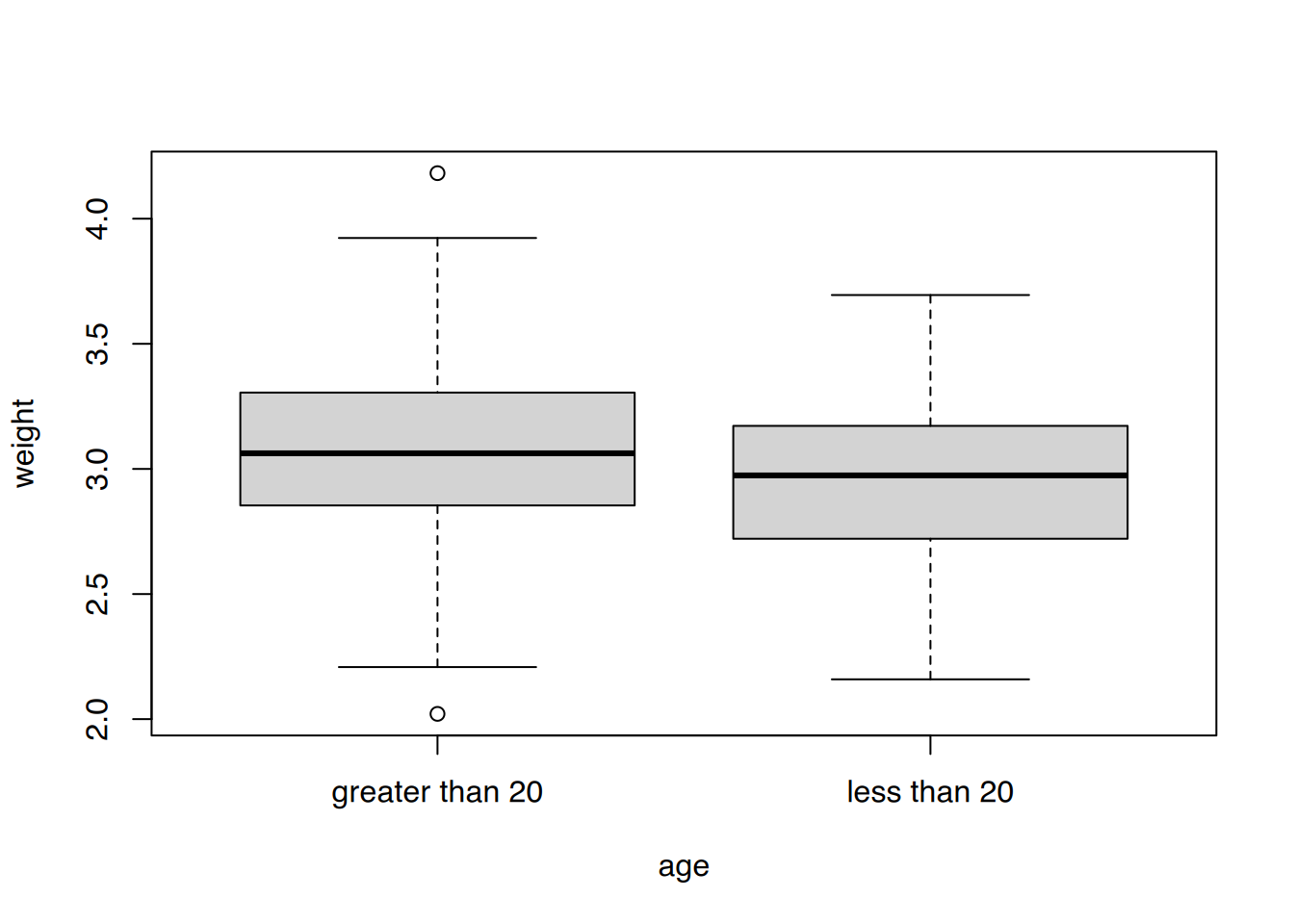
# ggplot Rauchen
ggplot(neonates, aes(y=weight, x=smoke)) +
geom_boxplot() +
stat_boxplot(geom="errorbar") +
theme(axis.ticks.x=element_blank(),
axis.text.x=element_blank())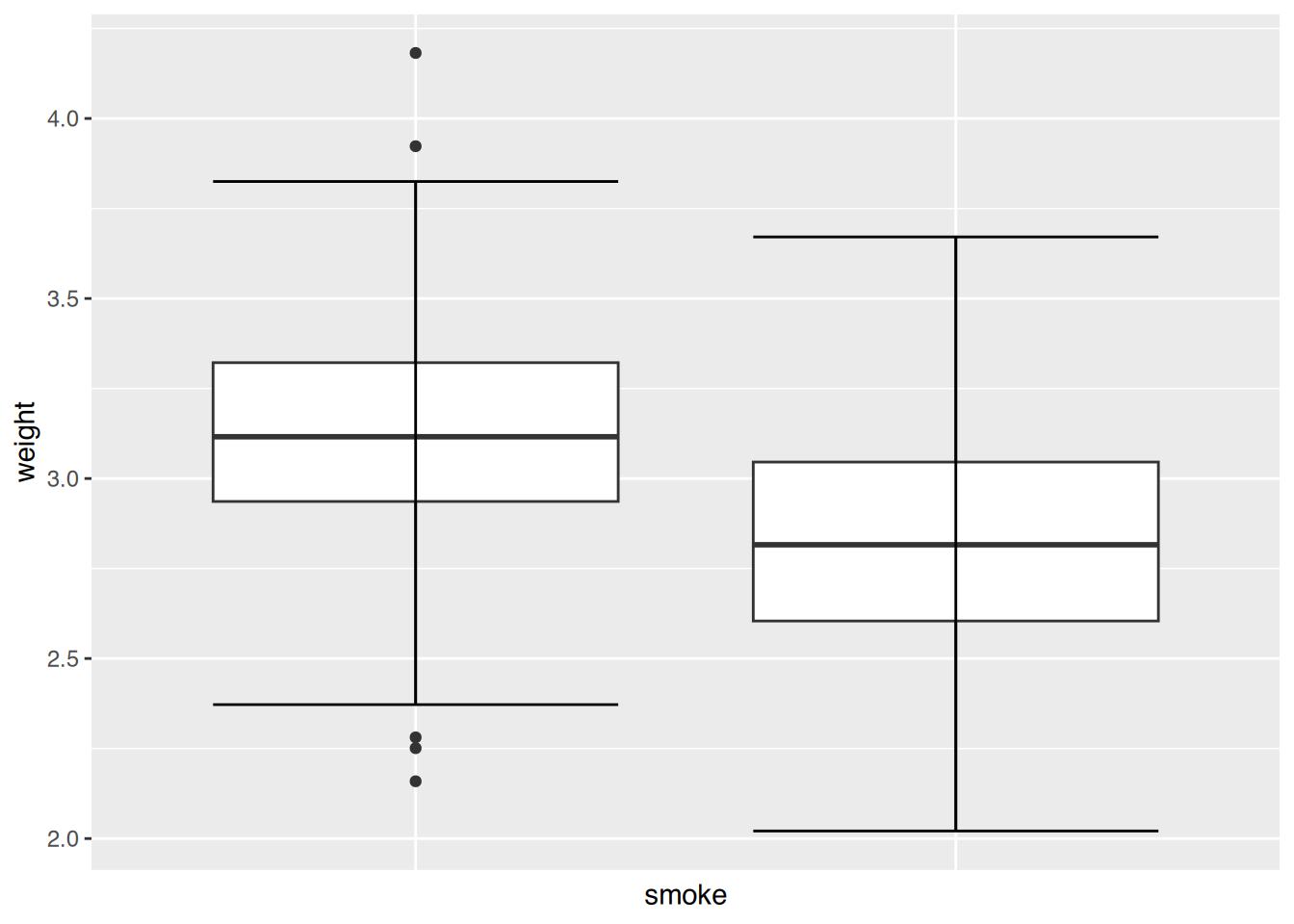
# 20 Jahre alt
ggplot(neonates, aes(y=weight, x=age)) +
geom_boxplot() +
stat_boxplot(geom="errorbar") +
theme(axis.ticks.x=element_blank(),
axis.text.x=element_blank())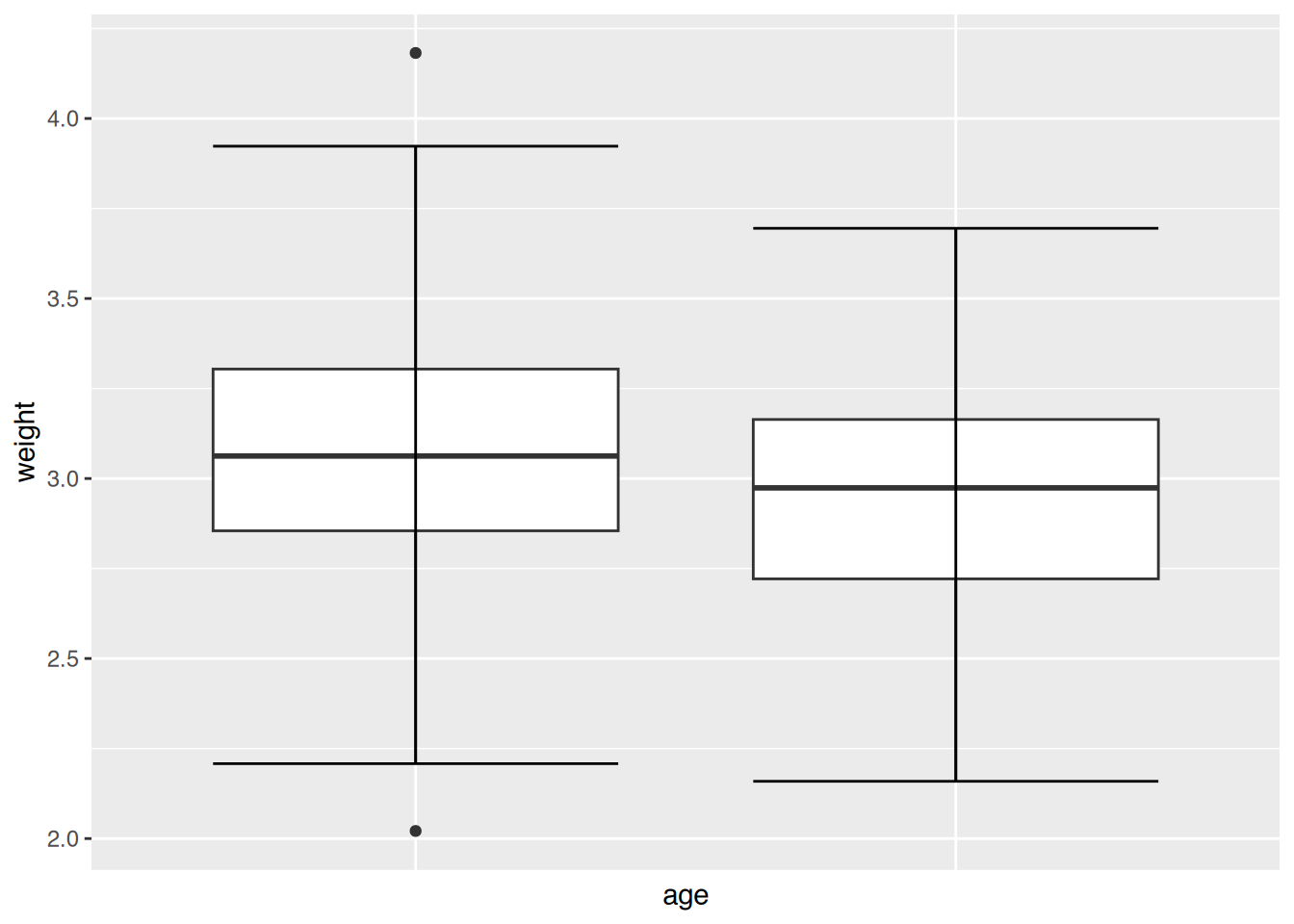
Das Gewicht ist in der Gruppe der Raucherinnen und in der Gruppe der unter-20jährigen geringer.
o) Vergleichen Sie die Boxplots der APGAR-Scores nach 1 Minute und nach 5 Minuten. Welche Variable hat eine größere zentrale Streuung?
# daten tidy machen
df <- pivot_longer(neonates, apgar1:apgar5,
names_to = "minute",
values_to = "wert")
# boxplot
boxplot(wert ~ minute, data=df)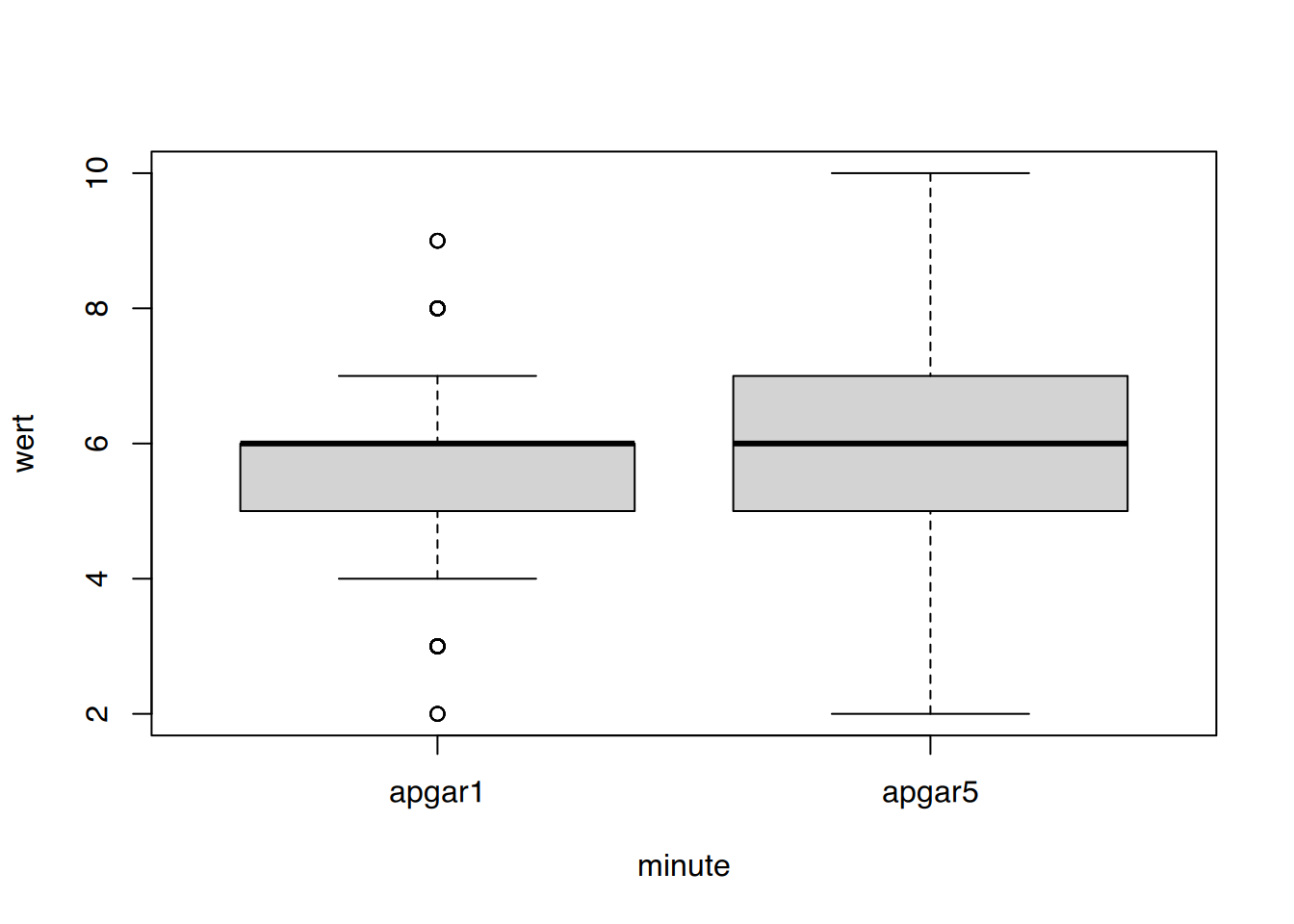
# ggplot
ggplot(df, aes(y=wert, fill=minute)) +
geom_boxplot() +
stat_boxplot(geom="errorbar") +
theme(axis.ticks.x=element_blank(),
axis.text.x=element_blank())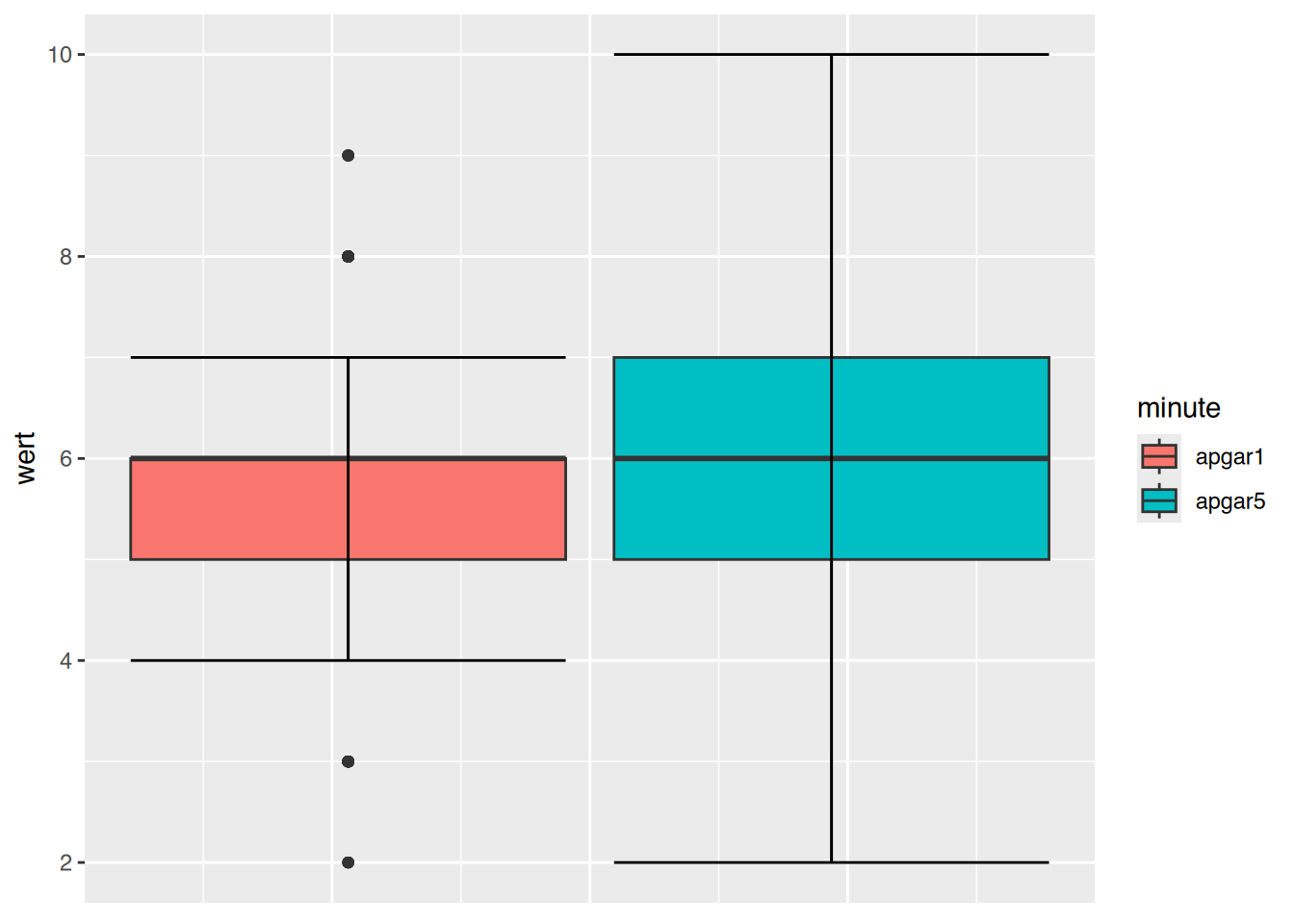
Die Streuung in apgar5 ist größer.