Statistik mit R und RStudio - Ein Nachschlagewerk für Gesundheitsberufe

Jörg große Schlarmann

52 Lösungen Konfidenzintervalle (eine Stichprobe)

Autor:in

Zugehörigkeit

Hier finden Sie die Lösungen zu den Übungsaufgaben von Abschnitt 44.8.

Die hier vorgestellten Lösungen stellen immer nur eine mögliche Vorgehensweisen dar und sind sicherlich nicht der Weisheit letzter Schluss. In R führen viele Wege nach Rom, und wenn Sie mit anderem Code zu den richtigen Ergebnissen kommen, dann ist das völlig in Ordnung.

52.1 Lösung zur Aufgabe 44.8.1

a) Übertragen Sie die Daten in ein Datenframe mit der Variable Konzentration.

Konzentration <- c(17.6, 19.2, 21.3, 15.1, 17.6, 18.9, 16.2, 18.3, 19.0, 16.4)

b) Berechnen Sie das Konfidenzintervall für die mittlere Konzentration bei einem Konfidenzniveau von 95% (Signifikanzlevel \(\alpha = 0,05\)).

d <-t.test(Konzentration, mu=0, conf.level=0.95)
d


    One Sample t-test

data:  Konzentration
t = 31.78, df = 9, p-value = 1.485e-10
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 16.68158 19.23842
sample estimates:
mean of x 
    17.96

# nur Konfidenzintervall ausgeben
as.numeric(d$conf.int)

[1] 16.68158 19.23842

c) Berechnen Sie das Konfidenzintervall für die mittlere Konzentration bei einem Konfidenzniveau von 99% (Signifikanzlevel \(\alpha = 0,01\)).

d <-t.test(Konzentration, mu=0, conf.level=0.99)
d


    One Sample t-test

data:  Konzentration
t = 31.78, df = 9, p-value = 1.485e-10
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
 16.1234 19.7966
sample estimates:
mean of x 
    17.96

# nur Konfidenzintervall ausgeben
as.numeric(d$conf.int)

[1] 16.1234 19.7966

d) Wenn wir die Genauigkeit des Intervalls als den Kehrwert seiner Breite definieren, wie ändert sich die Genauigkeit eines Intervalls, wenn wir das Konfidenzniveau erhöhen?

Mit höherem Konfidenzniveau sinkt die Genauigkeit der Aussagen.

e) Welche Stichprobengröße wird benötigt, um den mittleren Konzentrationswert mit einem Fehler von \(\pm 0.5\)mg/mm\(^{3}\) und einem Konfidenzniveau von 95% Sicherheit zu bestimmen?

# Berechnung der Standardabweichung der Stichprobe
sigma <- sd(Konzentration)

# Gegebene Werte
# z-Wert für 95% Konfidenzniveau
z <- 1.96  

# Fehlermarge
E <- 0.5  

# Berechnung der Stichprobengröße
n <- (z * sigma / E)^2

# Aufrunden auf die nächste ganze Zahl
ceiling(n)

[1] 50

f) Wenn die Konzentration des Wirkstoffs mindestens 16 mg/mm\(^{3}\) betragen muss, um wirksam zu sein, ist dann unsere Medikamentencharge wirksam?

t.test(Konzentration, mu = 16, alternative = "greater")


    One Sample t-test

data:  Konzentration
t = 3.4682, df = 9, p-value = 0.003534
alternative hypothesis: true mean is greater than 16
95 percent confidence interval:
 16.92404      Inf
sample estimates:
mean of x 
    17.96

Der Test ist signifikant. Wir können also sagen, dass unserer Medikamentencharge wirksam ist.

52.2 Lösung zur Aufgabe 44.8.2

a) Übertragen Sie die Daten in ein Datenframe mit den Variablen Hof und Fett.

# Daten übertragen
Hof1 <- data.frame(Fett = c(0.34, 0.34,
          0.32, 0.35,
          0.33, 0.33,
          0.32, 0.32,
          0.33, 0.30,
          0.31, 0.32))
Hof1$Hof <- "Hof 1"     

Hof2 <- data.frame(Fett = c(0.28, 0.29,
          0.30, 0.32,
          0.32, 0.31,
          0.29, 0.29,
          0.31, 0.32,
          0.29, 0.31,
          0.33, 0.32,
          0.32, 0.33))
Hof2$Hof <- "Hof 2"     

milch <- rbind(Hof1, Hof2)
milch$Hof <- factor(milch$Hof)

b) Berechnen Sie das 95%-Konfidenzintervall für den durchschnittlichen Fettgehalt.

t.test(milch$Fett, conf.level=0.95)


    One Sample t-test

data:  milch$Fett
t = 96.537, df = 27, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 0.3090040 0.3224246
sample estimates:
mean of x 
0.3157143

c) Berechnen Sie das 95%-Konfidenzintervall für den durchschnittlichen Fettgehalt, getrennt nach Höfen.

t.test(Hof1$Fett, conf.level=0.95)


    One Sample t-test

data:  Hof1$Fett
t = 81.853, df = 11, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 0.3170719 0.3345948
sample estimates:
mean of x 
0.3258333

t.test(Hof2$Fett, conf.level=0.95)


    One Sample t-test

data:  Hof2$Fett
t = 76.994, df = 15, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 0.299595 0.316655
sample estimates:
mean of x 
 0.308125

d) Plotten Sie das 95%-Konfidenzintervall für den durchschnittlichen Fettgehalt, getrennt nach Höfen..

# Vorbereitung
h1 <- t.test(Hof1$Fett, conf.level=0.95)
h2 <- t.test(Hof2$Fett, conf.level=0.95)

# Als Datenframe für ggplot zusammenbauen
df <- data.frame(unten = c(h1$conf.int[1], h2$conf.int[1]),
                 oben  = c(h1$conf.int[2], h2$conf.int[2]),
                 mitte = c(h1$estimate, h2$estimate ),
                 Hof = c("Hof 1", "Hof 2"))

# ggplot
ggplot(df, aes(x=Hof, color=Hof)) +
  geom_point(aes(y=mitte)) +
  geom_segment(aes(xend=Hof, y=unten, yend=oben))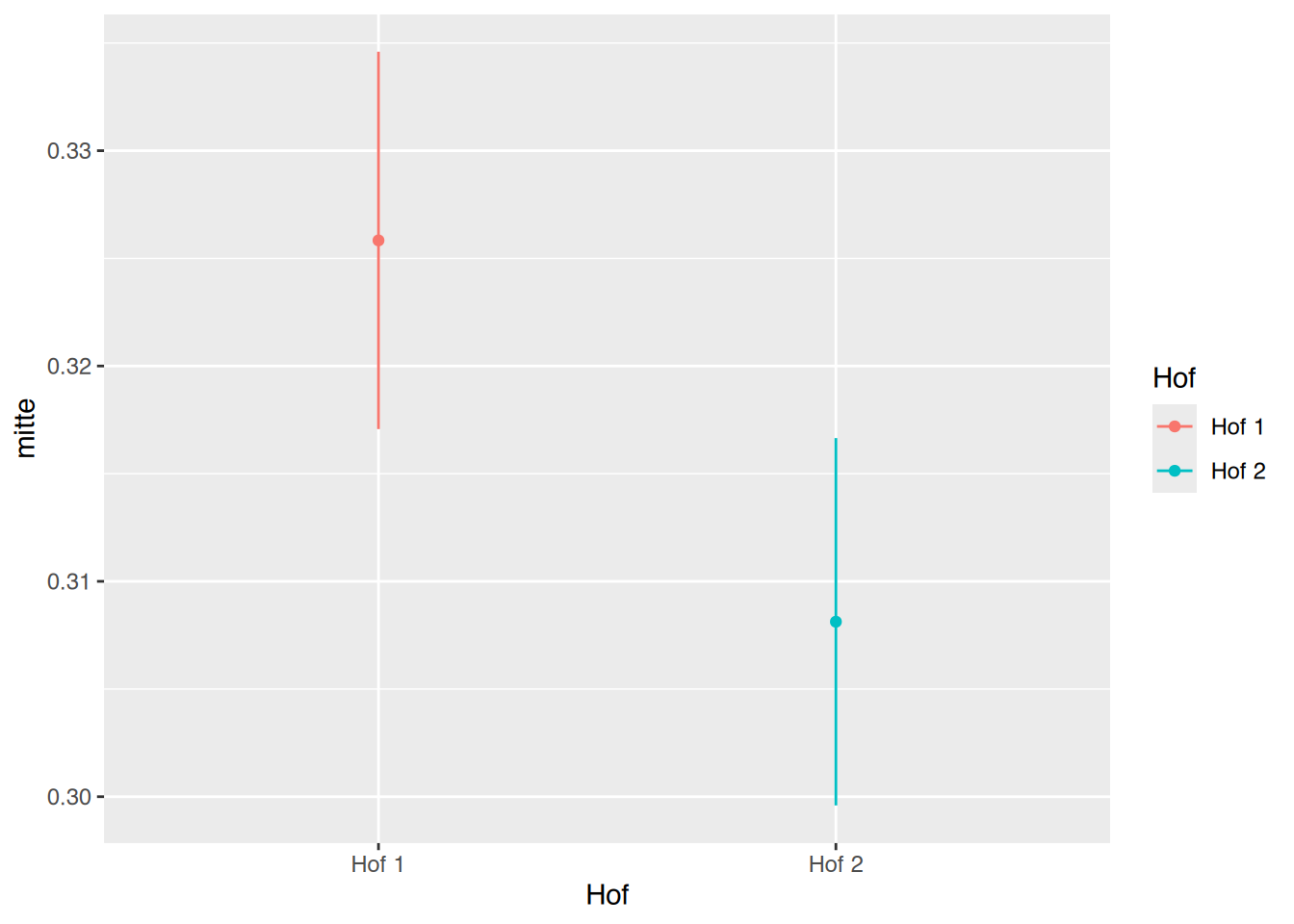

e) Lässt sich aus den Konfidenzintervallen ein signifikanter Untschied zwischen den Höfen feststellen?

df

      unten      oben     mitte   Hof
1 0.3170719 0.3345948 0.3258333 Hof 1
2 0.2995950 0.3166550 0.3081250 Hof 2

Die beiden Konfidenzintervalle überschneiden sich nicht. Das heisst, es kann ein signifikanter Unterschied abgeleitet werden.

52.3 Lösung zur Aufgabe 44.8.3

a) Übertragen Sie die Daten in ein Datenframe mit der Variable Antwort.

# Daten übertragen
Antwort <- c("nein",  "ja",  "nein",  "nein",  "nein",  "ja",  "nein",  
             "ja", "ja",  "ja",  "ja",  "nein",  "ja",  "nein", "ja",  
             "nein",  "nein", "nein",  "ja",  "ja",  "ja",  "nein",  
             "nein",  "ja",  "nein",  "nein", "ja",  "ja",  "nein",  
             "nein",  "ja",  "nein",  "ja", "nein")

b) Berechnen Sie das Konfidenzintervall für den Anteil an Studierenden, welche die Bibliothek wöchentlich nutzen mit einem Signifikanzlevel von \(\alpha=0,01\).

freq <- table(Antwort)
bib <- prop.test(freq[["ja"]], sum(freq), 
                 alternative="two.sided", 
                 p=0.5, conf.level=0.99)
bib


    1-sample proportions test with continuity correction

data:  freq[["ja"]] out of sum(freq), null probability 0.5
X-squared = 0.029412, df = 1, p-value = 0.8638
alternative hypothesis: true p is not equal to 0.5
99 percent confidence interval:
 0.2617050 0.6896622
sample estimates:
        p 
0.4705882

c) Wie präzise ist das Intervall?

bib$conf.int[2] - bib$conf.int[1]

[1] 0.4279572

Das Intervall ist sehr breit und daher unpräzise.

d) Welcher Stichprobenumfang ist erforderlich, um eine Schätzung des Anteils der Studenten zu erhalten, die die Bibliothek mindestens einmal pro Woche nutzen, mit einem Fehler von \(\pm1\)% und einem Konfidenzniveau von 95%?

# gemessene Proportionen
prop <- bib$estimate

# Z-Wert für 95% Konfidenz
z <- 1.96

# Fehlerspanne +-1%
e <- 0.01

# Fallzahl berechnen
n <- (z^2 * prop * (1 - prop)) / (e^2)

Es werden 9571 Probanden benötigt.

52.4 Lösung zur Aufgabe 44.8.4

a) Berechnen Sie das 95%-Konfidenzintervall für den Anteil an geimpften Probanden in der Grundgesamtheit.

# Daten übertragen
prop.test(154, 200, p=0.5, conf.level=0.95)


    1-sample proportions test with continuity correction

data:  154 out of 200, null probability 0.5
X-squared = 57.245, df = 1, p-value = 3.848e-14
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.7042503 0.8251428
sample estimates:
   p 
0.77

b) Wenn das Gesundheitsministerium das Ziel verfolgt, dass mindestens 70% der Menschen über 65 mit Atemwegserkrankungen geimpft sind, können wir dann sagen, dass das Ministerium das Ziel erreicht hat?

# Daten übertragen
prop.test(154, 200, p=0.5, conf.level=0.95)$conf.int[1]

[1] 0.7042503

Da die untere Grenze des Konfidenzintervalls größer als 0,7 ist, können wir bestätigen, dass das Ministerium sein Ziel erreicht hat.

52.5 Lösung zur Aufgabe 44.8.5

a) Berechnen Sie die Konfidenzintervalle für den Mittelwert mit den Signifikanzniveaus \(0.1\), \(0.05\) und \(0.01\).

# Daten übertragen
cholesterin <- c(196, 212, 188, 206, 203, 210, 201, 198)

t.test(cholesterin, conf.level=0.90)


    One Sample t-test

data:  cholesterin
t = 72.849, df = 7, p-value = 2.416e-11
alternative hypothesis: true mean is not equal to 0
90 percent confidence interval:
 196.5031 206.9969
sample estimates:
mean of x 
   201.75

t.test(cholesterin, conf.level=0.95)


    One Sample t-test

data:  cholesterin
t = 72.849, df = 7, p-value = 2.416e-11
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 195.2014 208.2986
sample estimates:
mean of x 
   201.75

t.test(cholesterin, conf.level=0.99)


    One Sample t-test

data:  cholesterin
t = 72.849, df = 7, p-value = 2.416e-11
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
 192.0585 211.4415
sample estimates:
mean of x 
   201.75

b) Kann man schließen, dass der Mittelwert des Cholesterinspiegels der Bevölkerung unter 210 mg/dl liegt?

# Daten übertragen
as.numeric(t.test(cholesterin, conf.level=0.90)$conf.int)

[1] 196.5031 206.9969

as.numeric(t.test(cholesterin, conf.level=0.95)$conf.int)

[1] 195.2014 208.2986

as.numeric(t.test(cholesterin, conf.level=0.99)$conf.int)

[1] 192.0585 211.4415

Die obere Grenze des 99%-Konfidenzintervall ist größer als 210. Wird dies berücksichtigt, lässt dich die Aussage nicht bestätigen.

52.6 Lösung zur Aufgabe 44.8.6

a) Berechnen Sie für jede Therapie das 95% Konfidenzintervall für den Anteil an Personen, die geheilt wurden.

# Daten übertragen
a <- c(rep("geheilt", 18), rep("nicht", 7))
b <- c(rep("geheilt", 21), rep("nicht", 14))

freqA <- table(a)
freqB <- table(b)
A <- prop.test(freqA[["geheilt"]], sum(freqA), 
                 alternative="two.sided", 
                 p=0.5, conf.level=0.95)
B <- prop.test(freqB[["geheilt"]], sum(freqB), 
                 alternative="two.sided", 
                 p=0.5, conf.level=0.95)
# Konfidenzintervalle
A$conf.int[2] - A$conf.int[1]

[1] 0.3672662

B$conf.int[2] - B$conf.int[1]

[1] 0.3343891

Das Konfidenzintervall von Gruppe B ist schmaler, und damit auch präziser.

52.7 Lösung zur Aufgabe 44.8.7

# lade Datensatz
load(url("https://www.produnis.de/R/data/neonates.RData"))

a) Berechnen Sie das 99% Konfidenzintervall für den Mittelwert des Gewichts der Neugeborenen.

# t-Test
d <- t.test(neonates$weight, conf.level = 0.99)

# Konfidenzgrenzen
as.numeric(d$conf.int)

[1] 2.975844 3.075531

b) Berechnen Sie die Konfidenzintervalle für den APGAR-Score nach 1 Minute und für den APGAR-Score nach 5 Minuten und vergleiche sie beide Intervalle. Gibt es auf Grundlage der Konfidenzintervalle einen signifikanten Unterschied zwischen den Mittelwerten der beiden Scores?

# t-Test
a1 <- t.test(neonates$apgar1, conf.level = 0.99)
a5 <- t.test(neonates$apgar5, conf.level = 0.99)

# Konfidenzgrenzen
as.numeric(a1$conf.int)

[1] 5.422182 5.834068

as.numeric(a5$conf.int)

[1] 5.998597 6.426403

Die Konfidenzgrenzen schneiden sich nicht. Das bedeutet, wir können von einem signifikanten Unterschied ausgehen.

c) Berechnen Sie die Konfidenzintervalle für den Prozentsatz der Neugeborenen mit einem Gewicht von \(\leq 2,5\) kg für Raucher- und Nichtrauchermütter und vergleichen Sie die Intervalle.

# geringes Gewicht kategorisieren
neonates$GG <- "normal"
neonates$GG[neonates$weight<2.50001] <- "low"

# Subsets bilden
k1 <- subset(neonates, smoke=="Yes")
k2 <- subset(neonates, smoke=="No")
# Häufigkeitstabelle
freq1 <- table(k1$GG)
freq2 <- table(k2$GG)

# Proportion Test
m1 <- prop.test(freq1[["low"]], sum(freq1), 
                 alternative="two.sided", 
                 p=0.5, conf.level=0.95)

m2 <- prop.test(freq2[["low"]], sum(freq2), 
                 alternative="two.sided", 
                 p=0.5, conf.level=0.95)

# Konfidenzgrenzen anzeigen
as.numeric(m1$conf.int)

[1] 0.1049334 0.2610870

as.numeric(m2$conf.int)

[1] 0.008396857 0.055169043

Die Konfidenzgrenzen schneiden sich nicht. Das bedeutet, wir können von einem signifikanten Unterschied ausgehen.