2 Skalentypen

Nach diesem ersten einführenden Beispiel müssen wir näher auf den Begriff Skala eingehen. Im obigen Beispiel hatten wir für die Anzahl der Krankenhausaufenthalte eine Skala von 0 bis 7 gewählt, um die Daten zu ordnen.

Allgemein dient eine Skala dazu, irgend etwas einzuteilen, zu ordnen oder zu sortieren. In der Statistik gibt es verschieden Arten von Skalen, in die man Daten einsortieren kann (Skalierung der Daten). Die verschiedenen Skalen haben abhängig von ihrem Informationsgehalt und der Möglichkeit der statistischen Auswertung ein sehr unterschiedliches Niveau.

2.0.1 Nominalskala

Nomen (latein.) heißt Namen oder Benennung

Fragt man zufällig ausgewählte Personen nach ihrem Familienstand, so wird man die Antworten ledig, verheiratet, geschieden und verwitwet erhalten. Beim sortieren der Urliste spielt es keine Rolle, ob zuerst die ledigen oder zuerst die geschiedenen Personen aufgelistet werden.

Nominaskaliert soll zum Ausdruck bringen, dass die erhobenen Werte nur eine Art von Etiketten sind, “man gibt dem Kind einen Namen”, ohne dass irgendeine Wertigkeit oder Reihenfolge zugrunde liegt. Man kann auch sagen, Objekte oder Ereignisse werden in Kategorien eingeteilt, die sich gegenseitig ausschließen. Entweder hat ein Objekt bzw. Ereignis ein bestimmtes Merkmal oder nicht.

Weitere Beispiele für nominalskalierte Merkmale sind:

Geschlecht (männlich, weiblich)
Augenfarbe (grün, blau, braun,..)
Körperbau (leptosom, pyknisch, athletisch)
Krebslokalisation (Lunge, Magen, Darm, etc.)
Zufriedenheit mit der Pflege (ja, nein)
Religionszugehörigkeit (evangelisch, katholisch,...)
Prüfung (bestanden, nicht bestanden)

Die Möglichkeiten der deskriptiven Statistik beschränken sich auf die Ermittlung der Häufigkeiten sowie auf die Bestimmung der Kategorie, in der die meisten Personen (oder Objekte) zu finden sind. Nehmen wir das Beispiel einer Prüfung.

In der Tageszeitung lesen Sie: “An der Schule XY haben von 160 Schülern 120 die Abschlussprüfung bestanden. Leider sind 40 Schüler durchgefallen.”

	absolute Häufigkeit \(h_{i}\)	relative Häufigkeit in % \(f_{i} P 100\)
bestanden	120	75
nicht bestanden	40	25
Gesamt	n = 160	100

Dieses Beispiel soll verdeutlichen, dass in nominalskalierten Daten wenig Informationsgehalt steckt. Wir können nicht feststellen, mit welchen Noten die Schüler die Prüfung bestanden haben oder wieviel Punkte sie im einzelnen erreicht haben.

2.0.2 Ordinalskala

Ordinatus heißt im lateinischen soviel wie geordnet, ordentlich. Eine Ordinalzahl ist eine Ordnungszahl.

Zusätzlich zu den Eigenschaften der Nominalskala zeichnet sich dieses “nächst höhere” Skalenniveau dadurch aus, dass ordinale Merkmale oder Daten einer vorgegebenen Reihenfolge oder Rangfolge unterliegen.

“Gut - Besser - Am Besten”
“Schlecht - Schlechter - Am Schlechtesten”

Denkt man an die Stadieneinteilung von Krebserkrankungen, so wird zwar deutlich, dass mit Stadium 1 eine bessere Prognose verbunden ist als mit Stadium 2 oder Stadium 3. Auch wenn Stadium 4 sicherlich prognostisch am ungünstigsten beurteilt werden muss, können wir nicht das “wieviel besser” oder “wieviel schlechter genauer ausdrücken. Mit anderen Worten, die Abstände zwischen den Werten dieser Skala, also zwischen den verschiedenen Ausprägungen des Merkmals, sind nicht interpretierbar. Die Ziffern im o.g. Beispiel sind lediglich Ordnungs- oder Rangzahlen.

Beim Auflisten und Sortieren ordinaler Daten hat man sich in jedem Fall an die vorgegebene Reihen - oder Rangfolge zu halten. Zusätzlich zu der Information, in welche Kategorie eine Person oder ein Objekt gehört, lässt sich bei ordinalen Merkmalen noch die Zugehörigkeit zu einer bestimmten Rangstufe feststellen. Analog zu den nominalen Merkmalen lassen sich die entsprechenden Häufigkeiten ermitteln. Wie wir später noch sehen werden, existieren darüber hinaus Auswertungsmöglichkeiten, welche die zusätzlich in der Rangfolge liegenden Informationen berücksichtigen.

Ein typisches Beispiel für eine Ordinalskala sind die Schulnoten von sehr gut bis ungenügend, denen die entsprechenden Rangzahlen von eins bis sechs zugeordnet wurden. Kommen wir zurück zu dem Beispiel der Prüfung. Eine andere Tageszeitung veröffentlichte zusätzlich zu der Information “bestanden - nicht bestanden” den Notenspiegel. Der höhere Informationsgehalt der Ordinalskala wird sofort deutlich:

Zensur	absolute Häufigkeit (\(h_{i}\))	relative Häufigkeit in % (\(f_{i} \cdot 100\))
sehr gut	2	1,25	bestanden
gut	21	13,12	bestanden
befriedigend	37	23,12	bestanden
ausreichend	60	37,50	bestanden
mangelhaft	28	17,50	nicht bestanden
ungenügend	12	7,50	nicht bestanden
Gesamt	\(n = 160\)	100

2.0.3 Metrische Skala

das lateinische Metor bedeutet soviel wie: abstecken, ausmessen oder abgrenzen

Das höchste Niveau besitzt die metrische Skala. Die Werte einer metrischen Skala unterliegen nicht nur einer Reihenfolge, benachbarte Werte weisen auch gleiche Abstände auf. Die Abstände zwischen den Werten sind somit interpretierbar. Man unterscheidet bei der metrischen Skala weiterhin die Intervallskala und die Verhältnisskala.

Von einer Intervallskala spricht man, wenn kein natürlicher Nullpunkt vorliegt, z.B. °Celsius oder °Fahrenheit. Die Abstände auf einer Intervallskala sind zwar interpretierbar, nicht aber das Verhältnis. Zwischen 10 °C und 20 °C liegen genauso viele Werte, wie zwischen 20 °C und 30 °C, aber 30 °C bedeutet nicht doppelt so warm wie 15 °C, auch wenn dies auf den ersten Blick den Anschein hat. Umgerechnet in °Fahrenheit¹ ergibt sich: 15 °C = 59 °F und 30 °C = 86 °F. Wenn nun 30 °C doppelt so warm wären wie 15 °C, dann müßte es auch für die Werte in °Fahrenheit gelten. Wie man aber leicht erkennen kann, entspricht 86 °F nicht 2 * 59 °F .
Eine Verhältnisskala dagegen besitzt einen natürlichen Nullpunkt (Länge, Gewicht, Lebensalter, usw.). Dies erlaubt Aussagen über das Verhältnis der einzelnen Werte, so ist ein zehnjähriger Junge doppelt so alt wie ein fünfjähriger. Die Unterscheidung von Intervall- und Verhältnisskala ist für die Anwendung von statistischen Verfahren für uns nicht von Bedeutung, sie sollte nur der Vollständigkeit halber erwähnt werden. Wir werden daher im folgenden nur von der metrischen Skala sprechen.

Man könnte jetzt einwerfen, dass die Abstände bei Schulnoten auch immer gleich eins und damit konstant sind. Da z.B. eine 4 doppelt so schlecht erscheint wie eine 2, könnte man auf die Idee kommen, Schulnoten als metrische Größen einzustufen. Hierbei wird jedoch vergessen, dass es sich bei Schulnoten nur um Rangzahlen (bzw. Ordnungszahlen) handelt, die wenig über die Differenz der Leistung aussagen. Darf man sich beispielsweise für die Note 1 nur drei Fehler erlauben, sind es für die Note 2 schon 7 und für die Note 3 schon 20 Fehler. Hieran wird deutlich, dass die Leistungsdifferenz zwischen den Noten nicht konstant ist, obwohl die Differenz der Rangzahlen (der Noten) jeweils den Wert eins besitzt.

Werden in einer Klausur oder Klassenarbeit richtig gelöste Aufgaben mit einer Anzahl von Punkten bewertet, dann handelt es sich wirklich um eine metrische Skala. Erreicht ein Schüler 30 Punkte und ein anderer vielleicht 60 Punkte, so lassen sich klare Aussagen über die Leistungsdifferenz der Schüler machen. Der erste Schüler war nur halb so gut wie der zweite. Die Differenz der beiden beträgt 30 Punkte.

2.0.4 Anmerkungen

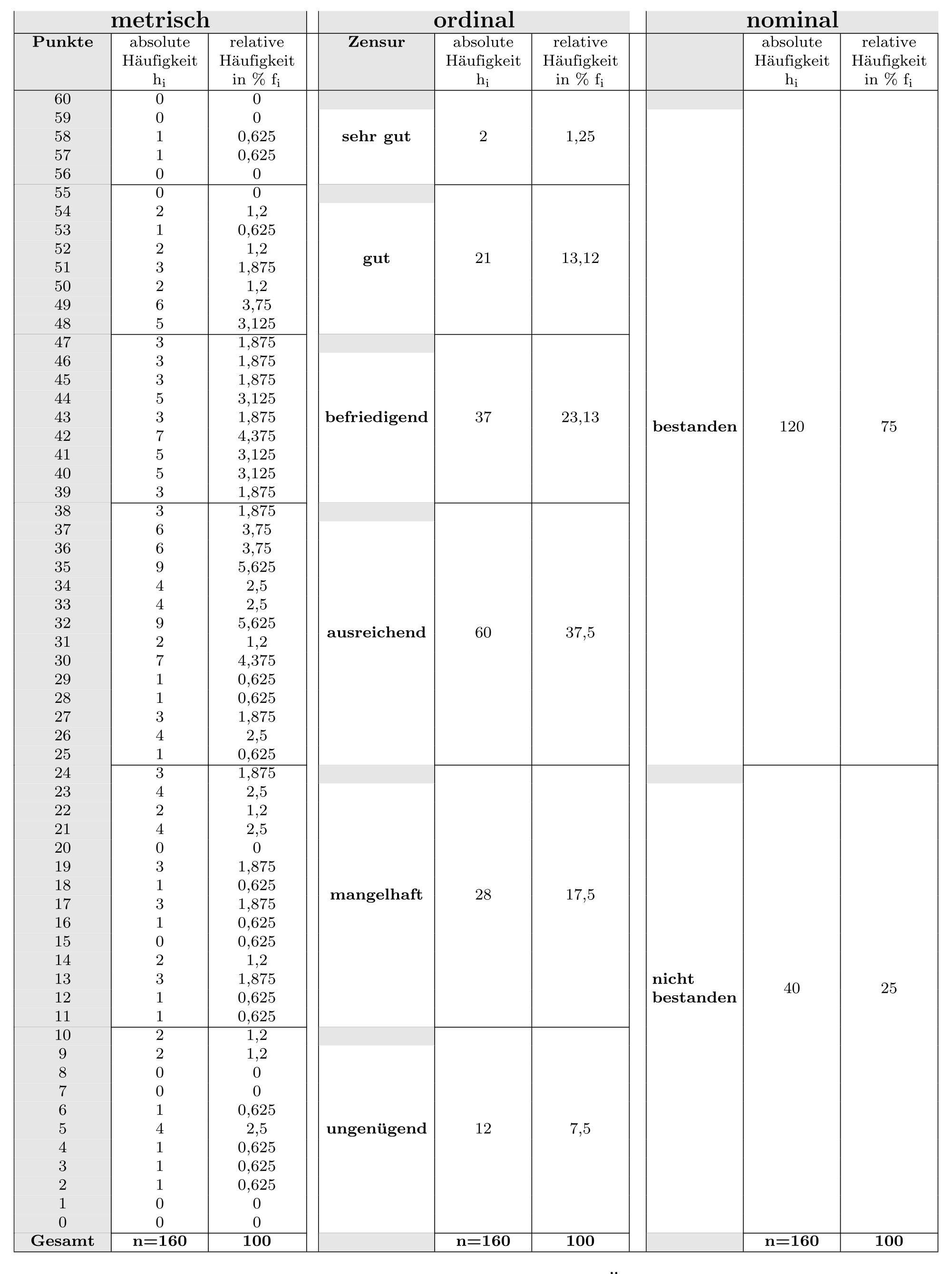
Für jeden Skalentyp stehen statistische Verfahren zur Verfügung, die den jeweiligen Informationsgehalt der Skalen optimal nutzen. Hierbei ist zu beachten, dass man Verfahren für nominale Merkmale auch auf ordinale und metrische Merkmale anwenden kann, und Verfahren für ordinale Daten auch bei metrischen Anwendung finden können. Dazu muß man die Daten allerdings auf das niedrigere Skalenniveau “herunter stufen”. Wollen oder müssen wir auf metrischskalierte Daten Verfahren für ordinale Merkmale anwenden, sind wir gezwungen, metrische Daten in ordinale umzuwandeln. Dabei nehmen wir allerdings immer einen erheblichen Informationsverlust in Kauf. Ein umgekehrtes Vorgehen ist nicht möglich, d.h. statistische Verfahren dürfen niemals “unter ihrem Niveau” angewendet werden. Vor jeder Datenerhebung ist daher zu überlegen, welches Skalenniveau benötigt wird, um die Fragestellung zu beantworten. Im Zweifelsfall sollte man das höhere Niveau vorziehen. Um noch einmal die verschiedenen Skalen mit ihrem unterschiedlichen Informationsgehalt deutlich zu machen, fügen wir dem Beispiel der Prüfung in Tabelle [tab:skalenniveausueberblick] auf der folgenden Seite die Information über die erreichten Punktzahlen hinzu.

die Umrechnungsformel lautet: \(°F = 1,8 * °C + 32\)↩︎