4 Statistische Kenngrößen

Eine Tabelle oder graphische Darstellung der Daten informiert über die gesamte Verteilung eines Merkmals mit seinen Ausprägungen. Demgegenüber sagen statistische Kennwerte etwas über spezielle Eigenschaften der Verteilung aus. Wie bereits im Kapitel zur Darstellung der Daten behandeln wir zunächst nur Kenngrößen für univariate Verteilungen, also Größen, die sich auf ein Merkmal beziehen.

Die zahlenmäßige Darstellung der Daten durch statistische Kenngrößen beruht auf einer Reduktion der Daten. Die Gesamtheit des Datenmaterials wird durch typische Vertreter repräsentiert, welche die Datenmenge zusammenfassend und gründlich charakterisieren. Dies geht jedoch mit dem Verlust der einzelnen individuellen Daten und deren Informationsgehalt einher.

Sicherlich ist es einleuchtend, dass repräsentative Vertreter einer Häufigkeitsverteilung nicht die selten beobachteten Werte sind. Denken wir an unser Beispiel “Schulnoten”, so sind die Zensuren “sehr gut” und “ungenügend” keine typischen Vertreter dieser Verteilung.

Abbildung 4.1: Verteilung der Abiturnoten Schule `X`

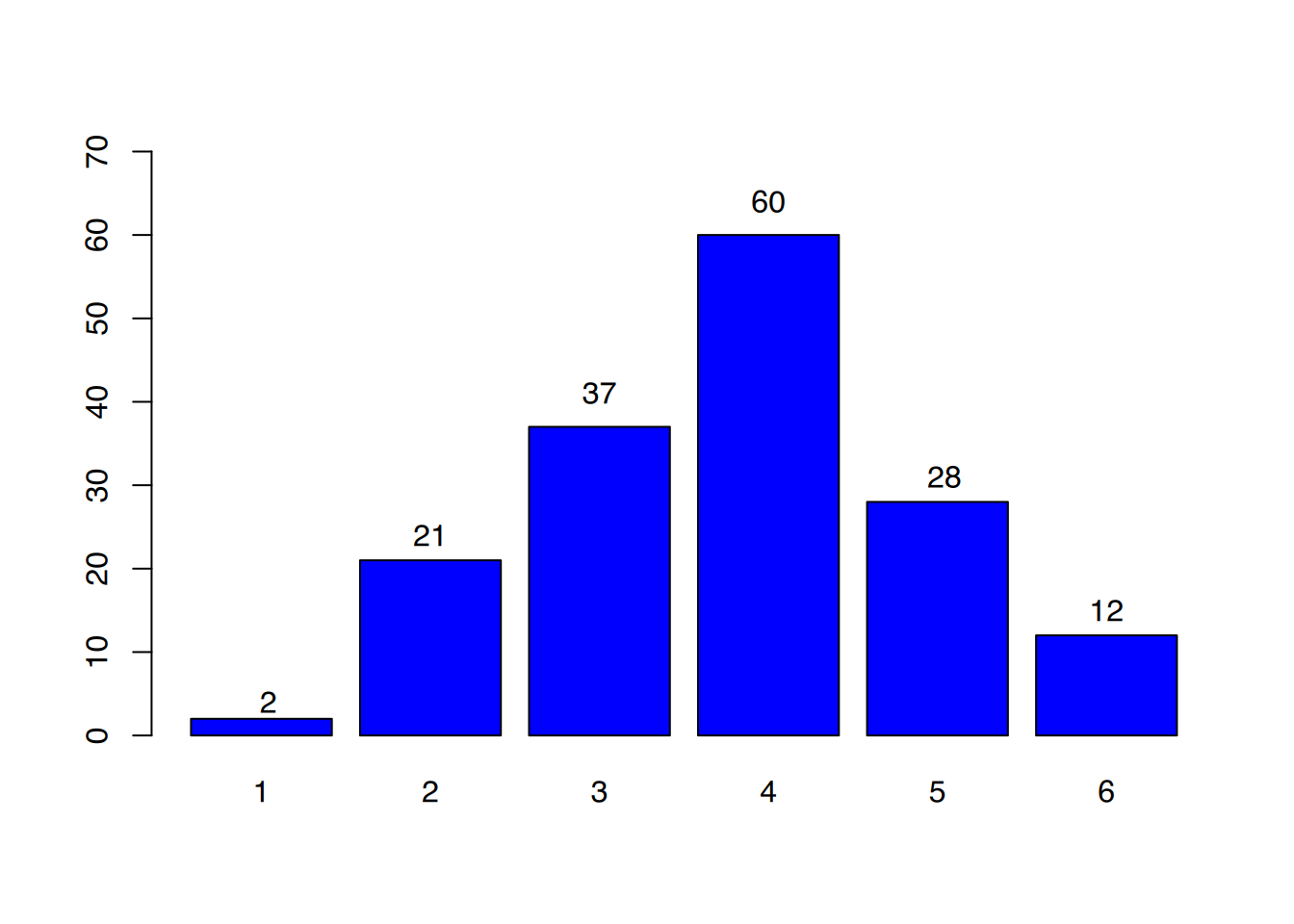
Abbildung 4.1 zeigt deutlich, dass der Hauptteil der Abiturienten die Note ausreichend erzielte. Das “Typische” dieser Verteilung lässt sich durch die Angabe, wo sich der “Hauptteil” der Werte befindet, also das Zentrum der Verteilung liegt, beschreiben. Allgemein spricht man von Maßen der zentralen Tendenz oder Lage-Kenngrößen. Maße der zentralen Tendenz, bzw. Lage-Kenngrößen allein genügen oft nicht, eine Häufigkeitsverteilung ausreichend zu beschreiben.

Dies soll das folgende Beispiel verdeutlichen:

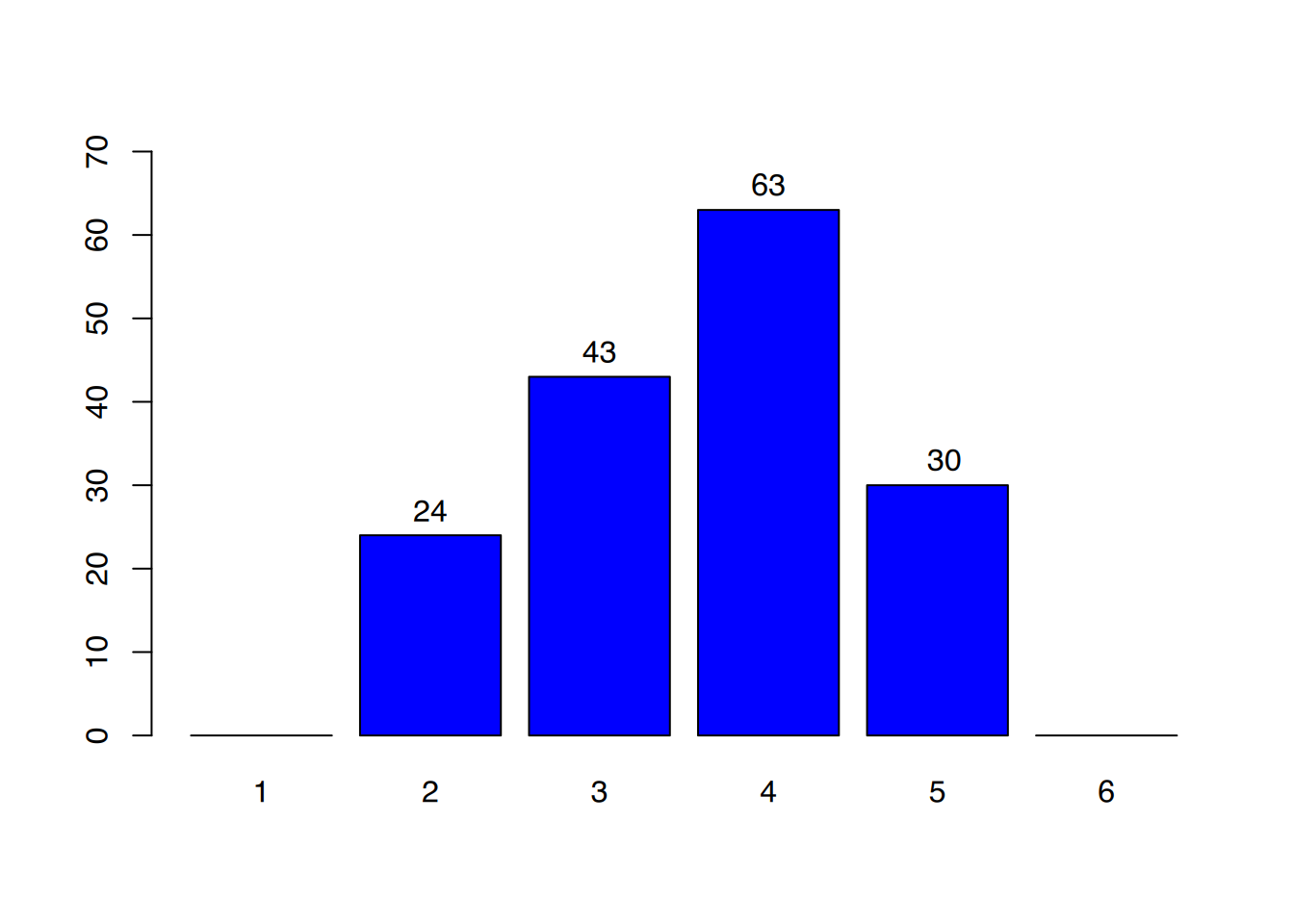
Betrachtet man die in Abbildung 4.2 dargestellte Verteilung der Noten der Schule “Y”, kann festgestellt werden, dass auch hier der Hauptteil der Schüler die Note “ausreichend” erreichte.

Abbildung 4.2: Verteilung der Abiturnoten Schule `Y`

Auffallend ist aber, dass es an dieser Schule anscheinend keine sehr guten und ebenfalls keine sehr schlechten Schüler gibt, während an Schule “X” durchaus auch die Noten sehr gut und ungenügend vergeben wurden. Gibt man für die Schulen “X” und “Y” lediglich die Lagemaße an (der Hauptteil der Schüler beider Schulen erreichte Noten zwischen befriedigend und ausreichend), kann der Eindruck entstehen, dass beide Schulen bei der Abiturprüfung gleich abgeschnitten haben. Erst die Angabe “Die Noten der Schule ”X” verteilten sich von sehr gut bis ungenügend, die der Schule ”Y” von gut bis mangelhaft” macht die Unterschiedlichkeit der beiden Verteilungen deutlich.

Kenngrößen, die Aussagen über die Unterschiedlichkeit oder auch Variabilität von Meßwerten zulassen, nennt man Streuungskenngrößen oder auch Dispersionsmaße. Zusammenfassend kann gesagt werden, dass durch die Angabe von Lage- und Streuungskenngrößen das Charakteristische einer Verteilung oft schon recht deutlich wird.

Die Verfahren zur Ermittlung der verschiedenen Lage- und Streuungskenngrößen reichen vom einfachen Ablesen aus der Häufigkeitsverteilung bis hin zur mathematischen Berechnung. Die Frage, welche Kenngrößen verwendet werden und verwendet werden dürfen, hängt direkt mit dem Informationsgehalt, also mit dem Skalenniveau der Daten zusammen. beginnen werden wir mit den Lagekenngrößen.

4.0.1 Lage-Kenngrößen

4.0.1.1 Der Modalwert

Der Modus oder Modalwert ist der in einer Verteilung am häufigsten auftretende Wert.

Liegen klassierte Daten vor, entspricht der Modalwert der Klassenmitte der Klasse mit der größten Häufigkeit. Die Kategorie (Gruppe, Klasse, etc.) mit den häufigsten Werten nennt man die Modalklasse. Es ist durchaus denkbar, dass innerhalb einer Verteilung mehrere Modalwerte ermittelt werden können. Sind jedoch die Häufigkeiten der Merkmalsausprägungen annähernd gleich verteilt, macht es keinen Sinn, den Modalwert zu bestimmen. Der Modalwert, bzw. die Modalklasse lässt sich für Daten jeglichen Skalenniveaus angeben. Andererseits bietet er für nominale Merkmale die einzige Möglichkeit, etwas typisches über die Verteilung der Merkmalsausprägungen aufzuzeigen.

Im eigentlichen Sinne (Lokalisation der Merkmalsausprägungen auf der Meßwertskala) gibt es keine Lage-Kenngrößen für nominale Daten, denn sie verteilen sich weder auf einer Meßwertskala, noch unterliegt die Anordnung der Merkmalsausprägungen einer vorgegebenen Reihenfolge. Lorenz (1996) weist darauf hin, dass der Modalwert / die Modalklasse ursprünglich nur auf metrische Merkmale angewendet und erst später auf nominale Daten ausgedehnt wurde.

Der Modalwert lässt sich ohne großen Rechenaufwand durch einfaches Ablesen aus der Häufigkeitsverteilung ermitteln.

Der Modalwert, man spricht auch vom Dichtemittel, veranschaulicht eine Häufigkeitsverteilung insofern sehr gut, als es sich ja um den relativ am häufigsten auftretenden Wert handelt.

Er vermittelt eine Vorstellung davon, welcher Wert “am ehesten auftreten wird und damit”am wahrscheinlichsten” ist. In unserm Beispiel zur Befragung nach der Anzahl der Krankenhausaufenthalte (Abbildung 4.3) tritt der Wert “bereits einmal im Krankenhaus” am häufigsten auf.

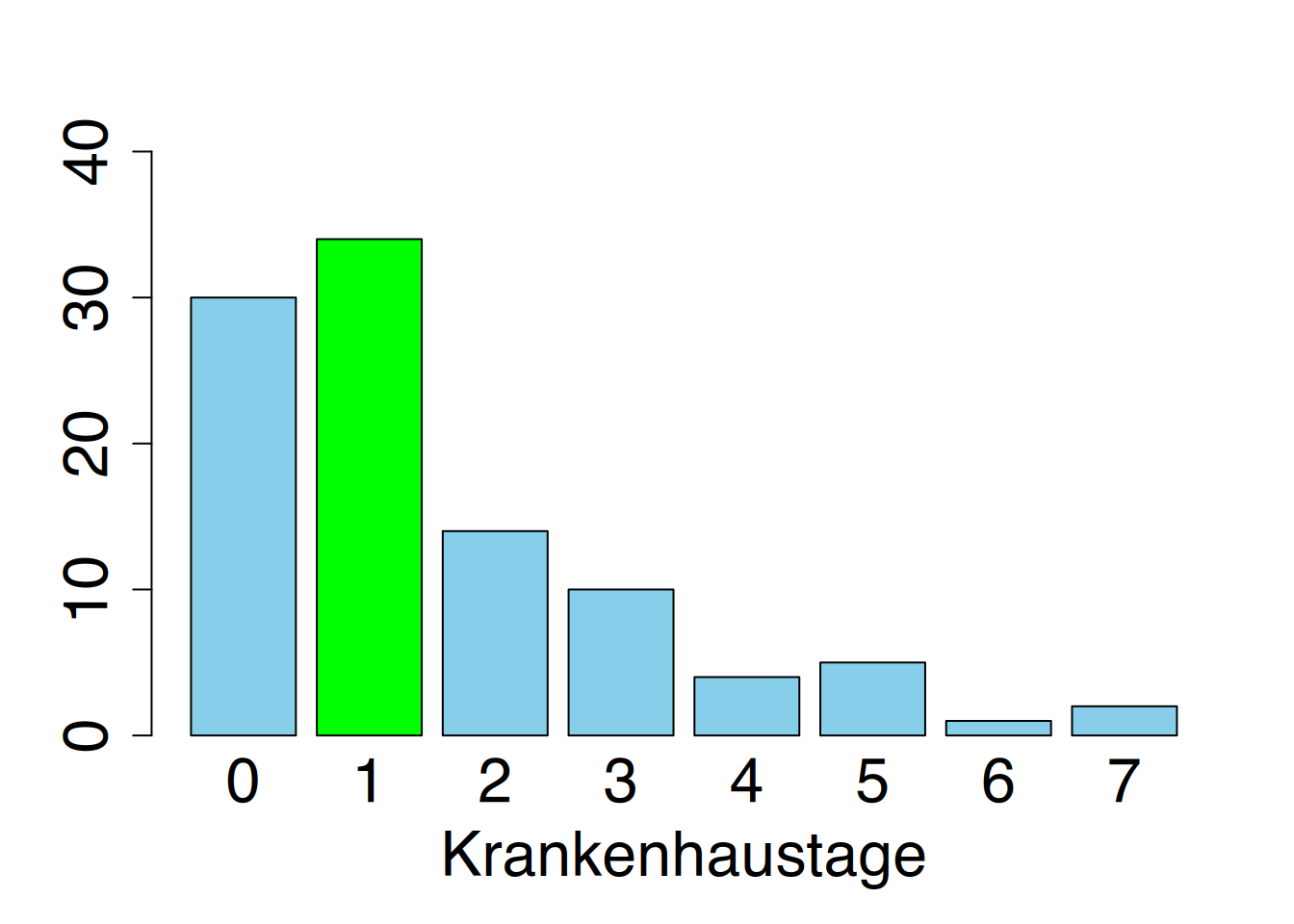
Allerdings ist der Modus relativ unzuverlässig. Betrachtet man im Balkendiagramm die Anzahl derjenigen, die noch nie in einem Krankenhaus waren, wird deutlich, dass eine geringe Änderung der Daten (z.B. durch eine Wiederholungsuntersuchung) eine entscheidende Verschiebung des Modus zur Folge haben kann.

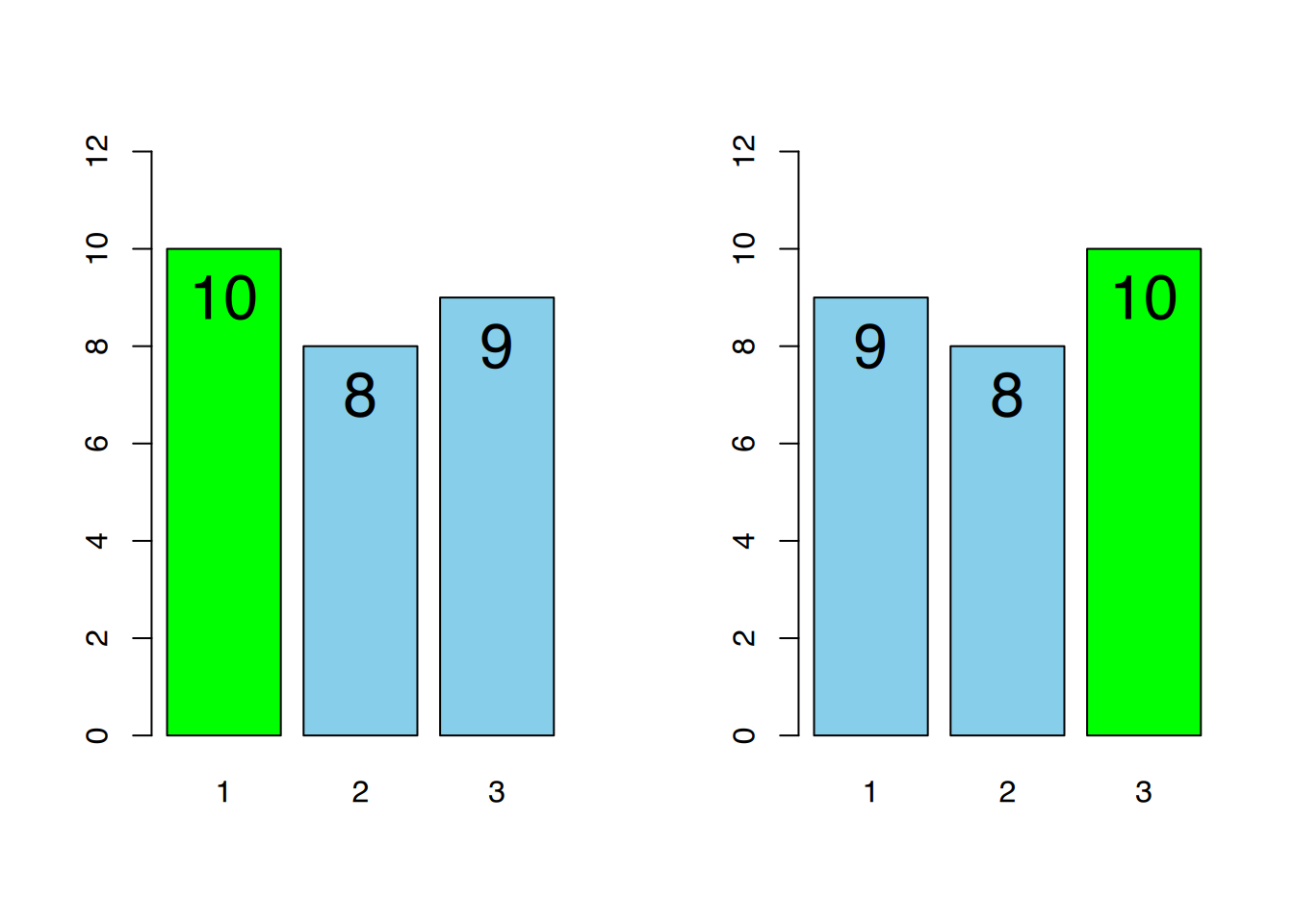
Abbildung 4.4: Verschiebung des Modus durch Änderung eines Wertes

Abbildung 4.4 zeigt dies am Beispiel von Zensuren. Durch die Veränderung eines Wertes verschiebt sich die Modalklasse von “sehr gut” nach “befriedigend”.

4.0.1.2 Der Median

Unter Median wird der “mittelste” Wert verstanden. Man spricht auch vom Zentralwert.

Der Median halbiert eine geordnete Meßwertreihe, d.h. je 50% der Werte befinden sich unterhalb und oberhalb des Medians.

Der Begriff “geordnete Meßwertreihe” weist auf das Skalenniveau hin, welches als Mindestanforderung für den Median vorliegen muß. Zur Erinnerung: Ordnen lassen sich lediglich ordinale Daten (nach Rangplätzen) und metrische Daten, bei nominalen Daten ist die Anordnung der Merkmalsausprägungen frei wählbar. Die Bestimmung des Medians ist somit nur für ordinale und metrische Merkmale zulässig.

Der Median kann bei geordneten Meßwertreihen mit geringer Anzahl einfach durch Ablesen des mittelsten Wertes ermittelt werden.

Beispiel:

Tabelle 4.1: Liegedauer
Patient	A	B	C	D	E	F	G
Liegedauer in Tagen	5	7	5	6	6	5	8

Aus der nun geordneten Meßwertreihe ergibt sich, dass der vierte Meßwert die Reihe halbiert. Es liegen sowohl drei Werte unterhalb wie auch oberhalb des Medians von 6 Tagen.

Nehmen wir nun an, es wäre nur bei 6 Patienten die Liegedauer in Tagen erfasst worden:

Der Median liegt in diesem Fall genau zwischen dem dritten und vierten Wert. Bei metrischen Daten ergibt der Durchschnitt aus 5 (dritter Wert) und 6 (vierter Wert) den Median, hier also 5,5 Tage. Beim Vorliegen von ordinalen Daten werden beide Rangplätze benannt, d.h. der Median ergibt sich aus dem dritten und vierten Rangplatz mit den Werten 5 und 6. Da die “Abzählmethode” bei umfangreichen Meßwertreihen sehr umständlich ist, ermittelt man den Median durch Anwendung nachfolgender Formeln.

Für Messwertreihen mit ungerader Anzahl gilt: \[\frac{n+1}{2} \tag{4.1}\]

Beispiel für 99 Messwerte: \[\frac{99+1}{2} = 50\] Die geordnete Messwertreihe wird durch den fünfzigsten Wert halbiert, sein Wert entspricht dem Median.

Bei gerader Anzahl gilt: \[\frac{n}{2}\ \ \mathbf{und}\ \ \frac{n}{2}+1 \label{formel:1b}\]

Beispiel für 100 Messwerte: \[\frac{100}{2} = 50\ \ \ \mathbf{und}\ \ \ \frac{100}{2}+1 = 51\] Der Median bestimmt sich aus dem fünfzigsten und einundfünfzigsten Wert der geordneten Messwertreihe.

Etwas schwieriger wird die Bestimmung des Medians bei Daten, die in klassierter Form vorliegen.

Abbildung 4.7: Median bei klassierten Daten

Greifen wir noch einmal auf unser Beispiel der Anzahl von Punkten von Seite zurück: Sicherlich haben Sie schnell ermittelt, dass der 80. und 81. Wert den Median bezeichnen, und dass diese Werte in der Klasse mit den Grenzen (24-36] liegen.

Möchte man genauere Angaben zum Median haben, benötigt man folgende Größen:

die Hälfte der Messwerte: \(\frac{n}{2} = \frac{\mathbf{160}}{2} = \mathbf{80}\)
die Klassenbreite \(b\): \(\mathbf{12}\)
die untere Grenze der Medianklasse \(x_{m}\): \(\mathbf{24}\)
die absolute Häufigkeit der Medianklasse \(h_{m}\): \(\mathbf{51}\)
die kumulierte Häufigkeit der Klasse, die unterhalb des Medians liegt \(H_{m-1}\): \(\mathbf{40}\)

Die Berechnung des Medians erfolgt dann nach der allgemeinen Formel: \[\tilde{x} = x_{m} + b \cdot \frac{\frac{n}{2}-H_{m-1}}{h_{m}} \label{formel:median}\]

Setzen wir unsere gegebenen Werte in diese Formel ein, ergibt sich für den Median: \[\tilde{x} = 24 + 12 \cdot \frac{\frac{160}{2}-40}{51}\ =\ \mathbf{33,41} \ \ \ \text{(gerundet)}\]

Eine weiter Möglichkeit zur Ermittlung des Medians bei klassierten Daten ist die graphische Methode (siehe Abbildung 11.1). Der Median entspricht unserem natürlichen Gefühl von “Mitte”. Liegen kumulierte Prozentwerte vor, lässt sich der Median leicht aus dem 50% Wert ablesen. Der Median ist nur eine Größe aus einer ganzen Reihe von Kenngrößen, die auf Rangreihen beruhen. Schließlich lässt sich eine Meßwertreihe nicht nur halbieren, man kann sie beispielsweise vierteln oder in 10 Teile teilen. Man spricht dann von den sogenannten Quantilen, die je nach Einteilung als Quartile (Viertel) oder Zentile (Zehntel) bezeichnet werden. Allgemein spricht man von p-Quantilen, die mit dem Symbol \(x_{p}\) abgekürzt werden. Nimmt man beispielsweise das 90%-Quantil oder 0,9-Quantil (\(x_{0,9}\)) bedeutet dies, dass 90% der Werte unterhalb und 10% der Werte oberhalb von \(X_{0,9}\) liegen.

Warum macht es keinen Sinn, bei nominalen Daten den Median zu bestimmen?

Betrachten wir nachfolgend die erhobenen Daten zu einigen Pflegediagnosen.

Tabelle 4.2: Häufigkeitsverteilung der Pflegediagnosen
	Häufigkeit	Prozenz	kumulierte Prozente
Störung des Körperbildes	10	40	40
soziale Isolation	5	20	60
Inkontinenz, funktional	8	32	92
Körpertemperatur, erhöht	2	8	100
Gesamt	25	100

Laut Gleichung 4.1 würde der 13. Wert den Median darstellen. Da die Pflegediagnose “Störung des Körperbildes” 10 Messwerte enthält, liegt der 13. Messwert in der nachfolgenden Diagnose “soziale Isolation” (denn diese enthält 5 Messwerte, also die Werte von 11 bis 15).

Aber: die Anordnung, also die Reihenfolge der Kategorien von nominalen Merkmalen (hier die Pflegediagnosen) spielt keine Rolle! Ordnen wir die Pflegediagnosen einmal anders an, ergibt sich folgende Häufigkeitstabelle:

Tabelle 4.3: Pflegediagnosen in veränderter Reihenfolge
Klassengrenzen	absolute Häufigkeit	kumuliert
Körpertemperatur, erhöht	2	8
soziale Isolation	5	28
Inkontinenz, funktional	8	60
Störung des Körperbildes	10	100
Gesamt	25

Jetzt fände sich der Median in der Kategorie “Inkontinenz, funktional”. Es erscheint uns nicht notwendig, alle Möglichkeiten, die Pflegediagnosen anzuordnen, vorzuführen. Eines sollte klar sein, der “13. Wert” liegt jedesmal in einer anderen Kategorie. Wie aber soll ein Wert, der je nach Anordnung in einer anderen Kategorie liegt, ein typischer Repräsentant einer Häufigkeitsverteilung sein?

Fazit: für nominale Merkmale bietet sich lediglich der Modalwert an. Egal, wie die Pflegediagnosen angeordnet werden, die Kategorie “Störung des Körperbildes” bleibt die am häufigsten vorkommende Größe!

4.0.1.3 Der arithmetische Mittelwert (\(\bar{x}\))

Der arithmetische Mittelwert \(\bar{x}\) (sprich: x quer) eines Merkmals ist die Summe aller Daten dividiert durch den Stichprobenumfang.

Der arithmetische Mittelwert beruht auf mathematischen Operationen und darf daher ausschließlich bei metrischen Daten angewendet werden. Dieser Mittelwert entspricht eher dem umgangssprachlichen “Durchschnitt”.

Die Berechnung von \(\mathbf{\bar{x}}\) erfolgt, indem man alle Einzelwerte addiert (\(\sum\)) und anschließend durch die Anzahl (n) der Werte dividiert. Die allgemeine Formel lautet: \[ \bar{x} = \frac{\sum{x_{i}}}{n} \tag{4.2}\]

Beispiel:

Tabelle 4.4: Liegedauer
Patient	A	B	C	D	E	F	G
Liegedauer in Tagen	5	7	5	6	6	5	8

Eingesetzt in Gleichung 4.2 ergibt sich:

\[\begin{aligned} \bar{x} &=& \frac{(5+7+5+6+6+5+8)}{7}\\ &=& \frac{42}{7}\\\\ &=& \mathbf{6} \end{aligned}\]

Der mittlere stationäre Aufenthalt beträgt für dieses Beispiel sechs Tage.

In der Praxis wird eher selten eine Meßwertreihe mit sieben Einzelwerten wie in diesem Beispiel vorliegen. Oder anders ausgedrückt: In der Regel werden einzelne Meßwerte mehrfach vorkommen. Entsprechend berücksichtigt man bei der Berechnung des arithmetischen Mittelwertes die absoluten Häufigkeiten. \[\bar{x} = \frac{ \sum{x_{i} \cdot h_{i} }}{n} \tag{4.3}\]

Beispiel:

Tabelle 4.5: Liegedauer
Stationärer Aufenthalt in Tagen (\(x_{i}\))	1	2	3	4	5	6	7
Anzahl der Patienten (abs. Häufigkeit (\(h_{i}\))	2	4	3	5	6	4	1

Eingesetzt in Gleichung 14.1 ergibt sich:

\[\begin{aligned} \bar{x} & = & \frac{ \sum{ (1\cdot 2) + (2\cdot 4) + (3\cdot 3) + (4\cdot 5) + (5\cdot 6) + (6\cdot 4) + (7\cdot 1) } }{25}\\ & = &\frac{ \sum{ (2 + 8 + 9 + 20 + 30 + 24 + 7 } }{25}\\ & = &\frac{100}{25}\\\\ & = & \mathbf{4} \end{aligned}\]

Der mittlere stationäre Aufenthalt beträgt für dieses Beispiel vier Tage.

Eine weitere “Variante” des arithmetischen Mittelwertes kommt zur Anwendung, wenn beispielsweise der Gesamtmittelwert aus beiden Stichproben (beide Beispiele) interessiert. Man spricht dann vom gewichteten arithmetischen Mittelwert. Eine Möglichkeit besteht darin, jeden Einzelwert der beiden Beispiele zu summieren und anschließend durch die Anzahl aller Werte zu dividieren.

\[\begin{aligned} \bar{x} & = & \frac{ Summe_{gesamt}}{Anzahl_{gesamt}} = \frac{Summe_{1} + Summe_{2}}{Anzahl_{1} + Anzahl_{2}}\\\\ \end{aligned}\] bzw. \[\begin{aligned} \bar{x} & = & \frac{\sum{x_{i1}} + \sum{x_{i2}}}{n_{1} + n_{2}} \label{formel:xquergewichtet} \end{aligned}\]

Das Addieren aller Einzelwerte dürfte bei umfangreichen Messwertreihen recht mühsam sein. Nutzen wir die folgende Tatsache:
\[\text{Da\ \ \ } \bar{x} = \frac{\sum{x_{i}}}{n}\ \ \text{gilt dementsprechend\ \ \ } n \cdot \bar{x} = \sum{x_{i}}\]

Das mühsame Aufaddieren der Einzelwerte kann demnach entfallen. Wir ersetzen \(\sum{x_{i1}}\) durch \(n_{1} \cdot \bar{x}_{1}\) und \(\sum{x_{i2}}\) entsprechend durch \(n_{2} \cdot \bar{x}_{2}\)
Die Berechnung des Gesamtdurchschnitts erfolgt nach folgender Formel:

\[ \begin{aligned} \bar{x}_{gesamt} & = & \frac{n_{1} \cdot \bar{x}_{1} + n_{2} \cdot \bar{x}_{2}}{n_{1} + n_{2}} \end{aligned} \tag{4.4}\]

Wir erinnern uns, dass in Beispiel 1 der stationäre Aufenthalt der 7 Patientinnen im Schnitt 6 Tage und in Beispiel 2 der Aufenthalt der 25 Patientinnen durchschnittlich 4 Tage betrug.

Eingesetzt in Gleichung 4.4 ergibt sich ein gesamter oder gemeinsamer Durchschnitt von 4,437 Tagen: \[\begin{aligned} \bar{x}_{gesamt} & = & \frac{7 \cdot 6 + 25 \cdot 4}{7 + 25}\\\\ &=& \frac{42 + 100}{32}\\\\ &=& 4,437\\\\ \end{aligned}\]

4.0.2 Streuungskenngrößen

Wie eingangs bereits erwähnt unterscheiden sich Häufigkeitsverteilungen nicht nur durch ihre Lage auf der Meßwertskala, sondern auch durch ihre Streuung. Streuungskenngrößen sind Maßzahlen zur Bewertung oder Quantifizierung der Variabilität der Meßwerte.

4.0.2.1 Die Spannweite “R” und der Quartilsabstand “Q”

Ein besonders einfaches Streuungsmaß ist die Spannweite, auch Variationsbreite genannt, die mit “R” (engl. range) abgekürzt wird. Sie bestimmt sich aus der Differenz zwischen dem größten und dem kleinsten Meßwert. \[\begin{aligned} R = x_{max} - x_{min} \end{aligned}\]

Der Quartilsabstand “Q”, auch Interquartilsabstand genannt, gibt die mittleren 50% der Verteilung an, d.h. sowohl das obere, als auch das untere Viertel entfallen. Mit anderen Worten bezeichnet “Q” den Abstand zwischen dem ersten und dritten Quartil.

\[\begin{aligned} Q = x_{0,75} - x_{0,25} \end{aligned}\]

Relativ einfach lassen sich diese beiden Streuungsmaße aus der geordneten Messwertreihe bestimmen. Abbildung 4.8 zeigt 15 Meßwerte, der Vollständigkeit halber wurde auch der Median gekennzeichnet.

\[\begin{aligned} \text{Aus diesen Werten ergibt sich eine Spannweite von:\ \ \ } R & = 9 - 5 & = 4\ \text{Tage}\\ \text{Der Quartilsabstand beträgt:\ \ \ } Q & = 8 - 6 & = 2\ \text{Tage} \end{aligned}\]

Andere Streuungsmaße berücksichtigen die Abweichung jedes einzelnen Wertes vom arithmetischen Mittelwert. Diese Abweichungen werden aufsummiert: \[\begin{aligned} \sum{x_{i} - \bar{x}} \end{aligned}\] Dabei gibt es allerdings (zunächst) ein Problem. Da sich sowohl oberhalb als auch unterhalb des Mittelwertes Einzelwerte befinden, somit also positive und negative Abweichungen vom Mittelwert vorhanden sind, ergibt die Summe dieser Abweichungen Null. \[\begin{aligned} \sum{x_{i} - \bar{x}} = 0 \end{aligned}\]

Für unser Beispiel auf dieser Seite beträgt der arithmetische Mittelwert 7 Tage, die nachfolgende Tabelle zeigt die jeweiligen Abweichungen vom arithmetischen Mittelwert:

Abbildung 4.9: Abweichungen vom arithmetischen Mittel

4.0.2.2 Summe der quadrierten Abweichungen “SQ”

Um dennoch etwas über die Streuung der Werte vom Mittelwert aussagen zu können, greift man auf das Quadrieren zurück. Durch dieses Verfahren ergibt die Summe der Abweichungen in jedem Fall eine positive Zahl. Grundlegender Begriff beim Aufbau der nachfolgenden Formeln der Streuungsmaße ist die Summe der quadrierten Abweichungen “SQ”.

\[\begin{aligned} SQ = \sum{(x_{i} - \bar{x})^2} \cdot h_{i} \label{formel:SQ} \end{aligned}\] Es versteht sich, dass selbstverständlich bei mehrfachen Auftreten eines Meßwertes die Häufigkeiten (\(h_{i}\)) berücksichtigt werden. Bleiben wir bei unserem Beispiel von Seite und setzen die Werte in die Formel [formel:SQ] ein:

\[\begin{aligned} SQ &=& (5-7)^2 \cdot 2 + (6-7)^2 \cdot 3 + (7-7)^2 \cdot 5 + (8-7)^2 \cdot 3 + (9-7)^2 \cdot 2\\ &=& (-2)^2 \cdot 2 + (-1)^2 \cdot 3 + (0)^2 \cdot5 + 1^2\cdot3 + 2^2\cdot2\\ &=& 4\cdot2 + 1\cdot3 + 0\cdot5 + 1\cdot3 + 4 \cdot 2\\ &=& 8 + 3 + 0 +3 +8\\ &=& 22 \end{aligned}\]

4.0.2.3 Varianz \(\mathbf{s^2}\)

Zugegebenermaßen ist die Summe der quadrierten Abweichungen nicht besonders anschaulich, wenn wir etwas über die Variabilität der Werte im Beispiel des stationären Aufenthaltes aussagen möchten. Der nächste Schritt ist nun, SQ auf die Anzahl der Meßwerte “n” zu beziehen. Handelt es sich bei den zu berechnenden Daten um eine Stichprobe (was meistens der Fall ist) rechnet man mit “\(n - 1\)”. Daraus ergibt sich die Varianz \(\mathbf{s^2}\)

\[\begin{aligned} s^2 &=& \frac{SQ}{n - 1} \end{aligned}\]

bzw. \[\begin{aligned} s^2 &=& \frac{\sum{(x_{i} - \bar{x})^2} \cdot h_{i}}{n - 1} \label{varianz} \end{aligned}\]

In unserem Beispiel errechneten wir \(SQ = 22\), welche wir nun durch \(n - 1\) dividieren. \[\begin{aligned} s^2 = \frac{SQ}{n - 1} = \frac{22}{15 -1} = 1,57 \end{aligned}\]

4.0.2.4 Standardabweichung \(\mathbf{s}\)

Konsequenterweise sollte nun die Quadrierung wieder rückgängig gemacht werden (Lorenz (1996) schreibt: “…den Ausdruck SQ/n-1 auf dieselbe Dimension zu bringen, welche die Meßwerte selbst besitzen”). Um die Quadrierung rückgängig zu machen, zieht man die Wurzel und erhält damit die Standardabweichung “s”:

\[\begin{aligned} s = \sqrt{s^2} \ \ \ \ \text{bzw.}\ \ \ \ s = \sqrt{\frac{\sum{(x_{i} - \bar{x})^2}}{n - 1} \cdot h_{i}} \label{formel:sd} \end{aligned}\]

Für unser Beispiel ergibt sich damit: \[\begin{aligned} s = \sqrt{s^2}\ \ = \sqrt{1,57}\ \ = 1,25 \end{aligned}\]

In Publikationen findet sich häufig die Abkürzung sd (standard deviation) für die Standardabweichung anstelle von s.

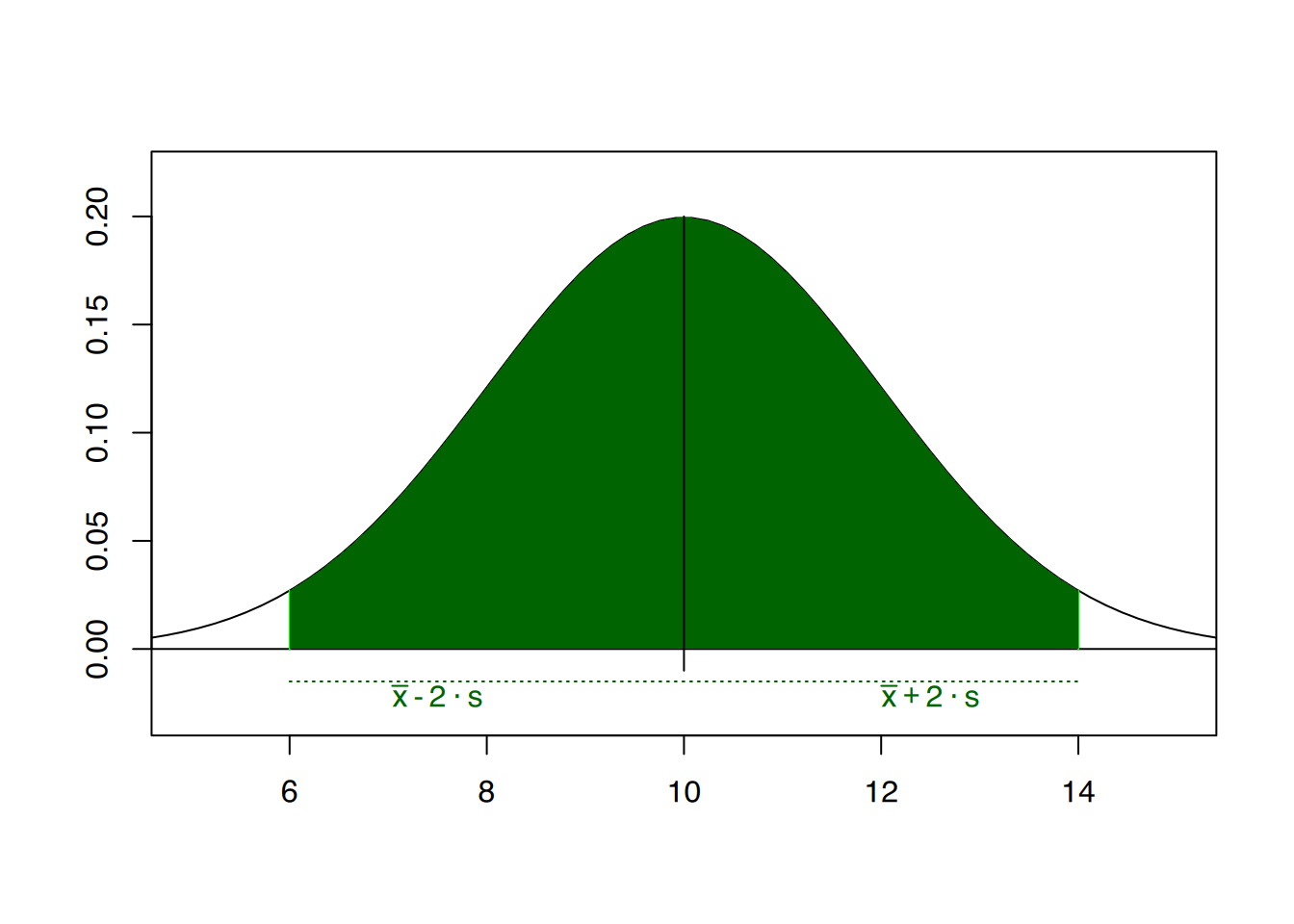
4.0.2.5 Die Bedeutung der Standardabweichung

Liegt eine glockenförmige, symmetrische Verteilung vor, eine sogenannte Normalverteilung (siehe Abbildung 4.10 (a)), so liegen in dem Bereich von einer Standardabweichung um den Mittelwert, d.h. innerhalb \(\bar{x} + s\) und \(\bar{x} - s\) ca. \(\frac{2}{3}\) aller Werte (genau 68,23%, siehe Abbildung 4.10 (b)). Innerhalb von 2 Standardabweichungen sind es bereits ca. 95% der Werte (siehe Abbildung 4.10 (c)).

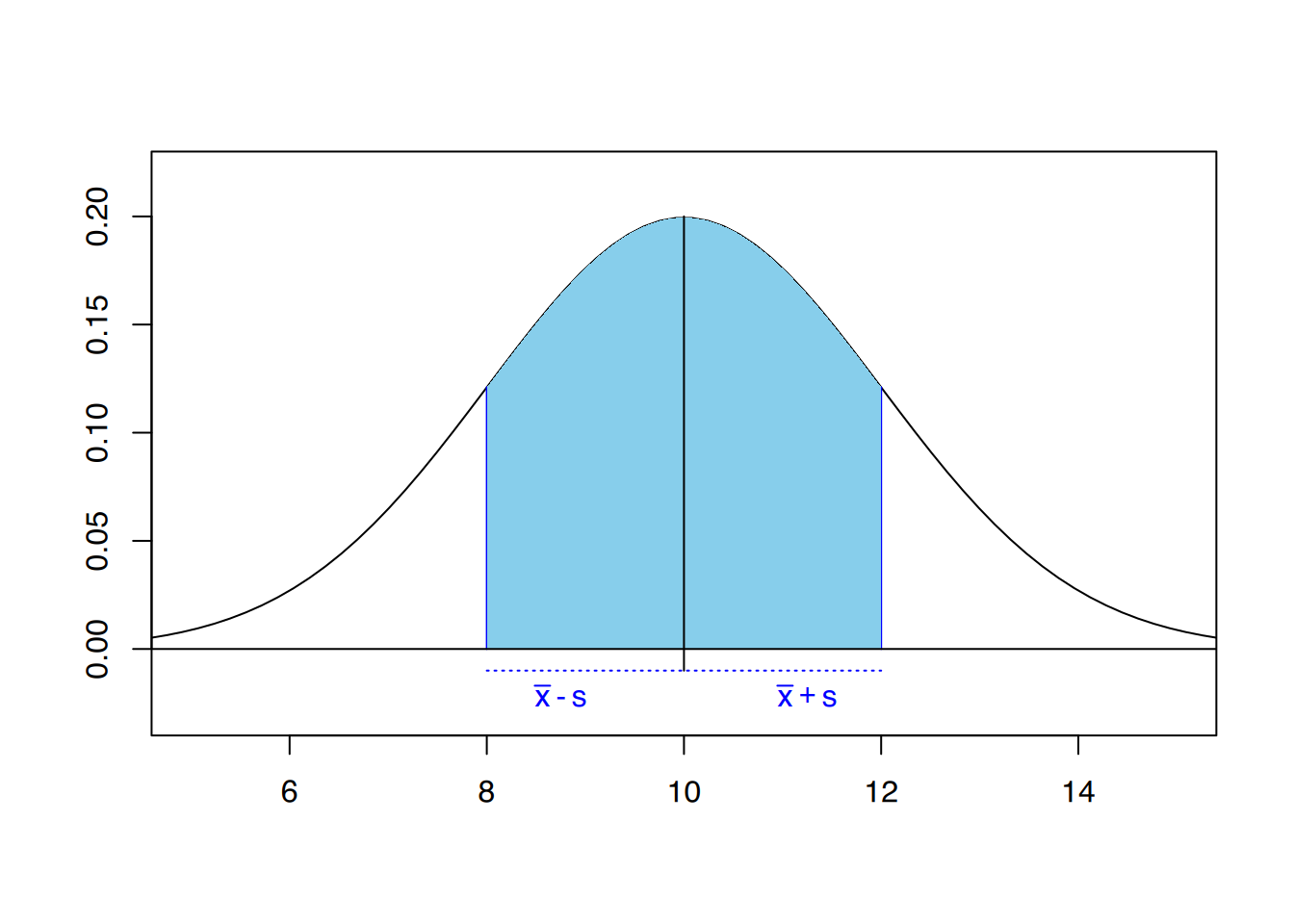
Für unser Beispiel bedeutet dies, dass 68,23% der Patientinnen \(7 -1,25\) bis \(7 +1,25\) Tage stationär im Krankenhaus lagen, also 68,23% der Patientinnen lagen zwischen 5,75 und 8,25 Tagen stationär.
95% der Patientinnen lagen zwischen 4,5 und 9,5 Tagen im Krankenhaus (\(7 \pm 2,5\)). Anders ausgedrückt kann man sagen, dass insgesamt nur 5% der Pat. weniger als 4,5 und mehr als 9,5 Tage im Krankenhaus verweilten.

4.0.2.6 Der Variationskoeffizient “Vk”

Bei Verteilungen mit unterschiedlichen Mittelwerten könnte die Frage interessieren, in welcher der beiden Verteilungen die Variabilität der Meßwerte größer ist. Um dies zu untersuchen, bietet sich der Variationskoeffizient an. Dieser setzt jeweils die Standardabweichung ins Verhältnis zum Mittelwert. Multipliziert man den Wert mit 100, so erhält man den Variationskoeffizienten in Prozent. \[\begin{aligned} VK = \frac{s}{\bar{x}}\quad\text{bzw.}\quad VK' = \frac{s}{\bar{x}} \cdot 100 \end{aligned}\] Beispiel:
Auf allgemeinchirurgischen Stationen fallen im Durchschnitt pro Patient/Tag Kosten in Höhe von 500,-€ (s=75) an. Auf den untersuchten Intensivstationen beliefen sich die Kosten auf 1000,-€ (s=100) täglich. Es errechnen sich die folgenden Variationskoeffizienten: \[\begin{aligned} VK_{Chirurgie} &= 550 = 0,15 \quad\text{bzw.}\quad 15\%\\\\ VK_{Intensiv} &= 1000 = 0,1 \quad\text{bzw.}\quad 10\% \end{aligned}\]

Die Verteilung der Werte auf den Intensivstationen ist demnach homogener, bzw. die Variabilität der Werte ist auf den chirurgischen Stationen ist höher.

Bleiben wir bei dem Beispiel und nehmen wir an, ein Verwaltungsleiter stellt fest, dass in seinem Haus die chirurgische Station im Schnitt täglich 650,-€ pro Patient aufwendet, und die Intensivstation sogar 1200,- €. Damit liegt die chirurgische Station 150,-€ und die Intensivstation 200.-€ über dem Durchschnitt. Auf den ersten Blick hat also die Intensivstation noch “schlechter” gewirtschaftet als die Chirurgie. Bevor man aber “Äpfel mit Birnen” vergleicht, also Werte vergleicht, die aus sehr unterschiedlichen Verteilungen stammen, muß man diese Verteilungen erst einmal vergleichbar machen.

4.0.2.7 Exkurs: z-Werte und z-Transformation

Sollen also Werte aus unterschiedlichen Verteilungen verglichen werden, so müssen sie laut Bortz (1999) S.45:

“.…zuvor an der Unterschiedlichkeit aller Werte im jeweiligen Kollektiv relativiert werden. Dies geschieht, indem die Abweichungen durch die Standardabweichungen im jeweiligen Kollektiv dividiert werden. Ein solcher Wert wird als z-Wert bezeichnet.”

Unter den unendlich vielen Normalverteilungen gibt es eine Normalverteilung, die sich dadurch auszeichnet, dass sie einen Erwartungswert von \(\mu=0\) und eine Streuung von \(\sigma=1\) aufweist. Dieser speziellen Normalverteilung wird deshalb eine besondere Bedeutung zugemessen, weil sämtliche übrigen Normalverteilungen durch eine einfache Transformation in sie überführbar sind. Dies erfolgt mit der Formel: \[\begin{aligned} z_{i} = \frac{x_{i} - \bar{x}}{s} \quad\quad\text{bzw.}\quad\quad z_{i} = \frac{x_{i} - \mu}{\sigma} \end{aligned} \tag{4.5}\]

Transformiert man mit Hilfe der Gleichung 4.5 alle vorliegenden Werte einer Verteilung, erhält man eine neue Verteilung mit einem Mittelwert von Null und einer Streuung von eins \[\begin{aligned} z = 0 \quad\text{und}\quad s_{z} = 1 \quad\quad\text{bzw.}\quad\quad \mu=0 \quad\text{und}\quad \sigma=1 \end{aligned}\]

Durch die z-Transformation können also sämtliche Normalverteilungen standardisiert werden. Deshalb wird die Normalverteilung mit \(\mu=0\) und \(\sigma=1\) auch als Standardnormalverteilung bezeichnet.

Setzen wir für unsere Stationen die Werte in die Gleichung 4.5 ein, ergibt sich: \[\begin{aligned} z_{chirurgie} = \frac{650 - 500}{75} = 2 \quad\text{und}\quad z_{intensiv} = \frac{1200 - 1000}{100} = 2 \end{aligned}\]

Durch die z-Transformation sind beide Stationen vergleichbar geworden. Beide Transformationen ergeben einen z-Wert von “2” d.h., beide Stationen weichen in gleicher Höhe vom Mittelwert ab.

Weitere Übungsaufgaben zur z-Transformation finden sich im Anhang [uebung:ztrans]

4.0.3 Streuungsmaße und Skalenniveau

Für nominalskalierte Daten gibt es im eigentlichen Sinne keine Streuungskenngrößen. Man kann lediglich die Zahl der Kategorien angeben. Alle besprochenen Streuungskenngrößen beruhen auf Rechenoperationen, selbst bei der Spannweite “R” wurde die Subtraktion des kleinsten vom größten Meßwert durchgeführt. Mathematische Operationen sind aber, - wie bereits mehrfach erwähnt -, lediglich bei metrischem Skalenniveau der Daten zulässig.

Trotzdem ist es möglich, auch bei ordinalen Daten die Spannweite und den Quartilsabstand anzugeben. Allerdings beschränken sich die Angaben dann darauf, über wie viele Skalenstufen bzw. Rangstufen sich die Spannweite oder der Quartilsabstand erstrecken. Es wird im eigentlichen Sinne nicht mehr gerechnet.

Als Beispiel sind in Abbildung 4.11 die Ergebnisse der Zwischenprüfung von 15 Altenpflegerinnen notiert worden. Die Ergebnisse erstrecken sich über vier Noten, es gibt bei diesem Beispiel demnach vier Rangstufen auf der Skala.

Abbildung 4.11: Ergebnisse der Zwischenprüfung

Die Spannweite “R” erstreckt sich über 4, der Quartilsabstand “Q” über 2 Ränge.

4.0.4 Zusammenfassung

Zusammenfassung
Nominale Skala	Ordinale Skala	Metrische Skala
- es gibt Unterschiede, aber nur im Sinne von Klassifizierung	- es gibt Unterschiede, größer oder kleiner, besser oder schlechter, die Abstände lassen sich aber nicht interpretieren	- die Größe des Unterschieds kann gemessen werden
- die Reihenfolge spielt keine Rolle	- die Reihenfolge der Klassen muss beachtet werden	- die Abstände sind interpretierbar
		- gleiche Abstände benachbarter Werte
		- ist der Ausgangspunkt/Nullpunkt frei wählbar, handelt es sich um eine Intervallskala, z.B. °C oder Fahrenheit, die Abstände sind interpretierbar, nicht aber das Verhältnis
		- liegt ein natürlicher Nullpunkt vor (Länge, Gewicht, Lebensalter) handelt es sich um eine Verhältnisskala. (10 Jahre ist doppelt so viel wie 5 Jahre). Abstände und Verhältnis der Werte sind interpretierbar.
Lagekenngrößen: Modalwert	Lagekenngrößen: Modalwert, Median	Lagekenngrößen: Modalwert, Median, arithmetisches Mittel
Streuungskenngrößen: Keine Streuungskenngrößen, allenfalls Zahl der Kategorien	Streuungskenngrößen: Spannweite und Quartilsabstand in Skalenstufen	Streuungskenngrößen: Spannweite, Quartilsabstand, Varianz, Standardabweichung, Variationskoeffizient