10 Signifikanztests
10.1 Einführung
Die Fragestellung, um die es beim Testen auf Signifikanz geht, ist die, inwieweit ein gefundenes Ergebnis, z.B. ein Unterschied zufällig oder nicht zufällig zufällig zustande gekommen sein kann. Im Rahmen dieses Skripts werden wir uns in der Hauptsache mit Unterschieden zwischen zwei Stichproben befassen. Der Grundgedanke, der sich dahinter verbirgt, ähnelt ein wenig dem Prinzip bei der Bestimmung von Konfidenzgrenzen. Greifen wir nochmals auf das Beispiel der durchschnittlichen Liegedauer zurück, die 9 Tage betrug. Unsere Stichprobe entstammte einer Grundgesamtheit mit einen Mittelwert \(\mu\) = 10 Tage und einen Standardfehler von \(\sigma_{\bar{x}}\) = 2 Tage. Im Bereich von 1,96 Standardfehlern rechts und links vom Mittelwert, also zwischen 6,08 und 13,92 Tagen, liegen 95% aller Werte. Die Wahrscheinlichkeit dafür, einen Stichprobenmittelwert von weniger als 6,08 Tagen oder einen von mehr als 13,92 Tage zu finden, beträgt jeweils nur 2,5%.
Wenn in einer weiteren Stichprobe eine durchschnittliche Liegedauer von 45 Tagen ermittelt wird, müssen wir fragen, ob diese Stichprobe wohl eher einer anderen Grundgesamtheit entstammt. Denn es ist sehr unwahrscheinlich, dass unsere Grundgesamtheit (\(\mu = 10, \sigma_{\bar{x}} = 2\)) einen Mittelwert von 45 Tagen und mehr „produziert" dass man sicherlich spontan sagen würde, der Unterschied zwischen Stichprobe A mit 9 Tagen und Stichprobe B mit 45 Tagen ist signifikant. Die beiden Stichproben entstammen zwei völlig verschiedenen Grundgesamtheiten (vielleicht Liegedauer in Allgemeinen Krankenhäusern und Liegedauer in Reha-Einrichtungen). Hätte Stichprobe B eine durchschnittliche Liegedauer von 7 oder 11 oder 12 Tagen angegeben, hätten wir mit unserem Vorwissen sofort gesagt, es ist sehr wahrscheinlich, dass Stichprobe B zu der gleichen Grundgesamtheit gehört wie Stichprobe A.
Wie schon bei der Bestimmung von Konfidenzgrenzen ist es auch bei Signifikanzaussagen nicht möglich, Aussagen mit 100%iger Sicherheit zu erhalten. So ist in unserem Beispiel eine durchschnittliche Liegedauer von 16 Tagen oder mehr Tagen sehr unwahrscheinlich (0,13%), es ist aber nicht unmöglich. Das heißt, wenn wir nach der Durchführung eines Signifikanztestes behaupten, das Krankenhaus gehöre zu einer anderen Grundgesamtheit, kann es sein, dass wir uns irren, dass wir also einen Fehler gemacht haben. Auf die Möglichkeit, Fehlentscheidungen zu treffen, gehen wir an späterer Stelle ausführlich ein. Vor der Durchführung eines Signifikanztestes legen wir (wie auch bei den Konfidenzgrenzen) fest, wie hoch denn das Irrtums-Risiko höchstens sein darf. Auch hierbei sind Irrtumswahrscheinlichkeiten \(\alpha\) von 5% oder 1% geläufig, so daß das Signifikanzniveau bei 95% oder 99% liegt.
Dadurch ergeben sich Schwellenwerte, die im Beispiel der Normalverteilung die \(z\)-Werte sind. Mittels \(z\)-Transformation unseres Stichprobenmittelwertes ist es uns dann möglich zu entscheiden, wo genau unser Stichprobenwert liegt. Findet er sich innerhalb des 95% (oder 99%) -Bereiches, so ist davon auszugehen, dass die Stichprobe zu dieser Grundgesamtheit gehört. Die vorher formulierte statistische Null-Hyothese (es gibt keinen Unterschied) kann somit nicht verworfen werden. Liegt er links vom unteren Wert bzw. rechts vom oberen Wert, so ist es sehr wahrscheinlich, dass unsere Stichprobe aus einer anderen Verteilung stammt. Dies würde die statistische Alternativ-Hypothese (es gibt einen Unterschied) bestätigen.
Zusammenfassend kann man sagen, dass es um die Frage geht, inwieweit die aufgetretenen Unterschiede „echt" sind (d.h. es existiert ein Unterschied) oder zufällig zustande kamen (es existiert kein Unterschied). Dazu formuliert man statistische Hypothesen. Gibt es tatsächlich Unterschiede, so stammen die beiden Stichproben aus zwei unterschiedlichen Grundgesamtheiten mit den Mittelwerten \(\mu_{1}\) und \(\mu_{2}\). Sind die Unterschiede in den Stichproben zufällig, so entstammen sie derselben Grundgesamtheit mit dem Mittelwert \(\mu\). Durch festlegen der Irrtumswahrscheinlichkeit \(\alpha\) lassen sich Schwellenwerte bestimmen, mit denen man den Stichprobenwert nach Transformation (Teststatistik) vergleicht. In unserem Beispiel ging es um eine Normalverteilung, so daß wir mit \(z\)-Werten und \(z\)-Transformation arbeiten konnten. Je nach Art der Daten (Skalenniveau, Verteilung, Variabilität) gibt es unterschiedliche Verfahrem zur Ermittlung der Teststatistik. Bevor wir auf die verschiedenen Signifikanzteste eingehen, müssen wir noch die angesprochenen statistischen Hypothesen und mögliche Fehlerarten besprechen.
10.2 Statistische Hypothesen
Grundsätzlich formulieren wir in der Statistik vor den Untersuchungen zwei Hypothesen. Zum ersten sprechen wir von der Null-Hypothese (\(\mathbf{H_{0}}\)), die vereinfacht ausgedrückt besagt, dass es keinen Effekt / Unterschied gibt, die Stichproben also aus der selben Grundgesamtheit stammen. Der transformierte Stichproben-Wert, die Teststatistik also, liegt innerhalb eines möglichen Bereiches, der vom Schwellenwert abgegrenzt wird.
Die Alternativ-Hypothese (\(\mathbf{H_{1}}\) oder \(\mathbf{H_{A}}\)) ist das (logische) Gegenteil der Nullhypothese, also es gibt einen Effekt / Unterschied. Somit gehören die Stichproben zu unterschiedlichen Grundgesamtheiten. Die Teststatistik hat den Schwellenwert überschritten (bzw. unterschritten).
Alle Testverfahren überprüfen die Nullhypothese. Wird diese nach Durchführung des Signifikanztestes abgelehnt, wird dadurch die Alternativhypothese bestätigt.
Beim Formulieren von Hypothesen unterscheidet man weiterhin, ob es sich um eine einseitige oder zweiseitige Fragestellung handelt. Man spricht dann von gerichteten oder ungerichteten Hypothesen. Formuliert man zur Liegedauer im Krankenhaus beispielsweise die folgenden Hypothesen:
\[ \begin{aligned} H_{0}: \mu_{1} = \mu_{2}\\ H_{1} : \mu_{1} \neq \mu_{2} \end{aligned} \]
Die Nullhypothese lautet: es gibt keinen Unterschied in der durchschnittlichen Liegedauer zwischen den beiden Stichproben und entsprechend sagt die Alternativhypothese aus, dass es einen Unterschied gibt. Dies ist eine ungerichtete Hypothese bei zweiseitiger Fragestellung, da wir nicht konkretisieren, ob die Verweildauer länger oder kürzer ist. Wir sagen lediglich, dass sie anders ist.
Sprechen wir unsere Vermutung deutlich aus, handelt es sich um eine gerichtete Hypothese bei einseitiger Fragestellung. Für unser Beispiel lautete die Nullhypothese, dass die durchschnittliche Verweildauer in Stichprobe 1 höchsten genauso lang ist wie in Stichprobe 2. Die Alternativhypothese wäre, dass die durchschnittliche Verweildauer in Stichprobe 1 länger ist als in Stichprobe 2.
\[ \begin{aligned} H_{0}: \mu_{1} \leq \mu_{2}\\ H_{1} : \mu_{1} > \mu_{2} \end{aligned} \]
Die Verwendung der Relationssymbole >, \(\geq\), \(\leq\), < richtet sich selbstverständlich nach der jeweiligen Fragestellung. Möchte man beispielsweise mit einem Signifikanztest herausfinden, dass ein neues Medikament (N) weniger Nebenwirkungen mit sich bringt als ein altes, bisher verwendetes Medikament (A), so könnten die Hypothesen lauten:
Nullhypothese \(H_{0}\): \(\mu_{N} \geq \mu_{A}\), das neue Medikament hat genauso viele oder mehr Nebenwirkungen wie das alte.
Alternativhypothese \(H_{1}\): \(\mu_{N} < \mu_{A}\), das neue Medikament hat weniger Nebenwirkungen als das alte.
Jetzt muß noch geklärt werden, welche Konsequenzen sich aus ein- bzw. zweiseitiger Fragestellung ergeben. Wir verdeutlichen dies am Beispiel der durchschnittlichen Kosten für Intensivbetten pro Tag.
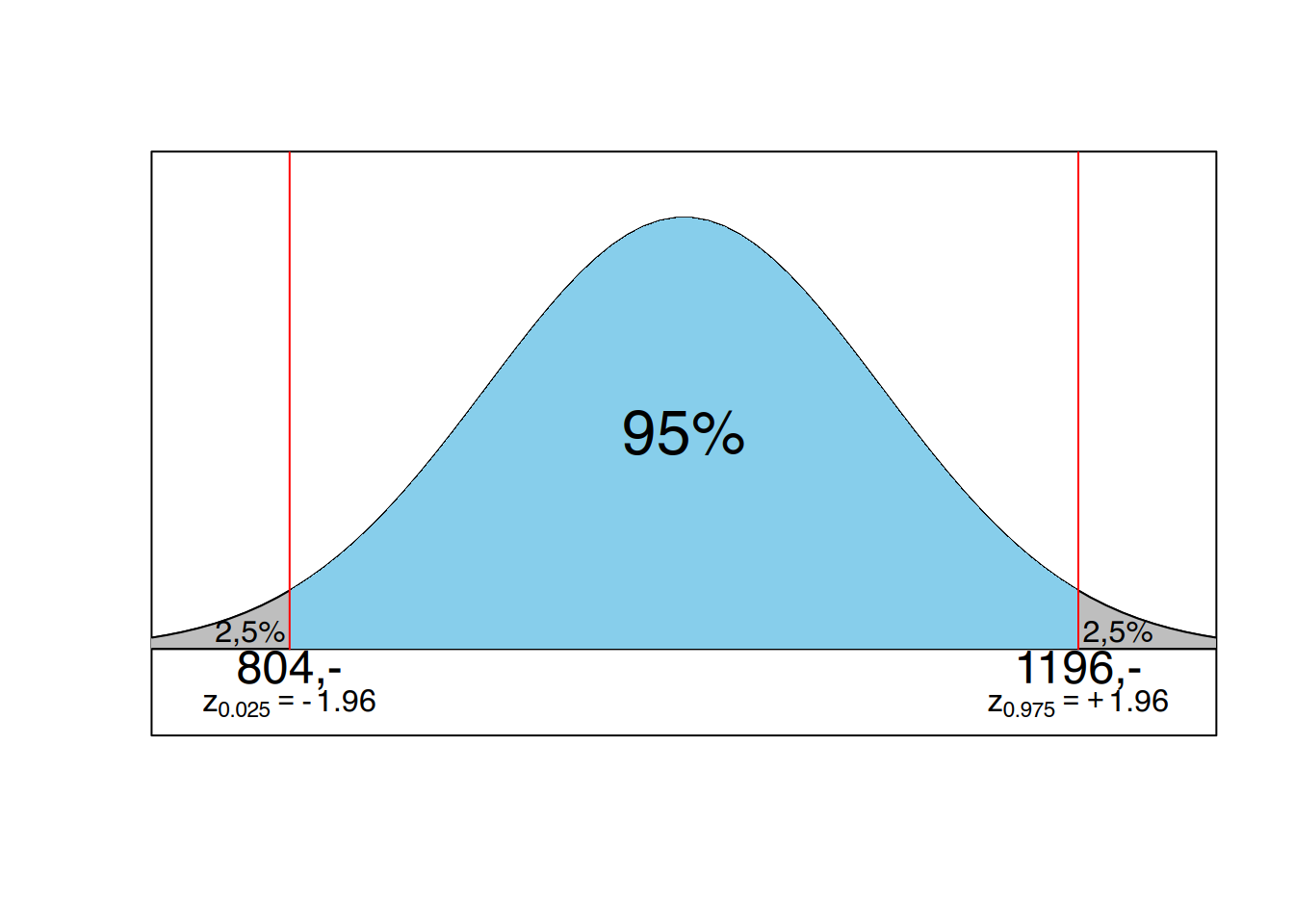
Angenommen wir wüßten, dass sich diese Kosten in Deutschland auf durchschnittlich 1000€ pro Tag belaufen. Bekannt sei ebenfalls der Standardfehler von 100 €. Finden wir jetzt in einer Stichprobe durchschnittliche Kosten von 1180€ und fragen, ob sich diese Klinik signifikant von der Grundgesamtheit unterscheidet. Bei zweiseitiger Fragestellung mit einem Signifikanzniveau von 95% liegt die Irrtumswahrscheinlichkeit gleichmäßig an beiden Seiten der Verteilung. Der Wert von 1180€ überschreitet nicht den oberen Schwellenwert, unserer Schlußfolgerung lautet, dass der Unterschied nicht signifikant ist. Man sagt auch, das Ergebnis ist mit der Nullhypothese (es gibt keinen Unterschied) verträglich.
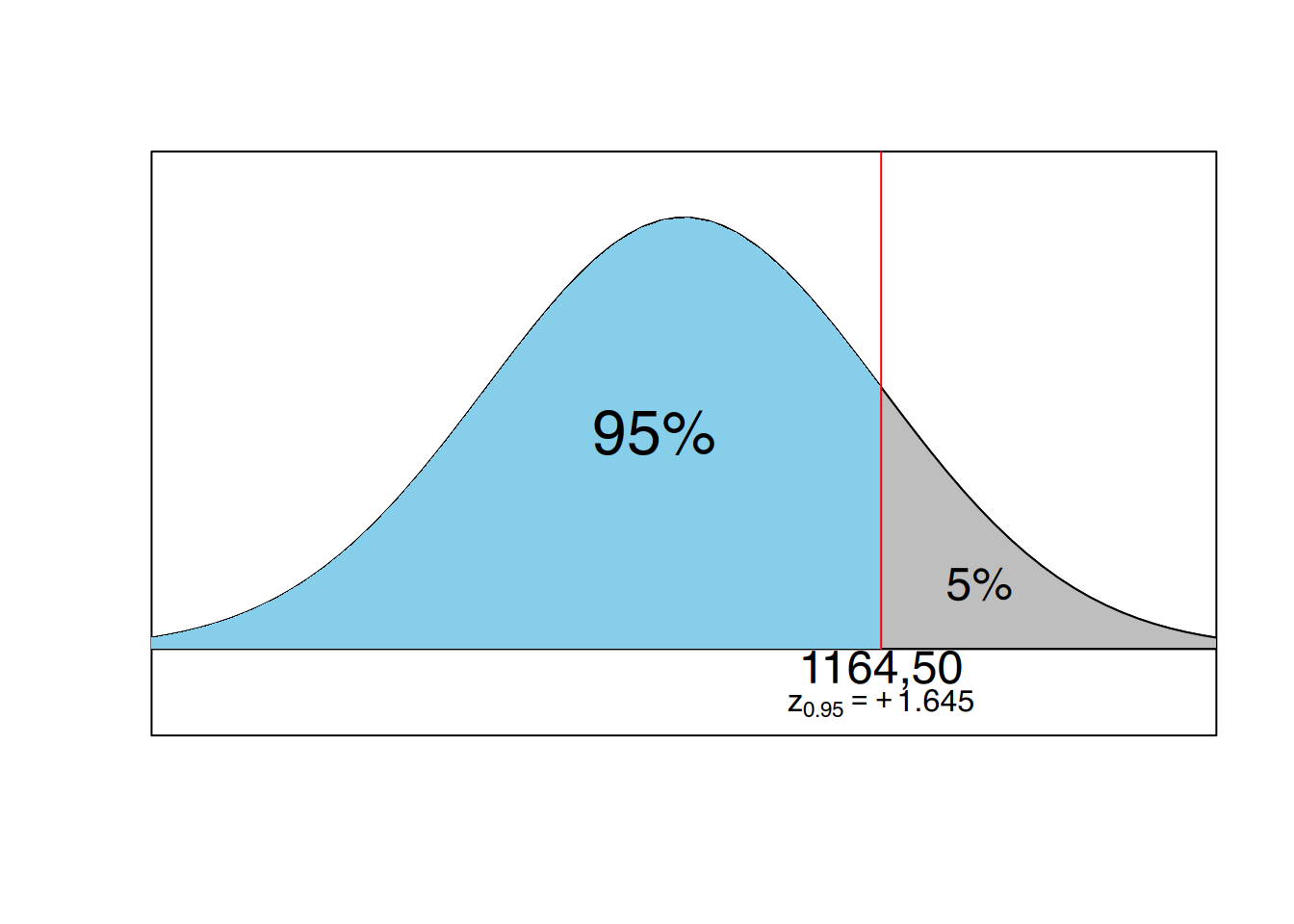
Nehmen wir jetzt die einseitige Fragestellung und formulieren die gerichtete Hypothese, dass der Wert von 1180 größer ist als der Mittelwert der Grundgesamtheit von 1000 €, dann bietet sich das Bild aus Abbildung 10.1 (b). Die Irrtumswahrscheinlichkeit von 5% findet sich hier an einer Seite der Verteilung. Der Wert von 1180 überschreitet den Schwellenwert und wir kämen zu dem Ergebnis, dass sich die untersuchte Klinik signifikant von der Grundgesamtheit unterscheidet. Man sagt auch, das Ergebnis ist mit der Nullhypothese nicht verträglich, die Nullhypothese wird abgelehnt.
Fassen wir zusammen: in unserem Beispiel wurde ein Ergebnis, welches bei zweiseitiger Fragestellung nicht signifikant war, bei einseitiger Fragestellung plötzlich signifikant. Man kann auch sagen, ein zweiseitiger Test entscheidet eher für die Nullhypothese, man bezeichnet dies als konservativ.
Das gleiche “Phänomen” tritt übrigens auch bei unterschiedlichem Signifikanzniveau auf. Ein Test auf dem Signifikanzniveau von 99% kann unter Umständen nicht signifikant ausfallen, während er bei einem Niveau von 90% signifikant ist (Allerdings liegt hier die Irrtumswahrscheinlichkeit bei 10%).
Vielleicht kommt an dieser Stelle wieder einmal der Gedanke auf, dass statistische Ergebnis willkürlich und manipulierbar sind. Bis zu einem gewissen Grad sind sie es sicherlich. Daher ist es ungeheuer wichtig, in Forschungsberichten und Veröffentlichungen genau zu begründen, warum man welche Methode angewendet oder aber die Fragestellung so und nicht anders formuliert oder auch, warum man welches Signifikanzniveau gewählt hat. Nur wenn ein Leser oder Anwender genau nachvollziehen kann, wie ein Ergebnis zustande kam und wie hoch das Risiko einer Fehlentscheidung ist, kann er Vertrauen in die Forschung haben.
Gerade bei der Überlegung, inwiefern man eine ein- oder zweiseitige Fragestellung wählt, weisen die meisten Autoren darauf hin, dass einseitige Fragestellungen nur sparsam zu verwenden sind. Guggenmoos-Holzmann & Wernecke (1995) gehen soweit zu sagen, dass eine einseitige Fragestellung nur dann berechtigt ist, wenn sich die postulierte Richtung der Änderung als absolut sicher (im deterministischen Sinne) erwiesen hat. Bei Polit & Hungler (1999) ist zu finden, dass die Frage ein- oder zweiseitig kontrovers diskutiert wird und die meisten Forscher der Konvention folgen, ihre Hypothese zwar gerichtet zu formulieren, den Test dann aber zweiseitig durchzuführen. Bei der Nutzung von Statistikprogrammen wie z.B. SPSS erübrigt sich die Überlegung, da dort meisten zweiseitig getestet wird.
Es ist in den vergangenen Abschnitten immer wieder von der Möglichkeit gesprochen worden, Fehlentscheidungen zu treffen. Dies wollen wir im folgenden näher ausführen.
10.3 Fehlerarten bei statistischen Entscheidungen
Jede Entscheidung in der schließenden Statistik ist mit einer gewissen Wahrscheinlichkeit behaftet, falsch zu sein. Denken wir an unser Beispiel. Eine durchschnittliche Liegedauer von mindestens 16 Tagen in einer Grundgesamtheit zu finden, deren Mittelwert 10 Tage (mit einem Standardfehler von 2 Tagen) betrug, war mit 0,13% sehr unwahrscheinlich. Unsere Testentscheidung würde bei solch einem Ergebnis die Nullhypothese (es gibt keinen Unterschied) verwerfen. Wir kämen zu einem „positiven Befund" nämlich den, dass es einen Unterschied gibt, der nicht zufällig ist. Anders als in unserem fiktiven Beispiel kennen wir üblicherweise die Verhältnisse in der Grundgesamtheit nicht. Genau genommen gibt es allerdings genau zwei Möglichkeiten, wie die tatsächlichen Verhältnisse sein können und es gibt genau zwei Testentscheidungen, so daß sich insgesamt vier Kombinationen ergeben.
Die untersuchte Klinik stammt tatsächlich aus einer anderen Grundgesamtheit und wir haben durch den Test eine richtige positive Entscheidung getroffen.
Die untersuchte Klinik gehört in Wirklichkeit doch noch zu der Grundgesamtheit der Allgemeinen Krankenhäuser. Der Test hat allerdings ein positives Ergebnis geliefert (es gibt einen Unterschied, die Nullhypothese wird verworfen), so daß wir zu einer falsch positiven Entscheidung kommen. Die Wahrscheinlichkeit dafür, eine falsch-positive Entscheidung zu treffen, betrug in unserem Beispiel 0,13%. Es wurde schon erwähnt, dass wir durch das Festlegen der Irrtumswahrscheinlichkeit \(\alpha\) von üblicherweise 5% oder 1% bestimmen, welche Wahrscheinlichkeit wir höchstens akzeptieren wollen, einen Irrtum zu begehen. Da die Möglichkeit einer falsch-positiven Entscheidung durch das Festlegen der Irrtumswahrscheinlichkeit a beeinflusst werden kann, spricht man von einem \(\alpha\)-Fehler, der oftmals auch Fehler 1. Art genannt wird. Die ausgerechnete Wahrscheinlichkeit, einen solchen Fehler zu begehen, nennt man \(\alpha\)-Fehlerwahrscheinlichkeit (nicht zu verwechseln mit der o.g. vorher festzulegenden Irrtumswahrscheinlichkeit) und sie betrug in unserem Beispiel 0,13%.
Der Signifikanztest findet keinen Unterschied, die Nullhypothese kann nicht verworfen werden, das Testergebnis ist negativ. Im günstigen Fall gibt es in der Realität auch tatsächlich keinen Unterschied. Dann handelt es sich um eine richtig-negative Entscheidung.
Verbleibt noch die letzte Möglichkeit. Der Signifikanztest ist negativ, in der Realität gibt es aber sehr wohl einen „Befund". Dann würden wir eine falsch-negative Entscheidung treffen. Dieser Fehler wird als \(\beta\)-Feher oder auch Fehler 2. Art bezeichnet. Das Problem bei diesem Fehler liegt darin, dass er nicht so leicht - zumindest nicht mit unserem jetzigen Wissen - kontrolliert werden kann.
Exkurs: \(p\)-Werte
Bisher war das allgemeine Vorgehen bei einem Signifikanztest so, dass man eine Teststatistik (z.B. der z-transformierter Mittelwert der Stichprobe) mit einem Schwellenwert (\(z\)-Wert, der 97,5% der Verteilung abschneidet) vergleicht und so zu einer Signifikanzaussage kommt. Genauso ist es möglich, die ausgerechnete a-Fehler-Wahrscheinlichkeit (im Beispiel 0,13%) mit der vorher festgelegten Irrtumswahrscheinlichkeit \(\alpha\) (z.B. 5%) zu vergleichen. Ist die ausgerechnete Wahrscheinlichkeit kleiner als \(\alpha\), so verwerfen wir die Null-Hypothese und sprechen von einem signifikanten Ergebnis. Ist die ausgerechnete Wahrscheinlichkeit größer als \(\alpha\), so behalten wir die Null-Hypothese bei, der Unterschied ist nicht signifikant, er ist zufällig. In Statistikprogrammen für Computer (z.B. SPSS oder R1) wird die entsprechende Teststatistik ausgerechnet und man kann diese dann anhand von tabellierten Schwellenwerten vergleichen. Einfacher ist allerdings, sich den „\(p\)-Wert" anzuschauen. Dieser gibt die ausgerechnete \(\alpha\)-Fehler-Wahrscheinlichkeit wieder. Für unser Beispiel hätte SPSS einen \(p\)-Wert von 0,0013 angegeben, der deutlich kleiner ist als \(\alpha=0,05\).
Wir wollen die vier möglichen Kombinationen zwischen Testentscheidung und tatsächlichen Verhältnissen in der Realität in einer Tabelle zusammen fassen:
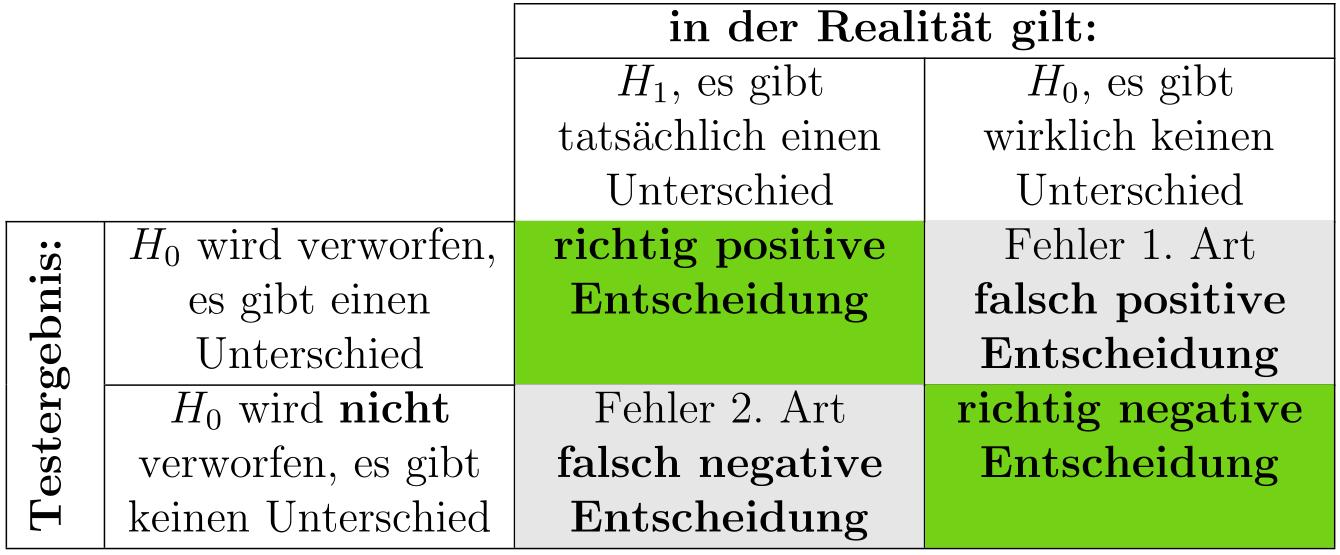
Wie eben erwähnt, ist es nicht so ohne weiteres möglich, den ß-Fehler zu kontrollieren, bzw. die ß-Fehler-Wahrscheinlichkeit zu berechnen. Da allerdings \(\alpha\)- und \(\beta\)-Fehler sich gegenseitig beeinflussen, können wir indirekt Einfluss auf den \(\beta\)-Fehler nehmen. Bleiben wir bei unserem Beispiel mit der durchschnittlichen Verweildauer (Grundgesamt ist die Liegedauer in Allgemeinen Krankenhäusern). Die Wahrscheinlichkeit, einen Mittelwert zu finden, der größer als 13,92 Tage ist, war sehr gering, allerdings nicht unmöglich. Wenn ein Signifikanztest entscheidet, ein solches Krankenhaus gehört zu einer anderen Grundgesamtheit, ist nicht auszuschließen, dass die \(H_{0}\) fälschlicherweise verworfen wurde, also ein \(\alpha\)-Fehler vorliegt.
Von den Langzeit- und Reha-Einrichtungen liegen uns keine Daten vor. Allerdings ist es denkbar, dass es auch dort angesichts der Sparmaßnahmen im Gesundheitswesen Kliniken gibt, die sich auf kurze Rehabilitationen eingerichtet haben und somit eventuell auch Stichproben mit Mittelwerten von 12 oder 13 Tagen dabei sein können. Ein Signifikanztest würde allerdings bei einem solchen Mittelwert entscheiden, die Nullhypothese (fälschlicherweise) nicht zu verwerfen. Das ist dann die Situation, die als \(\beta\)-Fehler bezeichnet wird.
Der Idealfall ist, wenn zwei völlig verschiedene (getrennt voneinander liegende) Verteilungen vorliegen, was aber in der Realität meist nicht der Fall ist (Abbildung 10.3)

Bei einer Irrtumswahrscheinlichkeit von 5% erhöht sich zwar das Risiko, fälschlicherweise die Nullhypothese zu verwerfen, gleichzeitig verringert sich die Wahrscheinlichkeit dafür, fälschlicherweise die Nullhypothese beizubehalten (Abbildung 10.4, roter Bereich).

Bei einer geringeren Irrtumswahrscheinlichkeit (z.B. 0,01) verhält es sich genau umgekehrt, der \(\alpha\)-Fehler verringert sich, der \(\beta\)-Fehler wird größer (Abbildung 10.5).
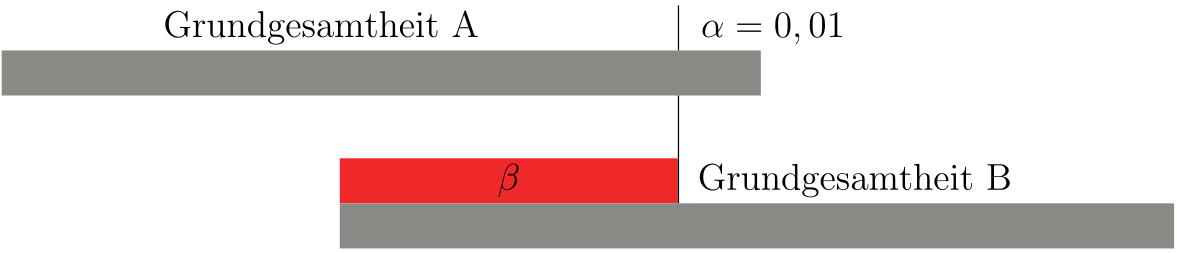
Wie man mit einem solchen Problem in der Praxis umgehen kann, kann an einem Beispiel (Lorenz (1996)) verdeutlicht werden:
Es sollen alle Fälle von Lungentuberkulose in der Bevölkerung erfasst werden. Dazu veranlasst man eine Röntgen-Reihenuntersuchung. Um möglichst niemanden mit einer TB zu übersehen, nimmt man erst einmal in Kauf, auch gesunde Personen fälschlicherweise als krank zu identifizieren (falsch-positiv, \(\alpha\)-Fehler) und wählt daher eine möglichst große Irrtumswahrscheinlichkeit (\(\alpha\)=10%,20% oder sogar mehr). Dadurch verringert sich das Risiko, kranke Personen irrtümlicherweise als gesund zu betrachten (falsch-negativ, \(\beta\)-Fehler). In einem zweiten Schritt werden dann alle erfassten Personen, die wirklich Erkrankten und fälschlicherweise als krank identifizierten, gründlich untersucht. Jetzt wählt man eine geringe Irrtumswahrscheinlichkeit (z.B. \(\alpha\)= 1% oder sogar 0,1%), damit wird das Risiko von falsch-positiven Diagnosen sehr klein und die Gesunden können heraus gefunden werden.
Die Entscheidung, welche Irrtumswahrscheinlichkeit a man für eine statistische Analyse wählt, hängt also unmittelbar damit zusammen, welche Konsequenzen jeweils der \(\alpha\)-Fehler bzw. der \(\beta\)-Fehler nach sich zieht. Auf die Frage, welcher Fehler denn „schlimmer" sei, wird häufig geantwortet, dies sei der \(\beta\)-Fehler. Allerdings lässt sich dies nur durch inhaltliche Überlegungen klären. Nachfolgend ein paar Beispiele.
Beispiel 1: Untersuchung einer neuen Unterrichtsmethode
- Nullhypothese: es gibt keinen Unterschied zwischen neuer und alter Methode.
- Alternativhypothese: die neue Methode ist besser
- \(\alpha\)-Fehler: die Nullhypothese wird fälschlicherweise verworfen, man geht davon aus, die neue Methode sei besser. Dies kann neben immensen Kosten für neue Schulmaterialen noch zur Folge haben, dass Kinder umgeschult werden etc.
- \(\beta\)-Fehler: die Nullhypothese wird fälschlicherweise nicht verworfen, die neue und wirklich bessere Methode wird nicht eingeführt.
Beispiel 2: Untersuchung eines neuen Medikaments
- Nullhypothese: es gibt keinen Unterschied zwischen dem neuem und dem altem Medikament
- Alternativhypothese: das neue Medikament ist besser
- \(\alpha\)-Fehler: das neue Medikament wird eingeführt, da es angeblich besser wirkt. Man nimmt ernsthafte Nebenwirkungen in Kauf, außerdem sind die Kosten sehr hoch.
- \(\beta\)-Fehler: es wird nicht erkannt, dass das neue Medikament besser ist, Es verschwindet in der „Schublade" obwohl vielen Menschen damit hätte geholfen werden können.
Beispiel 3: Untersuchung, inwieweit Fernsehen die Konzentrationsfähigkeit von Kindern senkt
- Nullhypothese: Fernsehen hat keinen Einfluss auf die Konzentration
- Alternativhypothese: Fernsehen senkt die Konzentrationsfähigkeit von Kindern
- \(\alpha\)-Fehler: Irrtümlicherweise wird angenommen, Fernsehen schadet der Konzentration und man empfiehlt den Eltern, die tägliche Fernsehzeit einzuschränken.
- \(\beta\)-Fehler: es wird fälschlicherweise angenommen, Fernsehen schadet nicht. Die Konsequenz daraus könnte sein, dass Kinder weiterhin uneingeschränkt fernsehen dürfen.
Einige letzte Anmerkungen bevor wir kurz auf die Schritte eines Signifikanztestes und auf einzelne Testverfahren eingehen: Eine Irrtumswahrscheinlichkeit \(\alpha\) von z.B. 5% mit einem Signifikanzniveau von 95% bedeutet nicht, dass mit 95%iger Wahrscheinlichkeit der Unterschied in der Realität vorhanden ist. Wie schon bei den Konfidenzgrenzen gibt es entweder einen Unterschied oder es gibt ihn nicht! Die Irrtumswahrscheinlichkeit von 5% sagt viel mehr aus, dass man bei 100 durchgeführten Untersuchungen im Schnitt 5 mal ein falsch-positives Ergebnis erhalten kann! (Natürlich besteht theoretisch auch hier wiederum die Gefahr, dass je nach Interessenlage nur diese falsch-positiven Ergebnisse veröffentlicht werden). Sowohl den \(\alpha\)-Fehler wie auch den \(\beta\)-Fehler möglichst klein zu halten gelingt nur über eine entsprechende große Stichprobe. Allerdings sprengt es den Rahmen eines Skriptes, das Thema Fallzahlschätzungen zu behandeln.
10.4 Die Struktur statistischer Tests
Formulierung von Hypothesen
Prinzipiell werden Hypothesen vor der Durchführung der Untersuchung formuliert. Wird Datenmaterial im Sinne von „Exploration" und „hypothesenerkundend" analysiert, muß dies kenntlich gemacht werden, indem die Untersuchung ausdrücklich als Erkundungsexperiment oder explorative Studie gekennzeichnet wird. Es ist unwissenschaftlich, aus dem selben Datenmaterial Hypothesen abzuleiten und gleichzeitig zu überprüfen.Auswahl eines Signifikanztests
Dabei spielt das Skalenniveau und die Verteilung der Daten eine wichtige Rolle. Hinzu kommt die Überlegung, ob es sich um verbundene oder unverbundene Daten (Stichproben) handelt. Von verbundenen oder auch abhängigen Stichproben geht man aus, wenn es sich um mehrere Meßwerte von ein und den selben Personen / Objekten handelt.Festlegen der Irrtumswahrscheinlichkeit \(\alpha\) und des notwendigen Stichprobenumfangs
Durchführung der Untersuchung / Datenerhebung
Berechnung der Teststatistik
Vergleich der Teststatistik mit einem (tabellierten) Schwellenwert
Testentscheidung
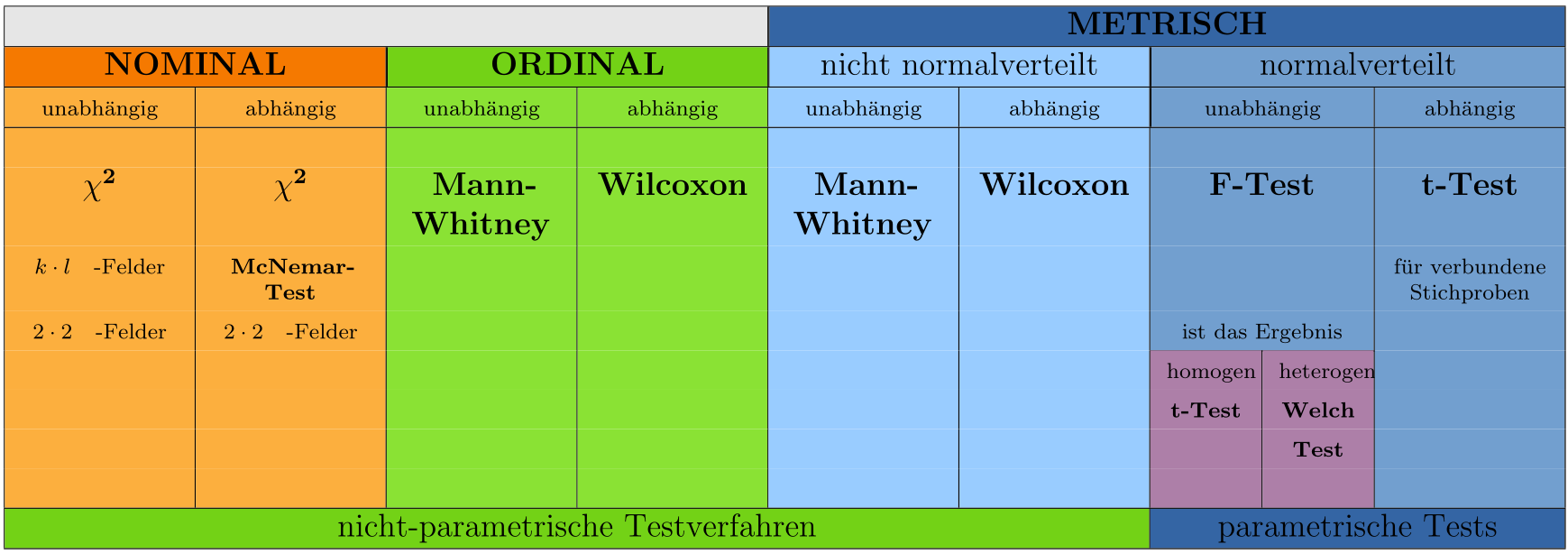
10.5 Überblick Signifikanztests
http://www.r-project.org, siehe hierzu auch große Schlarmann (2025)↩︎