3 Die Darstellung von Daten
Zunächst werden wir uns mit Daten befassen, welche die Ausprägungen eines Merkmals, also einer Variablen beschreiben. In der Literatur findet man Begriffe wie: univariat, monovariabel, eindimensional und ähnliches. Geht es um Beziehungen oder Zusammenhänge zwischen zwei oder mehr Variablen, spricht man von bivariat, bivariabel, zweidimensional oder auch mehrdimensional. Das Anliegen der deskriptiven Statistik ist das Ordnen, Zusammenfassen und Darstellen der Daten, damit sie übersichtlicher und anschaulicher werden. Ziel ist es u.a. zu verdeutlichen, wie häufig einzelne Merkmalsausprägungen vorkommen. Man spricht auch von Häufigkeitsverteilungen. Dazu stehen uns im wesentlichen die folgenden Möglichkeiten zur Verfügung:
die Darstellung in Tabellenform
die Darstellung durch Graphiken (Stabdiagramme, Histogramme, etc.)
Charakterisierung durch sogenannte Kenngrößen
Die zahlenmäßige Darstellung durch sogenannte Kenngrößen wie Mittelwerte, Streuungsmaße und Maße für den Zusammenhang von Merkmalen führt zu einer extremen Reduktion der Daten. Die Gesamtheit der Daten wird hierbei durch typische Vertreter repräsentiert. Diese Kenngrößen werden in einem späteren Kapitel behandelt.
3.0.1 Tabellen und Graphiken
Als erster Schritt bietet sich die tabellarische Darstellung der Daten an. Wir hatten dies bereits unter dem Punkt “Aufbereitung der Daten” angesprochen. Ausgehend von den in einer Tabelle geordneten Daten lassen sich die verschiedene Graphiken erstellen. Nehmen wir das Beispiel der Anzahl der Krankenhausaufenthalte aus Tabelle 1.3. Die Daten der Urliste wurden mittels Strichliste sortiert, wir erhielten die absoluten Häufigkeiten und konnten die relativen Häufigkeiten berechnen.
An dieser Stelle führen wir noch den Begriff der Häufigkeitssumme ein. Eine Häufigkeitssumme (absolut oder relativ) erhält man durch schrittweises aufaddieren der einzelnen Häufigkeiten. Dieses schrittweise aufaddieren nennt man kumulieren. Zur Veranschaulichung des Berechnens der Häufigkeitssumme (\(H_{i}\)) wurde in der folgenden Tabelle 3.1 eine Spalte eingefügt, in der die schrittweise Addition der absoluten Häufigkeit nachvollzogen werden kann. Mit dem gleichen Vorgehen wird die relative Häufigkeitssumme (F_{i}) errechnet.
| Anzahl der Krankenhausaufenthalte | absolute Häufigkeit \(h_{i}\) | schrittweise Addition | absolute Häufigkeit kumuliert \(H_{i}\) | relative Häufigkeit in % \(f_{i} P 100\) | relative Häufigkeit kumuliert \(F_{i}\) |
|---|---|---|---|---|---|
| 0 | 30 | 30 | 30 | 30 | 30 |
| 1 | 34 | 30+34=64 | 64 | 34 | 64 |
| 2 | 14 | 64+14=78 | 78 | 14 | 78 |
| 3 | 10 | 78+10=88 | 88 | 10 | 88 |
| 4 | 4 | 88+4=92 | 92 | 4 | 92 |
| 5 | 5 | 92+5=97 | 97 | 5 | 97 |
| 6 | 1 | 97+1=98 | 98 | 1 | 98 |
| 7 | 2 | 98+2=100 | 100 | 2 | 100 |
| Gesamt | n = 100 | 100 |
Sehen wir uns die relative Häufigkeitssumme in Tabelle 3.1 an. Auf einen Blick lässt sich z.B. sagen, dass mehr als \(\frac{3}{4}\) der Personen (78%) maximal zweimal im Krankenhaus waren.
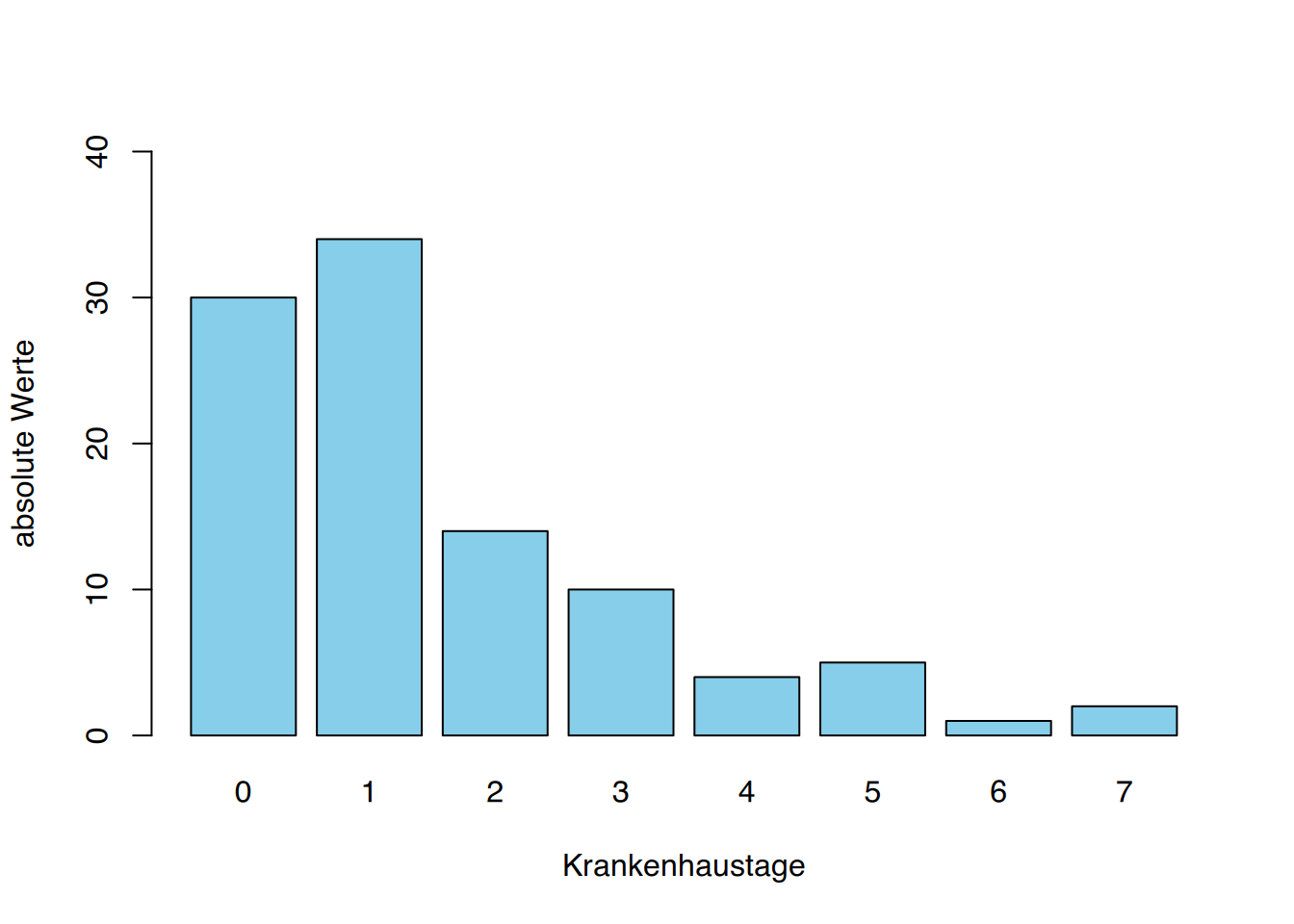
Kommen wir zur graphischen Darstellung unserer Daten und stellen die Anzahl der Krankenhausaufenthalte mittels eines Stab- oder Balkendiagramms dar.

Die Höhe der Balken entspricht den absoluten Häufigkeiten. Ebenso eignen sich die relativen Häufigkeiten zur Erstellung eines Balkendiagramms. Dabei sollte beachtet werden, dass die Gesamtzahl (n) angegeben wird. Dies gilt insbesondere dann, wenn es sich um eine zahlenmäßig sehr kleine Erhebung handelt. Breite und Abstand der Stäbe spielen keine Rolle und können nach ästhetischen Gesichtspunkten gewählt werden, wobei die Übersichtlichkeit der Darstellung im Vordergrund stehen sollte.
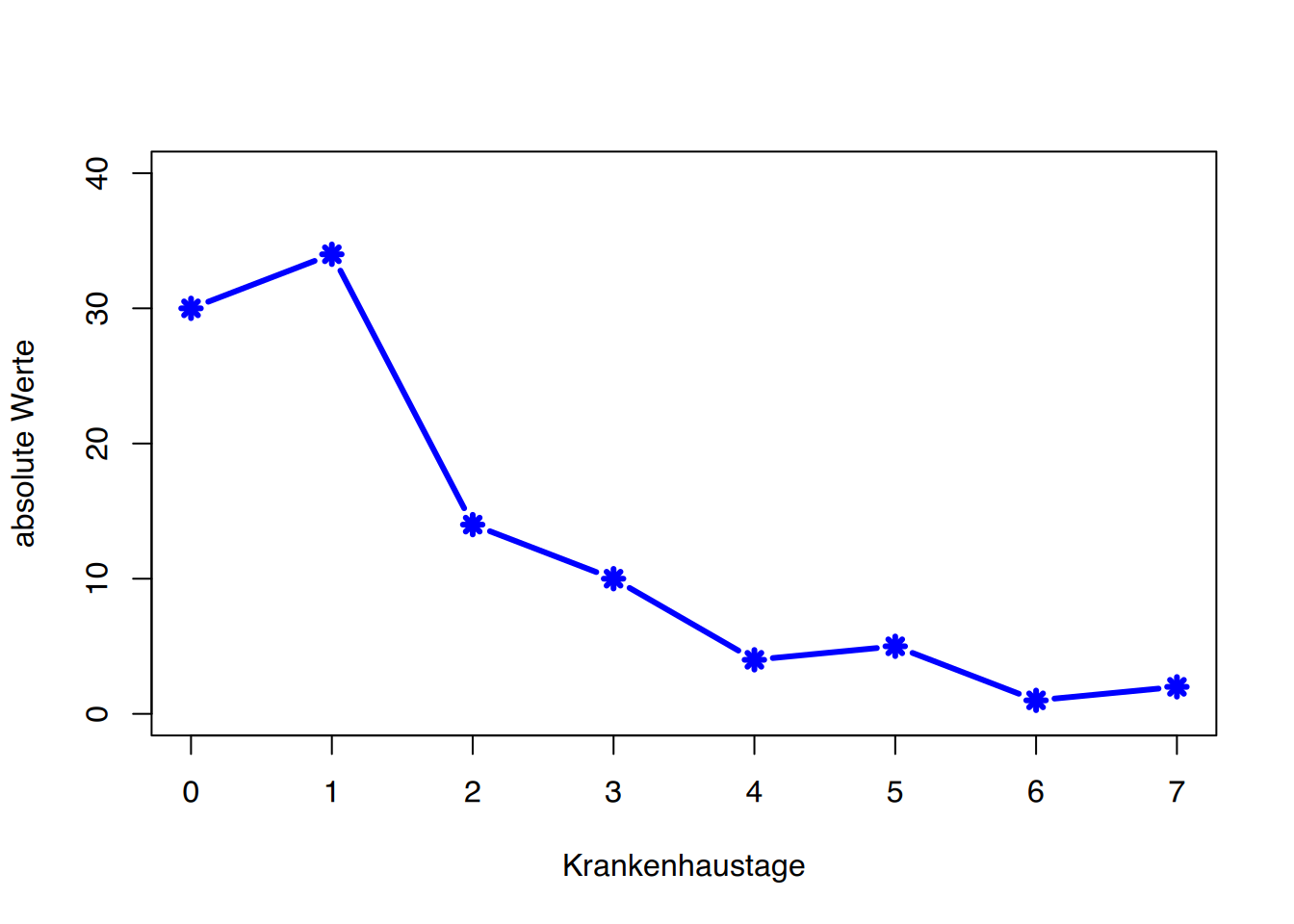
Eine weitere Form der Darstellung ist der Polygonzug (siehe Abbildung 3.2 (a)). Trägt man die einzelnen Häufigkeiten nicht als Balken, sondern als Punkte oder Kreuze über dem entsprechenden Wert ein und verbindet diese Punkte, erhält man den Polygonzug der Häufigkeitsverteilung.
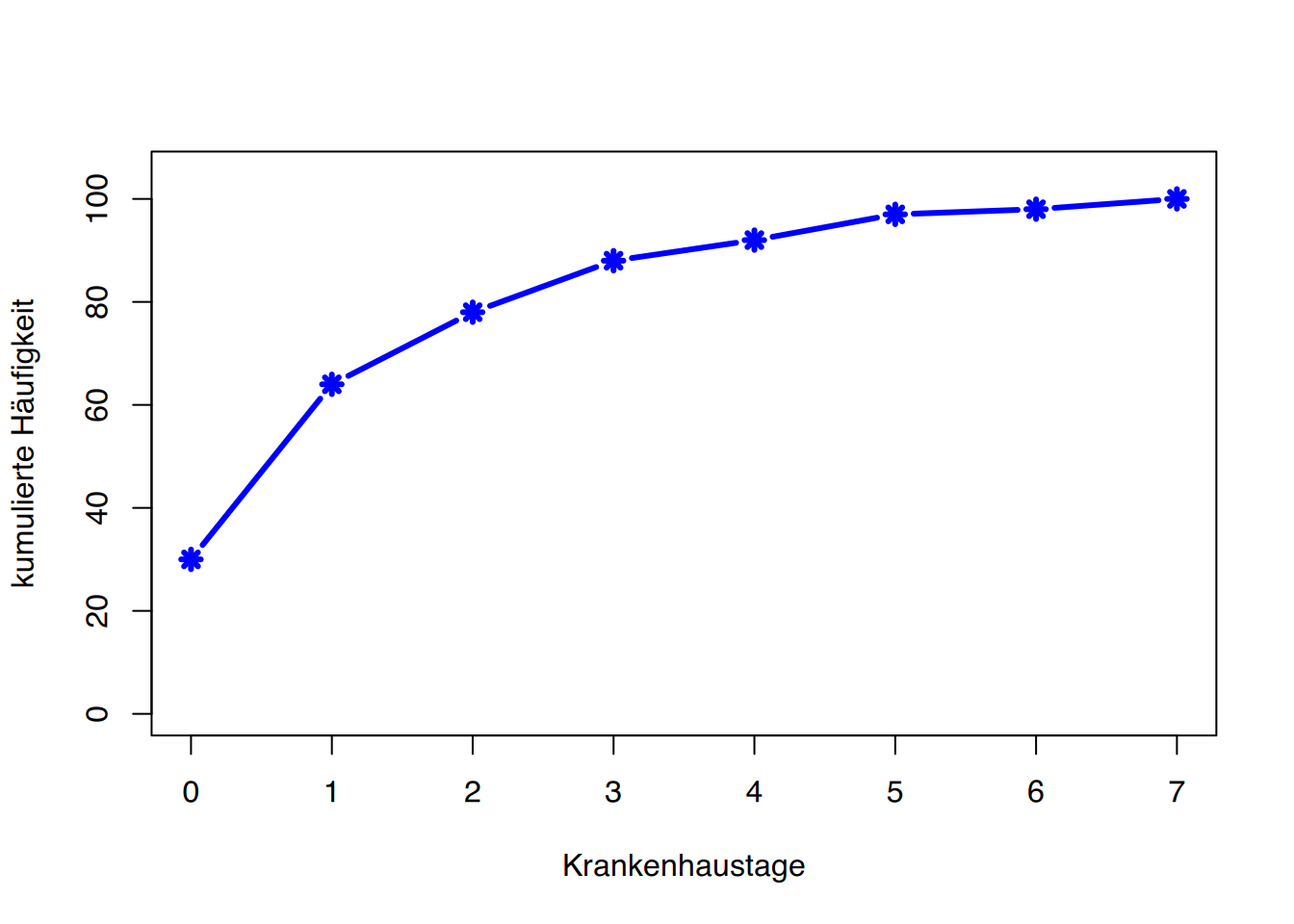
Ebenso lassen sich die Zwischenschritte der kumulierten Häufigkeiten darstellen. Man spricht dann vom Summenpolygon (siehe Abbildung 3.2 (b)). Analog zur relativen Häufigkeitssumme erlaubt auch das Summenpolygon durch einfaches Ablesen Aussagen vom Typ:
78% der Befragten waren maximal zweimal im Krankenhaus oder
50% der Schüler erreichten soundsoviel Punkte
Für unser Beispiel “Anzahl der Krankenhausaufenthalte” bieten die eben besprochenen Verfahren sicher eine gute Möglichkeit zur übersichtlichen und anschaulichen Darstellung der Daten.
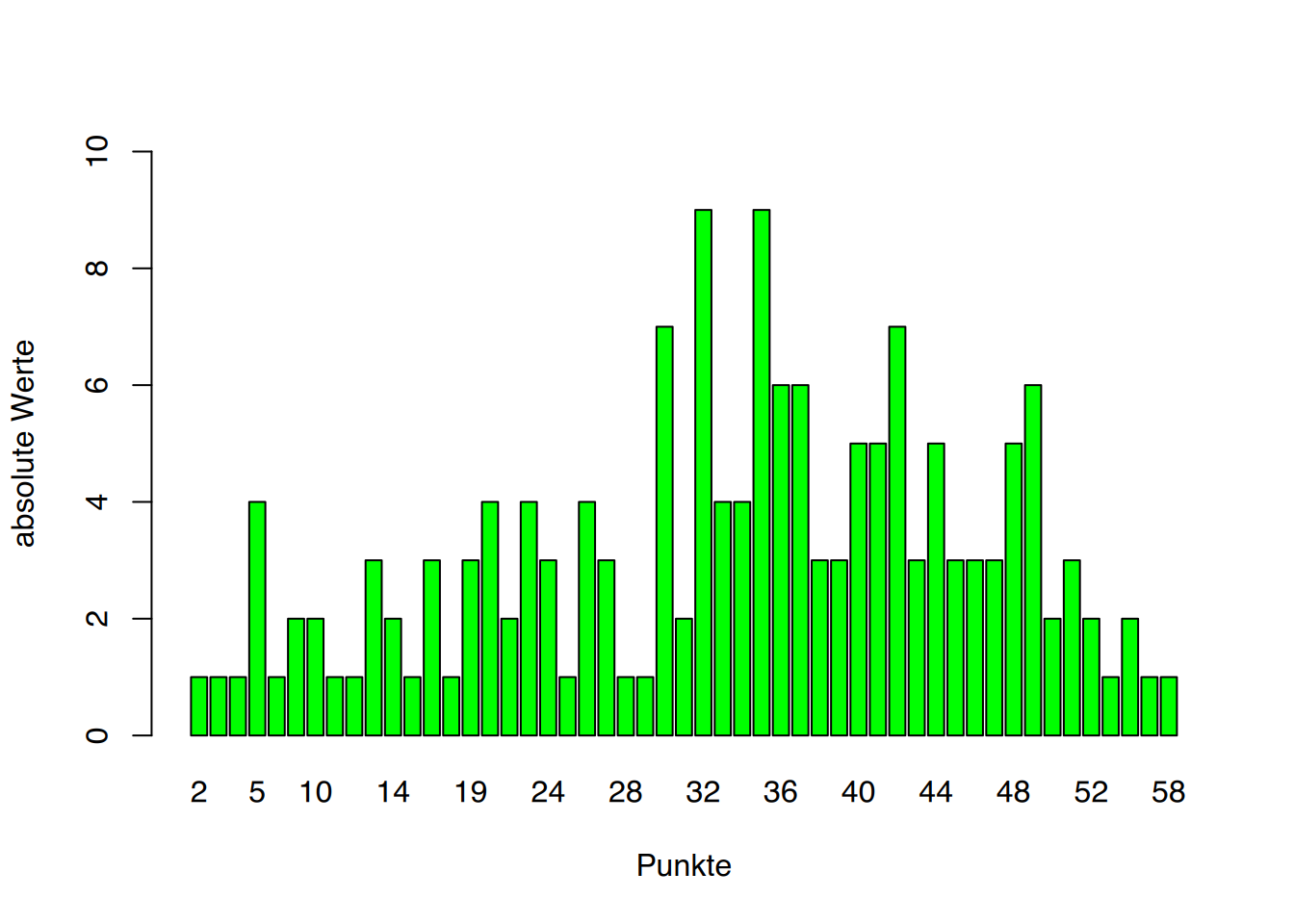
Stellen wir allerdings die Auflistung der einzelnen Punkte für die Prüfung mittels eines Balkendiagramms dar, so kann man sicherlich nicht mehr von Übersichtlichkeit sprechen (Abbildung 3.3).
Wenn also sehr viele Meßwerte vorliegen oder wenn es sich um kontinuierliche Daten (Körpergröße, Gewicht, etc.) handelt, ist es sinnvoller, mehrere benachbarte Werte zu einer Klasse zusammenzufassen. Dadurch lässt sich größere Klarheit und Übersicht erreichen. Man spricht von Gruppierung oder Klassierung der Daten.
Begriffsdefinitionen:
Eine Klasse ist die Menge sämtlicher Meßwerte, die innerhalb festgelegter Grenzen liegen.
Diese festgelegten Kassengrenzen werden durch den kleinsten und den größten Meßwert einer Klasse gebildet.
Die Kassenmitte ist das arithmetische Mittel (wird später eingehend besprochen) aus beiden Klassengrenzen.
Die Kassenbreite ist bei diskreten Merkmalen die Anzahl der in der Klasse zusammengefaßten Merkmalsausprägungen, bei kontinuierlichen Merkmalen die Differenz der Klassengrenzen.
Offene Kassen sind solche, in denen Meßwerte zusammengefaßt werden, die über oder unter einem Grenzwert liegen. Bei der Variablen Lebensalter wären z.B. “unter 18 Jahre” oder “über 70 Jahre” offene Klassen.
Es gibt keine verbindlichen Regeln zur Klassierung von Daten. Bei der Wahl einer zweckmäßigen Klassenbreite ist zu bedenken, dass sehr breite Klassen zuviel an Informationen über die Verteilung der Daten verwischen und zu schmale Klassen schnell unübersichtlich erscheinen. Auch bestimmt die Wahl der Klassenbreite unmittelbar die Anzahl der Klassen.
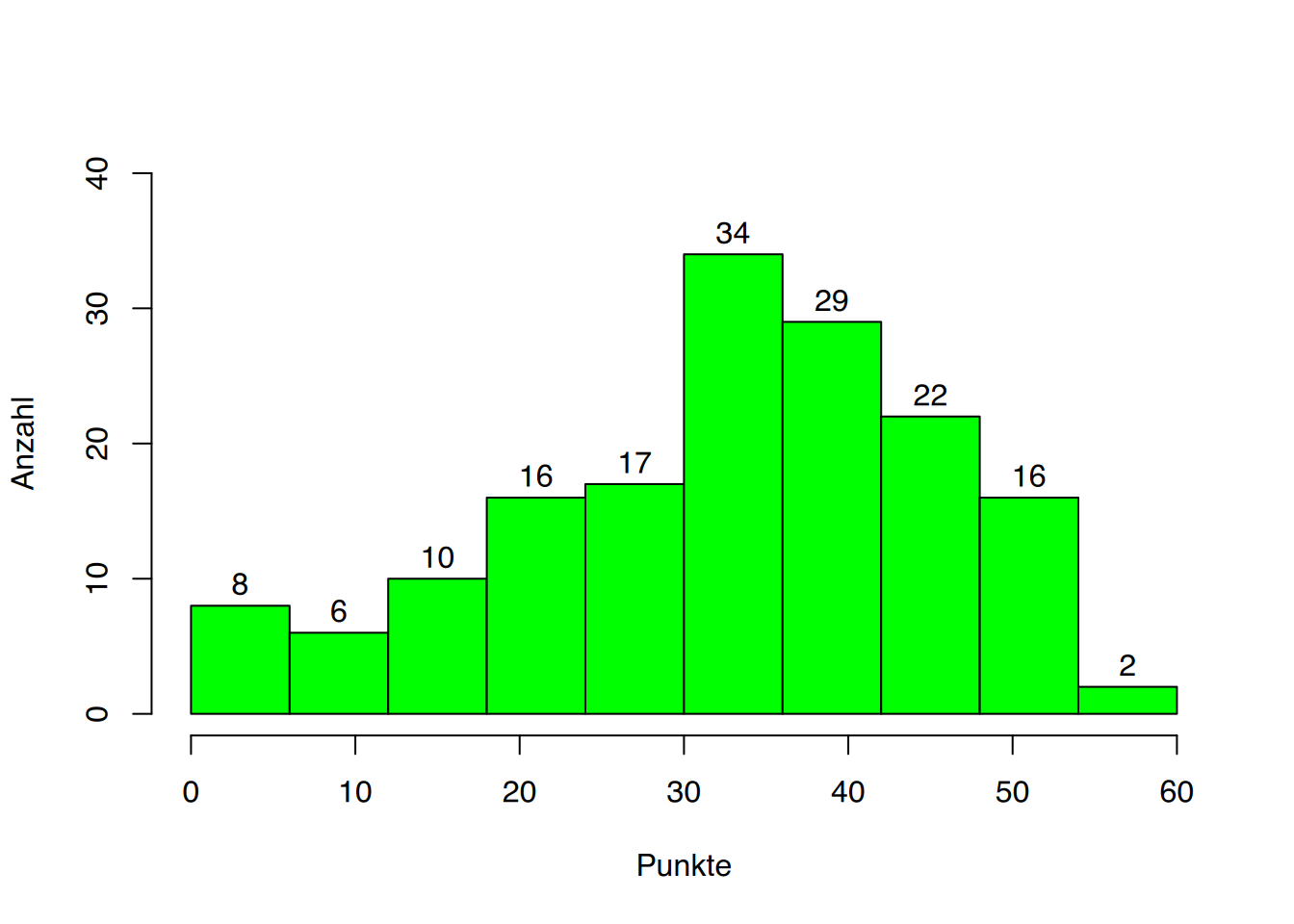
Klassierte oder gruppierte Daten lassen sich mit einem Histogramm graphisch gut darstellen. Ähnlich dem Balkendiagramm, allerdings ohne Abstände zwischen den einzelnen Balken. Bei einem Histogramm geht es um die Darstellung von Werten, die in einem Bereich : “von hier bis dort” liegen, also der Darstellung einer Fläche. Wir werden jetzt anhand des Beispiels “Punkte in der Prüfung” deutlich machen, wie unterschiedlich die Darstellung derselben Daten ausfallen kann, beeinflusst allein von der Art der Klassierung.
Die Schreibweise (0-6] in Tabelle 3.2 bedeutet, “mehr als 0 bis einschließlich 6”. Der Wert der Klassengrenze mit der runden Klammer wird nicht berücksichtigt, wohingegen der Wert mit der eckigen Klammer zu dieser Klasse zählt. Gerade bei kontinuierlichen Daten mit theoretisch unendlich vielen Zwischenwerten ist eine klare Abgrenzung wichtig, jeder Wert muß eindeutig einer Klasse zugeordnet werden können. Die Klassengrenzen (6-12] der zweiten Variante (Tabelle 3.3) bedeuten demnach: “mehr als 6 bis einschließlich 12”. Sollte also ein Schüler 6,3 oder 6,5 Punkte erhalten haben, gehört er eindeutig zur zweiten Klasse.
| Klassengrenzen | Klassenmitte | Absolute Häufigkeit |
|---|---|---|
| (0-6] | 3 | 8 |
| (6-12] | 9 | 6 |
| (12-18] | 15 | 10 |
| (18-24] | 21 | 16 |
| (24-30] | 27 | 17 |
| (30-36] | 33 | 34 |
| (36-42] | 39 | 29 |
| (42-48] | 45 | 22 |
| (48-54] | 51 | 16 |
| (54-60] | 57 | 2 |
| Gesamt | 160 |
| Klassengrenzen | Klassenmitte | Absolute Häufigkeit |
|---|---|---|
| (0-12] | 6 | 14 |
| (12-24] | 18 | 26 |
| (24-36] | 30 | 51 |
| (36-48] | 42 | 51 |
| (48-60] | 54 | 18 |
| Gesamt | 160 |
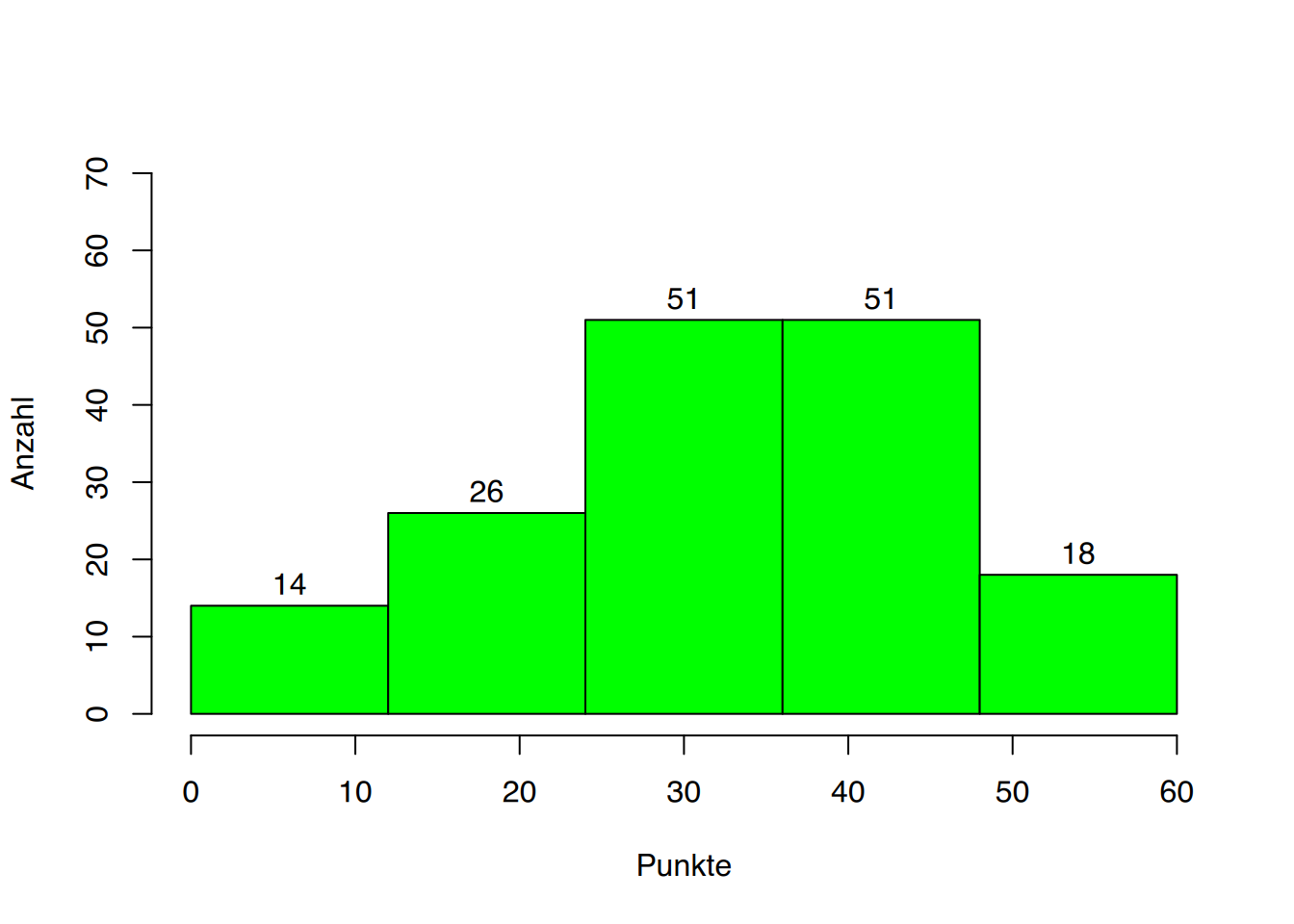
Wir könnten an dieser Stelle noch die unterschiedlichsten Histogramme derselben Daten liefern. Eines sollte jetzt klar geworden sein: Gerade weil es keine verbindlichen Richtlinien zur Klassierung von Daten gibt, ist die Gefahr der Manipulation sehr groß.
Ein weiteres Problem bei der Erstellung eines Histogramms tritt dann auf, wenn unterschiedliche Klassenbreiten gewählt werden.
| Klassengrenzen | Klassenmitte | Klassenbreite | Absolute Häufigkeit |
|---|---|---|---|
| (0-18] | 9 | 18 | 24 |
| (18-30] | 24 | 12 | 33 |
| (30-36] | 33 | 6 | 34 |
| (36-42] | 39 | 6 | 29 |
| (42-48] | 45 | 6 | 22 |
| (48-60] | 54 | 12 | 18 |
| Gesamt | 160 |
Liegen, wie in Tabelle 3.4, klassierte Daten mit unterschiedlichen Klassenbreiten vor, vermittelt ein nicht flächenproportionales Histogramm einen falschen Eindruck von den Daten.
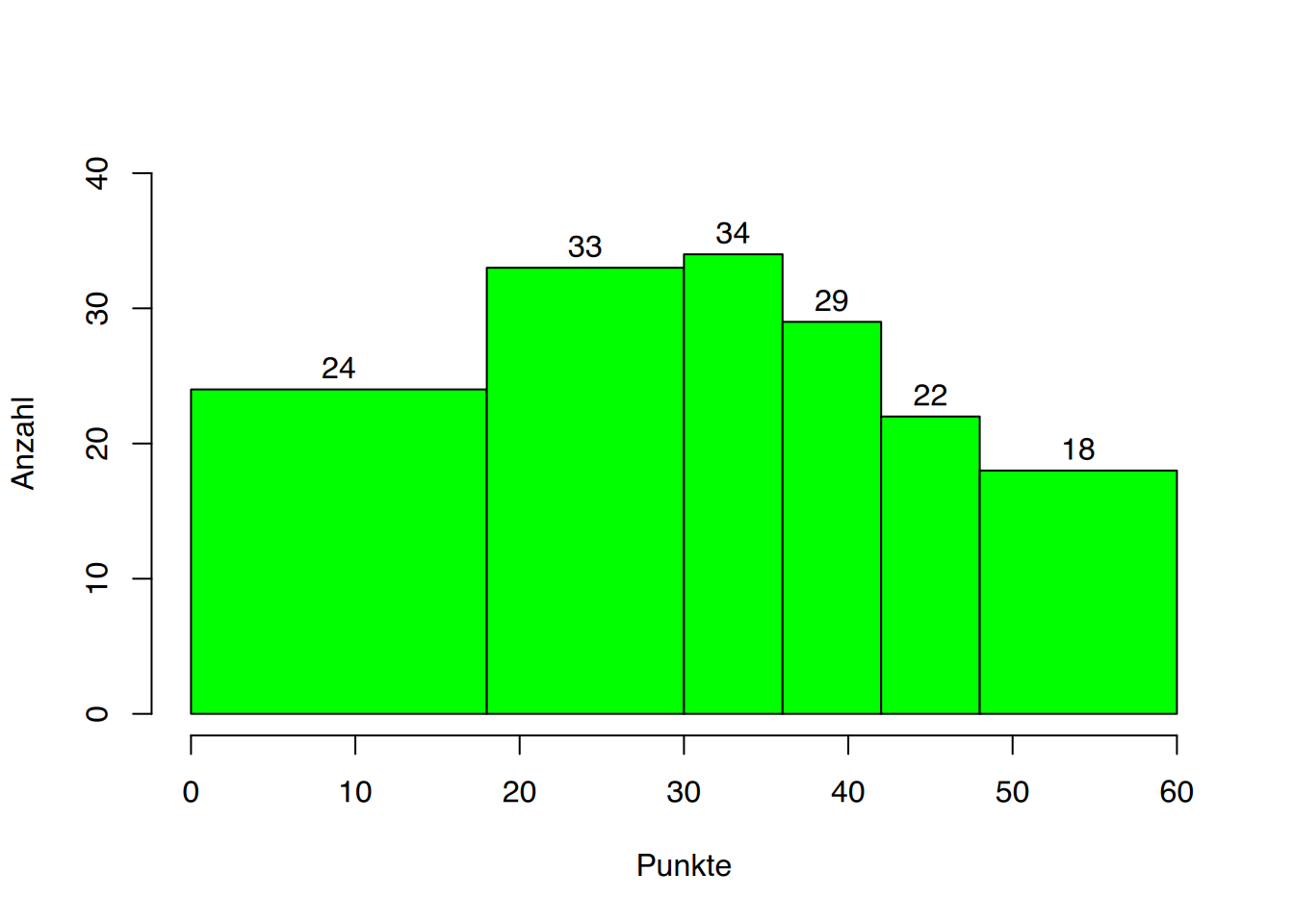
Die Abbildung 3.6 zeigt, dass die erste Klasse mit einer Breite von 18 Punkten größer erscheint als die dritte Klasse mit einer Breit von 6 Punkten, obwohl die absolute Häufigkeit dieser Klasse (=34) die der ersten Klasse (=24) deutlich übertrifft. Auch erscheint die zweite Klasse optisch doppelt so umfangreich wie die dritte klasse, obwohl die absoulte Häufigkeit (=33) sogar einen Wert niedriger ist als in der dritten Klasse (=34).
Nur ein flächenproportionales Histogramm spiegelt den tatsächlichen Sachverhalt wieder. Hierzu setzt man die absolute Häufigkeit ins Verhältnis zur Klassenbreite, d. h. für unser Beispiel:
| Klassengrenzen | Klassenmitte | Klassenbreite | Absolute Häufigkeit | Quotient aus absoluter Häufigkeit und Klassenbreite |
|---|---|---|---|---|
| (0-18] | 9 | 18 | 24 | \(24/18=1,3\) |
| (18-30] | 24 | 12 | 33 | \(33/12=2,7\) |
| (30-36] | 33 | 6 | 34 | \(34/6=5,6\) |
| (36-42] | 39 | 6 | 29 | \(29/6=4,8\) |
| (42-48] | 45 | 6 | 22 | \(22/6=3,6\) |
| (48-60] | 54 | 12 | 18 | \(18/12=1,5\) |
| Gesamt | 160 |
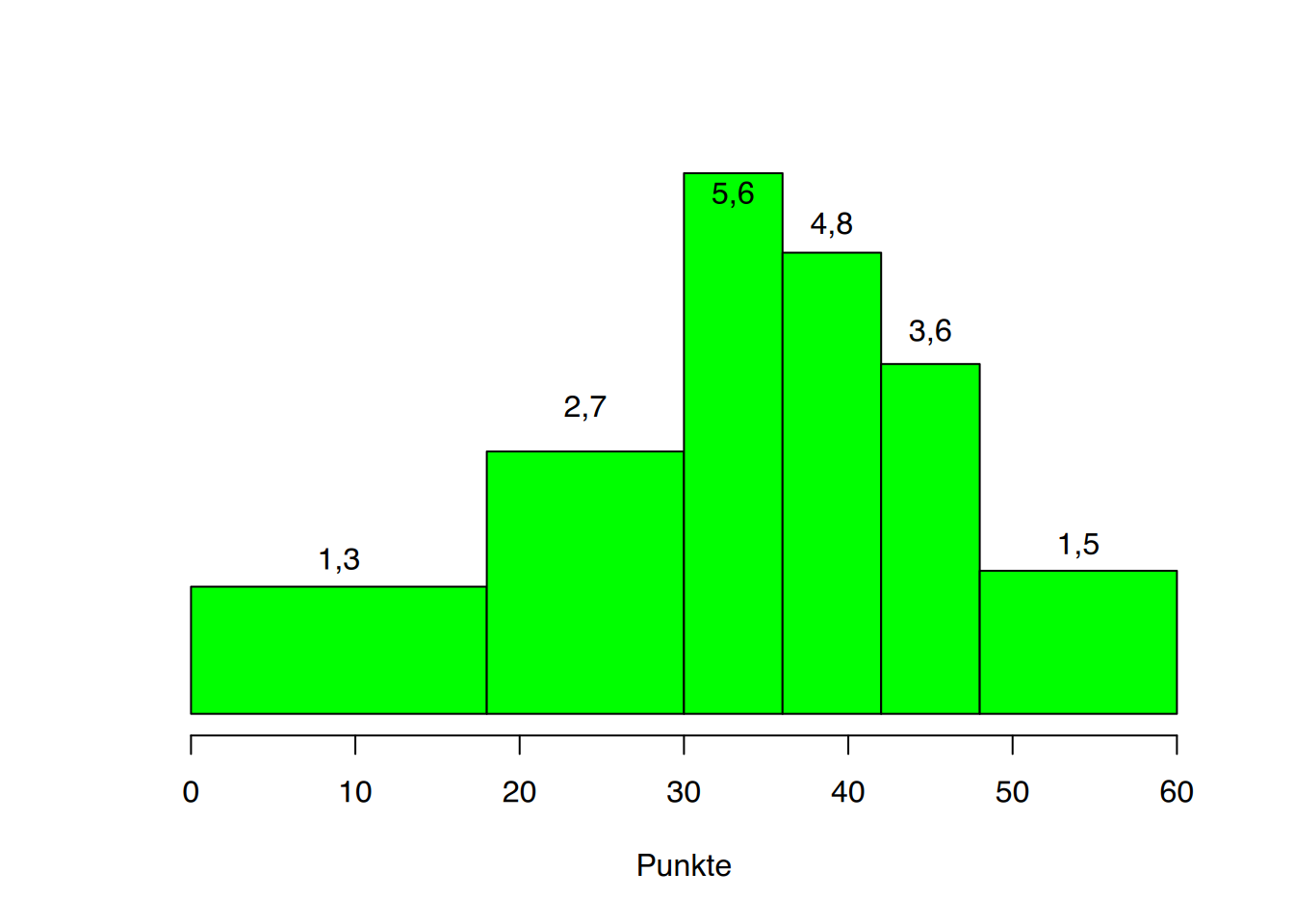
Die Y-Achse entspricht in diesem Histogramm (Abbildung 3.7) nicht mehr er absoluten Häufigkeit, sondern dem errechneten Quotienten.
Ein weiteres Beispiel soll den Unterschied verdeutlichen. Nehmen wir die folgende Altersverteilung von Personen, die in einem Londoner Stadtbezirk einen häuslichen Unfall erlitten haben (Tabelle 3.6).
| Klassengrenzen | Klassenmitte | Klassenbreite | Absolute Häufigkeit |
|---|---|---|---|
| (0-5] | 2,5 | 5 | 206 |
| (5-15] | 10 | 10 | 154 |
| (15-45] | 30 | 30 | 247 |
| (45-65] | 55 | 20 | 111 |
| (65-90] | 77,5 | 25 | 95 |
| Gesamt | 813 |
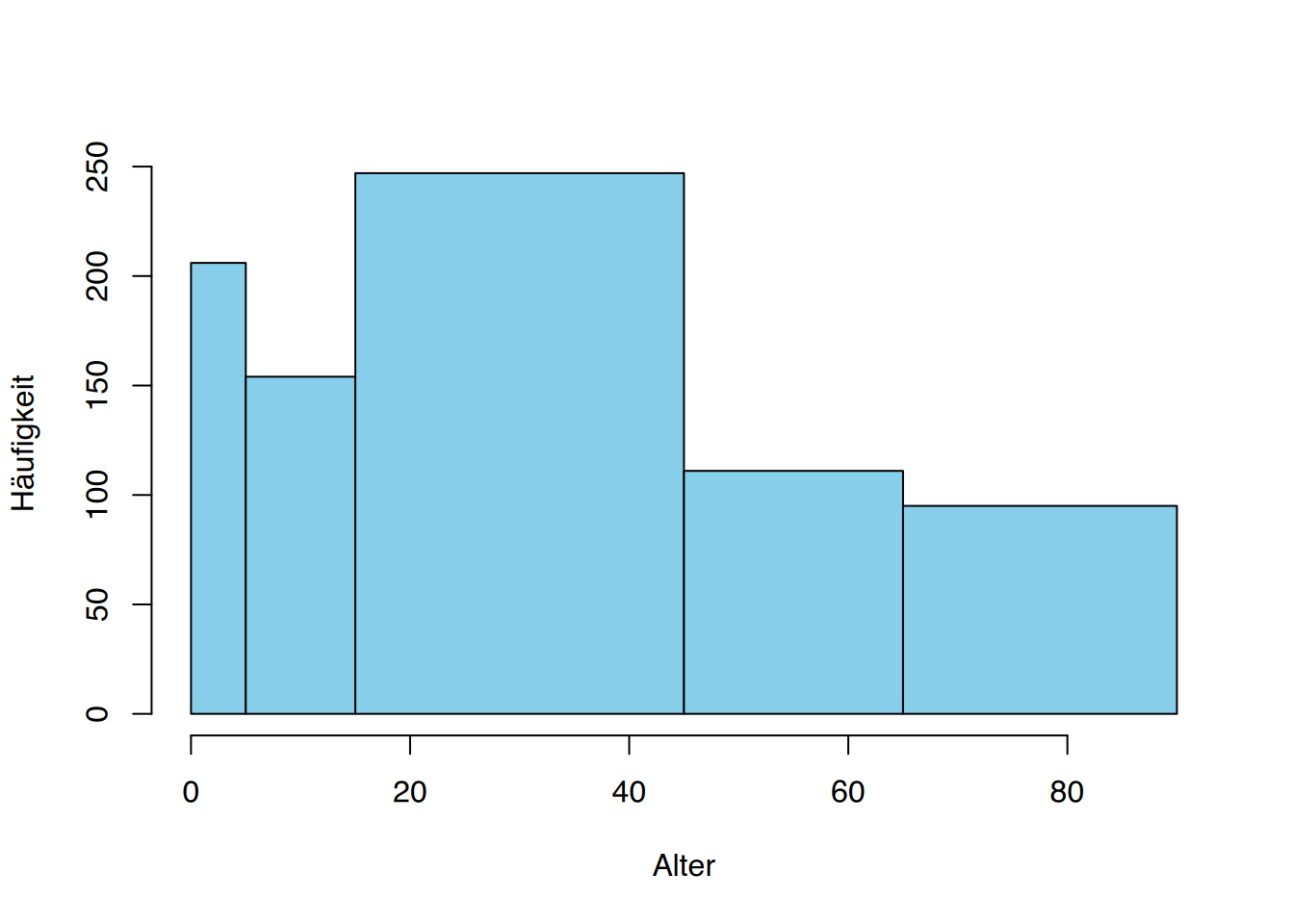
Schaut man sich Abbildung 3.8 an, so entsteht der Eindruck, dass Menschen im Alter von 15 bis 45 Jahren das höchste Unfallrisiko aufweisen. Zusätzlich scheint es so, als ob dieses Risiko bei Kleinkindern kleiner sei.
| Klassengrenzen | Klassenmitte | Klassenbreite | Absolute Häufigkeit | Quotient aus absoluter Häufigkeit und Klassenbreite |
|---|---|---|---|---|
| (0-5] | 2,5 | 5 | 206 | \(206/5=41,2\) |
| (5-15] | 10 | 10 | 154 | \(154/10=15,4\) |
| (15-45] | 30 | 30 | 247 | \(247/30=8,23\) |
| (45-65] | 55 | 20 | 111 | \(111/20=5,55\) |
| (65-90] | 77,5 | 25 | 95 | \(95/25=3,8\) |
| Gesamt | 813 |
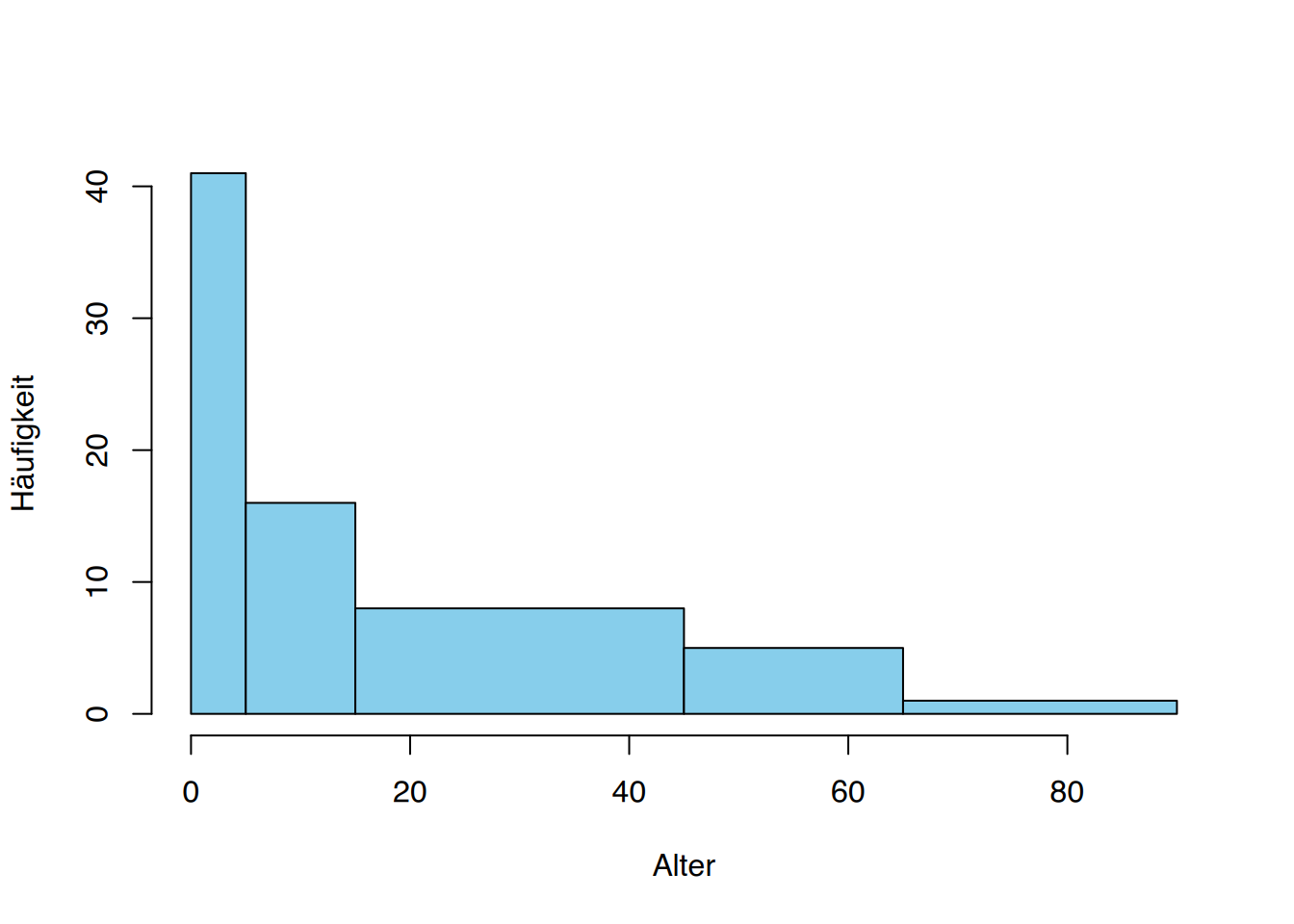
Erst durch ein flächenproportionales Histogramm wird auch in diesem Fall der falsche Eindruck entzerrt. Setzen wir also wieder die absolute Häufigkeit in Bezug zur Klassenbreite (Tabelle 3.7), so erhalten wir das Histogramm aus Abbildung 3.9. Wie man nun erkennen kann, haben in Wirklichkeit die Kleinkinder das höchste Risiko eines häuslichen Unfalls.
Es würde den Rahmen dieses Skriptes sprengen, auf alle Möglichkeiten der graphischen Darstellung einzugehen. Neben den besprochenen Diagrammen - Stab- oder Balkendiagramm, Polygonzüge, Histogramme - existieren noch vielfältige Möglichkeiten zur Präsentation der Daten.
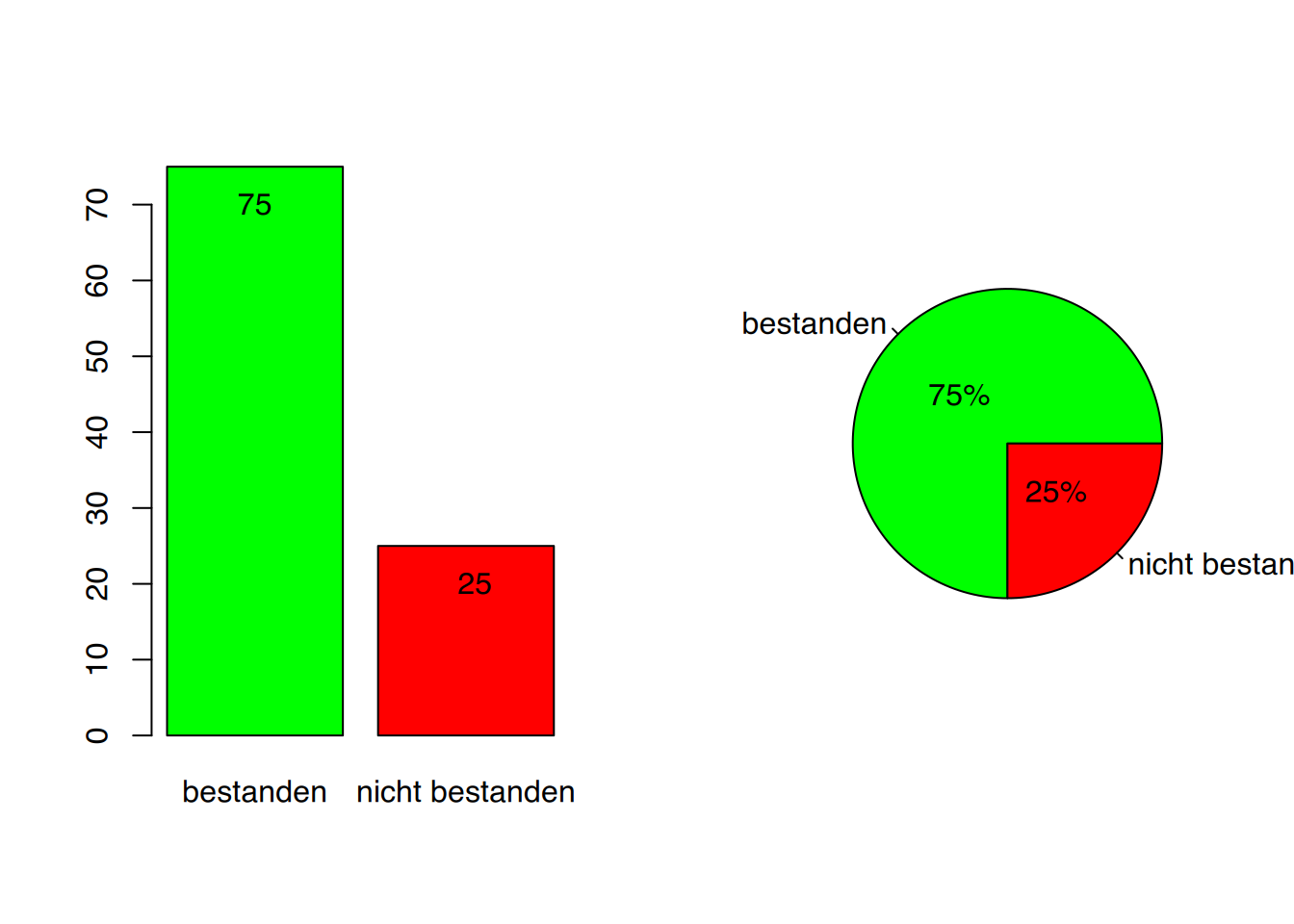
Spezielle Computerprogramme zur statistischen Datenverarbeitung bieten komfortable und vielfältige Optionen zur graphischen Darstellung des Materials. Hier sei nur noch das Kreisdiagramm erwähnt, welches eine sehr anschauliche Form zur Präsentation der Anteile bei nominalen Daten bietet.
Erinnern wir uns an das Beispiel der Prüfung. Auf nominalem Niveau konnten wir nur feststellen, wie viele Schüler die Prüfung bestanden, bzw. nicht bestanden hatten. Die Darstellung dieses Sachverhaltes ist sowohl als Balkendiagramm, als auch mittels eines Kreisdiagramms möglich. Wir überlassen natürlich dem Leser die Entscheidung, welche der beiden Möglichkeiten anprechender ist.
Nach dieser Darstellung der Daten mittels Tabellen und Kenngrößen werden wir uns im nächsten Kapitel mit statistischen Kenngrößen beschäftigen.