11 Die graphische Bestimmung des Medians bei klassierten Daten
Gegeben sind die Daten aus Tabelle 11.1.
| Häufigkeit | Prozent | kumulierte Prozente | |
|---|---|---|---|
| bis 12 | 14 | 8,8 | 8,8 |
| bis 24 | 26 | 16,3 | 25 |
| bis 36 | 51 | 31,9 | 56,9 |
| bis 48 | 51 | 31,9 | 88,8 |
| bis 60 | 18 | 11,3 | 100,0 |
| Gesamt | 160 | 100 |
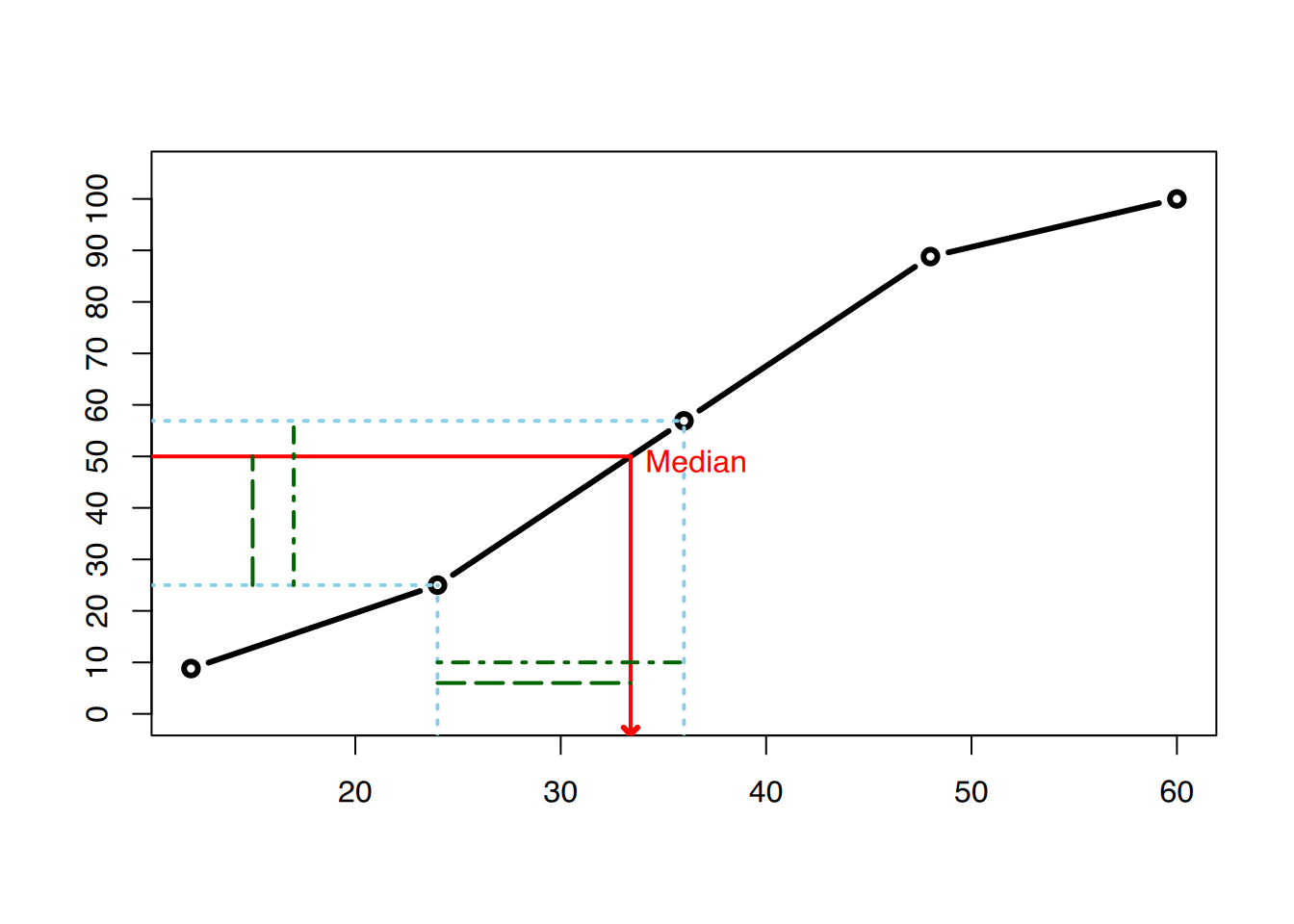
Für die graphische Ermittlung des Medians benötigen wir die kumulierten Prozentwerte, aus denen ein Summenpolygon (Abbildung 11.1) angefertigt wird.

Aus der Mathematik (Strahlensätze) wissen wir, dass das Verhältnis der beiden Strecken auf der x-Achse dem Verhältnis der Strecken auf der y-Achse entspricht.
Setzen wir also die Strecke ins Verhältnis, ergibt sich:
\[ \begin{aligned} \frac{x - 24}{36 - 24} = \frac{50 - 25}{56,9 - 25}\quad\quad\quad &\cdot 12\\[4mm] x - 24 = \frac{25}{31,9}\cdot 12 \quad\quad\quad &+ 24\\[4mm] x = 9,4 + 24 \quad\quad\quad\\[4mm] x = 33,4 \quad\quad \quad\quad \end{aligned} \]
11.1 Rechenweg der Beispielaufgabe
Hier nochmal der Rechenweg zum Beispiel aus Tabelle 5.3: