6 Regressionsanalysen

Im Kaptiel zur Korreltation wurde der Zusammenhang zweier Variablen statistisch untersucht. Als Ergebnis steht der Korrelationskoeffizient r, der die Stärke des Zusammenhangs in einer Zahl ausdrückt. Die zentrale Frage wird hierbei aber nicht beantwortet, nämlich: Wie ändert sich die Ausprägung eines Merkmals, wenn die Einflussgröße systematisch verändert wird? Anders ausgedrückt: Wie verhält sich die abhängige Variable (auch Zielgröße), wenn sich die unabhängige Variable verändert (Einflussgröße)? Wissen über die Art des Zusammenhangs zweier Merkmale erlaubt Vorhersagen wie beispielsweise: Eine Erhöhung der Dosis des Schlafmittels um 5 Milligramm verlängert die Schlafdauer um 4 Stunden.

6.1 Grundgedanken

Um die Art des Zusammenhanges zu berechnen, steht uns die Regressionsanalyse zur Verfügung. Im Gegensatz zur Korrelationsrechnung, die sich auf eine zweidimensionale oder bivariate Häufigkeitsverteilung bezieht, geht es bei der Regressionsrechnung um eine abhängige Variable (auch Zielgröße), die von einer unabhängigen Variablen (Einflussgröße) beeinflusst wird.

Die einfache lineare Regressionsanalyse ist ein Verfahren für metrische Daten. Im Rahmen dieses Skriptes werden wir wiederum nur auf lineare Zusammenhänge eingehen. Dementsprechend ist es auch bei der Regressionsrechnung wichtig, sich zunächst einen optischen Eindruck mittels Streudiagramm zu verschaffen.

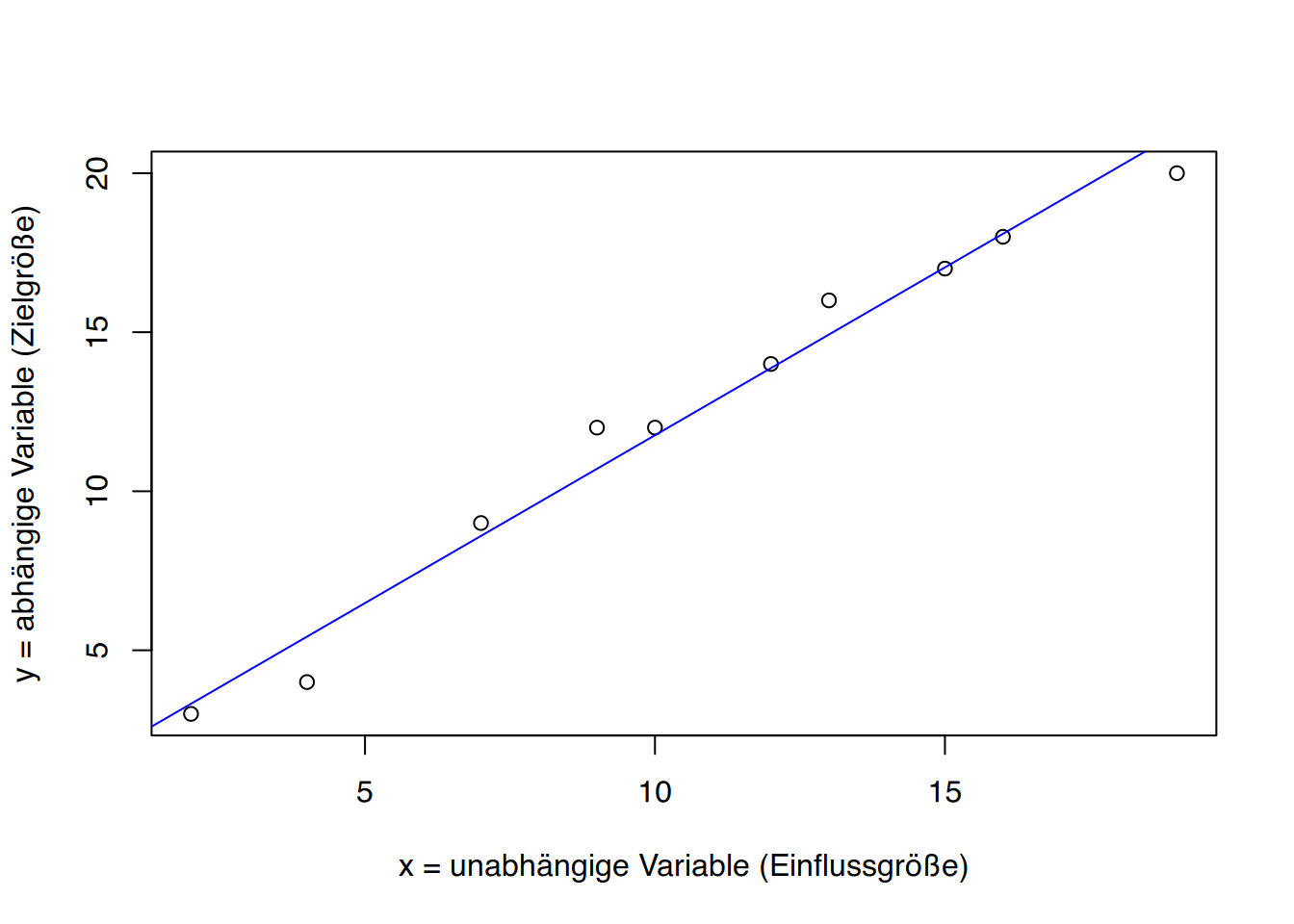
Grundgedanke der Regressionsanalyse ist es, die Beziehung zwischen x und y mittels einer Geraden zu veranschaulichen. Natürlich könnte man diese Linie nach “Augenmaß” durch die Punktwolke ziehen, wobei das Ziel ist, dass alle Punkte möglichst nahe an der Geraden liegen. Das Problem hierbei besteht darin, dass zehn Personen wahrscheinlich zehn verschiedene Linien zeichnen würden. Es bleibt uns also nichts anderes übrig, als die “beste” Gerade rechnerisch zu ermitteln, eine Gerade, von der die Abstände der einzelnen Punkte am geringsten sind.¹

Dazu benötigen wir die Gleichung einer geraden Linie: \[y = a + b\cdot x\]

wobei “a” den Schnittpunkt der Geraden durch die y-Achse angibt und “b” als der Steigungskoeffizient, bzw. linearer Regressionskoeffizient bezeichnet wird.

Die allgemeinen Formeln zur Berechnung von “a” und “b” lauten: \[\begin{aligned} a = \bar{y} - b \cdot\bar{x}\\[4mm] b = \frac{cov(x,y)}{s_{x}^2} \end{aligned} \tag{6.1}\]

Bleiben wir nochmals bei dem Beispiel der Schreib- und Lesefähigkeit. Nehmen wir an, es sei erwiesen, dass Lesen Einfluss auf die Rechtschreibung hat. Somit stellt sich das Lesen als die Einflussgröße und die Rechtschreibung als die Zielgröße oder abhängige Variable dar.

Es dürfte einleuchten, zunächst “b” zu berechnen, da diese Größe wiederum zur Bestimmung von “a” benötigt wird. Auf Seite wurden bereits Mittelwerte und Varianz, sowie Kovarianz für das Beispiel bestimmt. so dass wir diese jetzt in die Formeln einsetzen können:

\[b = \frac{30,5}{28,9} = 1,055 \quad\quad\quad\text{und}\quad\quad\quad a = 12,5 - (1,055 \cdot 10,7) = 1,211\]

Die Regressionsgleichung für das Beispiel lautet demnach (gerundet): \[y = 1.21 + 1,06 \cdot x\]

Setzt man jetzt einen beliebigen Punktwert für die Lesefähigkeit (x) ein , lässt sich der entsprechende Punktwert für die Rechtschreibung (y) voraussagen.

6.2 Interpolation und Extrapolation

Ein Vorteil der Regression besteht darin, dass für beliebige Wert \(x\) der passende \(y\)-Wert vorhergesagt werden kann. In Abbildung [fig:interextrapolation] sehen wir die Punkte einer Erhebung mit der dazugehörigen Regressionsgeraden. Zusätzlich ist jeweils beim Minimum und Maximum von \(x\) eine graue vertikale Hilfslinie in die Grafik eingezeichnet worden.

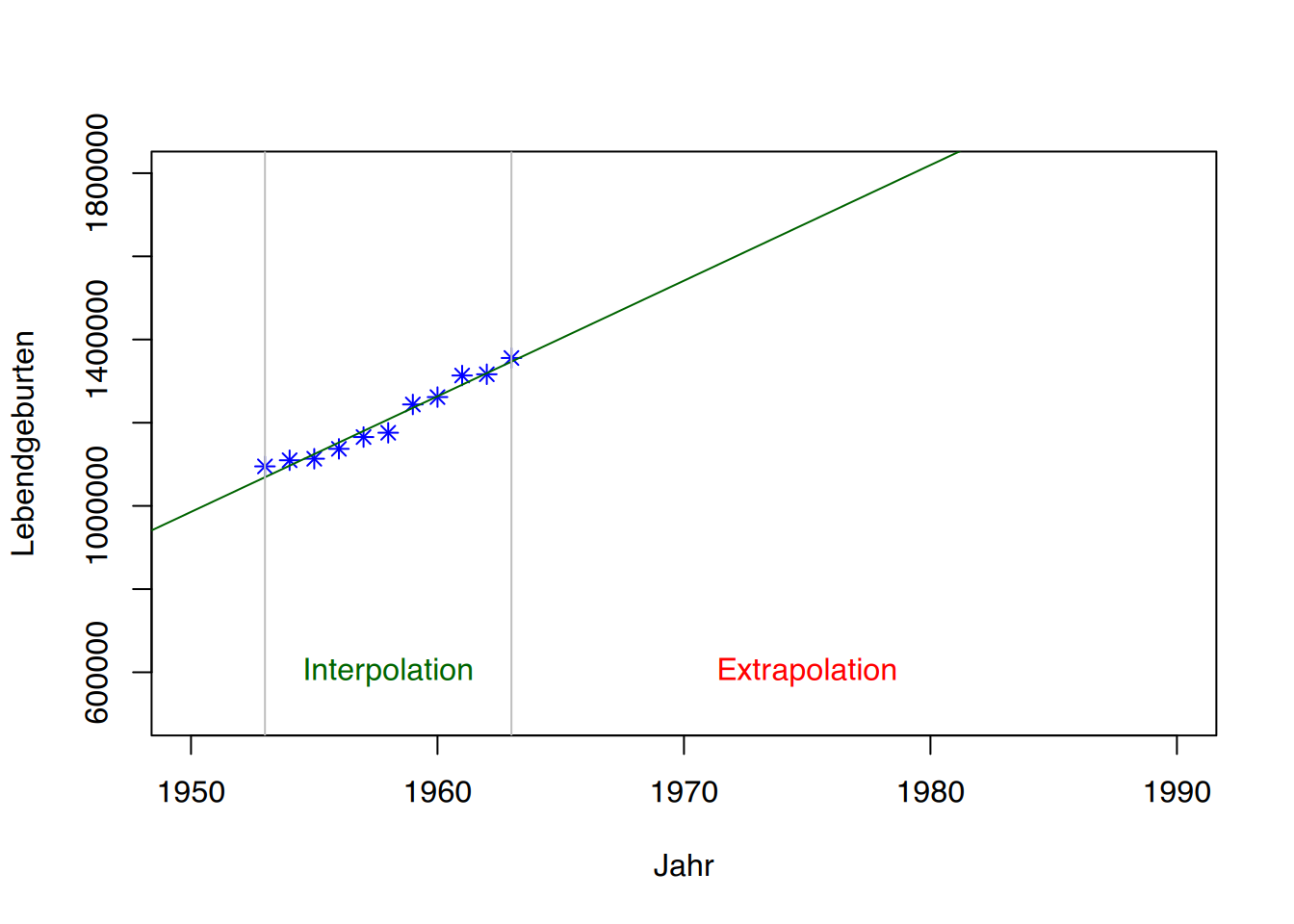
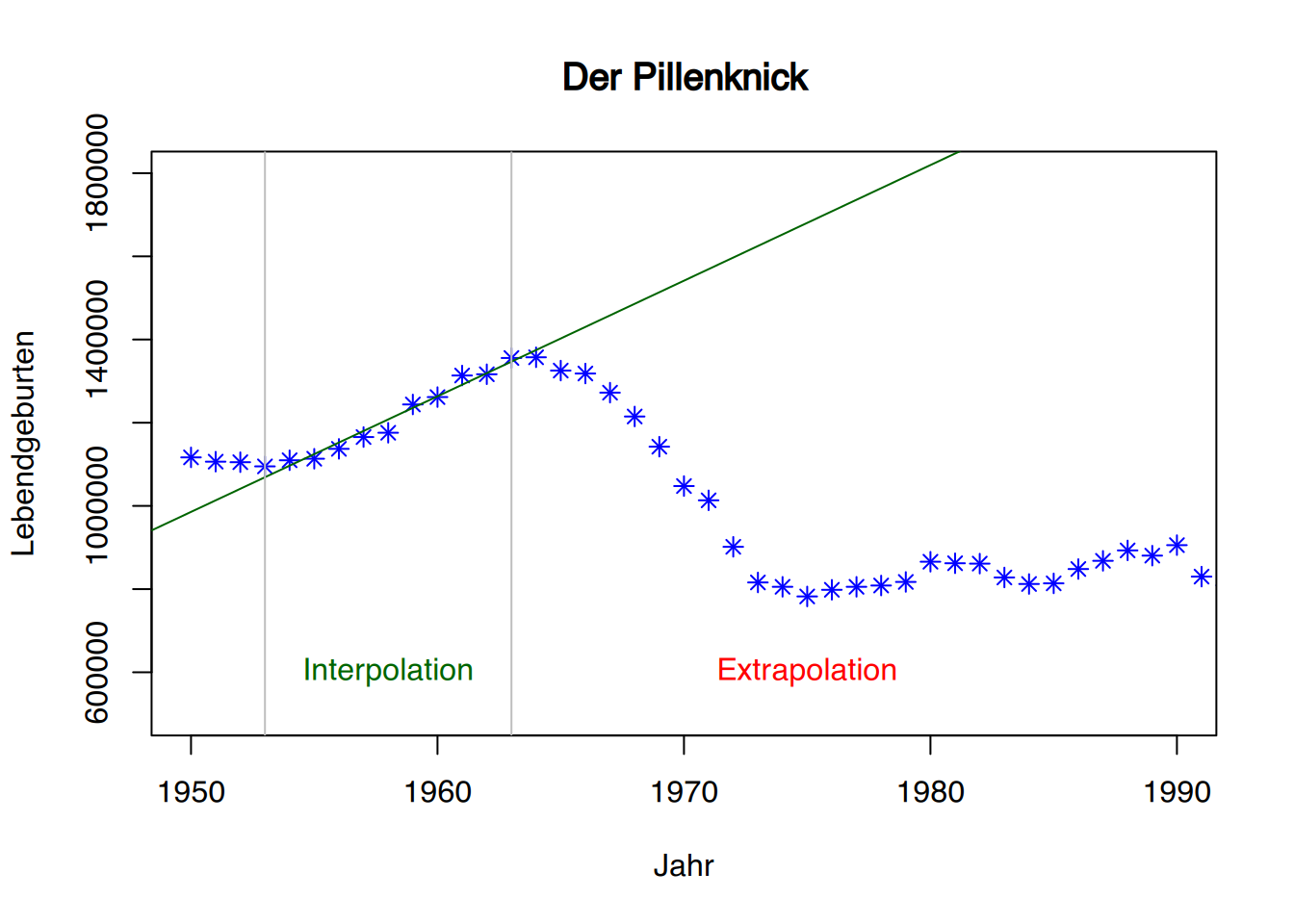
Macht man nun Vorhersagen innerhalb dieser Hilfslinien (das \(x\), für welches wir einen \(y\)-Wert vorhersagen wollen, liegt also zwischen dem gemessenen Minimum und Maximum von \(x\)), so spricht man von Interpolation. Möchten man jedoch einen passenden \(y\)-Wert für ein \(x\) vorhersagen, welches außerhalb des gemessenen Minimum und Maximum von \(x\) liegt, so spricht man von Extrapolation. Dass Vorhersagen mittels Extrapolation sehr kritisch gesehen werden müssen zeigt Abbildung 6.2. Laut der Geraden müsste die Anzahl der Lebendgeburten (Y-Achse) im Jahr 1980 bei ca. \(1.800.000\) liegen. Tatsächlich wurden 1980 aber nur \(865.789\) Kinder geboren. Dieser Abfall der Geburtenrate ist als “Pillenknick” bekannt, da sich die Geburtenrate mit Einführung der Anti-Baby-Pille (1965) deutlich verringerte. Die mittels Extrapolation getroffene Vorhersage für 1980 hat sich in diesem Beispiel um \(1.000.000\) Babys verschätzt.

6.3 Die einfache lineare Regression

Soll - wie in unserem Beispiel zur Schreib- und Lesefähigkeit - eine Zielvariabel \(y\) durch eine Einflussvariabel \(x\) erklärt werden, spricht man von der einfachen linearen Regression.

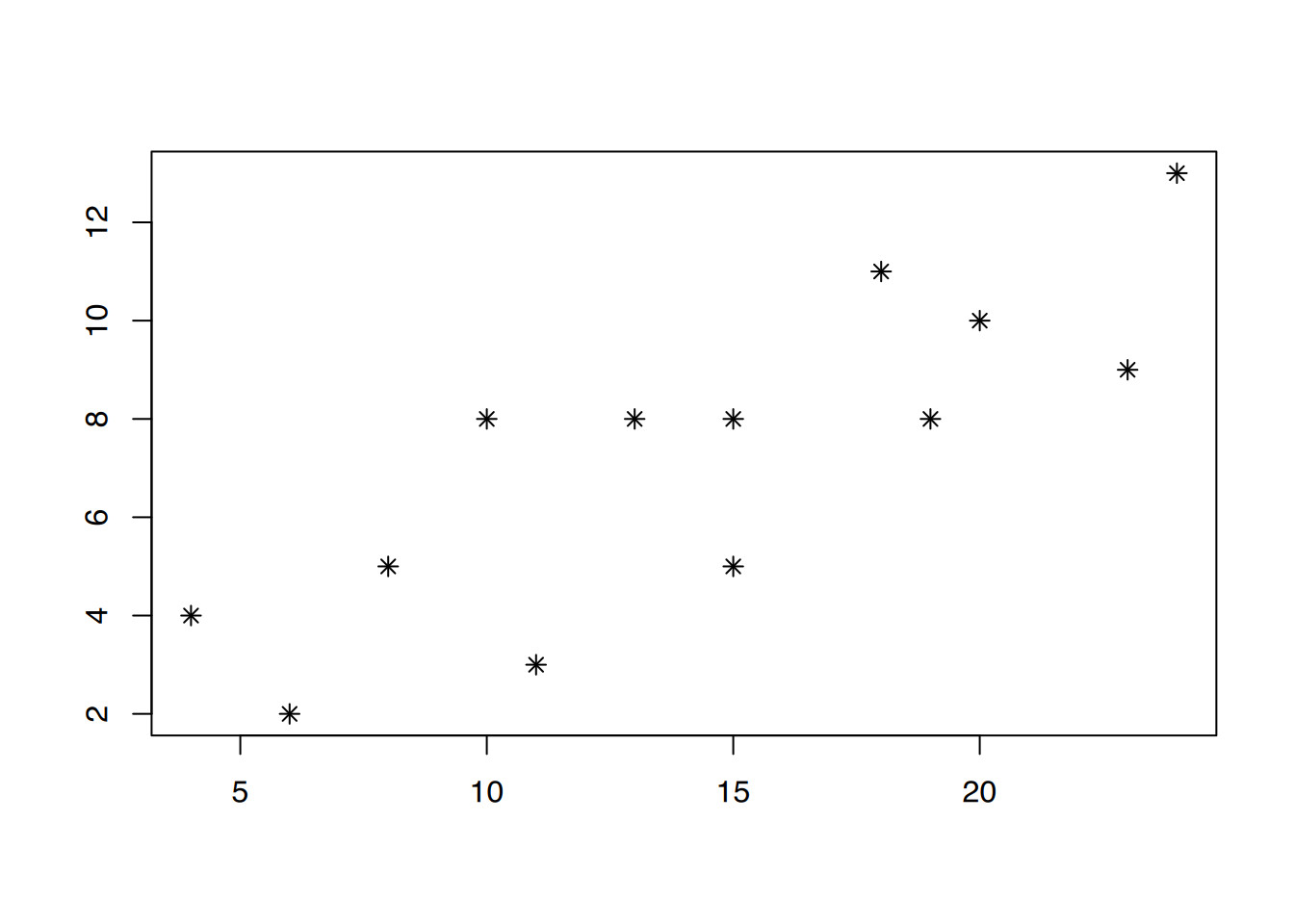
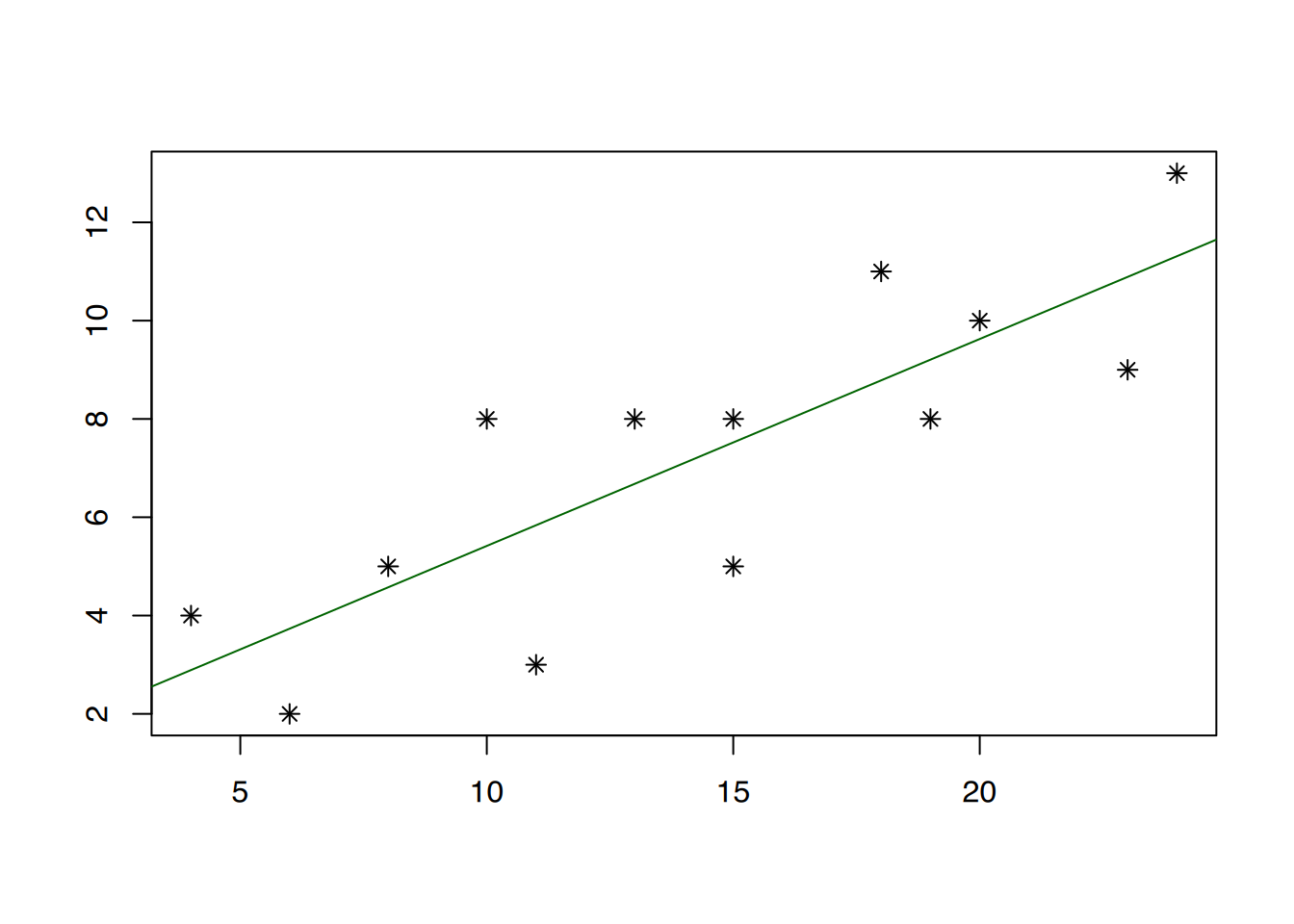
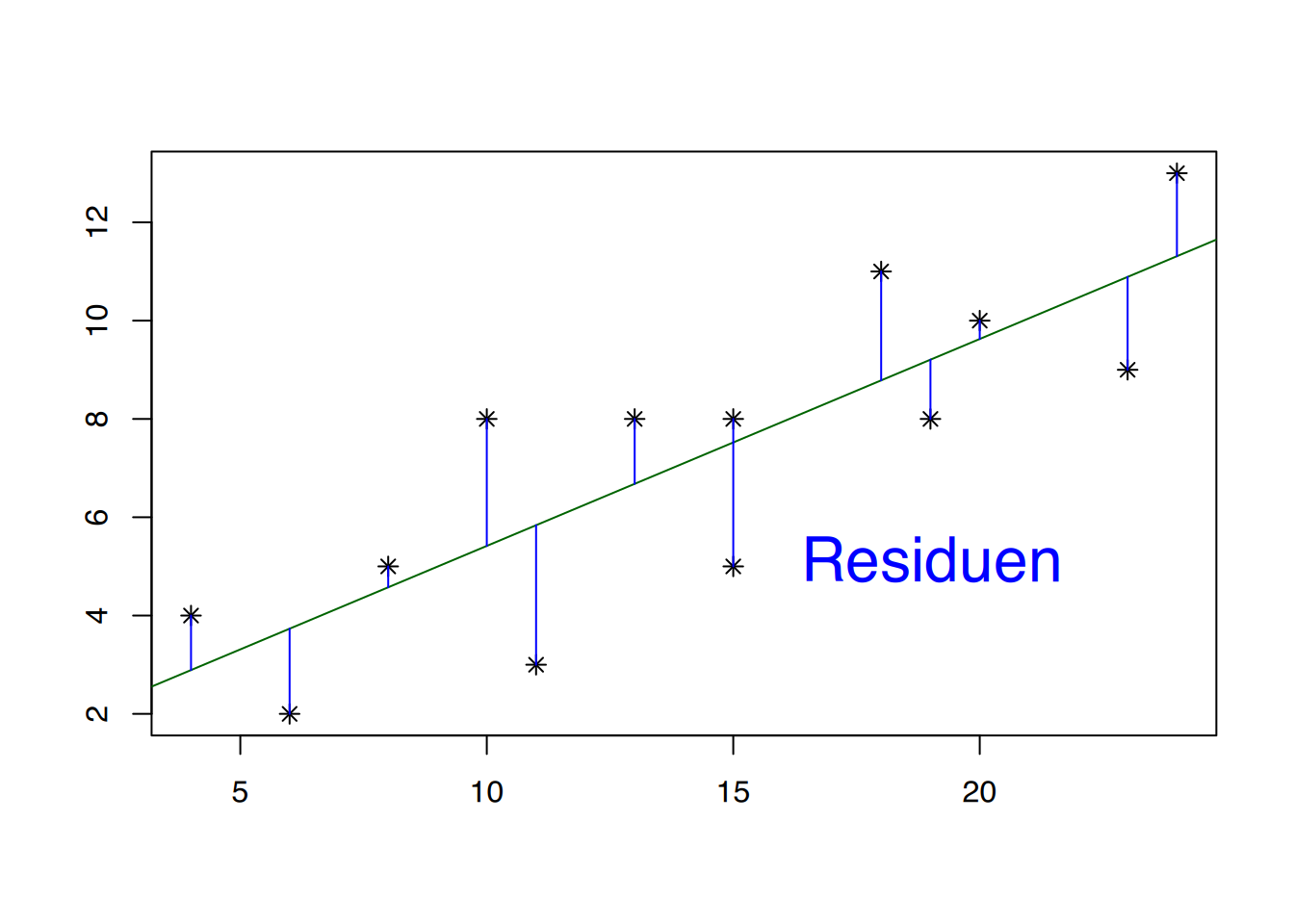
Abbildung 6.3 (a) zeigt eine Punktwolke, die einen linearen Trend aufzuweisen scheint. Daher wurde in Abbildung 6.3 (b) eine Regressionsgerade durch diese Punktwolke gezogen. Deutlich zu erkennen ist, dass die gemessenen Punkte nicht direkt auf der Geraden liegen, sondern durchaus nach oben oder unten abweichen können. Diese “Abweichler” nennt man Residuen. In Abbildung 6.3 (c) wurden die Abstände der Residuen zur Regressionsgeraden als blaue Linien eingezeichnet. Wenn man die Länge dieser blauen Linien misst, quadriert und dann zusammenzählt, erhält man die so genannte Summe der quadrierten Abweichungen. Carl-Friederich Gauß entdeckte im Jahr 1801, dass die “perfekte” Regressionsgerade bestimmt werden kann, indem man die Gerade so anlegt, dass die Summe der quadrierten Abweichungen minimal ist. Man nennt dies auch die “Methode der kleinsten Quadrate” (engl.: least squares). Wie bereits erwähnt lautet der mathematische Ausdruck einer Geraden: \[\begin{aligned} y = a + b \cdot x \end{aligned}\]

In der Statistik hat sich folgende Schreibweise etabliert:

\[\begin{aligned} \hat{y} = \beta_{0} + \beta_{1} \cdot x \end{aligned}\]

wobei \(\beta_{0}\) den Schnittpunkt (engl. Intercept) der Geraden durch die y-Achse angibt, und \(\beta_{1}\) als der Steigungskoeffizient bzw. linearer Regressionskoeffizient bezeichnet wird. Zur Erinnerung:

y = gemessene Werte
\(\mathbf{\hat{y}}\) = Modellwerte (auch: gefittete Werte)
\(\mathbf{\bar{y}}\) = arithmetisches Mittel

Während \(y\) (ohne Dach und ohne Querstrich) für die tatsächlich gemessenen Werte verwendet wird, bezeichnet \(\mathbf{\hat{y}}\) jene Werte, die durch die Regressionsgerade für \(y\) vorhergesagt werden. Man spricht hier auch von gefitteten Werten oder Modellwerte.

Genaugenommen geht es um die quadrierten Abstände, da die Summe der Abstände ansonsten wieder “Null” ergibt. Die Bestimmung der Regressionsgeraden geschieht nach der Methode der kleinsten Quadrate.↩︎