9 Das Schätzen unbekannter Größen: Punkt- und Intervallschätzungen
Nehmen wir an, die durchschnittliche Verweildauer in einer Stichprobe von 25 per Zufall ausgewählter Patientinnen des Krankenhauses A beträgt 9 Tage. Jedem wird es einleuchten, dass man jetzt nicht behaupten kann, dies sei die durchschnittliche Liegezeit für das gesamte Krankenhaus. In einer nächsten Stichprobe sind es vielleicht 10 Tage, in einer weiteren eventuell 11 Tage. Hiermit soll ausgedrückt werden, dass ein einzelner Befund einer Stichprobe nur ein ungefährer Wert, also ein Punktschätzwert für jenen unbekannten Wert sein kann, den man erhalten würden wenn man alle Patienten des Krankenhauses erfassen würde. Wo liegt nun dieser unbekannte wahre Wert? Es ist also unser Anliegen, den Punktschätzwert näher zu präzisieren.
Unter der Voraussetzung, dass es sich tatsächlich um Zufallsstichproben (des gleichen Umfanges) handelt, kann davon ausgegangen werden, dass einige Stichprobenmittelwerte etwas unterhalb und andere wiederum etwas oberhalb des wahren Wertes liegen. Die Wahrscheinlichkeit für extreme Abweichungen ist relativ gering. Theoretisch (siehe Wahrscheinlichkeitsrechnung) ist genau bekannt, wie sich die Werte einer Zufallsstichprobe um den wahren Wert herum verteilen. Demzufolge kann man fragen:
Wie weit kann der unbekannte wahre Wert von dem Schätzwert der Stichprobe mit einer großen Wahrscheinlichkeit höchstens entfernt sein?
Wir wollen die Überlegungen dazu an einem Beispiel mit normalverteilten Werten erläutern.
Wiederholen wir kurz unser Vorgehen aus der Wahrscheinlichkeitsrechnung, als es um die Bestimmung von Flächen (Wahrscheinlichkeiten) innerhalb einer Normalverteilung ging. Als fiktives Beispiel wollen wir davon ausgehen, dass von unserem Beispiel-Krankenhaus die durchschnittliche Liegedauer ermittelt worden ist und uns somit der wahre Wert der Grundgesamtheit bekannt sei. Nehmen wir an, die Liegedauer sei normalverteilt mit einem Mittelwert \(\mu\) von 10 Tagen.
Ausgehend von den Überlegungen zur Mittelwerte-Verteilung können wir dann behaupten, dass sich der Mittelwert einer beliebigen Zufallsstichprobe des Umfangs \(n\) mit einer Wahrscheinlichkeit von 95,44% im Bereich \(\mu \pm 2\cdot\sigma_{\bar{x}}\) befindet.
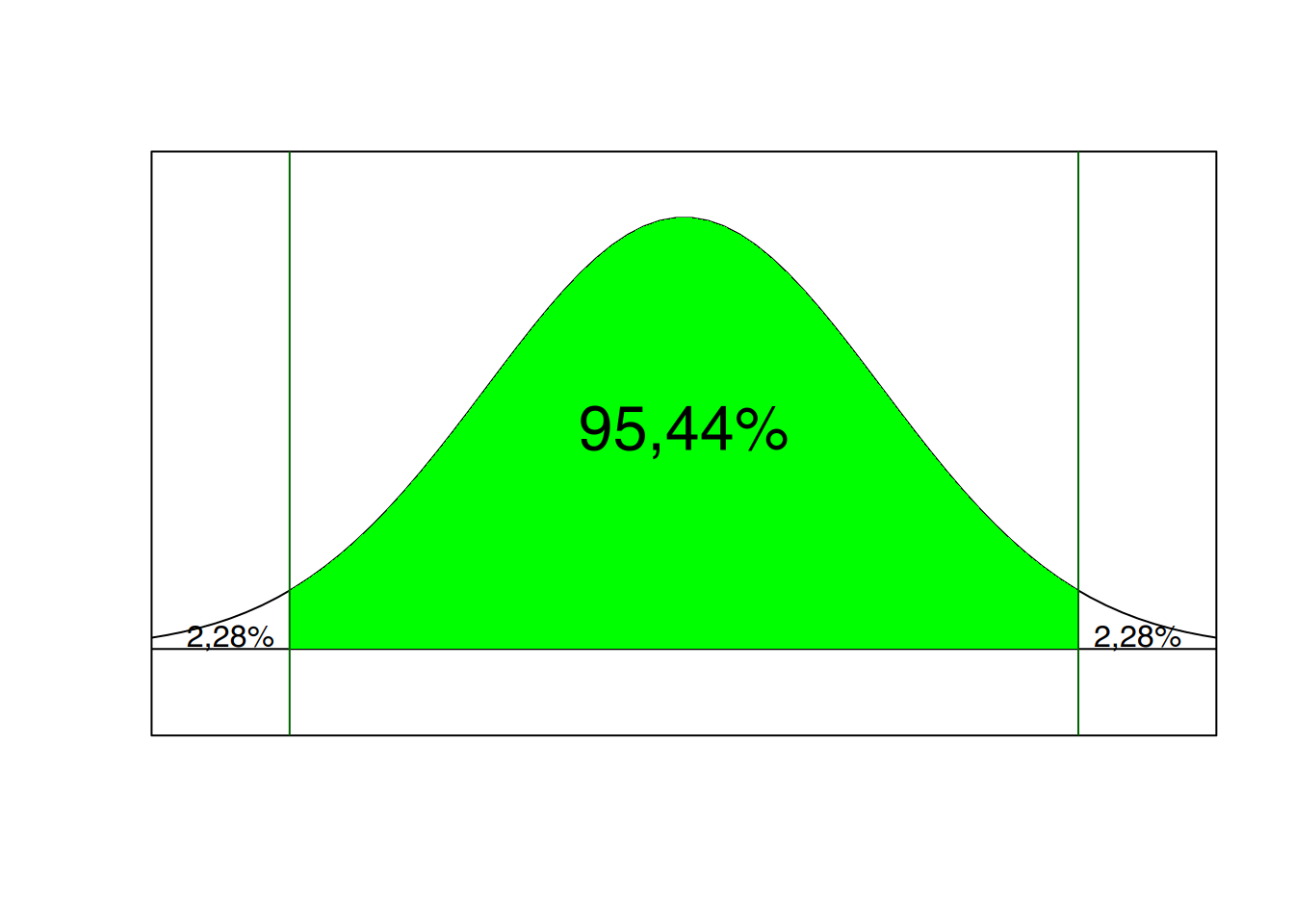
Angenommen, in unserem Beispiel sei \(\sigma = 2\) Tage, dann lautet dieser Bereich 6 bis 14 Tage. Dies bedeutet anders ausgedrückt, dass sich für 95,44% der Stichproben eine mittlere Verweildauerdauer ergibt, die zwischen 6 und 14 Tagen liegt. Umgekehrt heißt dies aber auch, es gibt lediglich bei 2,28% der Stichproben Verweildauern von weniger als 6 Tagen und ebenfalls bei 2,28% die länger als 14 Tage angaben. Drückt man dies als Wahrscheinlichkeitsaussage aus, so beträgt die Wahrscheinlichkeit bei einer zufällig gezogenen Stichprobe eine Liegedauer von weniger als 8 Tage zu finden, ganze 2,28%. Dieser Sachverhalt wird in Abbildung 9.1 nochmals verdeutlicht.

Wenn wir also per Zufall eine Stichprobe aus der Grundgesamtheit (hier das Krankenhaus) auswählen, ist die Wahrscheinlich sehr hoch (95,44%), eine mittlere Liegezeit zwischen 6 und 14 Tagen zu finden.
Anders herum könnte man auch sagen, dass sich aus den erhobenen Daten unseres Krankenhauses ein Wertebereich ergibt, in dem mit großer Wahrscheinlichkeit bestimmte Stichprobenmittelwerte zu finden sind. Nehmen wir jetzt an, die durchschnittliche Liegedauer betrüge 12 Tage mit einem Standardfehler von 2 Tagen. Daraus ergibt sich ein Bereich von 8 bis 16 Tagen.
Auch hier findet sich unser Stichprobenmittelwert von 9 Tagen innerhalb dieser Grenzen. D.h., eine mittlere Liegedauer von 12 Tagen ist mit unserem Stichprobenmittelwert vereinbar. Bei einer durchschnittlichen Liegedauer von 14 Tagen lautet der 95,44%-Bereich 10 bis 18 Tage. Jetzt liegt unser Stichprobenmittelwert von 9 Tagen jetzt nicht mehr innerhalb dieser Grenzen. Dies bedeutet, betrüge der tatsächliche Mittelwert (den wir normalerweise ja nicht kennen) 14 Tage, wäre es sehr unwahrscheinlich (weniger als 2,28%), einen Stichprobenmittelwert von 9 Tagen zu ermitteln.
Anders ausgedrückt heißt dies, dass bestimmte Mittelwerte der Grundgesamtheit als „Erzeuger" des Stichprobenmittelwertes von 9 Tagen als sehr unwahrscheinlich ausscheiden. Verdeutlichen wir dies mit einigen Mittelwerten der Grundgesamtheit bei gleichbleibendem Standardfehler von 2 Tagen und deren möglichen Wertebereichen (siehe Tabelle 9.1).
| \(\mu\) der Grundgesamtheit | Bereich \(\mu \pm 2\cdot\sigma_{\bar{x}}\) |
|---|---|
| 4 | 0 bis 8 |
| 5 | 1 bis 9 |
| 6 | 2 bis 10 |
| 7 | 3 bis 11 |
| 8 | 4 bis 12 |
| 9 | 5 bis 13 |
| 10 | 6 bis 14 |
| 11 | 7 bis 15 |
| 12 | 8 bis 16 |
| 13 | 9 bis 17 |
| 14 | 10 bis 18 |
In Tabelle 9.1 sind jene Populationsmittelwerte fett hinterlegt, bei denen die Wahrscheinlichkeit sehr gering ist, einen Stichprobenmittelwert von 9 Tagen zu „produzieren".
Setzen wir in die Formel, mit der wir den 95,44%-Werte-Bereich für den Mittelwert der Grundgesamtheit bestimmt haben jetzt einfach einmal unseren Stichprobenmittelwert von 9 ein: \[\bar{x} \pm 2 \cdot \sigma_{\bar{x}} = 9 \pm 2 \cdot 2\] dann ergibt sich ein 95,44%-Werte-Bereich von 5 bis 13 Tagen. Also genau jener Bereich, den wir unter der Annahme, dass die Verhältnisse in der Grundgesamtheit und damit der wahre Wert \(\mu\) bekannt sei, ermittelten. Die 95,44% bedeuten nicht, dass mit dieser Wahrscheinlichkeit der wahre Wert der Grundgesamtheit innerhalb dieses Bereichs liegt. Denn schließlich liegt der wahre Wert entweder innerhalb oder außerhalb. Es bedeutet lediglich, dass theoretisch in 95,44% der Stichproben Bereiche ermittelt werden können, die tatsächlich den wahren Wert umschließen.
Tatsache ist, dass unsere konkrete Stichprobe allerdings auch zu den 4,46% gehören könnte, die „daneben liegen".
Ganz vereinfacht ist dies der eingangs erwähnte Sachverhalt: Bei bekannter Grundgesamtheit sind Aussagen über die Stichprobe möglich und im Umkehrschluß lässt eine Stichprobe Aussagen über die zugrundeliegende Population zu.
Nachfolgend sollen einige Begriffe verdeutlicht werden. Im Beispiel der Liegedauer war der Mittelwert \(\bar{x}\) der Zufallsstichprobe ein Punktschätzwert für den wahren Wert \(\mu\) der Grundgesamtheit (das gesamte Krankenhaus). Weitere Punktschätzwerte, die wir aus Zufallsstichproben ermitteln können, sind z.B. Anteile (\(\hat{p}\)), Differenzen von Anteilen (\(\hat{d}\)), Korrelationskoeffizienten (\(\hat{r}\)), etc. Um diese Punktschätzwerte vom wahren Wert zu unterscheiden, versehen wir sie mit einem „Dach": \(\mathbf{\hat{}}\)
Es ist also möglich, ausgehend von Punktschätzwerten einer Zufallsstichprobe mit einer hohen Wahrscheinlichkeit (im folgenden sofern nichts anderes gesagt 95%) einen Bereich abzuschätzen, in dem der wahre Wert liegt. Bereiche werden üblicherweise mit Grenzen abgesteckt. Wie in Tabelle 9.1 dargestellt, benötigen wir die Angabe einer unteren und einer oberen Grenze, da der wahre Wert sowohl unterhalb als auch oberhalb unseres einzelnen Punktschätzwertes liegen kann.
Diese Grenzen nennt man Konfidenzgrenzen oder Vertrauensgrenzen (im englischen confidence limits), die mit einer bestimmten statistischen Wahrscheinlichkeit den wahren Wert einschließen. Üblicherweise geht man von 95% oder 99% Wahrscheinlichkeit aus und bezeichnet dies als Konfidenzniveau. Das Intervall zwischen den Konfidenzgrenzen bezeichnet man als Konfidenzintervall.
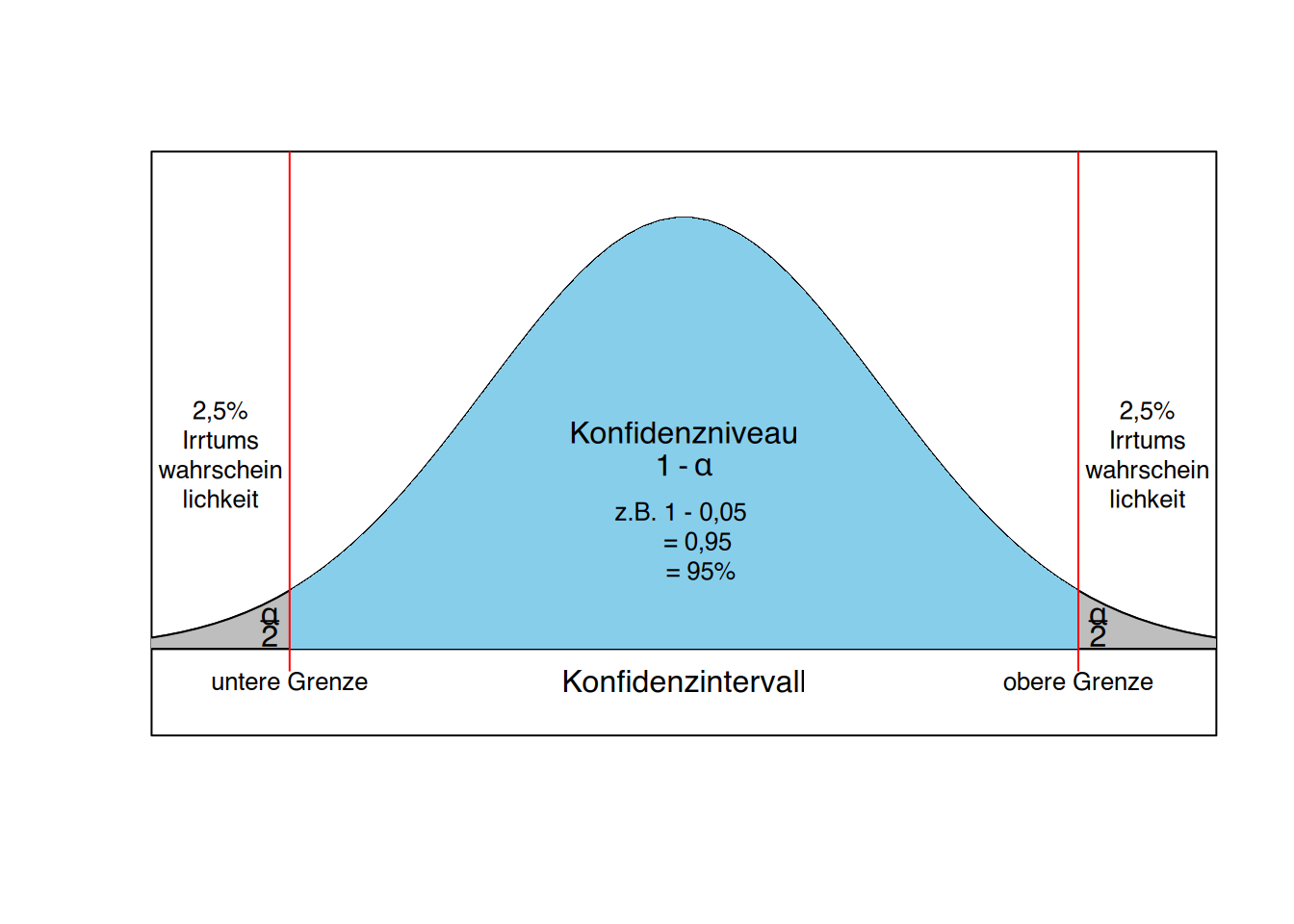
Die Wahrscheinlichkeit, dass der ermittelte Bereich den wahren Wert nicht einschließt, wird als Irrtumswahrscheinlichkeit \(\alpha\) (alpha) bezeichnet. Geläufig sind hierbei Werte von 5% oder 1%. Die Irrtumswahrscheinlichkeit liegt üblicherweise je zur Hälfte oberhalb und unterhalb der Konfidenzgrenzen, was mit dem Begriff „zweiseitig" ausgedrückt wird. Das Konfidenzniveau ergibt sich, indem man von der Gesamtwahrscheinlichkeit die Irrtumswahrscheinlichkeit abzieht (\(1 - \alpha\)). Abbildung 9.2 soll die Begriffe verdeutlichen.
Im Rahmen dieses Skripts beschränken wir uns auf die Bestimmung von Konfidenzgrenzen für Mittelwerte (Normalverteilungen), Anteile, sowie Differenzen von Anteilen (Binomialverteilungen).
9.1 Konfidenzgrenzen bei Normalverteilungen
Die wesentlichen Überlegungen zur Bestimmung von Konfidenzgrenzen bei Normalverteilung sind am Beispiel der Liegedauer in unserem Beispiel-Krankenhaus bereits besprochen worden. Zieht man sehr viele Zufallsstichproben aus einer Grundgesamtheit, so ist die Wahrscheinlichkeit für das Auftreten von Stichprobenmittelwerten, die extrem weit vom wahren Wert entfernt liegen, gering. Viel wahrscheinlicher dagegen ist es, einen Wert zu ermitteln, der innerhalb des Bereichs liegt, in dem 95% oder 99% aller Stichprobenmittelwerte liegen.
Bestimmt man für die Stichproben-Mittelwerte wiederum 95% oder 99% Wertebereiche, kann man im Umkehrschluss davon ausgehen, dass diese Bereiche (Intervalle) mit hoher Wahrscheinlichkeit den wahren beinhalten (einschließen).
Zur Bestimmung der Konfidenzintervalle legt man zunächst die Irrtumswahrscheinlichkeit \(\alpha\) fest. Geläufig sind Angaben von \(\alpha = 0,05\) und \(\alpha = 0,01\). Daraus ergibt sich das Konfidenzniveau (\(1-\alpha\)), zu 0,95 und 0,99 bzw. zu 95% und 99%. Wir erinnern uns, dass in der Mittelwertverteilung im Bereich von 2 Standardfehlern um \(\mu\) 95,44% der Werte liegen. Der 95%-Bereich einer Mittelwertverteilung (symmetrisch um den Mittelwert) wird von den z-Werten +1,96 und -1,96 begrenzt. Dies bedeutet, dass im Bereich von 1,96 Standardfehlern um \(\mu\) 95% der Stichprobenmittelwerte liegen.
Der Vollständigkeit halber soll noch angemerkt werden, dass für den 99%-Bereich ein z-Wert von 2,576 gilt. Mit anderen Worten liegen im Bereich von 2,576 Standardfehlern rechts und links vom Mittelwert 99% der Werte. Natürlich lässt sich jeder gewünschte Wertebereich (90%, 80%, etc.) ermitteln. Es sei daran erinnert, dass zur Ermittlung des entsprechenden z-Wertes die gesamte Fläche links von dem Wert berücksichtigt werden muß. Dies wird in Abbildung 9.3.
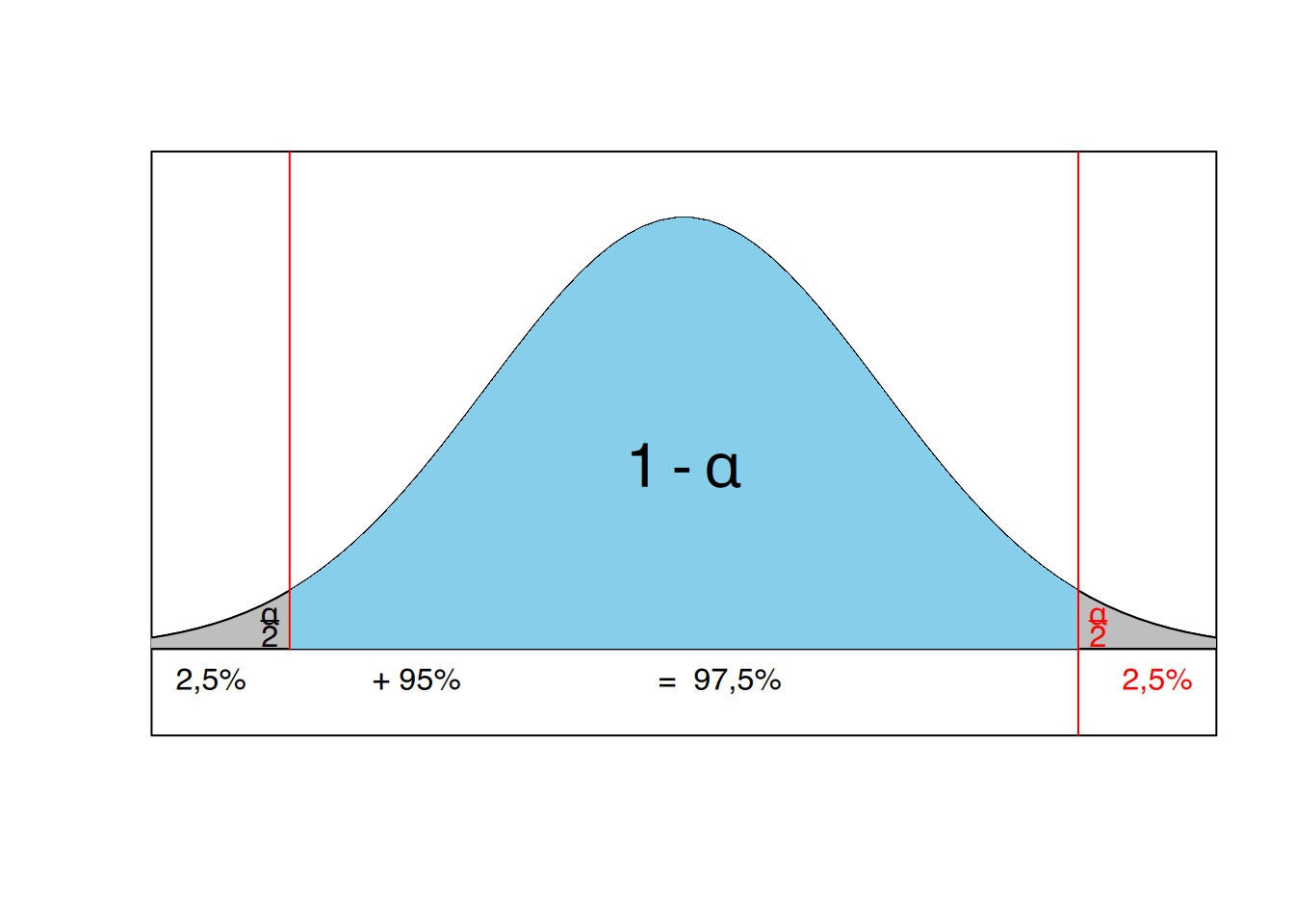
Suchen wir beispielsweise einen z- Wert zur Ermittlung der oberen Grenze des 95%-Konfidenzintervalls (d.h. \(\alpha\) entspricht 5%), so ist dies der z-Wert, der 97,5% der Verteilung „abschneidet". Er ergibt sich aus den Flächen \[ \begin{aligned} \frac{\alpha}{2} +1 - \alpha \quad\quad\text{oder}\quad\quad 1 - \frac{\alpha}{2}\\[4mm] \text{(d.h. hier}\quad 1 - \frac{0,05}{2} = 0,975 \text{)} \end{aligned} \]
Aus Referenztabellen (z.B. Tabelle 15.2) lässt sich dann ersehen, dass \(z_{0,975} = 1,96\) beträgt.
Kommen wir jetzt zur Ermittlung der Konfidenzintervalle, die nach der folgenden Formel berechnet werden: \[ \begin{aligned} \begin{array}{l l} \mu_{o}\\ \mu_{u}\\ \end{array}\Big\} \bar{x} \pm z \cdot \sigma_{\bar{x}} \label{formel:konfidenzgrenzen} \end{aligned} \]
R0.1p0.8 \(\mu_{o}, \mu_{u}\) & = die obere und untere Grenze des Intervalls
\(\bar{x}\) & = Mittelwert der Stichprobe
\(z\) & = Wert, der die entsprechende Fläche einer Normalverteilung “abschneidet”
\(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}\) & = Standardfehler des Mittelwerts
Wir verdeutlichen dies nochmals an einer Beispielaufgabe: Eine Zufalls-Erhebung über die jährlichen Ausgaben für Pflegehilfsmittel ergab bei 100 Befragten (\(n = 100\)) einen Mittelwert von 400,-€. Bekannt sei die Standardabweichung der Grundgesamtheit \(\sigma = 20\),-€. Bestimme das 95%- Konfidenzintervall für den wahren Wert \(\mu\). Der entsprechende z-Wert für den 95%-Bereich lautet 1,96.
\[\text{95\%-Konfidenzintervall} = 400 \pm (1,96 \cdot \frac{20}{\sqrt{100}}) = 400 \pm 3,92 \label{formel:phm}\]
Das 95%-Konfidenzinterval liegt zwischen 396,08€ und 403,92€. Eigentlich gestaltet sich die Bestimmung von Konfidenzintervallen rein rechnerisch nicht sehr schwierig. Allerdings gibt es das Problem, dass in den meisten Fällen nichts über die Standardabweichung der Grundgesamtheit bekannt ist. Dann wird mittels der Standardabweichung s der Stichprobe eine Punktschätzung für die Standardabweichung \(\sigma\) der Grundgesamtheit vorgenommen. Man geht dann allerdings davon aus, dass der geschätzte Standardfehler \(s_{\bar{x}}\)
\[s_{\bar{x}} = \frac{s}{\sqrt{n}}\quad\quad\text{häufig findet sich die Schreibweise}\quad\quad\hat{\sigma}_{\bar{x}} = \frac{\hat{\sigma}}{\sqrt{n}}\]
nicht einer Normalverteilung folgt, sondern einer \(t\)-Verteilung. Für die Bestimmung der Konfidenzintervalle bedeutet dies, das statt des \(z\)-Wertes der entsprechende \(t\)-Wert mit \(n - 1\) Freiheitsgraden (z.B. Lorenz (1996)) eingesetzt werden muß.
9.1.1 Exkurs: Freiheitsgrade (nach Bortz)
Freiheitsgrade bezeichnen die Anzahl der “frei wählbaren” Beobachtungen (Messungen). Beispiel: Eine Schulklasse mit 30 SchülerInnen hat einen Notenschnitt von \(2,9\). Nun kann man bei 29 SchülerInnen die Noten frei variieren – doch beim jeweils Letzten ist die Note vorgegeben, wenn der Mittelwert bei \(2,9\) liegen soll. Das arithmetische Mittel hat also \(n-1\) Freiheitsgrade.
Für die Berechnung des Standardfehlers benötigen wir die Varianz \(s^2\) in der die Summe der Abweichungsquadrate zunächst einmal - nämlich vor der Quadrierung - Null ergeben hätte
\[\sum_{i = 1}^{n} (x_{i} - \bar{x}) = 0\]
Ergeben sich beispielsweise bei einer Stichprobe von \(n = 5\) die ersten vier Abweichungen mit \(x_{1} - \bar{x} = -5, x_{2} - \bar{x} = +3, % x_{3} - \bar{x} = +1\) und \(x_{4} - \bar{x} = 2\), dann muss \(x_{5} - \bar{x} = -1\) sein, damit die Summe der Abweichungen wieder Null ergibt:
\(-5 +3 +1 +2 -1 = 0\)
Bei einer Stichprobe von \(n = 5\) ist eine der Abweichungen festgelegt. Die Varianz hat vier (\(n - 1\)) Freiheitsgrade. Freiheitsgrade kürzt man häufig mit \(v\) ( gesprochen "nü") oder mit \(df\) (englisch: degrees of freedom) ab.
Kehren wir zu unserem Beispiel der durchschnittlichen Ausgaben für Pflegehilfsmittel zurück. Aus der Stichrobe von \(n = 100\) errechnete sich ein Stichprobenmittelwert von \(\bar{x} = 400\) und eine Standardabweichung \(s = 20\). Da jetzt \(\sigma\) unbekannt ist, schätzen wir den Standardfehler mit der Standardabweichung aus der Stichprobe.
Die Formel zur Bestimmung des Konfidenzintervalls ändert sich dann wie folgt: \[\begin{aligned} \begin{array}{l l} \mu_{o}\\ \mu_{u}\\ \end{array}\Big\} = \bar{x} \pm t \cdot s_{\bar{x}} \label{formel:konfidenzgrenzen2} \end{aligned}\]
- \(\mu_{o}, \mu_{u}\) = die obere und untere Grenze des Intervalls
- \(\bar{x}\) = Mittelwert der Stichprobe
- \(t\) = Wert, der die entsprechende Fläche einer \(t\)-Verteilung “abschneidet”
- \(s_{\bar{x}} = \frac{s}{\sqrt{n}}\) = Standardfehler des Mittelwerts
Setzen wir unsere Werte jetzt in die Formel ein: \(400 \pm t \cdot \frac{20}{\sqrt{100}}\)
und ermitteln wir laut Tabelle (z.B. Tabelle 15.3) einen Wert für \(t_{\substack{\alpha = 0,05\\v=99}} = 1,985\) (gemittelt),
dann lautet das 95%-Konfidenzintervall = \(400 \pm 1,985 \cdot 2 = 400 \pm 3,97\)
Sicherlich fällt auf, dass der \(z\)-Wert (1,96) und der \(t\)-Wert (1,985) sich in unserem Beispiel nur unwesentlich unterscheiden. Wie in der Wahrscheinlichkeitsrechnung angesprochen, nähern sich einige Verteilungen (z.B. die Binomialverteilung) bei großen Stichproben einer Normalverteilung an. Dies gilt auch für die \(t\)-Verteilung. Hätte der Umfang der Stichprobe beispielsweise \(n = 5\) betragen, dann wäre der \(t\)-Wert mit 2,776 deutlich größer als der entsprechende \(z\)-Wert in der Normalverteilung und damit auch das Intervall breiter.
9.2 Schärfe und Sicherheit von Konfidenzaussagen
Die Länge eines Konfidenzintervalls - also der Abstand zwischen der oberen und unteren Grenze des Intervalls, ist ein Maß für die Präzision oder die Schärfe einer Konfidenzaussage. Das Konfidenzniveau, z.B. 95%, gibt die Sicherheit der Aussage an. Im Beispiel der durchschnittlichen Aufwendungen für Pflegehilfsmittel (Seite ) lag das 95%-Konfidenzintervall zwischen 396,08,-€ und 403,92,-€. Es hatte demnach eine Länge von 7,84,-€, was sicherlich als eine recht präzise Aussage gewertet werden kann (zumindest wenn es - wie in unserem Bespiel um mehrere 100€ geht). Nehmen wir an, uns reicht die Sicherheit von 95% nicht aus und wir hätten gerne eine Aussage mit 99%iger Sicherheit.
Dann ergibt sich laut Gleichung 14.10 von Seite für den Mittelwert der Stichprobe von 400,-€ mit bekannter Standardabweichung der Grundgesamtheit von 20,-€ bei \(n = 100\) das folgende Intervall:
\[400 \pm (2,576 \cdot \frac{20}{\sqrt{100}}) = 400 \pm 5,15\\[4mm]\]
Die untere Konfidenzgrenze lautet jetzt 394,85€, die obere 405,15€. Das heisst die Intervalllänge hat sich auf 10,30€ vergrößert. Anders ausgedrückt ist das Intervall hier bei höherer Sicherheit, nämlich 99%, breiter und damit unschärfer geworden. Es sieht also so aus, dass eine schärfere Konfidenzaussage zu Lasten der Sicherheit geht und umgekehrt eine höhere Sicherheit der Aussage diese wiederum unschärfer macht. Dies gilt zumindest solange die Stichprobengröße \(n\) konstant bleibt.
Die Breite und damit die Schärfe einer Konfidenzaussage wird von verschiedenen Größen beeinflusst:
die Irrtumswahrscheinlichkeit \(\alpha\), die direkt den \(z\)-Wert (bzw. \(t\)-Wert) beeinflusst. Ein großes \(\alpha\) bedeutet niedriges Konfidenzniveau (niedrige Sicherheit) und bewirkt ein schmaleres (schärferes) Intervall und umgekehrt bedeutet ein kleines \(\alpha\) ein höheres Konfidenzniveau (höhere Sicherheit) mit einem breiterem Intervall.
die Stichprobengröße \(n\), die (neben der Bestimmung des \(z\)- bzw. des \(t\)-Wertes) zur Berechnung des Standardfehlers der Mittelwertverteilung benötigt wird. Betrachtet man nochmals die Formel, müßte deutlich sein, dass ein „großes \(n\)" den Wert des Standardfehlers (und damit auch die Intervallbreite) verkleinert und umgekehrt (und zwar quadratisch, siehe unten).
die Variabilität des Merkmals in der Stichprobe, d.h. die Standardabweichung der Grundgesamtheit, bzw. der Stichprobe. Ein hoher Wert oberhalb des Bruchstriches wird den Standardfehler (und damit auch das Intervall) vergrößern und umgekehrt.
Möchten wir eine sichere (hohes Konfidenzniveau) und gleichzeitig präzise (schmales Intervall) Konfidenzaussage, so geht dies nur über den Stichprobenumfang.
Die Halbierung eines Konfidenzintervalls macht einen vierfachen Stichprobenumfang erforderlich!
9.3 Konfidenzgrenzen für Anteile (bei Binomialverteilungen)
Die Befragung über den Aufwand für Pflegehilfsmittel hatte neben den durchschnittlichen Ausgaben noch ergeben, dass insgesamt 25% der Befragten Zuzahlungen leisten müssen. Dieser Anteil von 25% ist wiederum der Punktschätzwert (\(\hat{p}\)) für den wahren Anteil (\(p\)) in der Grundgesamtheit, für den wir ein Konfidenzintervall mit \(p_{u}\) und \(p_{o}\) schätzen möchten. Für binomialverteilte Anteile gibt es verschiedene Methoden zur Bestimmung von Konfidenzintervallen. Wir werden uns hier auf die Beschreibung der graphischen Methode beschränken. Für die quantitative Bestimmung sei auf Lorenz (1996) verwiesen.
9.3.1 Die graphische Bestimmung von Konfidenzgrenzen für binomialverteilte Anteile
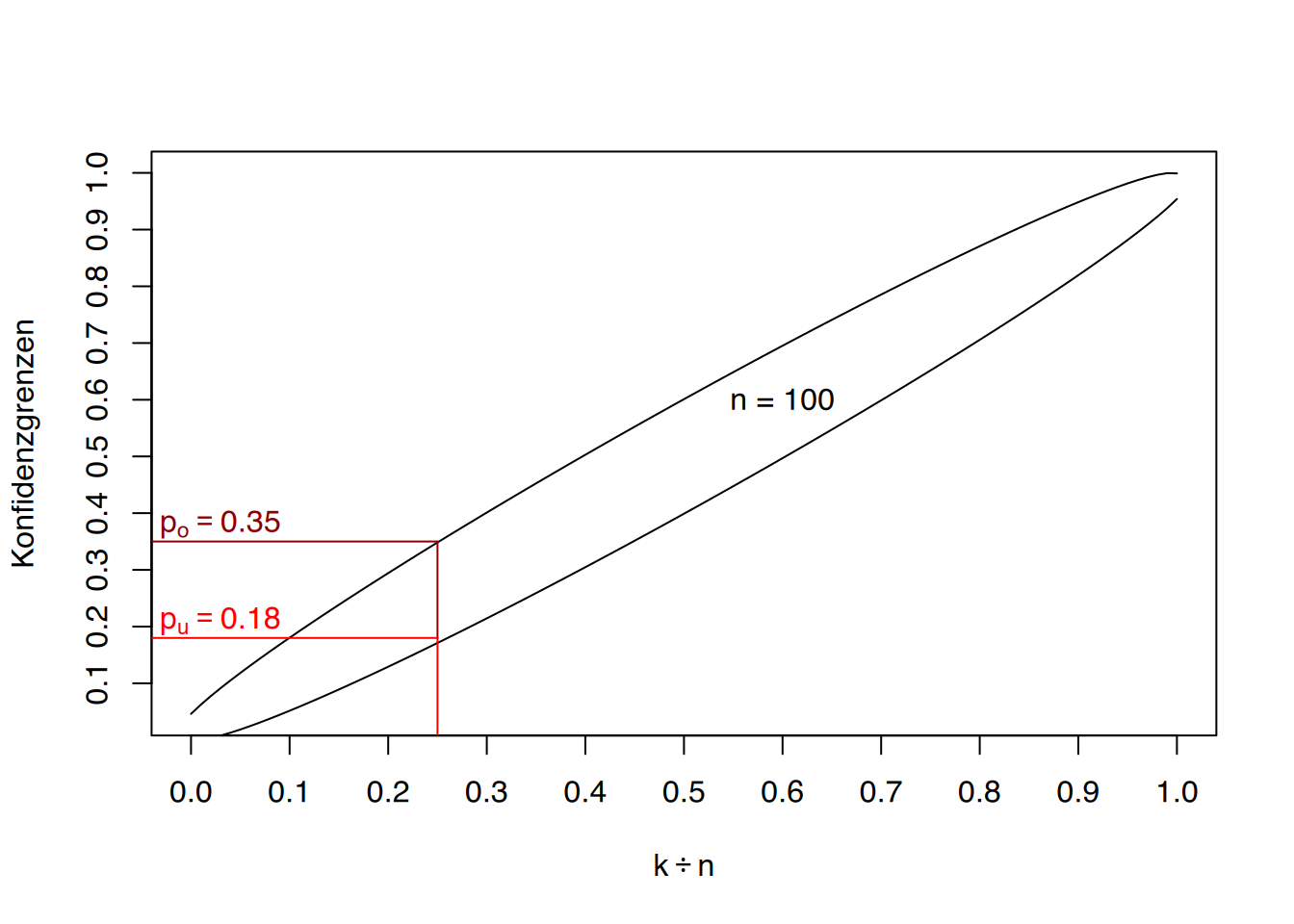
Die graphische Methode, die lediglich eine näherungsweise Bestimmung darstellt, erfolgt mittels Nomogrammen (wie z.B. im Lorenz (1996) für 95% und für 99%). Auf der unteren waagerechten Achse liest man den Anteil ab, den man über die Stichprobe geschätzt hat. Zieht man von diesem Anteil aus eine Linie nach oben, trifft man auf Kurven, die für verschieden Stichprobengrößen eingezeichnet sind, wobei sich jedesmal eine untere und eine obere Kurve (für die untere und obere Konfidenzgrenze) finden läßt. Geht man jetzt von den Kurven zur linken senkrechten Achse, lassen sich dort die Konfidenzgrenzen ablesen.
In der Abbildung 9.4 wurde das Vorgehen sehr vereinfacht dargestellt. Auch finden sich dort aus Gründen der Übersicht nur die Werte für unser Beispiel wieder. In unserem Beispiel liegt demnach der wahre Anteil derjenigen, die Zuzahlungen bei den Pflegehilfsmitteln leisten müssen, zwischen 18% und 35%.
Konfidenzgrenzen für binomialverteilte Anteile sind zunächst einmal nicht symmetrisch zu dem Punktschätzwert. Dies begründet sich durch die Schiefe der Binomialverteilung. Bei Anteilen, die nahe bei 0,5 liegen, sind auch die Grenzen annähernd symmetrisch. Konfidenzgrenzen für binomialverteilte Anteile lassen sich auch näherungsweise berechnen. Allerdings sind an die Berechnung entweder Bedingungen geknüpft (z.B. große Stichprobe) oder die Berechnung ist sehr aufwendig.
Bei vielen praktischen Fragestellungen interessieren wir uns allerdings für Unterschiede in Anteilen, so daß wir im Rahmen dieses Skripts darauf kurz eingehen werden.
9.3.2 Konfidenzgrenzen für den Unterschied von Anteilen (bei Binomialverteilungen)
Nehmen wir wieder unser Beispiel der Zuzahlungen bei Pflegehilfsmitteln. In Bundesland A gaben 25 von 100 Befragten an, Zuzahlungen leisten zu müssen. In Bundesland B wurden 150 Personen befragt, von denen 60 von Zuzahlungen betroffen waren. Bundesland A hat dementsprechend einen Anteil von 0,25 (25%) und Bundesland B einen Anteil von 0,40 (40%) Zuzahlern. Der Punktschätzwert für die Differenz \(\hat{d}\) beträgt folglich \(0,40 - 0,25 = 0,15\). Gesucht ist jetzt das 95% Konfidenzintervall für die wahre Differenz \(d\), welches wir mit der folgenden Formel bestimmen können:
\[ \begin{aligned} \begin{array}{l l} d_{o}\\ d_{u}\\ \end{array}\Big\} = \hat{d} \pm \frac{n_{1} + n_{2}}{2 \cdot n_{1} \cdot n_{2}} \pm c \cdot \sqrt{\frac{\hat{p}_{1} \cdot (1 - \hat{p}_{1})}{n_{1}} + \frac{\hat{p}_{2} \cdot (1 - \hat{p}_{2})}{n_{2}}} \end{aligned} \tag{9.1}\]
- \(n_{1}, n_{2}\) = die Umfänge der beiden Stichproben
- \(\hat{p}_{1}\), \(\hat{p}_{2}\) = die geschätzten Anteile in beiden Stichproben
- \(c\) = eine Konstante
So wie wir in den voran gegangenen Formeln \(z\)-Werte oder \(t\)-Werte benötigten, ist es bei der Ermittlung von Konfidenzintervallen für Unterschiede in Anteilen die Konstante \(c\), deren Werte der folgenden Tabelle zu entnehmen sind:
| \(\alpha\) | 0,01 | 0,05 | 0,10 | 0,20 |
|---|---|---|---|---|
| \(c\) | 2,58 | 1,96 | 1,64 | 1,28 |
Setzen wir jetzt die Zahlen in Gleichung 9.1 ein:
\[ \begin{aligned} d_{u}, d_{o} &=& 0,15 \pm \frac{100 + 150}{2 \cdot 100 \cdot 150} \pm 1,96 \cdot \sqrt{\frac{0,25 \cdot (1 - 0,25)}{100} + \frac{0,40 \cdot (1 - 0,40)}{150}}\\[4mm] &=& 0,15 \pm \frac{250}{30.000} \pm 1,96 \cdot \sqrt{\frac{0,1875}{100} + \frac{0,24}{150}}\\[4mm] &=& 0,15 \pm 0,00833 \pm 1,96 \cdot \sqrt{0,003475}\\ &=& 0,15 \pm 0,00833 \pm 1,96 \cdot 0,05895\\ &=& 0,15 \pm 0,00833 \pm 0,11554 \end{aligned} \]
\[ \begin{aligned} \text{Es ergibt sich für } &d_{u} &= 0,15 - 0,00833 - 0,11554 = 0,02613\\ \text{und für } &d_{o} &= 0,15 + 0,00833 + 0,11554 = 0,27387\\ \end{aligned} \]
Das 95%-Konfidenzintervall für die geschätzte Differenz von 15% zwischen den Bundesländern A und B wird begrenzt von den Werten 2,6% und 27,4%. Dies ist ein recht „breites" Intervall, d.h. die Aussage ist ziemlich unscharf (Wir erinnern uns, dass wir um die Intervalllänge zu verringern die Stichproben vergrößern müssen!). Nehmen wir an, die Differenz zwischen den Bundesländern hätte lediglich 7% betragen, da in Land B 48 von 150 Befragten Zuzahlungen leisten müssen (dies sollte zu Übungszwecken einmal nach gerechnet werden!), dann hätte sich das folgende Intervall ergeben: für die untere Grenze: -0,05 und für die obere Grenze +0,19
Errechnet sich ein Intervall, welches die „0" einschließt, bedeutet dies, dass der wahre Unterschied auch „0" sein könnte. Anders ausgedrückt, kann bei einer gefundenen Differenz von 7% zwischen den beiden Bundesländer nicht sicher genug ausgeschlossen werden, dass der Unterschied nicht zufällig entstanden ist. Der Unterschied ist nicht bedeutsam (signifikant). Würde man jetzt einen entsprechenden Sifnifikanztest durchführen, wie wir sie im nächsten Kapitel besprechen werden, müßte dieser ebenfalls ein nicht signifikantes Ergebnis liefern.
Bemerkung:
Konfidenzgrenzen für den Unterschied zweier Mittelwerte werden hier nicht besprochen. Wichtig hierbei ist, dass es zwei unterschiedliche Formeln zur Bestimmung gibt (siehe Lorenz (1996)), deren Anwendung sich danach richtet, ob die Varianzen der beiden Stichproben gleich (homogen) oder unterschiedlich (heterogen) sind. Kommen wir jetzt zu den bereits erwähnten Signifikanztests.