5 Bivariate Statistik
In den bisherigen Abschnitten haben wir uns mit der Beschreibung und Darstellung von einem Merkmal mit seinen Ausprägungen beschäftigt. In der Praxis liegt das Interesse häufig darin herauszufinden, ob es einen Zusammenhang oder eine Beziehung zwischen zwei (oder mehr) Merkmalen gibt.
Nehmen wir als fiktives Beispiel eine Dekubitusstudie, in der der Zustand der Haut, die Größe des Hautdefektes und die durchgeführte Dekubitusprophylaxe festgehalten wird. In einem solchen Beispiel könnte man den Dekubitus als eine Art von “Supermerkmal” bezeichnen, dass sich aus vielen verschiedenen Einzelkomponenten zusammensetzt. Man spricht dann von einem mehrdimensionalen Merkmal. Im Rahmen dieses Skriptes werden wir uns allerdings auf die Beschreibung von bivariaten Häufigkeitsverteilungen beschränken.
Der einfachste Fall einer solchen Verteilung liegt vor, wenn wir zwei Merkmale betrachten, die jeweils nur zwei Ausprägungen besitzen. Nehmen wir die Merkmale “Geschlecht” mit den Ausprägungen “weiblich und männlich” und “Rauchen” wobei wir nur zwischen Raucher und Nichtraucher unterscheiden. Es gibt dann insgesamt nur vier Kombinationsmöglichkeiten und jeder Proband kann eindeutig einer dieser Gruppen zugeordnet werden:
Weibliche Raucher
Weibliche Nichtraucher
Männliche Raucher
Männliche Nichtraucher
Für die übersichtliche Darstellung bieten sich sogenannte Kontingenztafeln an, die sich aus Reihen und Spalten zusammensetzen, in denen die Merkmale mit ihren Ausprägungen eingetragen werden können.
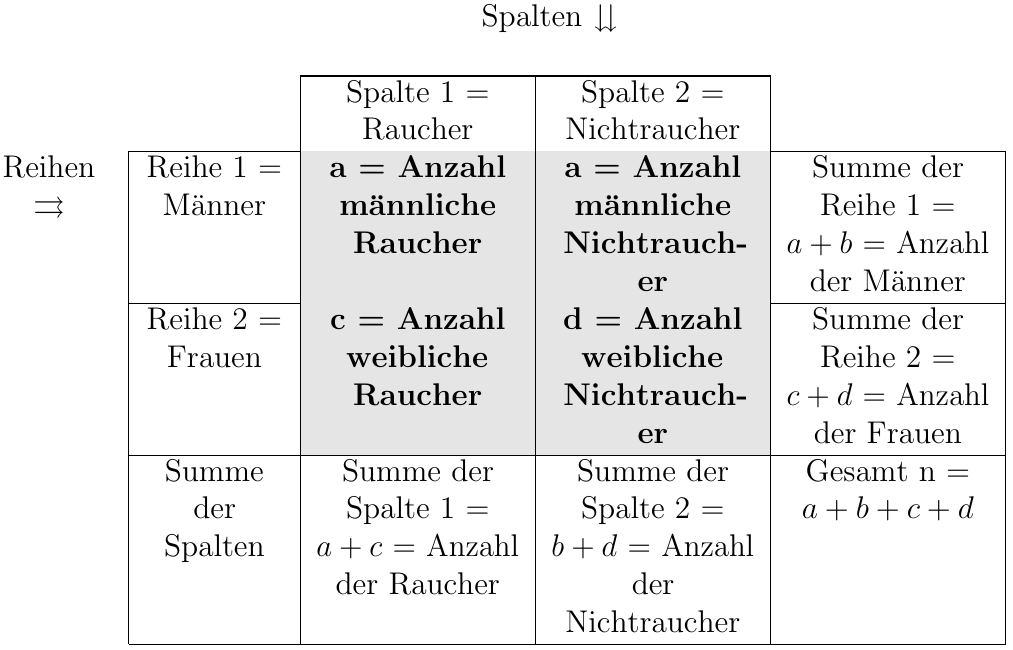
Die schwarz umrandeten Felder in der Mitte der Tabelle nennt man Zellen. Sie ergeben sich aus dem “Schnittpunkt” der Reihen und Spalten. In unserem Beispiel spricht man von einer 2x2 Felder-Tafel (allgemein r x s Tafel, für r = Anzahl der Reihen und s = Anzahl der Spalten). Da es sich in diesem Fall um nominale Merkmale handelt, ist die Anordnung der Merkmalsausprägung frei wählbar. Bei ordinalen oder metrischen Variablen, muß natürlich die Rang- bzw. Reihenfolge eingehalten werden. Nachfolgend findet sich eine Liste von Noten der Vorprüfung und der Abschlußprüfung von 20 Auszubildenden einer Krankenpflegeschule.

Die Anordnung der Merkmalsausprägung (hier die Noten von 1 bis 5) sind durch die Rangfolge vorgegeben.
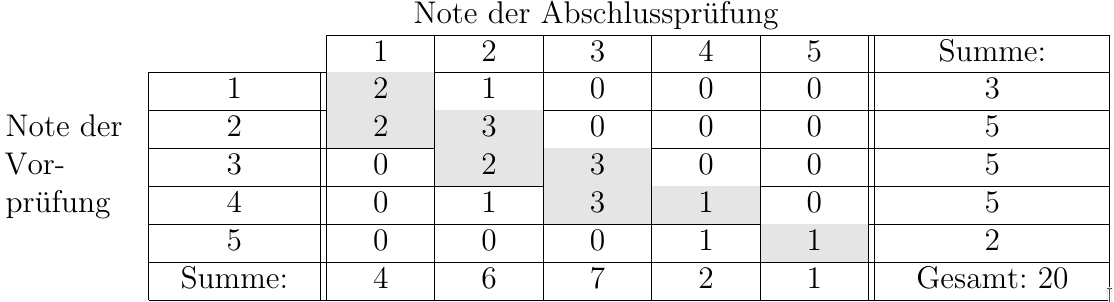
Das Lesen einer solchen Darstellung:
Es gibt z.B. 3 Auszubildende, die sowohl in der Vor- als auch in der Abschlußprüfung die Note “2” erzielten (2. Reihe, 2. Spalte) und 3 Personen, die in der Vorprüfung die Note “4” und in der Abschlußprüfung die Note “3” erhielten (4. Reihe, 3. Spalte). Weiterhin lässt die Darstellung die Vermutung zu, dass es einen Zusammenhang zwischen der Vorprüfung und der Abschlußprüfung gibt. Dafür spricht die stärkere Besetzung der Felder in der Diagonalen oder nahe der Diagonalen.
5.0.1 Der Zusammenhang zweier Merkmale
Greifen wir noch einmal das Beispiel “Rauchen und Geschlecht” auf. Nehmen wir an, die Stichprobe besteht aus 300 Probanden (100 Frauen und 200 Männer), von denen die Hälfte Raucher und die andere Hälfte Nichtraucher sind. Wenn es nun keinen Zusammenhang zwischen dem Merkmal Geschlecht und dem Rauchverhalten gibt, würden wir erwarten, dass sowohl die Hälfte der untersuchten Frauen als auch die Hälfte der Männer Raucher sind. In der nachfolgenden Abbildung 5.4 sind die Häufigkeiten, wie man sie bei Unabhängigkeit der Merkmale erwarten würde, dargestellt.
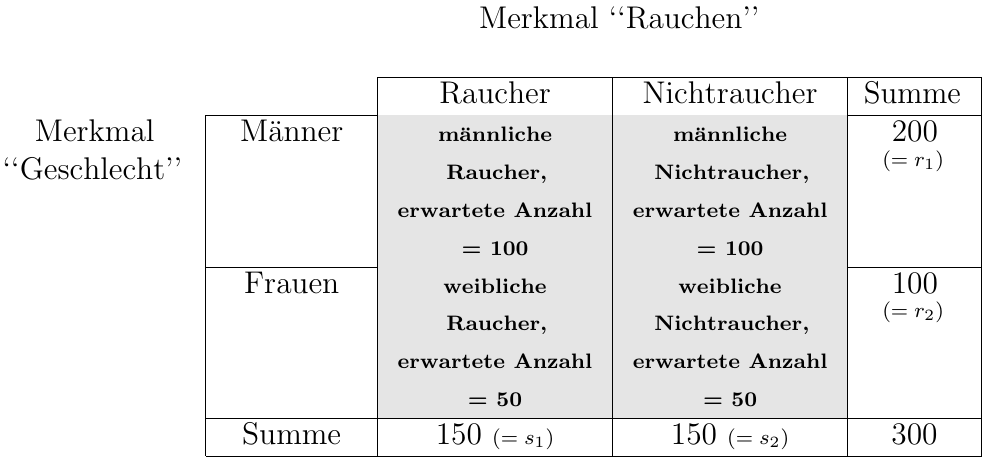
Natürlich sind die Verhältnisse bei tatsächlichen Untersuchungen nicht so “rund und glatt” und auf einen Blick sichtbar. Die erwarteten Häufigkeiten ergeben sich für die einzelnen Zellen, indem man die entsprechende Reihensumme mit der Spaltensumme multipliziert und dann durch die Gesamtzahl dividiert.
So errechnet sich zum Beispiel die erwartete Anzahl für die Zelle “männliche Raucher”: \[\frac{Summe_{Reihe 1} \cdot Summe_{Spalte 1}}{Summe_{Gesamt}}\quad\quad \text{bzw.}\quad\quad \frac{r_{1} \cdot s_{1}}{n}\]
Setzen wir die entsprechenden Zahlen ein, ergibt sich:
\[\frac{200 \cdot 150}{300} = 100\]
Die allgemeine Formel zur Berechnung der erwarteten Häufigkeiten für die Zelle der i-ten Reihe und j-ten Spalte (\(Z_{i,j}\)) lautet:
\[\begin{aligned} Z_{i,j} = \frac{r_{i} \cdot s_{j}}{n} \end{aligned}\]
Nachdem die erwarteten Häufigkeiten für alle vier Felder bestimmt sind, vergleichen wir diese jetzt mit den tatsächlich beobachteten Werten (130 männliche Raucher, 70 männliche Nichtraucher, 20 weibliche Raucher, 80 weibliche Nichtraucher):
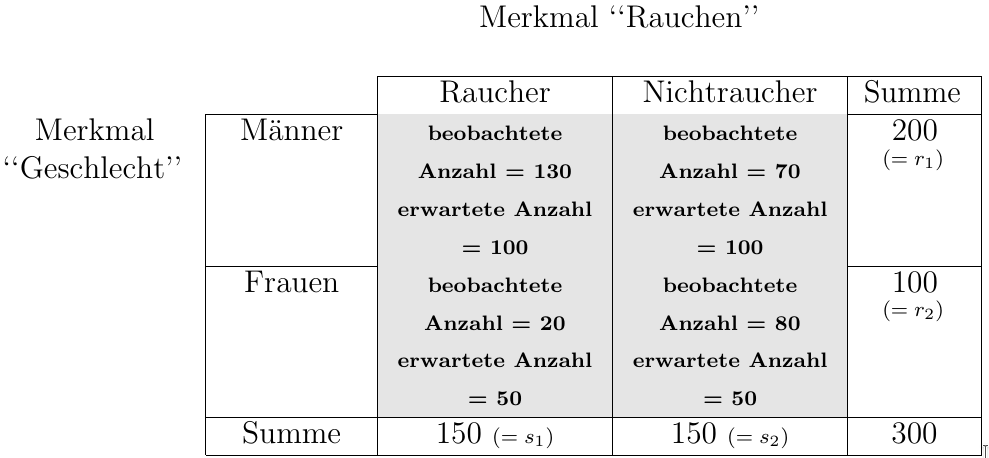
Die tatsächlich beobachteten weichen von den erwarteten Häufigkeiten ab. Dies spricht für einen Zusammenhang zwischen den Merkmalen “Geschlecht und Rauchen”. Der Anteil rauchender Männer ist größer als erwartet, bzw. der Anteil rauchender Frauen ist geringer als erwartet. Anders ausgedrückt: Würden die beobachteten mit den erwarteten Häufigkeiten übereinstimmen, so spräche dies für die Unabhängigkeit der beiden Merkmale.
Anmerkung
An dieser Stelle wird immer die Frage gestellt:
“Wie groß müssen die Abweichungen zwischen beobachteten und erwarteten Häufigkeiten denn sein, um von einem Zusammenhang sprechen zu können?”
Dies ist Inhalt eines späteren Kapitels sein, welches sich mit Signifikanztesten beschäftigt. Dort werden u.a. Verfahren zur Überprüfung der Unabhängigkeit von Merkmalen behandelt.
5.0.2 Die Stärke des Zusammenhanges zweier Merkmale
Bei der Berechnung der Stärke des Zusammenhanges kommt wiederum dem Skalenniveau der Daten entscheidende Bedeutung zu. Die folgende Tabelle gibt einen Überblick über einige Zusammenhangsmaße:
| Skalenniveau der Daten | Bezeichnung des Zusammenhangs | Kenngröße des Zusammenhangs |
|---|---|---|
| nominal (2x2-Felder-Tafel) | Assoziation/Kontingenz | Assoziationskoeffizient/Kontingenzkoeffizient |
| ordinal | Rangkorrelation | Rangkorrelationskoeffizient |
| metrisch | Maßkorrelation | Maßkorrelationskoeffizient |
In diesem Skript werden wir uns mit der
Rangkorrelation nach Spearman für ordinales Skalenniveau und der
Maßkorrelation nach Bravais-Pearson für metrische Daten befassen
Zudem beschränken wir uns auf die Beschreibung von linearen Zusammenhängen.
Bevor wir mit der Berechnung von Korrelationskoeffizienten beginnen, müssen wir uns zunächst mittels einer graphischen Darstellung davon überzeugen, dass ein linearer Zusammenhang vorliegt. Nehmen wir als Beispiel die Frage:
“Gibt es bei Kindern einen Zusammenhang zwischen Leistungen bei der Rechtschreibung und beim Lesen?”
Nachfolgend finden sich in der Tabelle die Punkte, die 10 Schüler in einem Rechtschreibtest (\(x_{i}\)) und in einem Lesetest (\(y_{i}\)) erreichten.
| Schüler | a | b | c | d | e | f | g | h | i | j |
|---|---|---|---|---|---|---|---|---|---|---|
| Lesetest \(x_{i}\) | 2 | 12 | 7 | 15 | 10 | 4 | 13 | 9 | 16 | 19 |
| Rechtschreibung \(y_{i}\) | 3 | 14 | 9 | 17 | 12 | 4 | 16 | 12 | 18 | 20 |
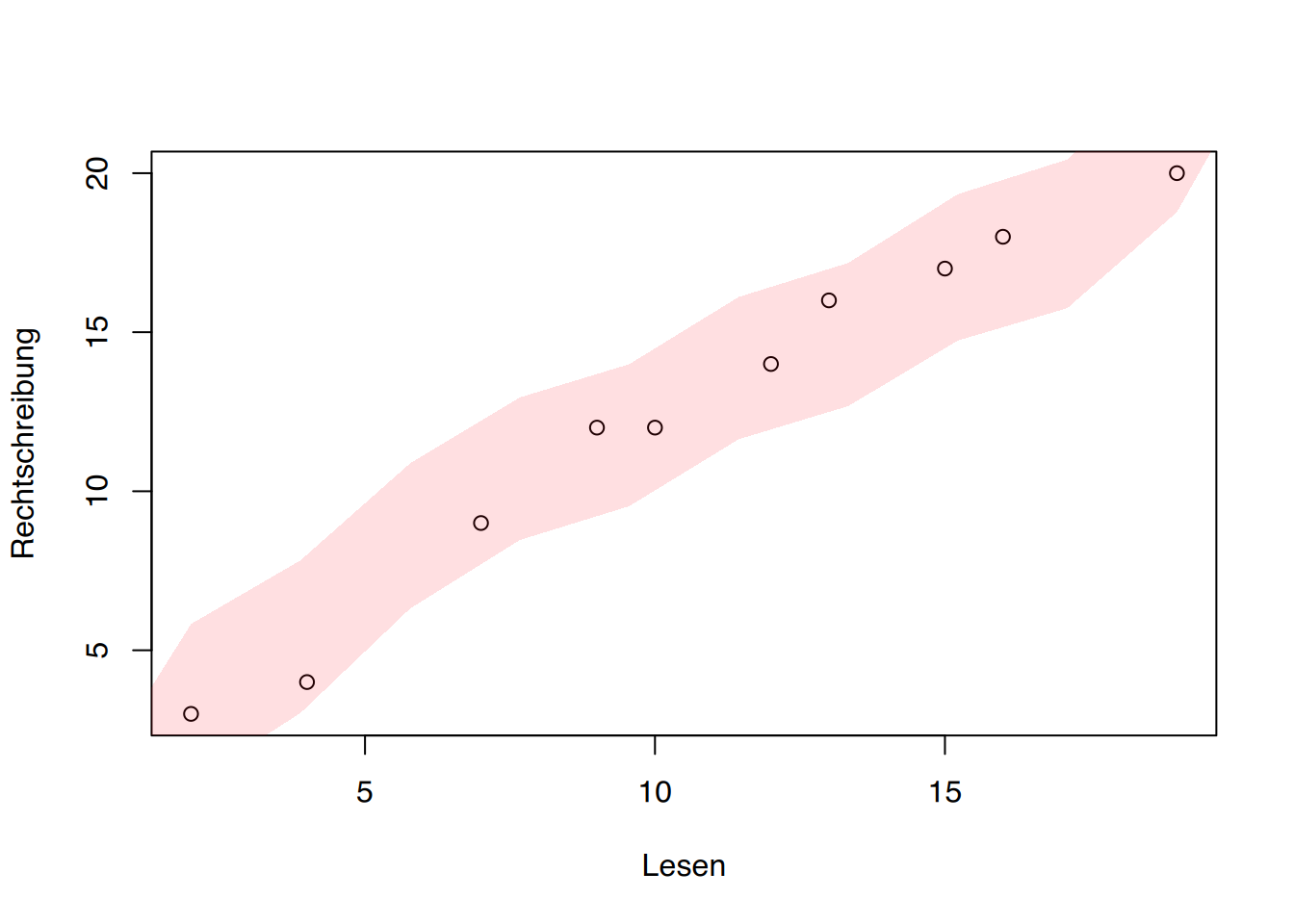
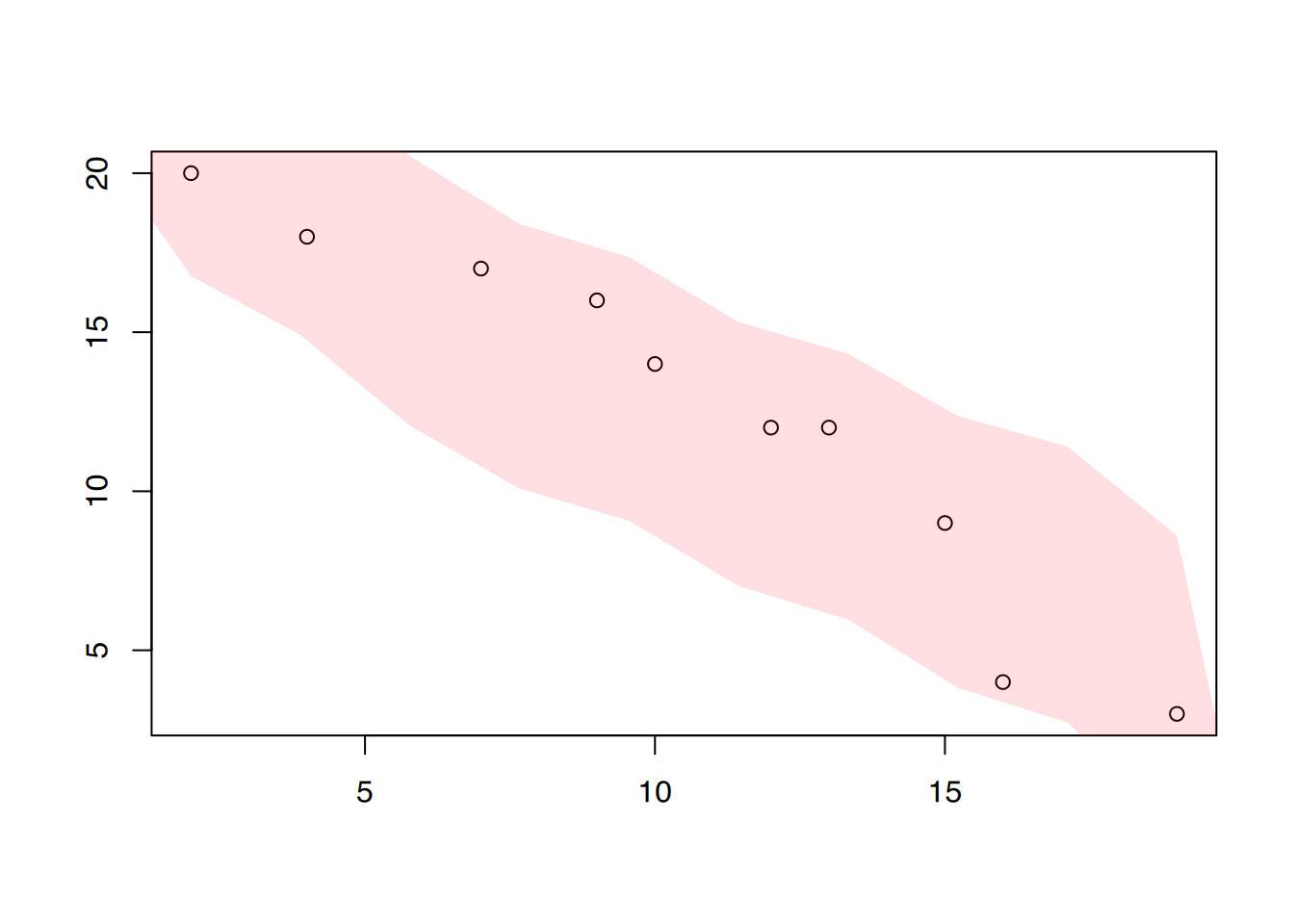
Zeichnet man die Wertepaare (x,y) in ein Koordinatensystem, so ergibt sich das Streudiagramm aus Abbildung 5.6, auch Scatterplot oder Punktwolke genannt. Zunächst einmal lässt sich durch ein solches Streudiagramm feststellen, inwieweit von einem linearen Zusammenhang ausgegangen werden kann.
Zur Verdeutlichung der Punktwolke zeichnet man eine Linie um die Punkte. Je “enger” oder auch ausgeprägter die Ellipsenform der Punktwolke, um so enger ist der Zusammenhang. Steigt die Punktwolke an, d.h. niedrige Punkte beim Schreiben gehen mit ebenfalls niedrigen Punkten beim Lesen, bzw. hohe Punktzahl beim Schreiben mit hoher Punktzahl beim Lesen einher, spricht man von einem positiven Zusammenhang. Einen sogenannten negativen Zusammenhang (Abbildung 5.6 (b)) findet man beispielsweise in dem Fall, dass aus der zunehmenden Dosierung eines blutdrucksenkenden Medikaments entsprechend sinkende Blutdruckwerte resultieren.
Erst nach der Feststellung, dass ein Zusammenhang, und zwar ein linearer Zusammenhang vorliegt, ist es sinnvoll, die Stärke des Zusammenhangs zu berechnen. Sowohl für den Maß-, als auch für den Rangkorrelationskoeffizienten gilt, dass sie Werte im Bereich von -1 bis + 1 annehmen können. Je näher der Korrelationskoeffient bei Eins liegt (sowohl -1 als auch + 1), um so stärker ist der Zusammenhang der beiden Variablen. Von einem schwachen, bzw. keinem Zusammenhang spricht man bei Annäherung des Wertes an Null.
Bleiben wir bei dem Beispiel des Rechtschreib- und Lesetests (Tabelle 5.2). Wie wir später sehen werden, errechnet sich hier ein Korrelationskoeffizient von 0,98. Dies bedeutet, dass es einen besonders starken Zusammenhang zwischen Rechtschreib- und Lesefähigkeiten gibt. Allerdings sagt ein Korrelationskoeffizient nichts über die Ursache des Zusammenhanges aus.
Folgende Möglichkeiten müssen in Betracht gezogen werden:
Beeinflusst die Rechtschreibfähigkeit (R) das Lesen (L)? oder
Hat die Lesefähigkeit Einfluss auf die Rechtschreibung? oder
Beeinflussen sich Lesen und Schreiben gegenseitig? oder
Werden Lese- und Schreibfähigkeiten von einer dritten oder weiteren Variablen wie z.B. Intelligenz oder Alter beeinflusst?
Allgemeiner Ausgedrückt:

Achtung: Nicht selten kommt es zu sogenannten “Scheinkorrelationen” oder “Nonsenskorrelationen”, wie bei Lorenz (1996) am Beispiel der Korrelation zwischen “Anzahl nistender Störche” und “Anzahl der Neugeborenen” sehr anschaulich beschrieben.
5.0.3 Der Maßkorrelationskoeffizient nach Pearson (\(r_{p}\))
Der Maßkorrelationskoeffizient nach Pearson (genau genommen nach Bravais-Pearson) eignet sich prinzipiell nur für metrische Daten und kann für Stichproben ungeachtet ihrer Verteilungseigenschaften berechnet werden. Bei der Berechnung von Pearson’s Maßkorrelationskoeffizient bedienen wir uns der Kovarianz \(cov (x,y)\) als Hilfsgröße.
\[\begin{aligned} r_{p} = \frac{cov(x,y)}{s_{x}\cdot s_{y}} \quad\quad\quad\text{wobei}\quad\quad\quad cov(x,y) = \frac{\sum{(x_{i} - \bar{x}) \cdot (y_{i} - \bar{y})}}{n - 1} \label{formel:rp} \end{aligned}\]
Für die Punktwerte aus unserem Beispiel (Schreib- und Lesetest) ergeben sich folgende Größen:
| \(\mathbf{x_{i}}\) | \(\mathbf{y_{i}}\) | \(\mathbf{(x_{i} - \bar{x})}\) | \(\mathbf{(x_{i} - \bar{x})^2}\) | \(\mathbf{(y_{i} - \bar{y})}\) | \(\mathbf{(y_{i} - \bar{y})^2}\) | \(\mathbf{(x_{i} - \bar{x}) \cdot (y_{i} - \bar{y})}\) |
|---|---|---|---|---|---|---|
| 2 | 3 | -8,7 | 75,69 | -9,5 | 90,25 | 82,65 |
| 4 | 4 | -6,7 | 44,89 | -8,5 | 72,25 | 56,95 |
| 7 | 9 | -3,7 | 13,69 | -3,5 | 12,25 | 12,95 |
| 9 | 12 | -1,7 | 2,89 | -0,5 | 0,25 | 0,85 |
| 10 | 12 | -0,7 | 0,49 | -0,5 | 0,25 | 0,35 |
| 12 | 14 | 1,3 | 1,69 | 1,5 | 2,25 | 1,95 |
| 13 | 16 | 2,3 | 5,29 | 3,5 | 12,25 | 8,05 |
| 15 | 17 | 4,3 | 18,49 | 4,5 | 20,25 | 19,35 |
| 16 | 18 | 5,3 | 28,09 | 5,5 | 30,25 | 29,15 |
| 19 | 20 | 8,3 | 68,89 | 7,5 | 56,25 | 62,25 |
Die benötigten Werte errechnen sich nun wie folgt (siehe hierzu auch Abbildung 11.2 im Anhang):
\[ \begin{aligned} \bar{y} = \frac{\sum{y_{i}}}{n} = \frac{125}{10} = 12,5 \quad \quad \quad \quad \bar{x} = \frac{107}{10} = 10,7\\\\ \end{aligned}\] \[\begin{aligned} s_{y}^2 &= \frac{\sum{(y_{i} - \bar{y})^2}}{n - 1} = \frac{296,5}{9} = 32,94 \quad\quad\text{und}\quad &s_{y} = \sqrt{32,94} = 5,74 \\\\ %\end{eqnarray*} %\begin{eqnarray*} s_{x}^2 &= \frac{\sum{(x_{i} - \bar{x})^2}}{n - 1} =\frac{260,1}{9} = 28,9 \quad\quad\text{und}\quad &s_{x} = \sqrt{28,9} = 5,38 \\ \end{aligned}\] \[\begin{aligned} cov(x,y) = \frac{\sum{(x_{i} - \bar{x}) \cdot (y_{i} - \bar{y})}}{n - 1} = \frac{274,5}{9} = 30,5 \end{aligned} \]
Setzen wir die errechneten Größen in die Formel für den Maßkorrelationskoeffizienten ein, ergibt sich:
\[r_{p} = \frac{cov(x,y)}{s_{x}\cdot s_{y}} = \frac{30,5}{5,74 \cdot 5,38} = 0,9876\]
Wie bereits besprochen, kann \(r\) Werte zwischen -1 und +1 annehmen. Auf unser Beispiel angewendet bedeutet dies, dass es einen sehr starken Zusammenhang zwischen Lese- und Rechtschreibfähigkeiten gibt. Nehmen wir jetzt an, wir hätten Zweifel daran, dass die Punkte der beiden Teste metrisch skaliert sind. In einem solchen Fall weichen wir auf den Rangkorrelationskoeffizienten für ordinales Skalenniveau aus.
5.0.4 Der Rangkorrelationskoeffizient nach Spearman (\(r_{s}\))
Wie man aus dem Namen Rangkorrelationskoeffizient schon ableiten kann, spielen die Ränge, bzw. die Rangplätze der Daten eine entscheidende Rolle bei der Berechnung von Spearman’s Rho. Er bietet sich für ordinale oder aber für metrische, nicht normalverteilte Daten an. Bleiben wir bei unserem Beispiel der Schreib- und Leserfähigkeit der Schüler. Der erste Schritt zur Bestimmung des Rangkorrelationskoeffizienten besteht darin, den einzelnen Punktwerten - für jede Variable getrennt - Rangplätze zu zuordnen. Da bei der Berechnung der Rangkorrelation die Differenzen der Rangplätze, bzw. die quadrierten Differenzen eine große Rolle spielen, haben wir sie in der nachfolgenden Tabelle mit aufgenommen.
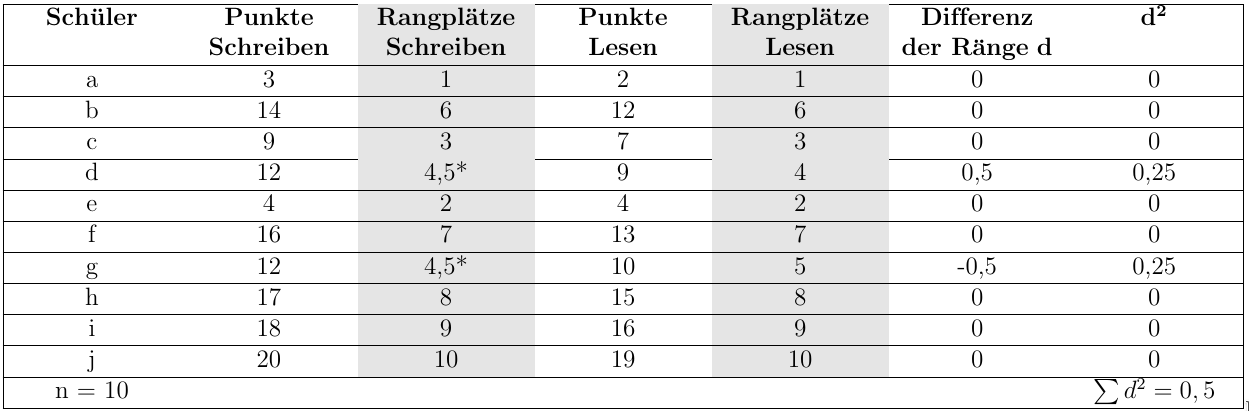
(*) Da der Punktwert “12” zweimal vorkommt, wird hier aus den Ranplätzen vier und fünf der Mittelwert gebildet. Man spricht in einem solchen Fall auch von gebundenen Rängen oder Rangbildungen. Läge der Wert “12” dreimal vor, würde man z.B. den Mittelwert der Rangplätze 4, 5, und 6 entsprechend vergeben. Es muss hier gleich angemerkt werden, dass die Gleichung 5.1 beim Vorliegen von mehr als 20% Rangbindungen nicht mehr angewendet werden darf. Liegen Daten “von Natur” aus auf ordinalem Niveau vor, wie beispielsweise Schulnoten, erhält man beim Zuordnen der Rangplätze sehr schnell einen großen Anteil gebundener Ränge. In den verschiedenen Lehrbüchern finden sich entsprechende Formeln zur Berechnung des Rangkorrelationskoeffizienten unter Berücksichtigung von gebundenen Rängen.
Die allgemeine Formel zur Berechnung der Rangkorrelationskoeffizienten nach Spearman (auch Spearman’s Rho) lautet:
\[\begin{aligned} r_{s} = 1 - \frac{6 \cdot \sum{d^2_{i}}}{n \cdot (n^2 - 1)} \end{aligned} \tag{5.1}\]
Setzen wir die aus Abbildung 5.7 ersichtlichen Werte in diese Formel ein, erhalten wir:
\[\begin{aligned} r_{s} &=& 1 - \frac{6 \cdot 0,5}{10 \cdot (100 - 1)}\\\\ &=& 1 - \frac{3}{990}\\\\ &=& 1 - 0,00303\\ &=& 0,9969\\ \end{aligned}\]
Auch Spearman’s Rho kann Werte zwischen -1 und +1 annehmen, auch hier gilt: je näher an Eins, um so enger/stärker der Zusammenhang. Nähert sich der Wert an Null an, liegt kein bzw. nur ein sehr schwacher Zusammenhang vor. Nachdem wir uns mittels der Korrelationsrechnung mit der Quantifizierung der Stärke des Zusammenhanges zweier Merkmale beschäftigt haben, interessiert im nachfolgenden Kapitel die Art des Zusammenhangs.
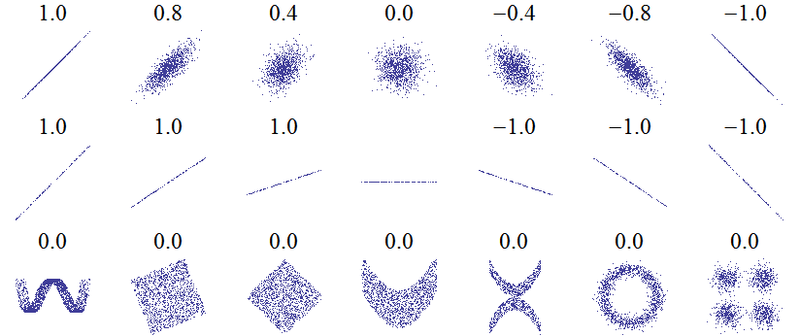
Abschließend sind in Abbildung 5.8 verschiedene Punktwolken mit ihrem Korrelationskoeffizienten angebildet.