5 Wahrscheinlichkeit

Die deskriptive Statistik bietet Methoden zur Beschreibung der in der Probe gemessenen Variablen und ihrer Beziehungen, ermöglicht jedoch keine Schlüsse aus dieser Probe auf die Grundgesamtheit.

Jetzt ist es Zeit, von der Stichprobe zur Grundgesamtheit zu gelangen, und die Brücke dafür ist die Wahrscheinlichkeitstheorie.

Bitte beachten Sie, dass die Stichprobe nur begrenzte Informationen über die Grundgesamtheit hat, und um gültige Schlüsse für diese zu ziehen, muss die Probe repräsentativ sein. Dies ist strenggenommen nur bei Zufallsstichproben gegeben.

Die Wahrscheinlichkeitstheorie wird uns Werkzeuge bieten, um den Zufall in der Stichprobenziehung zu kontrollieren und das Vertrauensniveau der aus der Stichprobe gezogenen Schlüsse zu bestimmen.

5.1 Experiment mit zufälligem Ergebnis

Die Untersuchung einer Eigenschaft der Grundgesamtheit erfolgt durch Experimente mit zufälligem Ergebnis.

Definition “Zufallsexperiment”

Ein Zufallsexperiment ist ein Experiment, das zwei Bedingungen erfüllt:

Alle möglichen Ergebnisse sind bekannt.
Es ist unmöglich, das Ergebnis mit absoluter Sicherheit vorherzusagen.

Beispiel: Glücksspiele

Glücksspiele sind typische Beispiele für Experimente mit zufälligem Ergebnis. Zum Beispiel ist das Werfen eines Würfels ein solches Experiment, weil:

Der Satz der möglichen Ergebnisse bekannt ist: $\{1, 2, 3, 4, 5, 6\}$.
Bevor der Würfel geworfen wird ist es unmöglich das Ergebnis mit absoluter Sicherheit vorherzusagen.

Ein weiteres Beispiel, das nichts mit Glücksspielen zu tun hat, ist die zufällige Auswahl einer Person aus einer menschlichen Grundgesamtheit und die Bestimmung ihrer Blutgruppe.

Grundsätzlich ist die Ziehung einer Stichprobe mittels einer Zufallsmethode ein Zufallsexperiment.

5.1.1 Wahrscheinlichkeitsraum

Definition “Wahrscheinlichkeitsraum $\Omega$”

Der Satz $\Omega$ der möglichen Ergebnisse eines Zufallsexperiments wird als Wahrscheinlichkeitsraum (Probabilitätsraum) bezeichnet.

Beispiele für Probabilitätsräume:

Beim Werfen einer Münze ist $\Omega = \{Kopf, Zahl\}$.
Beim Werfen eines Würfels ist $\Omega = \{1, 2, 3, 4, 5, 6 \}$.
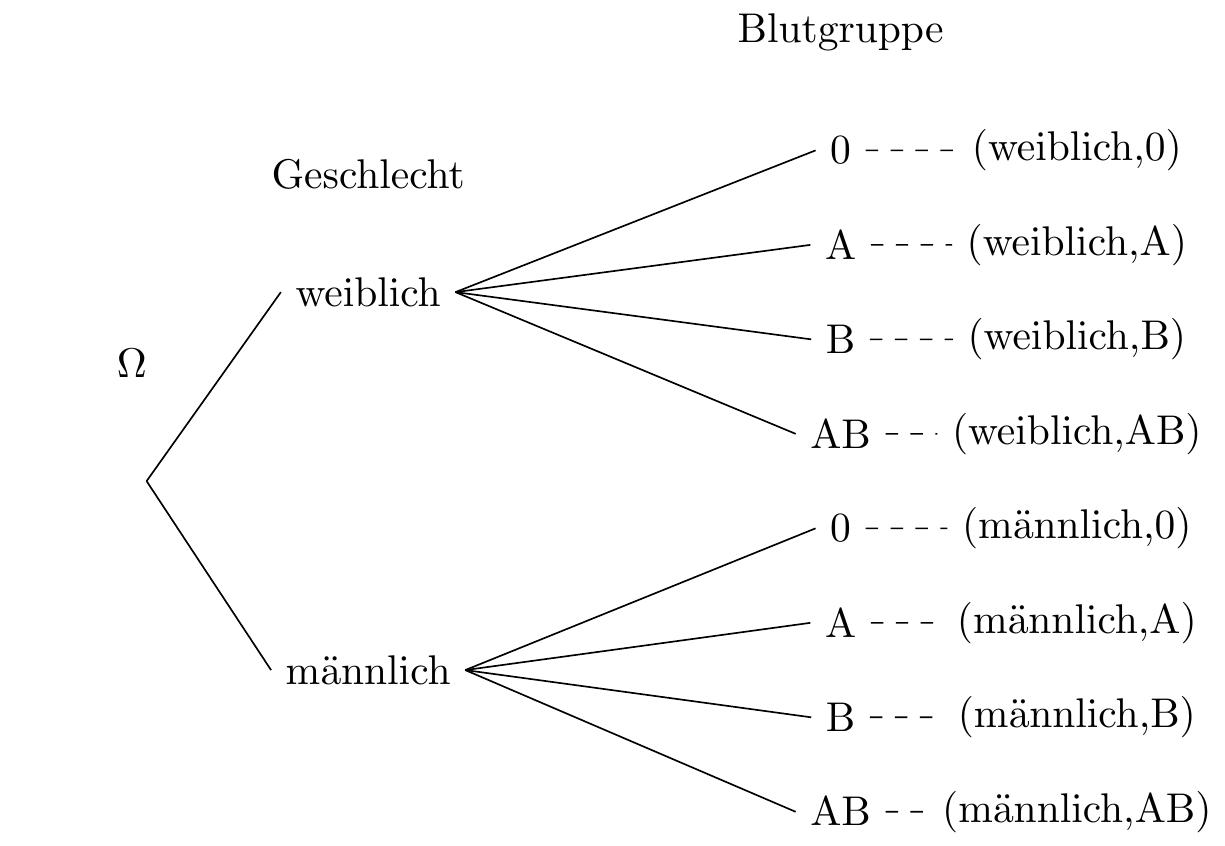
Beim Blutgruppentest einer zufällig ausgewählten Person ist $\Omega = \{0, A, B, AB \}$.
Bei der Körpergröße einer zufällig ausgewählten Person ist $\Omega=\mathbb{R}^+$.

5.1.2 Baumdiagramme

In Experimenten, bei denen mehr als eine Variable gemessen wird, kann die Bestimmung des Wahrscheinlichkeitsraums schwierig sein. In solchen Fällen ist es ratsam, ein Baumdiagramm zur Konstruktion des Probabilitätsraums zu verwenden.

In einem Baumdiagramm wird jede Variable auf einer Ebene des Baums dargestellt und jeder mögliche Wert der Variablen als Zweig.

5.1.3 Zufallsereignis

Definition Zufallsereignis

Ein zufälliges Ereignis ist jede Teilmenge des Probabilitätsraums $\Omega$ eines Zufallsexperimentes.

Es gibt verschiedene Arten von Ereignissen:

unmögliches Ereignis: Dies ist das Ereignis ohne Elemente $\emptyset$. Es hat keine Chance einzutreten.
elementare Ereignisse: Dies sind Ereignisse mit nur einem Element.
zusammengesetzte Ereignisse: Dies sind Ereignisse mit zwei oder mehr Elementen.
sicheres Ereignis: Dies ist das Ereignis, das den gesamten Probabilitätsraum $\Omega$ enthält. Es tritt immer ein.

5.2 Mengentheorie

5.2.1 Ereignisraum

Definition 32 Ereignisraum

Gegeben einen Wahrscheinlichkeitsraum $\Omega$ eines Zufallsexperimentes, ist die Ereignismenge von $\Omega$ die Menge aller möglichen Ereignisse von $\Omega$ und wird mit $\mathcal{P}(\Omega)$ bezeichnet.

Beispiel

Für den Probabilitätsraum $\Omega=\{a,b,c\}$ ist dessen Ereignismenge:

\[ \mathcal{P}(\Omega)=\left\{\emptyset, \{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\right\} \]

5.2.2 Ereignisoperationen

Da Ereignisse Teilmengen des Wahrscheinlichkeitsraums sind, haben wir mittels der Mengentheorie folgende Operationen an Ereignissen:

Vereinigung
Schnittmenge
Komplementärmenge
Differenzmenge

5.2.2.1 Vereinigung von Ereignissen

Definition “Vereinigungsereignis”

Gegeben zwei Ereignisse $A,B\subseteq \Omega$, ist die Vereinigung von $A$ und $B$, bezeichnet mit $A\cup B$, das Ereignis aller Elemente, die Mitglieder von $A$ oder $B$ oder beiden sind.

\[ A\cup B = \{x\,|\, x\in A\textrm{ oder }x\in B\}. \]

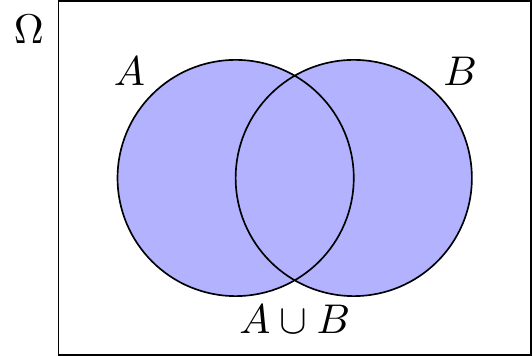
Das Vereinigungsereignis $A,B\subseteq \Omega$ tritt ein, wenn $A$ oder $B$ eintreten.

5.2.2.2 Schnittereignis

Definition “Schnittereignis”

Angenommen, wir haben zwei Ereignisse $A$ und $B$, die Teilmengen von $\Omega$ sind. Das Schnittereignis (Intersection) von $A$ und $B$, bezeichnet mit $A\cap B$, ist das Ereignis aller Elemente, die sowohl zu $A$ als auch zu $B$ gehören.

\[ A\cap B = \{x\,|\, x\in A\mbox{ und }x\in B\}. \]

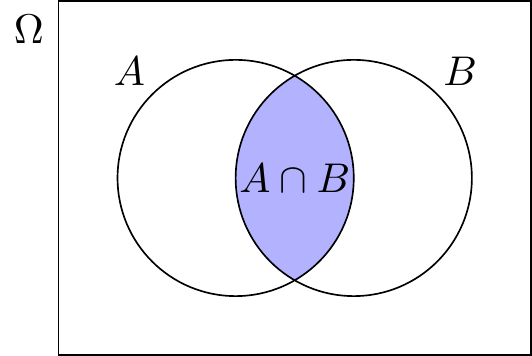
Das Ereignis $A\cap B$ tritt ein, wenn sowohl $A$ als auch $B$ eintreten. Zwei Ereignisse sind unmöglich, wenn ihr Schnitt leer ist.

5.2.2.3 Komplementärereignis

Definition “Komplementärereignis”

Angenommen, wir haben ein Ereignis $A$, das eine Teilmenge von $\Omega$ ist. Das komplementäre oder gegensätzliche Ereignis zu $A$, bezeichnet mit $\overline A$, ist das Ereignis aller Elemente in $\Omega$ außer denjenigen, die zu $A$ gehören.

\[ \overline A = \{x\,|\, x\not\in A\}. \]

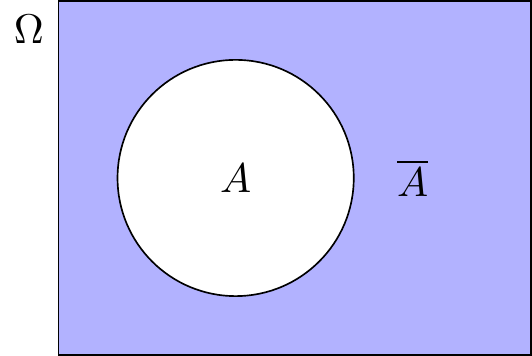
Das komplementäre Ereignis $\overline A$ tritt ein, wenn $A$ nicht eintritt.

5.2.2.4 Differenzereignis

Definition “Differenzereignis”

Gegeben sind zwei Ereignisse $A$ und $B$ als Teilmengen von $\Omega$. Die Differenz von $A$ und $B$, bezeichnet mit $A-B$, ist das Ereignis aller Elemente, die zu $A$ gehören, aber nicht zu $B$.

\[ A-B = \{x\,|\, x\in A\mbox{ und }x\not\in B\} = A \cap \overline B. \]

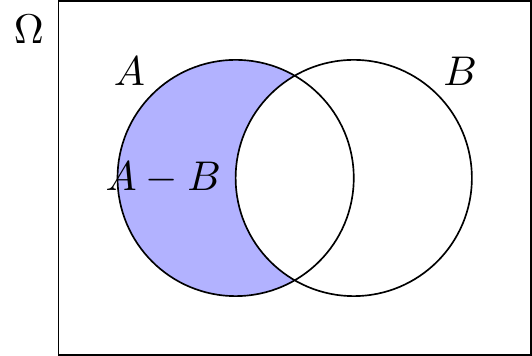
Das Differenzereignis $A-B$ tritt ein, wenn $A$ eintritt, aber $B$ nicht.

5.2.2.5 Beispiel

Beispiel

Der Ereignisraum beim Würfeln ist $\Omega=\{1,2,3,4,5,6\}$ und die Ereignisse sind

$A=\{2,4,6\}$ und
$B=\{1,2,3,4\}$,

dann gilt:

Die Vereinigungsmenge von $A$ und $B$ ist $A\cup B=\{1,2,3,4,6\}$.
Die Schnittmenge von $A$ und $B$ ist $A\cap B=\{2,4\}$.
Das Komplement von $A$ ist $\overline A=\{1,3,5\}$
Die Ereignisse $A$ und $\overline A$ schließen sich gegenseitig aus.
Die Differenz von $A$ und $B$ ist $A-B=\{6\}$ und die Differenz von $B$ und $A$ ist $B-A=\{1,3\}$

5.2.3 Algebra

Sind die Ereignisse $A,B,C\subseteq \Omega$ gegeben, treffen die folgenden algebra’schen Eigenschaften zu:

Idempotenz: $A\cup A=A,\quad A\cap A=A$
Kommutativität: $A\cup B=B\cup A,\quad A\cap B = B\cap A$
Assoziativität: $(A\cup B)\cup C = A\cup (B\cup C),\quad (A\cap B)\cap C = A\cap (B\cap C)$
Distributivität: $(A\cup B)\cap C = (A\cap C)\cup (B\cap C),\quad (A\cap B)\cup C = (A\cup C)\cap (B\cup C)$
Neutrales Element: $A\cup \emptyset=A,\quad A\cap \Omega=A$
absorbierendes Element: $A\cup \Omega=\Omega,\quad A\cap \emptyset=\emptyset$
komplementäres symmetrisches Element $A\cup \overline A = \Omega,\quad A\cap \overline A= \emptyset$
doppelte Negation: $\overline{\overline A} = A$
De Morgansche Gesetze: $\overline{A\cup B} = \overline A\cap \overline B,\quad \overline{A\cap B} = \overline A\cup \overline B$

5.3 Wahrscheinlichkeit

Defintion “Wahrscheinlichkeit” (nach Laplace)

Für ein Zufallsexperiment mit einem Ereignisraum $\Omega$, dessen Elemente alle gleich wahrscheinlich sind, ist die Wahrscheinlichkeit eines Ereignisses $A\subseteq \Omega$ der Quotient zwischen der Anzahl der Elemente von $A$ und der Anzahl der Elemente von $\Omega$

\[ P(A) = \frac{|A|}{|\Omega|} = \frac{\mbox{Anzahl gewünschter Ergebnisse}}{\mbox{Anzahl aller möglichen Ergebnisse}} \]

Diese Definition ist gut bekannt, hat aber wichtige Einschränkungen:

Es wird verlangt, dass alle Elemente des Ereignisraums gleich wahrscheinlich sind (Gleichwahrscheinlichkeit).
Sie kann nicht bei unendlichen großen Ereignisräumen angewendet werden.

Vorsicht!

Diese Bedingungen werden in vielen echten Experimenten nicht erfüllt.

Beispiel

Angenommen, der Ereignisraum beim Werfen eines Würfels ist $\Omega=\{1,2,3,4,5,6\}$ und das Ereignis $A=\{2,4,6\}$, dann beträgt die Wahrscheinlichkeit von $A$

\[ P(A) = \frac{|A|}{|\Omega|} = \frac{3}{6} = 0.5. \]

Allerdings ist es beim Ereignisraum der Blutgruppe einer zufällig ausgewählten Person $\Omega=\{O,A,B,AB\}$ nicht möglich, die klassische Definition zu verwenden, um die Wahrscheinlichkeit für Gruppe $A$ zu berechnen,

\[ P(A) \neq \frac{|A|}{|\Omega|} = \frac{1}{4} = 0.25, \]

…weil Blutgruppen in der menschlichen Bevölkerung nicht gleich wahrscheinlich sind.

5.3.1 Häufigkeitswahrscheinlichkeit

Definition “Gesetz der großen Zahlen”

Wenn ein zufälliges Experiment eine große Anzahl von Malen wiederholt wird, nähert sich die relative Häufigkeit eines Ereignisses der Wahrscheinlichkeit des Ereignisses an.

Die folgende Definition der Wahrscheinlichkeit basiert auf diesem Satz.

Definition “Frequenzwahrscheinlichkeit”

Gegeben ein Ereignisraum $\Omega$ eines reproduzierbaren zufälligen Experiments, beträgt die Wahrscheinlichkeit eines Ereignisses $A\subseteq \Omega$ die relative Häufigkeit des Ereignisses $A$ bei einer unbegrenzten Anzahl von Wiederholungen des Experiments.

\[ P(A) = lim_{n\rightarrow \infty}\frac{n_A}{n} \]

Auch diese Definition hat einige Nachteile:

Sie berechnet eine Schätzung der realen Wahrscheinlichkeit.
Die Wiederholung des Experiments muss unter identischen Bedingungen stattfinden.

Beispiel Münzwurf

Gegeben ist der Ereignisraum beim Werfen einer Münze $\Omega=\{Kopf, Zahl\}$. Wenn nach $100$ Würfen 54mal Kopf herauskam, beträgt die Wahrscheinlichkeit von $Kopf$ \[ P(Kopf) = \frac{n_{Kopf}}{n} = \frac{54}{100} = 0.54. \]

Beispiel Blutgruppen

Gegeben ist der Ereignisraum der Blutgruppe einer zufällig ausgewählten Person $\Omega=\{O,A,B,AB\}$. Wenn nach einer Zufallsstichprobe von 1.000 Personen 412 mit der Blutgruppe $A$ dabei waren, beträgt die Wahrscheinlichkeit von $A$

\[ P(A) = \frac{n_A}{n} = \frac{412}{1000} = 0.412. \]

5.3.2 Axiomatische Wahrscheinlichkeit

Definition “Wahrscheinlichkeit” (nach Kolmogórov)

Gegeben ein Ereignisraum $\Omega$ eines zufälligen Experiments, ist eine Wahrscheinlichkeitsfunktion eine Funktion, die jeden Ereigniswert $A\subseteq \Omega$ auf eine reelle Zahl $P(A)$ (bekannt als Wahrscheinlichkeit von $A$), abbildet und folgende Axiome erfüllt:

Die Wahrscheinlichkeit jedes Ereignisses ist nicht negativ, \[ P(A)\geq 0. \]
Die Wahrscheinlichkeit des Ereignisraums beträgt 1, \[ P(\Omega)=1 \]
Die Wahrscheinlichkeit der Vereinigung zweier inkompatibler Ereignisse ($A\cap B=\emptyset$) ist die Summe ihrer Wahrscheinlichkeiten \[ P(A\cup B) = P(A)+P(B). \]

5.3.2.1 Eigenschaften der axiomatischen Wahrscheinlichkeit

Aus diesen Axiomen lassen sich einige wichtige Eigenschaften einer Wahrscheinlichkeitsfunktion ableiten. Gegeben ein Ereignisruam $\Omega$ eines zufälligen Experiments und die Ereignisse $A,B\subseteq \Omega$, gelten folgende Eigenschaften:

$P(\overline A) = 1-P(A)$.
$P(\emptyset)= 0$.
Wenn $\ A\subseteq B\ $ dann $\ P(A)\leq P(B)$.
$P(A) \leq 1\ $. Das bedeutet $\ P(A)\in [0,1]$.
$P(A-B)=P(A)-P(A\cap B)$.
$P(A\cup B)= P(A) + P(B) - P(A\cap B)$.
Wenn $\ A=\{e_1,\ldots,e_n\}\ $, und $\ e_i$ $i=1,\ldots,n\ $ Elementarereignisse sind, dann gilt \[ P(A)=\sum_{i=1}^n P(e_i). \]

5.3.3 Wahrscheinlichkeitsinterpretation

Gemäß den vorherigen Axiomen ist die Wahrscheinlichkeit eines Ereignisses $A$ eine reelle Zahl $P(A)$, die stets im Bereich von 0 bis 1 liegt.

Auf gewisse Weise drückt diese Zahl die Glaubwürdigkeit des Ereignisses aus, d.h. die Chancen, dass das Ereignis $A$ in dem Experiment eintritt. Daher gibt sie auch ein Maß für die Unsicherheit bezüglich des Ereignisses an.

Die maximale Unsicherheit entspricht der Wahrscheinlichkeit $P(A) = 0,5\quad$ ($A$ und $\overline A$ haben die gleiche Chance, einzutreten).
Die minimale Unsicherheit entspricht der Wahrscheinlichkeit $P(A) = 1\quad$ ($A$ wird mit absoluter Sicherheit eintreten) und $P(A) = 0\quad$ ($A$ wird mit absoluter Sicherheit nicht eintreten).

Wenn $P(A)$ näher bei $0$ als bei $1$ liegt, sind die Chancen, dass $A$ nicht eintritt, größer als die Chancen, dass $A$ eintritt.

Im Gegensatz dazu, wenn $P(A)$ näher bei $1$ als bei $0$ liegt, sind die Chancen, dass $A$ eintritt, größer als die Chancen, dass $A$ nicht eintritt.

5.4 bedingte Wahrscheinlichkeit

Gelegentlich können wir bereits vor der Durchführung eines Experiments einige Informationen darüber erhalten. Üblicherweise wird diese Information als Ereignis $B$ des gleichen Ereignisraums gegeben, von dem wir wissen, dass es wahr ist, bevor wir das Experiment durchführen.

In einem solchen Fall werden wir sagen, dass $B$ ein konditionierendes Ereignis ist und die Wahrscheinlichkeit eines anderen Ereignisses $A$ als bedingte Wahrscheinlichkeit bezeichnen. Diese wird als $P(A|B)$ ausgedrückt.

Dies muss als “Wahrscheinlichkeit von $A$ unter der Bedingung $B$” oder “Wahrscheinlichkeit von $A$ gegeben $B$” gelesen werden.

Beispiel

Konditionierende Ereignisse ändern normalerweise den Ereignisraum und damit die Wahrscheinlichkeiten der Ereignisse. Angenommen, wir haben eine Stichprobe von 100 Frauen und 100 Männern mit den folgenden Häufigkeiten:

\[ \begin{array}{|c|c|c|} & \mbox{Nichtraucher} & \mbox{Raucher} \\ \hline \rowcolor{coral}\color{white} \mbox{Frauen} & \color{white}80 & \color{white}20 \\ \hline \mbox{Männer} & 60 & 40 \\ \hline \end{array} \]

Dann beträgt die Wahrscheinlichkeit, ein Raucher zu sein, basierend auf der gesamten Probe:

\[ P(\mbox{Raucher})= \frac{60}{200}=0.3. \]

Wenn wir jedoch wissen, dass die Person eine Frau ist, wird die Stichprobe auf die erste Zeile reduziert und die Wahrscheinlichkeit, eine Raucherin zu sein, beträgt:

\[ P(\mbox{Raucherin}|\mbox{Frau})=\frac{20}{100}=0.2. \]

Definition “bedingte Wahrscheinlichkeit”

Gegeben ist ein Ereignisraum $\Omega$ eines zufälligen Experiments und zwei Ereignisse $A,B\subseteq \Omega$, so ist die Wahrscheinlichkeit von $A$ unter der Bedingung, dass $B$ eintritt: \[ P(A|B) = \frac{P(A\cap B)}{P(B)}, \] solange $P(B)\neq 0$.

Diese Definition ermöglicht es, bedingte Wahrscheinlichkeiten zu berechnen, ohne den ursprünglichen Ereignisraum zu ändern.

Beispiel

In dem vorherigen Beispiel ist die bedingte Wahrscheinlichkeit, dass eine Person Raucher und weiblich ist:

\[ P(\mbox{Raucher}|\mbox{weiblich})= \frac{P(\mbox{Raucher}\cap \mbox{weiblich})}{P(\mbox{weiblich})} = \frac{20/200}{100/200}=\frac{20}{100}=0.2. \]

5.4.1 Wahrscheinlichkeit des Schnittmengen-Ereignisses:

Aus der Definition der bedingten Wahrscheinlichkeit kann die Formel für die Wahrscheinlichkeit der Schnittmenge zweier Ereignisse abgeleitet werden:

\[ P(A\cap B) = P(A)P(B|A) = P(B)P(A|B). \]

Beispiel: Brustkrebs

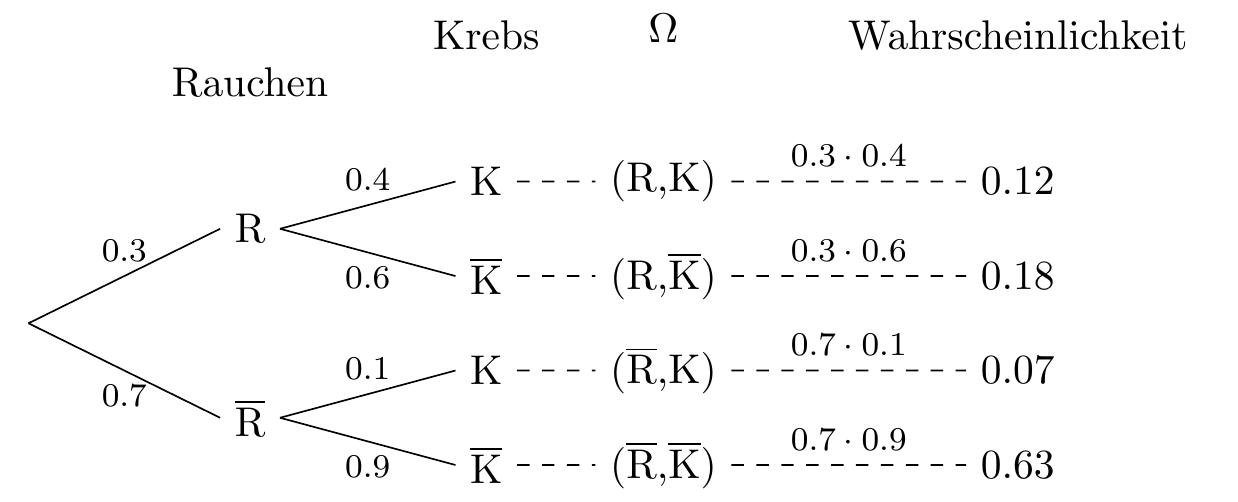
In einer Bevölkerung gibt es 30 % Raucherinnen und wir wissen, dass 40 % dieser Raucher Krebs haben. Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person raucht und Krebs hat, beträgt:

\[ P(\mbox{Raucher}\cap \mbox{Krebs})= P(\mbox{raucher})P(\mbox{Krebs}|\mbox{Raucher}) = 0.3\times 0.4 = 0.12. \]

5.4.2 Unabhängigkeit der Ereignisse

Manchmal ändert das bedingende Ereignis die ursprüngliche Wahrscheinlichkeit des Hauptereignisses nicht.

Definition “Unabhängige Ereignisse”

Gegeben einen Ereignisraum $\Omega$ eines zufälligen Experiments, sind zwei Ereignisse $A,B\subseteq \Omega$ unabhängig, wenn die Wahrscheinlichkeit von $A$ sich nicht ändert, wenn sie durch $B$ bedingt ist, und umgekehrt, d.h.,

\[ P(A|B) = P(A) \quad \mbox{und} \quad P(B|A)=P(B), \] wenn $P(A)\neq 0\ $ und $\ P(B)\neq 0$.

Das bedeutet, dass das Eintreten eines Ereignisses keine relevante Information liefert, um die Unsicherheit des anderen Ereignisses zu ändern.

Wenn zwei Ereignisse unabhängig sind, ist die Wahrscheinlichkeit ihrer Schnittmenge gleich dem Produkt ihrer Wahrscheinlichkeiten,

\[ P(A\cap B) = P(A)\cdot P(B) \]

Beispiel: Münzwurf

Der Ereignisraum für den doppelten Wurf einer Münze ist $\Omega=\{(K,K),(K,Z),(Z,K),(Z,Z)\}$ und alle Elemente sind gleich wahrscheinlich, wenn die Münze fair ist. Daher haben wir durch die klassische Definition der Wahrscheinlichkeit

\[ P((K,K)) = \frac{1}{4} = 0.25. \] Wenn wir $K_1=\{(K,K),(K,Z)\}$, d.h., Kopf beim ersten Wurf, und $H_2=\{(K,K),(Z,K)\}$ nennen, d.h., Kopf beim zweiten Wurf, können wir das gleiche Ergebnis erhalten, indem wir davon ausgehen, dass diese Ereignisse unabhängig sind,

\[ P(K,K)= P(K_1\cap K_2) = P(K_1)\cdot P(K_2) = \frac{2}{4}\cdot\frac{2}{4}=\frac{1}{4}=0.25. \]

5.5 Wahrscheinlichkeitsraum

Definition “Wahrscheinlichkeitsraum”

Ein Wahrscheinlichkeitsraum eines zufälligen Experiments ist ein Tripel $(\Omega,\mathcal{F},P)$ wobei

$\Omega\ $ der Ereignisraum des Experiments ist.
$\mathcal{F}\ $ eine Menge von Ereignissen des Experiments ist.
$P\ $ eine Wahrscheinlichkeitsfunktion ist.

Wenn wir die Wahrscheinlichkeiten aller Elemente von $\Omega$ kennen, können wir leicht den Wahrscheinlichkeitsraum konstruieren und die Wahrscheinlichkeit jedes Ereignisses in $\mathcal{F}$ berechnen.

5.5.1 Konstruktion des Wahrscheinlichkeitsraums

Um die Wahrscheinlichkeit jedes möglichen (elementaren) Ereignisses zu berechnen, können wir ein Baumdiagramm verwenden. Dabei gelten folgende Regeln:

Jede Kante im Baum erhält eine Wahrscheinlichkeit. Diese gibt an, wie wahrscheinlich der jeweilige Wert unter der Bedingung der vorherigen Knoten ist.
Die Wahrscheinlichkeit eines vollständigen Pfads (also eines Ereignisses ganz am Ende des Baums) ergibt sich, indem man die Wahrscheinlichkeiten aller Kanten entlang dieses Pfads miteinander multipliziert – vom Start (Wurzel) bis zum Ende (Blatt).

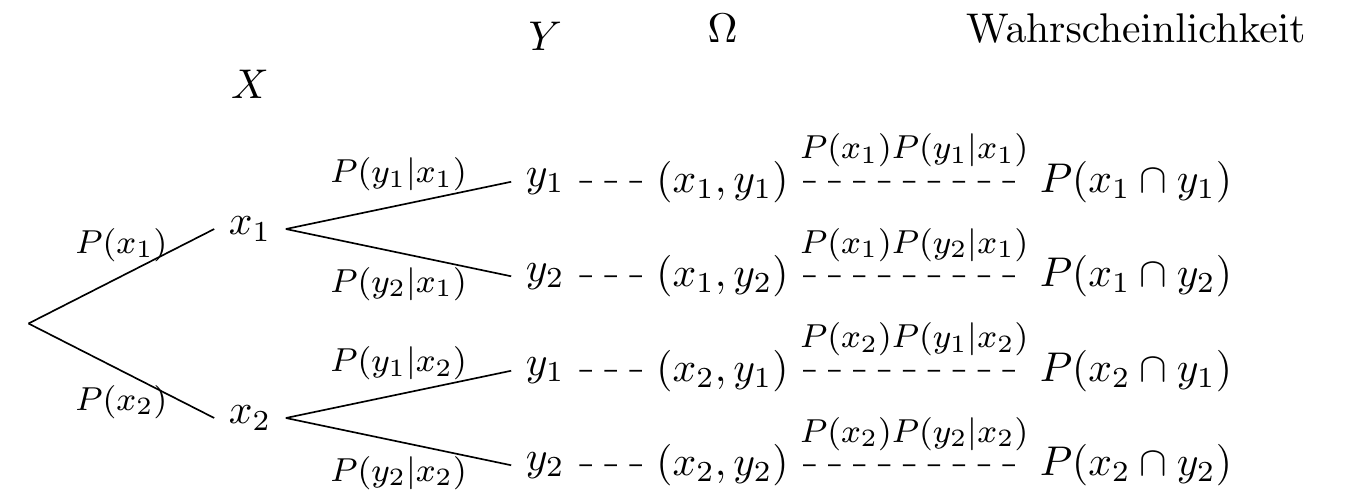
5.5.2 Wahrscheinlichkeitsbaum mit abhängigen Variablen

Beispiel: Rauchen und Krebs:

In einer Population gibt es 30 % Raucher und wir wissen, dass 40 % der Raucher Krebs haben, während nur 10 % der Nichtraucher an Krebs erkrankt sind. Der Wahrscheinlichkeitsbaum des Wahrscheinlichkeitsraums des zufälligen Experiments, das darin besteht, eine zufällig ausgewählte Person auszuwählen und die Variablen Rauchen und Brustkrebs zu messen, ist unten dargestellt.

5.5.3 Wahrscheinlichkeitsbaum mit unabhängigen Variablen

Beispiel Münzwurf

Der Wahrscheinlichkeitsbaum für das Zufallsexperiment zwei Münzen zu werfen ist:

Beispiel mit 3 Variablen

In einer Population gibt es 40% Männer und 60% Frauen. Der Wahrscheinlichkeitsbaum für das Ziehen einer zufälligen Stichprobe von drei Personen ist unten dargestellt.

5.6 Satz von der vollständigen Wahrscheinlichkeit:

Definition “Aufteilung des Wahrscheinlichkeitsraums”

Eine Menge von Ereignissen $A_1,A_2,\ldots,A_n$ aus demselben Ereignisraum $\Omega$ heißt eine Aufteilung des Wahrscheinlichkeitsraums, wenn sie die folgenden Bedingungen erfüllt:

Die Vereinigung der Ereignisse ist der Ereignisraum, das heißt, $A_1\cup \cdots\cup A_n =\Omega$
Alle Ereignisse sind paarweise ausschließend, das heißt $A_i\cap A_j = \emptyset$ $\forall i\neq j$.

Üblicherweise ist es einfach, eine Aufteilung des Wahrscheinlichkeitsraums zu erhalten, indem man eine Population entsprechend einer kategorischen Variable aufteilt, wie beispielsweise Geschlecht oder Blutgruppe usw.

Wenn wir eine Aufteilung des Ereignisraums haben, können wir sie verwenden, um die Wahrscheinlichkeiten anderer Ereignisse in demselben Wahrscheinlichkeitsraum zu berechnen.

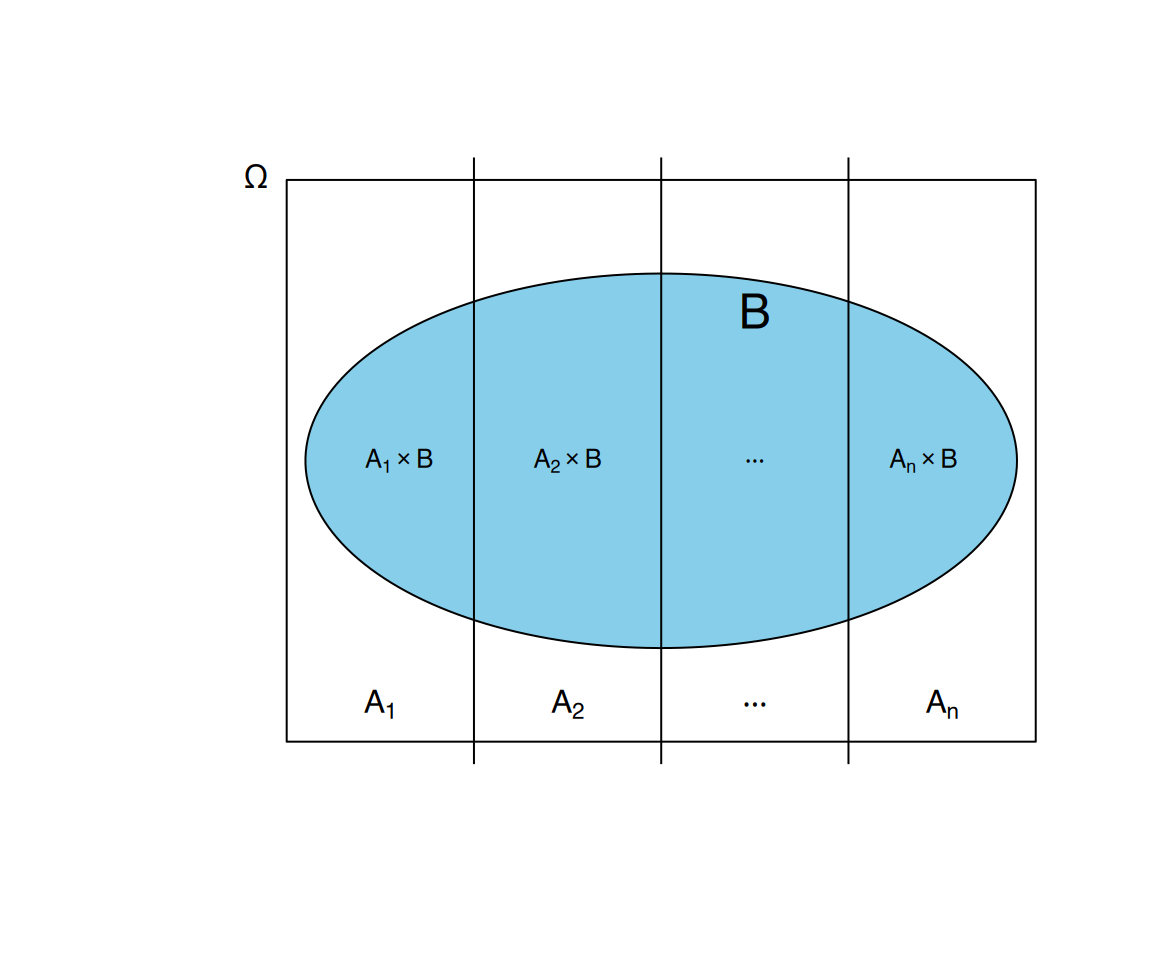
Definition “Gesamtwahrscheinlichkeit”

Gegeben eine Aufteilung $A_1,\ldots,A_n$ eines Wahrscheinlichkeitsraums $\Omega$, kann die Wahrscheinlichkeit jedes anderen Ereignisses $B$ des selben Wahrscheinlichkeitsraums mit der folgenden Formel berechnet werden:

\[ P(B) = \sum_{i=1}^n P(A_i\cap B) = \sum_{i=1}^n P(A_i)P(B|A_i). \]

Beweis

Der Beweis dieses Satzes ist recht einfach. Da $A_1,\ldots,A_n$ eine Aufteilung von $\Omega$ ist, haben wir:

\[ B = B\cap \Omega = B\cap (A_1\cup \cdots \cup A_n) = (B\cap A_1)\cup \cdots \cup (B\cap A_n). \]

Und alle Ereignisse dieser Vereinigung sind paarweise ausschließend, da $A_1,\ldots,A_n$. Daher gilt:

\[ \begin{aligned} P(B) &= P((B\cap A_1)\cup \cdots \cup (B\cap A_n)) = P(B\cap A_1)+\cdots + P(B\cap A_n) =\\ &= P(A_1)P(B|A_1)+\cdots + P(A_n)P(B|A_n) = \sum_{i=1}^n P(A_i)P(B|A_i). \end{aligned} \]

Beispiel: Diagnose

Ein Symptom $S$ kann durch eine Krankheit $K$ verursacht werden, kann aber auch bei Personen ohne die Krankheit auftreten. In einer Population beträgt der Anteil der Menschen mit der Krankheit 0,2. Es ist bekannt, dass 90 % der Personen mit der Krankheit das Symptom aufweisen, während nur 40 % der Personen ohne die Krankheit es haben.

Wie groß ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person aus der Bevölkerung das Symptom hat?

Um diese Frage zu beantworten, können wir den Satz von der vollständigen Wahrscheinlichkeit unter Verwendung der Aufteilung $\{K,\overline K\}$ anwenden:

\[ P(S) = P(K)P(S|K)+P(\overline K)P(S|\overline K) = 0.2\cdot 0.9 + 0.8\cdot 0.4 = 0.5. \] Das heißt, die Hälfte der Bevölkerung hat das Symptom.

Tatsächlich handelt es sich um einen gewichteten Mittelwert der Wahrscheinlichkeiten!

Beispiel Wahrscheinlichkeitsbaum

Das Ergebnis der vorherigen Frage wird durch den Wahrscheinlichkeitsbaum des Wahrscheinlichkeitsraums noch klarer:

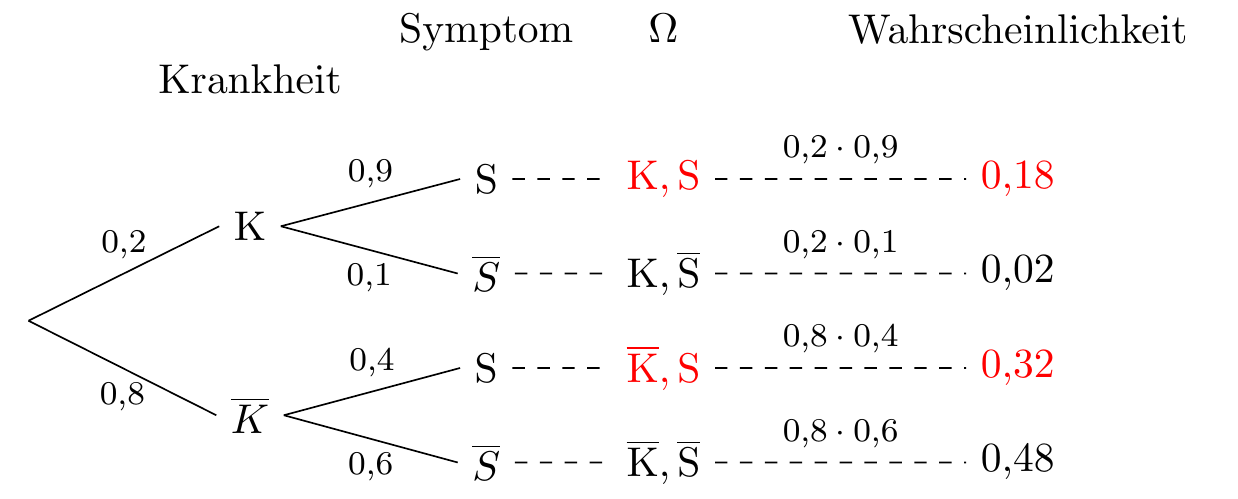
\[ \begin{aligned} P(S) &= P(K\cap S) + P(\overline K\cap S) = P(K)\cdot P(S|K)+P(\overline K)\cdot P(S|\overline K)\\ & = 0.2\cdot 0.9+ 0.8\cdot 0.4 = 0.18 + 0.32 = 0.5. \end{aligned} \]

5.7 Satz von Bayes

Eine Teilmenge eines Ereignisraums $A_1,\cdots,A_n$ kann auch als eine Menge von möglichen Hypothesen für ein Ereignis $B$ interpretiert werden. In solchen Fällen kann es hilfreich sein, die posteriori Wahrscheinlichkeit $P(A_i|B)$ jeder Hypothese zu berechnen.

Satz von Bayes

Gegeben eine Partition $A_1,\cdots,A_n$ eines Ereignisraums $\Omega$ und ein weiteres Ereignis $B$ desselben Mengenraums, kann die bedingte Wahrscheinlichkeit jedes Ereignisses $A_i$ $i=1,\ldots,n$ unter $B$ mit der folgenden Formel berechnet werden:

\[ P(A_i|B) = \frac{P(A_i\cap B)}{P(B)} = \frac{P(A_i)P(B|A_i)}{\sum_{i=1}^n P(A_i)P(B|A_i)}. \]

In dem vorherigen Beispiel sollte die Diagnose für eine Person mit Symptomen gestellt werden.

In diesem Fall können wir $K$ und $\overline K$ als die beiden möglichen Hypothesen für das Symptom $S$ interpretieren. Die vorab Wahrscheinlichkeiten dafür sind $P(K)=0.2$ und $P(\overline{K})=0.8$. Das bedeutet, dass wenn wir keine Informationen über das Symptom haben, die Diagnose nicht gestellt werden kann.

Allerdings ändert sich diese Unsicherheit bezüglich der Hypothese, wenn wir das Symptom beobachten. Dann müssen wir die posteriori Wahrscheinlichkeiten berechnen, um zu diagnostizieren, d.h.

\[ P(K|S) \mbox{ und } P(\overline{K}|S) \] Zur Berechnung nutzen wir den Satz von Bayes:

\[ \begin{aligned} P(D|S) &= \frac{P(D)P(S|D)}{P(D)P(S|D)+P(\overline{D})P(S|\overline{D})} = \frac{0.2\cdot 0.9}{0.2\cdot 0.9 + 0.8\cdot 0.4} = \frac{0.18}{0.5}=0.36,\\ P(\overline{D}|S) &= \frac{P(\overline{D})P(S|\overline{D})}{P(D)P(S|D)+P(\overline{D})P(S|\overline{D})} = \frac{0.8\cdot 0.4}{0.2\cdot 0.9 + 0.8\cdot 0.4} = \frac{0.32}{0.5}=0.64. \end{aligned} \]

Wie wir sehen können, hat sich die Wahrscheinlichkeit, die Krankheit zu haben, erhöht. Trotzdem ist die Wahrscheinlichkeit, sie nicht zu haben, immer noch größer als die Wahrscheinlichkeit, sie zu haben. Aus diesem Grund lautet die Diagnose, dass die Person die Krankheit nicht hat.

In diesem Fall wird gesagt, dass das Symptom $S$ nicht entscheidend ist, um die Krankheit zu diagnostizieren.

5.8 Epidemiologie

Einzelne Zweige der Medizin, die eine intensive Nutzung von Wahrscheinlichkeiten vornehmen, sind Epidemiologie und Präventionsmedizin.

Die Epidemiologie untersucht die Häufigkeit und Ursachen von Krankheiten in Populationen, indem sie Risikofaktoren für Krankheiten und Ziele zur präventiven Gesundheitsversorgung identifiziert.

In der Epidemiologie ist man daran interessiert, wie häufig ein medizinisches Ereignis 𝐷 (typischerweise eine Krankheit wie Grippe, ein Risikofaktor wie Rauchen oder ein Schutzfaktor wie eine Impfung) auftritt, das als nominale Variable mit zwei Kategorien (das Eintreten oder Nicht-Eintreten des Ereignisses) gemessen wird.

Es gibt verschiedene Messgrößen zur Häufigkeit eines medizinischen Ereignisses. Die wichtigsten sind:

Prävalenz
Inzidenz
Relatives Risiko
Odds Ratio

5.8.1 Prävalenz

Definition “Prävalenz”

Die Prävalenz eines medizinischen Ereignisses $K$ ist der Anteil einer bestimmten Bevölkerung, der von diesem medizinischen Ereignis betroffen ist.

\[ \mbox{Prävalenz}(K) = \frac{\mbox{Anzahl von } K \text{ betroffener}}{\mbox{Größe der Bevölkerung}} \]

Die Prävalenz wird häufig anhand einer Stichprobe geschätzt, indem man den relativen Anteil der Menschen berechnet, die in der Stichprobe von dem Ereignis betroffen sind. Es ist auch üblich, diesen Anteil als Prozentangabe auszudrücken.

Beispiel

Um die Prävalenz von Grippe zu schätzen, wurde eine Stichprobe von 1.000 Personen untersucht und 150 davon hatten Grippe. Daher beträgt die Prävalenz der Grippe etwa $150/1000 = 0,15\ $ oder 15%.

5.8.2 Inzidenz

Die Inzidenz misst die Wahrscheinlichkeit des Auftretens eines medizinischen Ereignisses in einer Bevölkerung innerhalb eines bestimmten Zeitraums. Die Inzidenz kann als kumulative Anteilszahl oder als Rate gemessen werden.

Definition “kumulative Inzidenz”

Die kumulative Inzidenz eines medizinischen Ereignisses $K$ ist der Anteil der Menschen, die das Ereignis in einem bestimmten Zeitraum erlitten haben, d.h. die Anzahl der neuen Fälle mit dem Ereignis in diesem Zeitraum geteilt durch die Größe der Risikobevölkerung. Anzahl neuer Fälle mit $K$

\[ R(K)=\frac{\mbox{Anzahl Neuerkrankungen}}{\mbox{Größe der Risikobevölkerung}} \]

Beispiel

Eine Bevölkerung enthält zu Beginn 1.000 Personen ohne Grippe und nach zweijähriger Beobachtungszeit hatten 160 davon die Grippe. Die Anteilszahl der Grippe-Inzidenz berechnet sich mit

\[ R(K) = \frac{160}{1.000} = 0,16 \]

Die kumulative Inzidenz liegt also beo 16% für zwei Jahre.

Definition “Inzidenzrate” (Absolutes Risiko)

Die Inzidenzrate oder das absolute Risiko eines medizinischen Ereignisse $K$ ist die Anzahl neuer Erkrankungen geteilt durch die Größe der Risikobevölkerung und die Anzahl der Zeiteinheiten in einem bestimmten Zeitraum.

\[ R(K)=\frac{\mbox{Anzahl Neuerkrankungen}}{\mbox{Größe der Risikobevölkerung}\times \mbox{Anzahl Zeiteinheiten}} \]

Beispiel

Eine Bevölkerung enthält zu Beginn 1.000 Personen ohne Grippe und nach zweijähriger Beobachtungszeit hatten 160 davon die Grippe. Wenn man das Jahr als Zeiteinheit betrachtet, beträgt die Inzidenzrate der Grippe

\[ R(K) = \frac{160}{1.000 \cdot 2} =0,08 \] Die Inzidenzrate liegt also bei 8% Personen pro Jahr.

5.8.3 Prävlenz oder Inzidenz

Die Prävalenz zeigt an, wie verbreitet ein medizinisches Ereignis ist und ist eher ein Maß für die Belastung des Ereignisses für die Gesellschaft ohne Berücksichtigung der gefährdeten Zeit oder wann Personen möglicherweise einem möglichen Risikofaktor ausgesetzt waren

Die Inzidenz liefert Informationen über das Risiko, von dem Ereignis betroffen zu sein.

Die Prävalenz kann in Querschnittsstudien zu einem bestimmten Zeitpunkt gemessen werden, während zur Messung der Inzidenz eine Längsschnittstudie erforderlich ist, bei der die Individuen über einen bestimmten Zeitraum beobachtet werden.

Beim Verständnis der Ereignis-Ätiologie ist die Inzidenz nützlicher als die Prävalenz: wenn sich beispielsweise die Inzidenz einer Krankheit in einer Bevölkerung erhöht, dann gibt es einen Risikofaktor, der dies fördert.

Wenn die Inzidenz für die Dauer des Ereignisses ungefähr konstant ist, ist die Prävalenz ungefähr das Produkt aus Ereignis-Inzidenz und durchschnittlicher Ereignisdauer.

\[ \text{Prävalenz} = \text{Inzidenz} \cdot \text{Dauer} \]

5.8.4 Risiko-Vergleich

Um zu bestimmen, ob ein Faktor oder eine Eigenschaft mit dem medizinischen Ereignis verbunden ist, müssen wir das Risiko des medizinischen Ereignisses in zwei Populationen vergleichen, von denen die eine dem Faktor ausgesetzt ist und die andere nicht. Die Gruppe von Menschen, die dem Faktor ausgesetzt sind, wird als Interventionsgruppe oder experimentelle Gruppe bezeichnet und die Gruppe von Menschen, die nicht ausgesetzt sind, als Kontrollgruppe.

In der Regel werden die beobachteten Fälle für jede Gruppe in einer 2x2-Tabelle wie der folgenden dargestellt.

\[ \begin{array}{|c|c|c|} \hline & \text{erkrankt}\ K & \text{gesund}\ \overline{K}\\ \hline \text{Interventionsgruppe}\newline (exponiert) & a & b\\ \hline \text{Kontrollgruppe}\newline (nicht\ exponiert) & c & d\\ \hline \end{array} \]

5.8.5 Zurechenbares Risiko

Definition “zurechendbares Risiko” (Risikodifferenz)

Das zurechenbare Risiko (attributales Risiko oder Risikodifferenz) eines medizinischen Ereignisses $K$ für Personen, die einem Faktor (Exposition) ausgesetzt sind, ist der Unterschied zwischen den absoluten Risiken der Interventionsgruppe und der Kontrollgruppe.

\[ AR(K)=R_{Intervention}(K)-R_{Kontrolle}(K)=\frac{a}{a+b}-\frac{c}{c+d}. \]

Das zurechenbare Risiko ist das Risiko eines Ereignisses, das spezifisch auf den Einflussfaktor von Interesse zurückzuführen ist. Beachten Sie, dass das zurechenbare Risiko positiv sein kann, wenn das Risiko der Interventionsgruppe größer als das Risiko der Kontrollgruppe ist, und umgekehrt.

Beispiel Impfung

Um die Wirksamkeit eines Impfstoffs gegen Grippe zu bestimmen, wurde zu Beginn des Jahres eine Stichprobe von 1.000 Personen ohne Grippe ausgewählt. Die Hälfte von ihnen wurde geimpft (Interventionsgruppe) und der Rest erhielt ein Placebo (Kontrollgruppe). Die folgende Tabelle fasst die Ergebnisse am Ende des Jahres zusammen.

\[ \begin{array}{|c|c|c|} \hline & \text{Grippe}\ K & \text{keine Grippe}\ \overline{K}\\ \hline \text{Interventionsgruppe}\newline (geimpft) & 20 & 480\\ \hline \text{Kontrollgruppe}\newline (nicht\ geimpft) & 80 & 420\\ \hline \end{array} \]

Für geimpfte Personen liegt das zurechenbare Risiko an Grippe zu erkranken bei

\[ AR(K) = \frac{20}{20+480}-\frac{80}{80+420} = -0.12. \] Das bedeutet, dass das Risiko an Grippe zu erkranken in der Gruppe der Geimpften 12% geringer ist als in der Gruppe der Ungeimpften.

5.8.6 Relatives Risiko

Definition “relatives Risiko”

Das relative Risiko eines medizinischen Ereignisses $K$ für Personen, die einer Exposition ausgesetzt sind, ist es der Quotient zwischen den Inzidenzen der Behandlungs- und Kontrollgruppe.

\[ RR(K)=\frac{\mbox{Risiko der Interventionsgruppe}}{\mbox{Risiko der Kontrollgruppe}}=\frac{R_I(K)}{R_K(K)}=\frac{a/(a+b)}{c/(c+d)} \]

Das relative Risiko vergleicht das Risiko eines medizinischen Ereignisses zwischen der Behandlungs- und Kontrollgruppe.

$RR = 1\ \ \rightarrow$ Es gibt keine Verbindung zwischen dem Ereignis und der Exposition.
$RR < 1\ \ \rightarrow$ Die Exposition verringert das Risiko des Ereignisses.
$RR > 1\ \ \rightarrow$ Die Exposition erhöht das Risiko des Ereignisses.

Je weiter entfern $RR$ von 1 ist, desto stärker die Verbindung.

Beispiel Impfung

Um die Wirksamkeit eines Impfstoffs gegen Grippe zu bestimmen, wurde zu Beginn des Jahres eine Stichprobe von 1.000 Personen ohne Grippe ausgewählt. Die Hälfte von ihnen wurde geimpft (Behandlungsgruppe) und der Rest erhielt ein Placebo (Kontrollgruppe). Die folgende Tabelle fasst die Ergebnisse am Ende des Jahres zusammen.

Das relative Risiko für geimpfte Personen an Grippe zu erkranken ist:

\[ RR(K) = \frac{20/(20+480)}{80/(80+420)} = 0,25. \]

Das bedeutet, dass geimpfte Personen im Vergleich zu ungeimpften nur ein Viertel des Risikos haben die Grippe bekommen. Das bedeutet, der Impfstoff verringerte das Risiko einer Grippe um 75%.

5.8.7 Odds

efinition “Odds”

Die Odds eines medizinischen Ereignisses $K$ in einer Bevölkerung ist der Quotient zwischen den Personen, die das Ereignis erlitten haben und den Personen, die es nicht in einem bestimmten Zeitraum erlitten haben.

\[ ODDS(K)=\frac{\mbox{Neue Fälle mit}\ K}{\mbox{Fälle ohne}\ K}=\frac{P(K)}{P(\overline K)} \]

Im Gegensatz zur Inzidenz, die ein Anteil von weniger als oder gleich 1 ist, kann das Odds größer als 1 sein. Es ist jedoch möglich, das Odds in eine Wahrscheinlichkeit umzuwandeln, indem man folgende Formel verwendet:

\[ P(K) = \frac{ODDS(K)}{ODDS(K)+1} \]

Beispiel

Eine Bevölkerung enthält initial 1.000 Personen ohne Grippe und nach einem Jahr haben 160 von ihnen die Grippe bekommen. Das Odds der Grippe ist somit \[ ODDS(\text{Grippe}) = \frac{160}{840} = 0,1905. \]

Beachten Sie, dass die Inzidenz $160/1000 =0,16 $ beträgt.

5.8.8 Odds Ratio

Definition “Odds Ratio”

Die Odds Ratio eines medizinischen Ereignisses $K$ für Personen, die einer Exposition ausgesetzt sind, ist der Quotient zwischen dem Odds des Ereignisses in der Behandlungs- und Kontrollgruppe.

\[ OR(K)=\frac{\mbox{Odds in Interventionsgruppe}}{\mbox{Odds in Kontrollgruppe}}=\frac{a/b}{c/d}=\frac{ad}{bc} \]

Die Odds Ratio vergleicht die Odds eines medizinischen Ereignisses zwischen der Behandlungs- und Kontrollgruppe. Die Interpretation ist ähnlich wie beim relativen Risiko.

$OR=1$ $\Rightarrow$ Es gibt keine Verbindung zwischen dem Ereignis und der Exposition.
$OR<1$ $\Rightarrow$ Die Exposition verringert das Risiko des Ereignisses.
$OR>1$ $\Rightarrow$ Die Exposition erhöht das Risiko des Ereignisses.

Je weiter $OR$ weg von 1 ist, desto stärker ist die Verbindung.

Beispiel Impfung

Die Odds Ratio der Grippe für geimpfte Personen ist:

\[ OR(K) = \frac{20/480}{80/420} = 0,21875. \]

Das bedeutet, dass die Chancen, an Grippe zu erkranken (im Vergleich dazu, nicht zu erkranken), bei geimpften Personen fast ein Fünftel derer bei ungeimpften Personen betragen. Das heißt: Auf etwa 22 geimpfte Personen mit Grippe kommen etwa 100 ungeimpfte Personen mit Grippe.

5.8.9 Relatives Risiko vs Odds ratio

Relatives Risiko und Odds Ratio sind zwei Kennzahlen, aber ihre Interpretation unterscheidet sich leicht. Während das Relative Risiko einen Vergleich der Risiken zwischen den Behandlungs- und Kontrollgruppen ausdrückt, beschreibt die Odds Ratio einen Vergleich der Chancen, was nicht dasselbe wie das Risiko ist. Daher bedeutet ein Odds Ratio von 2 nicht, dass die Behandlungsgruppe das doppelte Risiko hat, das medizinische Ereignis zu erwerben.

Die Interpretation des Odds Ratio ist komplizierter, da sie kontrarfaktisch ist und uns angibt, wie viele Male das Ereignis in der Behandlungsgruppe häufiger ist im Vergleich zur Kontrollgruppe unter der Annahme, dass in der Kontrollgruppe das Ereignis so häufig wie das Nicht-Ereignis ist.

Der Vorteil des Odds Ratio besteht darin, dass sie nicht von der Prävalenz oder der Inzidenz des Ereignisses abhängt und notwendigerweise verwendet werden muss, wenn die Anzahl der Menschen mit dem medizinischen Ereignis in beiden Gruppen willkürlich ausgewählt wird, wie z.B. bei Fall-Kontroll-Studien.

Beispiel Rauchen und Lungenkrebs

Um die Assoziation zwischen Lungenkrebs und Rauchen zu bestimmen, wurden zwei Proben ausgewählt (die zweite mit der doppelten Anzahl von Nicht-Krebs-Individuen), wobei folgende Ergebnisse erzielt wurden:

\[ \begin{array}{|c|c|c|} \hline & \text{Krebs} & \text{kein Krebs}\\ \hline \text{Raucher} & 60 & 80\\ \hline \text{Nichtraucher} & 40 & 320\\ \hline \end{array} \]

\[ \begin{aligned} RR(K) &= \frac{60/(60+80)}{40/(40+320)} = 3.86.\\ OR(K) &= \frac{60/80}{40/320} = 6. \end{aligned} \]

\[ \begin{array}{|c|c|c|} \hline & \text{Krebs} & \text{kein Krebs}\\ \hline \text{Raucher} & 60 & 160\\ \hline \text{Nichtraucher} & 40 & 640\\ \hline \end{array} \]

\[ \begin{aligned} RR(K) &= \frac{60/(60+160)}{40/(40+640)} = 4.64.\\ OR(K) &= \frac{60/160}{40/640} = 6. \end{aligned} \]

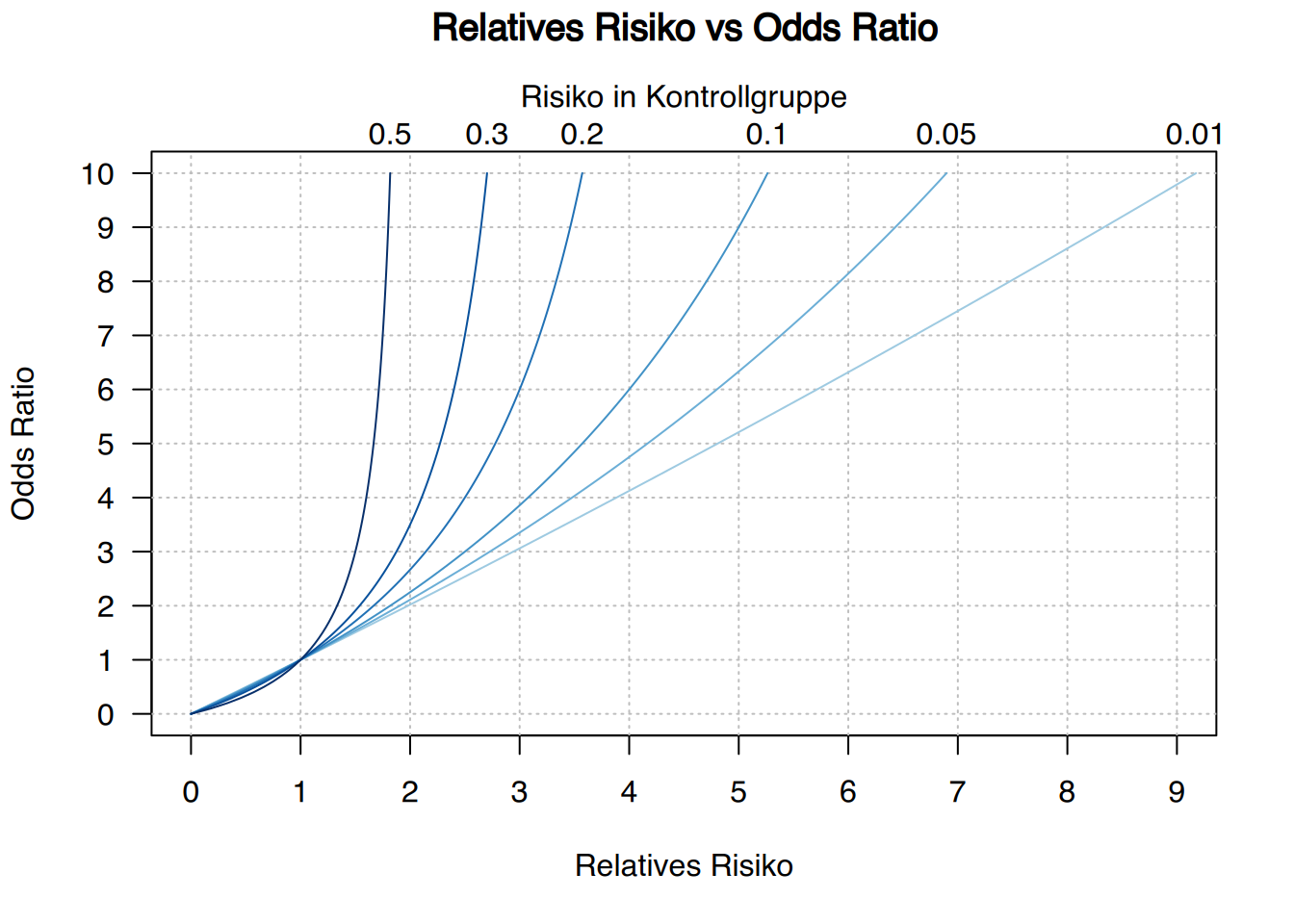
Das Relative Risiko verändert sich, wenn wir die Inzidenz oder Prävalenz des Ereignisses (Lungenkrebs) ändern, während sich die Odds Ratio nicht verändert.

Die Beziehung zwischen dem Relative Risiko und dem Odds Ratio wird durch die folgende Formel gegeben:

\[ RR = \frac{OR}{1-R_{Kontrolle}+R_{Kontrolle}\cdot OR}=OR \cdot \frac{1-R_{Intervention}}{1-R_{Kontrolle}} \] Die Odds Ratio überschätzt stets das Relative Risiko, wenn es größer als 1 ist, und unterschätzt es, wenn es kleiner als 1 ist. Allerdings sind Relatives Risiko und Odds Ratio für seltene medizinische Ereignisse (mit sehr kleiner Prävalenz oder Inzidenz) fast gleich.

5.9 Diagnosetests

In der Epidemiologie ist es üblich, diagnostische Tests zur Diagnose von Krankheiten zu verwenden. Im Allgemeinen sind diese jedoch nicht vollständig zuverlässig und haben ein gewisses Risiko einer Fehldiagnose, wie in der folgenden Tabelle dargestellt:

\[ \begin{array}{|c|c|c|} \hline & \text{krank}\ K & \text{gesund}\ \overline K\\ \hline \text{Testergebnis} & \textcolor{green}{\text{richtig positiv}} & \textcolor{red}{\text{falsch positiv}} \\ positiv \mathbf{+} & (RP) & (FP) \\ \hline \text{Testergebnis} & \textcolor{red}{\text{falsch negativ}} & \textcolor{green}{\text{richtig negativ}} \\ negativ \mathbf{-} & (FN) & (RN)\\\hline \end{array} \]

Die Leistung eines diagnostischen Tests hängt von den folgenden beiden Wahrscheinlichkeiten ab:

Sensitivität und
Spezifität

5.9.1 Sensitivität und Spezifität

Definition “Sensitivität”

Die Sensitivität eines diagnostischen Tests ist der Anteil positiver Ergebnisse bei erkrankten Personen.

\[ P(+|K)=\frac{RP}{RP+FN} \]

Definition “Spezifität”

Die Spezifität eines diagnostischen Tests ist der Anteil negativer Ergebnisse bei gesunden Personen.

\[ P(-|\overline{K})=\frac{RN}{RN+FP} \]

Ein Test mit hoher Sensitivität wird die Krankheit bei den meisten erkrankten Personen erkennen, jedoch auch mehr falsche Positive produzieren als ein weniger empfindlicher Test. Daher ist ein positives Ergebnis eines Tests mit hoher Sensitivität nicht nützlich zur Bestätigung der Krankheit, aber ein negatives Ergebnis ist nützlich zum Ausschluss der Krankheit, da es selten bei erkrankten Personen zu falsch-negativen Ergebnissen kommt.

Andererseits wird ein Test mit hoher Spezifität die Krankheit bei den meisten gesunden Personen ausschließen, jedoch auch mehr falsche Negative produzieren als ein weniger spezifischer Test. Daher ist ein negatives Ergebnis eines Tests mit hoher Spezifität nicht nützlich zum Ausschluss der Krankheit. Aber ein positives Ergebnis ist nützlich zur Bestätigung der Krankheit, da es selten bei gesunden Personen zu falsch-positiven Ergebnissen kommt.

Die Entscheidung für einen Test mit größerer Sensitivität oder einen Test mit größerer Spezifität hängt von Art der Krankheit und dem Ziel des Tests ab. Im Allgemeinen werden wir einen sensitiven Test verwenden, wenn:

die Krankheit ernst ist und es wichtig ist, sie zu erkennen.
die Krankheit behandelbar ist.
Falsch-positive Ergebnisse keine schweren Schäden verursachen.

Und wir werden einen spezifischen Test verwenden, wenn:

die Krankheit ernst ist, aber schwierig oder unmöglich zu behandeln ist.
falsch-positive Ergebnisse schwerwiegende Schäden verursachen.
die Behandlung von falsch-positiven Fällen gefährliche Folgen haben kann.

5.9.2 prädiktive Werte

Der wichtigste Aspekt eines diagnostischen Tests ist jedoch seine Vorhersagekraft, die mit den folgenden beiden posterioren Wahrscheinlichkeiten gemessen wird:

positiv prädiktiver Wert und
negativ prädiktiver Wert

Definition “positiv prädiktiver Wert

Der positiv prädiktive Wert eines diagnostischen Tests ist der Anteil von Personen mit der Krankheit unter allen Personen mit einem positiven Ergebnis.

\[ P(K|+) = \frac{RP}{RP+FP} \]

Definition “Negativ prädiktiver Wert”

Der negativ prädiktive Wert eines diagnostischen Tests ist der Anteil von Personen ohne die Krankheit unter allen Personen mit einem negativen Ergebnis.

\[ P(\overline{K}|-) = \frac{RN}{RN+FN} \]

Positiv und negativ prädiktive Werte ermöglichen es, die Krankheit zu bestätigen oder auszuschließen, besonders, wenn sie mindestens einen Schwellenwert von 0,5 erreichen.

$PPW>0.5 \ \Rightarrow\ $ Hinweis auf das Vorliegen der Krankheit

$PPV<0.5 \ \Rightarrow\ $ Hinweis auf das Nichtvorliegen der Krankheit

Diese Wahrscheinlichkeiten hängen jedoch von der Häufigkeit der Krankheit $P(K)$ ab und können aus der Sensitivität und Spezifität des diagnostischen Tests unter Verwendung des Satzes von Bayes berechnet werden.

\[ \begin{aligned} PPW=P(K|+) &= \frac{P(K)P(+|K)}{P(K)P(+|K)+P(\overline{K})P(+|\overline{K})}\\ NPW=P(\overline{K}|-) &= \frac{P(\overline{K})P(-|\overline{K})}{P(K)P(-|K)+P(\overline{K})P(-|\overline{K})} \end{aligned} \]

Daher steigt der positiv prädiktive Wert bei häufigen Krankheiten und der negativ prädiktive Wert bei seltenen Krankheiten.

Beispiel

Bei 1.000 Personen wurde ein Grippetest durchgeführt. Die Ergebnisse sind in der Tabelle dargestellt.

\[ \begin{array}{|c|c|c|} \hline & \text{Grippe}\ K & \text{keine Grippe}\ \overline K\\ \hline \text{Testergebnis} + & 95 & 90 \\ \hline \text{Testergebnis} - & 5 & 810\\\hline \end{array} \]

Die Prävalenz der Grippe ist $P(K) = \frac{95+5}{1000} = 0,1$.
Die Sensitivität des Tests ist $P(+|K) = \frac{95}{95+5}= 0,95$.
Die Spezifität des Tests ist $P(-|\overline{K}) = \frac{810}{90+810}=0,9$.
Der positiv prädiktive Wert ist $PPW = P(K|+) = \frac{95}{95+90} = 0,5135$. Da dieser Wert über 0,5 liegt, bedeutet dies, dass wir bei einem positiven Testergebnis wahrscheinlich wirklich Grippe gefunden haben. Allerdings wird das Vertrauen in diesesehr gering, da der Wert sehr nahe an 0,5 liegt.
Der negativ prädiktive Wert ist $NPW = P(\overline{K}|-) = \frac{810}{5+810} = 0,9939$. Da dieser Wert fast 1 ist, bedeutet dies, dass es fast sicher ist, dass eine Person keine Grippe hat, wenn sie ein negatives Testergebnis erhält.

Daher ist dieser Test sehr leistungsfähig, um die Grippe auszuschließen, aber nicht so leistungsfähig, um sie zu bestätigen.

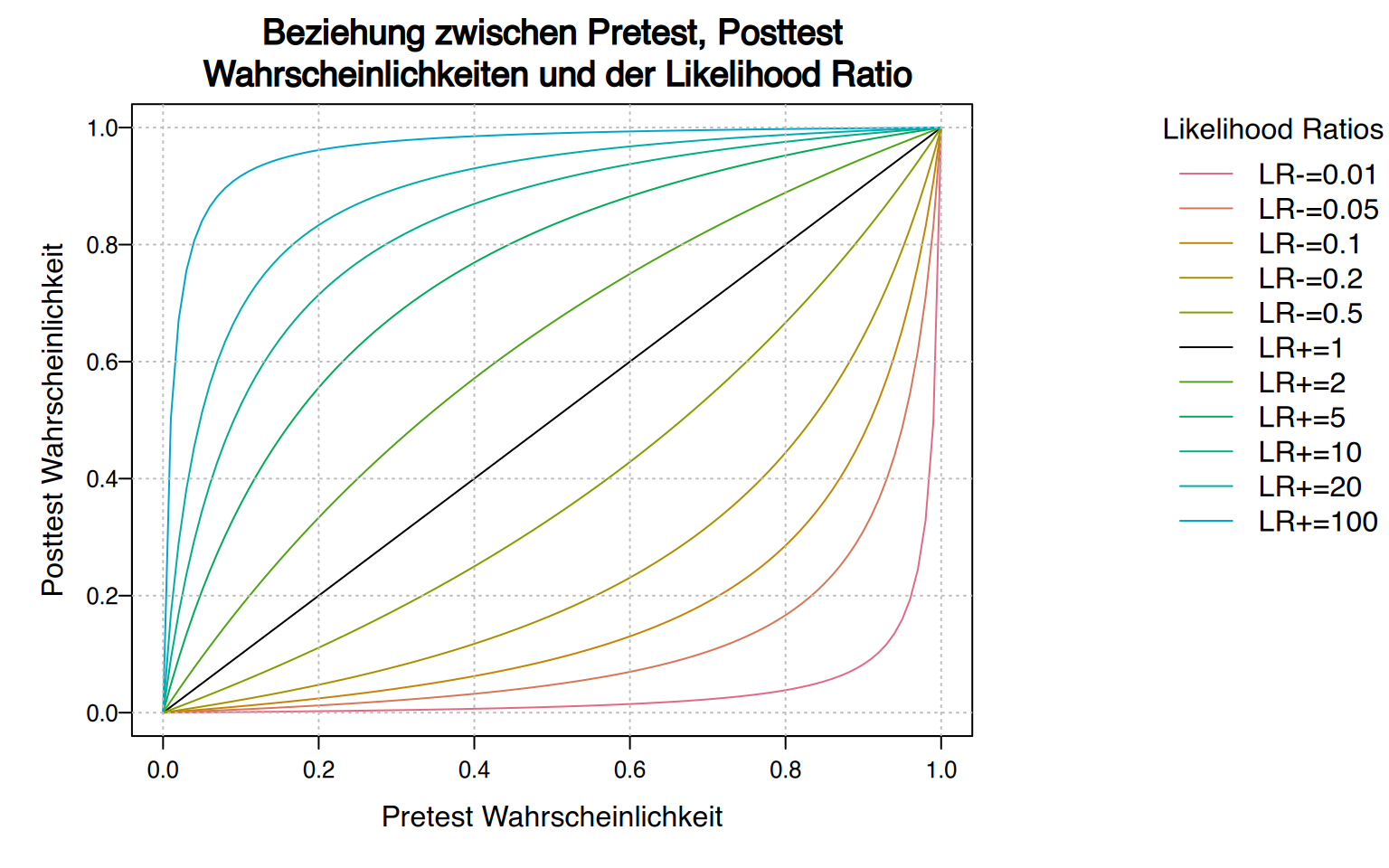
5.9.3 Likelihood Ratio

Die folgenden Maße werden normalerweise aus Sensitivität und Spezifität abgeleitet.

Definition “Positive Likelihood Ratio”

Die positive Likelihood Ratio eines diagnostischen Tests ist das Verhältnis zwischen der Wahrscheinlichkeit positiver Ergebnisse bei Personen mit der Krankheit und gesunden Personen.

\[ LR+=\frac{P(+|K)}{P(+|\overline{K})} = \frac{\mbox{Sensitivität}}{1-\mbox{Spezifität}} \]

Definition “Negative Likelihood Ratio”

Die negative Likelihood Ratio eines diagnostischen Tests ist das Verhältnis zwischen der Wahrscheinlichkeit negativer Ergebnisse bei Personen mit der Krankheit und gesunden Personen.

\[ LR-=\frac{P(-|K)}{P(-|\overline{K})} = \frac{1-\mbox{Sensitivität}}{\mbox{Spezifität}} \]

Die positive Likelihood Ratio kann als die Anzahl interpretiert werden, wie oft ein positives Ergebnis bei Personen mit der Krankheit gegenüber Personen ohne sie wahrscheinlicher ist.

Andererseits kann die negative Likelihood Ratio als die Anzahl interpretiert werden, wie oft ein negatives Ergebnis bei Personen mit der Krankheit gegenüber Personen ohne sie wahrscheinlicher ist.

Post-Test-Wahrscheinlichkeiten können durch Likelihood Ratio aus Pre-Test-Wahrscheinlichkeiten berechnet werden.

\[ P(K|+) = \frac{P(K)P(+|K)}{P(K)P(+|K)+P(\overline{K})P(+|\overline{K})} = \frac{P(K)LR+}{1-P(K)+P(K)LR+} \]

Daher gilt:

Eine Likelihood Ratio größer als 1 erhöht die Wahrscheinlichkeit der Erkrankung.
Eine Likelihood Ratio kleiner als 1 verringert die Wahrscheinlichkeit der Erkrankung.
Eine Likelihood Ratio von 1 ändert die Pre-Test-Wahrscheinlichkeit nicht.