3 Stichprobenstatistik
Die deskriptive Statistik hat zum Ziel, empirische Daten durch Tabellen und Grafiken übersichtlich darzustellen und zu ordnen, sowie durch geeignete grundlegende Kenngrößen zahlenmäßig zu beschreiben.
Eine Tabelle oder Grafik informiert über die gesamte Verteilung eines Merkmals mit seinen Ausprägungen. Demgegenüber sagen statistische Kenngrößen etwas über spezielle Eigenschaften der Verteilung aus.
- Lagekenngrößen: beschreiben Stellen, an denen sich die Daten konzentrieren oder die die Verteilung in gleiche Teile unterteilen.
- Streuungskenngrößen: messen die Ausbreitung und Variabilität der Daten.
- Formmaße: messen die Symmetrie und den “Schwanz” der Verteilung.
Diese Werte werden auch genannt Stichprobenstatistiken genannt.
Die zahlenmäßige Darstellung durch statistische Kenngrößen beruht auf einer Reduktion der Daten. Die Gesamtheit des Datenmaterials wird hierbei durch typische Vertreter repräsentiert.
3.1 Lagekenngrößen
Es werden zwei Gruppen von Lagekenngrößen unterschieden:
- Zentrale Lagewerte messen die Werte, an denen sich die Daten konzentrieren, meist im Zentrum der Verteilung. Diese Werte sind diejenigen, die die Stichprobe am besten darstellen. Die wichtigsten sind:
- Arithmetisches Mittel (Mittelwert)
- Median
- Modal (Modus)
- Nicht-zentrale Lagewerte teilen die Stichprobe in gleichgroße Teile. Die wichtigsten sind:
- Quartile.
- Dezile.
- Perzentile.
- Quartile.
3.1.1 Arithmetischer Mittelwert
Das arithmetische Mittel (umgangssprachlich Mittelwert) einer Variablen \(X\) ist die Summe der beobachteten Werte in der Stichprobe geteilt durch die Stichprobengröße \(n\) und wird durch das Symbol \(\overline x\) (sprich “x quer”) dargestellt.
\[ \overline x = \frac{\sum x_{i}}{n} \]
Er kann wie folgt auch aus der Häufigkeitstabelle berechnet werden:
\[ \overline x = \frac{\sum x_{i} \cdot n_{i}}{n} = \sum x_{i} \cdot f_{i} \]
In den meisten Fällen ist der arithmetische Mittelwert derjenige Wert, der die beobachteten Werte in der Stichprobe am besten darstellt.
Das arithmetische Mittel kann nur bei metrischen Daten berechnet werden!
Für das Beispiel der Erhebung von Kindern in Familien lautet das arithmetische Mittel:
\[ \begin{aligned} \overline{x} &= \frac{1+2+4+2+2+2+3+2+1+1+0+2+2}{25}+\\ &+\frac{0+2+2+1+2+2+3+1+2+2+1+2}{25} = \frac{44}{25} = 1.76 \mbox{ Kinder}. \end{aligned} \]
Die Berechnung von \(\overline x\) über die Häufigkeitstabelle
| \(x_{i}\) | \(n_{i}\) | \(f_{i}\) | \(x_{i} \cdot n_{i}\) | \(x_{i} \cdot f_{i}\) |
|---|---|---|---|---|
| 0 | 2 | 0.08 | 0 | 0 |
| 1 | 6 | 0.24 | 6 | 0.24 |
| 2 | 14 | 0.56 | 28 | 1.12 |
| 3 | 2 | 0.08 | 6 | 0.24 |
| 4 | 1 | 0.04 | 4 | 0.16 |
| \(\sum\) | 25 | 1 | 44 | 1.76 |
erfolgt mit:
\[ \overline{x} = \frac{\sum x_{i} \cdot n_i}{n} = \frac{44}{25}= 1.76\mbox{ Kinder} \qquad \overline{x}=\sum{x_{i} \cdot f_i} = 1.76 \mbox{ Kinder}. \] Dies ist die Anzahl an Kinder, durch welche die Familien in der Stichprobe am besten repräsentiert werden.
Verwenden wir die Daten der Körpergröße von Studierenden, berechnet sich \(\overline x\) wie folgt:
\[ \overline{x} = \frac{179+173+\cdots+187}{30} = 175.07 \mbox{ cm}. \]
Über die klassierte Häufigkeitstabelle kann \(\overline x\) bestimmt werden, indem jeweils die Klassenmitte als \(x_i\) verwendet wird.
| X | \(x_i\) | \(n_i\) | \(f_i\) | \(x_i \cdot n_i\) | \(x_i \cdot f_i\) |
|---|---|---|---|---|---|
| (150,160] | 155 | 2 | 0.07 | 310 | 10.33 |
| (160,170] | 165 | 8 | 0.27 | 1320 | 44.00 |
| (170,180] | 175 | 11 | 0.36 | 1925 | 64.17 |
| (180,190] | 185 | 7 | 0.23 | 1295 | 43.17 |
| (190,200] | 195 | 2 | 0.07 | 390 | 13.00 |
| ∑ | 30 | 1 | 5240 | 174.67 |
\[ \overline{x} = \frac{\sum x_i \cdot n_i}{n} = \frac{5240}{30}= 174.67 \mbox{ cm}\qquad \overline{x}=\sum{x_i \cdot f_i} = 174.67 \mbox{ cm}. \]
Beachten Sie, dass der Mittelwert, der aus der Tabelle berechnet wird, etwas von dem realen Wert abweicht. Da in den Berechnungen jeweils die Klassenmitten anstelle der tatsächlichen Werte verwendet werden, ergeben sich dadurch leichte Rundungsfehler.
3.1.2 Gewichtetes Mittel
In einigen Fällen haben die Werte der Stichprobe unterschiedlich starke Bedeutungen. In diesem Fall muss das jeweilige Gewicht der Werte berücksichtigt werden, wenn das Mittel berechnet wird.
Das gewichtete Mittel der Werte \(x_1, \ldots, x_n\) - wobei jeder Wert \(x_i\) ein Gewicht \(w_i\) hat - berechnet sich durch die Summe der Produkte jedes Wertes mit seinem Gewicht, dividiert durch die Summe der Gewichtwerte:
\[ \overline{x}_w = \frac{\sum x_i w_i}{\sum w_i} \]
Aus der Häufigkeitstabelle kann das gewichtete Mittel mit folgender Formel berechnet werden:
\[ \overline{x}_w = \frac{\sum x_i w_i n_i}{\sum w_i} \]
Ein Student möchte den Punktedurchschnitt seiner Studienleistungen in den folgenden drei Kursen berechnen
| Kurs | Credits | Punkte |
|---|---|---|
| Mathe | 8 | 15 |
| Wirtschaft | 5 | 10 |
| Chemie | 6 | 12 |
Das arithmetische Mittel der Punkte beträgt
\[ \overline x = \frac{\sum x_i}{n}= \frac{15+10+12}{3}=12,\overline 3 \text{ Punkte}. \]
Fächer mit mehr Creditpunkten erfordern mehr Arbeit und sollten bei der Berechnung des Durchschnitts ein größeres Gewicht erhalten. In diesem Fall ist es ratsam, das gewichtete Mittel mit den Creditpunkten als Gewichten zu berechnen.
\[ \overline{x}_w = \frac{\sum x_i w_i}{\sum w_i} = \frac{15\cdot8 + 10\cdot5 + 12\cdot6}{8+5+6} =\frac{242}{19} = 12,74\ \text{Punkte.} \]
3.1.3 Median
Der Median einer Variablen \(X\) ist der Wert, der in der Mitte der geordneten Stichprobe liegt.
Der Median teilt die Stichprobenwerte in zwei gleich große Teile, das heißt, es gibt dieselbe Anzahl von Werten über und unter dem Median.
Der Median kann nicht für nominale Variablen berechnet werden.
3.1.3.1 Nicht-klassierte Daten
Bei nicht-klassierten Daten gibt es zwei Möglichkeiten:
- Gerade Stichprobengröße: Der Median ist der Wert an Position \(\frac{n}{2}\).
- Ungerade Stichprobengröße: Der Median ist das arithmetische Mittel der Werte an den Positionen \(\frac{n}{2}\) und \(\frac{n}{2}+1\).

Verwenden wir die Daten des Beispiels mit der Anzahl an Kindern in Familien. Die Stichprobengröße beträgt 25, was ungerade ist. Daher ist der Median der Wert an Position \(\frac{25+1}{2} = 13\) der sortierten Stichprobe.
\[ 0,0,1,1,1,1,1,1,2,2,2,2,\fbox{2},2,2,2,2,2,2,2,2,2,3,3,4 \]
Der Median liegt also bei 2 Kindern.
Mithilfe der relativen Häufigkeitstabelle ist der Median der kleinste Wert mit einer kumulativen absoluten Häufigkeit \(N_i\) größer oder gleich 13 bzw. einer kumulativen relativen Häufigkeit \(F_i\) größer oder gleich 0,5.
\[ \definecolor{color1}{RGB}{24,81,145} \begin{array}{rrrrr} \hline x_i & n_i & f_i & N_i & F_i\\ \hline 0 & 2 & 0.08 & 2 & 0.08\\ 1 & 6 & 0.24 & 8 & 0.32\\ \rowcolor{coral} \color{white}2 & 14 & 0.56 & 22 & 0.88\\ 3 & 2 & 0.08 & 24 & 0.96\\ 4 & 1 & 0.04 & 25 & 1 \\ \hline \sum & 25 & 1 \\ \hline \end{array} \]
3.1.3.2 klassierte Daten
Sind die Werte in Klassen gruppiert, kann die Berechnung des Median geometrisch hergeleitet werden.
Die Werte unseres Beispiels der Körpergrößen liegen als klassierte Häufigkeitstabelle vor:
| X | \(x_i\) | \(n_i\) | \(f_i\) | \(F_i\) | |
|---|---|---|---|---|---|
| (150,160] | 155 | 2 | 0.07 | 0.07 | |
| (160,170] | 165 | 8 | 0.27 | 0.34 | |
| (170,180] | 175 | 11 | 0.36 | 0.70 | |
| (180,190] | 185 | 7 | 0.23 | 0.97 | |
| (190,200] | 195 | 2 | 0.07 | 1 | |
| \(\sum\) | 30 | 1 |
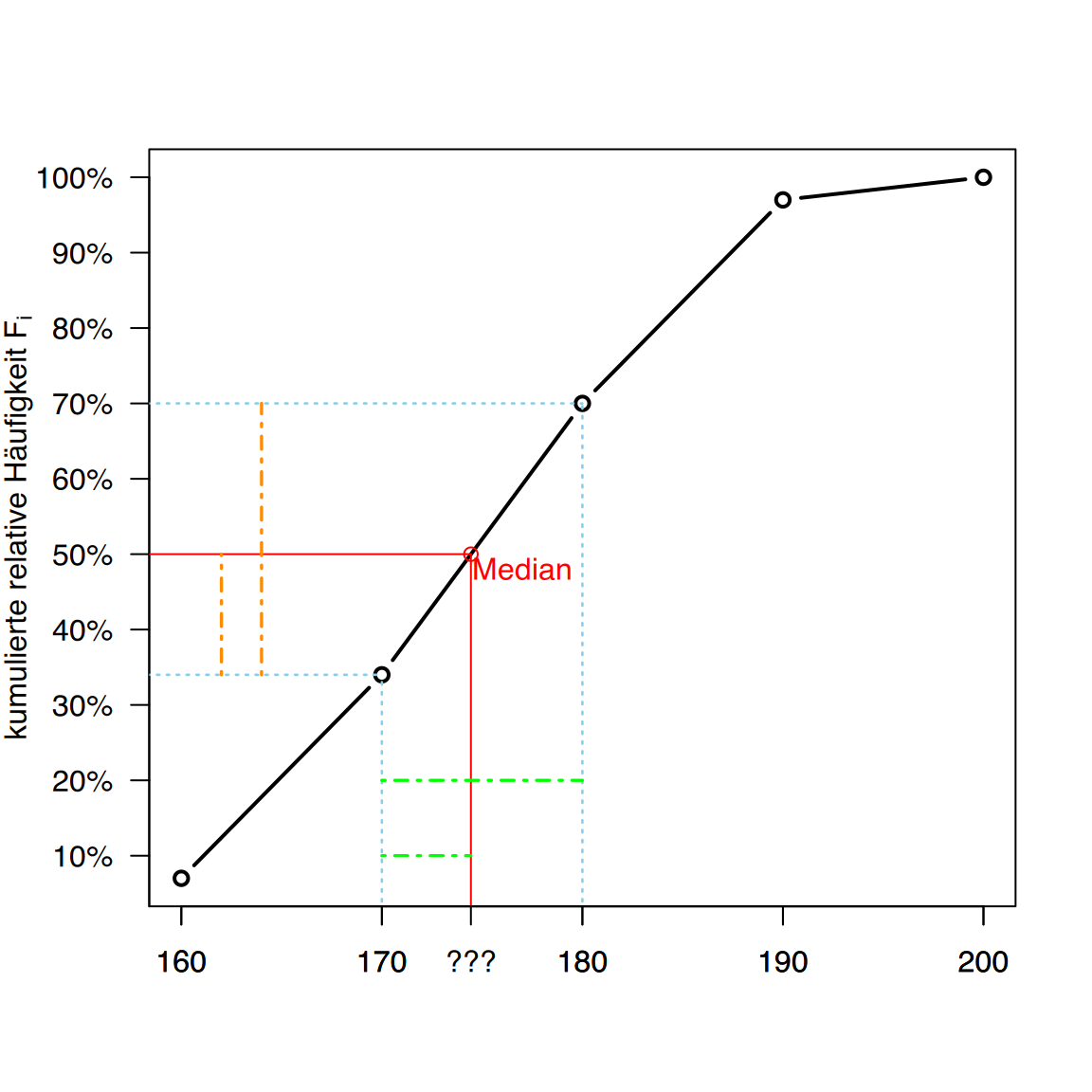
Der Median liegt irgendwo zwischen 170 und 180.
Für die graphische Ermittlung des Medians benötigen wir die kumulierten Prozentwerte \(F_i\), aus denen ein Summenpolygon angefertigt wird. Zusätzlich zeichnen wir ein paar Hilfslinien ein.
Der Median entspricht dem gesuchten Wert “???” auf der \(x\)-Achse.
Aus der Mathematik (Strahlensätze) wissen wir, dass das Verhältnis der beiden grünen Strecken auf der \(x\)-Achse dem Verhältnis der orangenen Strecken auf der \(y\)-Achse entspricht. Setzen wir also die Strecke ins Verhältnis, ergibt sich
\[ \frac{x_Me - x_u}{x_o - x_u} = \frac{50 - y_u}{y_o - y-u} \] Dabei entspricht
- \(x_Me\) dem Median
- \(x_u\) dem unteren Klassengrenze
- \(x_o\) der oberen Klassengrenz
- \(y_u\) der kumulierten relativen Häufigkeit der darunter liegenden Klasse
- \(y_o\) der kumulierten relativen Häufigkeit der Klasse
Die Gleichung kann nun nach \(x_Me\) umgestellt werden.
\[ x_{Me} = x_u + (x_o - x_u) \cdot \frac{50 - y_u}{y_o - y_u} \]
Jetzt können wir unsere Werte einsetzen.
\[ \begin{aligned} \text{Median} &= 170 + (180 - 170) \cdot \frac{50 - 34}{70 - 34}\\ &= 170+ 10\cdot \frac{4}{9} \approx 174,44\\ \end{aligned} \]
3.1.4 Modus
Der Modus oder Modalwert ist der in einer Verteilung am häufigsten auftretende Wert.
Liegen klassierte Daten vor, entspricht der Modalwert der Klassenmitte der Klasse mit der größten Häufigkeit. Die Kategorie (Gruppe, Klasse, etc.) mit den häufigsten Werten nennt man die Modalklasse. Es ist durchaus denkbar, dass innerhalb einer Verteilung mehrere Modalwerte ermittelt werden können. Sind jedoch die Häufigkeiten der Merkmalsausprägungen annähernd gleich verteilt, macht es keinen Sinn, den Modalwert zu bestimmen. Der Modalwert, bzw. die Modalklasse lässt sich für Daten jeglichen Skalenniveaus angeben. Andererseits bietet er für nominale Merkmale die einzige Möglichkeit, etwas typisches über die Verteilung der Merkmalsausprägungen aufzuzeigen.

3.1.4.1 Modusberechnung
Unter Verwendung der Daten der Stichprobe zur Anzahl an Kindern in Familien ist der Wert mit der höchsten Häufigkeit = 2.
\[ \begin{array}{rr} \hline x_i & n_i \\ \hline 0 & 2 \\ 1 & 6 \\ \rowcolor{coral}\color{white} 2 & 14 \\ 3 & 2 \\ 4 & 1 \\ \hline \end{array} \]
Der Modus beträgt also = \(2\) Kinder.
Unter Verwendung der Daten der Stichprobe zur Körpergröße von Studenten ist die Klasse mit der höchsten Häufigkeit (170, 180].
\[ \begin{array}{rr} \hline X & n_i \\ \hline (150,160] & 2 \\ (160,170] & 8 \\ \rowcolor{coral} \color{white}(170,180] & 11 \\ (180,190] & 7 \\ (190,200] & 2 \\ \hline \end{array} \]
Das bedeutet, die modale Klasse ist = \((170, 180]\).
3.1.5 Welchen Lagekennwert soll ich verwenden?
Welche Lagekenngröße hat die größte Aussagekraft bezüglich der Stichprobe? Als Faustregel kann folgende Reihenfolge verwendet werden:
- Mittelwert: Der Mittelwert nutzt mehr Information aus der Stichprobe als die anderen Maße, da er die Größenordnung der Daten berücksichtigt.
- Median: Der Median nutzt weniger Informationen als der Mittelwert, aber mehr als der Modus, da er die Ordnung der Daten berücksichtigt.
- Modus: Der Modus ist das Maß, das am wenigsten Information aus der Stichprobe nimmt, da er nur die absolute Häufigkeit der Werte berücksichtigt.
Der Mittelwert wird stärker von Ausreißern beeinflusst als der Median!
Stellen wir uns vor, die Befragung zur Anzahl an Kinder in 7 Familien ergäbe folgende Werte
0, 0, 1, 1, 2, 2, 15
Dann wären die Lagekenngrößen
- \(\overline x\) = 3 Kinder
- Median = 1 Kind
In diesem Fall hat der Median die größte Aussagekraft bezüglich der Stichprobe.
3.1.6 nicht-zentrale Lagewerte
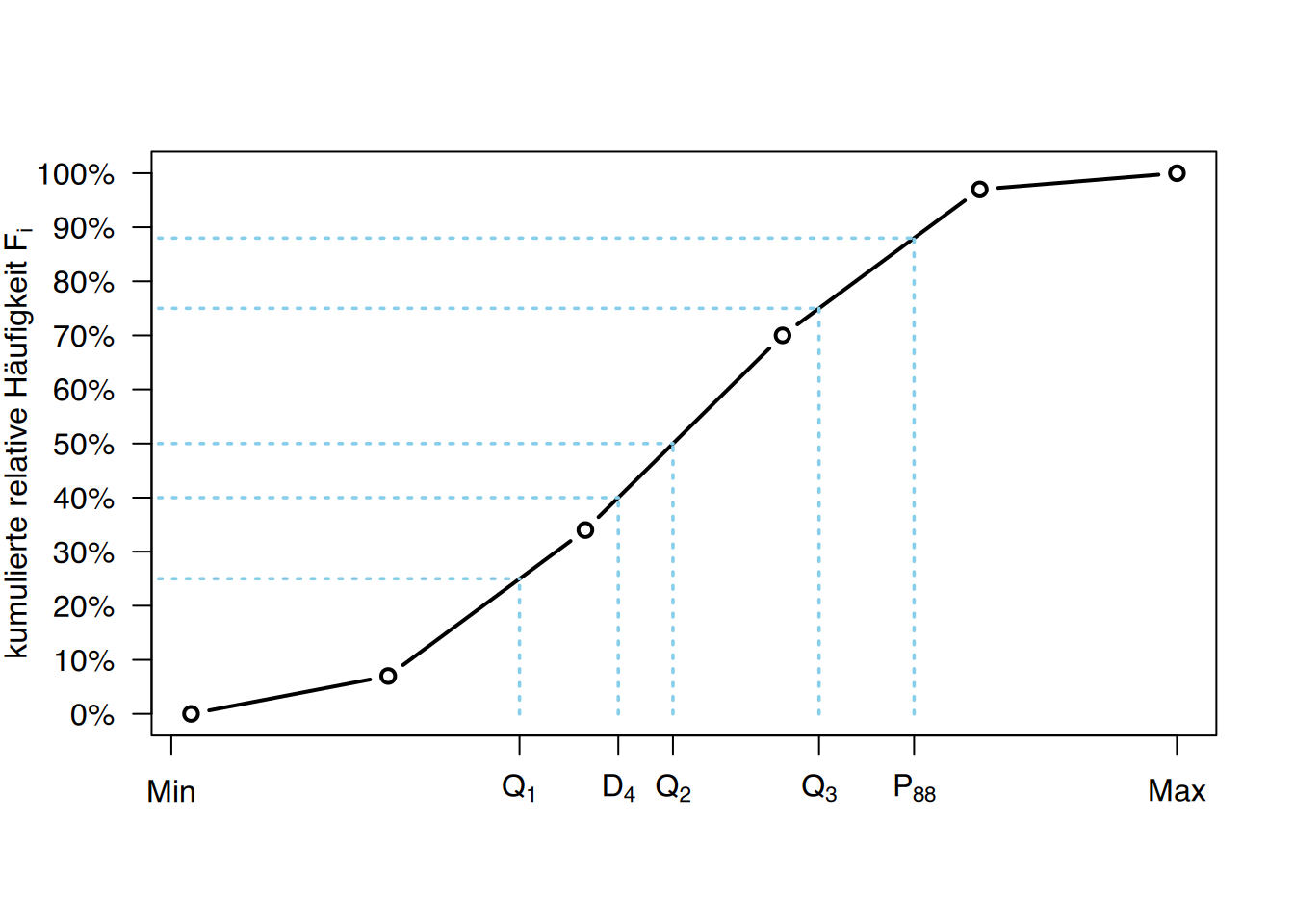
Die nichtzentralen Lagewerte (Quantile) teilen die Stichprobenverteilung in gleich große Teile. Die am häufigsten verwendeten sind:
- Quartile: Teilen die Verteilung in 4 gleich große Teile. Es gibt 3 Quartile:
- \(Q_1\) (25% kumuliert)
- \(Q_2\) (50% kumuliert),
- \(Q_3\) (75% kumuliert).
- Dezile: Teilen die Verteilung in 10 gleich große Teile. Es gibt 9 Dezile:
- \(D_1\) (10% kumuliert),
- \(\vdots\),
- \(D_9\) (90% kumuliert).
- Perzentile: Teilen die Verteilung in 100 gleich große Teile. Es gibt 99 Perzentile:
- \(P_1\) (1% kumuliert),
- \(\vdots\),
- \(P_{99}\) (99% kumuliert).

Beachten Sie, dass es Übereinstimmungen zwischen den Quartilen, Dezilen und Perzentilen gibt es. Zum Beispiel stimmt das erste Quartil mit dem 25. Perzentil überein, und das vierte Dezil stimmt mit dem 40. Perzentil überein.
3.1.6.1 Bestimmung der Quantile
Quantile werden ähnlich wie die Median berechnet. Der einzige Unterschied liegt in der kumulierenden relativen Häufigkeit \(F_i\), die jedem Quantil zugeordnet ist.
Die Häufigkeitstabelle der Anzahl an Kindern in Familien ist
\[ \begin{array}{rr} \hline x_i & F_i \\ \hline 0 & 0.08\\ 1 & 0.32\\ 2 & 0.88\\ 3 & 0.96\\ 4 & 1\\ \hline \end{array} \]
Anhand der Spalte \(F_i\) kann das gewünschte Perzentil, Dezentil oder Quartil abgelesen werden.
\[ \begin{aligned} F_{Q_1}=0.25 &\Rightarrow Q_1 = 1 \text{ Kinder},\\ F_{Q_2}=0.5 &\Rightarrow Q_2 = 2 \text{ Kinder},\\ F_{Q_3}=0.75 &\Rightarrow Q_3 = 2 \text{ Kinder},\\ F_{D_4}=0.4 &\Rightarrow D_4 = 2 \text{ Kinder},\\ F_{P_{92}}=0.92 &\Rightarrow P_{92} = 3 \text{ Kinder}.\\ \end{aligned} \]
Die Bestimmung kann ebenfalls (wie beim Median) geometrisch hergeleitet werden.
3.2 Streuungskenngrößen
Häufigkeitsverteilungen lassen sich nicht nur durch ihre Lage auf der Messwertskala, sonder auch durch ihre Streuung beschreiben.
Streuungskenngrößen sind Maßzahlen zur Bewertung oder Quantifizierung der Variablilität der Messwerte. Es gibt diverse Streuungskenngrößen. Die wichtigsten sind:
- Spannweite \(R\)
- Quartilsabstand \(Q\)
- Varianz \(s^2\)
- Standardabweichung \(s\)
- Variationskoeffizient \(vk\)
3.2.1 Spannweite
Ein besonders einfaches Streuungsmaß ist die Spannweite (auch: Variationsbreite), die mit “\(R\)” (englisch “range”) abgekürzt wird.
Die Spannweite \(R\) bestimmt sich aus der Differenz zwischen dem größten und dem kleinsten Messwert.
\[ R = \max_{x_i} -\min_{x_i} \]

3.2.2 Interquartilsabstand
Der Interquartilsabstand einer Variablen \(x\) ist der Unterschied zwischen dem dritten und dem ersten Stichproben-Quartil.
\[ IQR = Q_3-Q_1 \]
Der IQR gibt die mittleren 50% der Verteilung an. Daher reagiert er - ähnlich wie der Median - robuster auf Ausreisser.

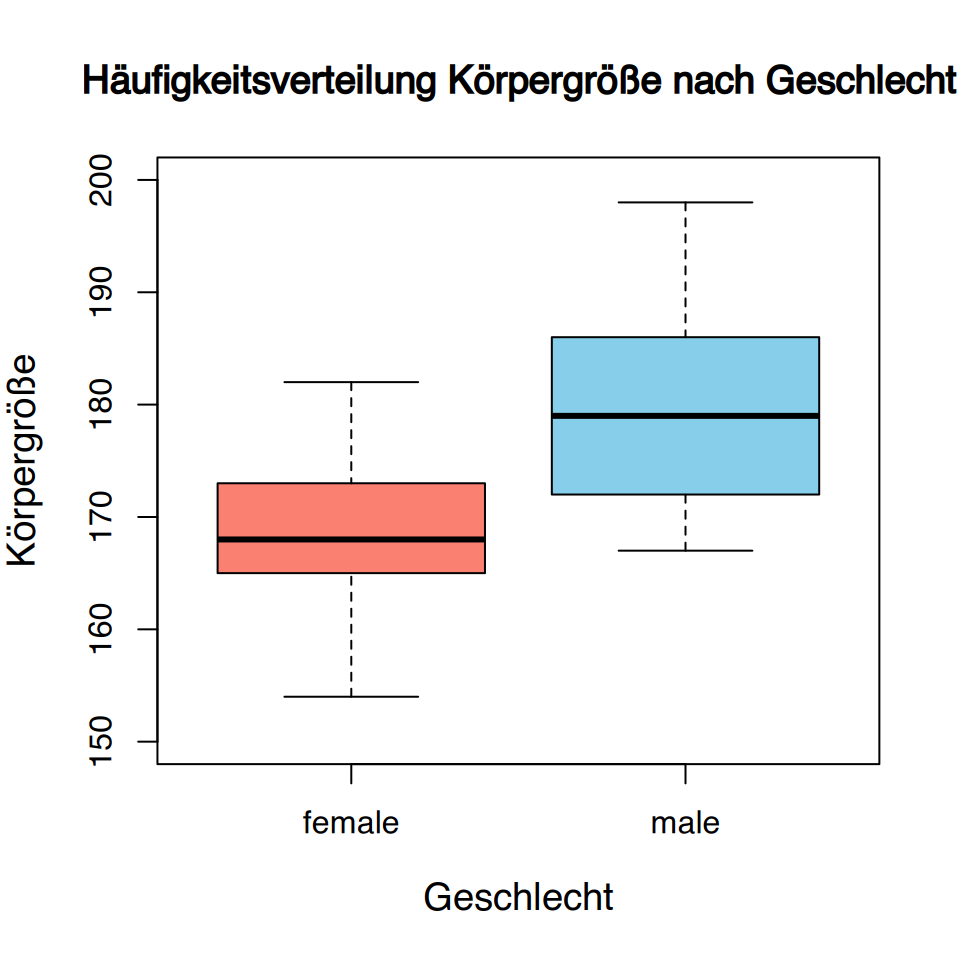
3.2.3 Boxplot
Die Streuung einer Variablen in einer Stichprobe kann graphisch mit einem Boxplot dargestellt werden. An ihm lassen sich die fünf wichtigsten Kennwerte (Minimum, Quartile und Maximum) ablesen.
Es besteht aus einem Block (Box), der vom ersten bis zum dritten Quartil gezeichnet wird. Dies entspricht dem Interquartilsabstand.
Zusätzlich werden an den Rändern zwei Segmenten, die als untere und obere Antennen (Whisker) bezeichnet werden. Normalerweise wird die Box durch den Median in zwei Teile gesplittet.
Das Boxplot erfreut sich großer Beliebtheit, da es mehrere Funktionen erfüllt:
- Es dient zur Einschätzung der Streuung, da es die Spannweite sowie den Interquartilabstand darstellt.
- Es dient zum Erkennen von Ausreißern, die außerhalb der Whiskers liegen.
- Es dient zur Bestimmung der Symmetrie der Verteilung, indem die Länge der Boxen und Whisker über und unter dem Median verglichen werden.
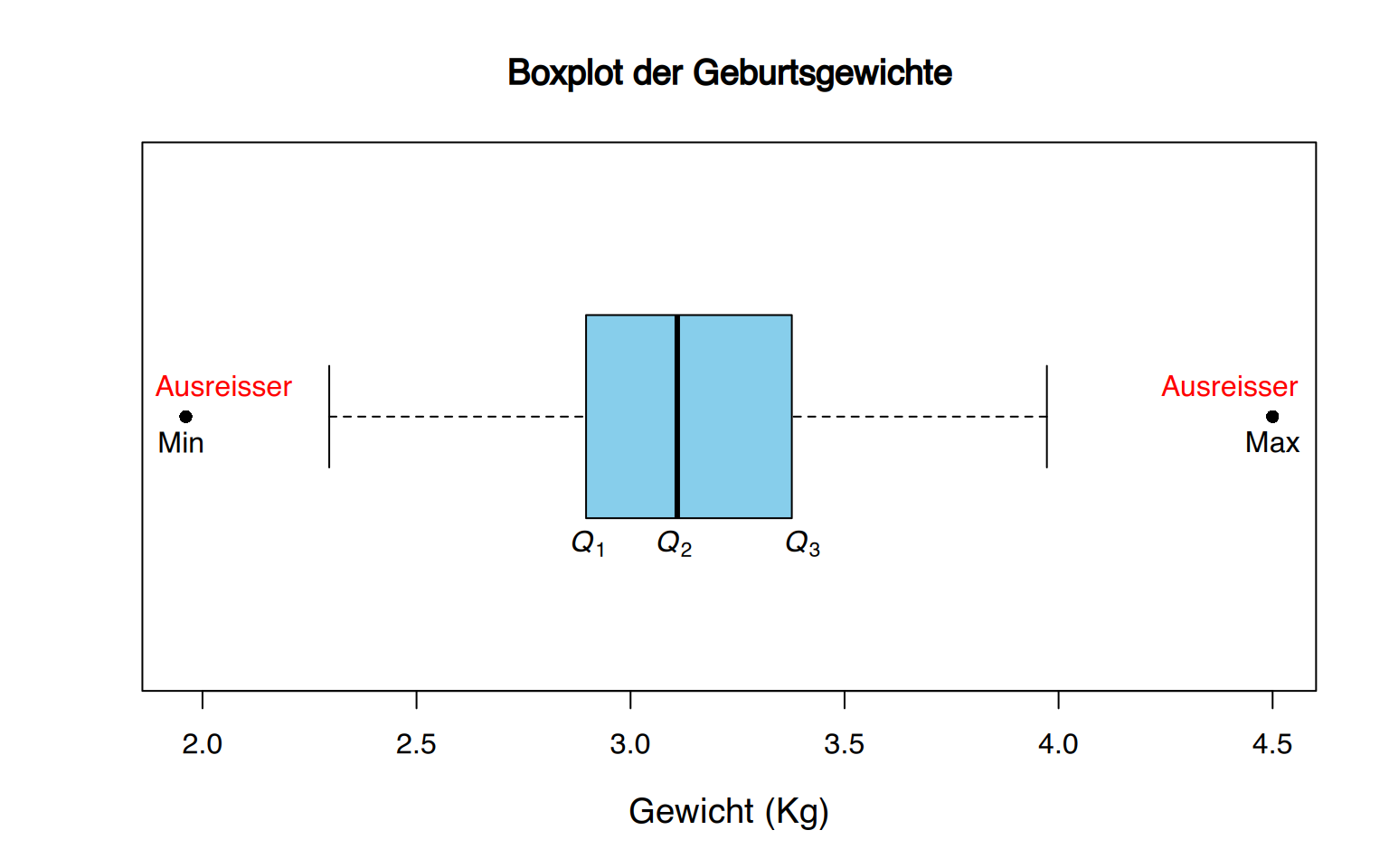
Um einen Boxplot zu erstellen, folgen Sie den nachfolgenden Schritten:
- Berechnen Sie die Quartile.
- Zeichnen Sie eine Box vom ersten zum dritten Quartil.
- Teilen Sie die Box mit dem Median
- Die Whiskers berechnen sich über die Hilfsgrößen \(f_1\) und \(f_2\) wie folgt:
\[ \begin{aligned} f_1&=Q_1-1.5\,\text{IQR}\\ f_2&=Q_3+1.5\,\text{IQR} \end{aligned} \] Diese Grenzen definieren den Bereich, in dem die Daten als normal betrachtet werden. Jeder Wert außerhalb dieses Bereichs wird als Ausreisser betrachtet. Zeichnen Sie für den unteren Whisker einen Strich vom unteren Quartil zum kleinsten Wert in der Stichprobe, der größer oder gleich \(f_1\) ist, und für den oberen Whisker einen Strich vom oberen Quartil zum größten Wert in der Stichprobe, der kleiner oder gleich \(f_2\) ist. 5. Zeichnen Sie schließlich je einen Punkt für alle Werte kleiner \(f_1\) oder größer \(f_2\) (Ausreisser).
3.2.4 Abweichungen zur Mitte
Bei der Abweichungen zur Mitte wird die Entfernung von jedem Wert in der Stichprobe zum Mittelwert gemessen.
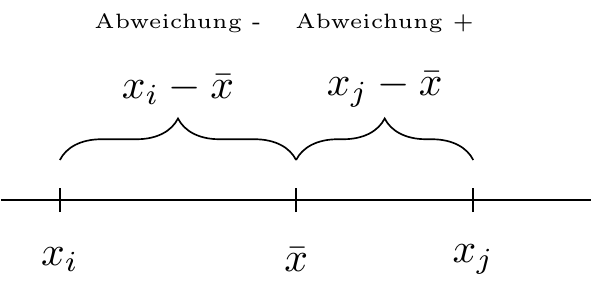
Wenn die Abweichungen groß sind, ist der Mittelwert weniger repräsentativ als bei kleinen Abweichungen.
Üblicherweise wird an dieser Stelle die Summe der quadrierten Abweichungen (SQA) bestimmt, indem die Abweichungen quadriert und aufsummiert werden.
\[ SQA = \sum (x_i - \overline x)^2 \]
3.2.5 Varianz
Die Varianz \(s^2\) ist ein Maß für die Streuung oder Variabilität von Datenwerten. Sie gibt an, wie weit die einzelnen Werte eines Datensatzes im Durchschnitt vom Mittelwert (Durchschnitt) entfernt sind.
\[ s^2 = \frac{SQA}{n-1} = \frac{\sum (x_i - \overline x)^2}{n-1} \]
Die Varianz hat die quadrierte Einheiten der Variablen. Um ihre Deutung zu vereinfachen ist es üblich, ihre Wurzel zu berechnen.
3.2.6 Standardabweichung
Die Standardabweichung \(s\) (auch: \(\sigma\) oder sd (englisch: standard deviation )) ist das wichtigste und bekannteste Maß für die Streuung der Messwerte um den Mittelwert.
\[ s = \sqrt{s^2} = \sqrt{\frac{\sum (x_i - \overline x)^2}{n-1}} \]
Liegen metrische Messwerte vor, so sind das arithmetische Mittel \(\overline x\) und die Standardabweichung \(s\) die wichtigsten Maßwerte, um die Eigenschaften der Messreihe ausreichend zu beschreiben.
3.2.6.1 Interpretation
Varianz und Standardabweichung messen die Ausbreitung der Daten um den Mittelwert herum.
- Wenn die Varianz oder die Standardabweichung klein sind, sind die Werte um den Mittelwert herum konzentriert, und der Mittelwert ist ein gutes repräsentatives Maß.
- Wenn sie groß sind, sind die Stichprobenwerte weit von der Mitte entfernt, und der Mittelwert ist kein guter Repräsentant der Stichprobe.
Von 2 Studierenden wurden die Modulpunkte von 2 Kursen erhoben.
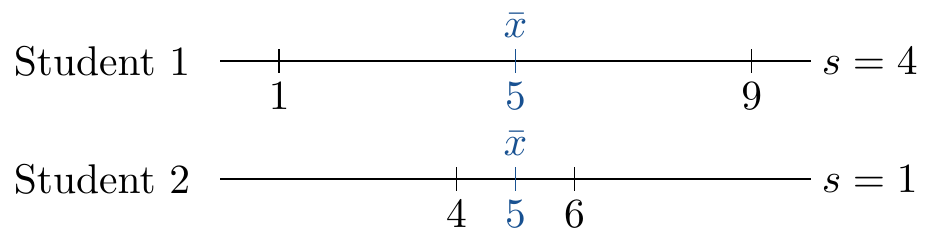
Welcher Mittelwert beschreibt die Leistung besser?
3.2.7 Variationskoeffizient
Um einschätzen zu können, ob die Standardabweichung eher groß oder klein ist, bietet sich der Variationskoeffizient an (englisch coefficient of variance).
Der Variationskoeffizient setzt die Streuung (Standardabweichung) ins Verhältnis zum Mittelwert (\(\overline x\)).
\[ vk = \frac{s}{|\overline x|} \]
Es entsteht ein dezimaler Prozentwert, der den Anteil der Standardabweichung am Mittelwert wiedergibt. Je größer \(vk\) ist, umso mehr streuen die Werte um den Mittelwert. Da er keine Einheiten hat, ist der Variationskoeffizient sehr hilfreich, um die Streuung in Verteilungen verschiedener Variablen zu vergleichen (je kleiner der \(vk\), desto besser).
Bei der Anzahl an Kindern in Familien lag der Mittelwert bei \(\overline x = 1,76\) Kindern und die Standardabweichung bei \(s=0,8616\) Kindern. Der Variationskoeffizient beträgt demnach:
\[ vk = \frac{1,76\ \text{Kinder}}{0,8616\ \text{Kinder}} = 0,49 \] Bei der Stichprobe zur Körpergröße lag der Mittelwert bei \(\overline x = 174,67\) cm und die Standardabweichung bei \(s=10,1\) cm. Der Variationskoeffizient beträgt demnach:
\[ vk = \frac{174,67\ \text{cm}}{10,1\ \text{cm}} = 0,06 \]
Das bedeutet, dass die Streuung in der Verteilung der Körpergrößen geringer ist als in der Verteilung der Anzahl an Kindern, und dass daher der Mittelwert der Körpergröße repräsentativer ist als der Mittelwert der Anzahl an Kindern.
3.3 Formmaße
Formmaße sind Maße, die die Form der Verteilung beschreiben. Besonders wichtige Aspekte sind:
- Schiefe (skewness): misst die Symmetrie der Verteilung hinsichtlich des Mittels.
- Wölbung: (kurtosis) misst die Länge der Verteilungsenden (Schwanz) oder die Spitzigkeit der Verteilung. Das am meisten verwendete
3.3.1 Schiefekoeffizient
Der Stichproben-Schiefekoeffizient \(g_1\) einer Variablen \(X\) ist der Durchschnitt der hoch drei genommenen Abweichungen der Werte vom Stichprobenmittel, geteilt durch die hoch drei genommene Standardabweichung.
\[ g_1 = \frac{\sum (x_i-\bar x)^3 n_i/n}{s^3} = \frac{\sum (x_i-\bar x)^3 f_i}{s^3} \]
Skewness misst die Symmetrie der Verteilung, das heißt, wie viele Werte in der Stichprobe über oder unter dem Mittel liegen und wie weit sie von diesem entfernt sind.
3.3.1.1 Interpretation des Schiefekoeffizienten
Je nach Vorzeichen von \(g_1\) gilt:
- \(g_1 = 0\) bedeutet, dass es dieselbe Anzahl an Werten im Stichprobenmaterial oberhalb und unterhalb des Mittelwerts gibt und diese gleich weit von ihm entfernt sind. Die Verteilung ist symmetrisch.
- \(g_1 < 0\) bedeutet, dass es mehr Werte oberhalb des Mittelwerts als unterhalb davon gibt, aber die darunter liegenden Werte weiter entfernt sind. Die Verteilung ist links-schiefs (sie hat eine längere Schwanzspitze nach links).
- \(g_1 > 0\) bedeutet, dass es mehr Werte unterhalb des Mittelwerts als oberhalb davon gibt, aber die darüber liegenden Werte weiter entfernt sind. Die Verteilung ist rechts-schiefs (sie hat eine längere Schwanzspitze nach rechts).
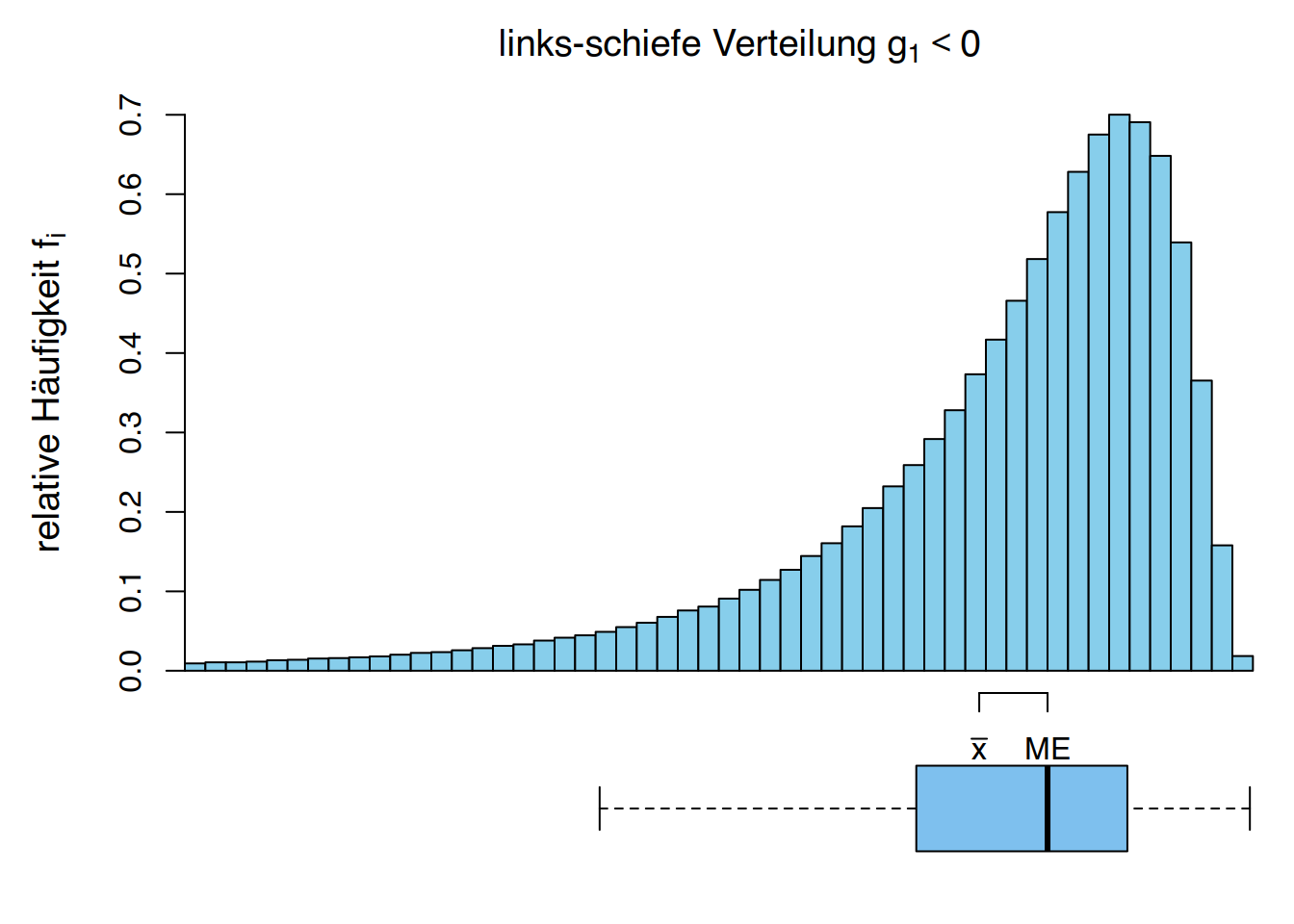
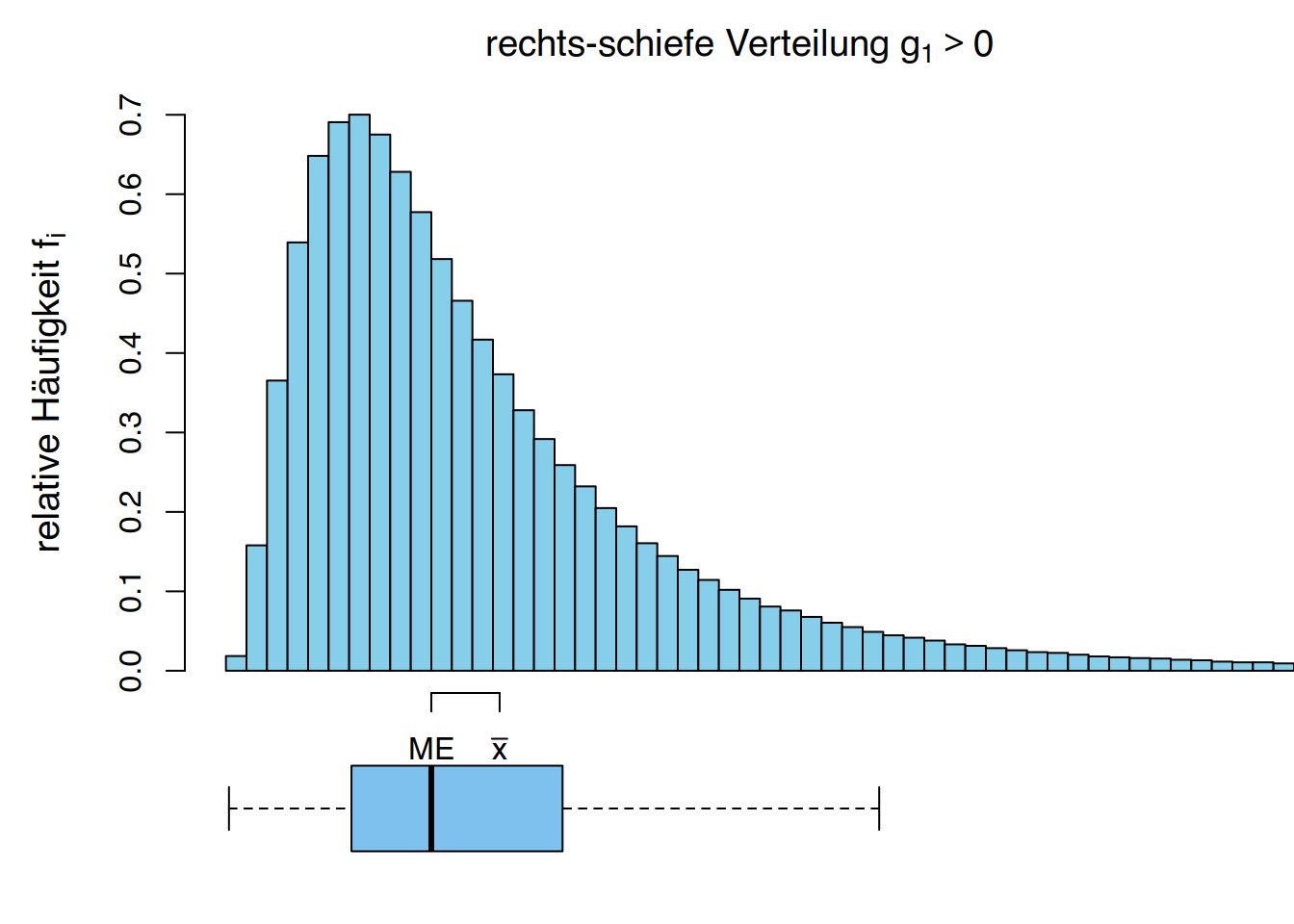
Verwenden wir die Daten der Körpergrößen von Studierenden, können wir der Häufigkeitstabelle eine weitere Spalte mit den kubierten Abweichungen vom Mittelwert \(\overline x = 174,67\) cm hinzufügen:
\[ \begin{array}{rrrrr} \hline {X} & {x_i} & {n_i} & {x_i-\bar x} & {(x_i-\bar x)^3\cdot n_i} \\ \hline (150,160] & 155 & 2 & -19.67 & -15221.00\\ (160,170] & 165 & 8 & -9.67 & -7233.85\\ (170,180] & 175 & 11 & 0.33 & 0.40\\ (180,190] & 185 & 7 & 10.33 & 7716.12\\ (190,200] & 195 & 2 & 20.33 & 16805.14\\ \hline \sum & & 30 & & 2066.81 \\ \hline \end{array} \]
Die Skewness berechnet sich nun wie folgt:
\[ g_1 = \frac{\sum (x_i-\bar x)^3n_i/n}{s^3} = \frac{2066,81/30}{10,1^3} = 0,07. \]
Der Wert liegt nahe bei \(0\), was bedeutet, dass die Verteilung nahezu symmetrisch (normalverteilt) ist.
3.3.2 Wölbungskoeffizient
Der Wölbungskoeffizient \(g_2\) (coefficient of kurtosis) einer Variablen \(X\) ist der Durchschnitt der zur vierten Potenz erhobenen Abweichungen der Werte vom Stichprobenmittelwert, geteilt durch die Standardabweichung hoch vier, und anschließend minus 3.
\[ g_2 = \frac{\sum (x_i-\bar x)^4 n_i/n}{s^4}-3 = \frac{\sum (x_i-\bar x)^4 f_i}{s^4}-3 \]
Der Koeffizient misst die Konzentration der Werte um die Mitte und die Länge der Schwanzenden der Verteilung. Die Normalverteilung dient als Bezugsgröße.
3.3.2.1 Interpretation des Wölbungskoeffizienten
Je nach Vorzeichen von \(g_1\) gilt:
- \(g_2 = 0\) zeigt an, dass die Wölbung normal ist, das heißt, die Konzentration der Werte um den Mittelwert wie bei einer gaußschen Glockenkurve (mesokurtisch).
- \(g_2 < 0\) zeigt an, dass die Wölbung weniger als normal ist, das heißt, die Konzentration der Werte um den Mittelwert ist geringer als bei einer gaußschen Glockenkurve (plattikurtisch).
- \(g_2 > 0\) zeigt an, dass die Kurtosis größer als normal ist, das heißt, die Konzentration der Werte um den Mittelwert ist größer als bei einer gaußschen Glockenkurve (leptokurtisch).
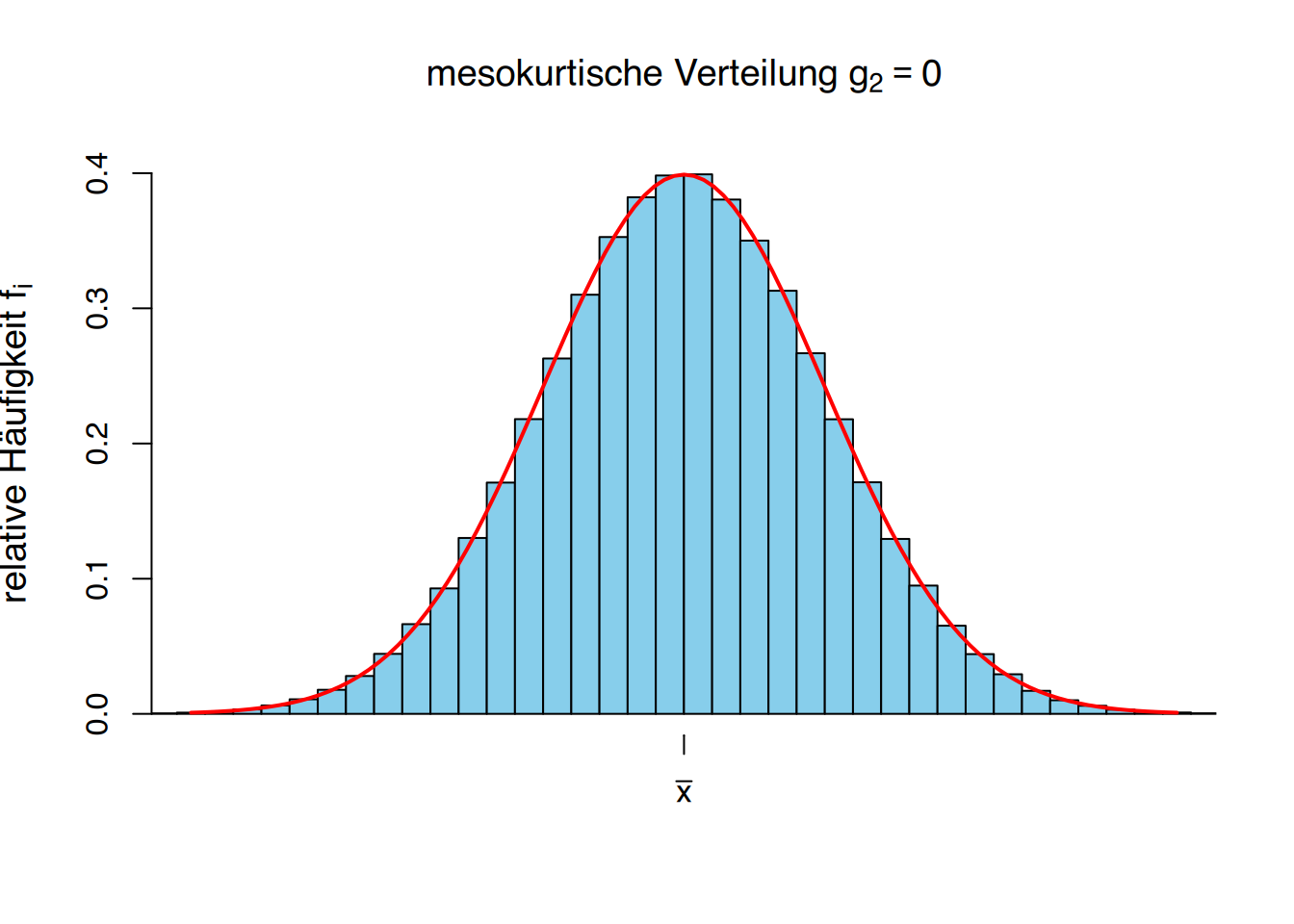
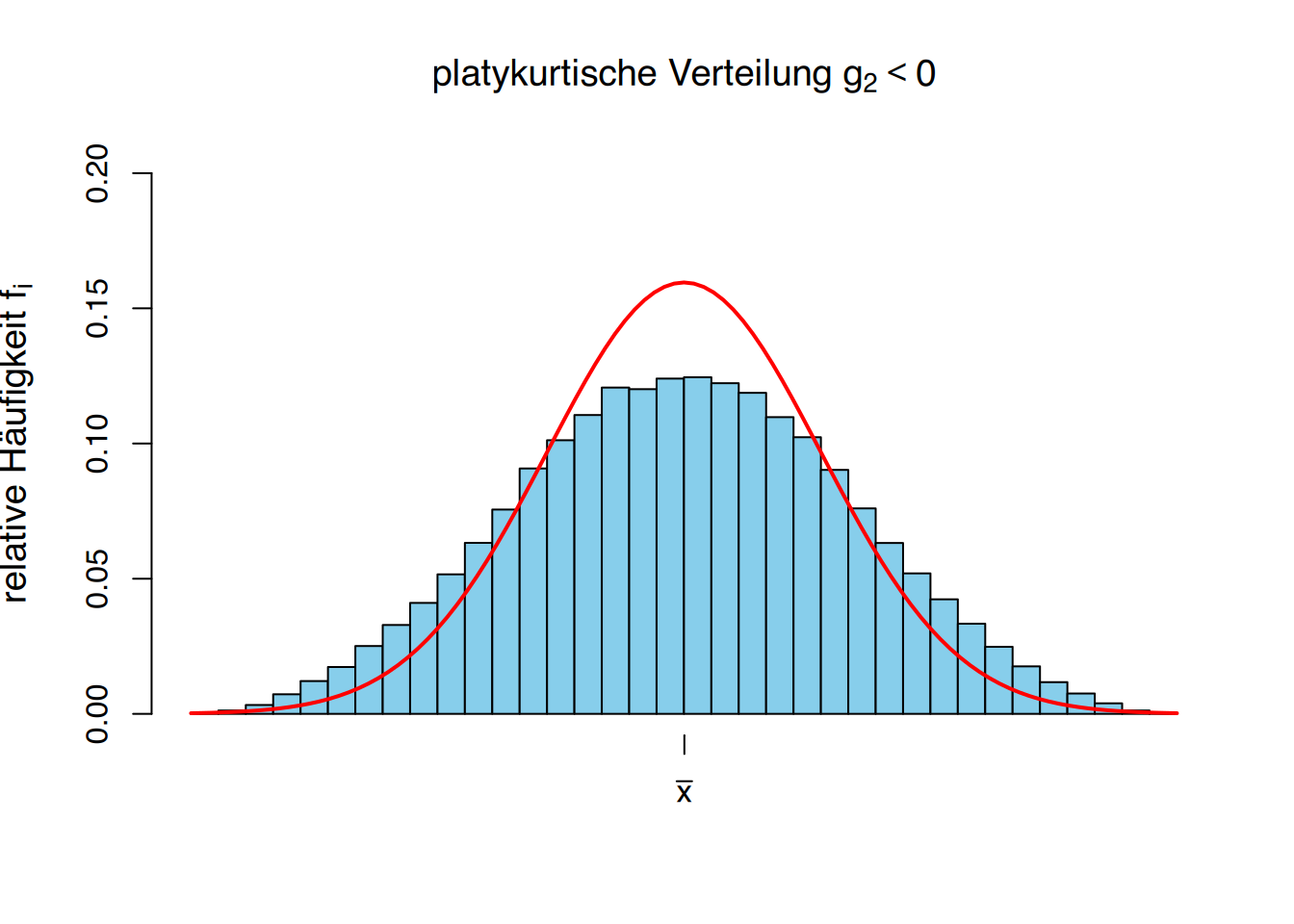
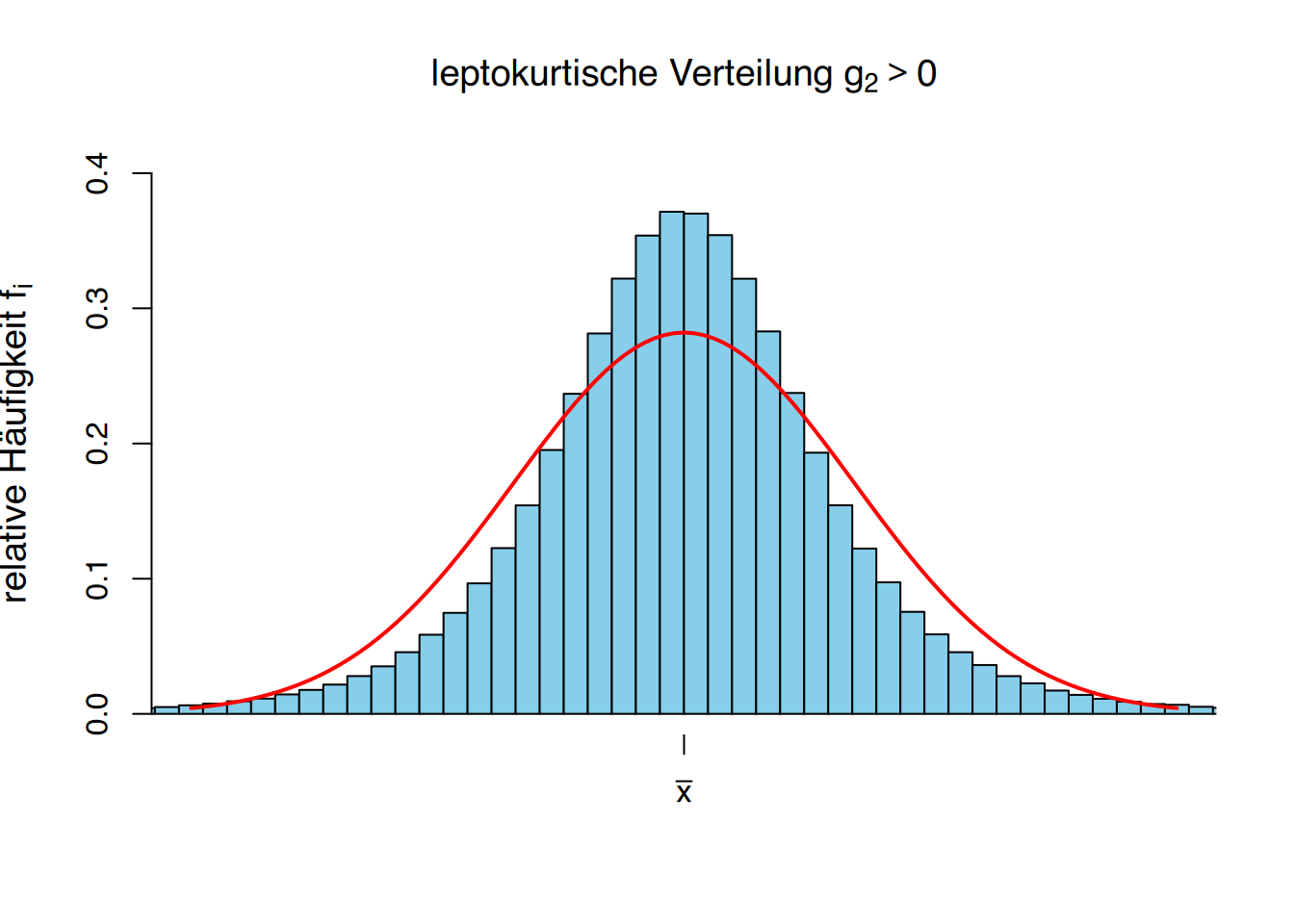
Verwenden wir die die Häufigkeitstabelle der Körpergrößen von Studierenden, können wir eine neue Spalte mit den Abweichungen vom Mittelwert \(\overline x = 174,67\) cm zur vierten Potenz hinzufügen.
\[ \begin{array}{rrrrr} \hline {X} & {x_i} & {n_i} & {x_i-\bar x} & {(x_i-\bar x)^4 n_i} \\ \hline (150,160] & 155 & 2 & -19.67 & 299396.99\\ (160,170] & 165 & 8 & -9.67 & 69951.31\\ (170,180] & 175 & 11 & 0.33 & 0.13\\ (180,190] & 185 & 7 & 10.33 & 79707.53\\ (190,200] & 195 & 2 & 20.33 & 341648.49\\ \hline \sum & & 30 & & 790704.45 \\ \hline \end{array} \] Nun kann die Kurtosis wie folgt berechnet werden:
\[ g_2 = \frac{\sum (x_i-\bar x)^4n_i/n}{s^4} - 3 = \frac{790704.45/30}{10.1^4}-3 = -0.47. \]
Der Wert ist negativ, aber nahe bei \(0\). Das bedeutet, dass die Kurve leicht platykurtisch (niedriger als normalverteilt) ist.
Wie wir im Kapitel zur schließenden Statistik sehen werden, können viele statistische Tests nur auf normalverteilte (glockenförmigen) Verteilungen angewendet werden.
Normalverteilungen sind symmetrisch und mesokurtisch, weshalb ihre Symmetriekoeffizienten und Kurtosiskoeffizienten den Wert 0 haben. Daher ist eine Möglichkeit, eine Variable auf Normalverteilung zu testen, die Abweichungen der Skewness- und Kurtosis-Koeffizienten von 0 zu betrachten.
Im Allgemeinen wird die Normaverteilung abgelehnt, wenn \(g_1\) oder \(g_2\) außerhalb des Intervalls \([−2, 2]\) liegen. In diesem Fallist es üblich, eine Transformation anzuwenden, um diese Abweichung zu korrigieren.
3.4 Transformationen
In vielen Fällen werden die rohen Stichprobendaten transformiert, um eine passendere Skala zu erhalten, oder um Daten zu korrigieren, die nicht normalverteilt sind.
Nehmen wir z.B. folgende Werte zur Körpergröße
\[ 1.75m, 1.65m, 1.80m, \]
Wenn die Werte mit \(100\) multipliziert werden, ändert sich die Einheit von Meter in Zentimeter, und aus den Dezimalzahlen werden ganze Zahlen.
\[ 175cm, 165cm, 180cm, \]
Darüber hinaus ist es möglich, die Größen der Werte durch Subtraktion des kleinsten Wertes in der Stichprobe zu verringern. In unserem Beispiel würden wir von jedem Wert \(165\) cm abziehen:
\[ 10 cm, 0 cm, 15 cm \]
Es ist offensichtlich, dass diese Daten leichter zu handhaben sind als die ursprünglichen. Im Grunde haben wir folgende Transformation auf die Daten angewendet:
\[ Y= 100\cdot X-165 \]
3.4.1 lineare Transformation
Eine der am häufigsten verwendeten Transformationen ist die lineare Transformation:
\[ Y=a+b\cdot X \]
Bei der linearen Transformation veränderen sich das arithmetische Mittel und die Standardabweichung der transformierten Variablen wie folgt:
\[ \begin{aligned} \bar y &= a+ b\bar x,\\ s_{y} &= |b|s_{x} \end{aligned} \]
Zudem bleibt der Wölbungskoeffizient (Kurtosis) unverändert, während der Koeffizient der Schieflage (Skewness) nur das Vorzeichen ändert, falls \(b\) negativ ist.
3.4.1.1 Standardisierung und z-Transformation
Die standardisierte Variable \(Z\) einer Variablen \(X\) ist die Variable, die durch Abzug des Mittelwertes von \(X\) und anschließendes Dividieren durch die Standardabweichung entsteht:
\[ Z = \frac{X − \bar{x}}{s_x} \]
Für jeden Wert \(x_i\) der Stichprobe ist der Standardiserungsscore (\(z\)-Wert) der Wert, der durch Anwendung der Standardisierungstransformation entsteht:
\[ z_i = \frac{x_i − \bar{x}}{s_x} \]
Der Standardiserungsscore gibt die Anzahl an Standardabweichungen an, um welche ein Wert über oder unter dem Mittelwert liegt, und ist nützlich, um die Abhängigkeit der Variablen von ihren Maßeinheiten zu vermeiden. Die standardisierte Variable hat immer einen Mittelwert von \(0\) und eine Standardabweichung von \(1\).
\[ \bar z = 0 \qquad s_{z} = 1 \]
Die Leistungspunkte von 5 Studierenden in 2 Fächern sind
\[ \begin{array}{rccccccccc} \mbox{Student:} & Hans & Tina & Kim & Flo & Karl\\\hline Mathe: & 2 & 5 & 4 & \cellcolor{coral} \color{white}\mathbf{8} & 6 & \qquad & \bar x = 5 & \quad s_x = 2\\ Musik: & 1 & 9 &\cellcolor{coral} \color{white} \mathbf{8} & 5 & 2 & \qquad & \bar y = 5 & \quad s_y = 3.16\\ \end{array} \] Hat Student Flo im Fach Mathe mit 8 Punkten eine bessere Leistung erbracht als Studentin Kim im Fach Musik (ebenfalls 8 Punkte)?
Es mag den Anschein haben, dass Kim und Flo die gleiche Leistung in den Fächern erbracht haben, da sie die gleichen Leistungspunkte erzielen. Aber um die Leistung der Studierenden zum Rest der Gruppe zu bestimmen, müssen wir die Abweichungen der Leitungspunkte in jedem Fach betrachten. Aus diesem Grund ist es besser, die \(z\)-Werte als Maßstab für die Leistungsfähigkeit zu verwenden.
\[ \begin{array}{cccccc} Mathe: & -1.5 & 0 & -0.5 & \cellcolor{coral} \color{white}\mathbf{1.5} & 0.5 \\ Musik: & -1.26 & 1.26 &\cellcolor{coral} \color{white} \mathbf{0.95} & 0 & -0.95\\ \end{array} \]
Nun ist erkennbar, dass Flo mit 8 Punkten im Fach Mathe um 1,5 Standardabweichungen über dem Leistungsdurchschnitt liegt, während Kim mit 8 Punkten im Fach Musik nur um 0,95 Standardabweichungen über dem Leistungsmittelwert liegt. In Relation zu allen Studierenden hat Flo eine bessere Leistung erbracht als Kim.
Fragen wir uns nun, wer der beste Studierende ist.
\[ \begin{array}{rccccc} \mbox{Student:} & Hans & Tina & Kim & Flo & Karl\\\hline Mathe: & 2 & 5 & 4 & 8 & 6 \\ Musik: & 1 & 9 & 8 & 5 & 2 \\ \hline \sum & 3 &\cellcolor{coral} \color{white} \mathbf{14} & 12 & 13 & 8 \end{array} \]
Wenn wir nur den Leistungspunktsummen folgen, ist dies Studentin Tina mit insgesamt 14 Punkten.
Wenn wir allerdings die relative Leistung betrachten und die \(z\)-transformierten Werte aufsummieren…
\[ \begin{array}{rccccc} \mbox{Student:} & Hans & Tina & Kim & Flo & Karl\\\hline Mathe: & -1.5 & 0 & -0.5 & 1.5 & 0.5 \\ Musik: & -1.26 & 1.26 & 0.95 & 0 & -0.95\\ \hline \sum & -2.76 & 1.26 & 0.45 &\cellcolor{coral} \color{white} \mathbf{1.5} & -0.45 \end{array} \] …ist Student Flo der beste.
3.4.2 nicht-lineare Transformation
Nicht-lineare Transformationen werde verwendet, um die Nicht-Normalität der Verteilungen zu korrigieren.
Die Quadrat-Transformation \(Y = X^2\) verringert kleine Werte und verstärkt große Werte. Daher wird sie verwendet, um links-schiefe Verteilungen zu korrigieren.
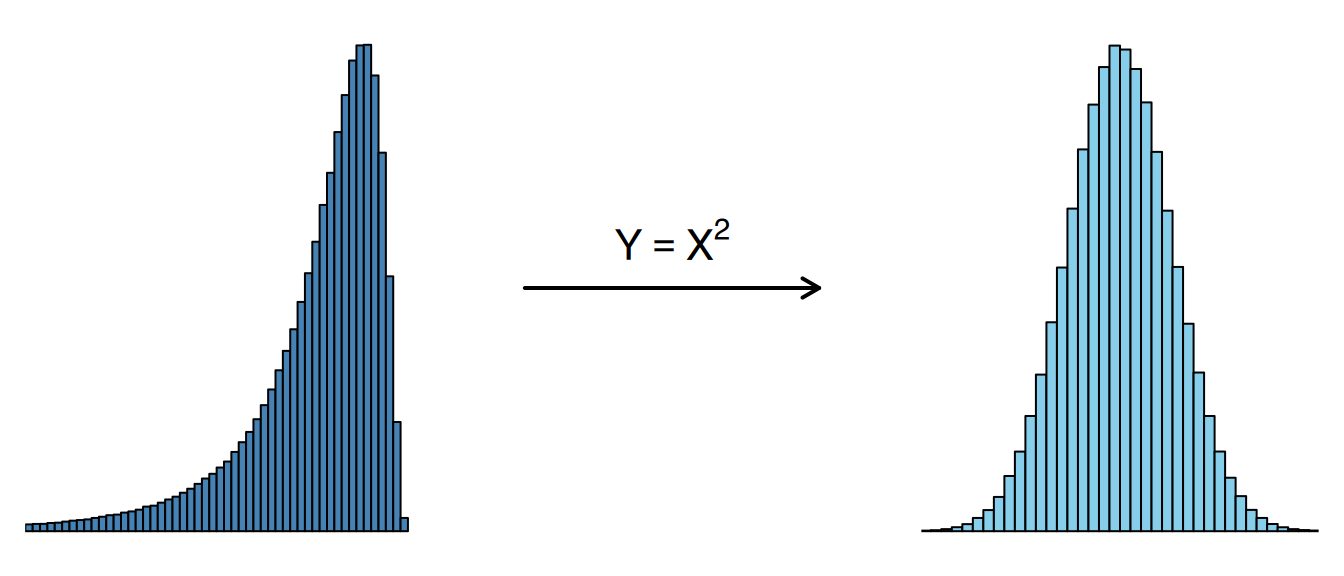
Die Wurzeltransformation \(Y = \sqrt{X}\), die logarithmische Transformation \(Y = \log(X)\) und die inverse Transformation \(Y = \frac{1}{X}\) verringern große Werte und verstärken kleine Werte. Daher werden sie verwendet, um rechts-schiefe Verteilungen zu korrigieren.
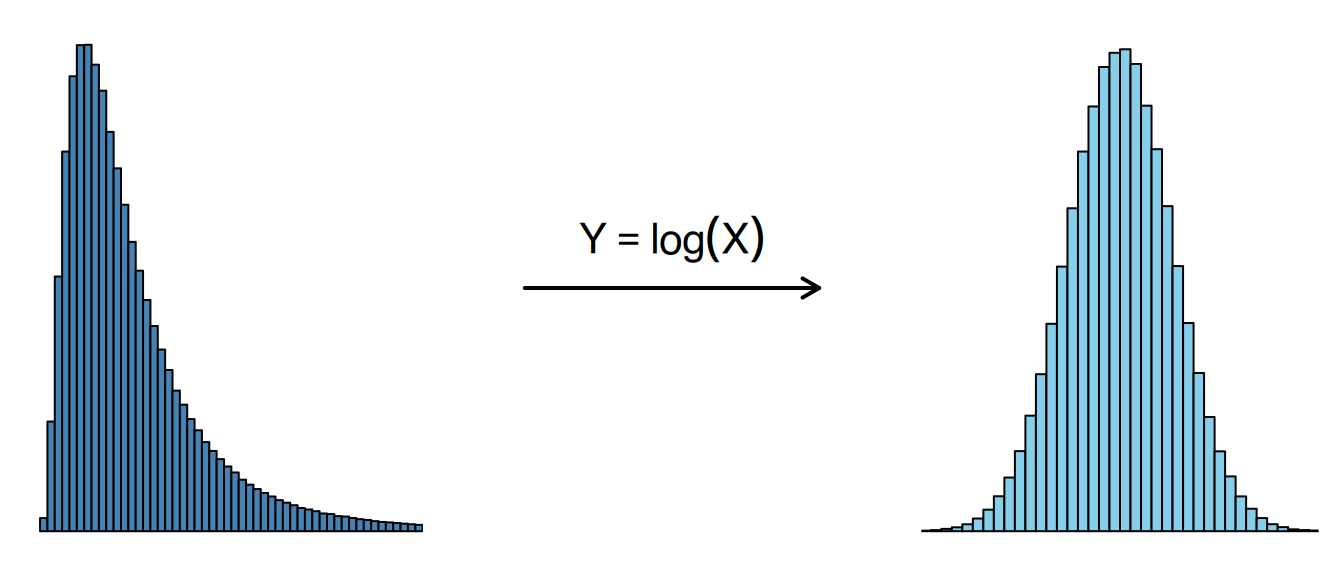
3.4.2.1 Faktoren
Manchmal ist es interessant, die Häufigkeitsverteilung der Stichprobe für verschiedene Teilproben zu beschreiben, die den Kategorien einer anderen Variablen entsprechen (z.B Geschlecht oder Beruf). Solche Klassifikationsvariablen werden als Faktor bezeichnet.
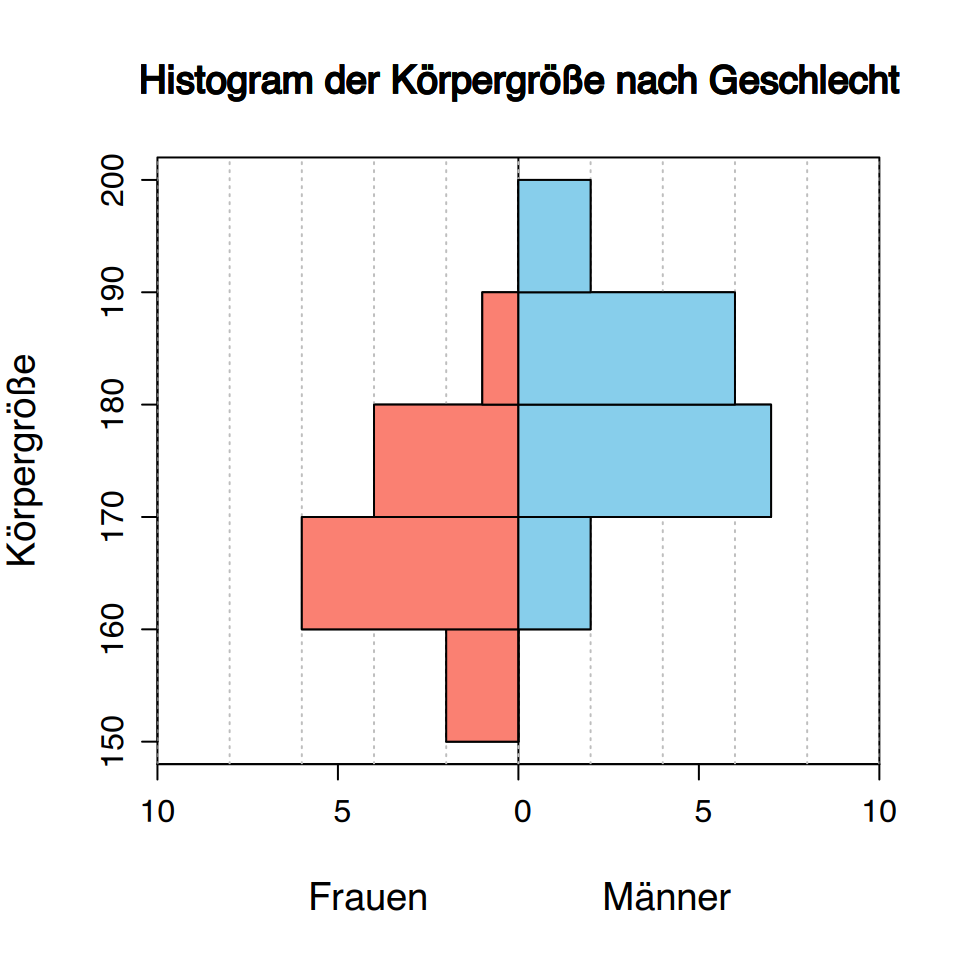
Das Aufteilen der Stichprobe “Körpergrößen” nach der Variable “Geschlecht” ergibt zwei Teilproben.
\[ \begin{array}{lll} \hline \textit{Frauen} & 173, 158, 174, 166, 162, 177, 165, 154, 166, 182, \\ & 169, 172, 170, 168. \\ \hline \textit{Männer} & 179, 181, 172, 194, 185, 187, 198, 178, 188, 171,\\ & 175, 167, 186, 172, 176, 187. \\ \hline \end{array} \]