6 Diskrete Zufallsvariablen
6.1 Zufallsvariable
Das Ziehen einer Probe auf zufällige Weise ist ein Zufallsexperiment und jede Variable, die in der Probe gemessen wird, ist eine Zufallsvariable, da die Werte, die die Variable bei den Individuen der Probe annimmt, dem Zufall unterliegen.
Definition “Zufallsvariable”
Eine Zufallsvariable \(X\) ist eine Funktion, die jedes Element einer Zufallsstichprobe auf eine reelle Zahl abbildet.
\[ X:\Omega \rightarrow \mathbb{R} \]
Der Satz von Werten, den die Variable annehmen kann, wird Reichweite (range) genannt und durch \(Ran(X)\) dargestellt.
Im Grunde genommen ist eine Zufallsvariable eine Variable, deren Werte aus einem Zufallsexperiment stammen und jeder Wert hat eine bestimmte Wahrscheinlichkeit für das Auftreten.
Beispiel Würfel
Die Variable \(X\), die das Ergebnis des Würfelns misst, ist eine Zufallsvariable und ihre Reichweite ist
\[ \mbox{Ran}(X)=\{1,2,3,4,5,6\} \]
6.1.1 Arten von Zufallsvariablen
Es gibt zwei Arten von Zufallsvariablen:
- Diskret: Sie nehmen isolierte Werte an und ihre Reichweite ist abzählbar, zum Beispiel Anzahl der Kinder einer Familie, Anzahl gerauchter Zigaretten, Anzahl bestandener Prüfungen usw.
- Kontinuierlich: Sie können jeden Wert in einem echten Intervall annehmen und ihre Reichweite ist nicht abzählbar, z.B. Beispiel Gewicht, Größe, Alter, Cholesterinspiegel usw.
Die Art der Modellierung ist für jede Art von Variable unterschiedlich. In diesem Kapitel werden wir untersuchen, wie diskrete Zufallsvariablen modelliert werden.
6.2 Wahrscheinlichkeitsverteilung diskreter Zufallsvariablen
Da die Werte einer diskreten Zufallsvariablen mit den elementaren Ereignissen eines Zufallsexperiments verknüpft sind, hat jeder Wert eine Wahrscheinlichkeit.
Definition “Wahrscheinlichkeitsfunktion”
Die Wahrscheinlichkeitsfunktion einer diskreten Zufallsvariablen \(X\) ist die Funktion \(f(x)\), die jeden Wert \(x_i\) der Variablen auf seine Wahrscheinlichkeit abbildet,
\[ f(x_i) = P(X=x_i). \]
Wir können auch Wahrscheinlichkeiten auf die gleiche Weise kumulieren wie wir Häufigkeiten in der Stichprobe kumuliert haben.
Definition “Verteilungsfunktion”
Die Verteilungsfunktion einer diskreten Zufallsvariablen \(X\) ist die Funktion \(F(x)\), die jeden Wert \(x_i\) der Variablen auf die Wahrscheinlichkeit abbildet, einen Wert kleiner oder gleich \(x_i\) zu haben,
\[ F(x_i) = P(X\leq x_i) = f(x_1)+\cdots +f(x_i). \]
Der Bereich einer diskreten Zufallsvariablen und ihre Wahrscheinlichkeitsfunktion wird als Wahrscheinlichkeitsverteilung der Variablen bezeichnet und normalerweise in einer Tabelle dargestellt:
\[ \begin{array}{|c|cccc|c|} \hline X & x_1 & x_2 & \cdots & x_n & \sum\\ \hline f(x) & f(x_1) & f(x_2) & \cdots & f(x_n) & 1\\ \hline F(x) & F(x_1) & F(x_2) & \cdots & F(x_n) =1 & \\\hline \end{array} \]
Auf die gleiche Weise, wie die Tabelle der Häufigkeiten in der Stichprobe die Verteilung der Werte einer Variablen in der Stichprobe zeigt, zeigt die Wahrscheinlichkeitsverteilung einer diskreten Zufallsvariablen die Verteilung der Werte in der Gesamtpopulation.
Beispiel Münzenwurf
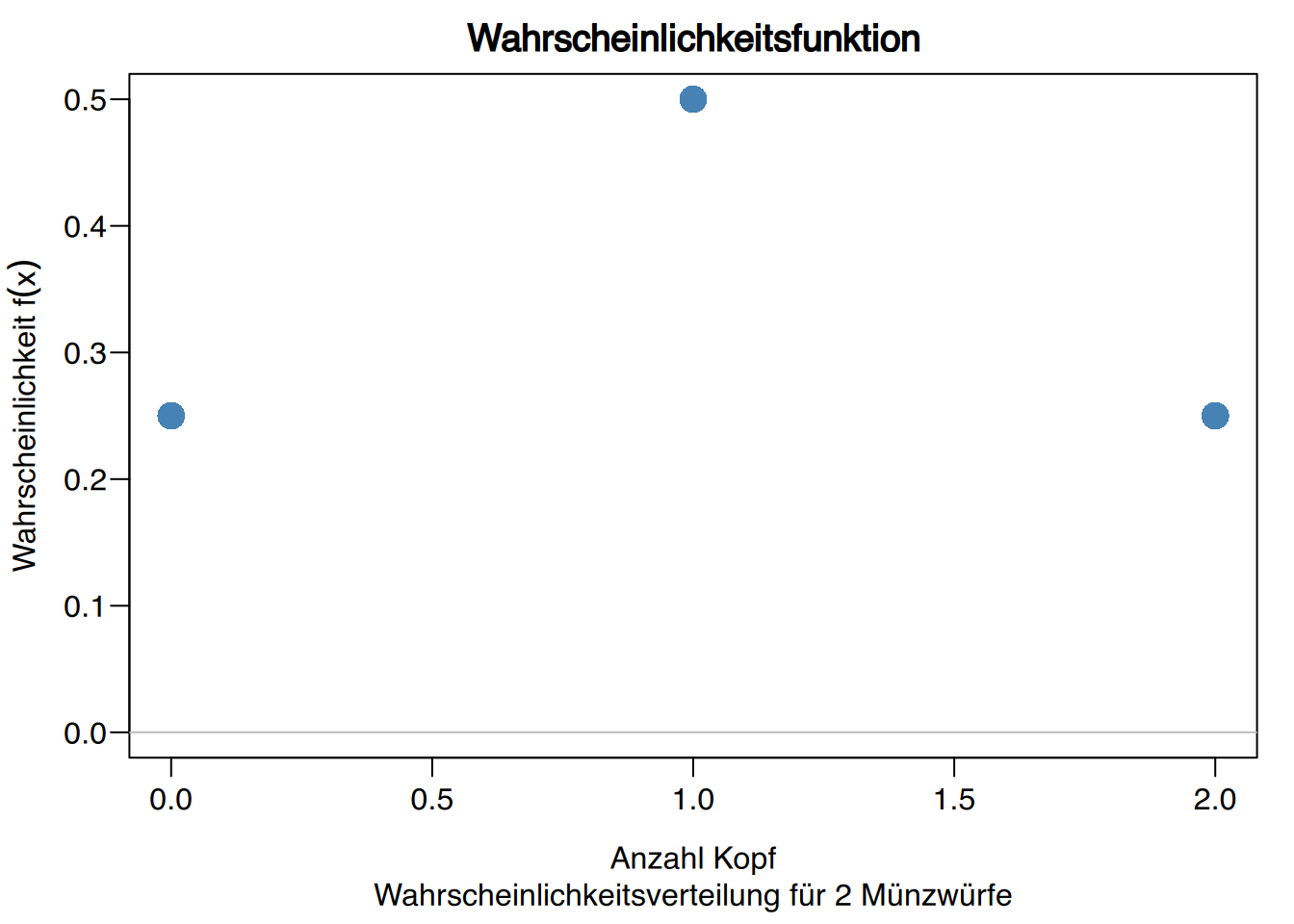
Sei \(X\) die diskrete Zufallsvariable, die die Anzahl der Köpfe nach dem Werfen von zwei Münzen misst. Der Wahrscheinlichkeitbaum des Wahrscheinlichkeitsraums des Zufallsexperiments ist wie folgt dargestellt.
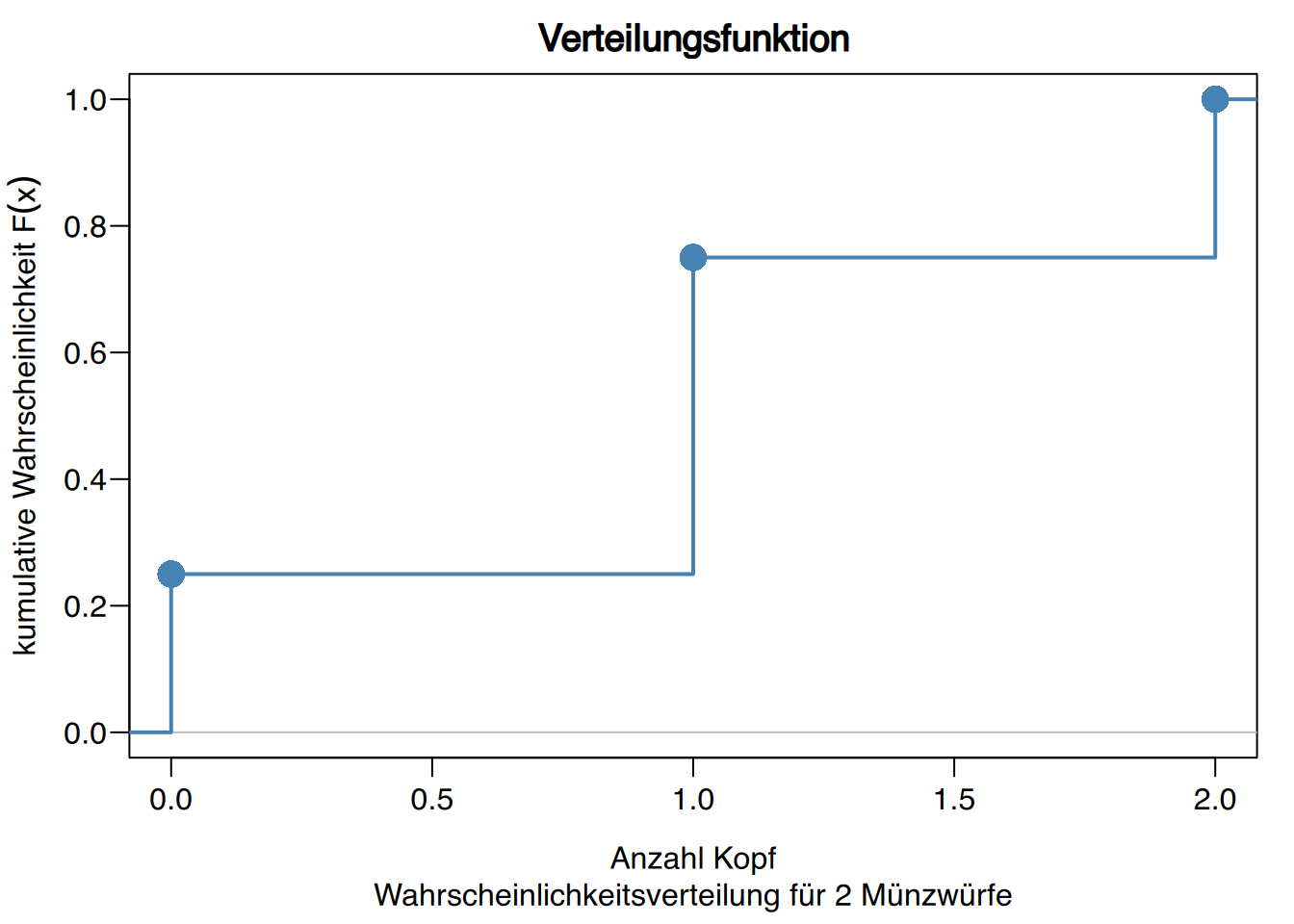
Die Wahrscheinlichkeitsverteilung ist daher
\[ \begin{array}{|c|ccc|} \hline X & 0 & 1 & 2\\ \hline f(x) & 0.25 & 0.5 & 0.25\\ \hline F(x) & 0.25 & 0.75 & 1 \\ \hline \end{array} \qquad F(x) = \left\{ \begin{array}{ll} 0 & \text{wenn } x < 0 \\ 0{,}25 & \text{wenn } 0 \leq x < 1 \\ 0{,}75 & \text{wenn } 1 \leq x < 2 \\ 1 & \text{wenn } x \geq 2 \end{array} \right. \]
6.2.1 Populationsstatistik
Auf die gleiche Weise, wie wir Stichprobestatistiken verwenden, um die Häufigkeitsverteilung einer Variablen in der Stichprobe zu beschreiben, verwenden wir Populationsstatistiken, um die Wahrscheinlichkeitsverteilung einer Zufallsvariablen in der Gesamtpopulation zu beschreiben.
Die Definition von Populationsstatistiken entspricht analog der Definition von Stichprobestatistiken, jedoch unter Verwendung von Wahrscheinlichkeiten anstelle von relativen Häufigkeiten.
Die wichtigsten sind:
- Mittelwert: \(\quad\mu = E(X) = \sum_{i=1}^n x_i f(x_i)\)
- Varianz: \(\quad \sigma^2 = Var(X) = \sum_{i=1}^n x_i^2 f(x_i) -\mu^2\)
- Standardabweichung: \(\quad \sigma = +\sqrt{\sigma^2}\)
Um sie besser von Stichprobenkennwerten zu unterscheiden, werden für die Populationsstatistiken griechische Buchstaben verwendet,
Beispiel Münzwurf
Aus einem Zufallsexperiment, bei dem 2 Münzen geworfen wurden, ergab sich folgende Wahrscheinlichkeitsverteilung
\[ \begin{array}{|c|ccc|} \hline X & 0 & 1 & 2\\ \hline f(x) & 0.25 & 0.5 & 0.25\\ \hline F(x) & 0.25 & 0.75 & 1 \\ \hline \end{array} \]
Daraus ergeben sich folgende Populationskennwerte:
\[ \begin{aligned} \mu &= \sum_{i=1}^n x_i f(x_i) = 0\cdot 0.25 + 1\cdot 0.5 + 2\cdot 0.25 = 1 \mbox{ Kopf},\\ \sigma^2 &= \sum_{i=1}^n x_i^2 f(x_i) -\mu^2 = (0^0\cdot 0.25 + 1^2\cdot 0.5 + 2^2\cdot 0.25) - 1^2 = 0.5 \mbox{ Kopf}^2,\\ \sigma &= +\sqrt{0.5} = 0.71 \mbox{ Kopf}. \end{aligned} \]
6.2.2 Diskrete Wahrscheinlichkeitsverteilungsmodelle
Je nach Art des Experiments, bei dem die Zufallsvariable gemessen wird, gibt es verschiedene Wahrscheinlichkeitsverteilungsmodelle. Die wichtigsten sind:
- Diskrete Gleichverteilung
- Binomialverteilung
- Poissonverteilung
6.3 Diskrete Gleichverteilung
Wenn alle Werte einer zufälligen Variablen \(X\) die gleiche Wahrscheinlichkeit haben, ist die Wahrscheinlichkeitsverteilung von \(X\) gleichförmig.
Definition 63 “Diskrete Gleichverteilung U(a, B)”
Eine diskrete Zufallsvariable \(X\) folgt einem diskreten Gleichverteilungsmodell mit Parametern \(a\) und \(b\), notiert als \(X\sim U(a,b)\), wenn ihr Bereich \(\mbox{Ran}(X) = \{a, a+1, \ldots,b\}\) ist und ihre Wahrscheinlichkeitsfunktion
\[ f(x)=\frac{1}{b-a+1}. \]
Beachten Sie, dass \(a\) und \(b\) das Minimum bzw. das Maximum des Bereichs sind.
Der Mittelwert (Erwartungswert) und die Varianz sind
\[ \mu = \sum_{i=0}^{b-a}\frac{a+i}{b-a+1}=\frac{a+b}{2} \qquad \sigma^2 =\sum_{i=0}^{b-a}\frac{(a+i-\mu)^2}{b-a+1}= \frac{(b-a+1)^2-1}{12} \]
Beispiel Würfeln
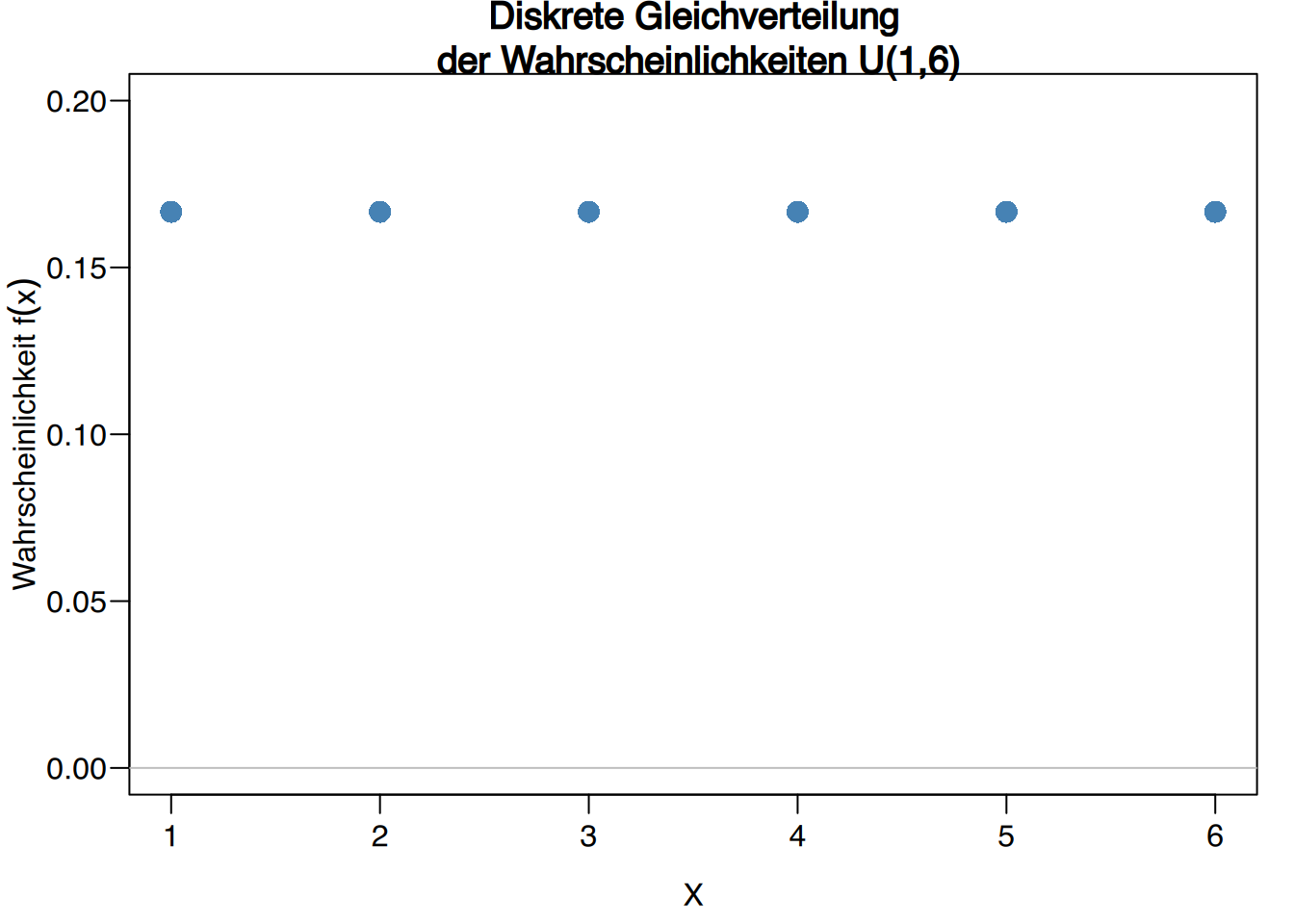
Die Variable, die das Ergebnis beim Würfeln misst, folgt einem diskreten Gleichverteilungsmodell \(U(1, 6)\).
6.4 Binomialverteilung
Die Binomialverteilung entspricht in der Regel einer Variablen, die in einem zufälligen Experiment mit den folgenden Merkmalen gemessen wird:
- Das Experiment besteht aus einer Sequenz von \(n\) Wiederholungen desselben Versuchs.
- Jeder Versuch wird unter identischen Bedingungen wiederholt und produziert zwei mögliche Ergebnisse namens Erfolg oder Misserfolg.
- Die Versuche sind unabhängig voneinander.
- Die Wahrscheinlichkeit für einen Erfolg ist in allen Versuchen gleich und beträgt \(P(\text{Erfolg}) = p\).
Unter diesen Bedingungen folgt die diskrete Zufallsvariable \(X\), die die Anzahl der Erfolge bei den \(n\) Versuchen misst, einem Binomialverteilungsmodell mit Parametern \(n\) und \(p\).
Definition “Binomialverteilung \((B(n, p)\)”
Eine diskrete Zufallsvariable \(X\) folgt einem binomialen Verteilungsmodell mit Parametern \(n\) und \(p\), notiert als \(X\sim B(n,p)\), wenn ihr Bereich \(\mbox{Ran}(X) = \{0,1,\ldots,n\}\) ist und ihre Wahrscheinlichkeitsfunktion
\[ f(x) = \binom{n}{x}p^x(1-p)^{n-x} = \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x} \]
ist.
Beachten Sie, dass \(n\) als die Anzahl der Wiederholungen eines Versuchs bekannt ist und \(p\) als die Wahrscheinlichkeit für einen Erfolg bei jeder Wiederholung.
Der Erwartungswert und die Varianz sind:
\[ \mu = n\cdot p \qquad \sigma^2 = n\cdot p\cdot (1-p). \]
Beispiel: Werfen von 10 Münzen:
Die Variable, die die Anzahl der Köpfe nach dem Werfen von 10 Münzen misst, folgt einem binomialen Verteilungsmodell \(B(10,\ 0.5)\).
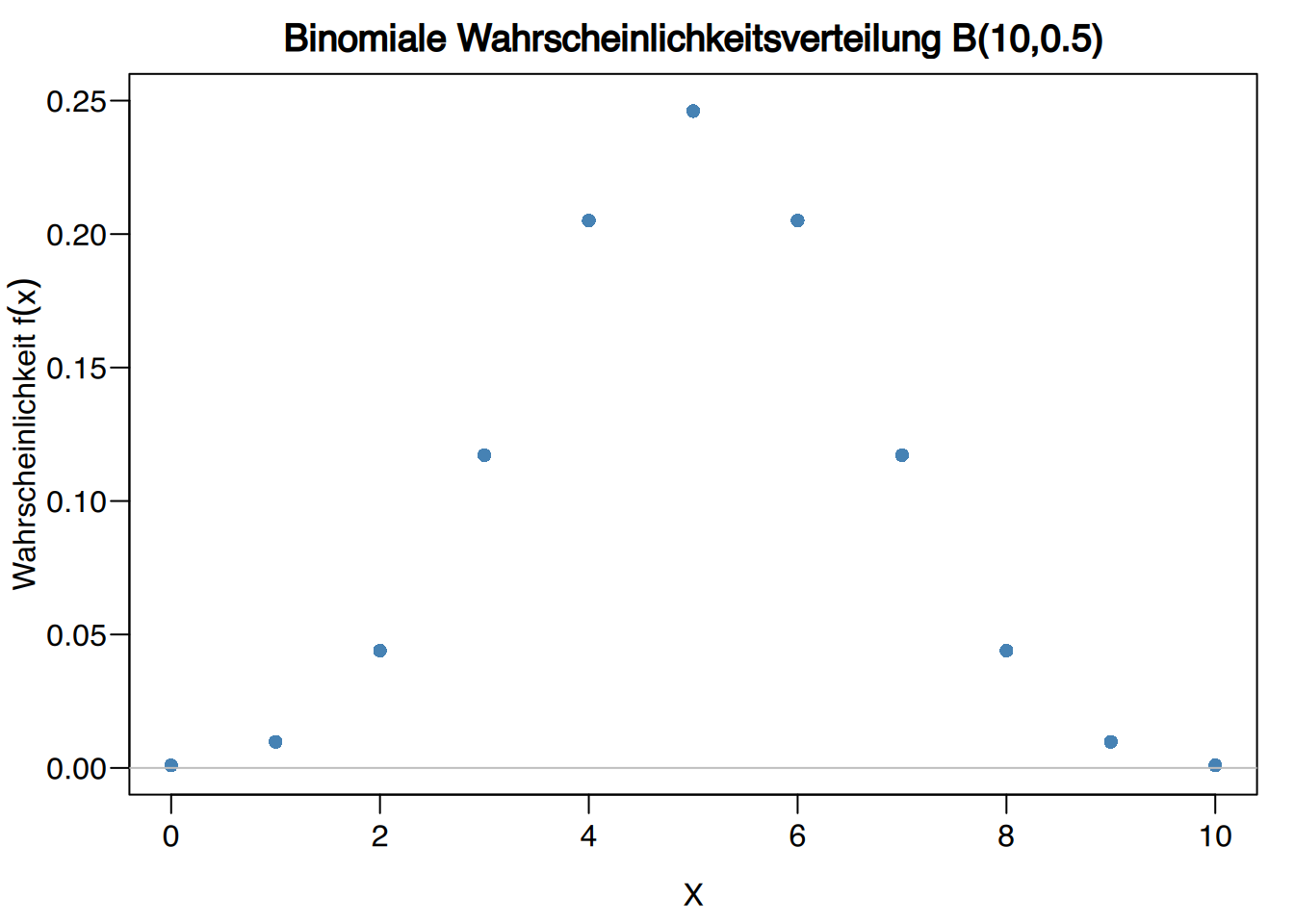
Wenn \(X\sim B(10,\,0.5)\) die zufällige Variable ist, die die Anzahl der Köpfe nach dem Werfen von 10 Münzen misst, dann ist:
die Wahrscheinlichkeit, 4 mal Kopf zu werfen: \[ f(4) = \binom{10}{4}0.5^4 (1-0.5)^{10-4} = \frac{10!}{4!6!}0.5^40.5^6 = 210\cdot 0.5^{10} = 0.2051. \]
die Wahrscheinlichkeit, 2 mal oder weniger Kopf zu werfen: \[ \begin{aligned} F(2) &= f(0) +f(1) + f(2) =\\ &= \binom{10}{0}0.5^0 (1-0.5)^{10-0} + \binom{10}{1}0.5^1 (1-0.5)^{10-1} + \binom{10}{2}0.5^2 (1-0.5)^{10-2} =\\ &= 0.0547. \end{aligned} \]
der erwartete Wert für die Anzahl an Kopfwürfen: \[ \mu = 10\cdot 0.5 = 5 \mbox{ mal Kopf}. \]
Beispiel für eine zufällige Stichprobe mit Zurücklegen:
In einer Population gibt es 40% Raucher. Die Variable \(X\), die die Anzahl der Raucher in einer zufälligen Stichprobe mit Zurücklegen von 3 Personen misst, folgt einem binomialen Verteilungsmodell \(X\sim B(3,\,0.4)\).
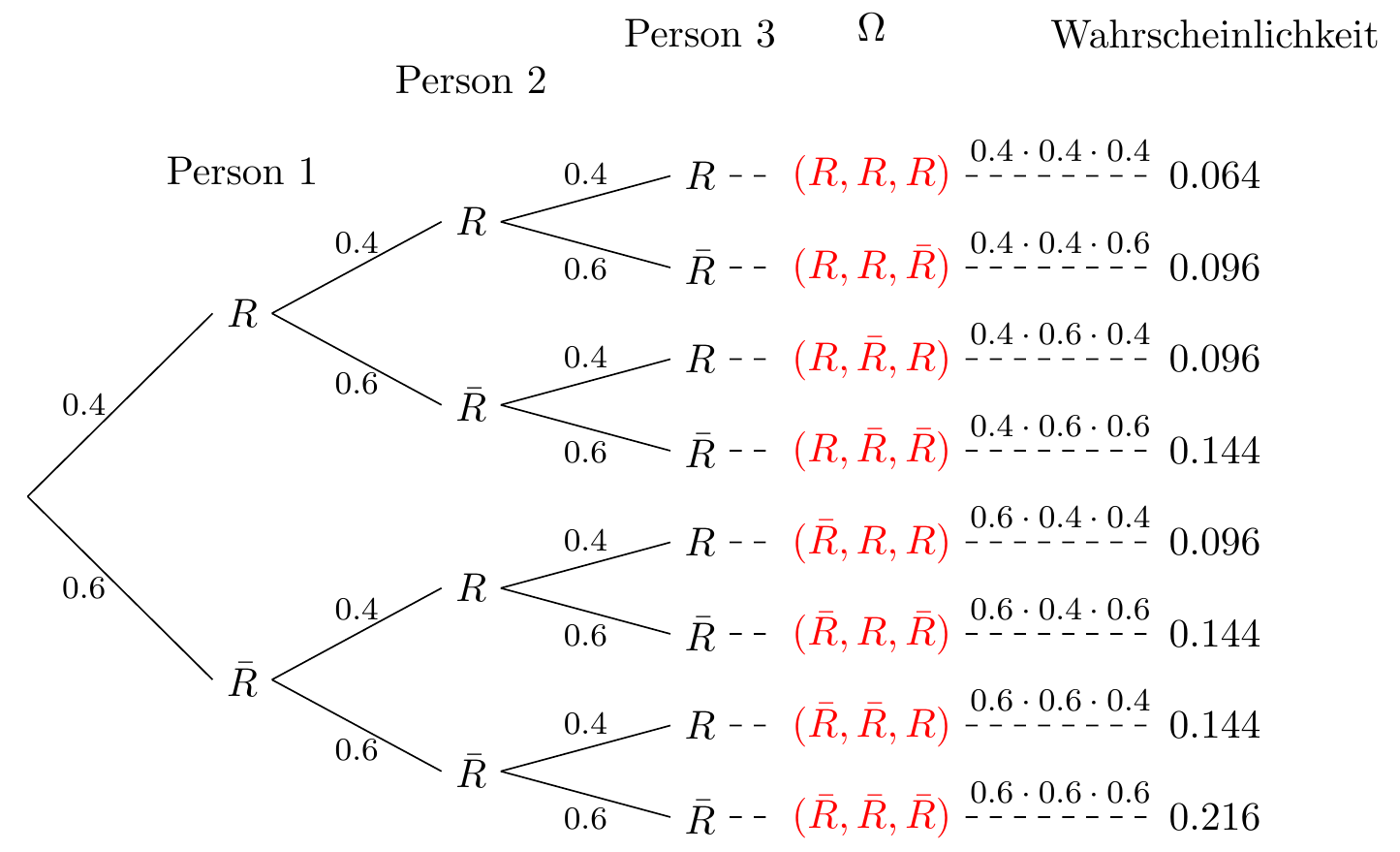
\[ \begin{array}{lll} f(0)=\binom{3}{0}0.4^0(1-0.4)^{3-0}= 0.6^3, & \quad & f(1)=\binom{3}{1}0.4^1(1-0.4)^{3-1}= 3\cdot 0.4\cdot 0.6^2,\\ f(2)=\binom{3}{2}0.4^2(1-0.4)^{3-2}= 3\cdot 0.4^2\cdot 0.6, & & f(3)=\binom{3}{3}0.4^3(1-0.4)^{3-3}= 0.4^3. \end{array} \]
6.5 Poissonverteilung
Die Poisson-Verteilung entspricht in der Regel einer Variablen, die in einem zufälligen Experiment gemessen wird, für welches folgenden Merkmalen gelten:
- Das Experiment besteht darin, die Anzahl der Ereignisse zu beobachten, die in einem festgelegten Zeit- oder Raumintervall auftreten, zum Beispiel: Anzahl der Geburten in einem Monat, Anzahl der E-Mails in einer Stunde, Anzahl der roten Blutkörperchen in einem Blutvolumen usw.
- Die Ereignisse treten unabhängig voneinander auf.
- Das Experiment produziert dieselbe durchschnittliche Ereignisrate \(\lambda\) für jedes Intervall.
Unter diesen Bedingungen folgt die diskrete Zufallsvariable \(X\), die die Anzahl der Ereignisse in einem Intervall misst, einem Poisson-Verteilungsmodell mit dem Parameter \(\lambda\).
Definition “Poisson-Verteilung” \(P(\lambda)\)
Eine diskrete Zufallsvariable \(X\) folgt einem Poisson-Verteilungsmodell mit dem Parameter \(\lambda\), notiert als \(X\sim P(\lambda)\), wenn ihr Bereich \(\mbox{Ran}(X) = \{0,1,\ldots,\infty\}\) ist und ihre Wahrscheinlichkeitsfunktion
\[ f(x) = e^{-\lambda}\frac{\lambda^x}{x!} \]
ist.
Beachten Sie, dass \(\lambda\) die durchschnittliche Ereignisrate für ein Intervall ist und sich ändern wird, wenn das Intervall verändert wird.
Der Erwartungswert und die Varianz sind:
\[ \mu = \lambda \qquad \sigma^2 = \lambda. \]
Beispiel: Anzahl der Geburten in einer Stadt
In einer Stadt gibt es durchschnittlich 4 Geburten pro Tag. Die Zufallsvariable \(X\), die die Anzahl der Geburten an einem Tag in der Stadt misst, folgt einem Poisson-Verteilungsmodell \(X\sim P(4)\).
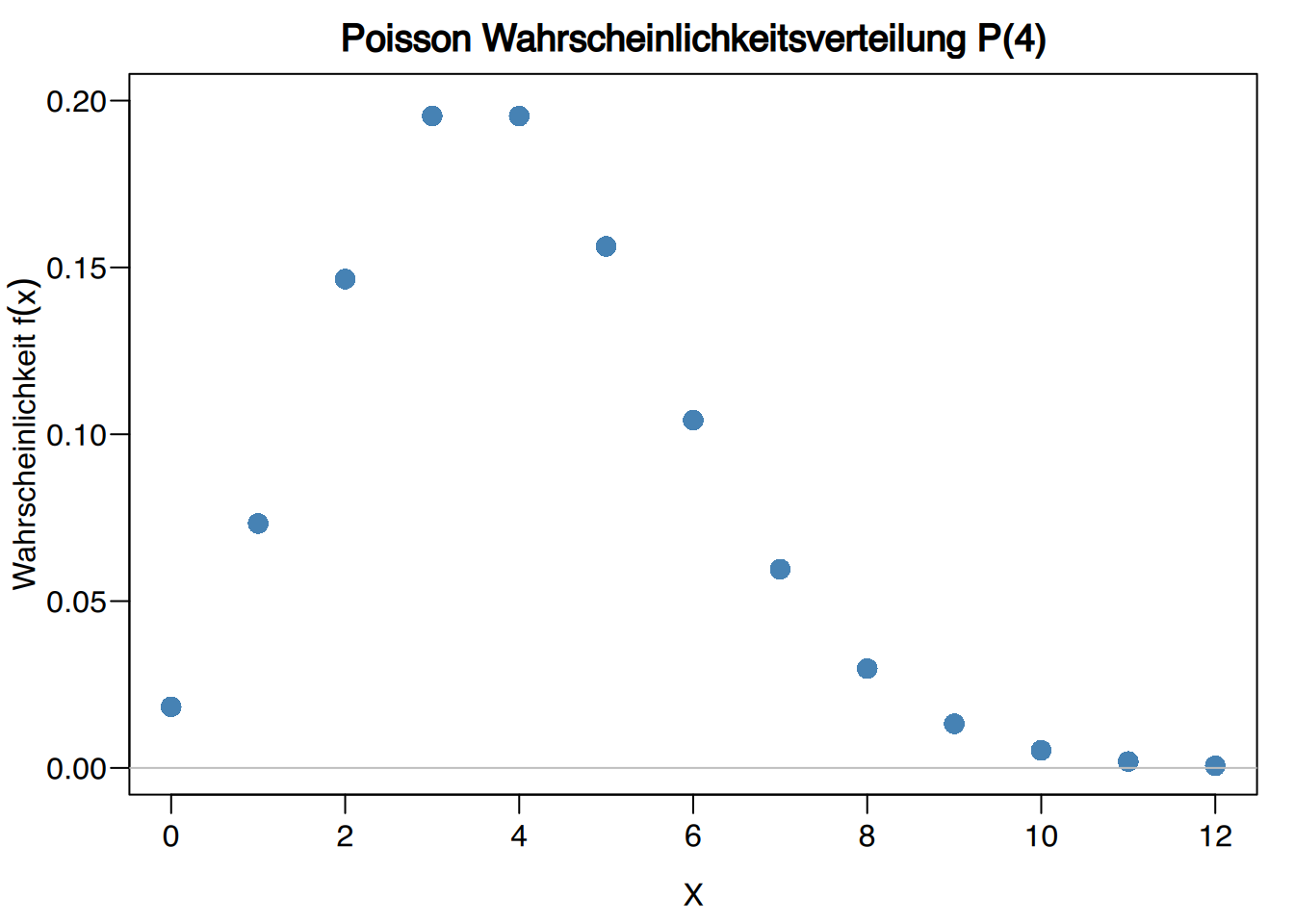
Wenn \(X\sim P(4)\) die Zufallsvariable ist, die die Anzahl der Geburten in der Stadt misst, dann ist:
die Wahrscheinlichkeit, dass es 5 Geburten an einem Tag gibt: \[ f(5) = e^{-4}\frac{4^5}{5!} = 0.1563. \]
die Wahrscheinlichkeit, dass es weniger als 2 Geburten an einem Tag gibt: \[ F(1) = f(0)+f(1) = e^{-4}\frac{4^0}{0!} + e^{-4}\frac{4^1}{1!} = 5e^{-4} = 0.0916. \]
die Wahrscheinlichkeit, dass es mehr als 1 Geburt an einem Tag gibt: \[ P(X>1) = 1-P(X\leq 1) = 1-F(1) = 1-0.0916 = 0.9084. \]
6.5.1 Annäherung an die Binomialverteilung durch die Poisson-Verteilung
Die Poisson-Verteilung kann aus der Binomialverteilung erhalten werden, wenn die Anzahl der Versuche gegen unendlich geht und die Wahrscheinlichkeit für den Erfolg gegen Null tendiert.
Gesetz der seltenen Ereignisse
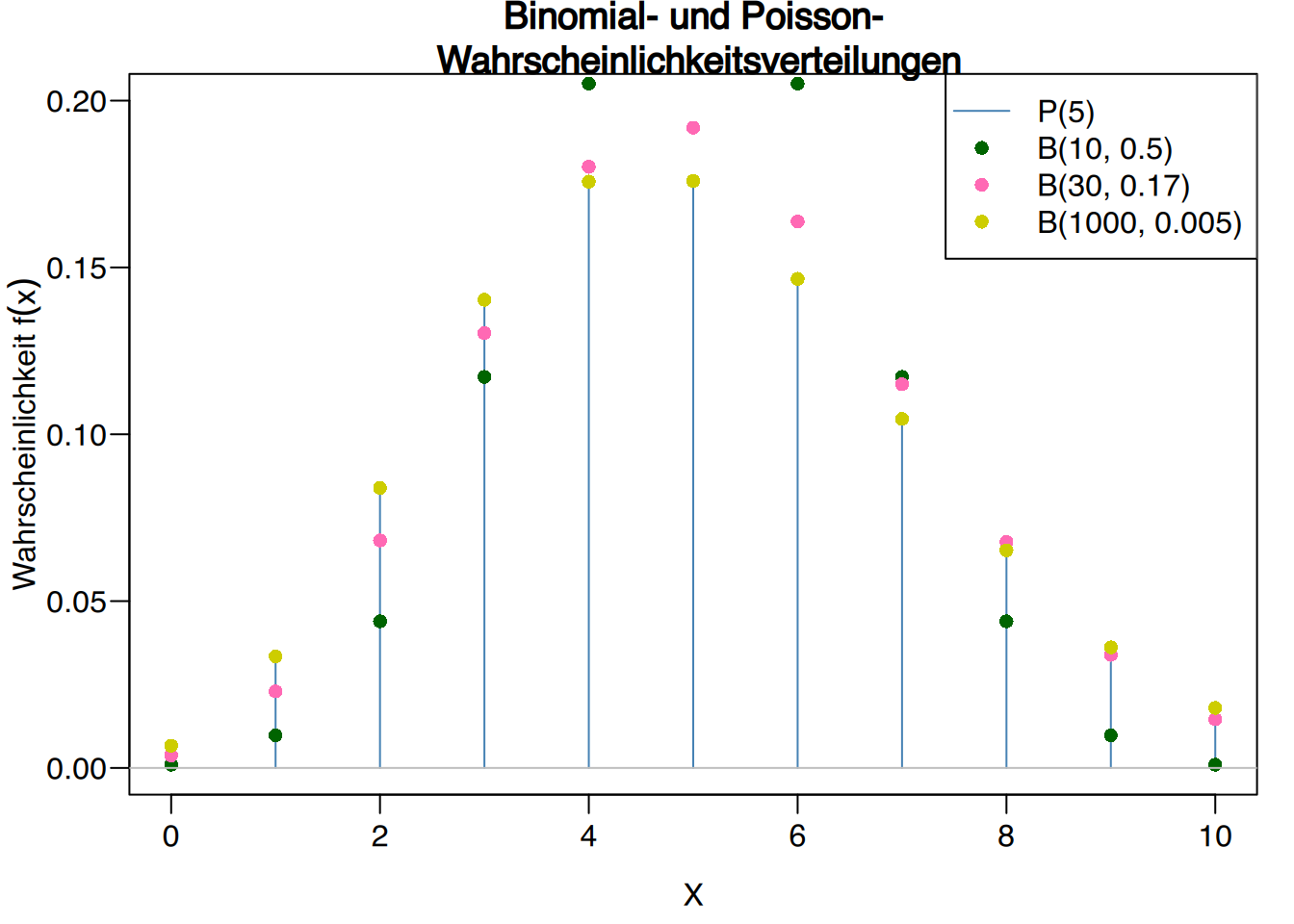
Die Binomialverteilung\(X\sim B(n,p)\) tendiert gegen die Poisson-Verteilung \(P(\lambda)\), mit \(\lambda=n\cdot p\), wenn \(n\) gegen unendlich geht und \(p\) gegen Null geht, d.h.:
\[ \lim_{n\rightarrow \infty, p\rightarrow 0}\binom{n}{x}p^x(1-p)^{n-x} = e^{-\lambda}\frac{\lambda^x}{x!}. \]
In der Praxis kann diese Annäherung für \(n\geq 30\) und \(p\leq 0.1\) verwendet werden.
Beispiel
Ein Impfstoff löst in 4% der Fälle eine unerwünschte Reaktion aus. Wenn 50 Personen geimpft werden, was ist die Wahrscheinlichkeit, dass mehr als 2 Personen eine unerwünschte Reaktion haben?
Die Zufallsvariable, die die Anzahl der Personen mit einer unerwünschten Reaktion im Sample misst, folgt einem Binomialverteilungsmodell \(X\sim B(50,0.04)\). Da aber \(n=50>30\) und \(p=0.04<0.1\) sind, können wir das Gesetz der seltenen Ereignisse anwenden und das Poisson-Verteilungsmodell \(P(50\cdot 0.04)=P(2)\) verwenden, um die Berechnungen durchzuführen.
\[ \begin{aligned} P(X>2) &= 1-P(X\leq 2) = 1-f(0)-f(1)-f(2) =\\ &= 1-e^{-2}\frac{2^0}{0!}-e^{-2}\frac{2^1}{1!}-e^{-2}\frac{2^2}{2!} =\\ &= 1-5e^{-2} = 0.3233. \end{aligned} \]