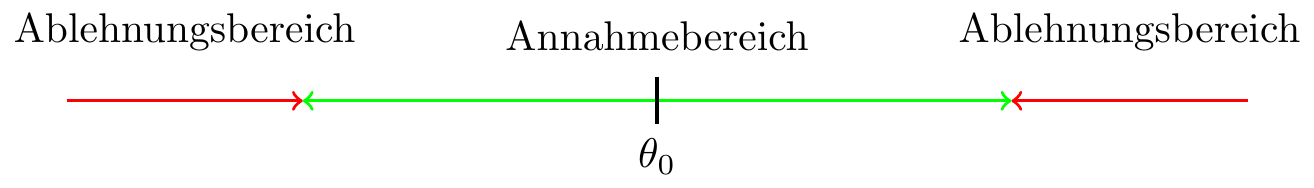
9 Parametrische Hypothesentests

9.1 Statistische Hypothese und Arten von Tests

In vielen statistischen Studien besteht das Ziel eher darin, die Richtigkeit einer über die untersuchte Population aufgestellten Hypothese zu überprüfen, als den Wert eines unbekannten Parameters in der Population zu schätzen.

Der Forscher hat aufgrund seiner Erfahrung oder früherer Studien oft Vermutungen über die untersuchte Population, die er in Form von Hypothesen formuliert.

Definition “Statistische Hypothese”

Eine statistische Hypothese ist jede Aussage oder Vermutung, die die Verteilung einer oder mehrerer Variablen in der Population ganz oder teilweise bestimmt.

Beispiel

Um die akademische Leistung einer Studierendengruppe in einem bestimmten Fach zu überprüfen, könnten wir die Hypothese aufstellen, ob die Bestehensquote über 50% liegt.

9.1.1 Hypothesentest

Im Allgemeinen wird man nie mit absoluter Sicherheit wissen, ob eine statistische Hypothese wahr oder falsch ist, da hierfür alle Individuen der Population untersucht werden müssten.

Um die Richtigkeit oder Falschheit dieser Hypothesen zu überprüfen, müssen sie mit den empirischen Ergebnissen der Stichproben verglichen werden. Wenn die beobachteten Ergebnisse der Stichproben – innerhalb der durch den Zufall bedingten Fehlertoleranz – mit dem übereinstimmen, was bei Gültigkeit der Hypothese zu erwarten wäre, wird die Hypothese als wahr akzeptiert. Andernfalls wird sie als falsch verworfen, und es werden neue Hypothesen gesucht, die die beobachteten Daten erklären können.

Da Stichproben zufällig gezogen werden, wird die Entscheidung, eine statistische Hypothese anzunehmen oder abzulehnen, auf probabilistischer Basis getroffen.

Die Methodik, die sich mit der Überprüfung der Richtigkeit statistischer Hypothesen befasst, wird als Hypothesentest bezeichnet.

9.1.2 Arten von Hypothesentests

Anpassungstests (Goodness-of-Fit-Tests): Ziel ist die Überprüfung einer Hypothese über die Verteilungsform der Population. Beispiel: Testen, ob die Noten einer Schülergruppe einer Normalverteilung folgen.
Verträglichkeitstests (Konformitätstests): Ziel ist die Überprüfung einer Hypothese über einen Parameter der Population. Beispiel: Testen, ob der Notendurchschnitt einer Schülergruppe gleich 2 ist.
Homogenitätstests: Ziel ist der Vergleich zweier Populationen hinsichtlich bestimmter Parameter. Beispiel: Testen, ob die Leistung zweier Schülergruppen gleich ist, indem ihre Durchschnittsnoten verglichen werden.
Unabhängigkeitstests: Ziel ist die Überprüfung, ob ein Zusammenhang zwischen zwei Variablen der Population besteht. Beispiel: Testen, ob ein Zusammenhang zwischen den Noten zweier unterschiedlicher Fächer besteht.

Wenn Hypothesen über Parameter der Population aufgestellt werden, spricht man auch von parametrischen Tests.

9.1.3 Nullhypothese und Alternativhypothese

In den meisten Fällen geht es bei einem Hypothesentest darum, eine Entscheidung zwischen zwei gegensätzlichen Hypothesen zu treffen:

Nullhypothese: Dies ist die konservative Hypothese, die beibehalten wird, solange die Stichprobendaten ihre Falschheit nicht eindeutig belegen. Sie wird als \(H_0\) bezeichnet.
Alternativhypothese: Sie stellt die Verneinung der Nullhypothese dar und entspricht in der Regel der Aussage, die nachgewiesen werden soll. Sie wird als \(H_1\) bezeichnet.

Die Wahl beider Hypothesen folgt dem Prinzip der wissenschaftlichen Einfachheit (Ockhams Rasiermesser):

“Ein einfaches Modell sollte nur dann durch ein komplexeres ersetzt werden, wenn es starke Beweise für das komplexere Modell gibt.”

Ein Beispiel aus der Rechtsprechung: Wenn ein Richter entscheiden muss, ob ein Angeklagter schuldig oder unschuldig ist, sollten die Hypothesen wie folgt lauten:

\[ \begin{aligned} H_0:\ & \text{ Unschuldig} \\ H_1:\ & \text{ Schuldig} \end{aligned} \]

Denn Unschuld wird angenommen, während Schuld bewiesen werden muss.

Entsprechend würde der Richter die Alternativhypothese nur dann akzeptieren, wenn es signifikante Beweise für die Schuld des Angeklagten gibt.

Der Forscher übernimmt in diesem Vergleich die Rolle des Anklägers, da sein Ziel darin besteht, die Nullhypothese zu widerlegen – also die Schuld des Angeklagten nachzuweisen.

Achtung

Diese Methodik begünstigt immer die Nullhypothese!

9.1.4 Parametrische Hypothesentests

Bei vielen Tests, insbesondere bei Konformitäts- und Homogenitätstests, beziehen sich die Hypothesen auf unbekannte Parameter der Grundgesamtheit wie den Mittelwert, die Varianz oder einen Anteilswert.

In diesem Fall weist die Nullhypothese dem Parameter stets einen konkreten Wert zu, während die Alternativhypothese meist eine offene Aussage darstellt, die zwar der Nullhypothese widerspricht, aber keinen festen Wert für den Parameter vorgibt.

Daraus ergeben sich drei Arten von Tests:

Zweiseitig	Einsitig (links)	Einseitig (rechts)
\(H_0:\ \theta = \theta_0\)	\(H_0:\ \theta = \theta_0\)	\(H_0:\ \theta = \theta_0\)
\(H_1:\ \theta \neq \theta_0\)	\(H_1:\ \theta < \theta_0\)	\(H_1:\ \theta > \theta_0\)

Beispiel

Angenommen, es besteht der Verdacht, dass in einer Population weniger Männer als Frauen vorhanden sind.

Welche Art von Test sollte durchgeführt werden, um diesen Verdacht zu bestätigen oder zu widerlegen?

Der Verdacht bezieht sich auf den Anteilswert \(p\) der Männer in der Population, es handelt sich also um einen parametrischen Test.
Das Ziel ist die Überprüfung des Werts von \(p\), daher handelt es sich um einen Konformitätstest. In der Nullhypothese wird \(p\) auf \(0.5\) festgesetzt, da gemäß den Gesetzen der Genetik in der Population gleich viele Männer wie Frauen zu erwarten wären.
Schließlich besteht der Verdacht, dass der Männeranteil geringer ist als der Frauenanteil, daher lautet die Alternativhypothese \(p<0.5\).

Somit sollte folgender Test durchgeführt werden:

\[ \begin{aligned} H_0:\ & p=0,5 \\ H_1:\ & p<0,5 \end{aligned} \]

9.2 Methodik zur Durchführung eines Hypothesentests

9.2.1 Teststatistik

Die Annahme oder Ablehnung der Nullhypothese hängt letztlich von den Beobachtungen in der Stichprobe ab.

Die Entscheidung wird basierend auf dem Wert einer Stichprobenstatistik getroffen, die mit dem zu testenden Parameter oder Merkmal in Zusammenhang steht. Die Wahrscheinlichkeitsverteilung dieser Statistik muss unter der Annahme der Nullhypothese und bei festgelegtem Stichprobenumfang bekannt sein. Diese Statistik wird als Teststatistik bezeichnet.

Für jede Stichprobe liefert die Teststatistik eine Schätzung, auf deren Grundlage die Entscheidung getroffen wird: Wenn die Schätzung zu stark vom unter \(H_0\) erwarteten Wert abweicht, wird die Nullhypothese verworfen, andernfalls wird sie beibehalten.

Die zugrundeliegende Logik folgt dem Prinzip, die Nullhypothese beizubehalten, es sei denn, die Stichprobe liefert eindeutige Beweise gegen sie. In Analogie zum Gerichtsverfahren würde dies bedeuten, die Unschuldsvermutung aufrechtzuerhalten, solange keine klaren Schuldbeweise vorliegen.

Beispiel

Kehren wir zum Beispiel des Tests über den Männeranteil in einer Population zurück:

\[ \begin{aligned} H_0:\ & p=0,5 \\ H_1:\ & p<0,5 \end{aligned} \]

Wenn für den Test eine Zufallsstichprobe von 10 Personen gezogen wird, könnte die Anzahl der Männer in der Stichprobe \(X\) als Teststatistik gewählt werden.

Unter der Annahme, dass die Nullhypothese zutrifft, folgt die Teststatistik einer Binomialverteilung \(X\sim B(10,\,0.5)\), sodass die erwartete Anzahl von Männern in der Stichprobe 5 beträgt.

Daher ist es logisch, die Nullhypothese zu akzeptieren, wenn die Stichprobe eine Anzahl von Männern in der Nähe von 5 ergibt, und sie zu verwerfen, wenn die Anzahl deutlich unter 5 liegt.

Doch wo genau sollte die Grenze zwischen den X-Werten gezogen werden, die zur Annahme bzw. zur Ablehnung führen?

9.2.2 Annahme- und Ablehnungsbereich

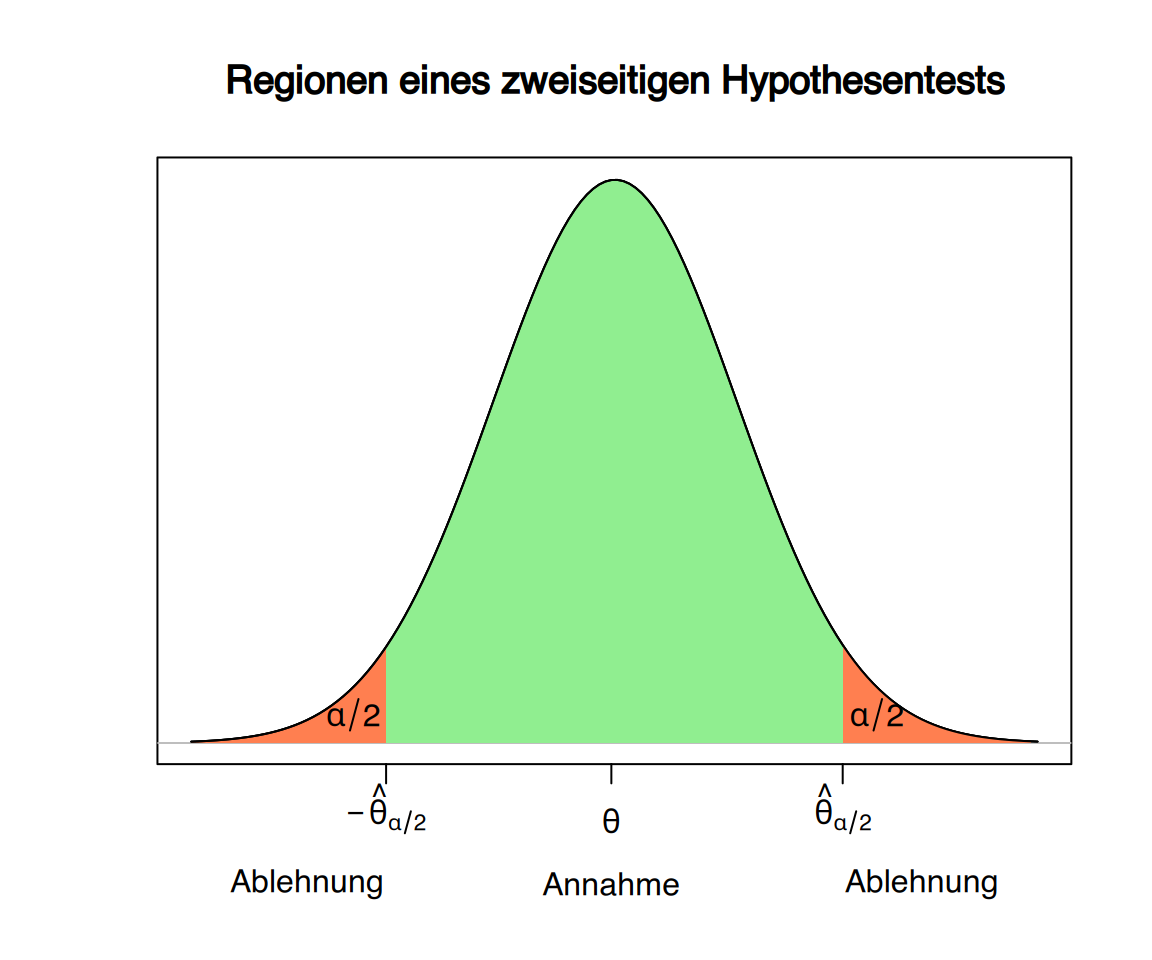
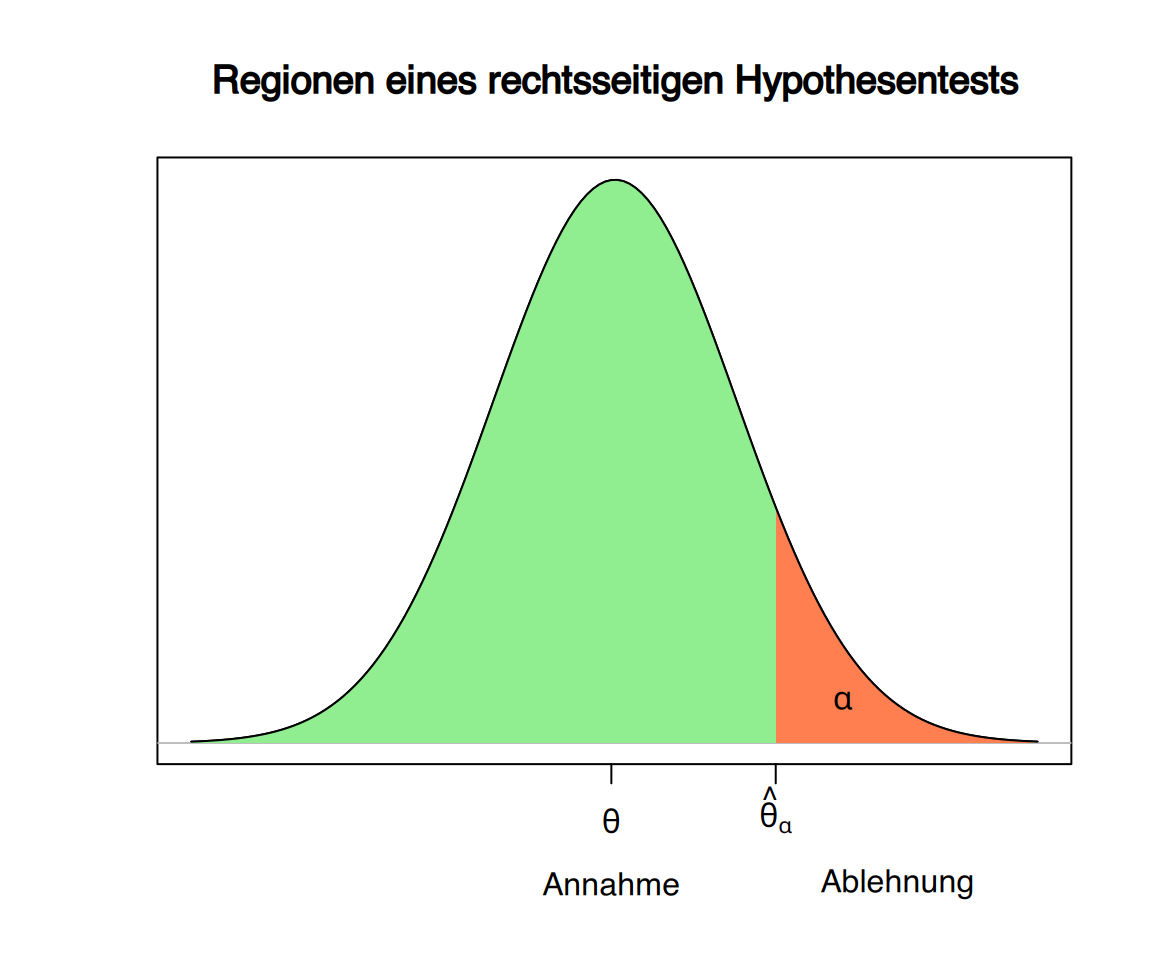
Nach Auswahl der Teststatistik gilt es festzulegen, für welche Werte dieser Statistik die Nullhypothese angenommen bzw. verworfen wird. Dadurch wird der Wertebereich der Statistik in zwei Regionen unterteilt:

Annahmebereich: Die Menge der Werte der Teststatistik, für die die Nullhypothese angenommen wird.
Ablehnungsbereich: Die Menge der Werte der Teststatistik, für die die Nullhypothese verworfen und folglich die Alternativhypothese angenommen wird.

Abhängig von der Art des Tests (einseitig/zweiseitig) befindet sich der Ablehnungsbereich entweder links, rechts oder auf beiden Seiten des unter der Nullhypothese erwarteten Werts der Teststatistik.

Zweiseitiger Hypothesentest \[ \begin{aligned} H_0:\ \theta=\theta_{0}\\ H_1:\ \theta\neq\theta_0 \end{aligned} \]

Einseitiger Test (linksseitig) \[ \begin{aligned} H_0:\ \theta = \theta_0\\ H_1:\ \theta < \theta_0 \end{aligned} \]

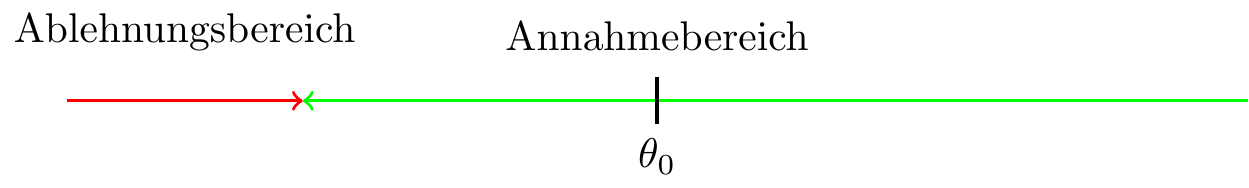
Einseitiger Test (rechtsseitig) \[ \begin{aligned} H_0:\ \theta=\theta_{0}\\ H_1:\ \theta > \theta_{0} \end{aligned} \]

Beispiel

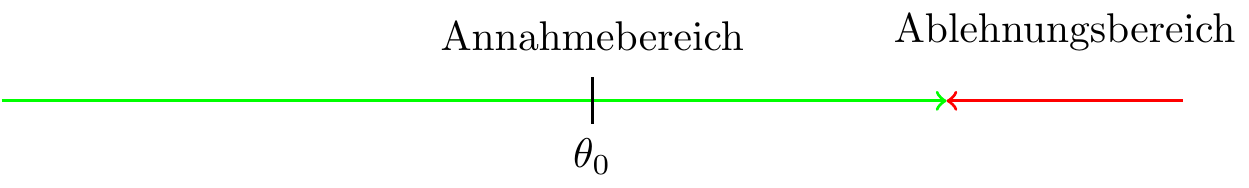
Im fortgesetzten Beispiel des Hypothesentests zum Bevölkerungsanteil von Männern

\[ \begin{aligned} H_0:\ & p=0,5 \\ H_1:\ & p<0,5 \end{aligned} \]

folgt die Teststatistik bei gültiger Nullhypothese einer \(B(10,0.5)\)-Verteilung. Ihr Wertebereich reicht somit von 0 bis 10 bei einem Erwartungswert von 5. Da ein linksseitiger Test vorliegt (\(H_1:\ p < 0,5\)), konzentriert sich der Ablehnungsbereich auf die Werte deutlich unter 5. Die entscheidende Frage bleibt jedoch:

An welchem kritischen Wert soll die Trennlinie zwischen Annahme und Verwerfung der Nullhypothese festgelegt werden?

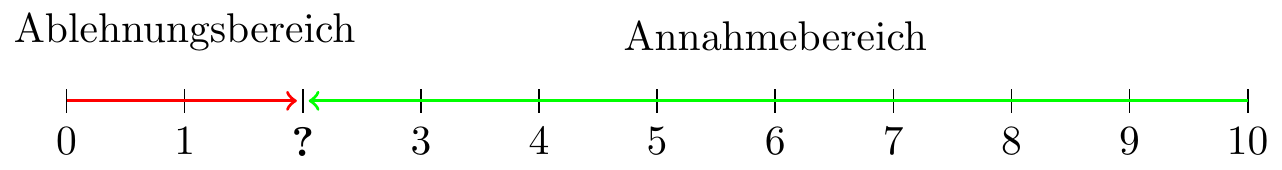
9.2.3 Fehler bei einem Hypothesentest

Wir haben gesehen, dass ein Hypothesentest auf einer Entscheidungsregel basiert, die je nach Wert der Teststatistik die Annahme oder Ablehnung der Nullhypothese ermöglicht.

Letztlich führt der Test zu einer Entscheidung gemäß dieser Regel. Das Problem ist, dass man niemals mit absoluter Sicherheit weiß, ob eine Hypothese wahr oder falsch ist. Daher besteht bei jeder Entscheidung - ob Annahme oder Ablehnung - die Möglichkeit eines Fehlers.

Bei einem Hypothesentest können zwei Arten von Fehlern auftreten:

Fehler 1. Art (\(\alpha\)-Fehler): Tritt auf, wenn die Nullhypothese abgelehnt wird, obwohl sie wahr ist.
Fehler 2. Art (\(\beta\)-Fehler): Tritt auf, wenn die Nullhypothese angenommen wird, obwohl sie falsch ist.

\[ \begin{array}{|c|c|c|} \hline \mbox{Entscheidung} & H_0 \mbox{ gilt} & H_1 \mbox{ gilt} \\ \hline H_0 \mbox{ annehmen} & \color{green}{\mbox{korrekte Entscheidung}} & \color{red}{\mbox{Fehler 2. Art } (\beta)} \\ \hline H_0 \mbox{ ablehnen}& \color{red}{\mbox{Fehler 1. Art } (\alpha)} & \color{green}{\mbox{korrekte Entscheidung}} \\ \hline \end{array} \]

9.2.4 Fehlerrisiko von Hypothesentests

Die Risiken der beiden Fehlerarten werden durch Wahrscheinlichkeiten quantifiziert:

Definition “Alpha- und Betarisiko”

Bei einem Hypothesentest wird das \(\alpha\)-Risiko definiert als die maximale Wahrscheinlichkeit, einen Fehler 1. Art zu begehen, d.h.

\[ P(\mbox{Ablehnung }H_0|H_0) \leq \alpha, \]

und das \(\beta\)-Risiko als die maximale Wahrscheinlichkeit, einen Fehler 2. Art zu begehen, also

\[ P(\mbox{Annahme }H_0|H_1) \leq \beta. \]

Vorsicht

Da diese Methodik grundsätzlich die Nullhypothese begünstigt, gilt der Fehler 1. Art als gravierender als der Fehler 2. Art. Daher wird das \(\alpha\)-Risiko üblicherweise auf niedrige Werte von \(0,1\), \(0,05\) oder \(0,01\) festgelegt, wobei \(0,05\) der gebräuchlichste Wert ist.

Bei der Interpretation des \(\alpha\)-Risikos ist Vorsicht geboten, da es sich um eine bedingte Wahrscheinlichkeit unter der Annahme handelt, dass die Nullhypothese wahr ist. Wenn man die Nullhypothese mit einem \(\alpha\)-Risiko von \(0,05\) verwirft, ist die Aussage “in 5 von 100 Fällen liegen wir falsch” nur dann korrekt, wenn die Nullhypothese tatsächlich immer wahr wäre.

Ebenso wenig sinnvoll ist es, nach einer konkreten Testentscheidung von der “Wahrscheinlichkeit eines Fehlers” zu sprechen - denn für die getroffene Entscheidung gilt:

Entweder man hat richtig entschieden (Fehlerwahrscheinlichkeit 0)
oder falsch (Fehlerwahrscheinlichkeit 1).

9.2.5 Festlegung von Annahme- und Ablehnungsbereich basierend auf dem \(\alpha\)-Risiko

Nach Festlegung des tolerierbaren \(\alpha\)-Risikos können die Regionen für Annahme und Ablehnung der Nullhypothese so bestimmt werden, dass die kumulierte Wahrscheinlichkeit des Ablehnungsbereichs unter der Annahme der Nullhypothese genau \(\alpha\) beträgt.

Beispiel: Fortsetzung des Tests zum Männeranteil in einer Population

Wird die Nullhypothese verworfen, wenn höchstens 2 Männer in der Stichprobe sind, ergibt sich unter \(X\sim B(10,0.5)\) eine Fehlerwahrscheinlichkeit 1. Art von:

\[ P(X\leq 2)= f(0)+f(1)+f(2)= 0.0010 + 0.0098 + 0.0439 = 0.0547. \]

Wenn die maximal tolerierbare Wahrscheinlichkeit für einen Fehler 1. Art auf \(\alpha=0,05\) festgelegt ist, für welche Werte der Teststatistik darf dann die Nullhypothese verworfen werden?

\[ P(X\leq 1)= f(0)+f(1) = 0.0010 + 0.0098 = 0.0107. \]

Das bedeutet, die Nullhypothese könnte nur verworfen werden, wenn die Stichprobe 0 oder 1 Mann enthält.

9.2.6 Betarisiko und Effektgröße

Obwohl der Fehler 2. Art weniger gravierend erscheinen mag, ist es dennoch wünschenswert, das \(\beta\)-Risiko gering zu halten. Andernfalls wird es schwierig sein, die Nullhypothese zu verwerfen (was meist das Ziel ist), selbst wenn es deutliche Anzeichen für ihre Falschheit gibt.

Das Problem bei parametrischen Tests besteht darin, dass die Alternativhypothese eine offene Hypothese ist, die keinen festen Wert für den zu testenden Parameter vorgibt. Um das \(\beta\)-Risiko berechnen zu können, muss daher ein spezifischer Parameterwert angenommen werden.

Üblicherweise wird der Parameterwert auf die kleinste praktisch oder klinisch relevante Differenz festgelegt. Diese minimal als bedeutsam erachtete Differenz wird als Effektgröße bezeichnet und mit \(\delta\) (Delta) symbolisiert.

9.2.7 Teststärke (Power) eines Hypothesentests

Da das Forschungsziel meist in der Ablehnung der Nullhypothese besteht, ist oft besonders interessant, wie gut ein Test in der Lage ist, die Falschheit der Nullhypothese zu erkennen, wenn tatsächlich eine Differenz größer als \(\delta\) zwischen dem wahren Parameterwert und dem unter der Nullhypothese angenommenen Wert besteht.

Definition “Teststärke (Power)”

Die Teststärke (Power) eines Hypothesentests ist definiert als

\[ \mbox{Teststärke} = P(\mbox{Ablehnung }H_0|H_1) = 1 - P(\mbox{Annahme }H_0|H_1) = 1-\beta. \]

Somit führt eine Verringerung des \(\beta\)-Risikos zu einer Erhöhung der Teststärke.

Ein Test mit geringer Power ist meist wenig aussagekräftig, da er die Nullhypothese selbst dann nicht verwerfen kann, wenn es deutliche gegen sie sprechende Evidenzen gibt.

9.2.8 Berechnung des Betarisikos und der Teststärke \(1-\beta\)

Angenommen, beim Test des Männeranteils wird eine Abweichung von weniger als 10% vom Wert der Nullhypothese als nicht signifikant betrachtet, d.h. \(\delta=0.1\).

Dies ermöglicht die Festlegung der Alternativhypothese:

\[ H_1:\ p=0,5-0,1=0,4. \]

Unter der Annahme, dass diese Hypothese zutrifft, folgt die Teststatistik einer Binomialverteilung \(X\sim B(10,,0.4)\).

In diesem Fall beträgt das β-Risiko für die zuvor definierten Annahme- und Ablehnungsbereiche:

\[ \beta = P(\mbox{Annahme }H_0|H_1) = P(X\geq 2) = 1 - P(X<2) = 1-0,0464 = 0,9536. \]

Wie zu erkennen ist, handelt es sich um ein sehr hohes \(\beta\)-Risiko, sodass die Teststärke nur:

\[ 1-\beta = 1-0,9536 = 0,0464 \]

beträgt. Dies zeigt, dass dieser Test ungeeignet wäre, um Unterschiede von 10% im Parameterwert zu erkennen.

9.2.9 Zusammenhang zwischen \(\beta\)-Risiko und Effektgröße \(\delta\)

Das \(\beta\)-Risiko hängt direkt von der minimalen Differenz \(\delta\) ab, die im Vergleich zum unter der Nullhypothese angenommenen Parameterwert erkannt werden soll.

Beispiel

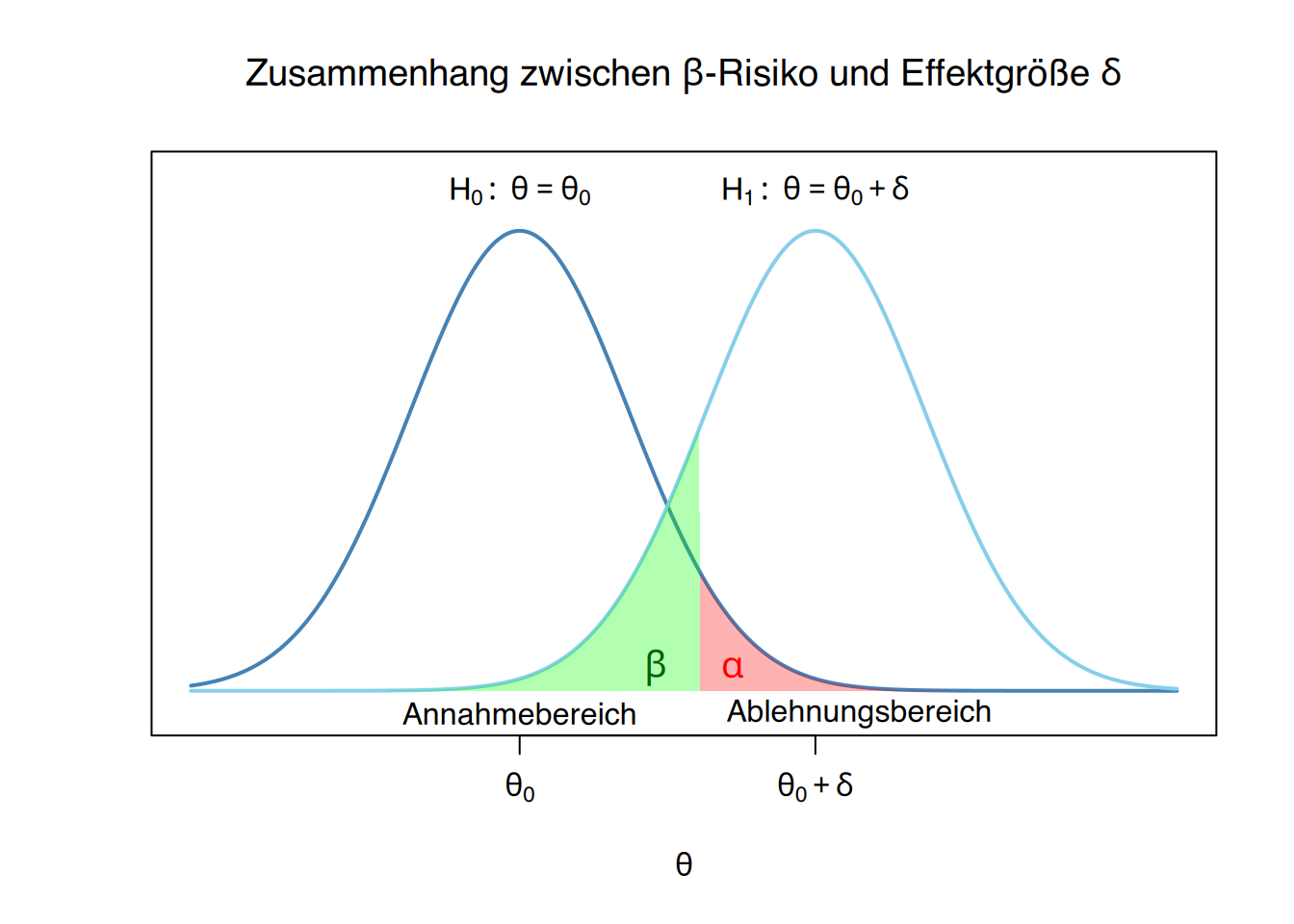
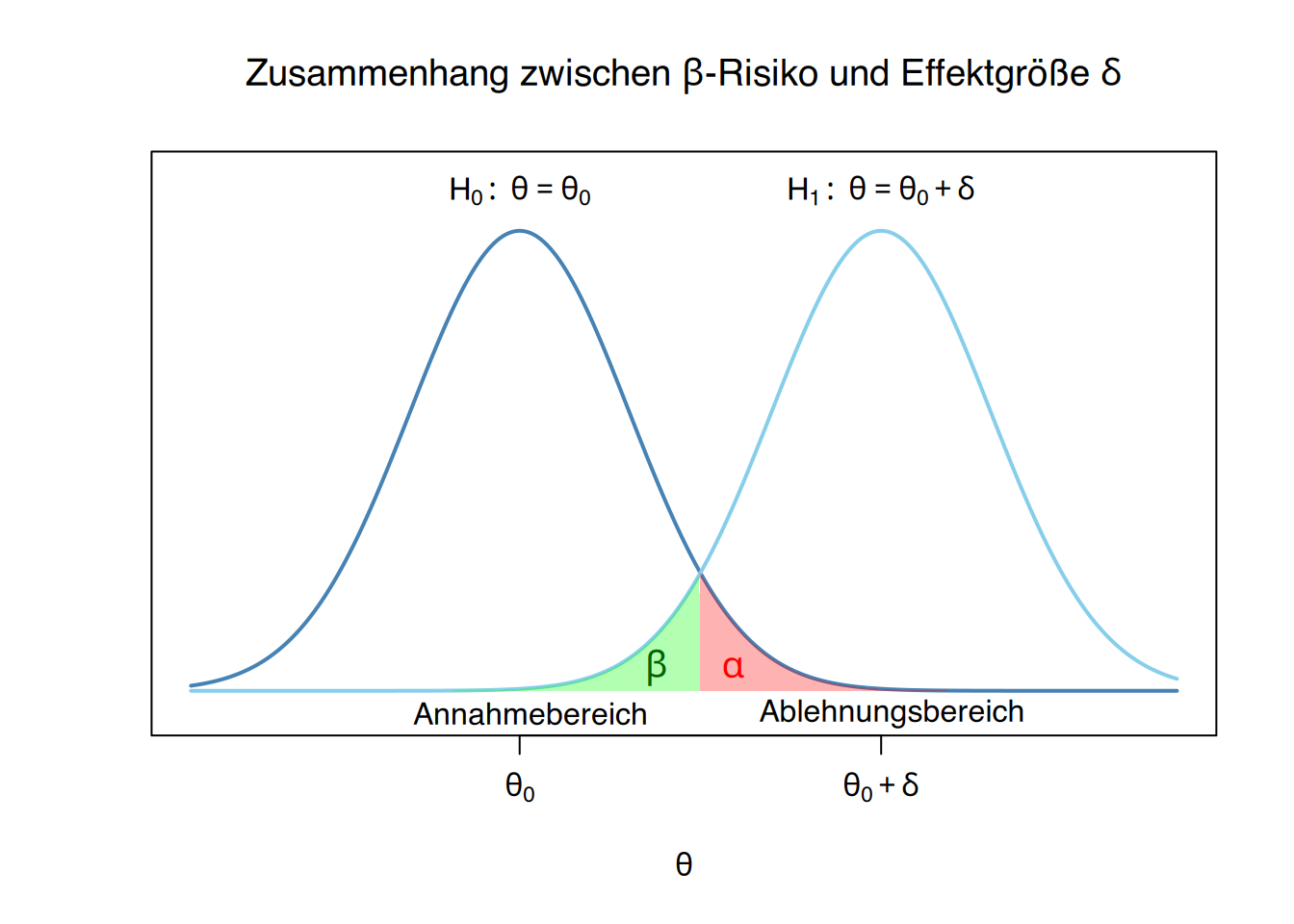
Wenn beim Test des Männeranteils eine Abweichung von mindestens 20% vom Wert der Nullhypothese erkannt werden soll, also \(\delta=0.2\), dann würde die Alternativhypothese auf

\[ H_1:\ p=0.5-0.2=0.3 \]

festgelegt werden.

Unter dieser Annahme folgt die Teststatistik einer Binomialverteilung \(X\sim B(10,,0.3)\).

In diesem Fall beträgt das \(\beta\)-Risiko für die zuvor definierten Annahme- und Ablehnungsbereiche:

\[ \beta = P(\mbox{Annahme }H_0|H_1) = P(X\geq 2) = 1 - P(X<2) = 1-0,1493 = 0,8507 \]

sodass das \(\beta\)-Risiko sinkt und die Teststärke steigt:

\[ 1-\beta = 1-0,8507 = 0,1493 \] wobei der Test damit immer noch eine geringe Power aufweist.

9.2.10 Beziehung zwischen \(\alpha\)- und \(\beta\)-Fehlern

Die Fehlerwahrscheinlichkeiten \(\alpha\) und \(\beta\) stehen in einem Spannungsverhältnis: Wenn die eine steigt, sinkt in der Regel die andere – und umgekehrt.

Beispiel

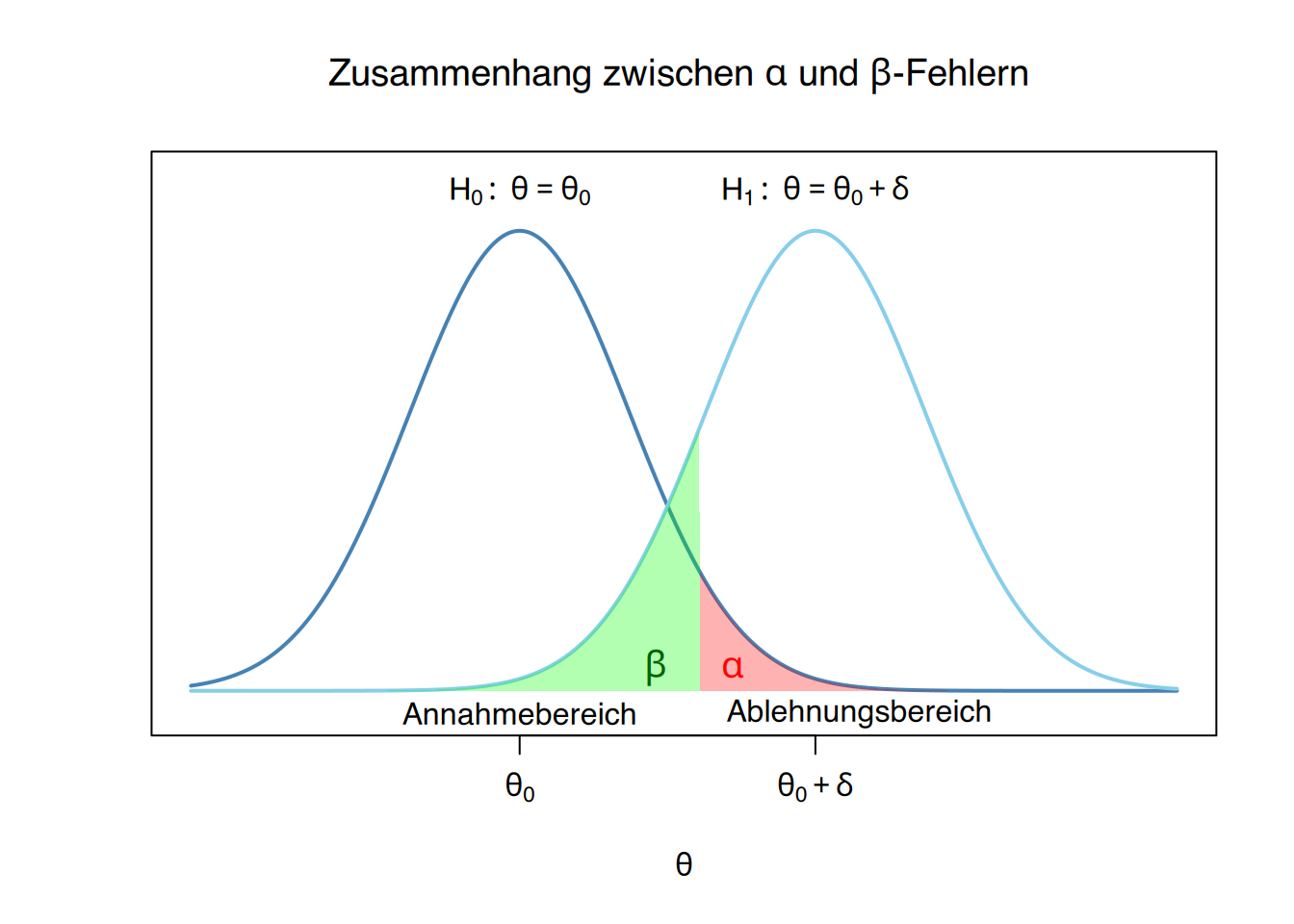
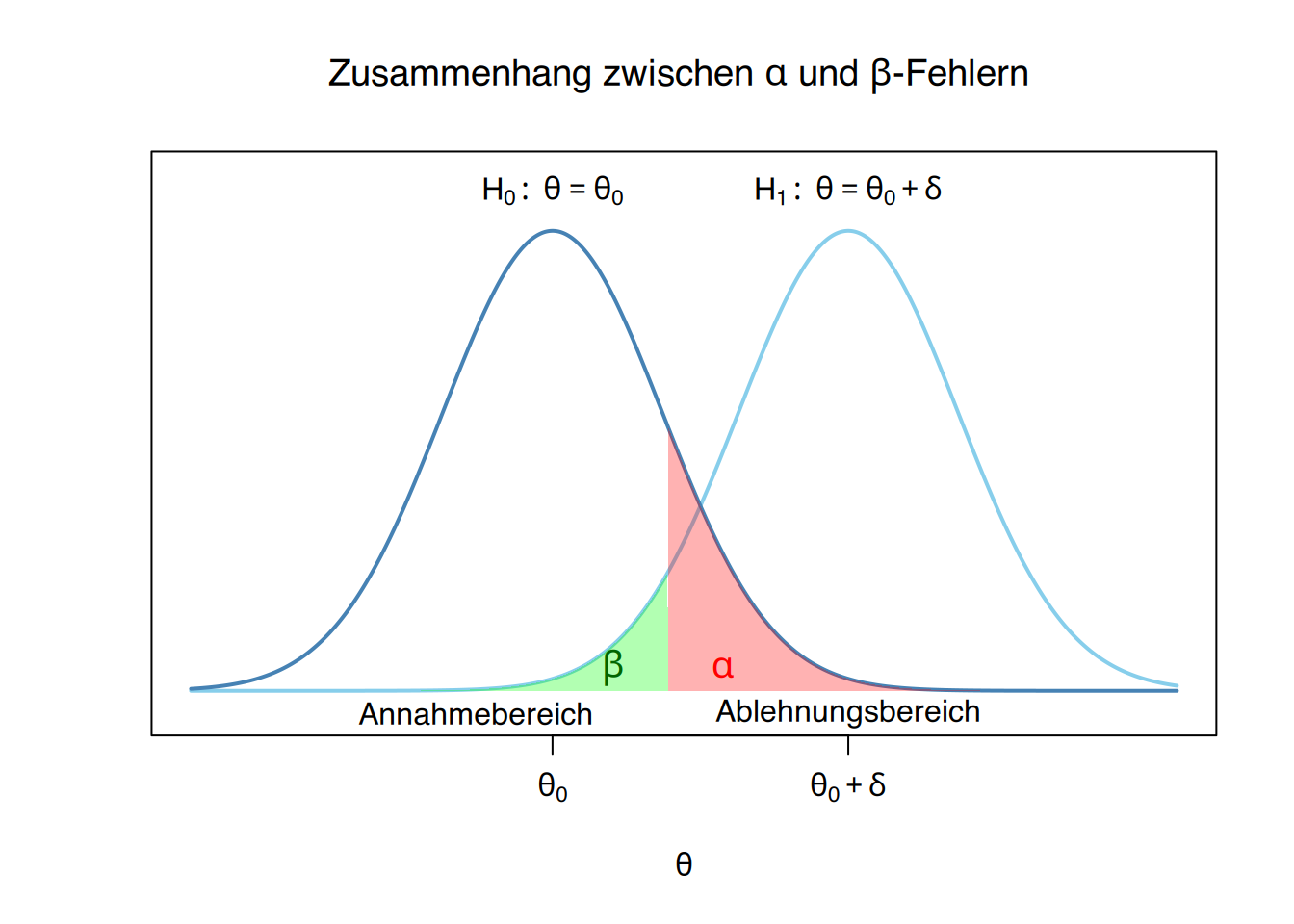
Wenn beim Test des Männeranteils ein Risiko von \(\alpha=0.1\) festgelegt wird, dann wäre der Ablehnungsbereich \(X\leq 2\), da unter der Annahme der Nullhypothese \(X\sim B(10, 0.5)\) gilt und

\[ P(X\leq 2) = 0.0547 \leq 0.1=\alpha. \]

Für eine minimale Differenz von \(\delta=0.1\) und unter Annahme der Alternativhypothese \(X\sim B(10, 0.4)\) beträgt das \(\beta\)-Risiko dann:

\[ \beta = P(\mbox{Annahme }H_0|H_1) = P(X\geq 3) = 1- P(X<3) = 1-0,1673 = 0,8327 \]

sodass die Teststärke nun auf

\[ 1-\beta = 1-0,8327 = 0,1673 \]

angestiegen ist.

9.2.11 Zusammenhang zwischen Fehlerrisiken und Stichprobenumfang

Die Fehlerrisiken hängen ebenfalls vom Stichprobenumfang ab, denn mit zunehmender Stichprobengröße verringert sich die Streuung der Teststatistik und damit auch die Fehlerrisiken.

Beispiel

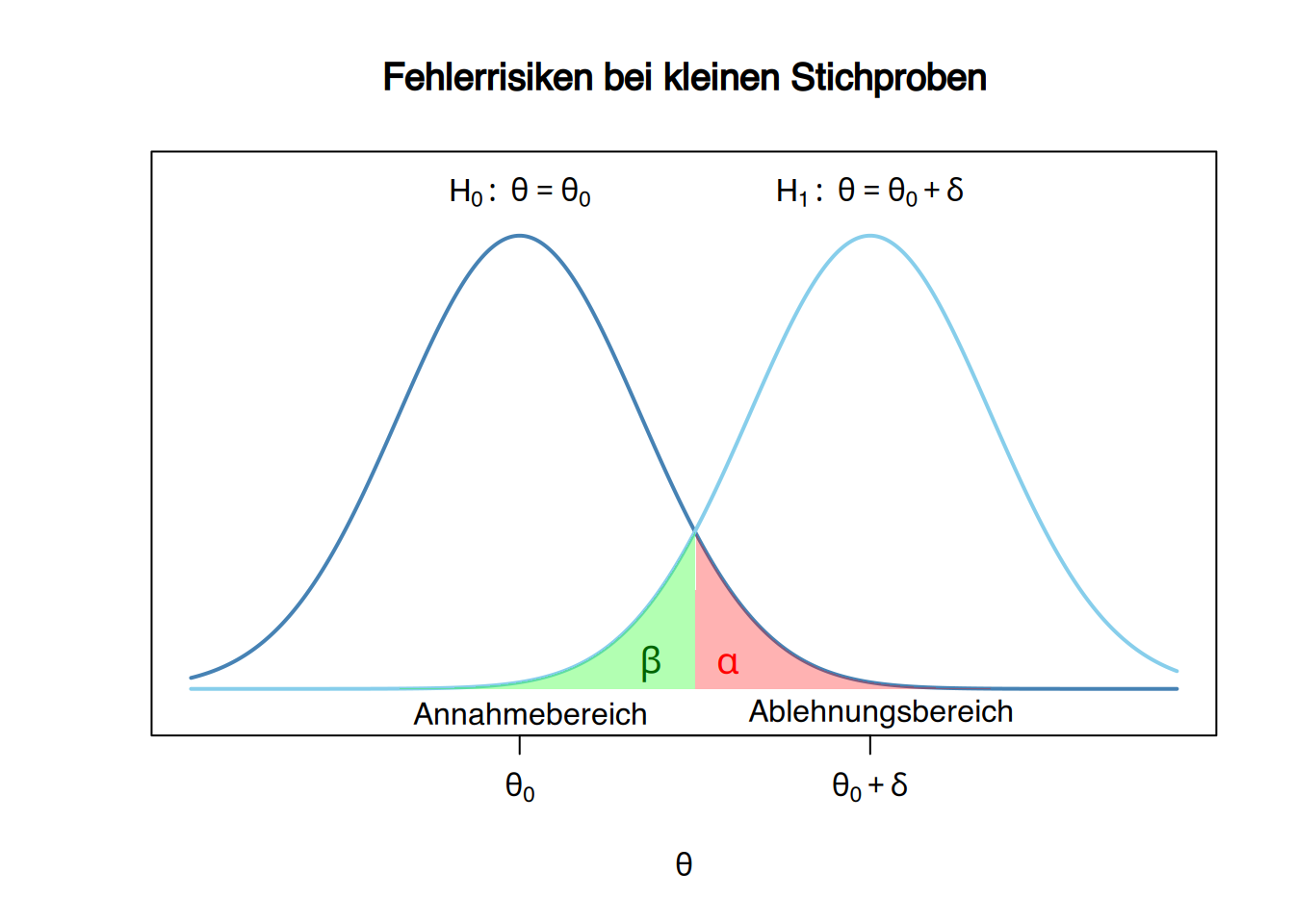
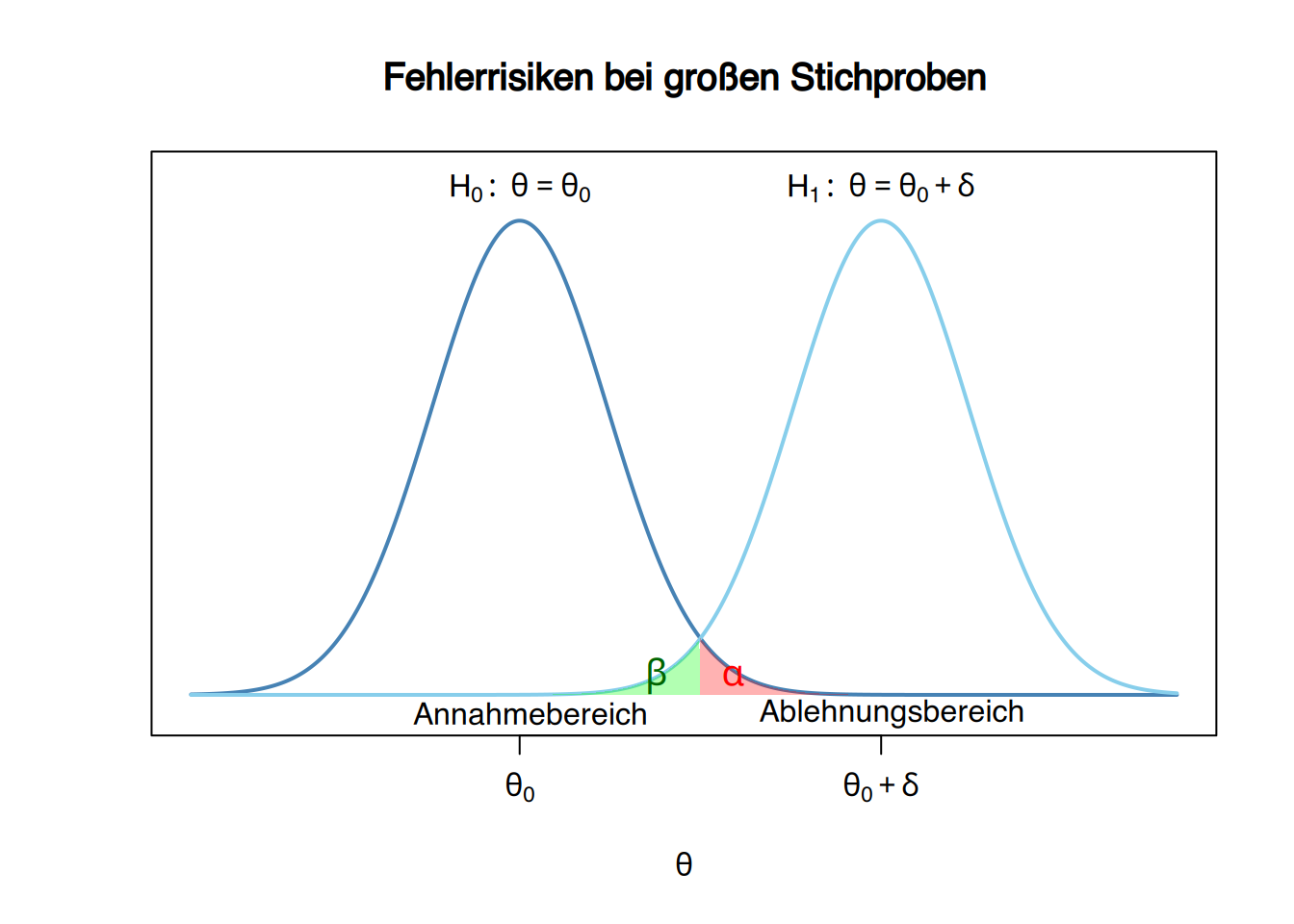
Wenn für den Test des Männeranteils eine Stichprobe des Umfangs 100 (statt 10) verwendet worden wäre, würde die Teststatistik unter Gültigkeit der Nullhypothese einer Binomialverteilung \(B(100 ,0.5)\) folgen. In diesem Fall wäre der Ablehnungsbereich \(X\leq 41\), da

\[ P(X\leq 41) = 0,0443 \leq 0,05 =\alpha. \]

Für \(\delta=0.1\) und unter Annahme der Alternativhypothese \(X\sim B(100,,0.4)\) würde das \(\beta\)-Risiko dann

\[ \beta = P(\mbox{Annahme }H_0|H_1) = P(X\geq 42) = 0.3775 \]

betragen, und die Teststärke hätte sich deutlich erhöht auf

\[ 1-\beta = 1-0,3775 = 0,6225. \]

Dieser Test wäre wesentlich besser geeignet, um eine Abweichung von mindestens 10% vom unter der Nullhypothese angenommenen Parameterwert zu erkennen.

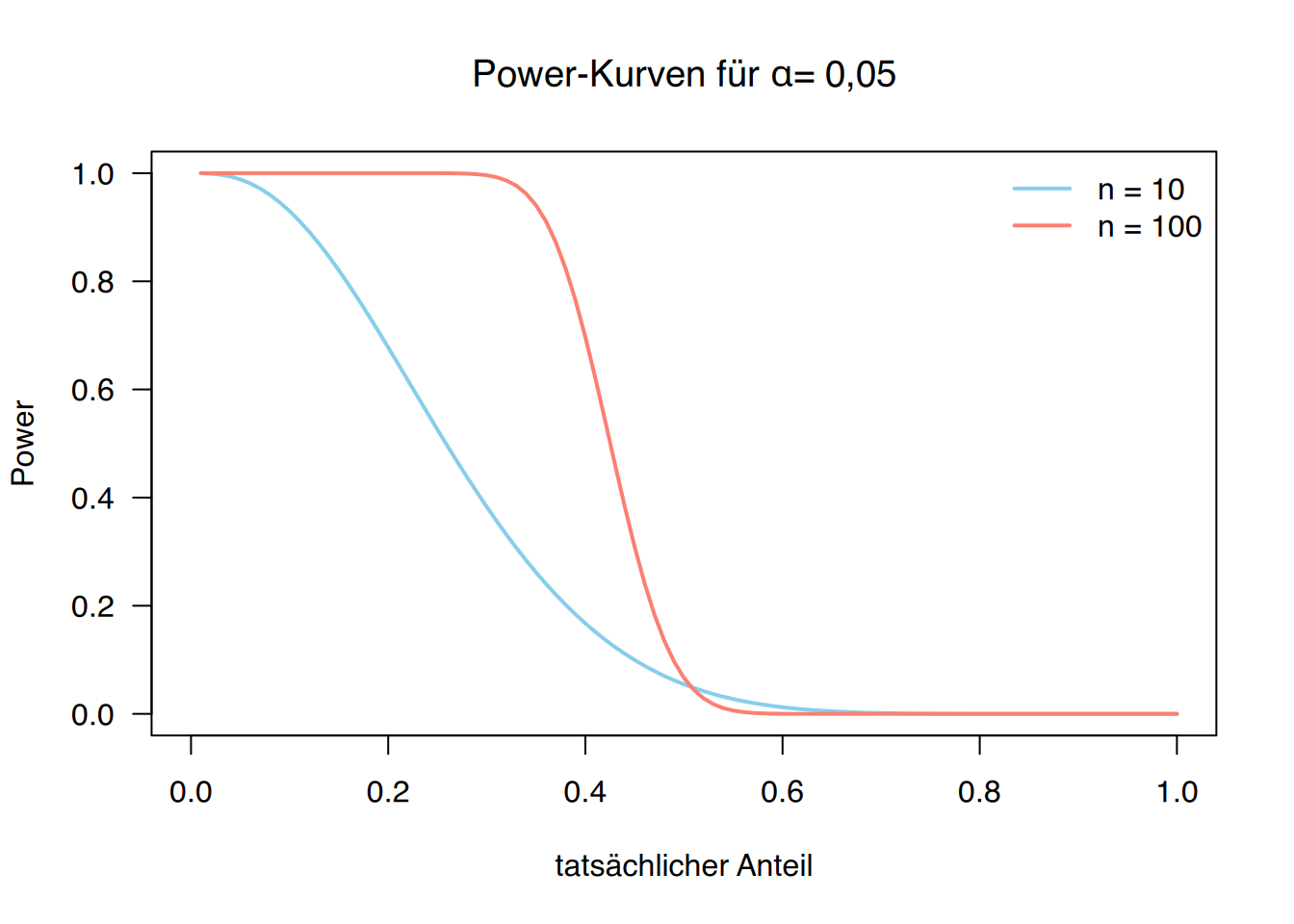
9.3 Power-Kurve

Die Teststärke (Power) eines Hypothesentests hängt vom unter der Alternativhypothese angenommenen Parameterwert ab und ist somit eine Funktion dieses Parameters:

\[ \mbox{Power}(x)= P(\mbox{Ablehnung }H_0|\theta=x). \]

Diese Funktion gibt die Wahrscheinlichkeit an, die Nullhypothese für jeden möglichen Parameterwert zu verwerfen und wird als Power-Kurve oder Trennschärfekurve bezeichnet.

Wenn der genaue Parameterwert der Alternativhypothese nicht festgelegt werden kann, ist die Darstellung dieser Kurve besonders nützlich, um die Güte des Tests bei Nicht-Ablehnung der Nullhypothese zu beurteilen. Ebenso hilfreich ist sie, wenn nur eine begrenzte Stichprobengröße verfügbar ist, um die Sinnhaftigkeit der Untersuchung einzuschätzen.

Die Qualität eines Tests ist umso höher, je größer die Fläche unter der Power-Kurve ist.

Beispiel

Die zugehörige Power-Kurve des Tests zur Prüfung des Männeranteils in der Bevölkerung ist die folgende:

9.3.1 Der p-Wert eines Hypothesentests

Grundsätzlich wird die Nullhypothese verworfen, wenn die Schätzung der Teststatistik in den Ablehnungsbereich fällt. Jedoch haben wir deutlich mehr Vertrauen in die Ablehnung, wenn die Schätzung weit vom Annahmebereich entfernt liegt, als wenn sie nahe an der Grenze zwischen Annahme- und Ablehnungsbereich liegt.

Aus diesem Grund wird bei der Durchführung eines Tests zusätzlich die Wahrscheinlichkeit berechnet, mit der eine Abweichung auftritt, die mindestens so groß ist wie die beobachtete Differenz zwischen der Schätzung der Teststatistik und ihrem erwarteten Wert gemäß der Nullhypothese.

Definition “p-Wert”

In einem Hypothesentest wird für jede Schätzung \(x_0\) der Teststatistik \(X\) - abhängig von der Art des Tests - der \(p\)-Wert definiert als:

\[ \begin{array}{lc} \mbox{zweiseitiger Test}: & 2P(X\geq x_0|H_0) \\ \mbox{einseitiger Test (links)}: & P(X\leq x_0|H_0) \\ \mbox{einseitiger Test (links)}: & P(X\geq x_0|H_0) \end{array} \]

In gewisser Weise drückt der \(p\)-Wert das Vertrauen in die Entscheidung aus, die Nullhypothese abzulehnen. Je näher der \(p\)-Wert bei \(1\) liegt, desto größer ist das Vertrauen in die Annahme der Nullhypothese, und je näher er bei \(0\) liegt, desto größer ist das Vertrauen in ihre Ablehnung.

9.3.2 Entscheidungsregel eines Tests

Nach Festlegung des Risikos \(\alpha\) kann die Entscheidungsregel für einen Test auch wie folgt formuliert werden:

Entscheidungsregel

\[ \begin{array}{ccc} \mbox{Wenn } p\leq \alpha & \rightarrow & \mbox{Ablehnung von } H_0 \\ \mbox{Wenn } p>\alpha & \rightarrow & \mbox{Annehmen von } H_0. \end{array} \]

Somit gibt der \(p\)-Wert Auskunft darüber, bei welchen Signifikanzniveaus die Nullhypothese verworfen werden kann und bei welchen nicht.

Beispiel

Wenn beim Test des Männeranteils eine Stichprobe der Größe 10 gezogen wird und 1 Mann beobachtet wird, dann beträgt der p-Wert unter Annahme der Nullhypothese \(X\sim B(10,, 0.5)\):

\[ p = P(X\leq 1)= 0,0107 \]

während bei einer Beobachtung von 0 Männern der p-Wert:

\[ p = P(X\leq 0)= 0,001 \]

beträgt. Im ersten Fall würde die Nullhypothese für ein Risiko \(\alpha=0.05\) verworfen werden, aber nicht für \(\alpha=0.01\), während sie im zweiten Fall auch für \(\alpha=0.01\) verworfen würde. Offensichtlich würde im zweiten Fall die Entscheidung zur Ablehnung der Nullhypothese mit größerer Sicherheit getroffen werden.

9.3.3 Vorgehensweise bei der Durchführung eines Hypothesentests

Formulierung der Nullhypothese \(H_0\) und Alternativhypothese \(H_1\)
Festlegung der gewünschten Risiken \(\alpha\) und \(\beta\)
Auswahl der geeigneten Teststatistik
Bestimmung der klinisch relevanten Mindestdifferenz (Effektgröße) \(\delta\)
Berechnung des erforderlichen Stichprobenumfangs \(n\)
Abgrenzung von Annahme- und Ablehnungsbereich
Ziehung einer Stichprobe des Umfangs \(n\)
Berechnung der Teststatistik für die Stichprobe
Ablehnung der Nullhypothese, wenn der Schätzwert in den Ablehnungsbereich fällt oder der \(p\)-Wert kleiner als \(\alpha\) ist; andernfalls Beibehaltung der Nullhypothese

9.4 Wichtigste parametrische Tests

Anpassungstests (Goodness-of-Fit-Tests):

Test für den Mittelwert einer Normalverteilung mit bekannter Varianz
Test für den Mittelwert einer Normalverteilung mit unbekannter Varianz
Test für den Mittelwert einer Population mit unbekannter Varianz bei großen Stichproben
Test für die Varianz einer normalverteilten Population
Test für einen Anteilswert in einer Population

Homogenitätstests:

Vergleichstest für Mittelwerte zweier Normalverteilungen mit bekannten Varianzen
Vergleichstest für Mittelwerte zweier Normalverteilungen mit unbekannten, aber gleichen Varianzen
Vergleichstest für Mittelwerte zweier Normalverteilungen mit unbekannten und ungleichen Varianzen
Vergleichstest für Varianzen zweier Normalverteilungen
Vergleichstest für Anteilswerte zweier Populationen

9.5 Test für den Mittelwert einer Normalverteilung mit bekannter Varianz

Gegeben sei eine Zufallsvariable \(X\) mit folgenden Eigenschaften:

Normalverteilung \(X\sim N(\mu,\sigma)\)
Unbekannter Mittelwert \(\mu\), aber bekannte Varianz \(\sigma^2\)

Testproblem:

\[ \begin{aligned} H_0 &: \mu=\mu_0 \\ H_1 &: \mu\neq \mu_0 \end{aligned} \]

Teststatistik:

\[ \bar x\sim N\left(\mu_0,\frac{\sigma}{\sqrt{n}}\right) \Rightarrow Z=\frac{\bar x-\mu_0}{\sigma/\sqrt{n}}\sim N(0,1). \]

Annahmebereich: \(z_{\alpha/2}< Z < z_{1-\alpha/2}\)

Ablehnungsbereich: \(Z\leq z_{\alpha/2}\) oder \(Z\geq z_{1-\alpha/2}\)

9.6 Test für den Mittelwert einer normalverteilten Grundgesamtheit mit unbekannter Varianz

Sei \(X\) eine Zufallsvariable, die die folgenden Bedingungen erfüllt:

Ihre Verteilung ist normal \(X\sim N(\mu,\sigma)\).
Sowohl ihr Mittelwert \(\mu\) als auch ihre Varianz \(\sigma^2\) sind unbekannt.

Testproblem:

\[ \begin{aligned} H_0 &: \mu=\mu_0 \\ H_1 &: \mu\neq \mu_0 \end{aligned} \]

Teststatistik: Unter Verwendung der Stichprobenvarianz als Schätzer der Populationsvarianz ergibt sich

\[ \bar x\sim N\left(\mu_0,\frac{\sigma}{\sqrt{n}}\right) \Rightarrow T=\frac{\bar x-\mu_0}{\hat s/\sqrt{n}}\sim T(n-1). \]

Annahmebereich: \(t^{n-1}{\alpha/2} < T < t^{n-1}{1-\alpha/2}\).

Ablehnungsbereich: \(T\leq t^{n-1}{\alpha/2}\) und \(T\geq t^{n-1}{1-\alpha/2}\).

Beispiel

In einer Gruppe von Studierenden soll getestet werden, ob die durchschnittliche Note in Statistik höher als 5 Punkte ist. Dazu wird die folgende Stichprobe entnommen:

\[ 6,3 - 5,4 - 4,1 - 5,0 - 8,2 - 7,6 - 6,4 - 5,6 - 4,3 - 5,2 \]

Der formulierte Test lautet:

\[ H_0:\ \mu=5 \quad H_1:\ \mu>5 \]

Für die Durchführung des Test ergibt sich:

\(\bar x = \frac{6.3+\cdots+5.2}{10}=\frac{58.1}{10}=5.81\) Punkte.
\(\hat s^2 = \frac{(6.3-5.81)^2+\cdots+(5.2-5.81)^2}{9} = \frac{15.949}{9}=1.7721\) Punkte\(^2\), und \(\hat s=1.3312\) Punkte.

Die Teststatistik beträgt

\[ T=\frac{\bar x-\mu_0}{\hat s/\sqrt{n}} = \frac{5,81-5}{1,3312/\sqrt{10}}= 1,9246. \]

Der \(p\)-Wert des Tests ist \(P(T(9)\geq 1,9246) = 0,04323\), was bedeutet, dass die Nullhypothese für \(\alpha=0.05\) abgelehnt würde.

Der Ablehnungsbereich ist

\[ T=\frac{\bar x-5}{1,3312/\sqrt{10}} \geq t^9_{0,95} = 1,8331 \Leftrightarrow \bar x \geq 5+1,8331\frac{1,3312}{\sqrt 10} = 5,7717 \] sodass die Nullhypothese abgelehnt wird, wenn der Stichprobenmittelwert größer als \(5,7717\) ist, andernfalls wird sie angenommen.

Unter der Annahme, dass in der Praxis ein minimaler wichtiger Unterschied in der Durchschnittsnote ein Punkt \(\delta=1\) wäre, dann unter der Alternativhypothese \(H_1:\mu=6\), wenn die Nullhypothese abgelehnt würde, wäre das Risiko \(\beta\)

\[ \beta = P\left(T(9)\leq \frac{5,7717-6}{1,3312\sqrt 10}\right) = P(T(9)\leq -0,5424) = 0,3004 \]

sodass die Teststärke zur Erkennung einer Differenz von \(\delta=1\) Punkt \(1-\beta=1-0,3004 = 0,6996\) beträgt.

9.6.1 Bestimmung des Stichprobenumfangs für einen Test des Mittelwerts

Es wurde gezeigt, dass für ein Risiko \(\alpha\) der Ablehnungsbereich

\[ T=\frac{\bar x-\mu_0}{\hat s/\sqrt{n}} \geq t^{n-1}_{1-\alpha} \approx z_{1-\alpha}\quad \mbox{ für } n\geq 30. \]

oder äquivalent

\[ \bar x \geq \mu_0+z_{1-\alpha}\frac{\hat s}{\sqrt n}. \]

Wenn die Effektgröße \(\delta\) beträgt, ergibt sich für eine Alternativhypothese \(H_1:\mu=\mu_0+\delta\) das Risiko \(\beta\) zu

\[ \beta = P\left(Z< \frac{\mu_0+z_{1-\alpha}\frac{\hat s}{\sqrt n}-(\mu_0+\delta)}{\frac{\hat s}{\sqrt n}} \right) = P\left(Z< \frac{z_{1-\alpha}\frac{\hat s}{\sqrt n}-\delta}{\frac{\hat s}{\sqrt n}} \right). \]

sodass

\[ z_\beta = \frac{z_{1-\alpha}\frac{\hat s}{\sqrt n}-\delta}{\frac{\hat s}{\sqrt n}} \Leftrightarrow \delta = (z_{1-\alpha}-z_\beta)\frac{\hat s}{\sqrt n} \Leftrightarrow n = (z_{1-\alpha}-z_\beta)^2\frac{\hat s^2}{\delta^2} = (z_\alpha+z_\beta)^2\frac{\hat s^2}{\delta^2}. \]

Beispiel

Im vorherigen Beispiel wurde gezeigt, dass die Teststärke zur Erkennung einer Differenz in der Durchschnittsnote von 1 Punkt bei \(69,96%\) lag.

Um die Teststärke auf \(90%\) zu erhöhen, wie viele Schüler müssten in die Stichprobe aufgenommen werden?

Da eine Teststärke von \(1-\beta=0,9\) gewünscht ist, beträgt das Risiko \(\beta=0.1\) und aus der Tabelle der Standardnormalverteilung ergibt sich \(z_\beta = z_{0,1}=1,2816\).

Unter Anwendung der obigen Formel zur Bestimmung des erforderlichen Stichprobenumfangs ergibt sich

\[ n = (z_\alpha+z_\beta)^2\frac{\hat s^2}{\delta^2} = (1,6449+1,2816)^2\frac{1,7721}{1^2} = 15,18, \]

sodass mindestens 16 Schüler hätten untersucht werden müssen.

9.7 Test für den Mittelwert einer Grundgesamtheit mit unbekannter Varianz und großen Stichproben

Sei \(X\) eine Zufallsvariable, die die folgenden Bedingungen erfüllt:

Ihre Verteilung kann beliebig sein.
Sowohl ihr Mittelwert \(\mu\) als auch ihre Varianz \(\sigma^2\) sind unbekannt.

Testproblem:

\[ \begin{aligned} H_0 &: \mu=\mu_0 \\ H_1 &: \mu\neq \mu_0 \end{aligned} \]

Teststatistik: Unter Verwendung der Stichprobenvarianz als Schätzer der Populationsvarianz und dank des zentralen Grenzwertsatzes (da große Stichproben \(n\geq 30\) vorliegen) gilt:

\[ \bar x\sim N\left(\mu_0,\frac{\sigma}{\sqrt{n}}\right) \Rightarrow Z=\frac{\bar x-\mu_0}{\hat s/\sqrt{n}}\sim N(0,1). \]

Annahmebereich: \(-z_{\alpha/2}< Z < z_{\alpha/2}\).

Ablehnungsbereich: \(Z\leq -z_{\alpha/2}\) y \(Z\geq z_{\alpha/2}\).

9.8 Test für die Varianz einer normalverteilten Grundgesamtheit

Sei \(X\) eine Zufallsvariable, die folgende Annahmen erfüllt:

Ihre Verteilung ist normal
Sowohl ihr Mittelwert \(\mu\) als auch ihre Varianz \(\sigma^2\) sind unbekannt

Testproblem:

\[ \begin{aligned} H_0 &: \sigma^2 = \sigma_0^2 \\ H_1 &: \sigma^2 \neq \sigma_0^2 \end{aligned} \]

Teststatistik: Ausgehend von der Stichprobenvarianz als Schätzer für die Populationsvarianz gilt:

\[ J=\frac{nS^2}{\sigma_0^2} = \frac{(n-1)\hat{S}^2}{\sigma_0^2}\sim \chi^2(n-1), \]

die einer Chi-Quadrat-Verteilung mit \(n-1\) Freiheitsgraden folgt.

Annahmebereich: \(\chi_{\alpha/2}^{n-1} < J < \chi_{1-\alpha/2}^{n-1}\)

Ablehnungsbereich: \(J\leq \chi_{\alpha/2}^{n-1}\) oder \(J\geq \chi_{1-\alpha/2}^{n-1}\)

Beispiel

In einer Schülergruppe soll getestet werden, ob die Standardabweichung der Noten größer als 1 Punkt ist. Dazu wird folgende Stichprobe erhoben:

\[ 6,3 - 5,4 - 4,1 - 5,0 - 8,2 - 7,6 - 6,4 - 5,6 - 4,3 - 5,2 \]

Es wird folgender Test durchgeführt:

\[ H_0: \sigma=1 \quad H_1: \sigma>1 \]

Für die Testdurchführung ergibt sich:

\(\bar x = \frac{6.3+\cdots+5,2}{10}=\frac{58,1}{10}=5,81\) Punkte
\(\hat s^2 = \frac{(6,3-5,81)^2+\cdots+(5,2-5,81)^2}{9} = \frac{15,949}{9}=1,7721\) Punkte\(^2\)

Die Teststatistik beträgt:

\[ J= \frac{(n-1)\hat{S}^2}{\sigma_0^2} = \frac{9\cdot1,7721}{1^2} = 15,949, \]

und der \(p\)-Wert des Tests ist \(P(\chi(9)\geq 15,949) = 0,068\), sodass die Nullhypothese für \(\alpha=0.05\) nicht verworfen werden kann.

9.9 Test für einen Anteilswert in einer Grundgesamtheit

Sei \(p\) der Anteil von Individuen in einer Population, die eine bestimmte Eigenschaft aufweisen.

Testproblem:

\[ \begin{aligned} H_0 &: p=p_0 \\ H_1 &: p\neq p_0 \end{aligned} \]

Teststatistik: Die Zufallsvariable, die die Anzahl der Individuen mit der Eigenschaft in einer Zufallsstichprobe des Umfangs \(n\) zählt, folgt einer Binomialverteilung \(X\sim B(n,p_0)\). Gemäß dem zentralen Grenzwertsatz gilt für große Stichproben (\(np\geq 5\) und \(n(1-p)\geq 5\)) die Approximation \(X\sim N(np_0,\sqrt{np_0(1-p_0)})\), und somit:

\[ \hat{p}=\frac{X}{n} \sim N\left(p_0,\sqrt{\frac{p_0(1-p_0)}{n}}\right) \Rightarrow Z = \frac{\hat p-p_0}{\sqrt{p_0(1-p_0)/n}}\sim N(0,1). \]

Annahmebereich: \(z_{\alpha/2}< Z < z_{1-\alpha/2}\).

Ablehnungsbereich: \(Z\leq z_{\alpha/2}\) oder \(Z\geq z_{1-\alpha/2}\).

Beispiel

In einer Gruppe von Studierenden soll untersucht werden, ob die Durchfallquote über 50% liegt. Dazu wird eine Stichprobe von 80 Studierenden gezogen, von denen 50 bestanden haben.

Das Testproblem lautet:

\[ \begin{aligned} H_0\ &: p=0.5 \\ H_1\ &: p>0.5 \end{aligned} \]

Für die Testdurchführung ergibt sich \(\hat p= 50/80 = 0,625\). Da die Approximationsbedingungen \(n\hat p=80\cdot 0,625 = 50\geq 5\) und \(n(1-\hat p)=80(1-0,625)=30\geq 5\) erfüllt sind, berechnet sich die Teststatistik zu:

\[ Z = \frac{\hat p-p_0}{\sqrt{p_0(1-p_0)/n}} = \frac{0,625-0.5}{\sqrt{0,5(1-0,5)/80}} = 2,2361. \]

Der p-Wert des Tests beträgt \(P(Z\geq 2,2361)=0,0127\), sodass die Nullhypothese für \(\alpha=0,05\) verworfen werden kann. Es lässt sich schließen, dass die Bestehensquote signifikant über 50% liegt.

9.10 Vergleichstest für Mittelwerte zweier Normalverteilungen mit bekannten Varianzen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen, die folgende Bedingungen erfüllen:

Ihre Verteilung ist normal: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\)
Ihre Mittelwerte \(\mu_1\) und \(\mu_2\) sind unbekannt, aber ihre Varianzen \(\sigma^2_1\) und \(\sigma^2_2\) sind bekannt.

Testproblem:

\[ \begin{aligned} H_0 &:\ \mu_1=\mu_2 \\ H_1 &:\ \mu_1\neq \mu_2 \end{aligned} \]

Teststatistik:

\[ \left. \begin{array}{l} \bar{X}_1\sim N\left(\mu_1,\frac{\sigma_1}{\sqrt{n_1}} \right) \\ \bar{X}_2\sim N\left(\mu_2,\frac{\sigma_2}{\sqrt{n_2}} \right) \end{array} \right\} \Rightarrow \]

\[ \Rightarrow \bar{X}_1-\bar{X}_2 \sim N\left(\mu_1-\mu_2,\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\right) \Rightarrow Z= \frac{\bar{X}_1-\bar{X}_2}{\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}}\sim N(0,1). \]

Annahmebereich: \(-z_{\alpha/2}< Z < z_{\alpha/2}\)

Ablehnungsbereich: \(Z\leq -z_{\alpha/2}\) oder \(Z\geq z_{\alpha/2}\)

9.11 Vergleichstest für Mittelwerte zweier Normalverteilungen mit unbekannten aber gleichen Varianzen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen, die folgende Bedingungen erfüllen:

Ihre Verteilung ist normal: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\)
Ihre Mittelwerte \(\mu_1\) und \(\mu_2\) sind unbekannt und ihre Varianzen ebenfalls, aber sie sind gleich: \(\sigma^2_1=\sigma^2_2=\sigma^2\)

Testproblem:

\[ \begin{aligned} H_0 &:\ \mu_1=\mu_2 \\ H_1 &:\ \mu_1\neq \mu_2 \end{aligned} \]

Teststatistik:

\[ \left. \begin{array}{l} \bar{X}_1-\bar{X}_2\sim N\left(\mu_1-\mu_2,\sigma\sqrt{\frac{n_1+n_2}{n_1n_2}} \right) \\ \displaystyle \frac{n_1S_1^2+n_2S_2^2}{\sigma^2} \sim \chi^2(n_1+n_2-2) \end{array} \right\} \Rightarrow T=\frac{\bar{X}_1-\bar{X}_2}{\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}} \sim T(n_1+n_2-2). \]

Annahmebereich: \(-t_{\alpha/2}^{n_1+n_2-2} < T < t_{\alpha/2}^{n_1+n_2-2}\)

Ablehnungsbereich: \(T\leq -t_{\alpha/2}^{n_1+n_2-2}\) oder \(T\geq t_{\alpha/2}^{n_1+n_2-2}\)

Beispiel

Es soll die akademische Leistung zweier Schülergruppen (10 bzw. 12 Schüler) mit unterschiedlichen Lehrmethoden verglichen werden. Dazu werden folgende Prüfungsergebnisse erzielt:

\[ \begin{aligned} X_1 &: 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \\ X_2 &: 8 - 9 - 5 - 3 - 8 - 7 - 8 - 6 - 8 - 7 - 5 - 7 \end{aligned} \]

Das Testproblem lautet:

\[ H_0: \mu_1=\mu_2\qquad H_1: \mu_1\neq \mu_2 \]

Für die Testdurchführung ergibt sich:

\(\bar{X}_1 = \frac{4+\cdots +3}{10}=5.3\) Punkte und \(\bar{X}_2=\frac{8+\cdots +7}{12}=6.75\) Punkte
\(S_1^2= \frac{4^2+\cdots + 3^2}{10}-5.3^2=3.21\) Punkte\(^2\) und \(S_2^2= \frac{8^2+\cdots +3^2}{12}-6.75^2=2.69\) Punkte\(^2\)
\(\hat{S}_p^2 = \frac{10\cdot 3.21+12\cdot 2.6875}{10+12-2}= 3.2175\) Punkte\(^2\), und \(\hat S_p=1.7937\)

Unter Annahme gleicher Varianzen beträgt die Teststatistik:

\[ T=\frac{\bar{X}_1-\bar{X}_2}{\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}} = \frac{5,3-6,75}{1,7937\sqrt{\frac{10+12}{10\cdot 12}}} = -1,8879 \]

Der \(p\)-Wert des Tests ist \(2P(T(20)\leq -1,8879) = 0,0736\), sodass die Nullhypothese nicht verworfen werden kann. Es gibt keine signifikanten Unterschiede zwischen den Durchschnittsnoten der Gruppen.

9.12 Vergleichstest für Mittelwerte zweier Normalverteilungen mit unbekannten und ungleichen Varianzen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen, die folgende Bedingungen erfüllen:

Ihre Verteilung ist normal: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\)
Ihre Mittelwerte \(\mu_1\), \(\mu_2\) und Varianzen \(\sigma_1^2\), \(\sigma_2^2\) sind unbekannt, wobei \(\sigma^2_1 \neq \sigma^2_2\)

Testproblem:

\[ \begin{aligned} H_0 &:\ \mu_1=\mu_2 \\ H_1 &:\ \mu_1\neq \mu_2 \end{aligned} \]

Teststatistik:

\[ T=\frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}} \sim T(g), \]

mit \(g=n_1+n_2-2-\Delta\) und

\[ \Delta = \frac{(\frac{n_2-1}{n_1}\hat{S}_1^2-\frac{n_1-1}{n_2}\hat{S}_2^2)^2}{\frac{n_2-1}{n_1^2}\hat{S}_1^4+\frac{n_1-1}{n_2^2}\hat{S}_2^4}. \]

Annahmebereich: \(-t_{\alpha/2}^{g} < T < t_{\alpha/2}^{g}\)

Ablehnungsbereich: \(T\leq -t_{\alpha/2}^{g}\) oder \(T\geq t_{\alpha/2}^{g}\)

9.13 Vergleichstest für Varianzen zweier Normalverteilungen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen mit:

Normalverteilung: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\)
Unbekannten Mittelwerten \(\mu_1\), \(\mu_2\) und Varianzen \(\sigma_1^2\), \(\sigma_2^2\)

Testproblem:

\[ \begin{aligned} H_0 &: \sigma_1=\sigma_2 \\ H_1 &: \sigma_1\neq \sigma_2 \end{aligned} \]

Teststatistik:

\[ \left. \begin{array}{l} \displaystyle \frac{(n_1-1)\hat{S}_1^2}{\sigma_1^2}\sim \chi^2(n_1-1) \\ \displaystyle \frac{(n_2-1)\hat{S}_2^2}{\sigma_2^2}\sim \chi^2(n_2-1) \end{array} \right\} \Rightarrow F= \frac{\frac{\frac{(n_1-1)\hat{S}_1^2}{\sigma_1^2}}{n_1-1}}{\frac{\frac{(n_2-1)\hat{S}_2^2}{\sigma_2^2}}{n_2-1}} = \frac{\sigma_2^2}{\sigma_1^2}\frac{\hat{S}_1^2}{\hat{S}_2^2}\sim F(n_1-1,n_2-1). \]

Annahmebereich: \(F_{\alpha/2}^{n_1-1,n_2-1} < F < F_{1-\alpha/2}^{n_1-1,n_2-1}\)

Ablehnungsbereich: \(F\leq F_{\alpha/2}^{n_1-1,n_2-1}\) oder \(F\geq F_{1-\alpha/2}^{n_1-1,n_2-1}\)

Beispiel

Fortsetzung des Beispiels mit den Punktzahlen zweier Gruppen:

\[ \begin{aligned} X_1 &: 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \\ X_2 &: 8 - 9 - 5 - 3 - 8 - 7 - 8 - 6 - 8 - 7 - 5 - 7 \end{aligned} \]

Für den Varianzvergleich lautet das Testproblem:

\[ H_0: \sigma_1=\sigma_2\qquad H_1: \sigma_1\neq \sigma_2 \]

Berechnungen:

\(\bar{X}_1 = \frac{4+\cdots +3}{10}=5,3\) Punkte
\(\bar{X}_2=\frac{8+\cdots +7}{12}=6,75\) Punkte
\(\hat{S}_1^2= \frac{(4-5,3)^2+\cdots + (3-5,3)^2}{9}=3,5667\) Punkte\(^2\)
\(\hat{S}_2^2= \frac{(8-6,75)^2+\cdots + (3-6,75)^2}{11}=2,9318\) Punkte\(^2\)

Teststatistik:

\[ F = \frac{\hat{S}_1^2}{\hat{S}_2^2} = \frac{3,5667}{2,9318}=1,2165 \]

Der p-Wert beträgt \(2P(F(9,11)\leq 1.2165)=0.7468\), sodass die Nullhypothese gleicher Varianzen beibehalten wird.

9.14 Vergleichstest von Anteilen zweier Populationen

Seien \(p_1\) und \(p_2\) die jeweiligen Anteile von Individuen, die ein bestimmtes Merkmal in zwei Populationen aufweisen.

Testproblem:

\[ H_0: p_1=p_2\qquad H_1: p_1\neq p_2 \]

Teststatistik: Die Zufallsvariablen, die die Anzahl der Individuen mit dem Merkmal in zwei unabhängigen Stichproben der Größen \(n_1\) und \(n_2\) messen, folgen binomialverteilten Zufallsvariablen \(X_1\sim B(n_1,p_1)\) und \(X_2\sim B(n_2,p_2)\). Wenn die Stichproben groß sind (\(n_ip_i\geq 5\) und \(n_i(1-p_i)\geq 5\)), folgt gemäß dem zentralen Grenzwertsatz:

\[ X_1\sim N(np_1,\sqrt{np_1(1-p_1)})\quad \text{und} \quad X_2\sim N(np_2,\sqrt{np_2(1-p_2)}) \]

und es gilt:

\[ \left. \begin{array}{l} \hat{p}_1=\frac{X_1}{n_1} \sim N\left(p_1,\sqrt{\frac{p_1(1-p_1)}{n_1}}\right) \\ \hat{p}_2=\frac{X_2}{n_2} \sim N\left(p_2,\sqrt{\frac{p_2(1-p_2)}{n_2}}\right) \end{array} \right\} \Rightarrow Z = \frac{\hat{p}_1-\hat{p_2}}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}\sim N(0,1) \]

Annahmebereich: \(z_{\alpha/2}< Z < z_{1-\alpha/2}\)

Ablehnungsbereich: \(z\leq z_{\alpha/2}\) und \(z\geq z_{1-\alpha/2}\)

Beispiel

Es soll geprüft werden, ob sich die Bestehensquoten zweier Gruppen unterscheiden, die unterschiedliche Lehrmethoden durchlaufen haben. In der ersten Gruppe haben 24 von insgesamt 40 Schülern bestanden, in der zweiten Gruppe 48 von 60.

Der formulierte Test lautet:

\[ H_0:\ p_1=p_2\qquad H_1:\ p_1\neq p_2 \]

Für den Test ergibt sich: \(\hat{p}_1=24/40= 0.6\) und \(\hat{p}_2=48/60=0.8\). Damit sind die Voraussetzungen erfüllt:

\(n_1\hat{p}_1=40\cdot 0.6=24\geq 5\),
\(n_1(1-\hat{p}_1)=40(1-0.6)=16\geq 5\),
\(n_2\hat{p}_2=60\cdot 0.8=48\geq 5\) und
\(n_2(1-\hat{p}_2)=60(1-0.8)=12\geq 5\).

Die Teststatistik ergibt:

\[ Z = \frac{\hat{p}_1-\hat{p_2}}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}} = \frac{0,6-0,8}{\sqrt{\frac{0,6(1-0,6)}{40}+\frac{0,8(1-0,8)}{60}}} = -2,1483 \]

und der \(p\)-Wert des Tests ist \(2P(Z\leq -2,1483)= 0,0317\), sodass die Nullhypothese bei einem Signifikanzniveau von \(\alpha=0,05\) verworfen wird. Es wird also geschlossen, dass es einen Unterschied zwischen den Gruppen gibt.

9.15 Durchführung von Tests mittels Konfidenzintervallen

Eine interessante Alternative zur Durchführung eines Hypothesentests

\[ H_0:\ \theta=\theta_0\qquad H_1:\ \theta\neq \theta_0 \]

mit einem Signifikanzniveau \(\alpha\) ist die Berechnung eines Konfidenzintervalls für \(\theta\) mit einem Vertrauensniveau von \(1-\alpha\). Dieses Intervall kann als die Menge akzeptabler Hypothesen für \(\theta\) interpretiert werden. Befindet sich \(\theta_0\) außerhalb des Intervalls, erscheint die Nullhypothese wenig glaubwürdig und kann verworfen werden. Befindet sich \(\theta_0\) hingegen innerhalb des Intervalls, wird die Hypothese als plausibel betrachtet und beibehalten.

Bei einem einseitigen Test mit der Alternativhypothese “kleiner” wird \(\theta_0\) mit der oberen Grenze eines Konfidenzintervalls für \(\theta\) mit einem Vertrauensniveau von \(1-2\alpha\) verglichen. Ist der Test einseitig mit der Alternativhypothese “größer”, so wird \(\theta_0\) mit der unteren Grenze des Intervalls verglichen.

Testart	Konfidenzintervall	Entscheidung
Zweiseitig	\([l_i,l_s]\) mit Vertrauensniveau \(1-\alpha\)	Verwerfe \(H_0\) wenn \(\theta_0\not \in [l_i,l_s]\)
Einseitig (kleiner)	\([-\infty,l_s]\) mit Vertrauensniveau \(1-2\alpha\)	Verwerfe \(H_0\) wenn \(\theta_0\geq l_s\)
Einseitig (größer)	\([l_i,\infty]\) mit Vertrauensniveau \(1-2\alpha\)	Verwerfe \(H_0\) wenn \(\theta_0\leq l_i\)

Beispiel

Zurück zum Test, der den schulischen Erfolg zweier Schülergruppen vergleicht. Diese haben folgende Punktzahlen erreicht:

\[ \begin{aligned} X_1 &: 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \\ X_2 &: 8 - 9 - 5 - 3 - 8 - 7 - 8 - 6 - 8 - 7 - 5 - 7 \end{aligned} \]

Der getestete Hypothesensatz lautete:

\[ H_0:\ \mu_1=\mu_2\qquad H_1:\ \mu_1\neq \mu_2 \]

Da es sich um einen zweiseitigen Test handelt, ergibt sich das Konfidenzintervall für die Differenz der Mittelwerte \(\mu_1-\mu_2\) bei einem Vertrauensniveau von \(1-\alpha=0,95\) (unter der Annahme gleicher Varianzen) zu \([-3{,}0521\ |\ 0{,}1521]\) Punkten.

Da unter der Nullhypothese \(\mu_1 - \mu_2 = 0\) gilt und 0 innerhalb dieses Intervalls liegt, wird die Nullhypothese beibehalten.

Der Vorteil eines Konfidenzintervalls besteht darin, dass es uns nicht nur erlaubt, einen Test durchzuführen, sondern auch eine Vorstellung von der Größenordnung der Differenz zwischen den Gruppenmittelwerten vermittelt.