10 Varianzanalysen

10.1 Varianzanalyse mit einem Faktor

Die Varianzanalyse mit einem Faktor (im Englischen ANOVA für Analysis of Variance) ist eine statistische Hypothesentest-Methode, die dazu dient, die Mittelwerte einer quantitativen Variablen – üblicherweise als abhängige Variable oder Antwortvariable bezeichnet – zwischen verschiedenen Gruppen oder Stichproben zu vergleichen. Diese Gruppen werden durch eine qualitative Variable definiert, die als unabhängige Variable oder Faktor bezeichnet wird. Die verschiedenen Ausprägungen des Faktors, die die zu vergleichenden Gruppen darstellen, nennt man Stufen oder Behandlungen des Faktors.

Es handelt sich dabei um eine Verallgemeinerung des t-Tests zum Vergleich der Mittelwerte zweier unabhängiger Stichproben für Versuchsanordnungen mit mehr als zwei Gruppen. Der Hauptunterschied zu einer einfachen Regressionsanalyse – bei der sowohl die abhängige als auch die unabhängige Variable quantitativ sind – besteht darin, dass beim einfaktoriellen Varianzanalysedesign die unabhängige Variable bzw. der Faktor eine qualitative Variable ist. Wie wir später bei den Regressionskontrasten sehen werden, lässt sich ein ANOVA-Test jedoch auch als Spezialfall eines linearen Regressionsmodells formulieren.

Ein typisches Beispiel für die Anwendung dieser Technik wäre der Vergleich des durchschnittlichen Cholesterinspiegels je nach Blutgruppe. In diesem Fall ist die unabhängige Variable oder der Faktor die Blutgruppe mit vier Stufen (A, B, 0, AB), während die Antwortvariable der Cholesterinspiegel ist.

Zum Vergleich der Mittelwerte der Antwortvariablen in den verschiedenen Stufen des Faktors wird ein Hypothesentest aufgestellt, bei dem die Nullhypothese \(H_0\) lautet, dass die Antwortvariable in allen Gruppen denselben Mittelwert hat. Die Alternativhypothese \(H_1\) besagt, dass es statistisch signifikante Unterschiede zwischen mindestens zwei der Mittelwerte gibt. Dieser Test basiert auf der Zerlegung der Gesamtvarianz der Antwortvariablen – daher der Name dieser Methode.

10.1.1 Der ANOVA-Test

Die übliche Notation in der ANOVA lautet:

\(k\): ist die Anzahl der Stufen (Niveaus) des Faktors.
\(n_i\): ist der Stichprobenumfang, der zur \(i\)-ten Stufe des Faktors gehört.
\(n = \sum_{i = 1}^k {n_i}\): ist die Gesamtanzahl der Beobachtungen.
\(X_{ij}\ (i = 1,...,k;\,j = 1,...,n_i)\): ist eine Zufallsvariable, die die Antwort des \(j\)-ten Individuums auf die \(i\)-te Stufe des Faktors angibt.
\(x_{ij}\): ist der konkrete Wert von \(X_{ij}\) in einer gegebenen Stichprobe.

\[ \begin{array}{c} \text{Faktorstufen} \\ \begin{array}{cccc} \hline 1 & 2 & \cdots & k \\ \hline X_{11} & X_{21} & \cdots & X_{k1} \\ X_{12} & X_{22} & \cdots & X_{k2} \\ \vdots & \vdots & \vdots & \vdots \\ X_{1n_1} & X_{2n_2} & \cdots & X_{kn_k} \\ \hline \end{array} \end{array} \]

\(\mu_i\): ist der Mittelwert der Grundgesamtheit der \(i\)-ten Stufe.
\(\bar X_i = \sum_{j = 1}^{n_i} X_{ij}/n_i\): ist der Stichprobenmittelwert der \(i\)-ten Stufe und Schätzer für \(\mu_i\).
\(\bar x_i = \sum_{j = 1}^{n_i} x_{ij}/n_i\): ist der konkrete Wert dieses Mittelwerts in einer gegebenen Stichprobe.
\(\mu\): ist der Gesamtmittelwert der Grundgesamtheit (über alle Stufen hinweg).
\(\bar X = \sum_{i = 1}^k \sum_{j = 1}^{n_i } X_{ij}/n\): ist der Gesamtstichprobenmittelwert, Schätzer für \(\mu\).
\(\bar x = \sum_{i = 1}^k \sum_{j = 1}^{n_i }x_{ij}/n\): ist der konkrete Wert dieses Mittelwerts in einer gegebenen Stichprobe.

Mit dieser Notation lässt sich die Antwortvariable durch ein mathematisches Modell ausdrücken, das sie in Komponenten zerlegt, die verschiedenen Ursachen zugeordnet werden:

\[ X_{ij} = \mu + (\mu_i - \mu) + (X_{ij} - \mu_i), \]

Das heißt, die Antwort der \(j\)-ten Beobachtung in der \(i\)-ten Stufe setzt sich zusammen aus dem Gesamtmittelwert, einer Abweichung, die dem Einfluss des \(i\)-ten Faktors zugeschrieben wird, und einer weiteren Abweichung aufgrund zufälliger Schwankungen innerhalb der Stufe.

Auf Basis dieses Modells formulieren wir die Nullhypothese: Die Mittelwerte aller Stufen sind gleich. Die Alternativhypothese lautet: Mindestens zwei Mittelwerte unterscheiden sich.

\[\begin{align*} H_0: & \mu_1 = \mu_2 = \cdots = \mu _k \\ H_1: & \mu_i \neq \mu_j \quad \text{für einige } i\neq j \end{align*}\]

Damit dieser Test gültig ist, müssen folgende Modellannahmen erfüllt sein:

Unabhängigkeit: Die \(k\) Stichproben, die den \(k\) Stufen entsprechen, sind unabhängige Zufallsstichproben aus \(k\) Populationen mit unbekannten Mittelwerten \(\mu_1 = \mu_2 = \cdots = \mu_k\).
Normalverteilung: Jede der \(k\) Populationen ist normalverteilt.
Homoskedastizität: Alle Populationen haben die gleiche Varianz \(\sigma^2\).

Wird in obigem Modell der Populationsmittelwert durch seinen Stichprobenschätzer ersetzt, ergibt sich:

\[ X_{ij} = \bar X + (\bar X_i - \bar X) + (X_{ij} - \bar X_i), \]

oder umgestellt:

\[ X_{ij} - \bar X = (\bar X_i - \bar X) + (X_{ij} - \bar X_i). \]

Durch Quadrieren und unter Ausnutzung der Summeneigenschaften ergibt sich die sogenannte Identität der Quadratsummen:

\[ \sum_{i=1}^k \sum_{j=1}^{n_i} (X_{ij} - \bar X)^2 = \sum_{i=1}^k n_i(\bar X_i - \bar X)^2 + \sum_{i=1}^k \sum_{j = 1}^{n_i}(X_{ij} - \bar X_i)^2, \]

wobei:

\(\sum_{i=1}^k \sum_{j=1}^{n_i} (X_{ij} - \bar X)^2\): ist die Gesamtquadratsumme (\(SCT\)) – misst die gesamte Streuung der Daten.
\(\sum_{i=1}^k n_i(\bar X_i - \bar X)^2\): ist die Zwischengruppen-Quadratsumme (\(SCInter\)) – misst die Streuung aufgrund der Unterschiede zwischen den Gruppenmitteln.
\(\sum_{i=1}^k \sum_{j=1}^{n_i}(X_{ij} - \bar X_i)^2\): ist die Intragruppen-Quadratsumme (\(SCIntra\)) – misst die Streuung innerhalb der Gruppen.

Somit gilt:

\[ SCT = SCInter + SCIntra \]

Um zur Teststatistik zu gelangen, definiert man die mittleren Quadratsummen (mean squares), indem man jede Quadratsumme durch die entsprechenden Freiheitsgrade teilt:

Für \(SCT\): \(n - 1\)
Für \(SCInter\): \(k - 1\)
Für \(SCIntra\): \(n - k\)

Daraus folgt:

\[\begin{align*} CMT &= \frac{SCT}{n - 1} \\ CMInter &= \frac{SCInter}{k - 1} \\ CMIntra &= \frac{SCIntra}{n - k} \end{align*}\]

Man kann zeigen, dass unter der Annahme, dass \(H_0\) sowie die Modellvoraussetzungen zutreffen, der Quotient

\[ \frac{CMInter}{CMIntra} \]

einer \(F\)-Verteilung von Fisher mit \(k - 1\) und \(n - k\) Freiheitsgraden folgt.

Wenn also \(H_0\) gilt, liegt dieser Quotient für gegebene Stichproben nahe bei 1 (aber stets > 0). Ist \(H_0\) falsch, dann nimmt die Streuung zwischen den Gruppen zu – der Wert des Quotienten steigt. Daher handelt es sich um einen einseitigen Test (rechtsseitig) mit Hilfe der \(F\)-Verteilung. Wir berechnen den \(p\)-Wert der beobachteten \(F\)-Statistik und entscheiden, ob wir \(H_0\) beibehalten oder verwerfen – abhängig vom festgelegten Signifikanzniveau.

10.1.1.1 ANOVA-Tabelle

Alle im vorherigen Abschnitt eingeführten Statistiken werden in einer sogenannten ANOVA-Tabelle zusammengefasst. In dieser Tabelle werden die Schätzwerte dieser Statistiken für die konkret untersuchten Stichproben dargestellt. Solche Tabellen sind auch das Standardausgabeformat statistischer Softwareprogramme bei der Durchführung einer ANOVA. Am Ende der Tabelle wird üblicherweise der \(p\)-Wert des berechneten \(F\)-Statistikums angegeben, anhand dessen entschieden werden kann, ob die Nullhypothese – dass die Mittelwerte aller Faktorstufen gleich sind – akzeptiert oder verworfen wird.

	Quadratsumme	Freiheitsgrade	Mittlere Quadrate	\(F\)-Statistik	\(p\)-Wert
Zwischengruppen	\(SCInter\)	\(k-1\)	\(CMInter=\frac{SCInter}{k-1}\)	\(f=\frac{CMInter}{CMIntra}\)	\(P(F>f)\)
Intragruppen	\(SCIntra\)	\(n-k\)	\(CMIntra=\frac{SCIntra}{n-k}\)
Gesamt	\(SCT\)	\(n-1\)

10.1.2 Tests für multiple und paarweise Vergleiche

Nachdem eine einfaktorielle ANOVA durchgeführt wurde, um die \(k\) Mittelwerte der \(k\) Faktorstufen bzw. Behandlungen zu vergleichen, kann man im Ergebnis entweder die Nullhypothese beibehalten – in diesem Fall endet die Analyse hinsichtlich signifikanter Unterschiede – oder sie verwerfen. Wird die Nullhypothese verworfen, ist es sinnvoll, die Analyse fortzusetzen, um präzise zu bestimmen, zwischen welchen Gruppen signifikante Unterschiede bestehen.

Für diesen zweiten Fall existieren verschiedene Verfahren, die als Tests für multiple Vergleiche bezeichnet werden. Diese lassen sich weiter unterteilen in:

Tests für paarweise Vergleiche: Ziel ist es, alle möglichen Paare von Mittelwerten zwischen den Faktorstufen einzeln zu vergleichen. Die Ergebnisse werden meist in Tabellenform dargestellt, mit den Differenzen zwischen allen möglichen Mittelwertpaaren und den zugehörigen Konfidenzintervallen. Dabei wird angegeben, ob die Unterschiede signifikant sind oder nicht. Wichtig ist, dass diese Intervalle nicht dieselben wären wie bei einem isolierten Vergleich zweier Gruppen, da das Verwerfen von \(H_0\) im Gesamt-ANOVA-Test bedeutet, dass gleichzeitig mehrere Einzelvergleiche impliziert sind. Um das vorgegebene Signifikanzniveau \(\alpha\) aufrechterhalten zu können, muss deshalb ein deutlich kleineres korrigiertes Niveau \(\alpha'\) bei den Einzeltests verwendet werden.
Tests mit multiplen Rängen: Ziel ist es, homogene Gruppen von Mittelwerten zu identifizieren, zwischen denen keine signifikanten Unterschiede bestehen.

Für paarweise Vergleiche kann der Bonferroni-Test verwendet werden; für Ranggruppierungen der Duncan-Test. Für beide Arten zusammen eignen sich die Verfahren Tukey-HSD und Scheffé-Test.

10.2 ANOVA mit zwei oder mehr Faktoren

In vielen Fragestellungen liegen nicht nur ein Faktor mit \(k\) Stufen vor, sondern es treten zwei oder mehr Faktoren auf, mit denen die Stichprobe nach verschiedenen Kriterien in Gruppen eingeordnet werden kann. Ziel ist es zu prüfen, ob signifikante Unterschiede zwischen den Mittelwerten der abhängigen Variable bestehen.

Zur Behandlung solcher Fragestellungen existiert das ANOVA mit zwei oder mehr Faktoren (auch Mehrfaktorielle ANOVA), eine Verallgemeinerung der einfaktoriellen ANOVA. Sie ermöglicht neben der Analyse der Haupteffekte jedes Faktors auch die Untersuchung ihrer Interaktion.

Außerdem gibt es Situationen, in denen pro Versuchsperson mehrere Messungen einer quantitativen Variable erfolgen. Bei zwei Messungen verwendet man den gepaarten Student‑Test (oder bei nichtparametrischen Voraussetzungen den Wilcoxon-Test). Wird drei oder mehr Messwerte pro Subjekt erhoben, kommt die ANOVA für Messwiederholungen zum Einsatz.

Es kann auch vorkommen, dass eine Variable mehrfach pro Individuum gemessen wird und gleichzeitig zwei oder mehr Klassifikationsfaktoren vorliegen. Dann kombiniert man repetierte Messungen mit einer mehrfaktoriellen ANOVA.

Die komplexeste Variante ist die ANCOVA (Analyse der Kovarianz), die in einem Design mit Messwiederholungen, mehreren Faktoren und zusätzlich Kovariablen (quantitative Einflussgrößen) durchgeführt wird. Die ANCOVA untersucht die Faktoren- und Messwiederholungseffekte, bereinigt um den Einfluss der Kovariablen.

10.2.1 Zweifaktorielle ANOVA mit zwei Faktorstufen

Um eine zweifaktorielle oder mehrfaktorielle ANOVA zu verstehen, ist es hilfreich, mit einem einfachen Fall mit zwei Faktoren und jeweils zwei Stufen zu beginnen. Beispielsweise könnte man ein Experiment durchführen, bei dem Personen entweder eine Diät einhalten (erster Faktor: Diät, mit zwei Stufen: ja und nein) und zusätzlich ein bestimmtes Medikament einnehmen (zweiter Faktor: Medikament, mit zwei Stufen: ja und nein), um ihr Körpergewicht zu reduzieren (numerische Zielvariable: Gewichtsreduktion in kg).

In diesem Fall ergeben sich vier verschiedene Gruppen:

Keine Diät und kein Medikament (Nein-Nein)
Keine Diät, aber Medikament (Nein-Ja)
Diät, aber kein Medikament (Ja-Nein)
Diät und Medikament (Ja-Ja)

Es können drei verschiedene Effekte untersucht werden:

Diät-Effekt: Untersucht, ob es signifikante Unterschiede in der Gewichtsabnahme zwischen Personen mit und ohne Diät gibt.
Medikamenten-Effekt: Untersucht, ob es signifikante Unterschiede in der Gewichtsabnahme zwischen Personen mit und ohne Medikament gibt.
Interaktionseffekt: Untersucht, ob die kombinierte Wirkung von Diät und Medikament unterschiedlich ist zur Summe ihrer Einzeleffekte. Bei einer Interaktion kann diese in zwei Richtungen wirken:

Synergie: Die Kombination führt zu einer stärkeren Gewichtsabnahme als die Summe der Einzeleffekte.
Antagonismus: Die Kombination führt zu einer schwächeren Gewichtsabnahme als die Summe der Einzeleffekte.

Beispiel

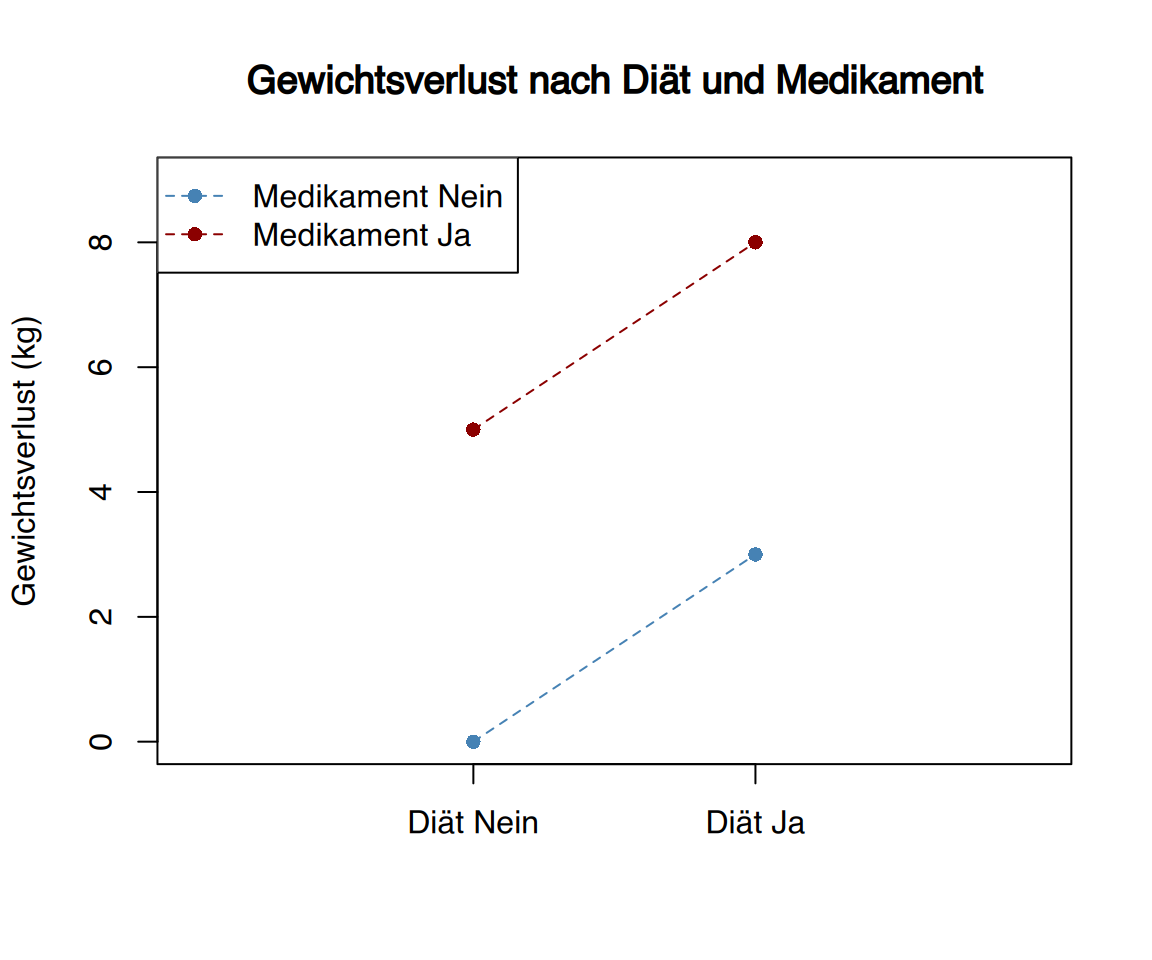
Angenommen, die folgende Tabelle zeigt die durchschnittliche Gewichtsabnahme (in kg) für jede Gruppe (ohne Berücksichtigung der individuellen Variabilität, die in einer echten ANOVA berücksichtigt würde):

	Medikament Nein	Medikament Ja
Diät Nein	0	5
Diät Ja	3	8

In diesem Fall gibt es keine Interaktion zwischen Diät und Medikament, denn:

Der Effekt des Medikaments allein (ohne Diät) beträgt +5 kg.
Der Effekt der Diät allein (ohne Medikament) beträgt +3 kg.
Die kombinierte Wirkung (Diät + Medikament) beträgt +8 kg, was exakt der Summe der Einzeleffekte (5 + 3) entspricht.

Grafische Darstellung: In einem Interaktionsplot wären die Linien für die Gruppen parallel (innerhalb eines gewissen Variabilitätsbereichs), was auf das Fehlen einer Interaktion hindeutet.

Im Gegensatz dazu könnte auch eine Tabelle entstehen, in der die Summe der Einzeleffekte geringer ist als der kombinierte Effekt von Diät und Medikament:

	Medikament Nein	Medikament Ja
Diät Nein	0	5
Diät Ja	3	12

In diesem Fall (wenn wir die Variabilität innerhalb jeder Gruppe vernachlässigen und annehmen, dass sie klein genug ist, damit die Unterschiede signifikant sind), wären die 8 kg durchschnittlicher Gewichtsabnahme, die sich aus der Summe der Einzeleffekte von Diät und Medikament ergeben, geringer als die 12 kg, die Personen im Durchschnitt verloren haben, die sowohl das Medikament einnahmen als auch die Diät befolgten.

Interpretation:

Es liegt eine Interaktion der beiden Faktoren vor, die ihre Einzeleffekte verstärkt hat.
Um das Endergebnis zu erklären, müsste man einen zusätzlichen Interaktionsterm in die Berechnung aufnehmen, der 4 kg zusätzlichen Gewichtsverlust beisteuert (über die Summe der Einzeleffekte hinaus).
Da dieser Term die Wirkung beider Faktoren verstärkt, handelt es sich um eine synergistische Interaktion.

Grafische Darstellung:

In einem Interaktionsplot wären die Linien nicht parallel, sondern würden sich annähern oder entfernen, was auf eine Interaktion hindeutet.

Zusammenfassung der Effekte:

Medikament allein: +5 kg
Diät allein: +3 kg
Erwarteter kombinierter Effekt (Summe): 5 + 3 = 8 kg
Tatsächlicher kombinierter Effekt: 12 kg
Interaktionsterm: 12 - 8 = +4 kg (Synergie)

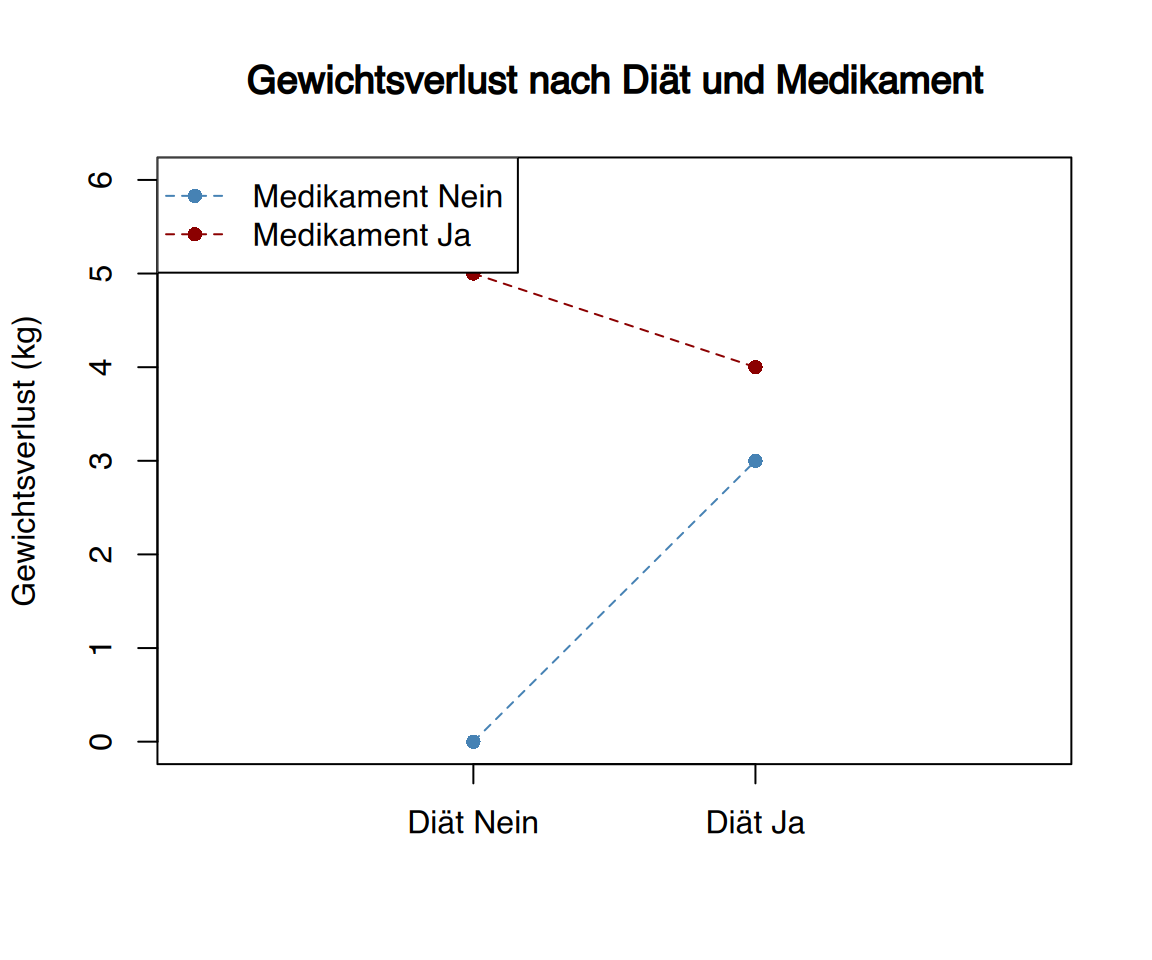
Schließlich könnte sich auch eine Tabelle ergeben, bei der die Summe der Einzeleffekte größer ist als der kombinierte Effekt beider Faktoren:

	Medikament Nein	Medikament Ja
Diät Nein	0	5
Diät Ja	3	4

In diesem Beispiel würden sich durch die Summe der Einzeleffekte (5 + 3 = 8 kg Gewichtsverlust) ein höherer Wert ergeben als die tatsächlich beobachteten 4 kg bei den Personen, die sowohl Diät hielten als auch das Medikament einnahmen.

Schlussfolgerungen:

Es liegt eine antagonistische Interaktion vor
Zur Erklärung der Ergebnisse muss ein negativer Interaktionsterm von -4 kg eingeführt werden (8 kg erwartet - 4 kg Interaktionseffekt = 4 kg beobachtet)
Die kombinierte Wirkung ist schwächer als die Summe der Einzeleffekte

Der Interaktionsterm wäre in diesem Fall statistisch signifikant negativ. Grafisch würden sich die Linien in einem Interaktionsplot kreuzen oder divergieren. Dies deutet darauf hin, dass die Faktoren sich gegenseitig in ihrer Wirkung abschwächen.

Zusammenfassung der Effekte:

\[ \begin{array}{lc} \text{Effekt} & \text{Gewichtsverlust}\\ \text{Medikament allein} & +5 \text{kg}\\ \text{Diät allein} & +3 \text{kg}\\ \text{Erwartete Kombination} & +8 \text{kg}\\ \text{Beobachtete Kombination} & +4 \text{kg}\\ \text{Interaktionseffekt} & -4 \text{kg}\\ \end{array} \]

Tatsächlich kann eine Interaktion sowohl synergistisch mit einem Faktor als auch antagonistisch mit dem anderen wirken, insbesondere wenn die Faktoren entgegengesetzte Effekte haben. Ein Beispiel wäre eine Studie, in der:

Eine kalorienreiche Diät (erwarteter Effekt: Gewichtszunahme)
Mit einem Gewichtsreduktionsmedikament (erwarteter Effekt: Gewichtsabnahme)kombiniert werden.

Wie anhand der Tabellen und Grafiken ersichtlich, zeigt eine Interaktion an, dass die Mittelwertdifferenzen zwischen den Gruppen nicht konsistent sind. Beispiel:

In der zweiten Tabelle betrug die Differenz zwischen Medikament und kein Medikament:
- Ohne Diät: 5 - 0 = 5 kg
- Mit Diät: 12 - 3 = 9 kg
Grafisch äußert sich dies in unterschiedlichen Steigungen der Verbindungslinien

Es werden drei zentrale Hypothesen geprüft:

Haupteffekt Diät

\(H_0: \mu_{\text{Diät}} = \mu_{\text{keine Diät}}\)
\(H_1: \mu_{\text{Diät}} \neq \mu_{\text{keine Diät}}\)

Haupteffekt Medikament

\(H_0: \mu_{\text{Medikament}} = \mu_{\text{kein Medikament}}\)
\(H_1: \mu_{\text{Medikament}} \neq \mu_{\text{kein Medikament}}\)

Interaktionseffekt (zwei äquivalente Formulierungen):
1. Unterschiedliche Medikamentenwirkung in Diät-Gruppen:
- \(H_0: (\mu_{\text{Med}} - \mu_{\text{kein Med}}){\text{keine Diät}} = (\mu{\text{Med}} - \mu_{\text{kein Med}}){\text{Diät}}\)
- \(H_1: (\mu{\text{Med}} - \mu_{\text{kein Med}}){\text{keine Diät}} \neq (\mu{\text{Med}} - \mu_{\text{kein Med}})_{\text{Diät}}\)
1. Unterschiedliche Diätwirkung in Medikamentengruppen:
- \(H_0: (\mu_{\text{Diät}} - \mu_{\text{keine Diät}}){\text{kein Med}} = (\mu{\text{Diät}} - \mu_{\text{keine Diät}}){\text{Med}}\)
- \(H_1: (\mu{\text{Diät}} - \mu_{\text{keine Diät}}){\text{kein Med}} \neq (\mu{\text{Diät}} - \mu_{\text{keine Diät}})_{\text{Med}}\)

Die Gesamtvarianz (Sum of Squares Total, SST) wird in vier Komponenten zerlegt:

Faktor A (Diät): \(SS_{Diät}\)
Faktor B (Medikament): \(SS_{Med}\)
Interaktion: \(SS_{Interaktion}\)
Residualvarianz: \(SS_{Residual}\)

Die ANOVA-Tabelle strukturiert diese Analyse:

Quelle	Quadratsumme	Freiheitsgrade	Mittelquadrate	F-Wert	p-Wert
Faktor A	\(SS_A\)	\(k_1 - 1\)	\(MS_A = \frac{SS_A}{df_A}\)	\(F_A = \frac{MS_A}{MS_{Res}}\)	\(P(F > F_A)\)
Faktor B	\(SS_B\)	\(k_2 - 1\)	\(MS_B = \frac{SS_B}{df_B}\)	\(F_B = \frac{MS_B}{MS_{Res}}\)	\(P(F > F_B)\)
Interaktion	\(SS_{AB}\)	\((k_1 - 1)(k_2 - 1)\)	\(MS_{AB} = \frac{SS_{AB}}{df_{AB}}\)	\(F_{AB} = \frac{MS_{AB}}{MS_{Res}}\)	\(P(F > F_{AB})\)
Residual	\(SS_{Res}\)	\(n - k_1 k_2\)	\(MS_{Res} = \frac{SS_{Res}}{df_{Res}}\)
Total	\(SS_{Total}\)	\(n - 1\)

Nach der Erstellung der ANOVA-Tabelle – üblicherweise mithilfe eines Statistikprogramms, um die umfangreichen Berechnungen zu vermeiden – folgt die Interpretation der erhaltenen p-Werte für die einzelnen Faktoren sowie für die Interaktion. Dabei kommt dem p-Wert der Interaktion eine zentrale Bedeutung zu, da er die gesamte Analyse maßgeblich beeinflusst:

Keine signifikante Interaktion Liegt der p-Wert der Interaktion oberhalb des festgelegten Signifikanzniveaus (meist 0,05), kann die Wirkung der beiden Faktoren unabhängig voneinander betrachtet werden. Das bedeutet, man prüft für jeden Faktor separat, ob es signifikante Unterschiede zwischen dessen Stufen gibt. Beispiel: Bei der Analyse von Gewichtsverlusten in Abhängigkeit von Diät und Medikament zeigt sich keine signifikante Interaktion. In diesem Fall untersucht man den Effekt der Diät anhand des entsprechenden p-Werts. Ist dieser kleiner als 0,05, so ist der Faktor Diät statistisch signifikant, was bedeutet, dass sich die Gewichtsverluste der Personen mit und ohne Diät signifikant unterscheiden – unabhängig davon, ob das Medikament eingenommen wurde oder nicht. Analog wird der Effekt des Medikaments geprüft.
Signifikante Interaktion Ist der p-Wert der Interaktion hingegen kleiner als das Signifikanzniveau, können die Faktoren nicht unabhängig voneinander betrachtet werden. Die Wirkung eines Faktors hängt vom jeweiligen Niveau des anderen Faktors ab. Deshalb ist es notwendig, die Effekte innerhalb der Stufen des jeweils anderen Faktors getrennt zu analysieren. Beispiel: Bei signifikantem Interaktionseffekt zwischen Diät und Medikament bedeutet dies, dass der Einfluss des Medikaments auf den Gewichtsverlust sich je nach Diätstatus unterscheidet – und umgekehrt. Es existiert somit kein allgemeingültiger Haupteffekt eines Faktors, sondern der Effekt ist kontextabhängig.

Wichtiger Hinweis:

Ein zweifaktorielles ANOVA mit je zwei Stufen pro Faktor ist nicht mit zwei unabhängigen T-Tests zu vergleichen. Selbst wenn keine Interaktion vorliegt, entsprechen die p-Werte aus dem ANOVA nicht zwangsläufig denen, die man durch separate T-Tests erhält. Das ANOVA berücksichtigt die gemeinsamen Einflüsse beider Faktoren und eliminiert den Anteil der Variabilität, der durch den jeweils anderen Faktor verursacht wird. Dadurch liefert es eine multivariate Betrachtung der Effekte. Im Beispiel bedeutet dies, dass der Einfluss der Diät auf den Gewichtsverlust unter Berücksichtigung der Wirkung des Medikaments (und gegebenenfalls deren Interaktion) bewertet wird – was bei einfachen T-Tests unberücksichtigt bliebe. Ebenso entspricht die Analyse der Interaktion nicht der Durchführung eines einfaktoriellen ANOVA mit einer Faktorstufe, die alle Kombinationen zusammenfasst, da die multivariate Struktur des zweifaktoriellen ANOVA eine differenziertere Betrachtung ermöglicht.

10.2.2 Zweifaktorielles ANOVA mit drei oder mehr Stufen in einem Faktor

Das Vorgehen bei einem zweifaktoriellen ANOVA, bei dem mindestens ein Faktor drei oder mehr Stufen aufweist, ähnelt dem bereits beschriebenen Fall mit je zwei Stufen pro Faktor. Lediglich die Nullhypothesen werden erweitert, indem die Gleichheit aller Mittelwerte der jeweiligen Stufen eines Faktors geprüft wird, und die Alternativhypothese besagt, dass mindestens ein Mittelwert sich unterscheidet. Bei den Interaktionen werden ebenfalls Mittelwertunterschiede betrachtet, wobei aufgrund der höheren Anzahl von Stufen mehr mögliche Unterschiede vorliegen.

Zur Interpretation der ANOVA-Ergebnistabelle gilt: Liegt keine signifikante Interaktion vor, aber signifikante Unterschiede in einem der Faktoren mit drei oder mehr Stufen, so folgt eine genauere Untersuchung, zwischen welchen Stufen diese Unterschiede bestehen. Beispiel: Wenn der Faktor 1 drei Stufen hat, keine Interaktion vorliegt und die Nullhypothese der Mittelwertgleichheit abgelehnt wird, prüft man, ob die Unterschiede beispielsweise zwischen Stufe 1 und 2, 1 und 3 oder 2 und 3 bestehen – und zwar unabhängig vom Faktor 2. Um die Unterschiede zwischen den Stufen zu identifizieren, führt man Multiple Paarvergleiche durch, etwa den Bonferroni-Test oder andere aus dem einfaktoriellen ANOVA bekannte Verfahren. Bei signifikanter Interaktion wird analog vorgegangen, jedoch werden die Unterschiede innerhalb jeder Stufe des jeweils anderen Faktors separat betrachtet.

Wie bereits beim zweifaktoriellen ANOVA mit zwei Stufen und den unabhängigen T-Tests erläutert, entspricht ein zweifaktorielles ANOVA mit drei oder mehr Stufen nicht der Durchführung zweier separater einfaktorieller ANOVAs. Die erhaltenen p-Werte unterscheiden sich – selbst wenn keine Interaktion vorliegt –, da die gemeinsame Varianzstruktur und Einflüsse berücksichtigt werden.

10.2.3 ANOVA mit drei oder mehr Faktoren

Die Grundprinzipien des ANOVA mit drei oder mehr Faktoren sind ähnlich denen des zweifaktoriellen ANOVA, und die Ergebnistabellen weisen vergleichbare Strukturen auf. Die Interpretation wird jedoch deutlich komplexer. Ein dreifaktorielles ANOVA enthält die Haupteffekte der drei Faktoren, die drei möglichen zweifachen Interaktionen (Faktor 1 mit 2, 1 mit 3, 2 mit 3) sowie optional die dreifache Interaktion aller Faktoren (je nach Software und Einstellungen können Interaktionen beliebiger Ordnung berücksichtigt werden).

Ist die dreifache Interaktion signifikant, kann kein allgemeiner Haupteffekt eines Faktors betrachtet werden. Stattdessen muss der Effekt dieses Faktors innerhalb jeder Stufe der beiden anderen Faktoren separat analysiert werden. Liegt keine signifikante dreifache Interaktion vor, wohl aber eine zweifache (beispielsweise zwischen Faktor 1 und 2), so wird der Effekt von Faktor 1 innerhalb der Stufen von Faktor 2 untersucht, unabhängig von Faktor 3.

Dies führt zu einer Vielzahl möglicher Analysen und multipler Vergleichstests. Daher liegt es in der Verantwortung des Forschers, die Anzahl der durchgeführten Tests sinnvoll zu begrenzen, den Versuchsaufbau klar zu definieren und ggf. höhere Interaktionen (dreifach oder mehr) nur dann zu berücksichtigen, wenn deren Interpretation auch tatsächlich möglich und sinnvoll ist.

Abschließend gilt auch hier: Ein ANOVA mit drei oder mehr Faktoren entspricht nicht der Durchführung mehrerer einfaktorieller ANOVAs für jeden Faktor einzeln.

10.2.4 Feste Faktoren und Zufallsfaktoren

Beim mehrfaktoriellen ANOVA unterscheiden sich der Umgang mit der durch jeden Faktor verursachten Variabilität und die daraus folgenden Schlussfolgerungen je nachdem, ob die Faktoren als feste oder zufällige Faktoren behandelt werden.

Ein fester Faktor (oder Faktor mit festen Effekten) ist ein Faktor, dessen Stufen vom Untersucher vorab festgelegt oder bestimmt werden (zum Beispiel festgelegte Dosierungen eines Medikaments oder vorgegebene Zeitpunkte) oder die sich aus der Natur des Faktors ergeben (z. B. Geschlecht oder Diät). Die Variabilität solcher Faktoren ist leichter kontrollierbar, und ihre Behandlung in den Berechnungen zum ANOVA-Endergebnis ist einfacher. Ein Nachteil besteht jedoch darin, dass nur für die konkret untersuchten Stufen Aussagen getroffen werden können. Das heißt, die Ergebnisse gelten nur für genau diese festen Stufen, und eine Verallgemeinerung auf andere, nicht untersuchte Stufen ist nicht zulässig.

Im Gegensatz dazu ist ein Zufallsfaktor (oder Faktor mit zufälligen Effekten) ein Faktor, dessen Stufen zufällig aus einer größeren Grundgesamtheit von möglichen Stufen ausgewählt wurden (beispielsweise eine Medikamentendosierung mit den Stufen 23 mg, 132 mg und 245 mg, die zufällig aus dem Bereich 0 bis 250 mg gezogen wurden). Die Analyse solcher Faktoren ist komplexer, da diese Stufen eine Stichprobe aller möglichen Stufen darstellen. Ziel ist es, Rückschlüsse auf die gesamte Population aller möglichen Stufen zu ziehen.

10.2.4.1 Modellannahmen des mehrfaktoriellen ANOVA

Wie beim einfaktoriellen ANOVA handelt es sich auch beim ANOVA mit zwei oder mehr Faktoren um einen parametrischen Test mit folgenden Voraussetzungen:

Die Daten innerhalb jeder Kategorie – definiert als Kombination aller Stufen aller Faktoren – folgen einer Normalverteilung. Beispiel: Bei einem zweifaktoriellen ANOVA mit je drei Stufen pro Faktor gibt es \(3^2=9\) Kategorien.
Die Varianzen dieser Normalverteilungen sind gleich (Varianzhomogenität bzw. Homoskedastizität).

Werden diese Voraussetzungen nicht erfüllt und liegen zudem kleine Stichproben vor, sollte ein mehrfaktorieller ANOVA nicht angewendet werden. Ein zusätzliches Problem ist, dass es für diesen Fall keinen entsprechenden nicht-parametrischen Ersatztest gibt. Zwar können mit nicht-parametrischen Tests (wie dem Kruskal-Wallis-Test) die Einflüsse der einzelnen Faktoren separat geprüft werden, die wichtige Untersuchung der Interaktion zwischen Faktoren ist jedoch nicht möglich.

10.3 ANOVA mit Messwiederholungen

In vielen Fragestellungen wird eine abhängige Variable mehrfach am selben Individuum gemessen (z. B. bei einer Gruppe, die eine bestimmte Diät verfolgt, wird das verlorene Gewicht nach einem, zwei und drei Monaten erfasst). Ziel ist es, den Mittelwert der Variable über die verschiedenen Messzeitpunkte zu vergleichen, also zu prüfen, ob sich die Variable über die Zeit verändert (im Beispiel: Entwicklung des Gewichtsverlusts). Konzeptuell entspricht dies der Situation bei paarweise gepaarten Messwerten, wie sie etwa mit dem gepaarten t-Test oder dem nichtparametrischen Wilcoxon-Test verglichen werden, jedoch liegen hier mehr als zwei gepaarte Messungen pro Individuum vor. In solchen Fällen verwendet man die ANOVA mit Messwiederholungen.

Diese ANOVA hat wie alle Tests mit gepaarten Daten den Vorteil, dass die Vergleiche innerhalb desselben Individuums (intraindividuell) erfolgen. Dadurch wird die Variabilität, die zwischen verschiedenen Individuen auftritt, reduziert. Zum Beispiel könnte man das Gewicht in drei verschiedenen Gruppen messen, die alle dieselbe Diät machen, aber mit unterschiedlichen Alters- oder Geschlechtsverteilungen – das würde die Ergebnisse beeinflussen. Mit Messwiederholungen werden alle Messungen innerhalb desselben Individuums verglichen, sodass z.B. Geschlecht, Alter oder sportliche Aktivität konstant bleiben. Dadurch werden kleine Unterschiede besser erkennbar.

10.3.1 ANOVA mit Messwiederholungen als zweifaktorieller ANOVA ohne Interaktion

Die ANOVA mit Messwiederholungen kann als zweifaktorieller ANOVA ohne Interaktion berechnet werden, wenn die Daten entsprechend aufbereitet werden.

Angenommen, es liegen \(k\) gepaarte Messungen einer numerischen abhängigen Variable bei \(n\) Individuen vor, dann können die Daten wie folgt dargestellt werden:

Individuum	VarDep 1	VarDep 2	\(\dots\)	VarDep \(k\)
Individuum 1	\(x_{1,1}\)	\(x_{1,2}\)	\(\dots\)	\(x_{1,k}\)
Individuum 2	\(x_{2,1}\)	\(x_{2,2}\)	\(\dots\)	\(x_{2,k}\)
\(\dots\)	\(\dots\)	\(\dots\)	\(\dots\)	\(\dots\)
Individuum n	\(x_{n,1}\)	\(x_{n,2}\)	\(\dots\)	\(x_{n,k}\)

Diese Daten können auch in einem “langen” Format angeordnet werden, das sich gut für eine zweifaktorielle ANOVA eignet:

Var Dep	Individuum	Messzeitpunkt
\(x_{1,1}\)	1	1
\(x_{2,1}\)	2	1
\(\dots\)	\(\dots\)	\(\dots\)
\(x_{n,1}\)	n	1
\(x_{1,2}\)	1	2
\(x_{2,2}\)	2	2
\(\dots\)	\(\dots\)	\(\dots\)
\(x_{n,2}\)	n	2
\(\dots\)	\(\dots\)	\(\dots\)
\(x_{1,k}\)	1	k
\(x_{2,k}\)	2	k
\(\dots\)	\(\dots\)	\(\dots\)
\(x_{n,k}\)	n	k

Hier sind Individuum und Messzeitpunkt kategoriale Variablen, die die Gesamtheit der Daten (\(n \times k\)) in Gruppen einteilen: \(n\) Gruppen für Individuen und \(k\) Gruppen für Messzeitpunkte. Die Kreuzung der beiden Variablen erzeugt \(n \times k\) Gruppen mit jeweils genau einem Messwert.

Die Variabilität der abhängigen Variablen wird aufgeteilt in drei Quellen:

Variabilität durch Messzeitpunkt
Variabilität durch Individuum
Residuale Variabilität

Eine Interaktion zwischen Messzeitpunkt und Individuum kann hier nicht analysiert werden, da jede Gruppe nur einen Wert enthält und somit keine Streuung berechnet werden kann. Daher wird eine zweifaktorielle ANOVA ohne Interaktion durchgeführt, die folgende Tabelle liefert:

Quelle	Quadratsumme	Freiheitsgrade	Mittelquadrat	F-Wert	p-Wert
F1 = Messzeitpunkt	\(SF1\)	\(GF1 = k-1\)	\(CF1 = \frac{SF1}{GF1}\)	\(f1 = \frac{CF1}{CR}\)	\(P(F>f1)\)
F2 = Individuum	\(SF2\)	\(GF2 = n-1\)	\(CF2 = \frac{SF2}{GF2}\)	\(f2 = \frac{CF2}{CR}\)	\(P(F>f2)\)
Residuale	\(SR\)	\(GR = (n \cdot k) - 1 - GF1 - GF2\)	\(CR = \frac{SR}{GR}\)
Total	\(ST\)	\(GT = (n \cdot k) - 1\)

Die Hypothesen, die mit diesem Modell getestet werden, sind:

Für den Faktor Messzeitpunkt:
\[ \begin{aligned} H_0: &\mu_{\text{Messzeitpunkt 1}} = \mu_{\text{Messzeitpunkt 2}} = \dots = \mu_{\text{Messzeitpunkt k}}\\ H_1: &\text{Mindestens ein Mittelwert ist unterschiedlich.} \end{aligned} \] Ist der p-Wert kleiner als das Signifikanzniveau, so gibt es einen signifikanten Effekt der Messzeitpunkte, d.h., die Variable ändert sich über die Zeit innerhalb der Individuen.
Für den Faktor Individuum:
\[ \begin{aligned} H_0: &\mu_{\text{Individuum 1}} = \mu_{\text{Individuum 2}} = \dots = \mu_{\text{Individuum n}} \\ H_1: &\text{Mindestens ein Mittelwert ist unterschiedlich.} \end{aligned} \] Ein signifikanter Effekt hier zeigt, dass Individuen sich im Mittel unterschiedlich verhalten. Dies ist jedoch meist erwartbar und weniger interessant im Kontext der Messwiederholungen.

Falls mindestens eine der Nullhypothesen verworfen wird, empfiehlt sich als nächster Schritt ein Multiple-Comparison-Test, z. B. der Bonferroni-Test, um herauszufinden, welche Mittelwerte sich unterscheiden – insbesondere bei den Messzeitpunkten.

10.3.1.1 Voraussetzungen der ANOVA mit Messwiederholungen

Wie bei jeder anderen ANOVA gilt auch für die ANOVA mit Messwiederholungen:

Die Daten der abhängigen Variablen sollten innerhalb jeder Gruppe normalverteilt sein, egal ob die Gruppen durch die Variable Messzeitpunkt oder durch die Variable Individuum gebildet werden. Da der wichtigste Test bei der Variable Messzeitpunkt durchgeführt wird, ist es besonders wichtig, dass die Verteilungen aller Messzeitpunkte normal sind.
Alle Normalverteilungen sollten die gleiche Varianz aufweisen (Homoskedastizität), besonders die der verschiedenen Messzeitpunkte.

Wenn bei einer ANOVA mit Messwiederholungen sowohl Normalität als auch Homoskedastizität erfüllt sind, spricht man von Sphärizität der Daten. Es gibt spezielle statistische Tests, um die Sphärizität zu überprüfen, beispielsweise den Mauchly-Test.

Werden die genannten Bedingungen nicht erfüllt und sind die Stichproben zudem klein, sollte die ANOVA mit Messwiederholungen nicht angewendet werden. Allerdings existiert zumindest ein nichtparametrischer Test, der überprüft, ob es signifikante Unterschiede zwischen den verschiedenen Stufen der Variable Messzeitpunkt gibt: der Friedman-Test.

10.3.2 ANOVA mit Messwiederholungen + ANOVA mit einem oder mehreren Faktoren

Es gibt viele Fälle, in denen neben der Analyse des intraindividuellen Effekts auf eine mehrfach gemessene quantitative abhängige Variable (ANOVA mit Messwiederholungen) auch qualitative Variablen berücksichtigt werden sollen, die vermutlich mit der abhängigen Variable zusammenhängen. Diese qualitativen Variablen führen zu Effekten, die üblicherweise als interindividuelle Effekte klassifiziert werden, die man aber auch als intergruppale Effekte verstehen kann, da sie Gruppen definieren, zwischen denen eine ANOVA mit einem oder mehreren Faktoren möglich ist.

Beispielsweise könnte man den Gewichtsverlust bei Individuen nach einem, zwei und drei Monaten (ANOVA mit Messwiederholungen) untersuchen, wobei die Individuen in sechs Gruppen aufgeteilt sind, die sich aus der Kreuzung zweier Faktoren ergeben: Diät (a, b, c) und Bewegung (niedrig, hoch). Um den Einfluss dieser beiden interindividuellen Faktoren zu untersuchen, wäre eine zweifaktorielle ANOVA mit Interaktion notwendig.

Obwohl die Daten ähnlich wie bei einer zweifaktoriellen ANOVA mit den Faktoren Messzeitpunkt und Individuum strukturiert werden könnten, um zwei weitere Faktoren (Diät und Bewegung) hinzuzufügen, ist es unpraktisch, für dasselbe Individuum mehrere Zeilen (eine pro Messzeitpunkt) einzufügen.

Deshalb erlauben bestimmte Statistikprogramme, wie z. B. PASW (SPSS), ANOVAs mit Messwiederholungen auf Basis des klassischen Formats (eine Zeile pro Individuum, eine Variable pro Messzeitpunkt). Dabei werden intraindividuelle Faktoren definiert, die alle Messzeitpunkte umfassen, und es können interindividuelle Faktoren (Kategorien) hinzugefügt werden, die die Antwortvariablen beeinflussen können. Zudem können Interaktionen zwischen den interindividuellen Faktoren sowie zwischen inter- und intraindividuellen Faktoren getestet werden.

Diese Verfahren kombinieren somit eine ANOVA mit Messwiederholungen und eine ANOVA mit einem oder mehreren Faktoren, wobei die Daten weiterhin klassisch eingegeben werden können: eine Zeile pro Individuum.

Die Ergebnisse ähneln den zuvor beschriebenen: Es werden ANOVA-Tabellen erzeugt, in denen für jeden Faktor (intraindividuell bzw. Messwiederholung, interindividuell bzw. Kategorien) sowie für die Interaktionen p-Werte berechnet werden.

10.4 Kovarianzanalyse: ANCOVA

Die Kovarianzanalyse (ANCOVA) ist eine Erweiterung der ANOVA (sei es einfaktorielle, mehrfaktorielle oder mit Messwiederholungen), die es erlaubt, den Einfluss aller kategorialen unabhängigen Variablen (Faktoren) und der Messwiederholungen auf die quantitative abhängige Variable zu analysieren, dabei aber zusätzlich den Effekt anderer quantitativer unabhängiger Variablen auf die Antwortvariable zu eliminieren. Diese unabhängigen Variablen, deren Effekt kontrolliert oder herausgerechnet werden soll, nennt man Kovariablen oder Kovariate, da man erwartet, dass sie mit der abhängigen Variable kovariieren, also korreliert sind.

Die detaillierte Durchführung einer ANCOVA geht über den Rahmen dieser Übung hinaus, die Grundidee ist aber einfach: Man kann eine Regressionsanalyse der abhängigen Variable in Abhängigkeit von der Kovariablen (oder mehreren Kovariablen) durchführen und den Teil der Variabilität der abhängigen Variable, der durch die Kovariable erklärt werden kann, eliminieren. Dies geschieht, indem man mit den Residuen des Regressionsmodells arbeitet anstatt mit den Originaldaten. Anschließend wird eine ANOVA mit einem oder mehreren Faktoren, auch mit Messwiederholungen, auf den Residuen durchgeführt.

Das Endergebnis der ANCOVA ist eine Tabelle, die der der ANOVA sehr ähnlich ist, aber mit zusätzlichen Zeilen für jede Kovariable. Diese Zeilen zeigen, wie viel Variabilität durch jede Kovariable erklärt wird, sowie deren zugehörigen \(p\)-Wert. Dieser \(p\)-Wert beantwortet die Frage, ob die Kovariable notwendig ist, um die abhängige Variable zu erklären (technisch ausgedrückt: ob die Steigung der Regressionsfunktion der unabhängigen Variable in Abhängigkeit von der Kovariable gleich Null sein kann oder nicht). In der ANCOVA-Tabelle gibt es keine zusätzliche Zeile für die mögliche Interaktion zwischen Kovariable und den verschiedenen interindividuellen Faktoren, weil ein ANCOVA-Modell bei vorhandener Interaktion nicht sinnvoll ist: Der Effekt des Faktors könnte nicht geschätzt werden, da er vom konkreten Wert der Kovariablen abhängt, welche als kontinuierliche Variable unendlich viele Werte annimmt. Dadurch gäbe es unendlich viele verschiedene Effekte des Faktors und kein eindeutiger \(p\)-Wert.

Allerdings enthält die Tabelle eine Zeile für die Interaktion jedes intraindividuellen Faktors mit jeder Kovariable, da jeder intraindividuelle Faktor aus mehreren quantitativen Variablen besteht, die in der Regression unterschiedliche Steigungen in Abhängigkeit von der Kovariable aufweisen können.

Wenn bei einer ANOVA zur Überprüfung des Einflusses verschiedener Faktoren auf eine quantitative Antwortvariable meist ein Mittelwertdiagramm verwendet wird, zeigt sich bei der ANCOVA der Effekt der Kovariablen auf die Antwortvariable durch ein Punktwolken-Diagramm der Antwortvariable in Abhängigkeit von der Kovariablen. Dieses wird je nach Grad der linearen Korrelation zwischen beiden mehr oder weniger linear aussehen. Zudem lässt sich erahnen, ob ein bestimmter Faktor nach Herausrechnung des Einflusses der Kovariablen noch einen Einfluss auf die Antwortvariable hat:

Wenn die Punktwolke durch eine einzige Gerade mit Null-Steigung gut beschrieben werden kann, unabhängig von den Faktorstufen, bedeutet dies, dass weder die Kovariable noch der Faktor signifikant sind, um die Antwortvariable zu erklären.
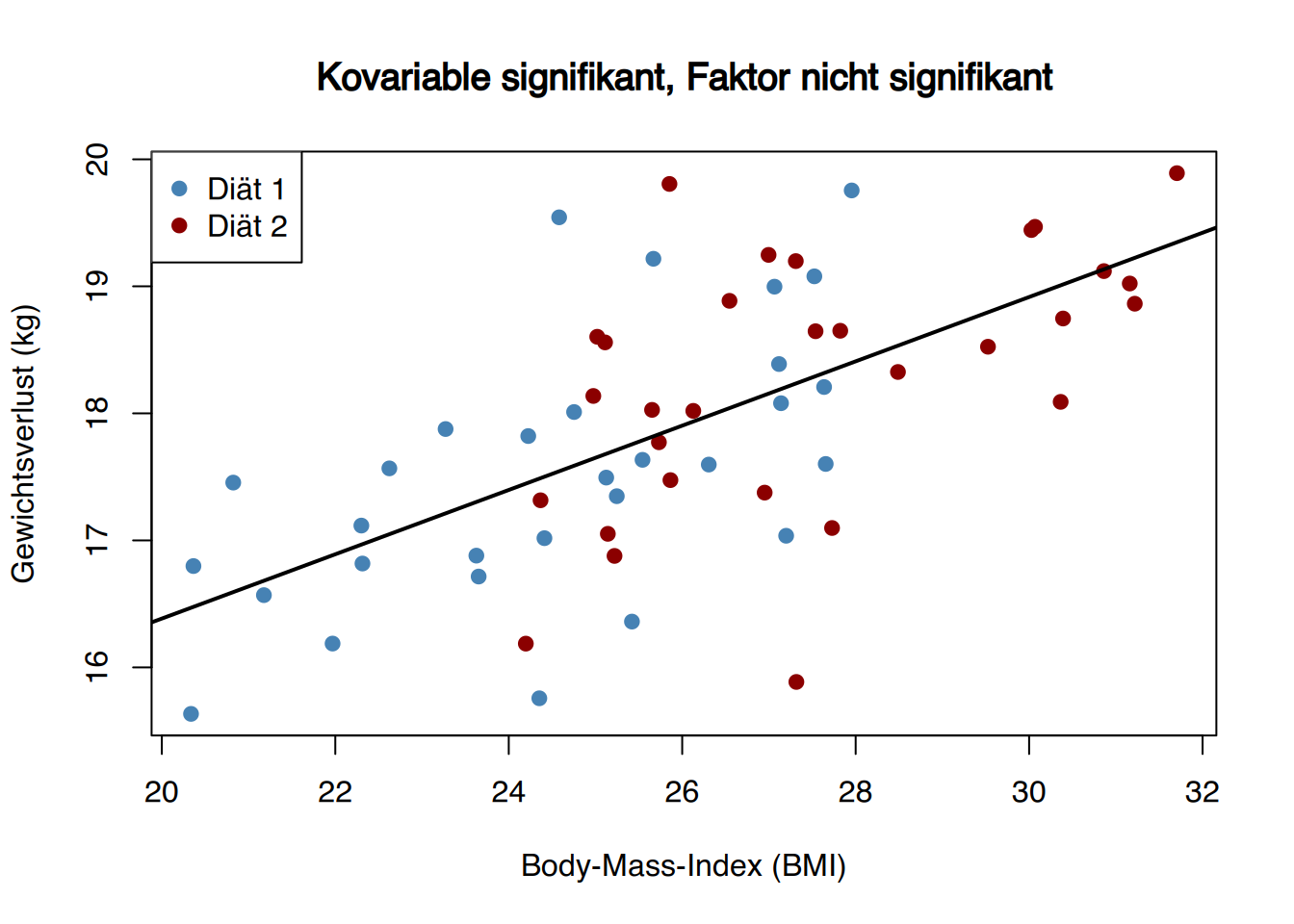
Wenn die Punktwolke durch eine einzige Gerade mit nicht null Steigung gut beschrieben werden kann, unabhängig von den Faktorstufen, bedeutet dies, dass die Kovariable signifikant ist, der Faktor aber nicht. Denn nach Herausrechnung des Einflusses der Kovariablen (also wenn man die Residuen der Anfangsregression betrachtet) gibt es keine Unterschiede zwischen den Faktorstufen (die Punkte der verschiedenen Kategorien liegen auf gleicher Höhe).

Zum Beispiel zeigt die folgende Abbildung das Ergebnis eines Experiments, bei dem die verlorenen Kilogramm von Personen gemessen wurden, die zwei verschiedene Diäten befolgten. Als Kovariable wurde der Body-Mass-Index (BMI) berücksichtigt, der ebenfalls Einfluss auf den Gewichtsverlust haben könnte, aber bei der Gruppeneinteilung nicht kontrolliert wurde. Die Gruppe mit Diät 2 hat im Mittel einen höheren BMI als die Gruppe mit Diät 1. Laut Abbildung scheint es signifikante Unterschiede im Gewichtsverlust zwischen den Diäten zu geben (Diät 2 führt zu mehr Gewichtsverlust), aber tatsächlich ist der Unterschied auf die Kovariable zurückzuführen. Wird der Effekt der Kovariablen eliminiert (also die Steigung der Geraden auf 0 gesetzt), hätten beide Gruppen etwa gleich viel Gewicht verloren. Das bedeutet, dass bei gleichem BMI Diät 2 nicht zu mehr Gewichtsverlust führt.

Wenn die Punktwolke durch mehrere Geraden mit Null-Steigung, eine pro Faktorstufe, gut beschrieben wird, ist die Kovariable nicht signifikant, aber der Faktor schon.
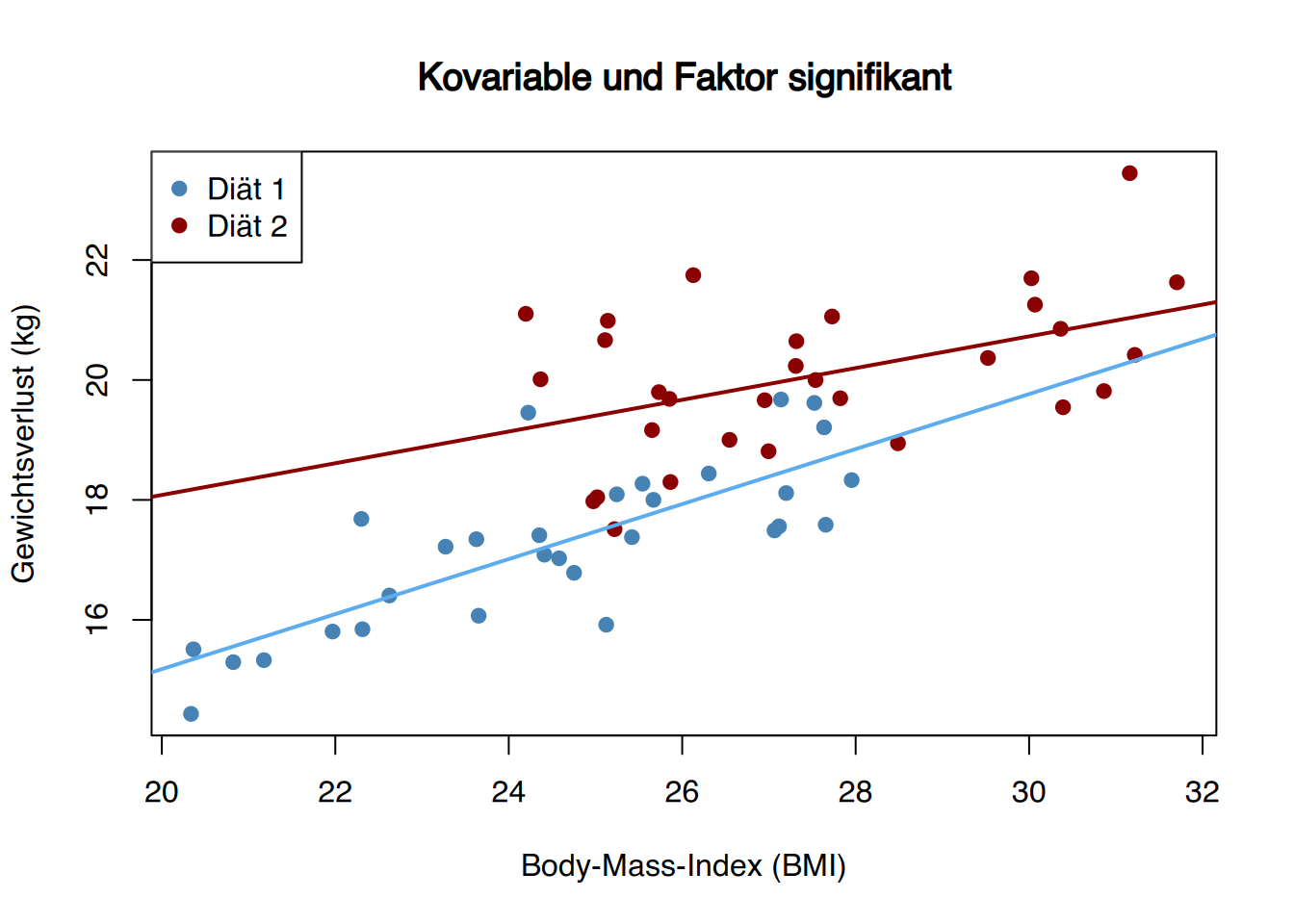
Wenn die Punktwolke durch Geraden mit gleicher, nicht null Steigung, eine pro Faktorstufe, beschrieben wird und mindestens eine Gerade sich von den anderen unterscheidet (mindestens eine Faktorstufe ist verschoben), sind sowohl Kovariable als auch Faktor signifikant bei der Erklärung der abhängigen Variable.

Zum Beispiel zeigt die folgende Abbildung das Ergebnis eines ähnlichen Experiments wie oben: Gewichtsverlust in Abhängigkeit von Diät und Kovariable BMI, die bei der Gruppeneinteilung nicht kontrolliert wurde (die Gruppe mit Diät 2 hat einen höheren BMI). Die Grafik deutet sogar auf signifikante Unterschiede im Gewichtsverlust hin, sodass die Diät 2 mehr Gewichtsverlust verursachen würde, was aber alles auf die Kovariable zurückzuführen ist. Nach Eliminierung des Kovariablen-Effekts ist der Gewichtsverlust der Diät-1-Gruppe größer (wenn die Steigung der Geraden entfernt wird, liegen die Punkte der Diät 1 höher).

Wenn die Punktwolke durch unterschiedliche Geraden, eine pro Faktorstufe, mit unterschiedlichen, nicht null Steigungen beschrieben wird, deutet dies auf eine Interaktion zwischen Kovariabler und Faktor hin, und es sollte kein ANCOVA-Modell verwendet werden.