4 Regression und Korrelation
Im vorherigen Kapitel haben wir gelernt, wie man die Verteilung einer einzelnen Variable in einer Stichprobe beschreibt. Allerdings müssen in den meisten Fällen mehrere Variablen beschrieben werden, die oft miteinander verbunden sind. Beispielsweise sollte eine Ernährungsstudie alle Variablen berücksichtigen, die mit dem Gewicht in Zusammenhang stehen könnten, wie z.B. Größe, Alter, Geschlecht, Rauchen, Ernährung und körperliche Betätigung.
Um ein Phänomen zu verstehen, das mehrere Variablen beinhaltet, reicht es nicht aus, jede Variable für sich allein zu studieren. Wir müssen alle Variablen gemeinsam untersuchen, um die Art ihrer Wechselbeziehungen und den Typ der Beziehung zwischen ihnen zu beschreiben.
In der Regel gibt es bei einer Abhängigkeitsstudie eine abhängige Variable \(Y\), die von einem Satz an unabhängigen Variablen \(X_1 , \dots , X_n\) beeinflusst wird. Der einfachste Fall ist eine einfache Abhängigkeitsstudie mit nur einer unabhängigen Variable.
4.1 Gemeinsame Häufigkeiten
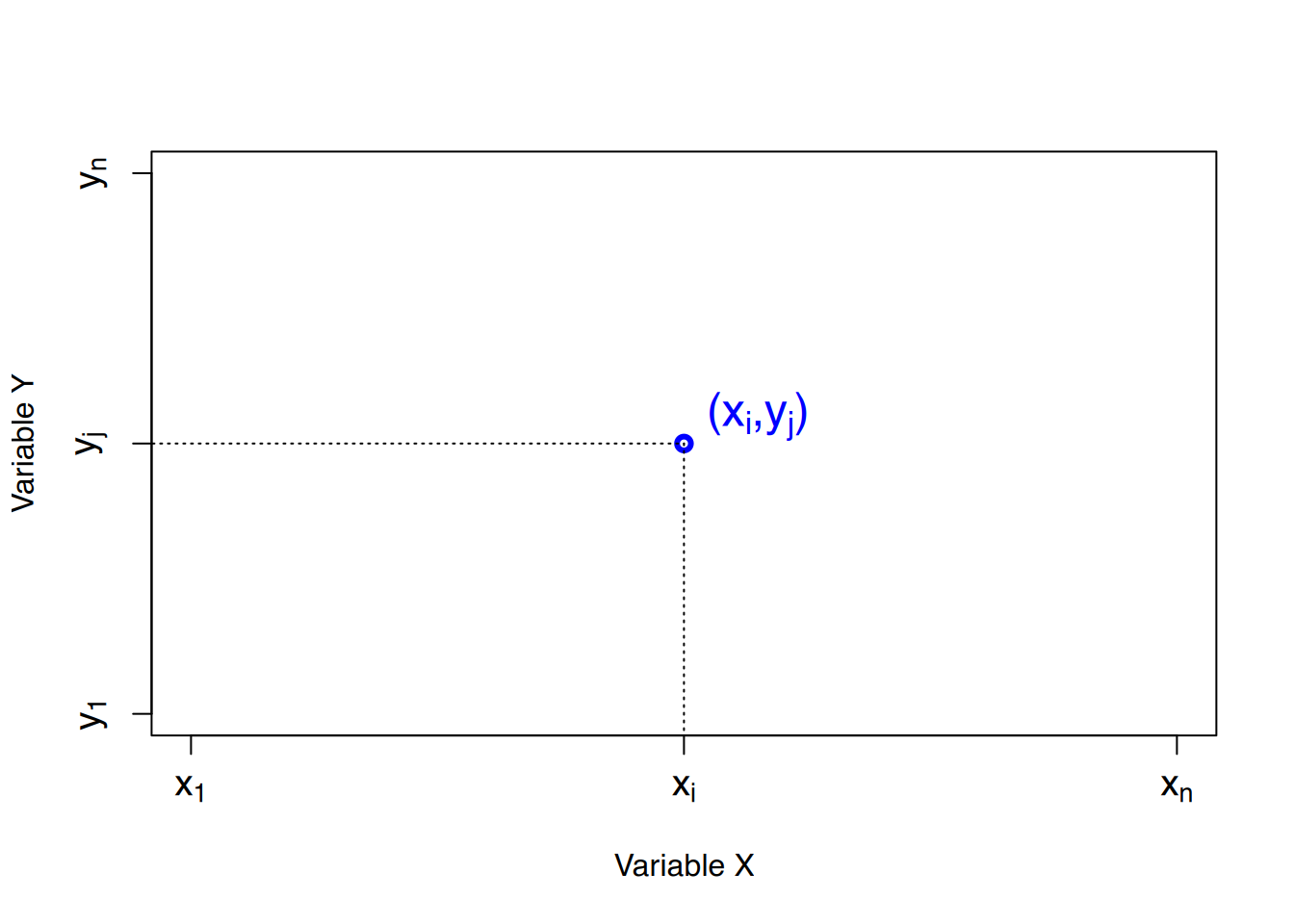
Um die Beziehung zwischen zwei Variablen \(X\) und \(Y\) zu untersuchen, müssen wir die gemeinsame Verteilung der zweidimensionalen Variable \((X, Y)\) studieren, deren Werte Paare \((x_i, y_j)\) sind, wobei das erste Element ein Wert von \(X\) und das zweite ein Wert von \(Y\) ist.
Bei einer Stichprobe mit \(n\) Werten und einer zweidimensionalen Variablen \((X, Y)\), wird für jeden Wert der Variablen \((x_i, y_j)\) folgendes definiert:
- Absolute Häufigkeit \(n_{ij}\): Ist die Anzahl der Male, die das Paar \((x_i, y_j)\) in der Stichprobe vorkommt.
- Relative Häufigkeit \(n_{ij}\): Ist der Anteil der Male, die das Paar \((x_i, y_j)\) in der Stichprobe vorkommt. \[ f_{ij}=\frac{n_{ij}}{n} \]
Für zweidimensionale Variablen ergeben kumulative Häufigkeiten keinen Sinn.
4.1.1 gemeinsame Häufigkeitsverteilung
Die Werte der zweidimensionalen Variablen mit ihren Häufigkeiten werden als gemeinsame Häufigkeitsverteilung bezeichnet und in einer gemeinsamen Häufigkeitstabelle dargestellt.
\[ \begin{array}{|c|ccccc|} \hline X\backslash Y & y_1 & \cdots & y_j & \cdots & y_q\\ \hline x_1 & n_{11} & \cdots & n_{1j} & \cdots & n_{1q}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ x_i & n_{i1} & \cdots & n_{ij} & \cdots & n_{iq}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ x_p & n_{p1} & \cdots & n_{pj} & \cdots & n_{pq}\\ \hline \end{array} \]
Von 30 Studierenden wurden Körpergröße (in cm) und Gewicht (in kg) wie folgt gemessen:
(179,85), (173,65), (181,71), (170,65), (158,51), (174,66), (172,62), (166,60), (194,90), (185,75), (162,55), (187,78), (198,109), (177,61), (178,70), (165,58), (154,50), (183,93), (166,51), (171,65), (175,70), (182,60), (167,59), (169,62), (172,70), (186,71), (172,54), (176,68),(168,67), (187,80).
Die gemeinsame Häufigkeitstabelle ist entsprechend:
\[ \begin{array}{|c||c|c|c|c|c|c|} \hline X/Y & [50,60) & [60,70) & [70,80) & [80,90) & [90,100) & [100,110) \\ \hline\hline (150,160] & 2 & 0 & 0 & 0 & 0 & 0 \\ \hline (160,170] & 4 & 4 & 0 & 0 & 0 & 0 \\ \hline (170,180] & 1 & 6 & 3 & 1 & 0 & 0 \\ \hline (180,190] & 0 & 1 & 4 & 1 & 1 & 0 \\ \hline (190,200] & 0 & 0 & 0 & 0 & 1 & 1 \\ \hline \end{array} \]
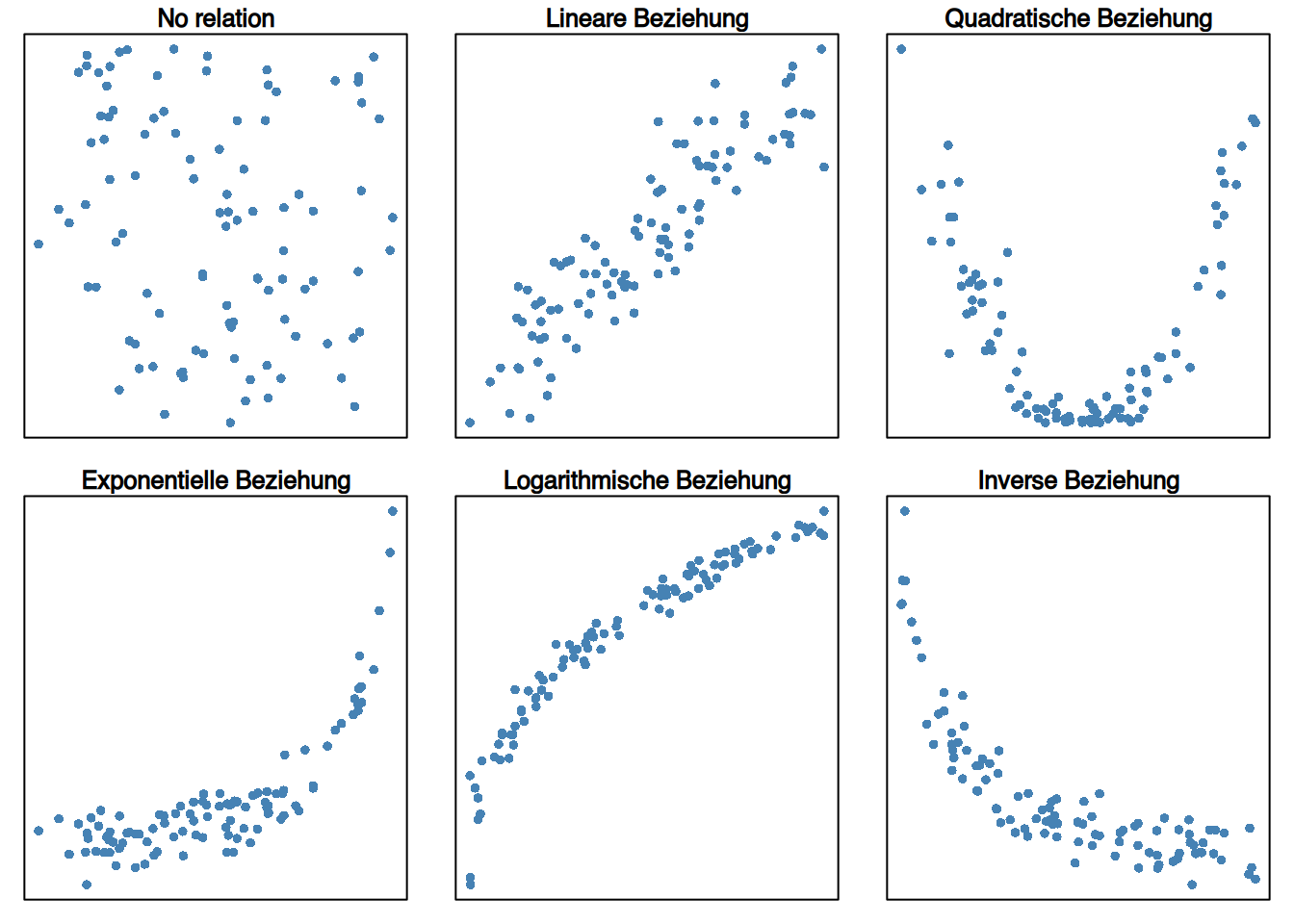
4.1.2 Streudiagramm
Die gemeinsame Häufigkeitsverteilung kann mit einem Streudiagramm (Punktwolke, Scatterplot) graphisch dargestellt werden, wobei die Daten als Sammlung von Punkten in einem \(XY\)-Koordinatensystem angezeigt werden.
Üblicherweise wird die unabhängige Variable auf der \(X\)-Achse und die abhängige Variable auf der \(Y\)-Achse dargestellt. Für jedes Datenpaar \((x_i, y_j)\) in der Stichprobe wird ein Punkt mit diesen Koordinaten auf der Ebene gezeichnet.
Das Ergebnis ist eine Ansammlung von Punkten, die auch Punktwolke genannt wird.
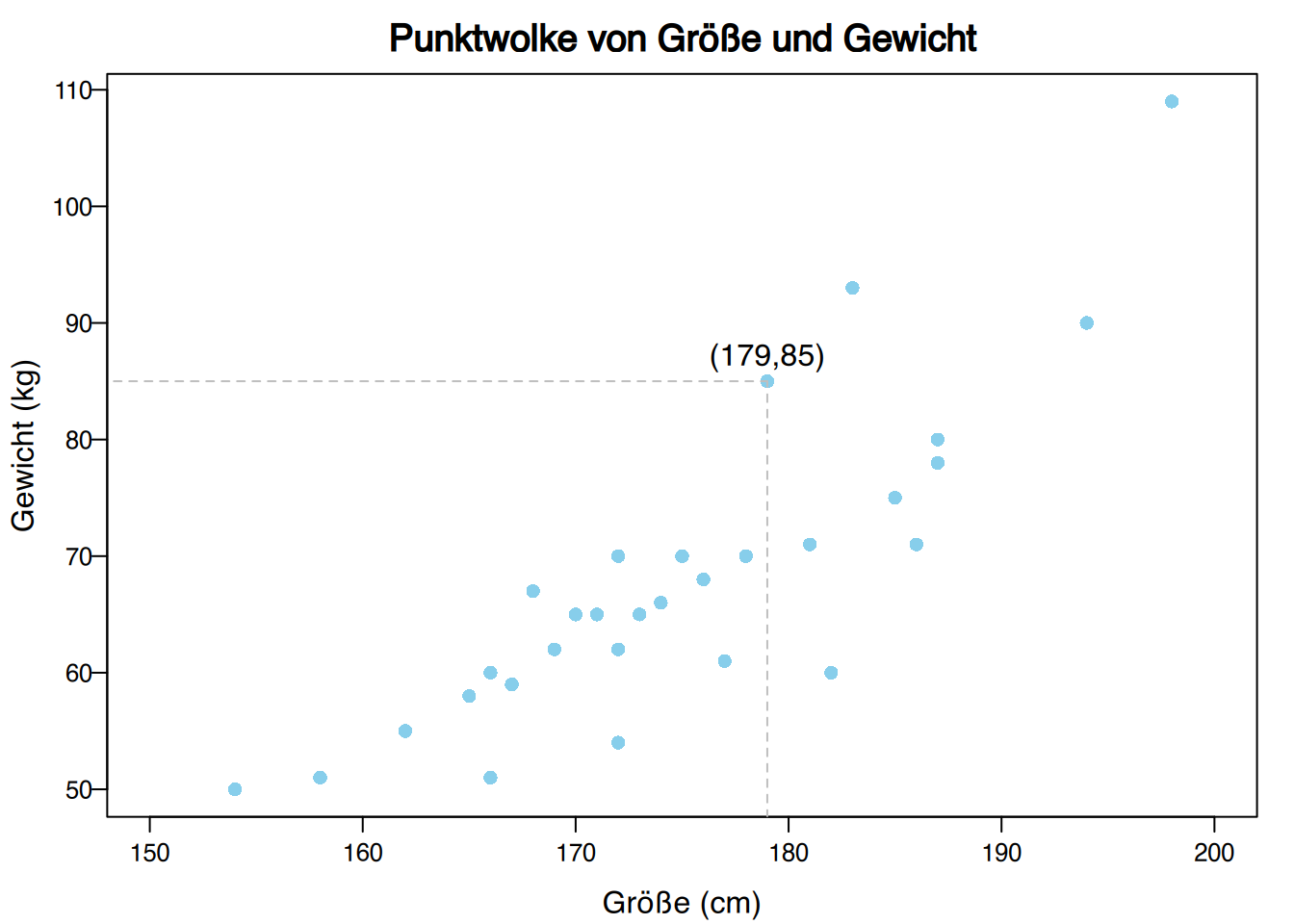
Die Form der Punktwolke gibt Aufschluss über die Art der Beziehung zwischen den Variablen \(X\) und \(Y\).
4.1.2.1 Häufigkeitsverteilungen an den Rändern
Die Häufigkeitsverteilungen jeder der zweidimensionalen Variablen werden als Randhäufigkeitsverteilungen bezeichnet. Wir können die Randhäufigkeitsverteilungen aus der gemeinsamen Häufigkeitstabelle erhalten, indem wir die Häufigkeiten nach Zeilen und Spalten summieren.
\[ \begin{array}{|c|ccccc|>{\columncolor{blue}}c|} \hline X\backslash Y & y_1 & \cdots & y_j & \cdots & y_q & \cellcolor{skyblue}n_x\\ \hline x_1 & n_{11} & \cdots & n_{1j} & \cdots & n_{1q} & \cellcolor{skyblue}n_{x_1}\\ \vdots & \vdots & \vdots & \cellcolor{coral}+ \downarrow& \vdots & \vdots & \cellcolor{skyblue}\vdots \\ x_i & n_{i1} & \cellcolor{skyblue}+\rightarrow & n_{ij} &\cellcolor{skyblue} +\rightarrow & n_{iq} & \cellcolor{skyblue} n_{x_i}\\ \vdots & \vdots & \vdots & \cellcolor{coral}+\downarrow & \vdots & \vdots & \cellcolor{skyblue}\vdots\\ x_p & n_{p1} & \cdots & n_{pj} & \cdots & n_{pq} & \cellcolor{skyblue}n_{x_p} \\ \hline \rowcolor{coral} n_y & n_{y_1} & \cdots & n_{y_j} & \cdots & n_{y_q} & \cellcolor{white} n\\ \hline \end{array} \]
Die Randhäufigkeitsverteilungen von Körpergröße und Gewicht sind
\[ \begin{array}{|c||c|c|c|c|c|c|>{\columncolor{blue}}c|} \hline X/Y & [50,60) & [60,70) & [70,80) & [80,90) & [90,100) & [100,110) &\cellcolor{skyblue} n_x\\ \hline\hline (150,160] & 2 & 0 & 0 & 0 & 0 & 0 & \cellcolor{skyblue}2\\ \hline (160,170] & 4 & 4 & 0 & 0 & 0 & 0 & \cellcolor{skyblue}8\\ \hline (170,180] & 1 & 6 & 3 & 1 & 0 & 0 & \cellcolor{skyblue}11 \\ \hline (180,190] & 0 & 1 & 4 & 1 & 1 & 0 & \cellcolor{skyblue}7 \\ \hline (190,200] & 0 & 0 & 0 & 0 & 1 & 1 & \cellcolor{skyblue}2\\ \hline \rowcolor{coral} n_y & 7 & 11 & 7 & 2 & 2 & 1 & \cellcolor{white} 30\\ \hline \end{array} \]
mit den den dazugehörigen Stichprobenstatistiken:
\[ \begin{array}{lllll} \bar x = 174.67 \mbox{ cm} & \quad & s^2_x = 102.06 \mbox{ cm}^2 & \quad & s_x = 10.1 \mbox{ cm}\\ \bar y = 69.67 \mbox{ Kg} & & s^2_y = 164.42 \mbox{ Kg}^2 & & s_y = 12.82 \mbox{ Kg} \end{array} \]
4.2 Kovarianz
4.2.1 Abweichungen von den Mittelwerten
Um die Beziehung zwischen zwei Variablen zu untersuchen, müssen wir ihre gemeinsame Variation analysieren.
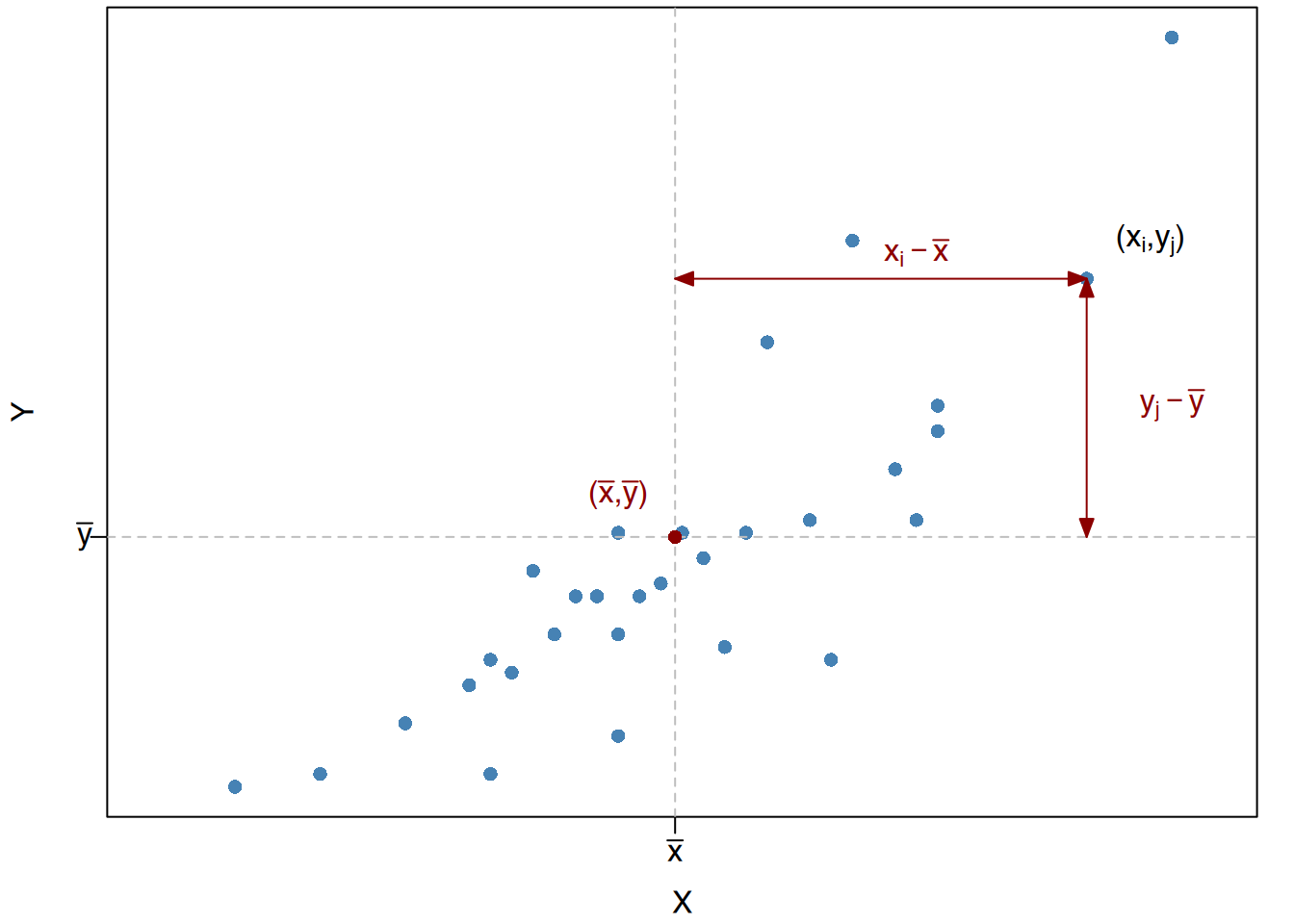
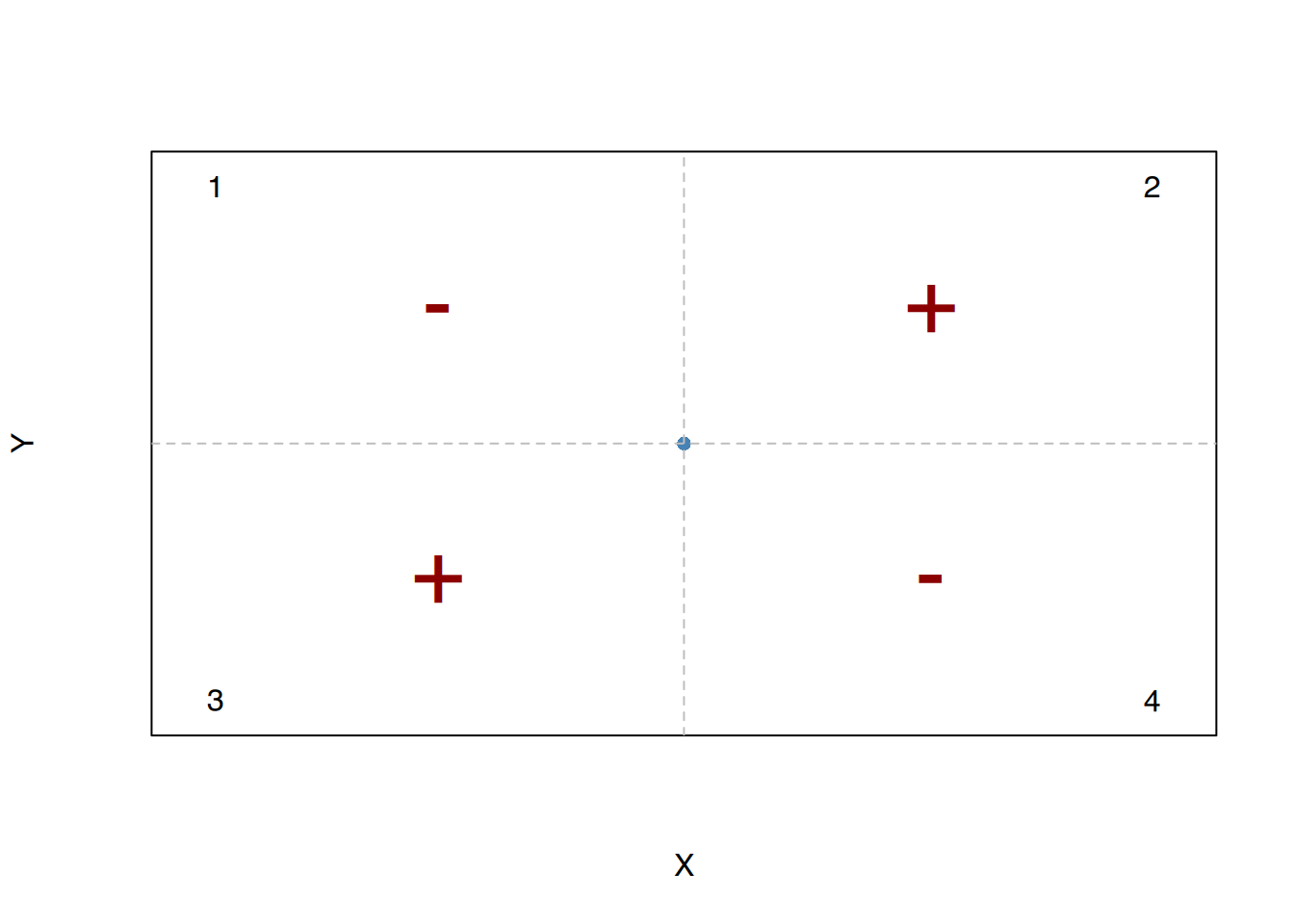
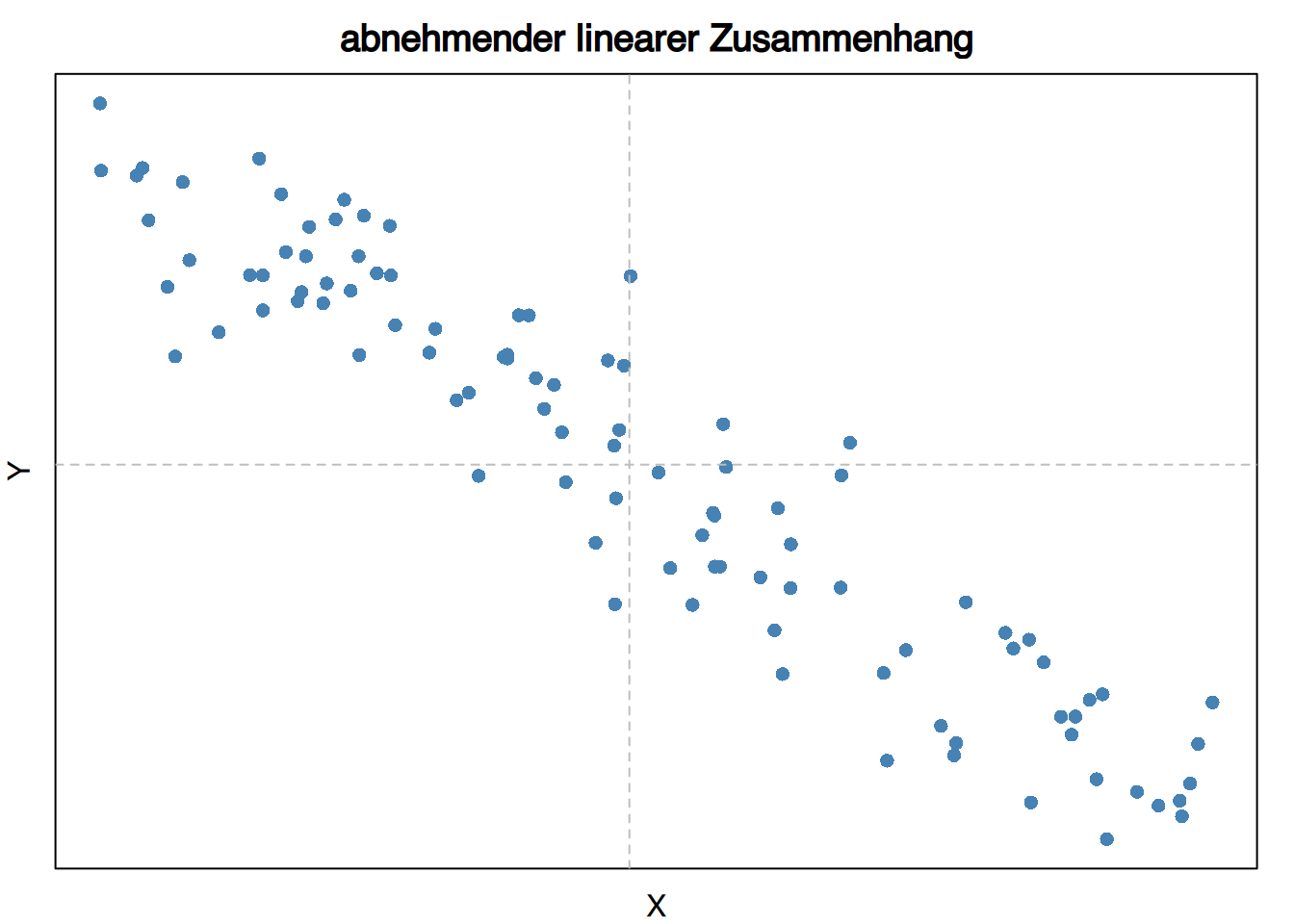
Wenn wir das Diagramm der Punktwolke in 4 Quadranten mit dem Mittelpunkt \((\bar x, \bar y)\) unterteilen, so sind die Vorzeichen der Abweichungen vom Mittelwert:
\[ \begin{array}{cccc} Quadrant & (x_i-\bar x) & (y_j-\bar y) & (x_i-\bar x)(y_j-\bar y)\\ \hline 1 & + & + & \mathbf{+}\\ 2 & - & + & \mathbf{-}\\ 3 & - & - & \mathbf{+}\\ 4 & + & - & \mathbf{-}\\ \hline \end{array} \]
4.2.2 Kovarianz
Die Kovarianz einer zweidimensionalen Variablen \((X, Y)\) ist der Durchschnitt der Produkte der Abweichungen von den jeweiligen Mitteln.
\[ s_{xy}=\frac{\sum (x_i-\bar x)(y_j-\bar y)n_{ij}}{n} \]
Sie kann auch unter Verwendung der folgenden Formel berechnet werden:
\[ s_{xy}=\frac{\sum x_iy_jn_{ij}}{n}-\bar x\bar y \]
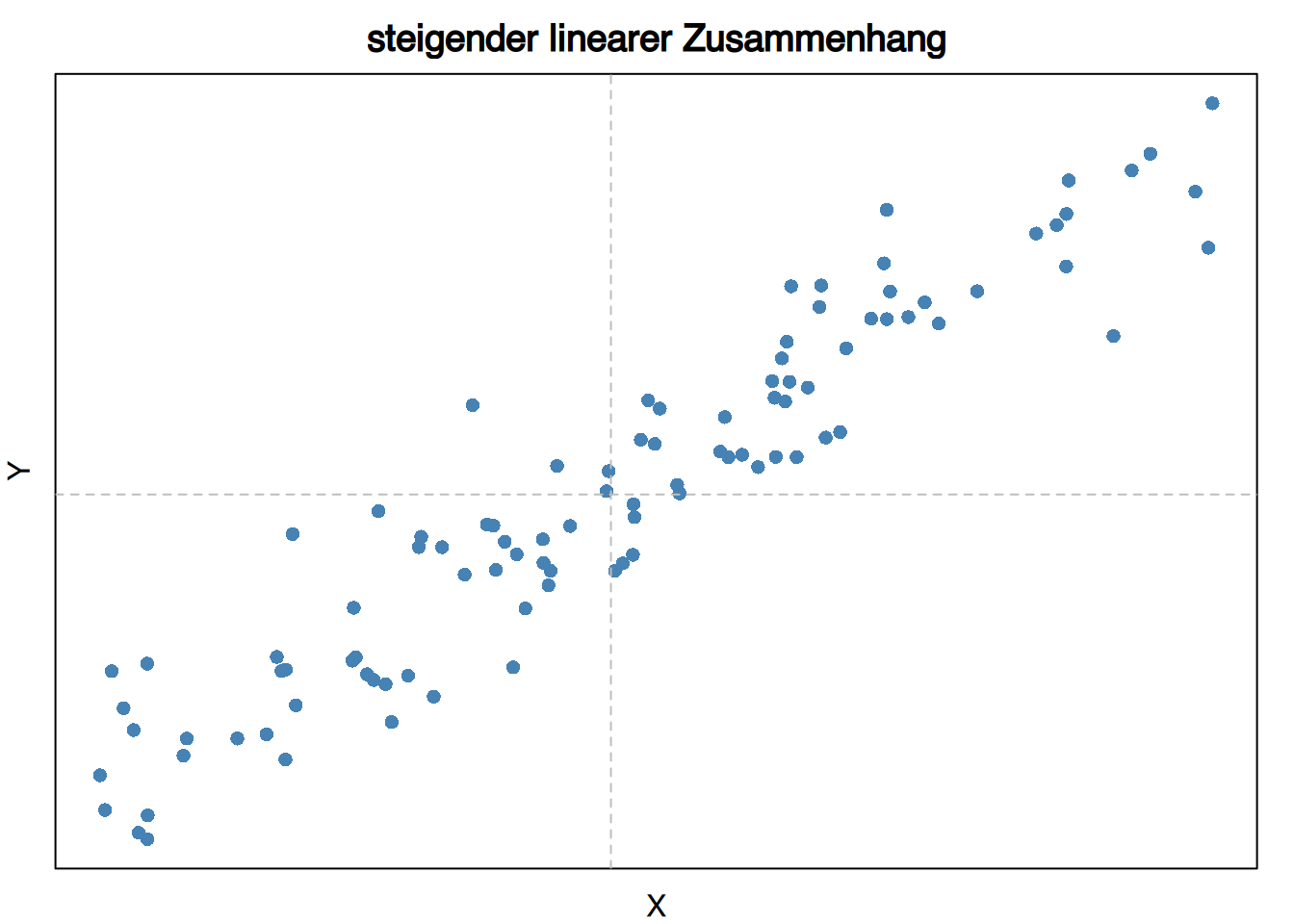
Die Kovarianz misst die lineare Beziehung zwischen zwei Variablen:
- Wenn \(s_{xy}\) > 0, besteht eine zunehmende lineare Beziehung.
- Wenn \(s_{xy}\) < 0, besteht eine abnehmende lineare Beziehung.
- Wenn \(s_{xy}\) = 0, gibt es keine lineare Beziehung.
Verwenden wir die Randhäufigkeitsverteilungen von Körpergröße und Gewicht
\[ \begin{array}{|c||c|c|c|c|c|c|c|} \hline X/Y & [50,60) & [60,70) & [70,80) & [80,90) & [90,100) & [100,110) & n_x\\ \hline\hline (150,160] & 2 & 0 & 0 & 0 & 0 & 0 & 2\\ \hline (160,170] & 4 & 4 & 0 & 0 & 0 & 0 & 8\\ \hline (170,180] & 1 & 6 & 3 & 1 & 0 & 0 & 11 \\ \hline (180,190] & 0 & 1 & 4 & 1 & 1 & 0 & 7 \\ \hline (190,200] & 0 & 0 & 0 & 0 & 1 & 1 & 2\\ \hline n_y & 7 & 11 & 7 & 2 & 2 & 1 & 30\\ \hline \end{array} \]
…mit den Mittelwerten. \[ \bar x = 174.67 \mbox{ cm} \qquad \bar y = 69.67 \mbox{ Kg} \]
So lässt sich die Kovarianz wie folgt berechnen:
\[ \begin{aligned} s_{xy} &=\frac{\sum x_iy_jn_{ij}}{n}-\bar x\bar y \\ & = \frac{155\cdot 55\cdot 2 + 165\cdot 55\cdot 4 + \cdots + 195\cdot 105\cdot 1}{30}-174.67\cdot 69.67 =\\ & = \frac{368200}{30}-12169.26 = 104.07 \text{cm} \cdot \text{Kg} \end{aligned} \]
Das bedeutet, dass eine positive lineare Beziehung zwischen den Variablen besteht.
4.3 Regression
In den meisten Fällen ist das Ziel einer Abhängigkeitsstudie nicht nur die Detektion einer Beziehung zwischen zwei Variablen, sondern auch die Expression dieser Beziehung mit einer mathematischen Funktion, \[ y=f(x) \]
um die abhängige Variable \(y\) für jeden Wert der unabhängigen \(x\) vorherzusagen.
Der Teil der Statistik, der sich mit dem Aufbau solch einer Funktion beschäftigt, wird Regression genannt, und die Funktion selbst heißt Regressionsfunktion oder Regressionsmodell.
4.3.1 Einfache Regressionsmodelle
Es gibt viele Arten von Regressionsmodellen. Die häufigsten Modelle sind in der folgenden Tabelle aufgeführt.
\[ \begin{array}{ll} \textbf{Model} & \textbf{Gleichung}\\ Linear & y=a+bx\\ Quadratisch & y=a+bx+cx^2\\ Kubisch & y=a+bx+cx^2+dx^3\\ Potenz & y=a\cdot x^b\\ Exponentiell & y=e^{a+bx}\\ Logarithmisch & y=a+b\cdot\log(x)\\ Invers & y = a+\frac{b}{x}\\ Sigmoidal & y= e^{a+\frac{b}{x}}\\ \end{array} \]
Die Wahl des Modells hängt von der Form der Punktwolke in der Streudiagramm ab.
4.3.2 Vorhersagefehler
Sobald der Typ des Regressionsmodells gewählt wurde, müssen wir entscheiden, welche Funktion dieser Familie die Beziehung zwischen der abhängigen und unabhängigen Variablen am besten erklärt, d.h. welche Funktion die abhängige Variable am besten vorhersagt.
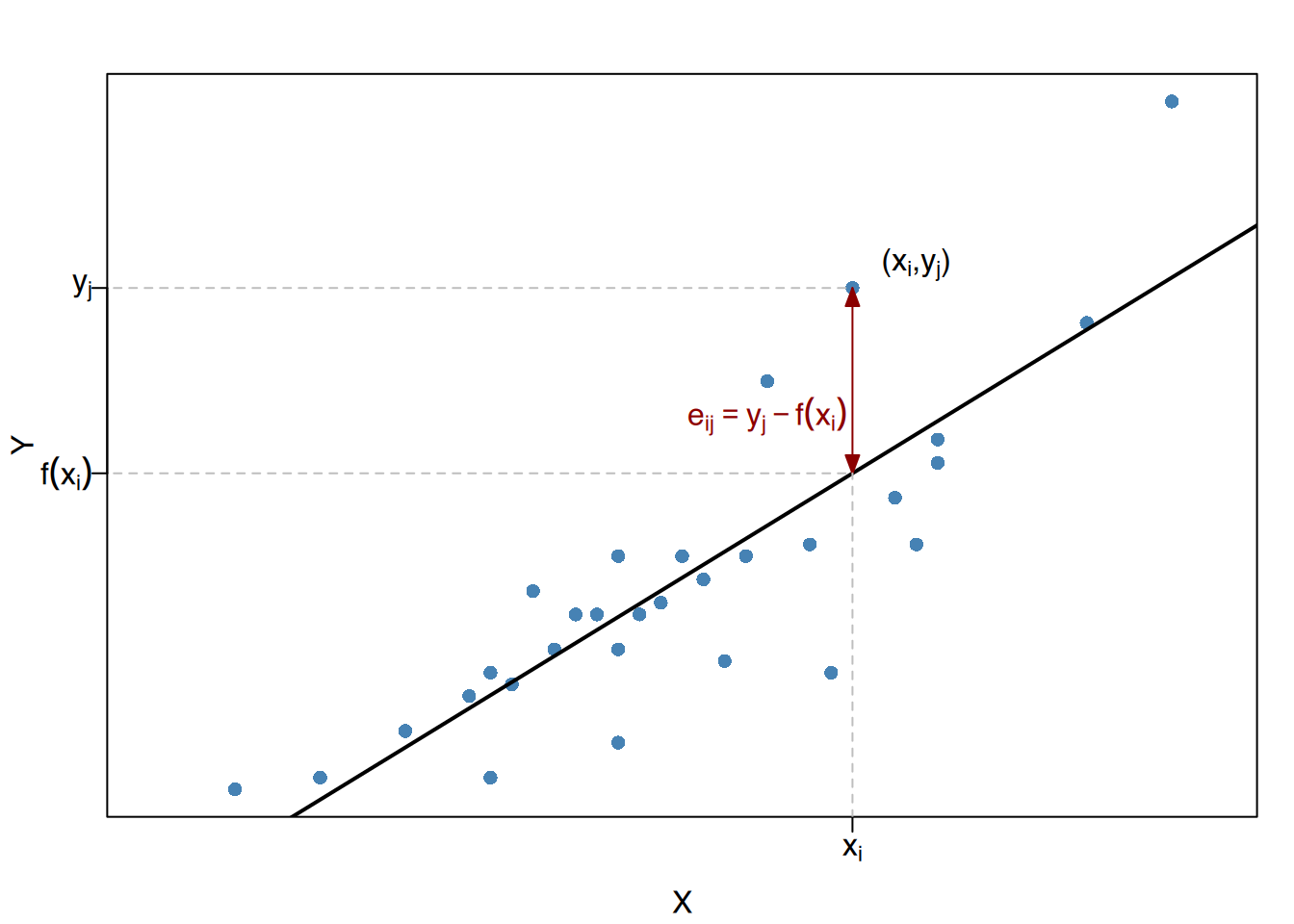
Diese Funktion ist diejenige, die die Abstände von den beobachteten Werten für \(Y\) in der Stichprobe zu den vorhergesagten Werten der Regressionsfunktion minimiert. Diese Abstände werden als Restterme, Residuen oder Vorhersagefehler bezeichnet.
Gegeben ein Regressionsmodell \(y = f(x)\) für eine zweidimensionale Variable \((X, Y)\), ist der Vorhersagefehler für jedes Paar \((x_i, y_j)\) der Stichprobe die Differenz zwischen dem beobachteten Wert der abhängigen Variablen \(y_j\) und dem vorhergesagten Wert der Regressionsfunktion für \(x_i\),
\[ e_{i,j} = y_j - f(x_i). \]
4.3.2.1 Methode der kleinsten Quadrate
Um die Regressionsfunktion zu erhalten, kann die Methode der kleinsten Quadrate angewendet werde. Mit ihr wird die Funktion bestimmt, welche die quadrierten Residuen minimiert.
\[ \sum e_{ij}^2. \]
Für ein lineares Modell \(f(x) = a + bx\) hängt die Summe von zwei Parametern ab, dem Schnittpunkt durch die Y-Achse \(a\) und der Steigung der Geraden \(b\),
\[ \theta(a,b) = \sum e_{ij}^2 =\sum (y_j - f(x_i))^2 =\sum (y_j-a-bx_i)^2. \]
Dies reduziert das Problem darauf, geeignete Werte für \(a\) und \(b\) zu bestimmen.
4.4 Regressionsgerade
Um das Minimierungsproblem zu lösen, müssen wir die partiellen Ableitungen bezüglich \(a\) und \(b\) auf Null setzen.
\[ \begin{aligned} \frac{\partial \theta(a,b)}{\partial a} &= \frac{\partial \sum (y_j-a-bx_i)^2 }{\partial a} =0\\ \frac{\partial \theta(a,b)}{\partial b} &= \frac{\partial \sum (y_j-a-bx_i)^2 }{\partial b} =0 \end{aligned} \]
Jetzt können wir das Gleichungssystem lösen zu:
\[ a= \bar y - \frac{s_{xy}}{s_x^2}\bar x \qquad b=\frac{s_{xy}}{s_x^2} \] Diese Formeln minimieren die Residuen von \(Y\) und ergeben das optimale lineare Modell.
Für eine Stichprobe mit den zweidimensionalen Variablen \((X, Y)\) ist die Regressionsgerade von \(Y\) auf \(X\):
\[ y = \bar y +\frac{s_{xy}}{s_x^2}(x-\bar x) \]
Die Regressionsgerade von \(Y\) auf \(X\) ist die Gerade, die die Vorhersagefehler von \(Y\) minimiert und daher das lineare Regressionsmodell mit den besten Vorhersagen für \(Y\) darstellt.
4.4.1 Regressionlinienberechnung
Wir verwenden die Daten der Körpergrößen (\(X\)) und Körpergewichten (\(Y\)) mit den folgenden Kennwerten
\[ \begin{array}{lllll} \bar x = 174.67 \text{ cm} & \quad & s^2_x = 102.06 \text{ cm}^2 & \quad & s_x = 10.1 \text{ cm}\\ \bar y = 69.67 \text{ Kg} & & s^2_y = 164.42 \text{ Kg}^2 & & s_y = 12.82 \text{ Kg}\\ & & s_{xy} = 104.07 \text{ cm}\cdot \text{ Kg} & & \end{array} \]
ergibt sich die Regressionsgerade für Körpergröße erklärt durch Gewicht (Größe gegen Gewicht, \(\text{Größe} = f(\text{Gewicht})\)) wie folgt:
\[ y = \bar y +\frac{s_{xy}}{s_x^2}(x-\bar x) = 69.67+\frac{104.07}{102.06}(x-174.67) = -108.49 +1.02 x \]
Die Regressionsgerade für Gewicht erklärt durch Körpergröße (Gewicht gegen Größe, \(\text{Gewicht} = f(\text{Größe})\)) ist
\[ x = \bar x +\frac{s_{xy}}{s_y^2}(y-\bar y) = 174.67+\frac{104.07}{164.42}(y-69.67) = 130.78 + 0.63 y \]
Beachten Sie, dass die Regressionsgeraden unterschiedlich sind!
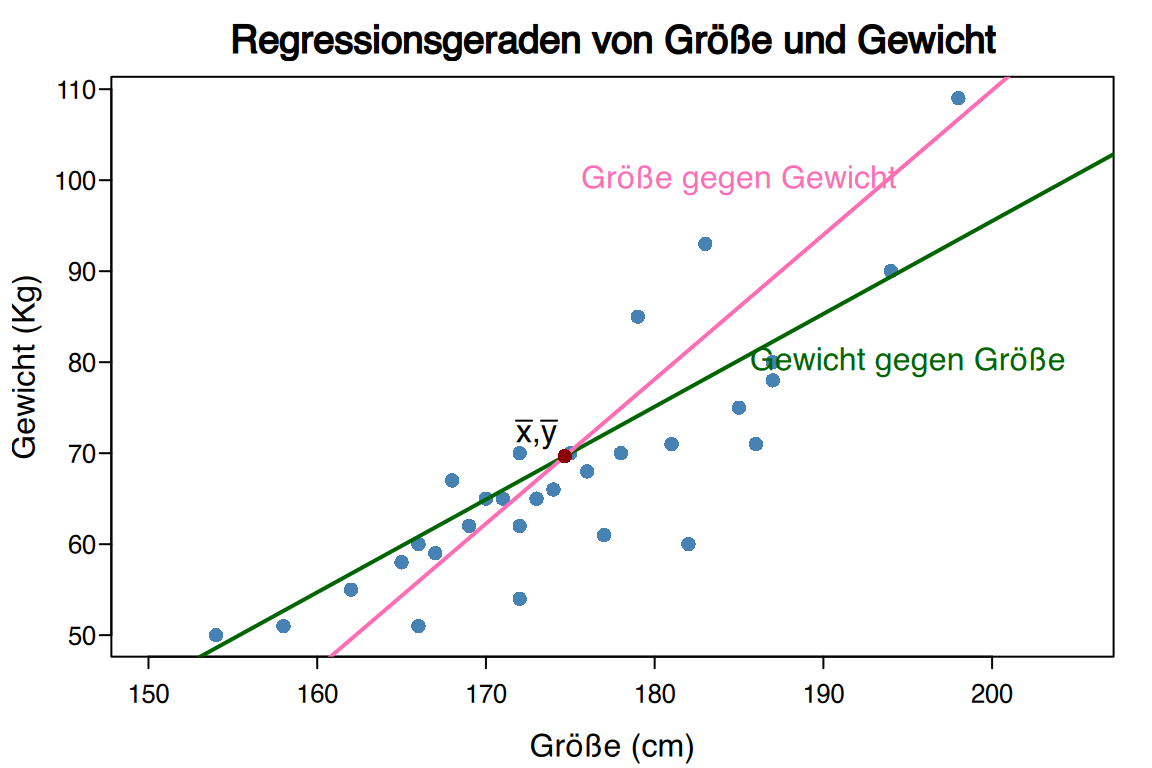
Üblicherweise sind die Regressionsgeraden von \(Y\) gegen \(X\) und \(X\) gegen \(Y\) nicht gleich, aber sie schneiden sich immer im Mittelpunkt \((\overline x, \overline y)\).
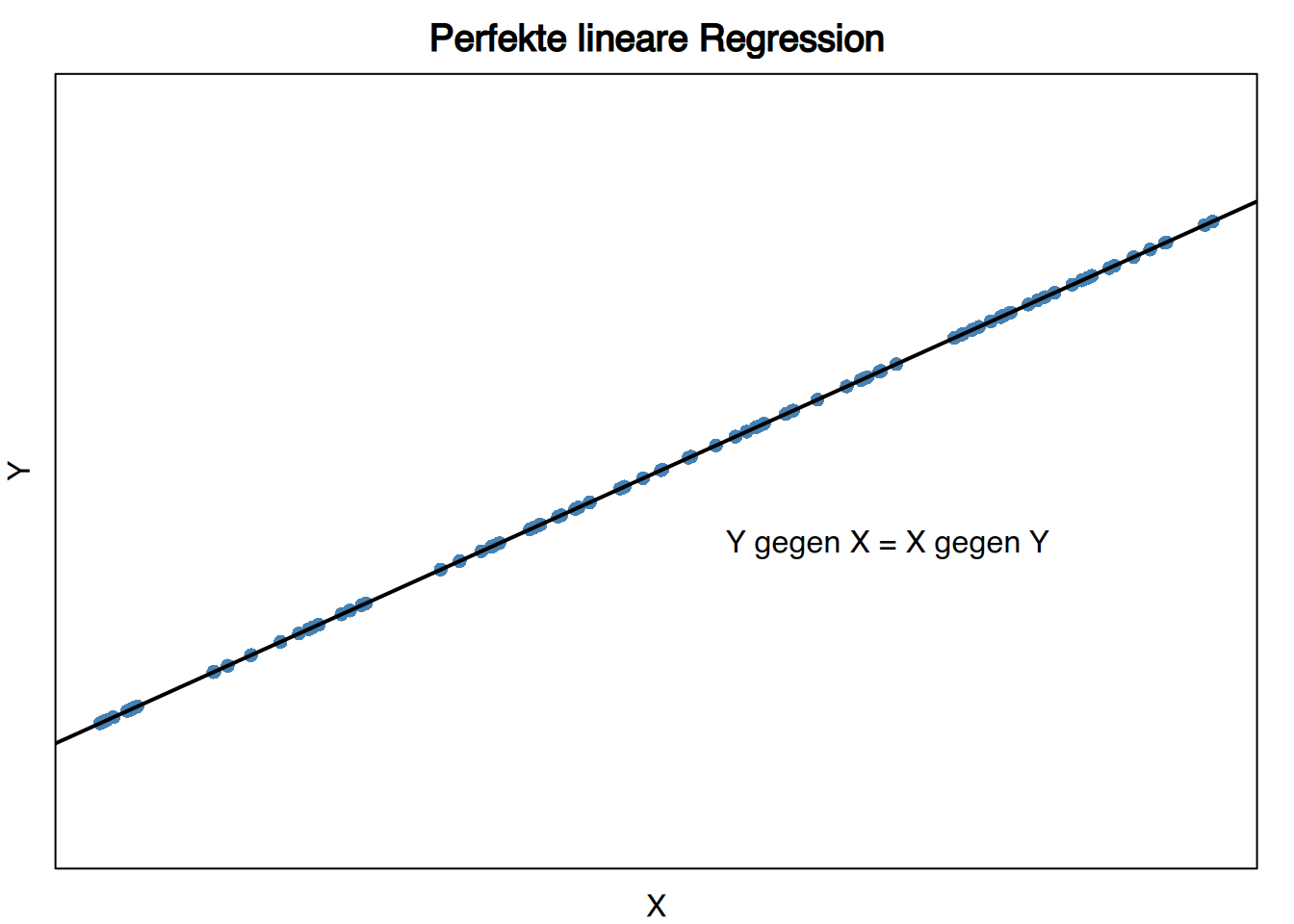
Wenn es eine perfekte lineare Beziehung zwischen den Variablen gibt, dann sind beide Regressionsgeraden gleich, da diese Linie sowohl \(X\)-Residuen als auch \(Y\)-Residuen auf null setzt.
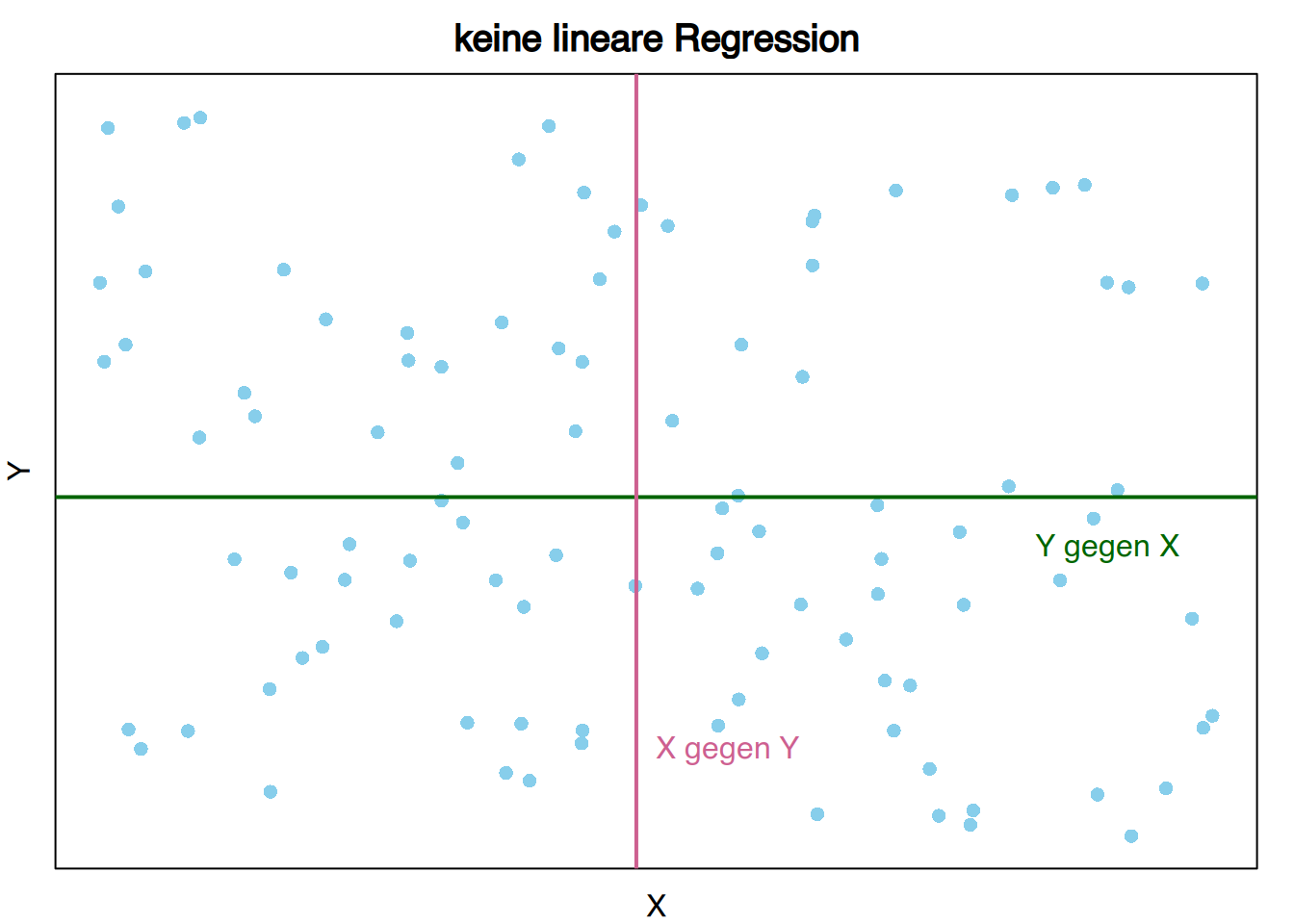
Wenn es keine lineare Beziehung zwischen den Variablen gibt, dann sind beide Regressionsgeraden konstant und gleich den jeweiligen Mittelwerten \[ y = \bar y, \qquad x = \bar x. \]
Daher schneiden sie sich senkrecht.
4.4.2 Regressionskoeffizient
Der wichtigste Parameter einer Regressionsgeraden ist die Steigung.
Für eine zweidimensionale Variable \((X, Y)\) gibt der Regressionskoeffizient der Regressionsgeraden von \(Y\) gegen \(X\) deren Steigung an,
\[ b_{yx} = \frac{s_{xy}}{s_x^2} \]
Der Regressionskoeffizient hat immer das gleiche Vorzeichen wie die Kovarianz. Er misst, wie sich die abhängige Variable \(Y\) in Bezug auf die unabhängige Variable \(X\) gemäß der Regressionsgerade verändert. Insbesondere gibt er an, um wie viele Einheiten die abhängige Variable pro Einheit, die die unabhängige Variable zunimmt, steigt oder fällt.
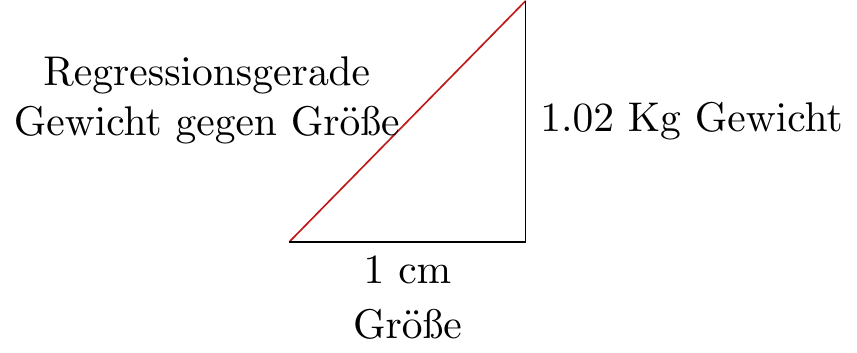
In unserer Stichprobe mit den Variablen Körpergröße und Gewicht war die Regressionsgerade für das Gewicht in Bezug auf die Körpergröße
\[ y=-108.49 +1.02 x. \]
Daher ist der Regressionskoeffizient für das Gewicht in Bezug auf die Körpergröße
\[ b_{yx}= 1.02 \text{ Kg/cm.} \]
Das bedeutet, dass das Gewicht gemäß der Regressionsgerade in Bezug auf die Körpergröße um 1.02 kg pro Zentimeter zunimmt, wenn die Körpergröße steigt.
4.4.3 Modellvorhersage
Üblicherweise werden Regressionsmodelle verwendet, um die abhängige Variable \(Y\) für bestimmte Werte der unabhängigen Variablen \(X\) vorherzusagen.
Um die besten Vorhersagen einer Variablen zu erhalten, müssen Sie die Regressionsgerade verwenden, bei der diese Variable die abhängige Rolle \(Y\) spielt.
Möchten wir das Gewicht einer Person mit einer Körpergröße von 180cm vorhersagen, müssen wir die Regressionsgerade für das Gewicht in Bezug auf die Körpergröße verwenden.
\[ y = -108.49 + 1.02 \cdot 180 = 75.11 \text{ Kg}. \]
Um hingegen die Körpergröße einer Person mit einem Gewicht von 79kg vorherzusagen, müssen wir die Regressionsgerade für die Körpergröße in Bezug auf das Gewicht verwenden,
\[ x = 130.78 + 0.63\cdot 79 = 180.55 \text{ cm}. \]
Aber wie zuverlässig sind diese Vorhersagen?
4.5 Korrelation
Sobald wir ein Regressionsmodell haben, müssen wir seine Vorhersagefähigkeit bewerten, indem wir die Anpassungsgüte des Modells und die Stärke der Beziehung, die es aufbaut, untersuchen. Dieser Teil der Statistik wird als Korrelation bezeichnet.
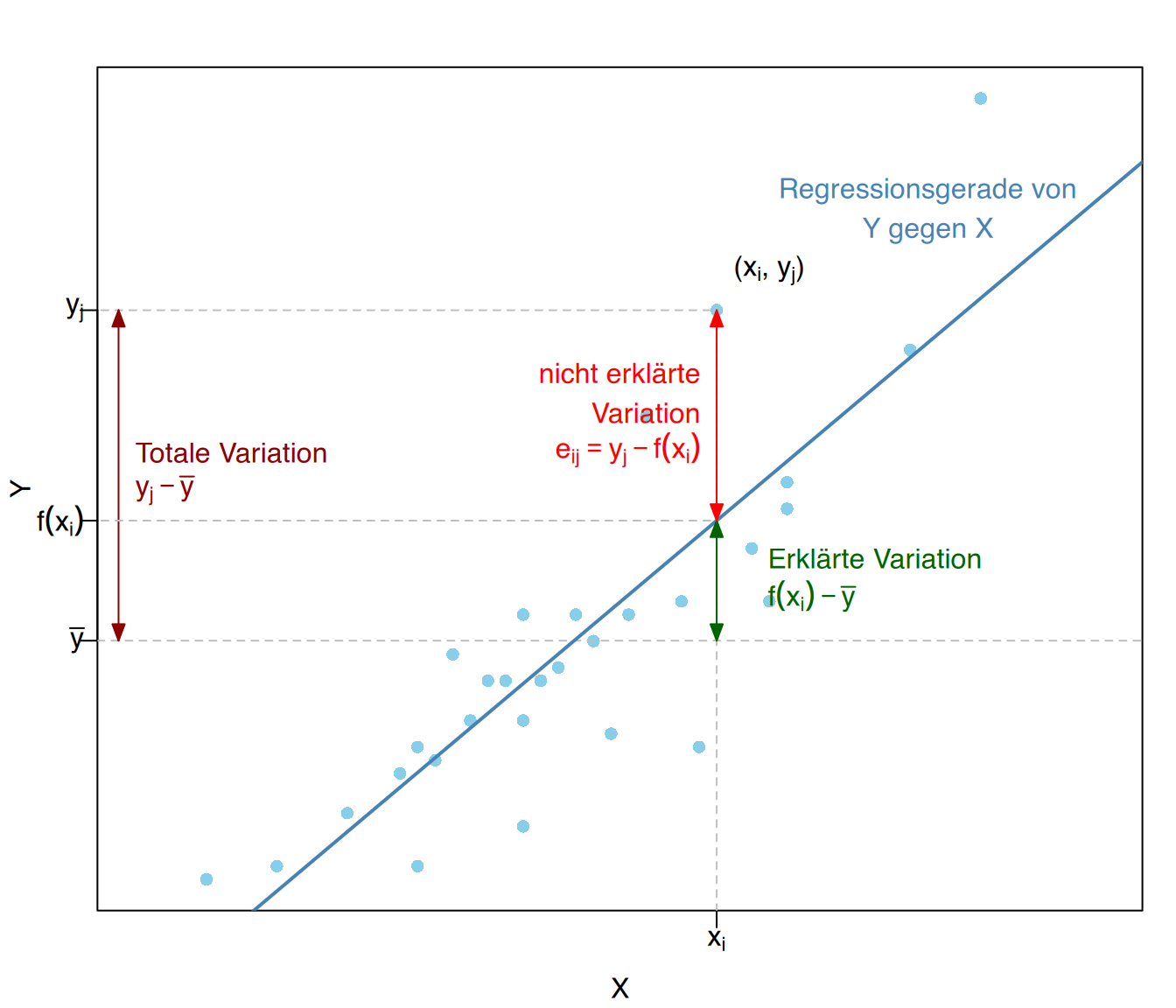
Die Korrelationsanalyse untersucht die Residuen eines Regressionsmodells: Je kleiner die Residuen, desto besser passt das Modell und desto stärker ist die Beziehung, die es aufbaut. Um die Anpassungsgüte eines Regressionsmodells zu messen, wird häufig die residuale Varianz verwendet.
Bei einem Regressionsmodell \(y = f(x)\) für eine zweidimensionale Variable \((X, Y)\) ist die residuale Varianz die durchschnittliche quadratische Abweichung der Residuen,
\[ s_{ry}^2 = \frac{\sum e_{ij}^2n_{ij}}{n} = \frac{\sum (y_j - f(x_i))^2n_{ij}}{n}. \]
Je größer die Residuen, desto größer die residuale Varianz und desto kleiner die Anpassungsgüte. Wenn die lineare Beziehung perfekt ist, sind die Residuen Null und die residuale Varianz ist ebenfalls Null. Umgekehrt gilt, dass wenn es keine Beziehung gibt, die Residuen mit den Abweichungen vom Mittelwert übereinstimmen und die residuale Varianz gleich der Varianz der abhängigen Variable ist.
\[ 0\leq s_{ry}^2\leq s_y^2 \]
4.6 Korrelationskoeffizienten
4.6.1 Bestimmheitsmaß
Es ist möglich, aus der Reststreuung eine andere Korrelationsstatistik zu definieren, die leichter interpretierbar ist.
Für ein Regressionsmodell \(y=f(x)\) einer zweidimensionalen Variablen \((X, Y)\), ist sein Bestimmtheitsmaß
\[ R^2 = 1- \frac{s_{ry}^2}{s_y^2} \]
Da die Reststreuung von 0 bis \(s_{y}^2\) reicht, gilt:
\[ 0\leq R^2\leq 1 \]
Je größer \(R^2\) ist, desto besser passt das Regressionsmodell und desto zuverlässiger werden seine Vorhersagen sein.
- Wenn \(R^2 = 0\), gibt es keine Beziehung gemäß dem Regressionsmodell.
- Wenn \(R^2 = 1\), ist die Beziehung gemäß dem Modell perfekt.
4.6.2 Lineares Bestimmtheitsmaß
Wenn das Regressionsmodell linear ist, beträgt die Reststreuung
\[ \begin{aligned} s_{ry}^2 & = \sum e_{ij}^2f_{ij} = \sum (y_j - f(x_i))^2f_{ij} = \sum \left(y_j - \bar y -\frac{s_{xy}}{s_x^2}(x_i-\bar x) \right)^2f_{ij}\\ & = \sum \left((y_j - \bar y)^2 +\frac{s_{xy}^2}{s_x^4}(x_i-\bar x)^2 - 2\frac{s_{xy}}{s_x^2}(x_i-\bar x)(y_j -\bar y)\right)f_{ij} \\ & = \sum (y_j - \bar y)^2f_{ij} +\frac{s_{xy}^2}{s_x^4}\sum (x_i-\bar x)^2f_{ij}- 2\frac{s_{xy}}{s_x^2}\sum (x_i-\bar x)(y_j -\bar y)f_{ij}\\ & = s_y^2 + \frac{s_{xy}^2}{s_x^4}s_x^2 - 2 \frac{s_{xy}}{s_x^2}s_{xy} = s_y^2 - \frac{s_{xy}^2}{s_x^2}. \end{aligned} \]
… und das Bestimmtheitsmaß ist ….
\[ \begin{aligned} R^2 &= 1- \frac{s_{ry}^2}{s_y^2} = 1- \frac{s_y^2 - \frac{s_{xy}^2}{s_x^2}}{s_y^2} = 1 - 1 + \frac{s_{xy}^2}{s_x^2s_y^2} = \frac{s_{xy}^2}{s_x^2s_y^2}. \end{aligned} \]
In der Stichprobe zu Körpergröße und Gewicht gelten folgende Kennwerte:
\[ \begin{array}{lll} \bar x = 174.67 \text{ cm} & \quad & s^2_x = 102.06 \text{ cm}^2\\ \bar y = 69.67 \text{ Kg} & & s^2_y = 164.42 \text{ Kg}^2\\ s_{xy} = 104.07 \text{ cm}\cdot\text{ Kg} \end{array} \]
Das Bestimmtheitsmaß errechnet sich also per
\[ R^2 = \frac{s_{xy}^2}{s_x^2s_y^2} = \frac{(104.07 \text{ cm}\cdot\text{Kg})^2}{102.06 \text{ cm}^2 \cdot 164.42 \text{ Kg}^2} = 0.65. \]
Das bedeutet, dass das lineare Modell Gewicht erklärt durch Größe 65% der Variation des Gewichts erklärt und das lineare Modell Körpergröße erklärt durch Gewicht ebenfalls 65% der Variation der Körpergröße erklärt.
4.6.3 Korrelationskoeffizient
Gegeben eine Stichprobe zweidimensionaler Variablen (X, Y), ist der Korrelationskoeffizient der Stichprobe die Wurzel des linearen Bestimmtheitsmaßes mit dem Vorzeichen der Kovarianz:
\[ r = \dfrac{s_{xy}}{s_xs_y}. \]
Das Bestimmheitsmaß \(R^2\) reicht von 0 bis 1, und \(r\) reicht von -1 bis 1,
\[ -1\leq r\leq 1 \]
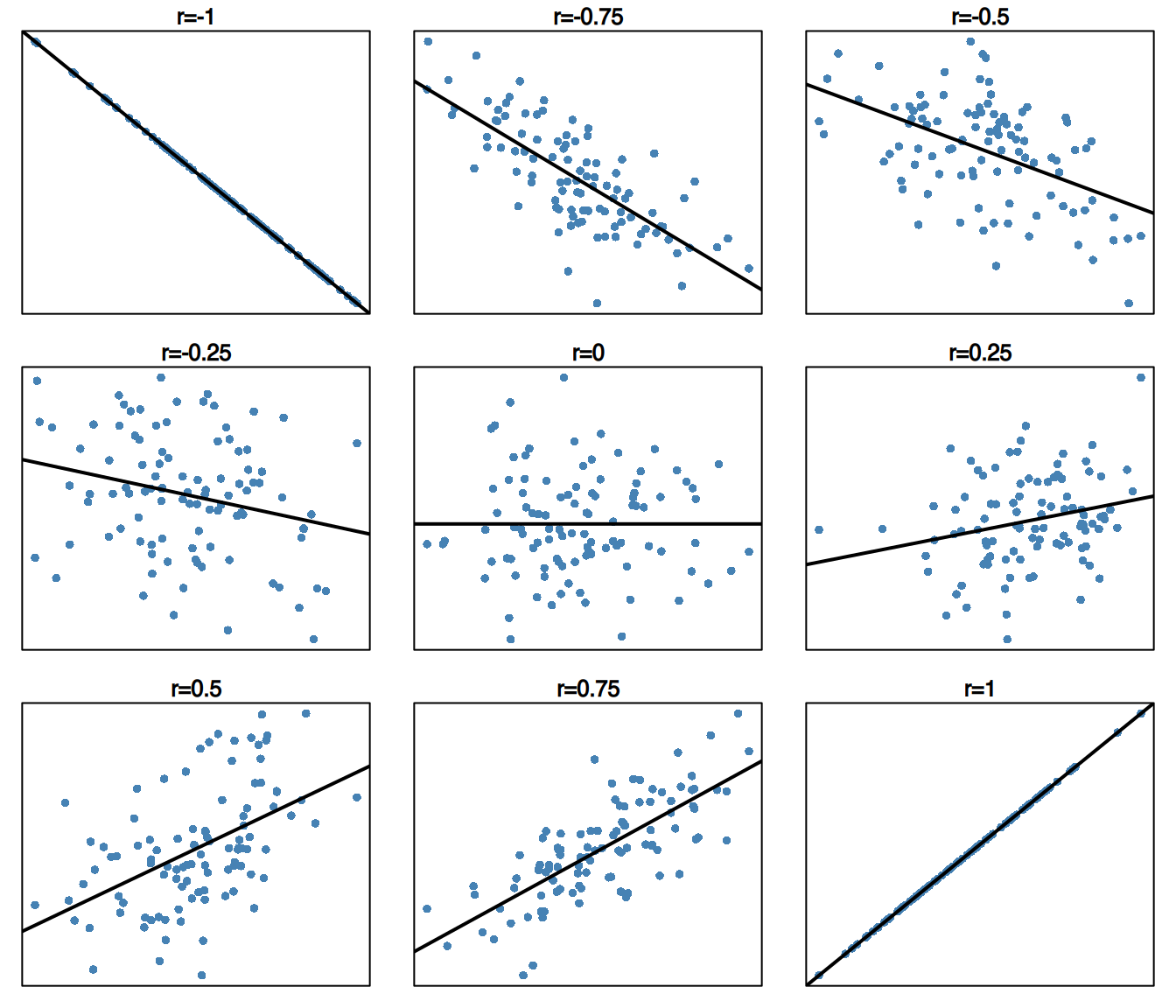
Der Korrelationskoeffizient misst nicht nur die Stärke, sondern auch die Richtung (steigend oder fallend) der linearen Beziehung:
- Wenn \(r = 0\), gibt es keine lineare Beziehung.
- Wenn \(r = 1\), gibt es eine perfekte steigende lineare Beziehung.
- Wenn \(r = -1\), gibt es eine perfekte fallende lineare Beziehung.
In der Stichprobe zu Körpergröße und Gewicht gelten folgende Kennwerte:
\[ \begin{array}{lll} \bar x = 174.67 \text{ cm} & \quad & s^2_x = 102.06 \text{ cm}^2\\ \bar y = 69.67 \text{ Kg} & & s^2_y = 164.42 \text{ Kg}^2\\ s_{xy} = 104.07 \text{ cm}\cdot\text{ Kg} \end{array} \]
Der Korrelationskoeffizient kann nun berechnet werden mit:
\[ r = \frac{s_{xy}}{s_xs_y} = \frac{104.07 \text{ cm}\cdot\text{Kg}}{10.1 \text{ cm} \cdot 12.82 \text{ Kg}} = +0.8. \]
Dies bedeutet, dass es eine relativ starke steigende lineare Beziehung zwischen Körpergröße und Gewicht gibt.
4.6.4 Zuverlässigkeit von Regressionsvorhersagen
Das Bestimmtheitsmaß erklärt, wie gut ein Regressionsmodell passt, aber andere Faktoren beeinflussen auch die Zuverlässigkeit von Regressionsvorhersagen:
- Ein höheres \(R^2\) bedeutet eine bessere Passung und zuverlässigere Vorhersagen.
- Eine höhere Variabilität der Grundgesamtheit macht Vorhersagen schwieriger und weniger zuverlässig.
- Eine größere Stichprobengröße bietet mehr Informationen und ermöglicht zuverlässigere Vorhersagen.
Darüber hinaus muss man beachten, dass ein Regressionsmodell nur für den in der Stichprobe beobachteten Wertebereich gültig ist. Daher sollten keine Vorhersagen für Werte weit außerhalb dieses Bereichs gemacht werden, da wir für diese keine Informationen haben.
4.7 nicht-lineare Regression
Eine nichtlineare Regression kann auch mit der Methode der kleinsten Quadrate durchgeführt werden. Allerdings kann in einigen Fällen die Anpassung eines nichtlinearen Modells durch eine einfache Transformation seiner Variablen auf die Anpassung eines linearen Modells reduziert werden.
4.7.1 Transformationen von nichtlinearen Regressionsmodellen
- Logarithmisches Modell: Ein logarithmisches Modell \(y = a+b \log x\) kann durch den Wechsel \(t=\log x\) in ein lineares Modell überführt werden:
\[ y=a+b\log x = a+bt \]
- Exponentielles Modell: Ein exponentielles Modell \(y = e^{a+bx}\) kann durch den Wechsel \(z = \log y\) in ein lineares Modell überführt werden:
\[ z = \log y = \log(e^{a+bx}) = a+bx \]
- Potenzialmodell: Ein Potenzialmodell \(y = ax^b\) kann durch die Wechsel \(t=\log x\) und \(z=\log y\) in ein lineares Modell überführt werden:
\[ z = \log y = \log(ax^b) = \log a + b \log x = a^\prime+bt. \]
- Inversmodell: Ein Inversmodell \(y = a+b/x\) kann durch den Wechsel \(t=1/x\) in ein lineares Modell überführt werden:
\[ y = a + b(1/x) = a+bt \]
- Sigmoidales Modell: Ein sigmoidales Modell \(y = e^{a+b/x}\) kann durch die Wechsel \(t=1/x\) und \(z=\log y\) in ein lineares Modell überführt werden:
\[ z = \log y = \log (e^{a+b/x}) = a+b(1/x) = a+bt \]
4.7.2 exponentieller Zusammenhang
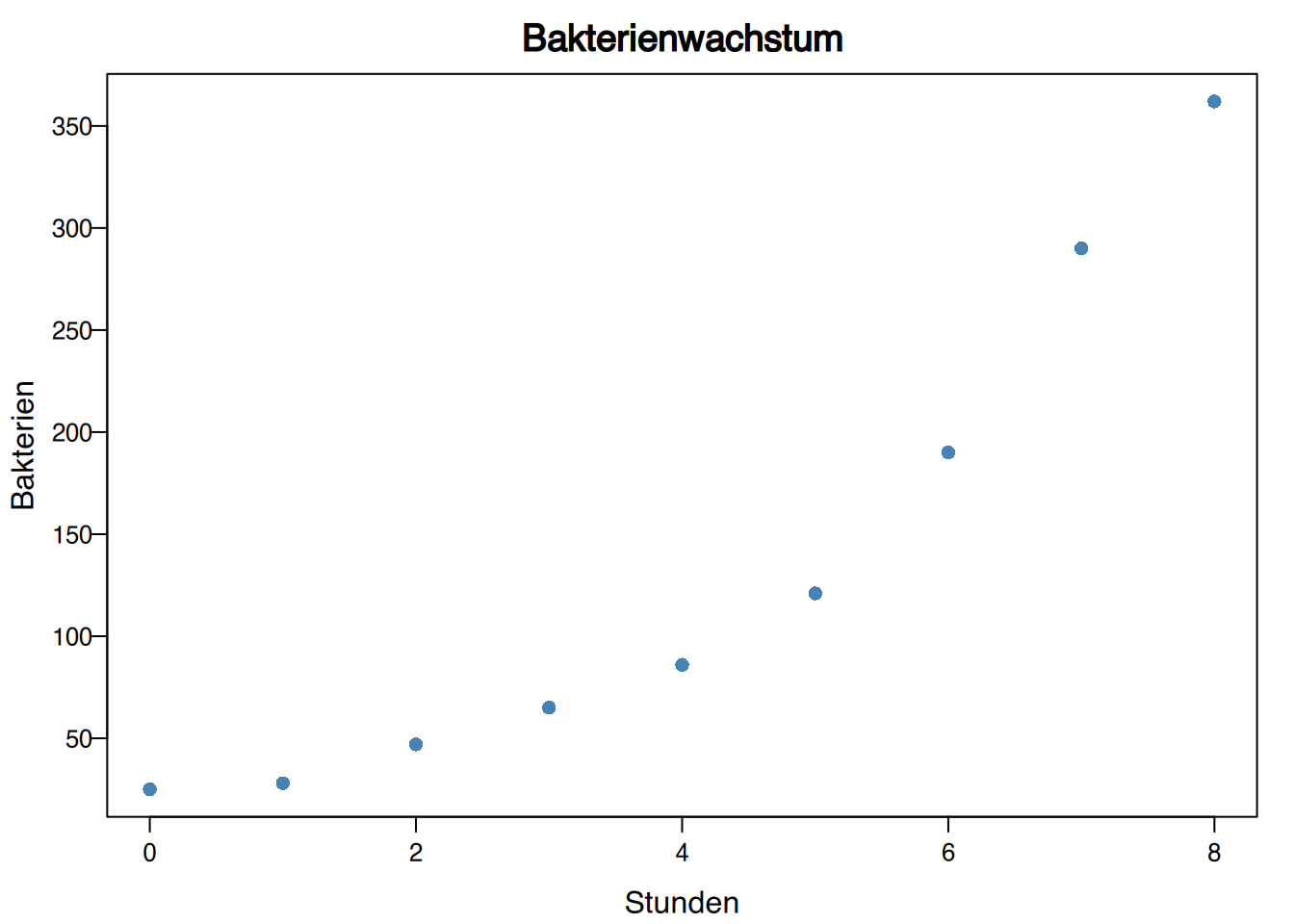
Die nachfolgende Tabelle zeigt die Anzahl an Bakterien in einer Kultur über mehrere Stunden.
\[ \begin{array}{c|c} \text{Stunden} & \text{Bakterien}\\ \hline 0 & 25 \\ 1 & 28 \\ 2 & 47\\ 3 & 65 \\ 4 & 86\\ 5 & 121\\ 6 & 190\\ 7 & 290\\ 8 & 362 \end{array} \]
Das dazugehörige Streudiagramm sieht so aus:
Wenn wir ein lineares Modell erstellen (engl: to fit, auch fitten genannt), erhalten wir
\[ \text{Bakterien} = -30,18+41,27\,\text{Stunden, mit } R^2=0,85. \] Die Regressionsgerade sieht so aus:
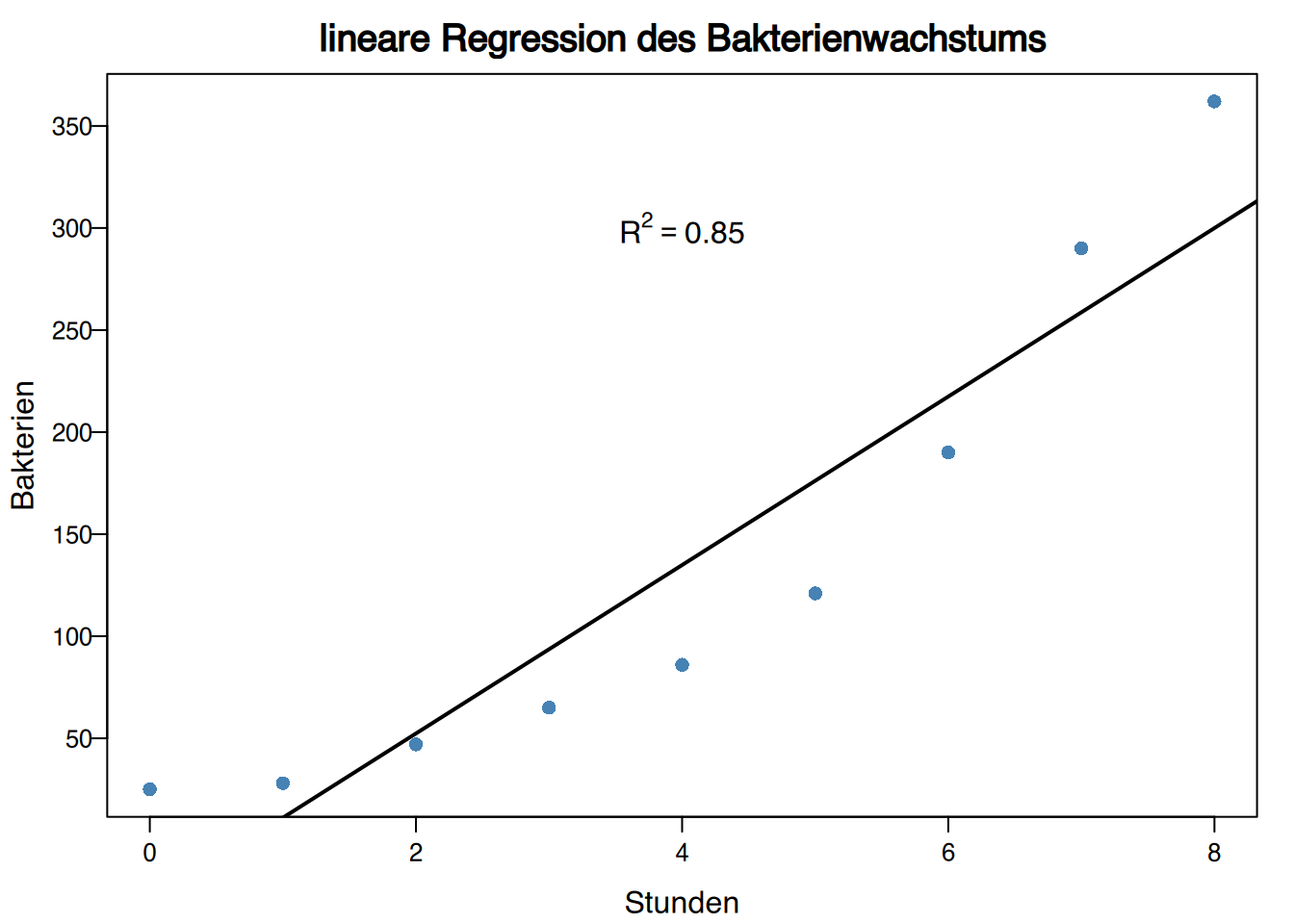
Ist dies ein gutes Modell?
4.7.2.1 exponentielles Modell
Obwohl das lineare Modell nicht schlecht ist, erscheint ein exponentielles Modell aufgrund der Form des Punktwolken-Clouds des Streuplots geeigneter zu sein.
Um ein exponentielles Modell \(y = e^{a+bx}\) zu konstruieren, können wir die Transformation \(z=\log y\) anwenden, indem wir also eine logarithmische Transformation der abhängigen Variablen durchführen.
\[ \begin{array}{c|c|c} \text{Stunden} & \text{Bakterien} & \log(Bakterien)\\ \hline 0 & 25 & 3.22\\ 1 & 28 & 3.33\\ 2 & 47 & 3.85\\ 3 & 65 & 4.17\\ 4 & 86 & 4.45\\ 5 & 121 & 4.80\\ 6 & 190 & 5.25\\ 7 & 290 & 5.67\\ 8 & 362 & 5.89 \end{array} \]
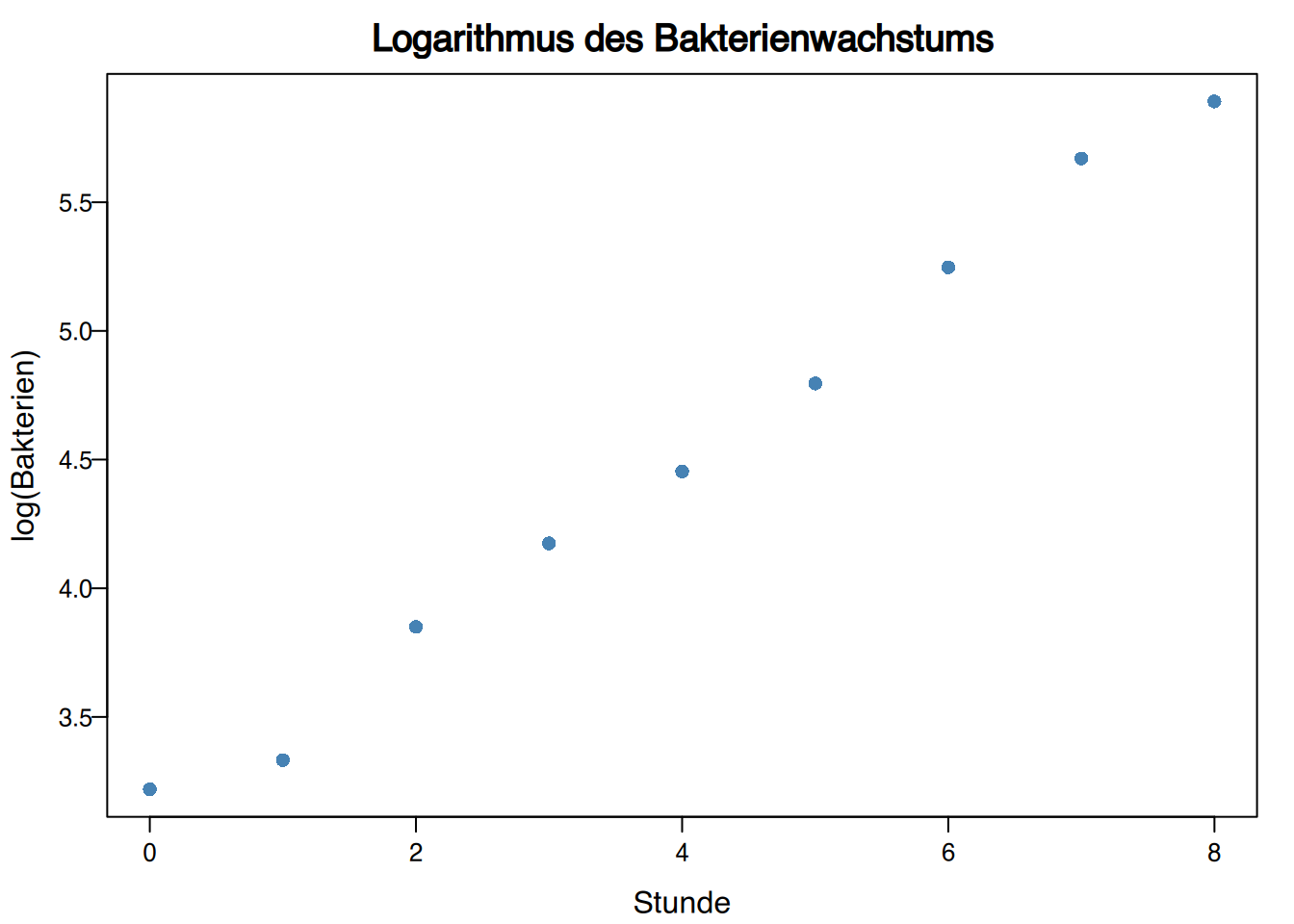
Jetzt bleibt nur noch, die Regressionslinie des Logarithmus der Bakterien über die Stunden zu berechnen:
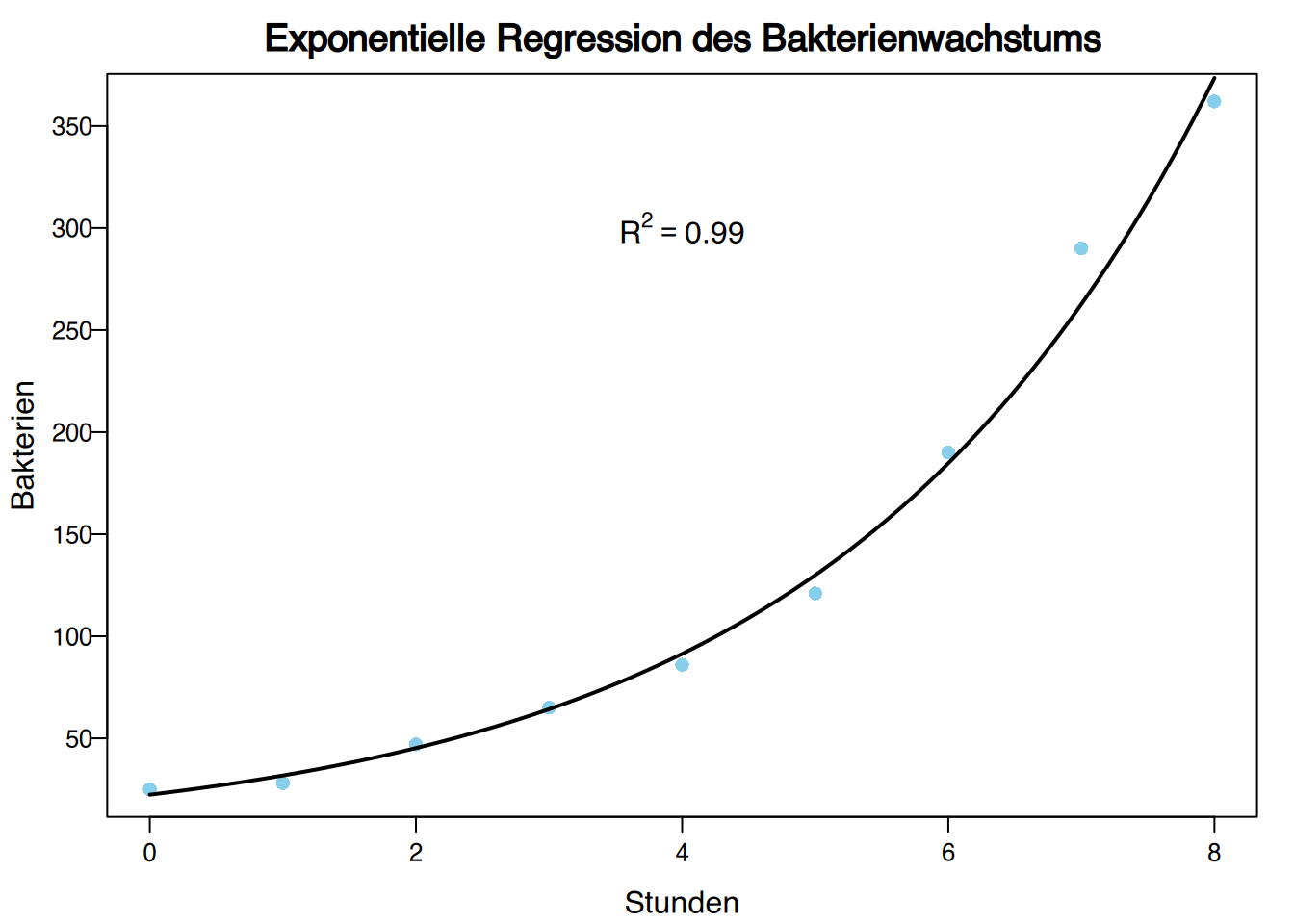
\[ \log(Bakterien) = 3.107 + 0.352 \text{ Stunden}, \]
und die Variable abschließend zurückzutransformieren,
\[ \text{Bakterien} = e^{3.107+0.352 \text{ Stunden}} \] errechnet sich \(R^2 = 0,99\).
Daher passt das exponentielle Modell deutlich besser als das lineare Modell.
4.7.3 Regressionsrisiken
Es ist wichtig zu beachten, dass jedes Regressionsmodell seinen eigenen Bestimmtheitskoeffizienten hat. Daher bedeutet ein nah an Null liegender Bestimmtheitskoeffizient, dass es keine vom Modell festgelegte Beziehung gibt. Aber das bedeutet nicht, dass die Variablen unabhängig sind, da es eine andere Art von Beziehung geben könnte.
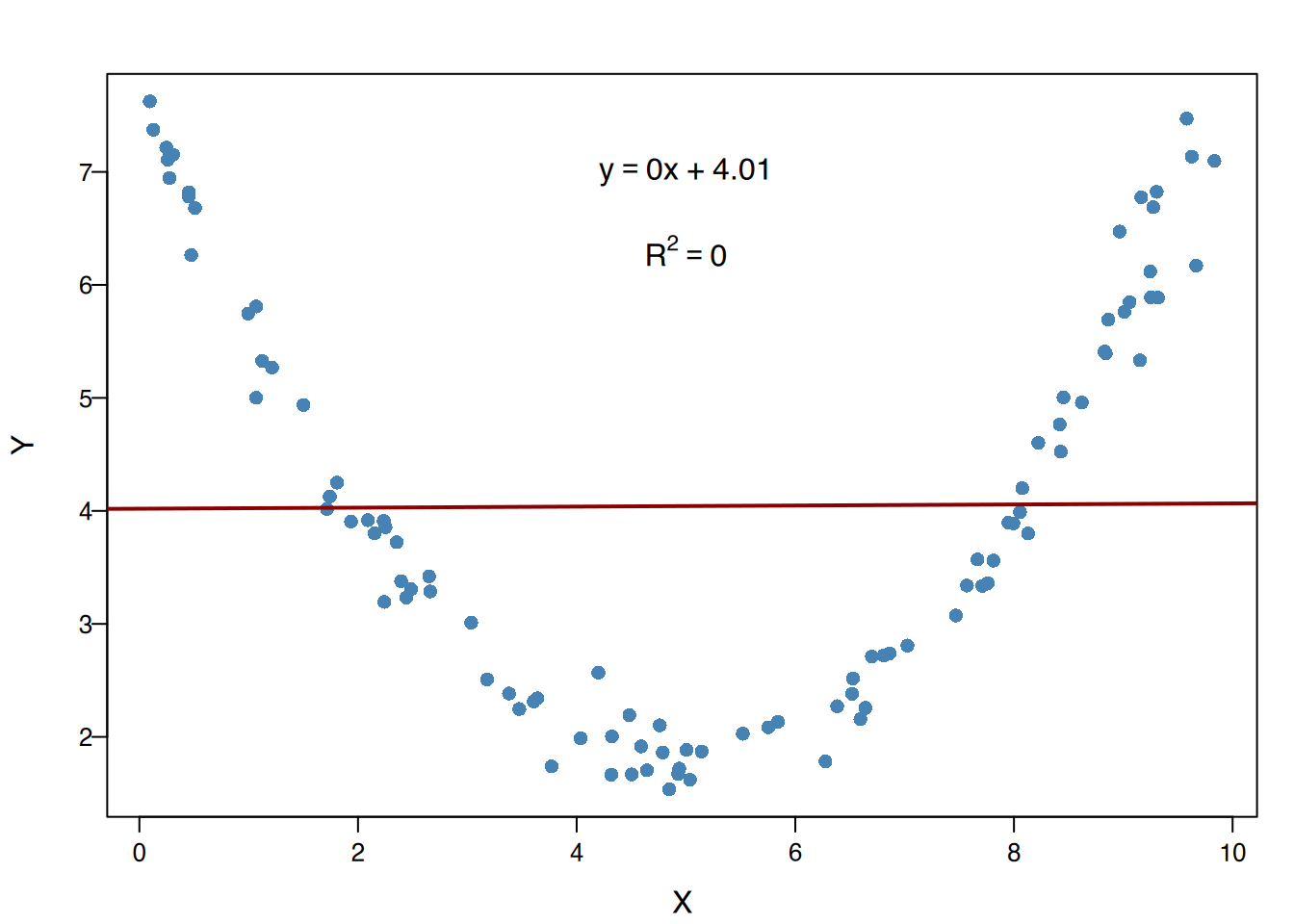
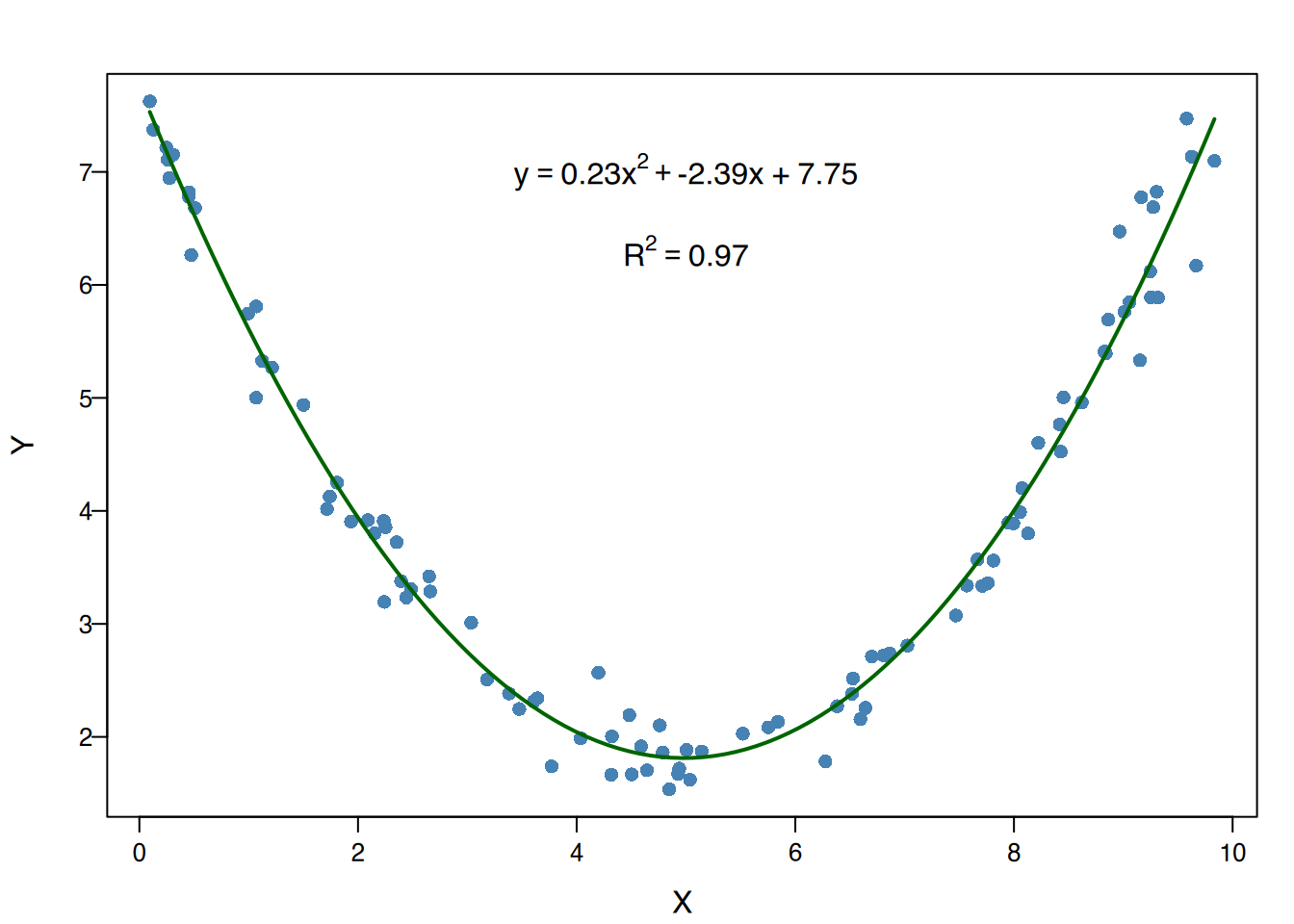
4.7.4 Ausreißer in Regressionsmodellen
In Regressionsstudien sind Ausreißer Punkte, die nicht der Tendenz der restlichen Punkte folgen, auch wenn die Werte des Paares für jede Variable separat keine Ausreißer sind.
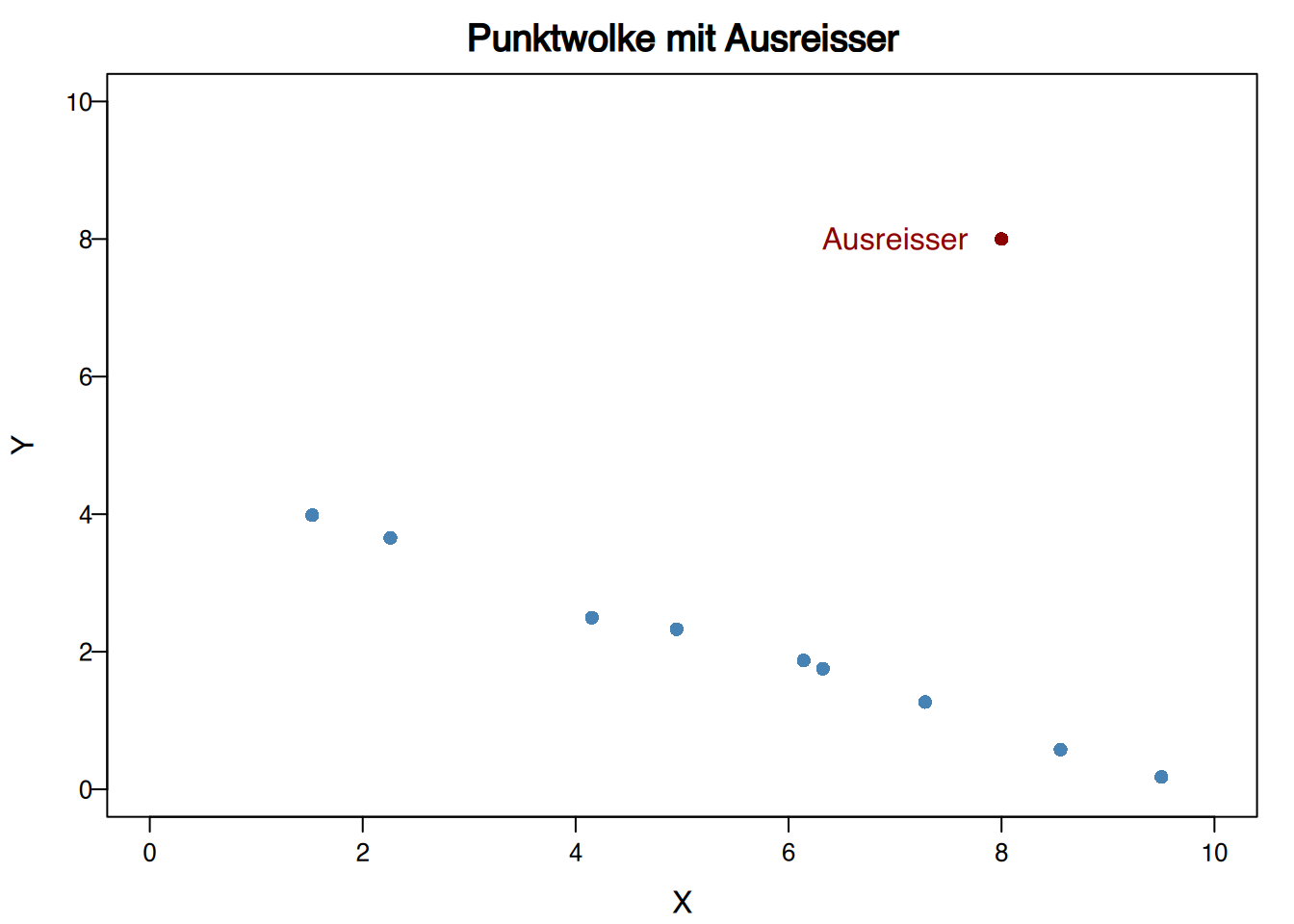
Ausreißer in Regressionsstudien können drastische Veränderungen in den Regressionsmodellen hervorrufen.
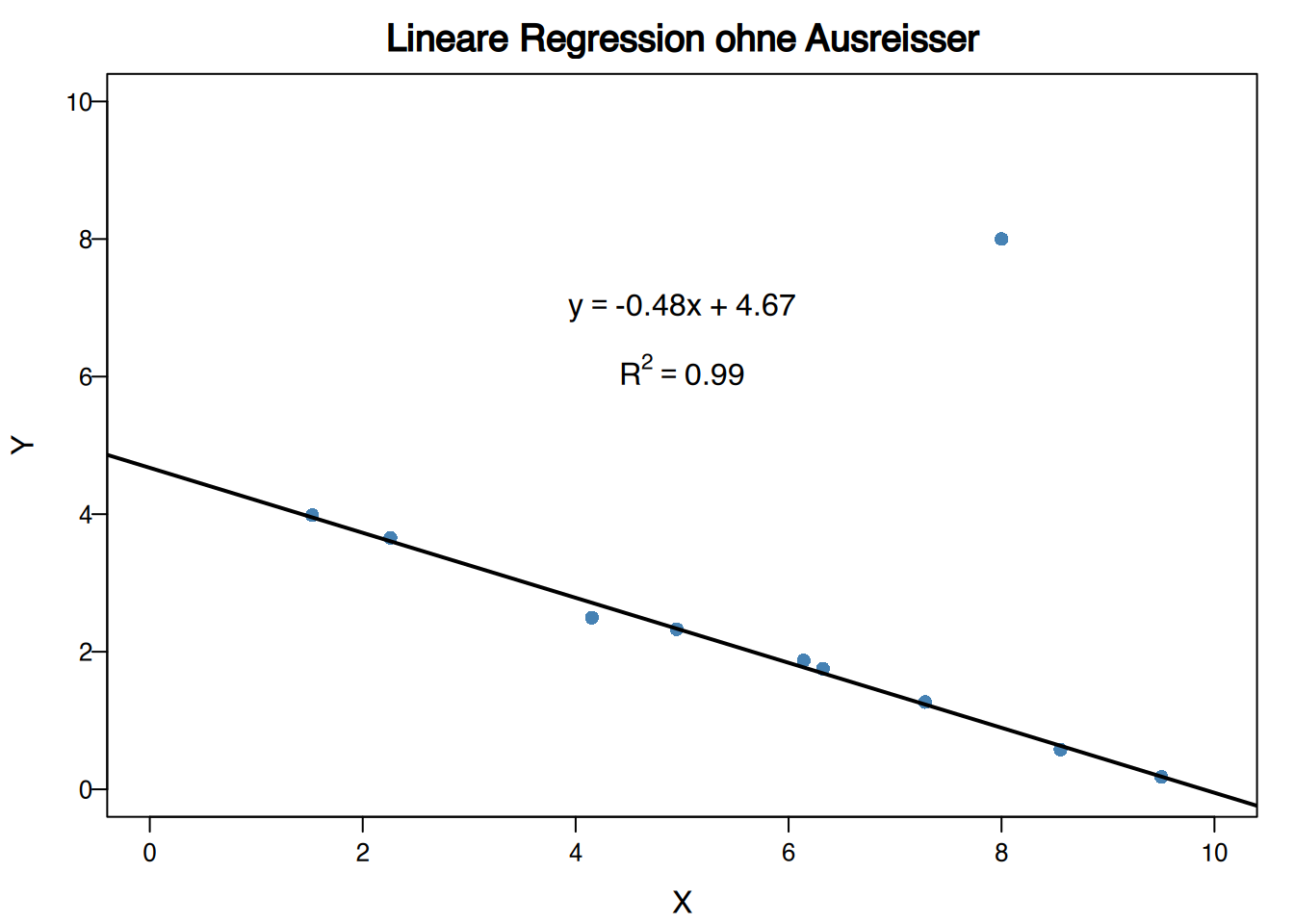
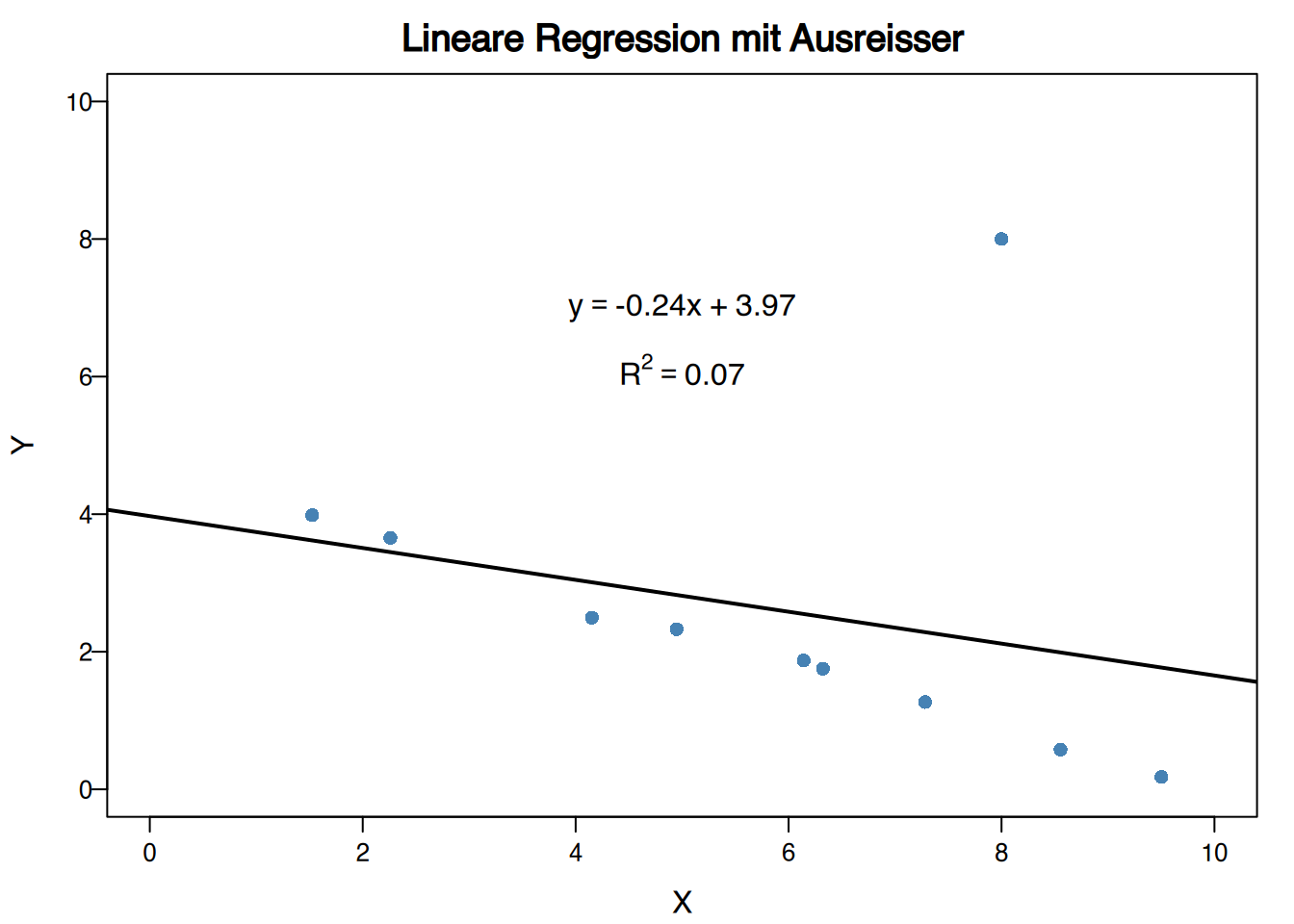
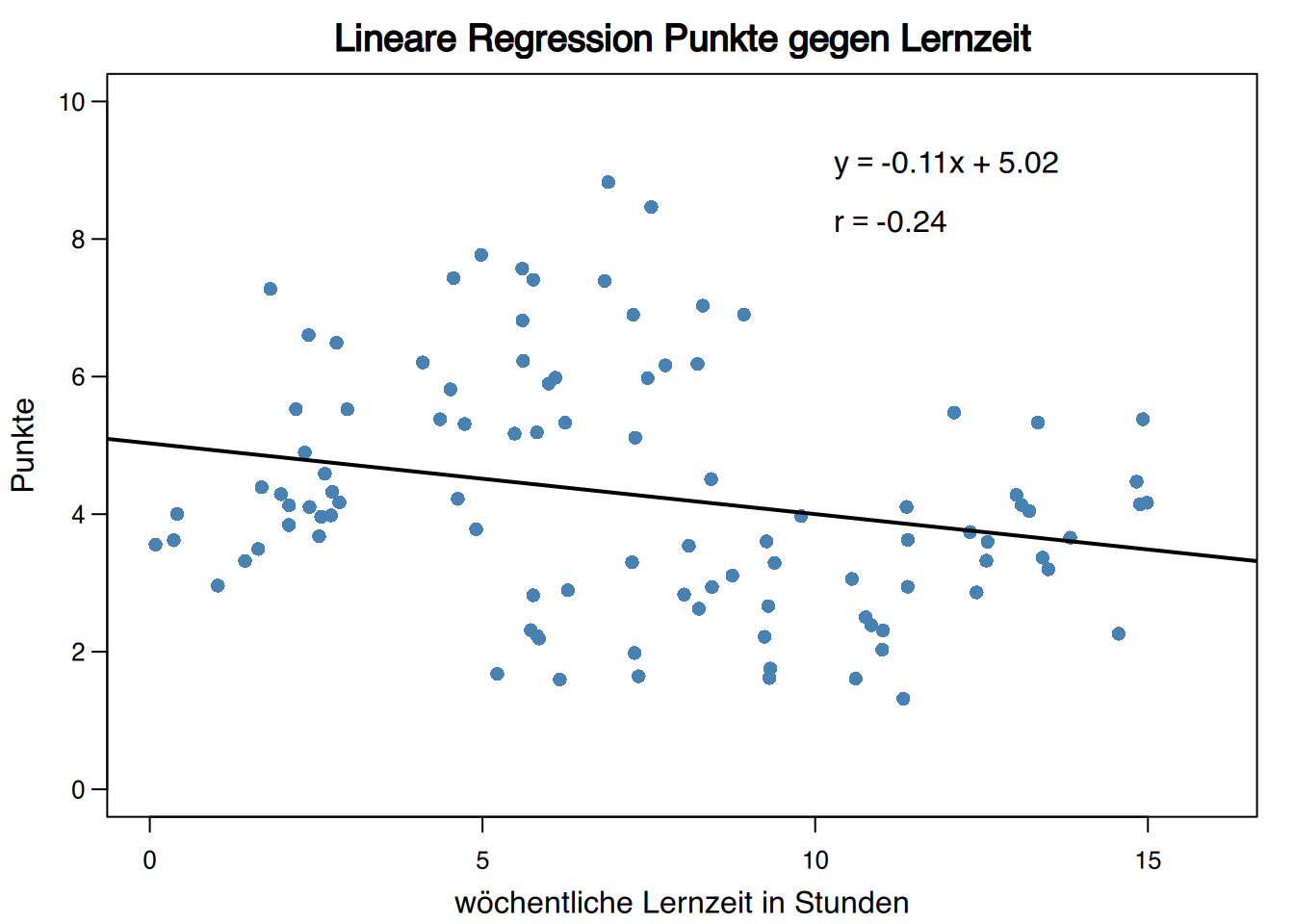
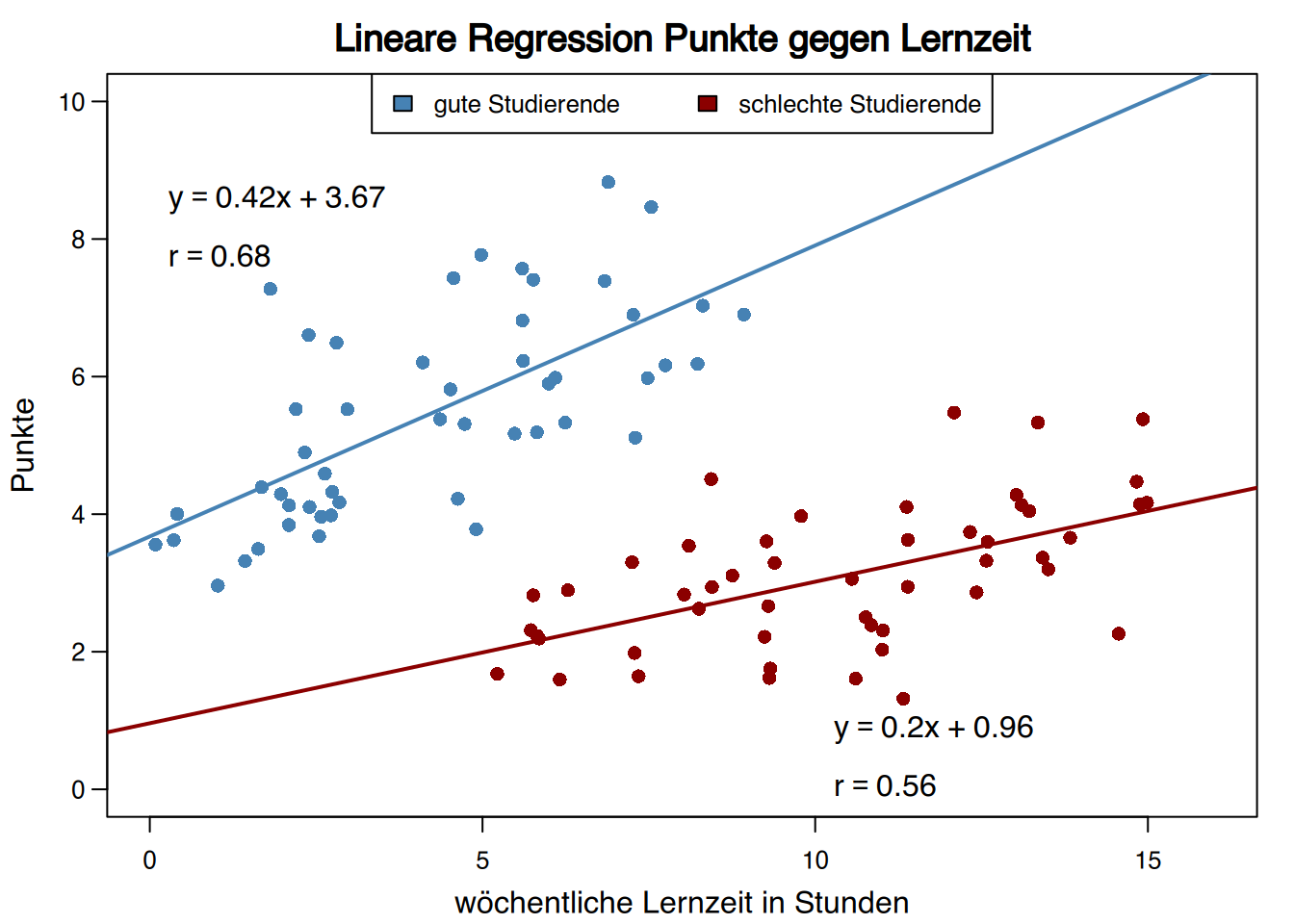
4.7.5 Simpsons Paradox
Manchmal verschwindet ein Trend oder kehrt sich sogar um, wenn man die Probe nach einer qualitativen Variable aufteilt, die mit der abhängigen Variablen zusammenhängt. Dies wird als Simpsons Paradox bezeichnet.