1 Einführung
1.1 Was ist Statistik?
Definition “Statistik”
Die Statistik ist ein mathematisches Gebiet, das sich mit der Sammlung, Zusammenfassung, Analyse und Interpretation von Daten befasst. Ihr Zweck besteht darin, Informationen aus Daten zu extrahieren, um Entscheidungen zu treffen.
Die Statistik spielt eine wichtige Rolle in jeder wissenschaftlichen oder technischen Disziplin, die mit Datenarbeit zu tun hat, besonders bei großen Datenvolumen, wie z.B. Physik, Chemie, Medizin, Psychologie, Wirtschaft oder Sozialwissenschaften.
Statistik…
- verschafft Überblick.
- bringt Ordnung ins Chaos.
- gibt Sicherheit.
- quantifiziert mögliche Fehler.
- ermöglicht Entscheidungen.
1.1.1 Warum ist Statistik notwendig?
Eine sich ändernde Welt: Wissenschaftler versuchen die Welt zu studieren. Die Welt ist hoch variabil, was es erschwert, das Verhalten von Dingen vorherzusagen.
Variabilität: Diese Variabilität ist der Grund, warum Statistik existiert. Sie dient als Brücke zwischen der realen Welt und den mathematischen Modellen, die diese Welt erklären möchten. Die Statistik bietet eine Methode zur Beurteilung der Unterschiede zwischen Realität und theoretischen Modellen.
Evidenzbasierung: wissenschaftliche Beweise (Evidenz) sind mathematische Beweise. Wenn beispielsweise die Überlegenheit von Anwendung A gegenüber Anwendung B gezeigt werden soll, muss dies mathematisch erfolgen. Statistik ist ein Dialekt der Mathematik, der hierfür verwendet werden kann.
1.2 Population und Stichprobe
Definition “Population”
Eine Population ist eine Gruppe von Elementen (z.B. Menschen), die durch eine oder mehrere Eigenschaften definiert sind. Diese Eigenschaften treffen auf jedes Element zu und sind nur bei ihnen vorhanden.
Definition “Grundgesamtheit”
Die Anzahl der Individuen in einer Population wird als Grundgesamtheit bezeichnet und durch \(N\) dargestellt.
Manchmal sind nicht alle Individuen für die Studie erreichbar. Dann unterscheiden wir zwischen:
- Theoretischer Grundgesamtheit: Die Individuen, auf die wir die Studienergebnisse übertragen möchten.
- Beforschbare Grundgesamtheit: Die Individuen, die wirklich in der Studie erreichbar sind.
1.2.1 Vollerhebung
Wissenschaftlerinnen studieren ein Phänomen in einer Bevölkerungsgruppe, um es zu verstehen, um Wissen über es zu erlangen und es dadurch möglichst zu kontrollieren.
Allerdings ist ein vollständiges Verständnis der Grundgesamtheit nur dann möglich, wenn alle ihre Individuen studiert werden (so genannte “Vollerhebung”). Doch dies ist aus mehreren Gründen nicht immer möglich:
- Die Population ist zu groß, um sämtliche Individuen untersuchen zu können.
- Die Interventionen, denen die Individuen unterzogen werden, sind gefährlich oder schädlich.
- Die Kosten – sowohl in Bezug auf Geld als auch Zeit –, die notwendig wären, um alle Individuen in der Bevölkerung zu studieren, sind unverhältnismäßig hoch.
1.2.2 Stichproben
Wenn es nicht möglich oder zu aufwendig ist, alle Individuen einer Population zu studieren, untersuchen wir nur eine Teilmenge von ihnen.
Definition “Stichprobe”
Eine Stichprobe ist eine Teilmenge der Population.
Definition “Stichprobenumfang”
Die Anzahl der Individuen in einer Stichprobe wird als Stichprobenumfang bezeichnet und mit \(n\) dargestellt.
Definition “Proband”
Probanden sind Menschen, die sich freiwillig dazu bereit erklärt haben, an einer Studie teilzunehmen.
Im Allgemeinen werden Studien anhand von Stichproben, die aus der Grundgesamtheit entnommen wurden, durchgeführt.
Zwar bieten die Ergebnisse einer Stichprobenanalyse nur Annäherungen über die Gegebenheiten in der Grundgesamtheit, doch in den meisten Fällen ist dies ausreichend.
1.2.3 Bestimmung des Stichprobenumfangs
Eine der interessantesten Fragen, die sich stellen, lautet:
Wie viele Probanden werden benötigt, um eine Stichprobe zu ziehen, die annehmbare Aussagen über die Grundgesamtheit zulässt?
Die Antwort hängt von mehreren Faktoren ab, wie z.B. der Variabilität innerhalb der Population oder der gewünschten Zuverlässigkeit für Schlussfolgerungen über die Grundgesamtheit. Im Allgemeinen gilt jedoch:
Je größer die Stichprobe ist, desto zuverlässiger werden die Schlussfolgerungen über die Grundgesamtheit sein, jedoch wird die Studie dadurch länger und teurer werden.
Beispiel
Um zu verstehen, was “ausreichende” Stichprobe bedeutet, können wir ein Beispiel mit einem Bild verwenden. Eine digitale Fotografie besteht aus vielen kleinen Punkten (Pixel), die in einer großen Matrix aus Zeilen und Spalten angeordnet sind. Je mehr Zeilen und Spalten vorhanden sind, desto höher die Auflösung des Bildes. In dieser Analogie entspricht das Bild der Grundgesamtheit und jeder Pixel stellt ein Individuum dar. Im Bild hat jeder Pixel eine Farbe, und es ist die Variabilität dieser Farben, die das Motiv des Bildes bildet.
Wie viele Pixel müssen wir in einer Stichprobe aufnehmen, um das Bild erkennen zu können?
Die Antwort hängt von der Variabilität der Farben im Bild ab. Wenn alle Pixelex im Bild dieselbe Farb haben, reicht nur ein Pixel aus, um das Motiv zu kennen. Wenn es eine hohe Variabilität in den Farben gibt, wird ein größerer Stichprobenumfang benötigt.
Die unten stehende Abbildung enthält eine kleine Stichprobe von Pixeln eines Fotos. Können Sie das Motiv des Bildes erkennen?
Wahrscheinlich ist es Ihnen schwer gefallen das Motiv zu erkennen, weil die Anzahl der ausgewählten Pixel in der Stichprobe zu gering ist, um die Farbenvielfalt im Bild zu verstehen.
Die nächste Abbildung unten enthält eine größere Stichprobe. Könnten Sie das Motiv des Bildes jetzt erkennen?
Der Vollständigkeit halber enthält nachfolgende Abbildung alle Pixeln der Grundgesamtheit.
Es ist häufig nicht erforderlich, alle Pixel eines Fotos zu verwenden, um das Motiv zu erkennen!
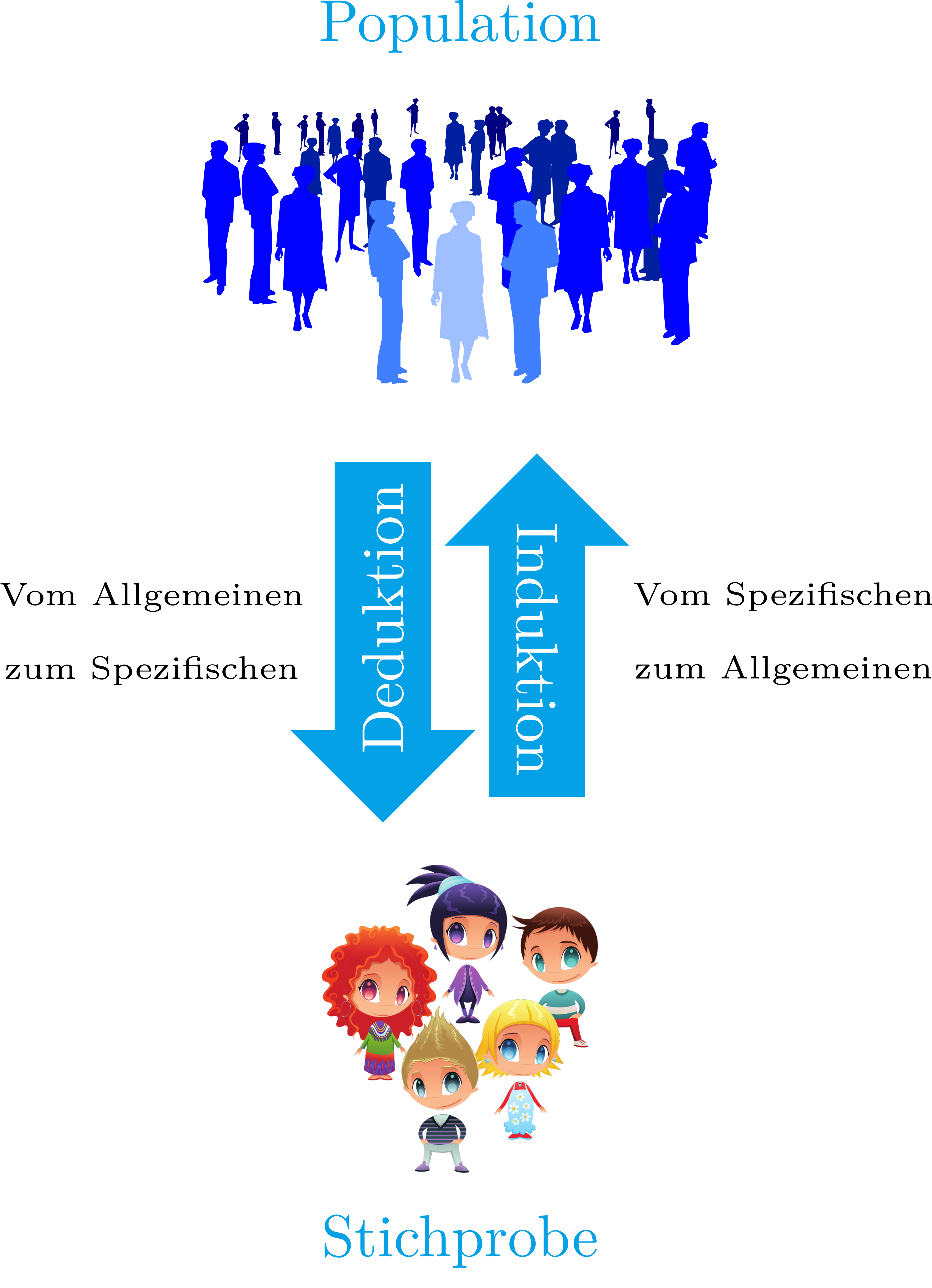
1.2.4 Typen des logischen Denkens
Deduktive Eigenschaften: Wir schließen vom Allgemeinen auf das Spezifische. Wenn etwas in der Population vorhanden ist, dann ist es auch in der Stichprobe vorhanden. Diese Art des Schlussfolgerns bringt keine wirklich neuen Kenntnisse, sondern verifiziert lediglich die Vorannahmen.
Induktive Eigenschaften: Wir schließen vom Spezifischen auf das Allgemeine. Wenn etwas in der Stichprobe vorhanden ist, muss es zwar nicht zwangsläufig in der Grundgesamtheit vorhanden sein (also vorsichtig mit Extrapolationen). Allerdings ist dies der einzige Weg, um neue Kenntnisse zu generieren.
Die Statistik basiert grundlegend auf der induktiven Schlußweise, weil sie die Informationen, die von Stichproben gewonnen wurden, verwendet, um Rückschlüsse über die Grundgesamtheit zu ziehen.
1.3 Sampling
Definition “Sampling”
Sampling beschreibt den Prozess, wie Elemente der Grundgesamtheit (Probanden) in die Stichprobe aufgenommen werden.
Um zuverlässige Informationen über die Grundgesamtheit zu erhalten, muss die Stichprobe repräsentativ sein (siehe hierzu von der Lippe (2002) (2011)). Das bedeutet, dass die Stichprobe die Variabilität der Grundgesamtheit auf kleinerem Maßstab nachbildet. Das Ziel des Sampling ist es, eine solche Stichprobe zu erhalten (was streng genommen nur bei Zufallsstichproben möglich ist, siehe von der Lippe (2002), (2010))!
1.3.1 Stichprobentypen
Es existieren viele Samplingmethoden, doch diese erzeugen immer eine der beiden nachfolgend genannten Stichprobentypen:
- Zufallsstichprobe: Die Individuen der Stichprobe werden zufällig ausgewählt. Jedes Mitglied der Grundgesamtheit hat dabei die selbe Chance, ausgewählt zu werden.
- keine Zufallsstichprobe: Die Individuen der Stichprobe werden nicht wirklich zufällig ausgewählt. Einige Mitglieder der Grundgesamtheit haben eine höhere Chance ausgewählt zu werden als andere.
Beispiel “Gelegenheitsstichprobe”
Sie wollen das Durchschnittseinkommen Ihrer Stadt ermitteln. Hierzu begeben Sie sich zum Hauptbahnhof, und befragen dort zufällig 100 Personen. In diesem Fall handelt es sich nicht um eine Zufallsstichprobe, da nicht alle Einwohner Ihrer Stadt (Grundgesamtheit) die selbe Chance hatten, von Ihnen befragt zu werden. Jedes Individuum, das nicht zu Ihrem Befragungszeitraum am Hauptbahnhof war, hatte eine Samplingchance von 0%.
Man spricht in diesem Fall auch von einer Gelegenheitsstichprobe, weil Sie “nur” diejenigen befragt haben, die “gerade da waren”.
Die meisten klinischen Studien sind Gelegenheitsstichproben. Man nimmt die Patienten, die gerade auf Station liegen.
Nur Zufallsstichproben können einer gewissen Repräsentativität nahe kommen.
Nicht-zufällige Stichproben eignen sich nicht zur Generalisierung, da sie wahrscheinlich von den Gegebenheiten in der Grundgesamtheit abweichen. Dennoch gibt es gerade in der klinischen Forschung häufig keine andere Möglichkeit zur Probandenrekrutierung.
1.3.2 Einfache Zufällige Stichprobenentnahme
Die beliebteste zufällige Samplingmethode ist die einfache zufällige Stichprobenentnahme, die folgende Eigenschaften aufweist:
- Chancengleichheit: Jedes Individuum in der Grundgesamtheit hat die selbe Chance zur Auswahl.
- Ziehen mit Zurücklegen: Die ausgewählten Individuen werden zurück in die Grundgesamtheit gegeben, bevor das nächste Individuum ausgewählt wird. Auf diese Weise bleibt die Population während der gesamten Entnahme unverändert.
- Unabhängigkeit: Die Auswahl eines Individuals ist unabhängig von der Auswahl anderer Individuen.
Die einzige Möglichkeit, eine Zufallsstichprobe zu ziehen, besteht darin, jedem Mitglied der Population eine eindeutige Identifikationsnummer zuzuordnen (was einem Zensus entspricht) und danach eine zufällige Auswahl vorzunehmen.
1.4 Statistische Variablen
In jeder statistischen Untersuchung interessieren wir uns für bestimmte Eigenschaften oder Merkmale von Individuen.
Definition “Statistische Variable”
Eine statistische Variable ist eine Eigenschaft oder ein Merkmal, das bei den Individuen einer Population gemessen wird.
Definition “Daten”
Die Daten sind die tatsächlichen Werte oder Ergebnisse, die für eine bestimmte Variable erhoben wurden.
1.4.1 Skalenniveau
Eine Skala dient dazu, irgend etwas einzuteilen, zu ordnen oder zu sortieren. In der Statistik unterscheiden sich die 3 Skalen in ihrem Informationsgehalt und in der Möglichkeit der statistischen Auswertung.
Laut der Art ihrer Werte und ihrem Skalenniveau lassen sich Variablen wie folgt unterscheiden:
- Qualitative Variablen: enthalten keine numerischen Werte, sondern Text.
- Nominal: Es gibt keine natürliche Reihenfolge zwischen den Werten. Beispiel: Haarfarbe oder Geschlecht.
- Ordinal: Es gibt eine natürliche Reihenfolge zwischen den Werten. Beispiel: Die Wochentage oder Schulnoten, oder alphabetisch sortierte Nachnamen.
- Nominal: Es gibt keine natürliche Reihenfolge zwischen den Werten. Beispiel: Haarfarbe oder Geschlecht.
- Quantitative Variablen: messen numerische Werte.
- Metrisch: alles, was man messen oder zählen kann.
- Diskret: Die Werte sind isolierte Zahlen (häufig ganze Zahlen). Beispiel: Die Anzahl der Kinder oder Autos in einer Familie.
- Kontinuierlich: Die Werte können jeden Wert in einem reellen Intervall annehmen. Beispiel: Körpergröße, Gewicht oder Alter eines Menschen.
- Diskret: Die Werte sind isolierte Zahlen (häufig ganze Zahlen). Beispiel: Die Anzahl der Kinder oder Autos in einer Familie.
- Metrisch: alles, was man messen oder zählen kann.
Qualitative und diskrete Variablen werden auch als kategoriale Variablen bezeichnet, und ihre Werte entsprechen Kategorien.
1.4.2 Nominalskala
Bei einer Nominalskala (lat. Nomen = Name, Bedeutung) entsprechen die erhobenen Werte nur einer Art von Etikett, “man gibt dem Kind einen Namen”, ohne dass irgendeine Wertigkeit oder Reihenfolge zugrunde liegt. Man kann auch sagen, dass Objekte oder Ereignisse in Kategorien eingeteilt werden, die sich gegenseitig ausschließen. Entweder hat ein Objekt ein bestimmtes Merkmal oder nicht.
Beispiele für nominalskalierte Daten
- Geschlecht (männlich, weiblich, \(\dots\))
- Augenfarbe (blau, grün, braun, \(\dots\))
- Körperbau (leptosom, pyknisch, athletisch, \(\dots\))
- bestanden (ja, nein)
1.4.3 Ordinalskala
Zusätzlich zu den Eigenschaften der Nominalskala unterliegen Daten einer Ordinalskala (lat. Ordinatus = Ordnung, ordentlich) einer vorgegebenen Reihenfolge oder Rangfolge.
Beispiele für ordinalskalierte Daten
- Steigerung (gut, besser, am besten)
- Schulnote (sehr gut, gut, befriedigend, ausreichend, mangelhaft, ungenügend)
- Siegerehrung (erster, zweiter, dritter)
1.4.4 metrische Skala
Das höchste Niveau besitzt die metrische Skala. Die Werte unterliegen nicht nur einer Reihenfolge, benachbarte Werte weisen auch gleiche Abstände auf.
Beispiele für metrische Daten
- Lebensalter in Jahren
- Gewicht in kg
- Länge in cm
- Lohn in Euro
Unterschied zwischen metrisch und ordinal
Die Abstände bei z.B. Schulnoten sind nicht gleich bzw. konstant! Darf man sich beispielsweise für die Note 1 nur drei Fehler erlauben, sind es bei der Note 2 schon sieben, und für die Note 3 schon zwanzig Fehler!
Die Leistungsdifferenz zwischen den Noten ist also nicht konstant!
1.4.5 Wählen der passenden Variablen
Manchmal kann eine Eigenschaft auf verschiedene Arten gemessen werden.
Beispiel Rauchen
Ob ein Mensch raucht oder nicht könnte auf folgende Weise gemessen werden:
- Raucht: Ja/Nein. (Nominal)
- Rauchstufe: Nichtrauchen/unüblich/mäßig/quasi/heftig. (Ordinal)
- Anzahl der Zigaretten pro Tag: 0,1,2,… (Diskret)
In solchen Fällen sind quantitative Variablen gegenüber qualitativen vorzuziehen, kontinuierliche Variablen werden den diskreten vorgezogen und ordinalen Variablen werden nominalen vorgezogen, da sie mehr Information liefern.
Laut ihrer Rolle in der Untersuchung unterscheiden wir:
- Unabhängige Variablen: Variablen, die nicht von anderen Variablen abhängig sind. Sie werden im Experiment oft manipuliert, um ihren Einfluss auf eine abhängige Variable zu beobachten. Sie werden auch als Prädiktionsvariablen bezeichnet.
- Abhängige Variablen: Variablen, die von anderen Variablen abhängig sind. Sie werden im Experiment nicht manipuliert und werden auch als Ergebnisvariablen bezeichnet.
Beispiel
In einer Studie über das Leistungsniveau von Studierenden in einem Kurs sind die Intelligenz der Schüler und die tägliche Lernzeit unabhängige Variablen, während die Note im Kurs eine abhängige Variable ist.
1.4.6 Arten statistischer Studien
- Experimentelle Studien: unabhängige Variablen werden manipuliert, um den Einfluss dieser Änderung auf die abhängigen Variablen zu beobachten.
Beispiel
In einer Studie über das Leistungsniveau von Studierenden bei einer Prüfung manipuliert die Dozentin bestimmte Rahmenbedingungen im Prüfungsraum. Sie bildet zwei oder mehr Gruppen mit unterschiedlichen Rahmenbedingungen (z.B. Kekse und Getränke zur Verfügung stellen) und vergleicht die Ergebnisse beider Gruppen.
- Nicht-experimentelle Studien: unabhängige Variablen werden nicht manipuliert. Das bedeutet nicht, dass es unmöglich wäre, sondern dass es entweder praktisch nicht möglich oder ethisch nicht vertretbar wäre.
Beispiel
In einer Studie interessieren sich Forschende für den Einfluss von Rauchen auf Lungenkrebs. Während es möglich ist, Menschen dazu zu bitten, zu rauchen, um den Einfluss dieser Tätigkeit auf ihre Lungen zu studieren, wäre es jedoch ethisch höchst fragwürdig. In diesem Fall können die Forschenden zwei Gruppen von Menschen untersuchen: Raucher und Nichtraucher, und deren Lungenfunktionen und Krebsquoten miteinander vergleichen.
Merke
Experimentelle Studien ermöglichen es, einen kausalen Zusammenhang zwischen Variablen zu identifizieren, während nicht-experimentelle Studien nur Beziehungen oder Verhältnisse zwischen Variablen identifizieren können.
1.4.7 Datentabelle
Die Variablen einer Studie werden bei jedem Individuum der Stichprobe gemessen. Das ergibt eine Datensammlung, die üblicherweise in tabellarischer Form angeordnet wird und als Datenstrom bezeichnet wird.
In dieser Tabelle enthält jede Spalte Informationen zu einer Variablen, während jede Zeile Informationen zu einem Individuum enthält.
Beispiel
| Name | Alter | Geschlecht | Gewicht (kg) | Größe (cm) |
|---|---|---|---|---|
| Anna Tomie | 42 | W | 85 | 179 |
| Bud Zillus | 31 | M | 115 | 173 |
| Dieter Mietenplage | 27 | M | 79 | 181 |
| Hella Scheinwerfer | 29 | W | 60 | 170 |
| Inge Danken | 36 | W | 57 | 158 |
| Jason Zufall | 54 | M | 96 | 174 |
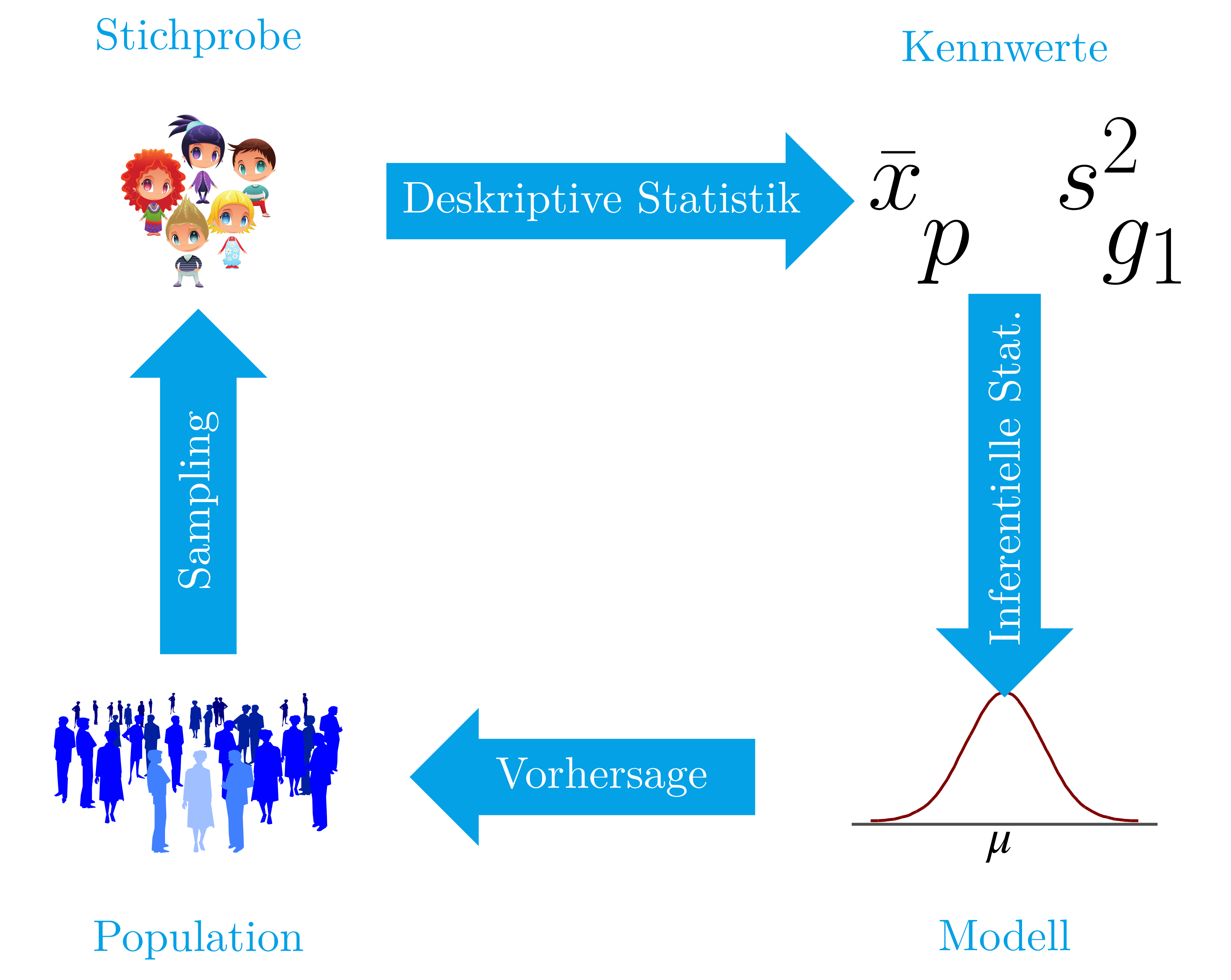
1.5 Phasen einer statistischen Untersuchung
Eine statistische Untersuchung durchläuft meist die folgenden Phasen:
- Die Studie beginnt mit einer vollständigen Planung, in der die Studienziele, die Population, die zu messenden Variablen und der benötigte Stichprobenumfang festgelegt werden.
- Anschließend wird eine Stichprobe aus der Population gezogen (Sampling), und die Variablen werden bei den Individuen der Stichprobe gemessen (was die Datentabelle ergibt).
- Der nächste Schritt besteht darin, die Informationen der Stichprobe zu beschreiben und zu zusammenzufassen. Das ist die Aufgabe der deskriptiven Statistik.
- Anschließend werden die erlangten Informationen auf ein mathematisches Modell projiziert, das beabsichtigt, die Vorgänge innerhalb der Grundgesamtheit zu erklären. Das Modell wird auf seine Gültigkeit überprüft. Dies ist Aufgabe der inferentiellen Statistik.
- Schließlich wird das validierte Modell verwendet, um Vorhersagen zu treffen und Schlussfolgerungen für die Grundgesamtheit zu ziehen.
