2 Häufigkeitsverteilungen
2.1 Deskriptive Statistik
Die deskriptive Statistik ist der Bereich innerhalb der Statistik, der sich mit dem Darstellen, Analysieren und Zusammenfassen von Informationen in einer Stichprobe beschäftigt. Nach dem Samplingprozess ist dies der nächste Schritt in jeder Studie und besteht meist aus folgenden Teilen:
- Ordnen und Klassifizieren der Daten sowie Einteilung in Gruppen.
- Tabellarische und grafische Darstellung der Daten nach ihrer Häufigkeit.
- Berechnung numerischer Maßzahlen, die die Informationen in der Stichprobe zusammenfassen (Stichprobenstatistiken).
die Stichprobenstatistik hat kein Inferenzpotential, weshalb keine Verallgemeinerungen auf die Population angewendet werden sollten!
2.2 Häufigkeitsverteilung
2.2.1 Stichprobenklassifizierung
Das Studium einer statistischen Variablen beginnt mit der Messung der Variable bei den Individuen der Stichprobe und der Klassifizierung der Werte. Es gibt zwei Weisen, Daten zu klassifizieren:
- Klassifizierung ohne Klassierung: Sortieren der Werte vom kleinsten zum größten (wenn eine Reihenfolge existiert). Diese Methode wird bei qualitativen Variablen und diskreten Variablen mit wenigen eindeutigen Werten verwendet.
- Klassifizierung mit Klassierung: Gruppieren der Werte in Intervalle (Klassen) und Sortieren dieser Intervalle vom kleinsten zum größsten. Diese Methode wird bei kontinuierlichen Variablen und diskreten Variablen mit vielen eindeutigen Werten verwendet.
2.2.2 Häufigkeiten
Bei einer Stichprobe mit \(n\) Werten der Variable \(X\) können wir für jedes \(x_{i}\) bestimmen:
- Absolute Häufigkeit (\(n_{i}\)): ist die Anzahl, mit der ein bestimmter Wert \(x_{i}\) in der Stichprobe auftritt.
- Relative Häufigkeit (\(f_{i}\)): ist das Verhältnis der Anzahl eines bestimmten Wertes \(x_{i}\) zur Gesamtanzahl der Beobachtungen in der Stichprobe.
\[ f_{i} = \frac{n_{i}}{n} \] - Kumulative absolute Häufigkeit (\(N_{i}\)): ist die Gesamtanzahl der Werte in der Stichprobe, die kleiner oder gleich \(x_{i}\) sind
\[ N_{i} = n_{1} + \dots + n_{i} \]
- Kumulative relativeHäufigkeit (\(F_{i}\)): ist das Verhältnis der kumulativen absoluten Häufigkeit zur Gesamtanzahl der Beobachtungen in der Stichprobe.
\[ F_{i} = \frac{N_{i}}{n} \]
2.2.3 Häufigkeitstabelle
Die Menge der Werte einer Variablen mit ihren jeweiligen Häufigkeiten nennt man Häufigkeitsverteilung, und sie wird üblicherweise als Häufigkeitstabelle dargestellt.
| Variable X | absolute Häufigkeit | relative Häufigkeit | kumulierte absolute Häufigkeit | kumulierte relative Häufigkeit |
|---|---|---|---|---|
| \(x_{1}\) | \(n_{1}\) | \(f_{1}\) | \(N_{1}\) | \(F_{1}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(x_{i}\) | \(n_{i}\) | \(f_{i}\) | \(N_{i}\) | \(F_{i}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(x_{k}\) | \(n_{k}\) | \(f_{k}\) | \(N_{k}\) | \(F_{k}\) |
Die Anzahl an Kindern wurde bei 25 Familien wie folgt erhoben:
1, 2, 4, 2, 2, 2, 3, 2, 1, 1, 0, 2, 2, 0, 2, 2, 1, 2, 2, 3, 1, 2, 2, 1, 2
Die Häufigkeitstabelle für die Anzahl an Kindern in der Stichprobe ist
| \(x_{i}\) | \(n_{i}\) | \(f_{i}\) | \(N_{i}\) | \(F_{i}\) |
|---|---|---|---|---|
| 0 | 2 | 0.08 | 2 | 0.08 |
| 1 | 6 | 0.24 | 8 | 0.32 |
| 2 | 14 | 0.56 | 22 | 0.88 |
| 3 | 2 | 0.08 | 24 | 0.96 |
| 4 | 1 | 0.04 | 25 | 1.00 |
| \(\sum\) | 25 | 1.00 |
2.2.4 Klassierung
Von 30 Studierenden wurde die Körpergröße wie folgt gemessen:
179, 173, 181, 170, 158, 174, 172, 166, 194, 185, 162, 187, 198, 177, 178, 165, 154, 188, 166, 171, 175, 182, 167, 169, 172, 186, 172, 176, 168, 187.
Die dazugehörige Häufigkeitstabelle wäre sehr lang, da sich nur sehr wenige Werte wiederholen. Es ist daher üblich, Werte aus bestimmten Bereichen in so genannten “Klassen” zusammenzufassen.
Eine Klasse ist die Menge sämtlicher Messwerte, die innerhalb festgelegter Grenzen liegt. Diese festgelegten Klassengrenzen werden durch den kleinsten und den größten Messwert einer Klasse gebildet. Die Klassenmitte ist das arithmetische Mittel aus beiden Klassengrenzen. Die Klassenbreite ist die Differenz der Klassengrenzen.
Bei der Klassierung sollten grundsätzlich folgende Regeln beachtet werden:
- die Anzahl der Klassen sollte nicht zu groß und nicht zu klein sein. Als Fausregel kann die Klassenanzahl auf \(\sqrt n\) bzw. \(log_{2}(n)\) gelegt werden. Für das Beispiel der Körpergrößen von 30 Studierenden gergeben sich \(\sqrt{30} = 5,48 \approx \mathbf{5}\) Klassen.
- die Klassen dürfen sich nicht überschneiden und müssen den gesamten Wertebereich abdecken. Ob die Intervalle links offen und rechts geschlossen sind oder umgekehrt, spielt keine Rolle.
- Der kleinste Wert muss in der ersten Klasse liegen und der größte Wert in der letzten.
- Die Klassengrenzen werden mir runde und eckigen Klammer angegeben. Eine eckige Klammer bedeutet, dass der nachstehen Wert in die Klasse eingeschlossen wird, eine runde Klammer schließt die nebenstehende Zahl aus.
Eine Häufigkeitstabelle der klassierten Körpergrößen mit 5 Klassen sieht so aus:
| \(x_{i}\) | \(n_{i}\) | \(f_{i}\) | \(N_{i}\) | \(F_{i}\) |
|---|---|---|---|---|
| (150,160] | 2 | 0.07 | 2 | 0.07 |
| (160,170] | 8 | 0.27 | 10 | 0.34 |
| (170,180] | 11 | 0.36 | 21 | 0.70 |
| (180,190] | 7 | 0.23 | 28 | 0.93 |
| (190,200] | 2 | 0.07 | 30 | 1.00 |
| ∑ | 30 | 1.00 |
2.2.5 Häufigkeitstabellen qualitativer Daten
Bei 30 Studierenden wurden die Blutgruppen wie folgt bestimmt:
A, B, B, A, AB, 0, 0, A, B, B, A, A, A, A, AB, A, A, A, B, 0, B, B, B, A, A, A, 0, A, AB, 0
Die Häufigkeitstabelle der Blutgruppen ist:
| \(x_{i}\) | \(n_{i}\) | \(f_{i}\) |
|---|---|---|
| 0 | 5 | 0.16 |
| A | 14 | 0.47 |
| B | 8 | 0.27 |
| AB | 3 | 0.10 |
| \(\sum\) | 30 | 1 |
Da es sich um nominale Werte handelt, gibt es keine natürliche Reihenfolge. Theoretisch gäbe es 24 Kombinationsmöglichkeiten, um eine Reihenfolge zu erzwingen. Diese sind aber alle aussagelos.
2.3 Diagramme
Häufigkeitsverteilungen werden üblicherweise auch grafisch dargestellt. Abhängig von dem Typ der Variablen und ob die Daten klassiert wurden, gibt es verschiedene Arten von Diagrammen:
- Säulendiagramm
- Histogramm
- Liniendiagramm
- Kreisdiagramm
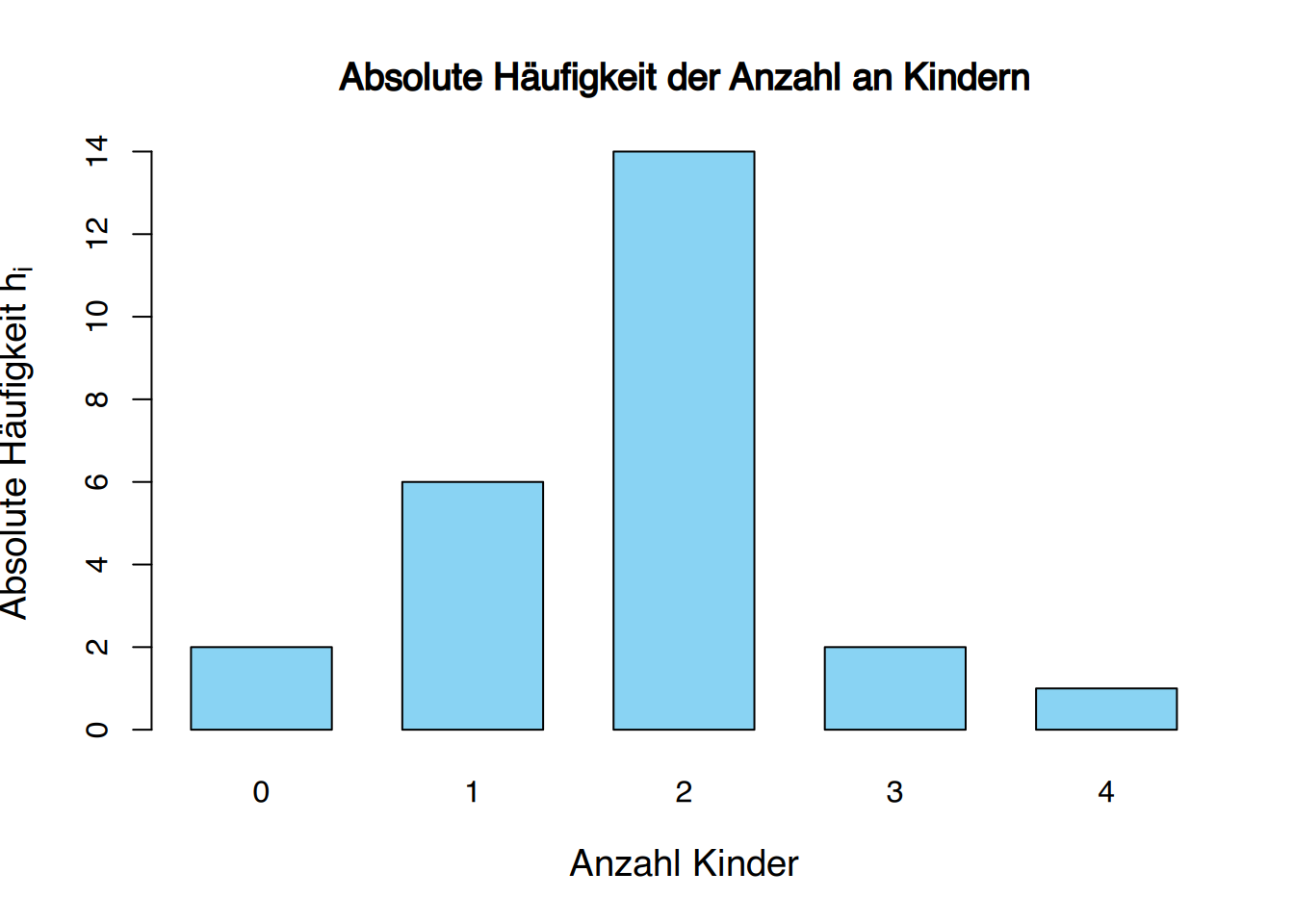
2.3.1 Säulendiagramm
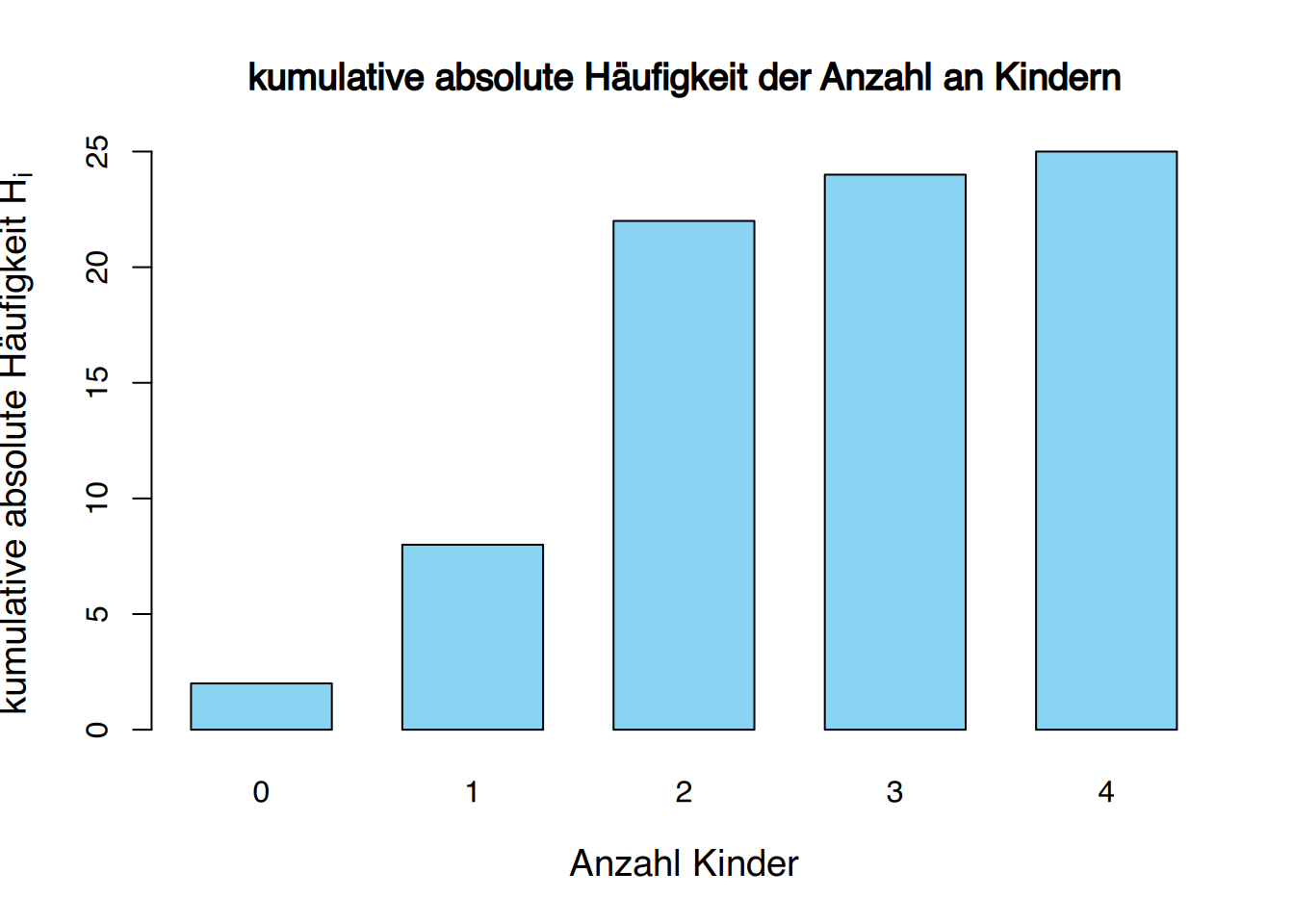
Ein Säulendiagramm besteht aus einer Reihe von Balken, einem für jeden Wert oder jede Kategorie der Variablen, die auf einem Koordinatensystem dargestellt sind. Üblicherweise werden die Werte oder Kategorien der Variable auf der \(x\)-Achse und die Häufigkeiten auf der \(y\)-Achse dargestellt. Für jeden Wert oder jede Kategorie der Variablen wird ein Balken in der Höhe seiner Frequenz gezeichnet. Die Breite des Balkens ist nicht wichtig, aber die Balken sollten klar voneinander getrennt sein.
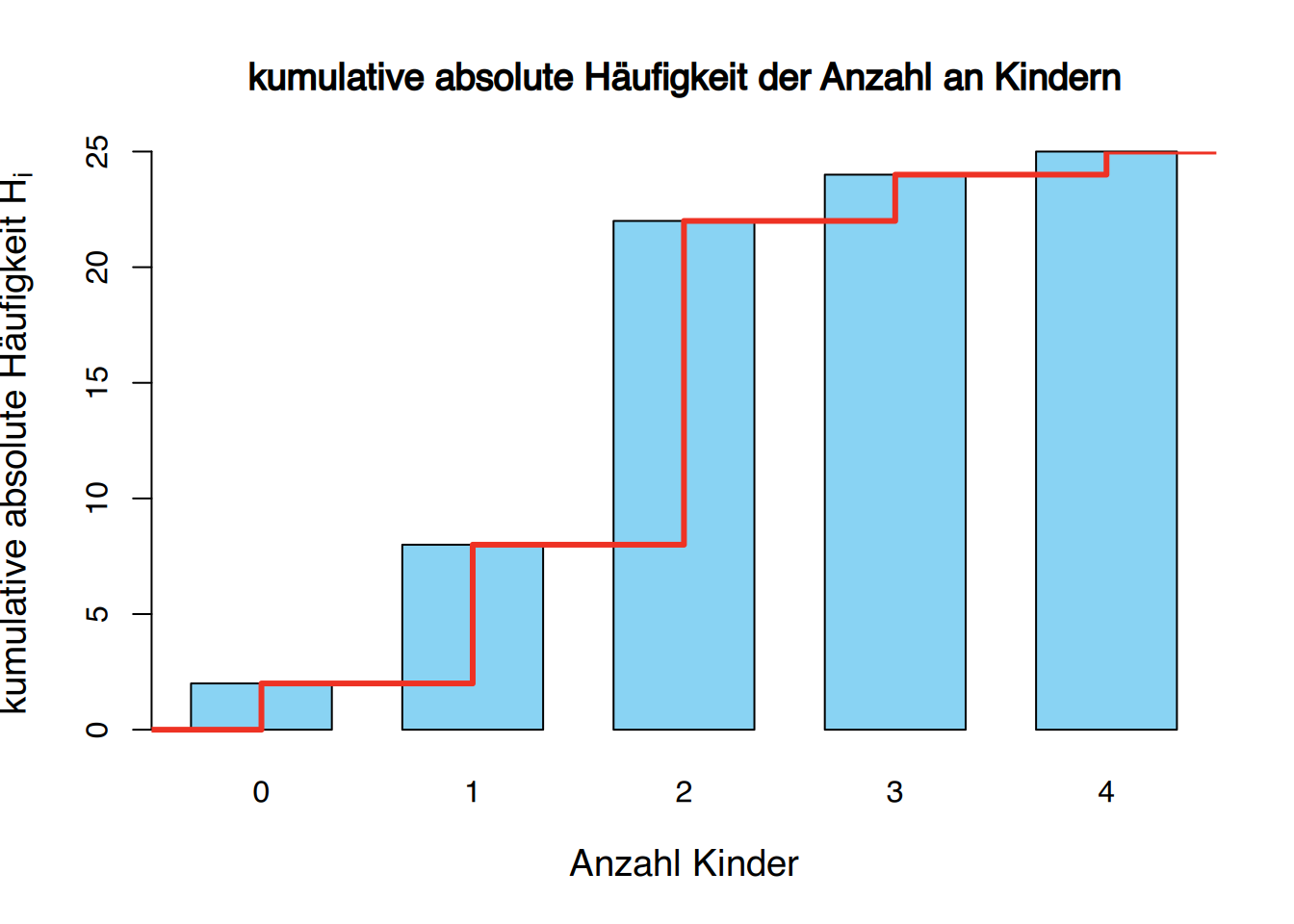
Abhängig von dem Typ der auf der \(y\)-Achse dargestellten Häufigkeit erhalten wir verschiedene Arten von Säulendiagrammen. Manchmal wird ein Polygon, bekannt als Frequenzpolygon, gezeichnet, indem die Spitzen jeder Bar durch gerade Linien verbunden werden.
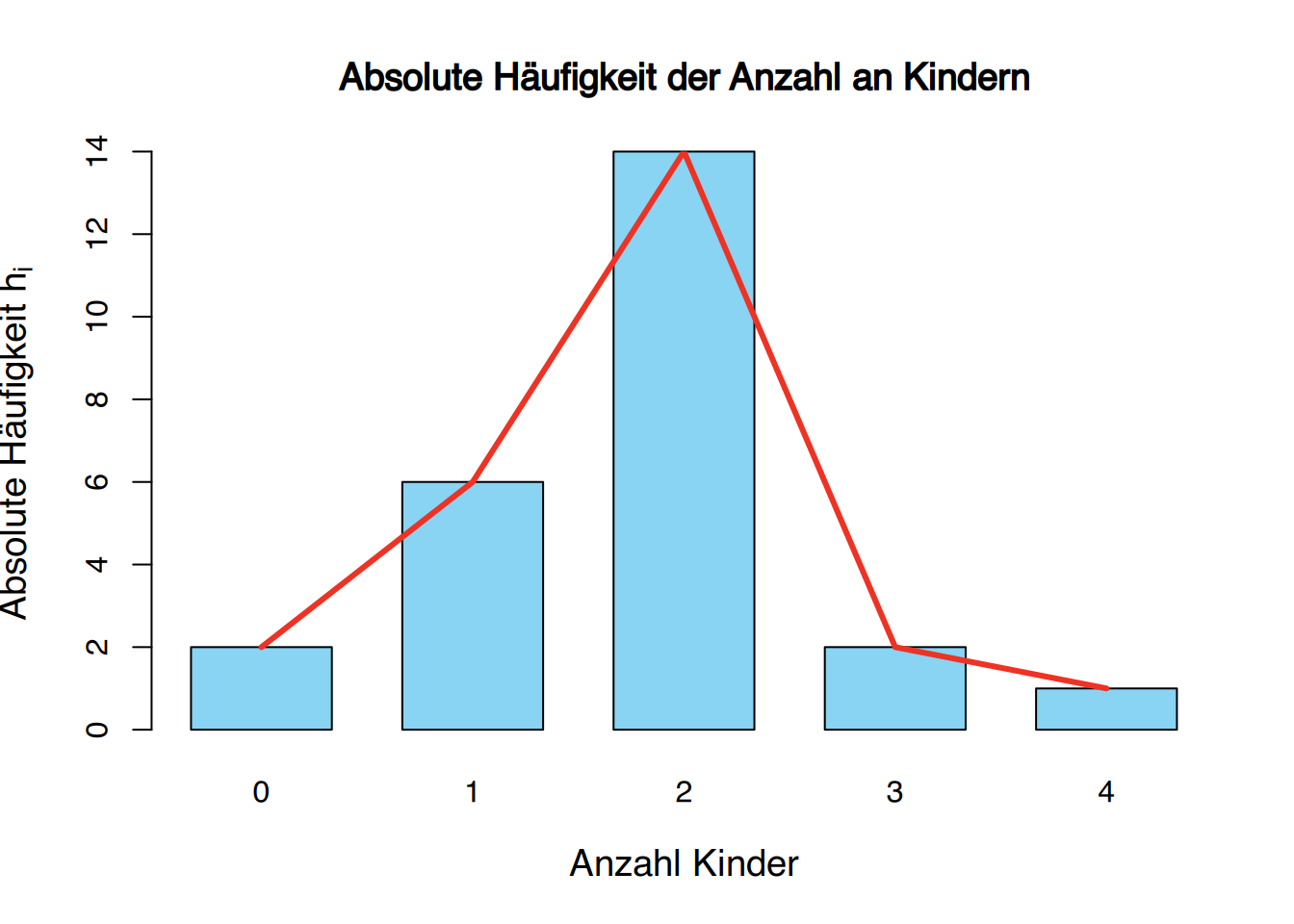
2.3.2 Histogramm
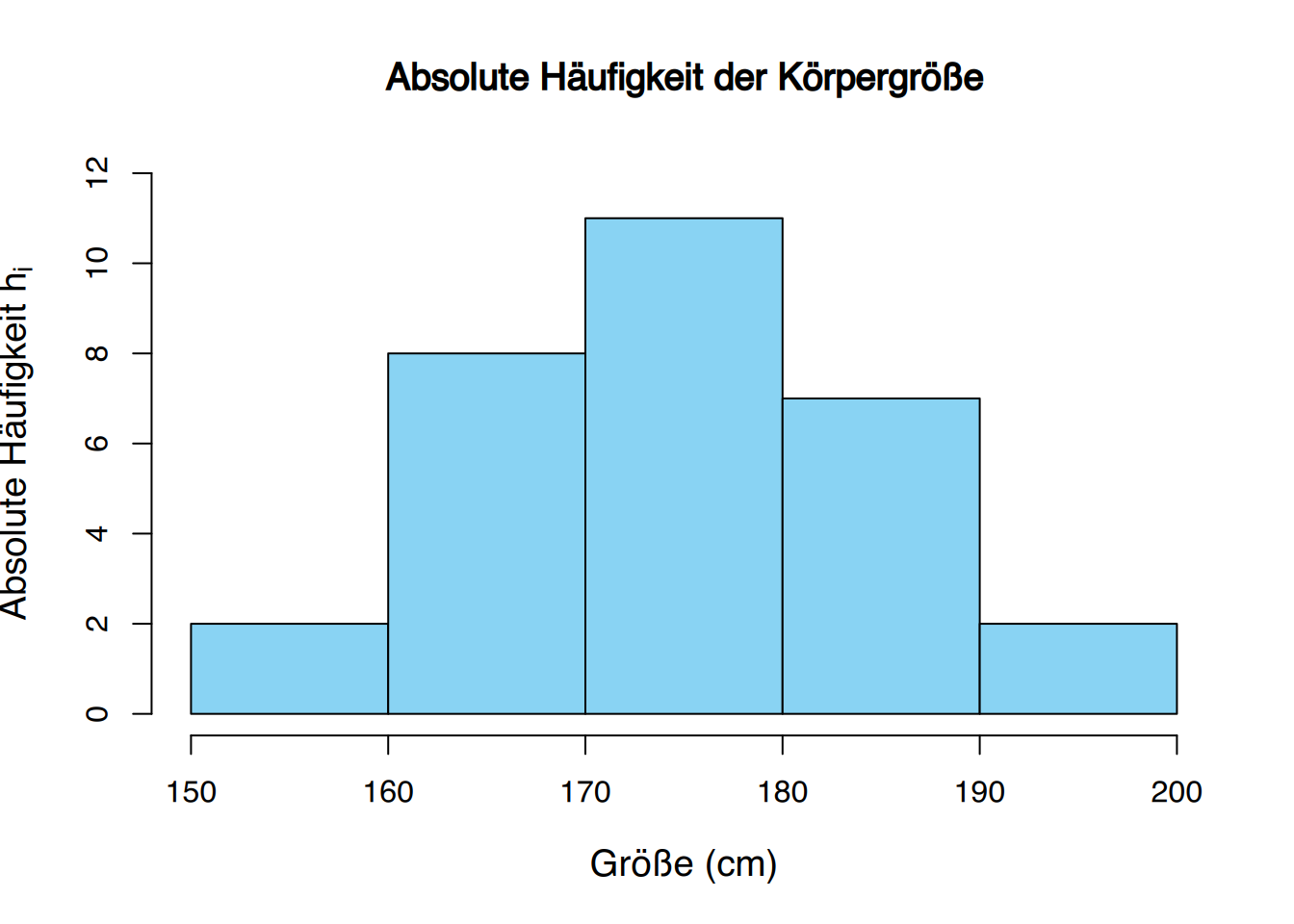
Ein Histogramm ist ähnlich wie ein Säulendiagramm, aber für klassierte Daten.
Die Klassen oder Gruppierungsintervalle werden üblicherweise auf der \(x\)-Achse dargestellt, und die Häufigkeiten auf der \(y\)-Achse. Für jede Klasse wird ein Balken in der Höhe seiner Frequenz gezeichnet.
Im Gegensatz zu Säulendiagrammen entspricht die Breite eines Balkens der Breite einer Klasse, und es gibt keinen Platz zwischen zwei aufeinanderfolgenden Balken. Abhängig von dem Typ der auf der \(y\)-Achse dargestellten Häufigkeit erhalten wir verschiedene Arten von Histogrammen. Manchmal wird ein Polygon, bekannt als Frequenzpolygon, gezeichnet, indem die Spitzen jeder Bar verbunden werden.
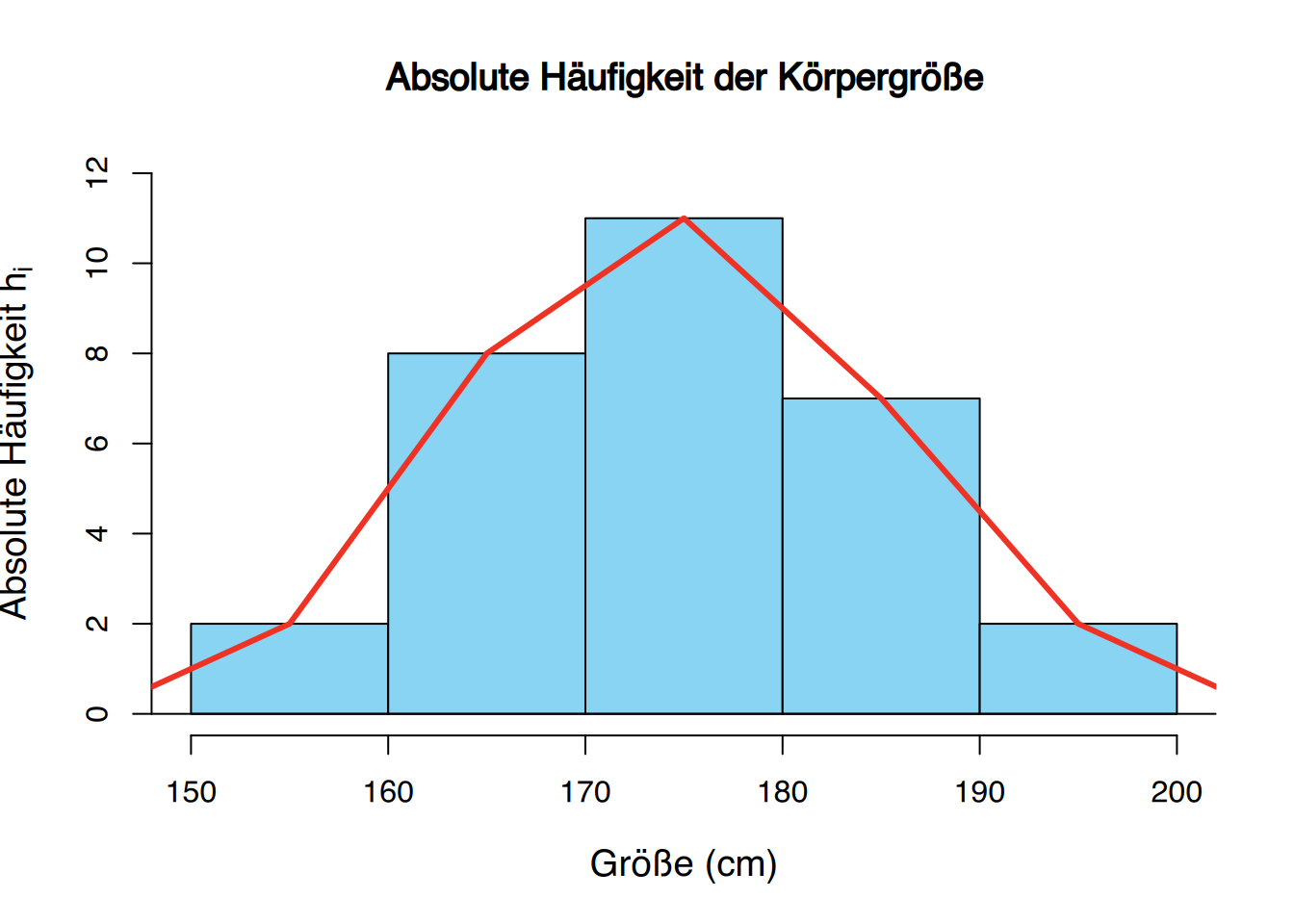
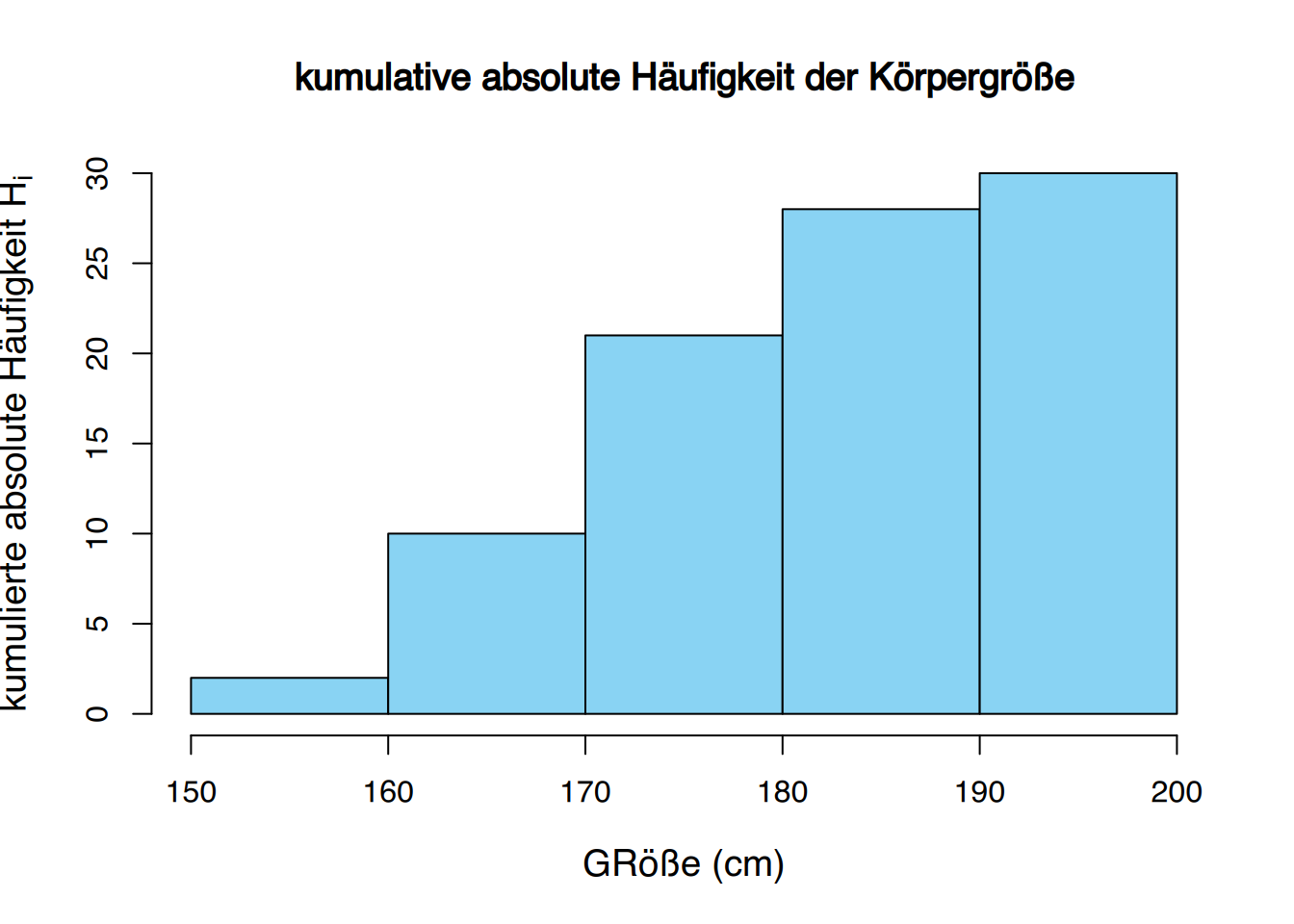
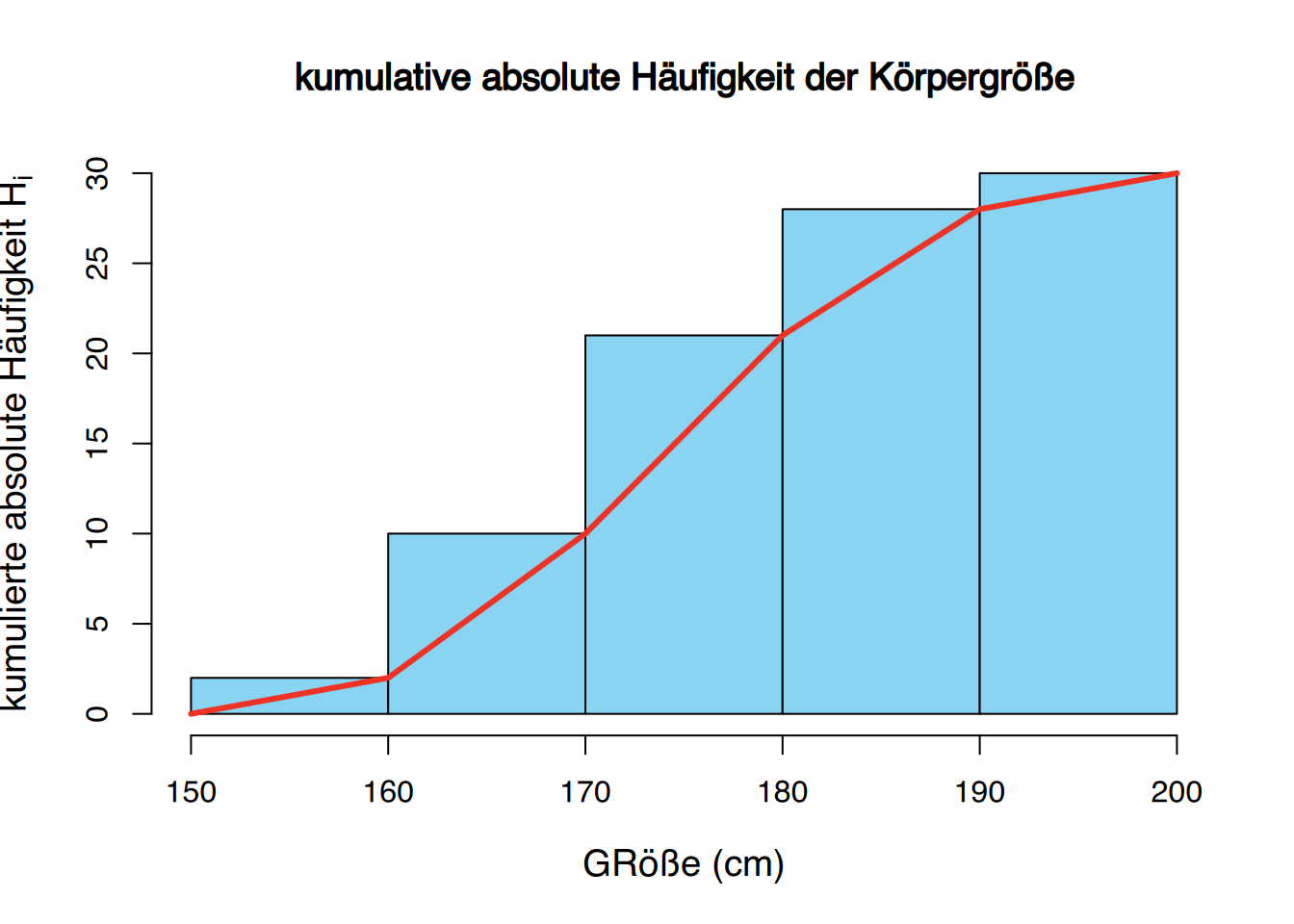
Das kumulative Häufigkeitspolynom (für absolute oder relative Häufigkeiten) wird als Ogive bezeichnet. Beachten Sie, dass in der Ogive die rechte obere Ecke jeder Bar mit der Linien verbunden wird, anstatt des mittleren Punkts, weil wir die akkumulierte Häufigkeit einer Klasse nur am Ende des Intervalls erreichen.
2.3.3 Kreisdiagramm
Ein Kreisdiagramm (auch Tortendiagramm) besteht aus einem Kreis, der in Scheiben geteilt ist, einer für jeden Wert oder jede Kategorie der Variablen. Jede Scheibe wird als Sektion bezeichnet, und ihr Winkel oder Gebiet ist proportional zur Häufigkeit des entsprechenden Wertes.
Tortendiagramme können absolute oder relative Häufigkeiten darstellen, aber nicht kumulative Häufigkeiten, und sie werden bei nominalen Variablen verwendet.
Für ordinal oder quantitative Variablen ist es besser, Säulendiagramme oder Histogramme zu verwenden, weil es einfacher ist, Unterschiede in einer Dimension (Länge der Balken) wahrzunehmen als in zwei Dimensionen (Gebiete der Sektionen).
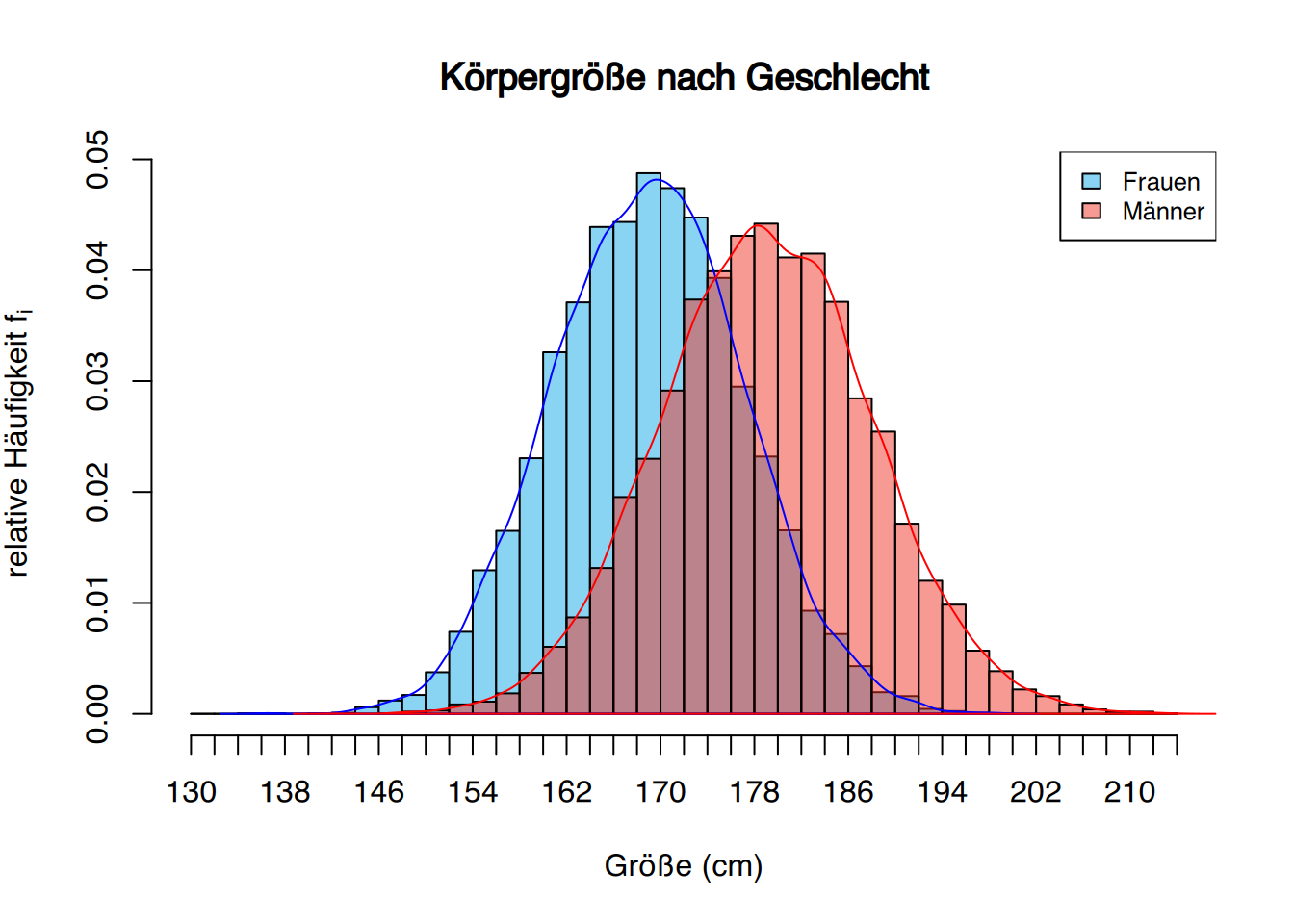
2.3.4 Verteilungsformen
Wenn wir metrische Daten erheben, wie z.B. die Anzahl der Krankenhausaufenthalte, dann stellen wir diese Daten als Häufigkeitstabelle oder Säulendiagramm dar.
Dabei nehmen die Diagramme häufig typische Formen an.
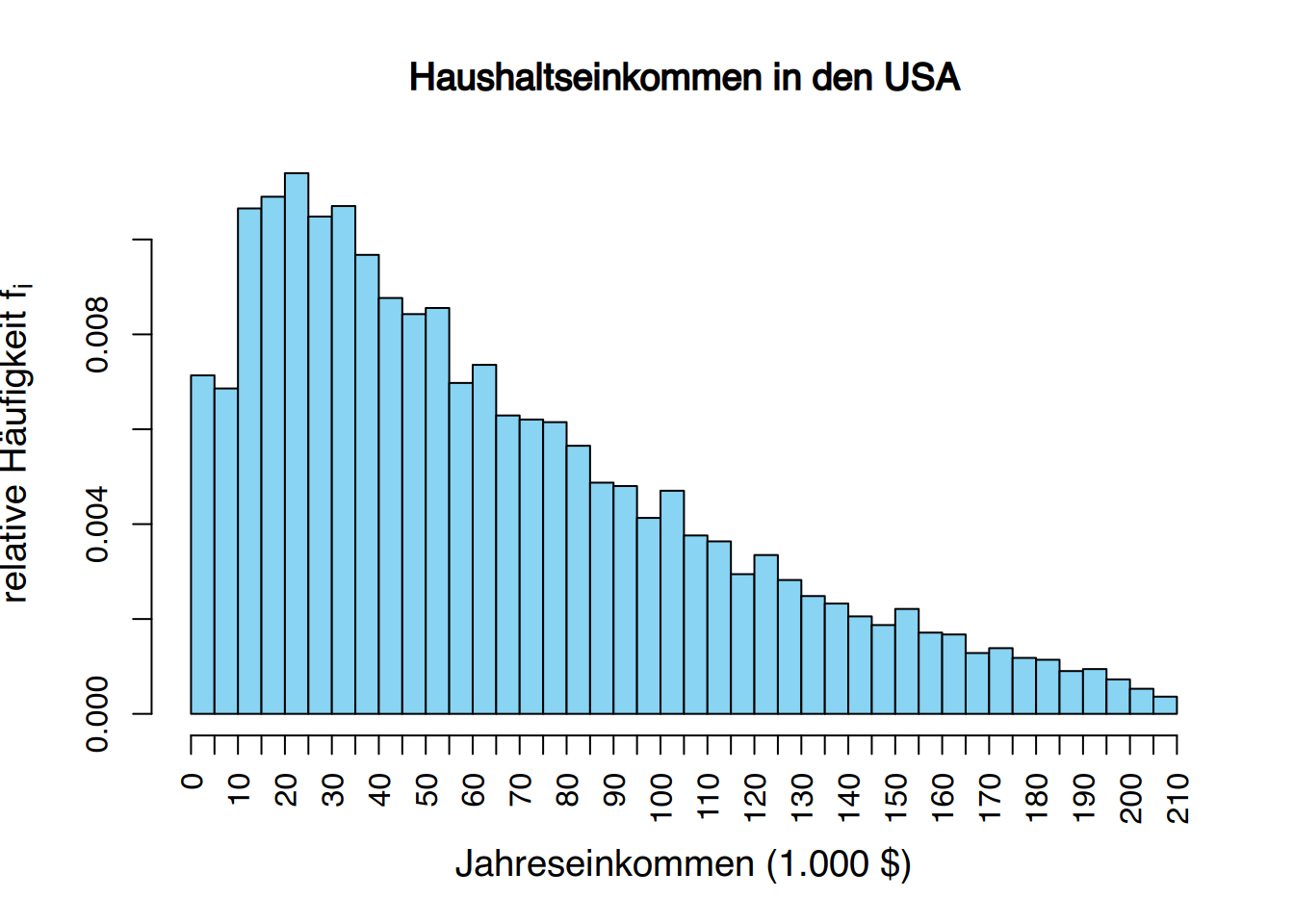
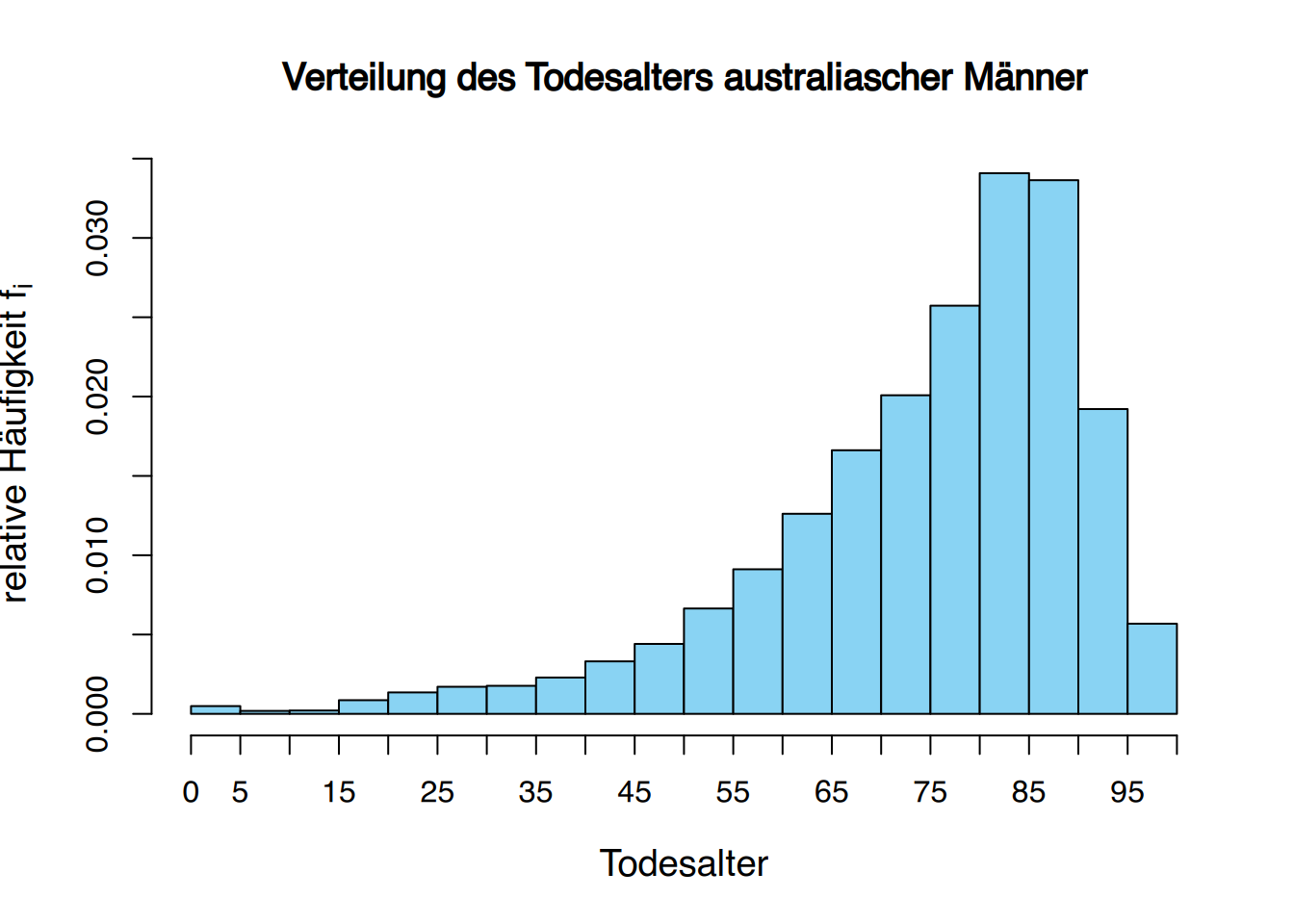
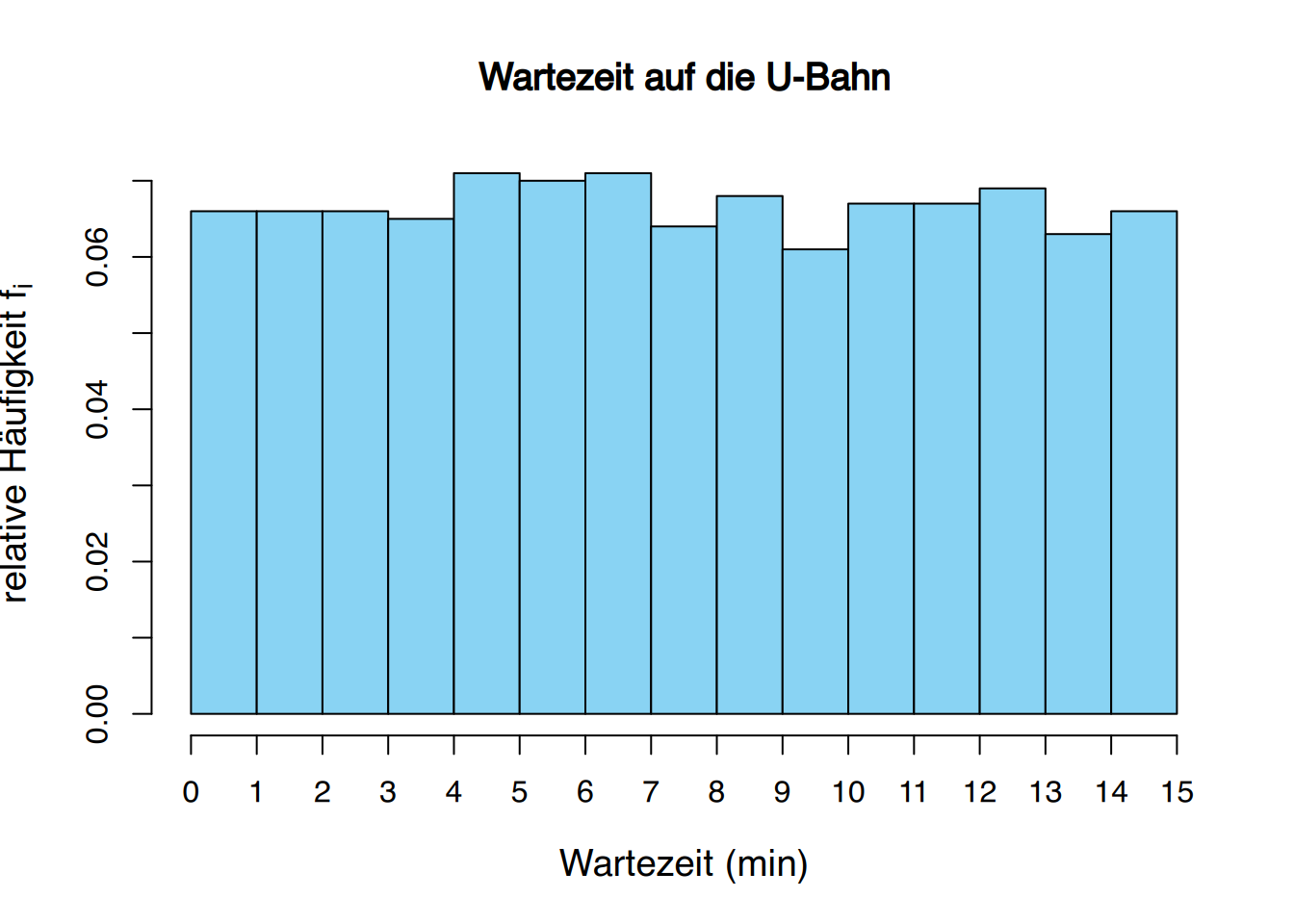
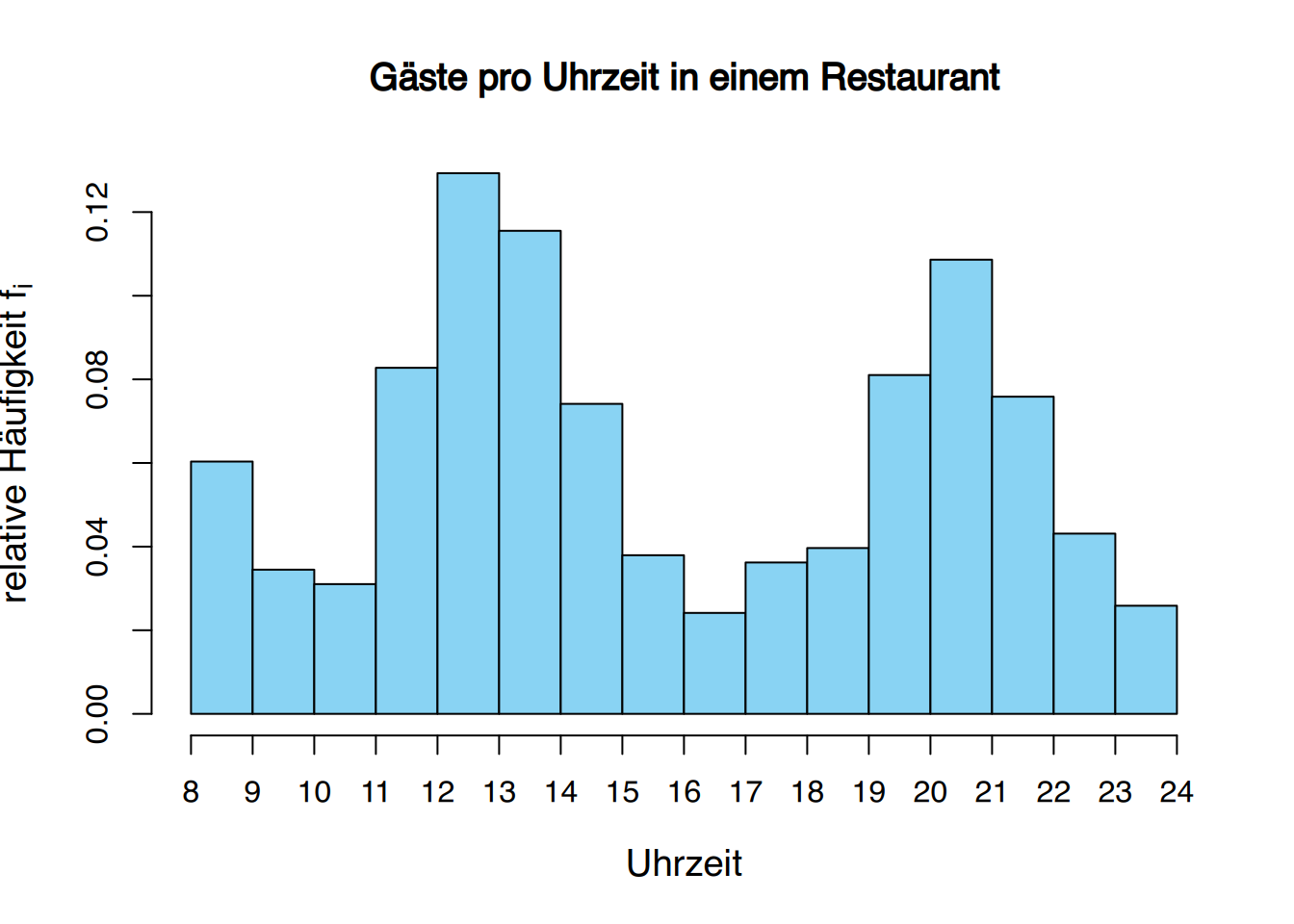
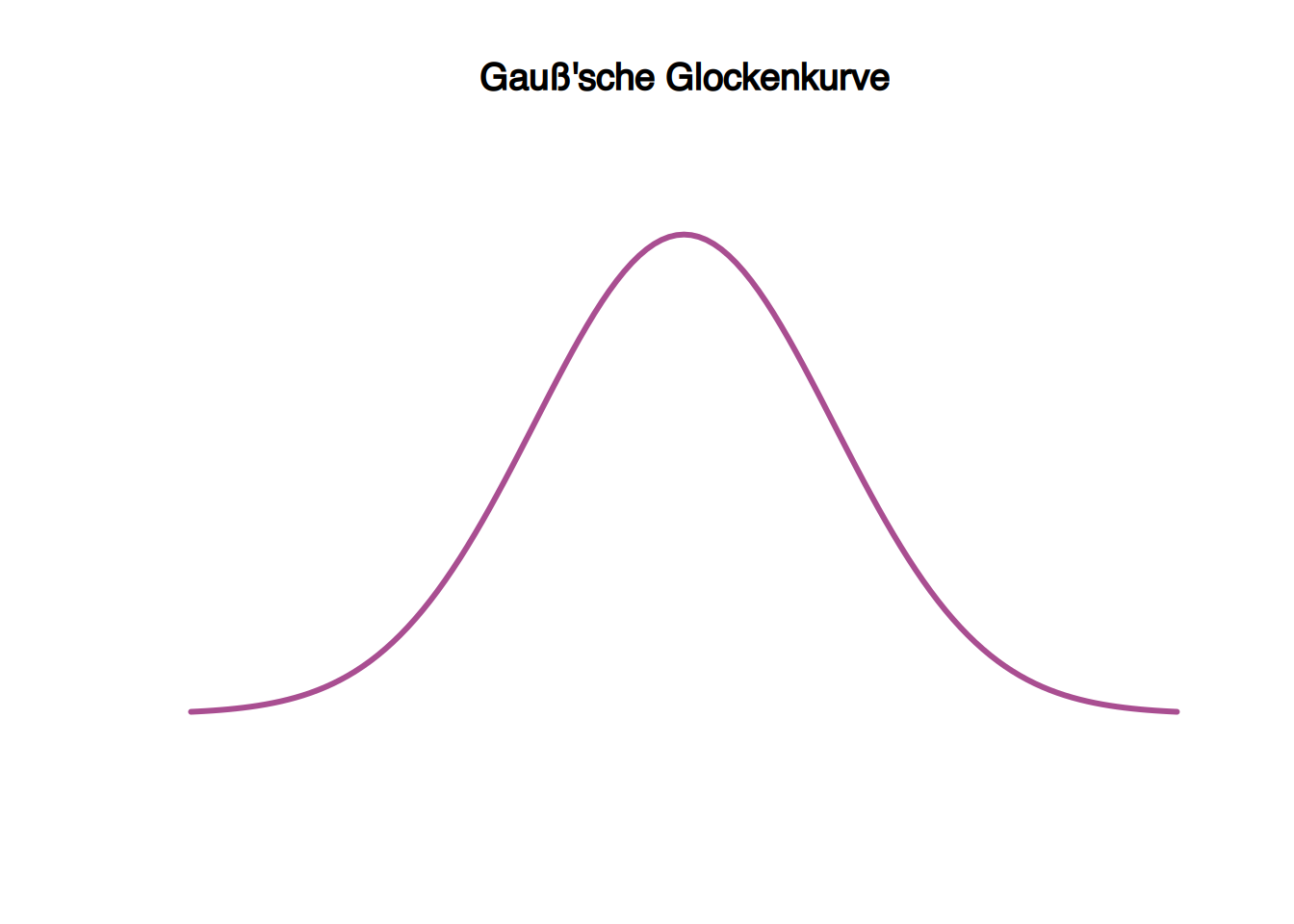
2.3.5 Glockenkurven
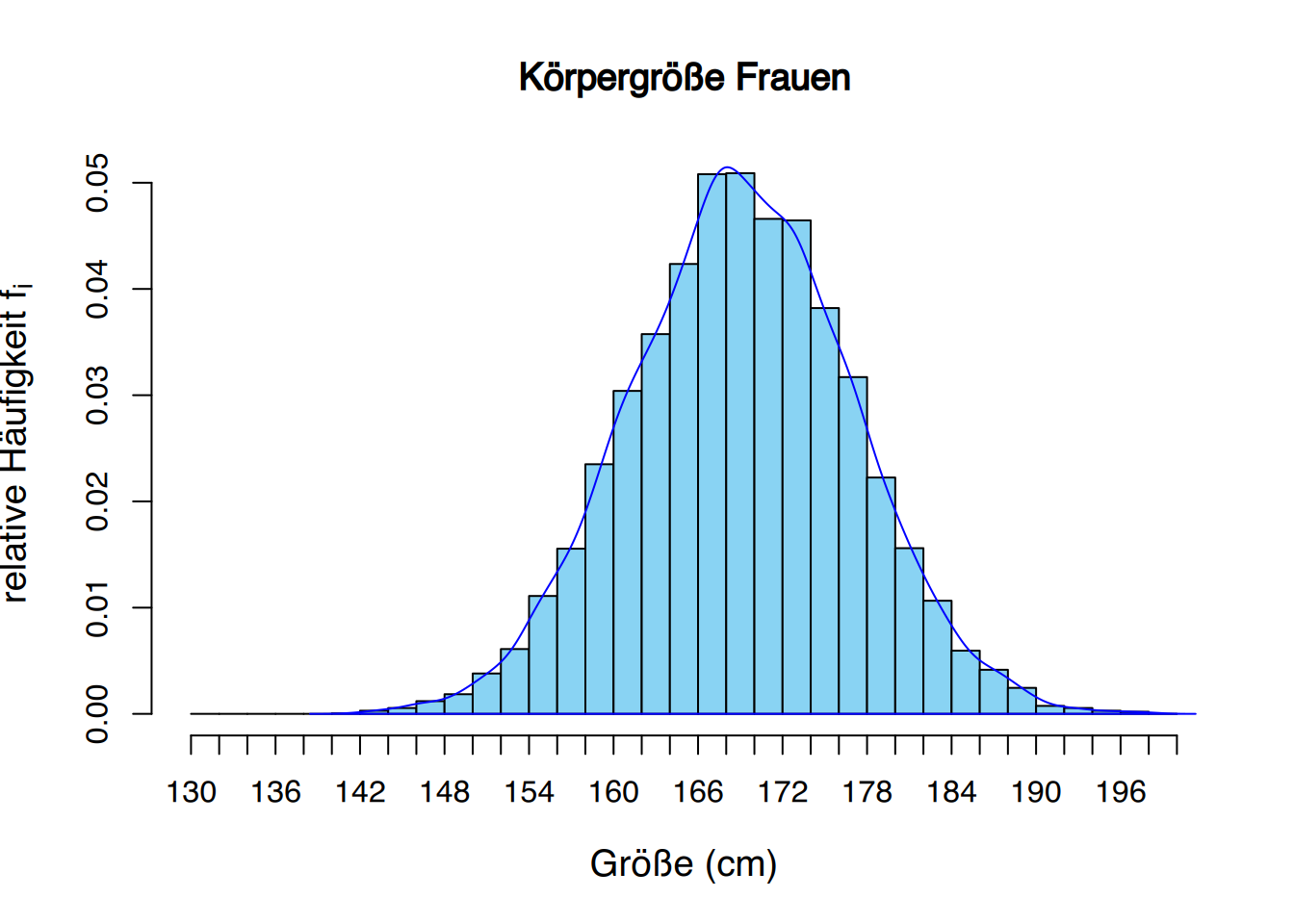
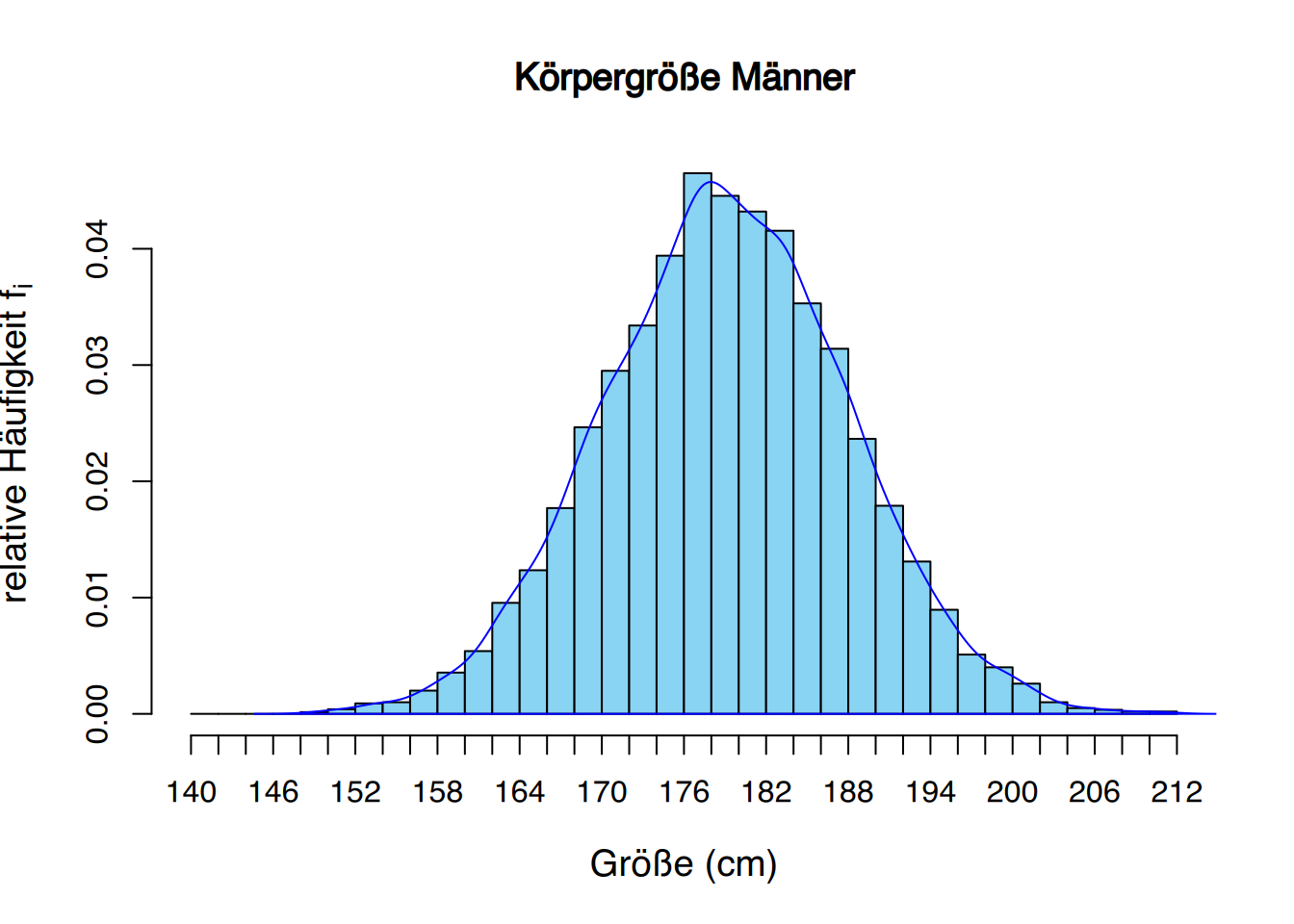
Die Glockenkurvenverteilung tritt so häufig in der Natur auf, dass sie als Normalverteilung oder Gaußsche Verteilung bekannt ist.
2.3.6 Liniendiagramme
Liniendiagramme (auch Polygonzüge) eignen sich, um zeitliche Verläufe darzustellen – und sollten auch nur dafür verwendet werden.
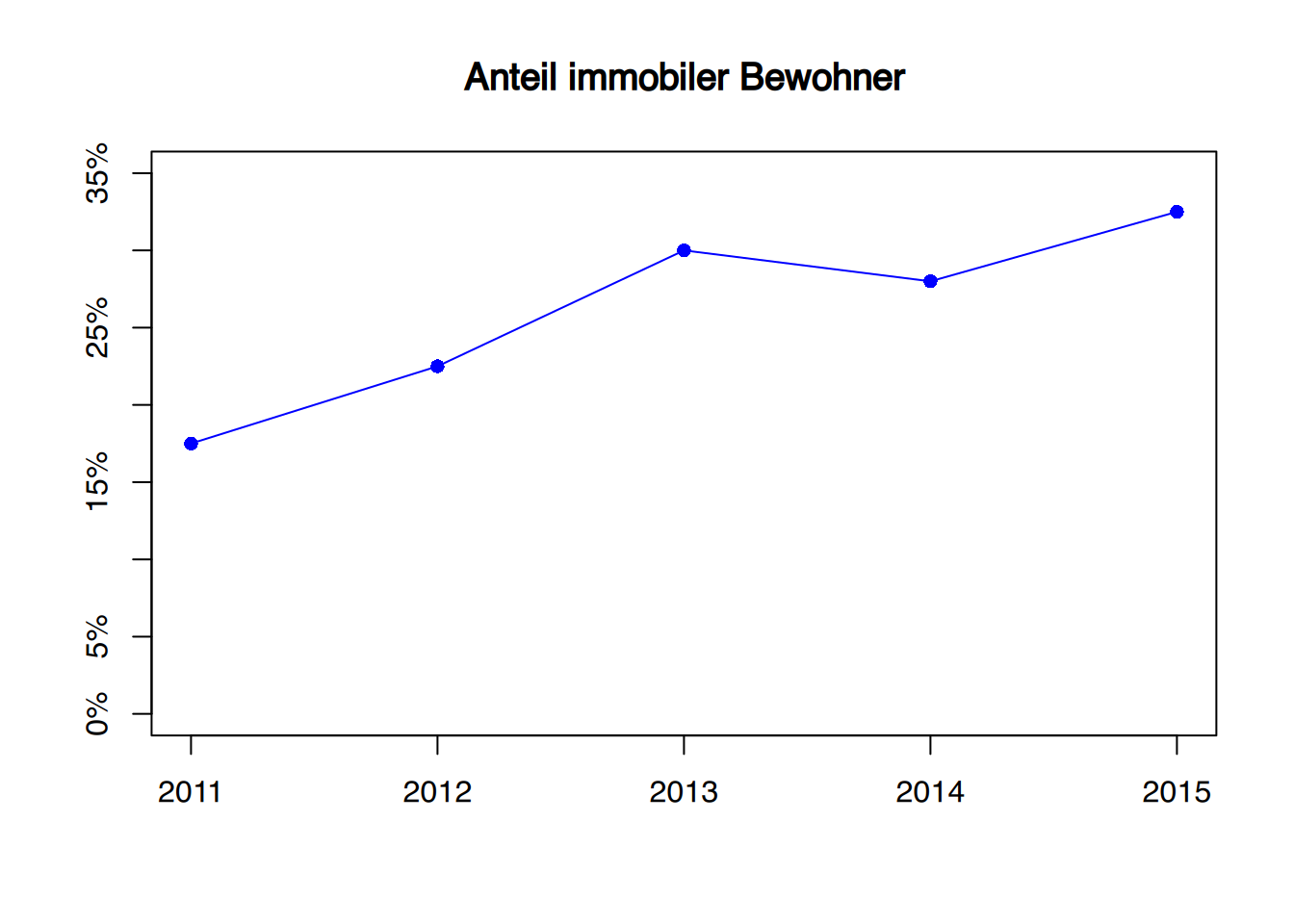
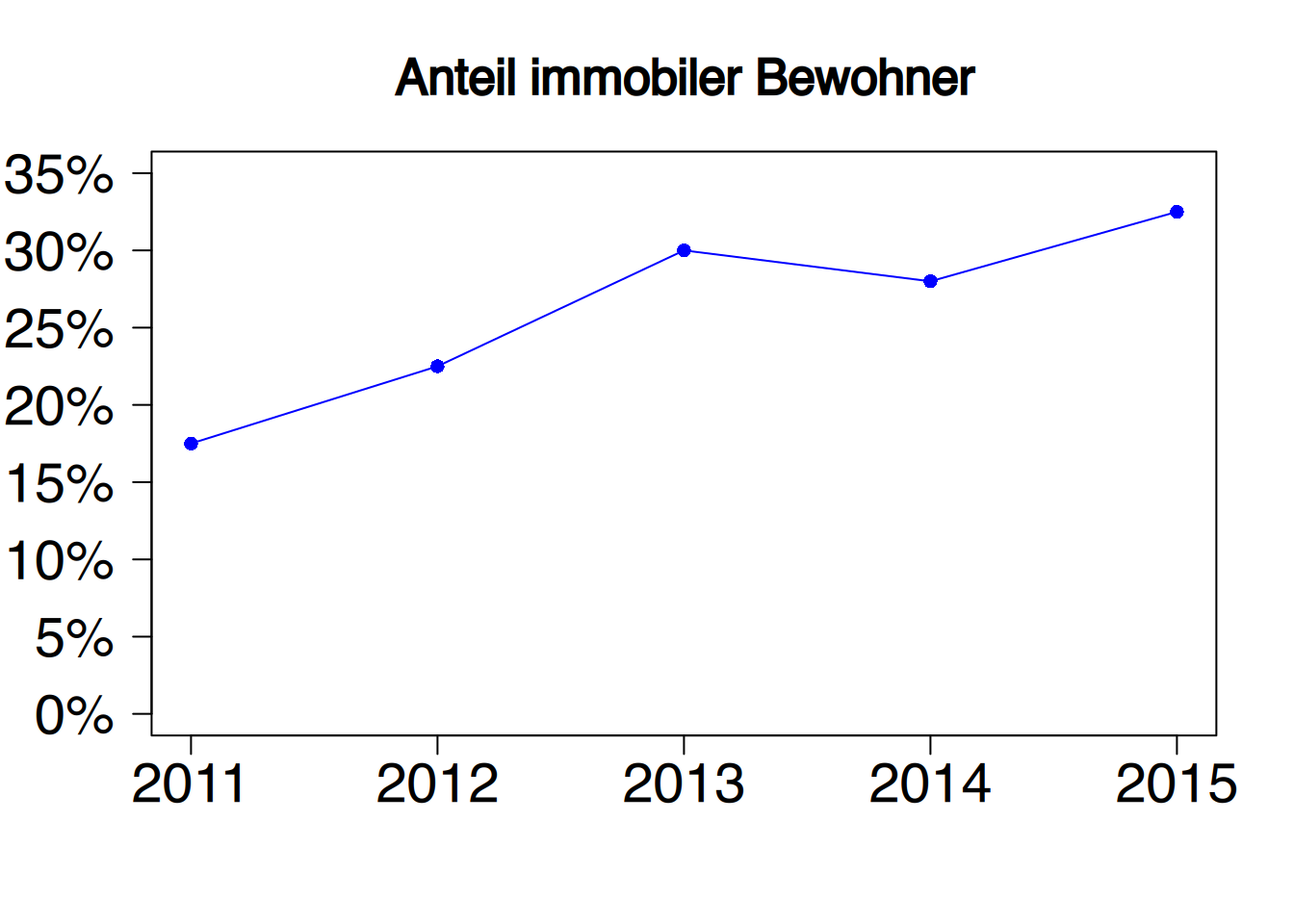
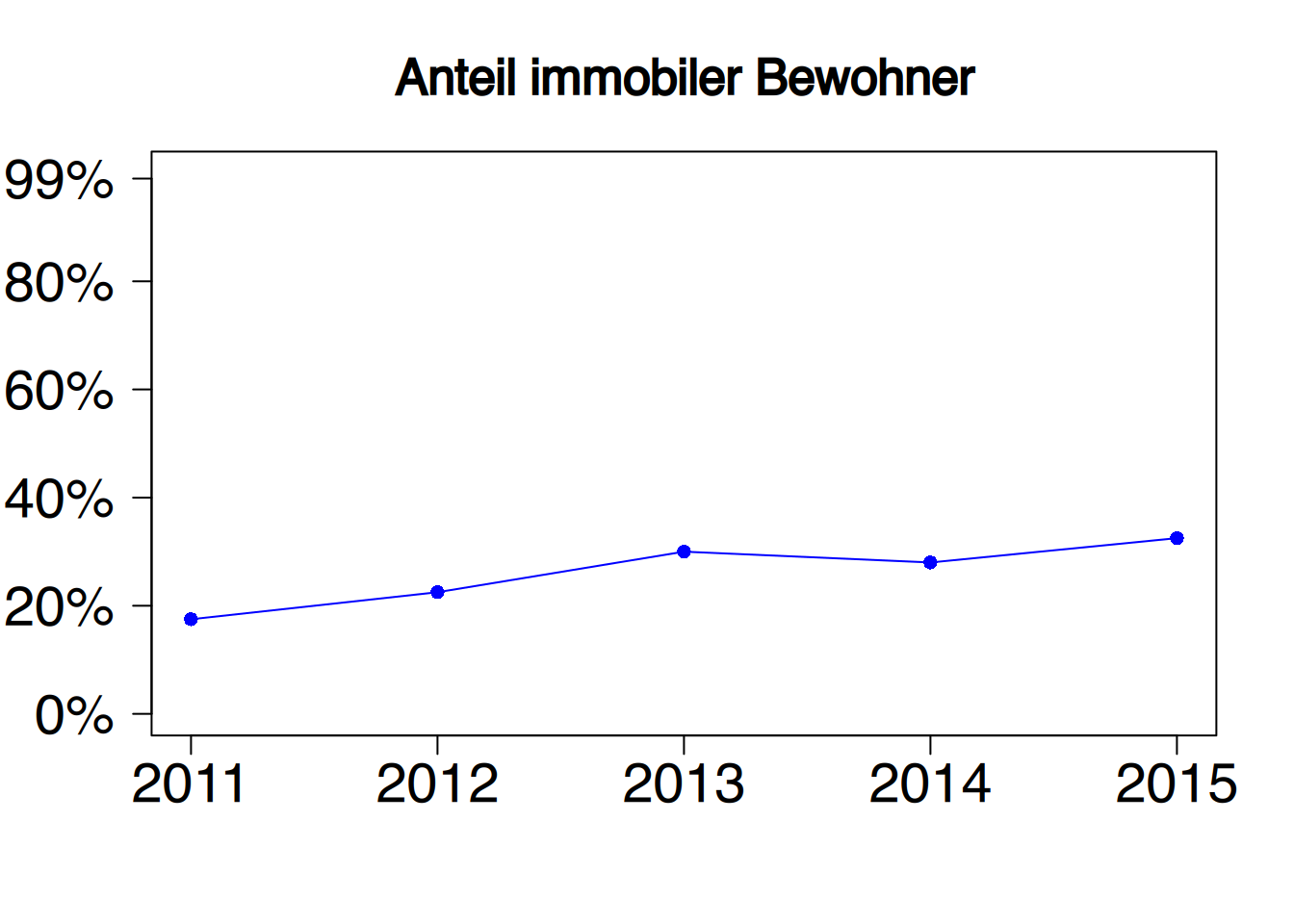
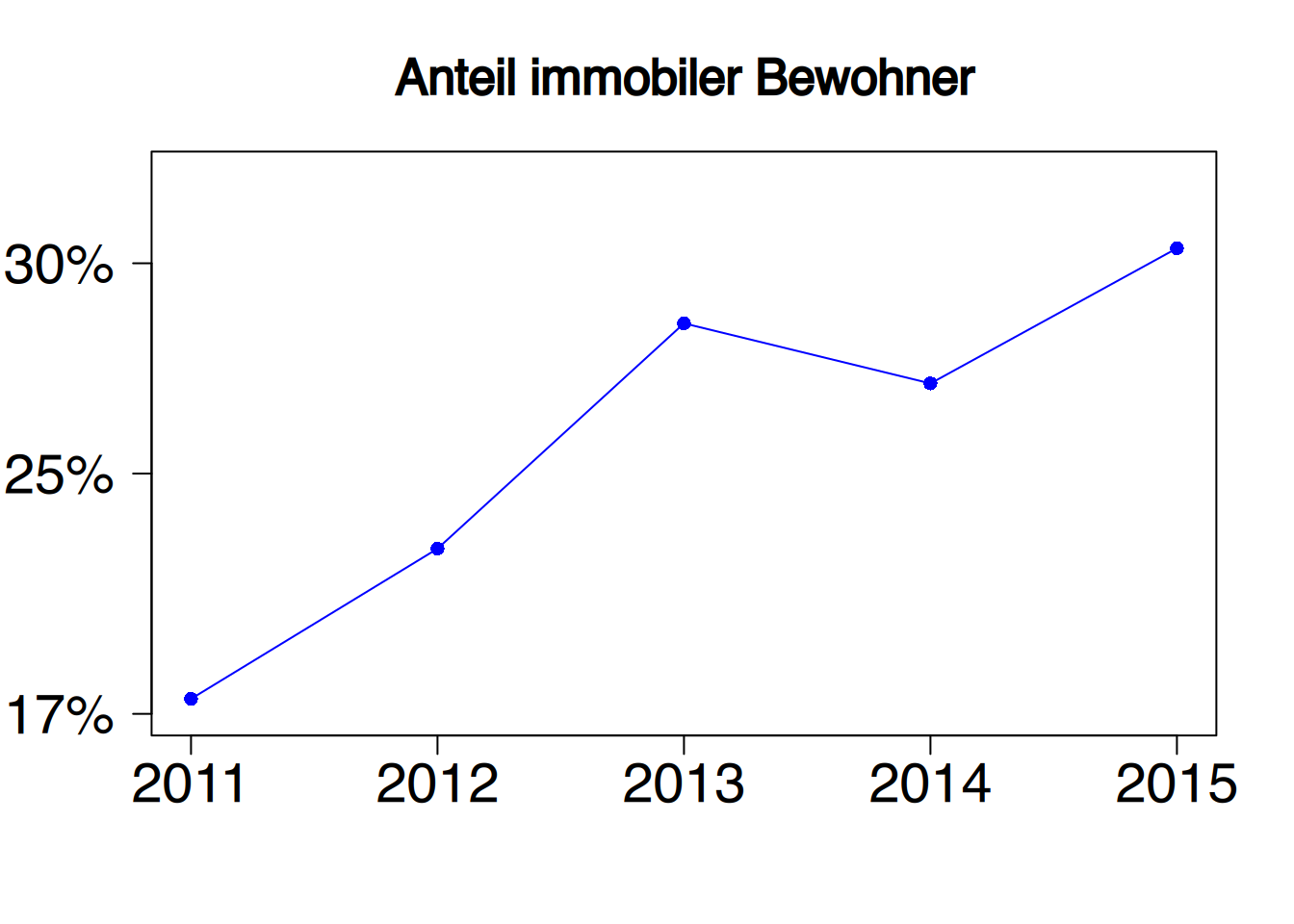
In allen drei Diagrammen sind identische Werte abgetragen. Durch die unterschiedliche Skalierung der \(y\)-Achse entsteht aber ein sehr unterschiedlicher Eindruck.
2.4 Ausreißer
Eines der größten Probleme in Stichproben sind Ausreißer, also Werte, die sehr von den restlichen Werten der Stichprobe abweichen. Es ist wichtig, Ausreißer zu identifizieren, bevor man irgendwelche Analysen durchführt, denn Ausreißer verzerren meistens die Ergebnisse.

Ausreißer tauchen immer am Ende der Verteilung auf und können mit einem Box-und-Whisker-Diagramm leicht identifiziert werden (wie später gezeigt wird).
2.4.1 Ausreißerhandhabung
Bei großen Stichproben haben Ausreißer weniger Bedeutung und können unbeachtet gelassen werden. Bei kleinen Stichproben gibt es mehrere Optionen:
- Entferne die Ausreißer, da es sich um fehlerhafte Werte handelt.
- Ersetze die Ausreißer durch den kleinsten oder größten Wert in der Verteilung, der selbst kein Ausreißer ist.
- Lasse die Ausreißer, und ändere das theoretische Modell, so dass die Ausreißer erklärbar werden.