7 Kontinuierliche Zufallsvariablen

Kontinuierliche Zufallsvariablen können im Gegensatz zu diskreten Zufallsvariablen jeden Wert in einem echten Intervall annehmen. Daher ist der Bereich einer kontinuierlichen Zufallsvariablen unendlich und nicht abzählbar. Diese Vielzahl von Werten macht es unmöglich, die Wahrscheinlichkeit für jeden einzelnen zu berechnen, wodurch es nicht möglich ist, ein Wahrscheinlichkeitsmodell über eine Wahrscheinlichkeitsfunktion wie bei diskreten Zufallsvariablen zu definieren.

Darüber hinaus wird die Messung einer kontinuierlichen Zufallsvariablen in der Regel durch die Genauigkeit des Messinstruments begrenzt. Zum Beispiel beträgt die wahre Größe einer Person, für die unser Messinstrument 1,68 Meter groß sagt, nicht genau 1,68 Meter, da die Genauigkeit des Messinstruments nur auf zwei Dezimalstellen cm (Zentimeter) beträgt. Dies bedeutet, dass die wahre Größe dieser Person zwischen 1,675 und 1,685 Metern liegt.

Daher ist es für kontinuierliche Variablen unsinnig, die Wahrscheinlichkeit eines einzelnen Werts zu berechnen, und wir werden Wahrscheinlichkeiten für Intervalle berechnen.

7.1 Verteilungsfunktion einer kontinuierlichen Zufallsvariablen

Um die Verteilungsfunktion einer kontinuierlichen Zufallsvariablen zu modellieren, wird eine Wahrscheinlichkeitsdichtefunktion verwendet.

Definition “Wahrscheinlichkeitsdichtefunktion”

Die Wahrscheinlichkeitsdichtefunktion einer kontinuierlichen Zufallsvariablen $X$ ist eine Funktion $f(x)$, die folgende Bedingungen erfüllt:

Sie ist nicht-negativ: $f(x)\geq 0$ $\forall x\in \mathbb{R}$.
Der von der Kurve der Dichtefunktion und der x-Achse begrenzte Bereich beträgt gleich 1, d.h.: \[ \int_{-\infty}^{\infty} f(x)\; dx = 1. \]
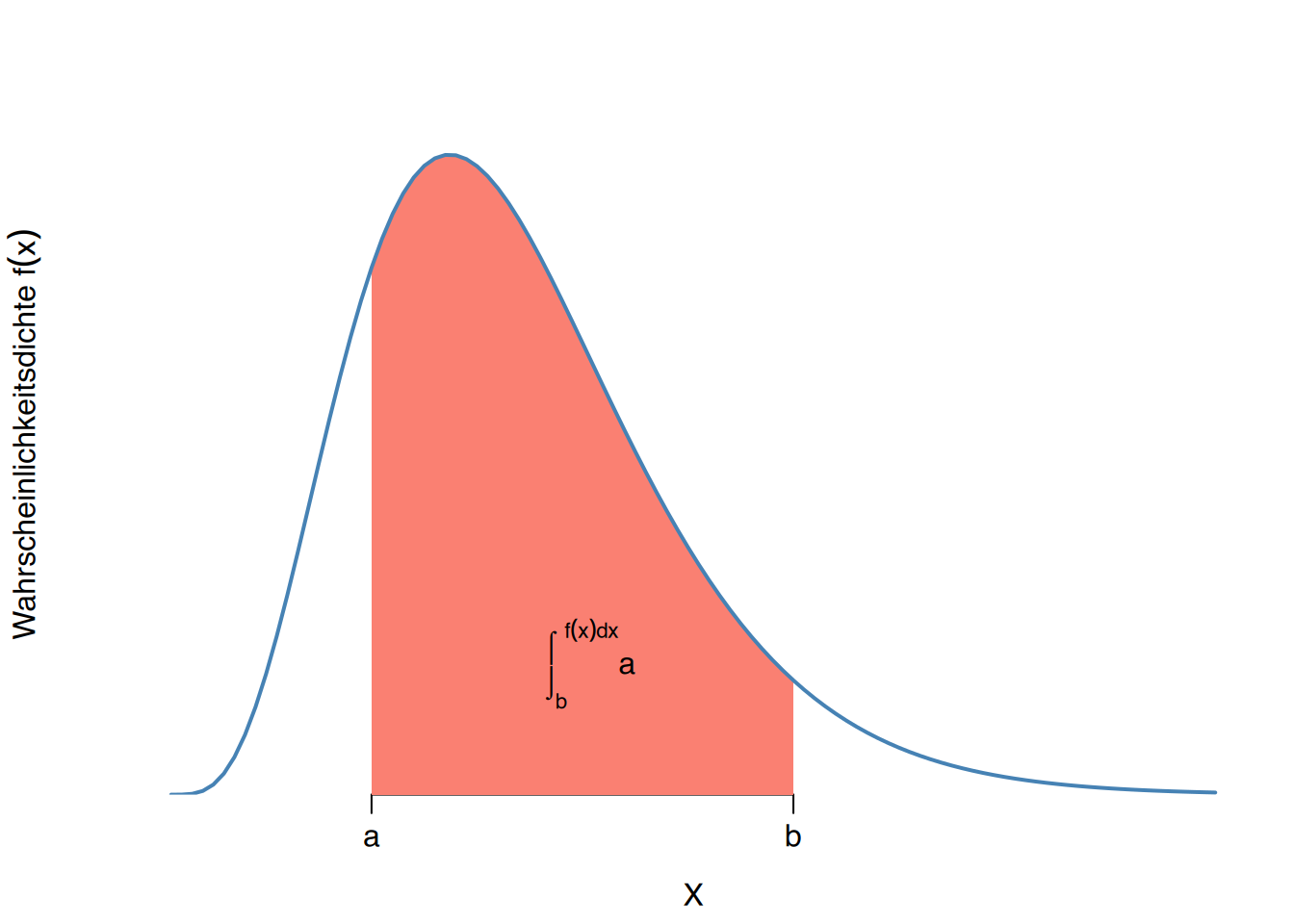
Die Wahrscheinlichkeit, dass $X$ einen Wert zwischen $a$ und $b$ annimmt, entspricht dem von der Dichtefunktion begrenzten Bereich unter $a$ und $b$, d.h.:

\[ P(a\leq X\leq b) = \int_a^b f(x)\; dx \]

Die Wahrscheinlichkeitsdichtefunktion misst die relative Wahrscheinlichkeit jedes Werts, jedoch ist $f(x)$ nicht die Wahrscheinlichkeit von $x$, da $P(X=x) = 0$ für jeden Wert $x$ gilt.

7.1.1 Verteilungsfunktion

Genauso wie bei diskreten Zufallsvariablen macht es auch bei kontinuierlichen Zufallsvariablen Sinn, kumulative Wahrscheinlichkeiten zu berechnen.

Definition “Verteilungsfunktion”

Die Verteilungsfunktion einer kontinuierlichen Zufallsvariablen $X$ ist eine Funktion $F(x)$, die jeden Wert $a$ auf die Wahrscheinlichkeit abbildet, dass $X$ einen Wert kleiner oder gleich $a$ annimmt, d.h.:

\[ F(a) = P(X\leq a) = \int_{-\infty}^{a} f(x)\; dx. \]

7.1.2 Wahrscheinlichkeitsbereiche

\[ \displaystyle P(a\leq X\leq b) = \int_a^b f(x)\, dx = F(b)-F(a) \]

Beispiel

Gegeben ist die folgende Funktion:

\[ f(x) = \left\{ \begin{array}{ll} 0 & \text{bei } x < 0 \\ e^{-x} & \text{bei } x \geq 0 \end{array} \right. \] Überprüfen wir, ob es sich um eine Dichtefunktion handelt.

Da diese Funktion klarerweise nicht-negativ ist, müssen wir prüfen, dass der Gesamtbereich, der durch die Kurve und die x-Achse begrenzt wird, gleich 1 beträgt:

\[ \begin{aligned} \int_{-\infty}^\infty f(x)\;dx &= \int_{-\infty}^0 f(x)\;dx +\int_0^\infty f(x)\;dx = \int_{-\infty}^0 0\;dx +\int_0^\infty e^{-x}\;dx =\\ &= \left[-e^{-x}\right]_0^{\infty} = -e^{-\infty}+e^0 = 1. \end{aligned} \]

Nun berechnen wir die Wahrscheinlichkeit, dass $X$ einen Wert zwischen 0 und 2 annimmt:

\[ \begin{aligned} P(0\leq X\leq 2) &= \int_0^2 f(x)\;dx = \int_0^2 e^{-x}\;dx = \left[-e^{-x}\right]_0^2 = -e^{-2}+e^0 = 0.8646. \end{aligned} \]

7.1.3 Populationsstatistik

Die Berechnung der Populationsstatistik erfolgt ähnlich wie im Fall diskreter Variabler, jedoch mit der Dichtefunktion anstelle der Wahrscheinlichkeitsfunktion und durch Ersetzen der diskreten Summe durch das Integral.

Die wichtigsten sind:

Mittelwert: $\mu = E(X) = \int_{-\infty}^\infty x f(x)\; dx$
Varianz: $\sigma^2 = Var(X) = \int_{-\infty}^\infty x^2f(x)\; dx -\mu^2$
Standardabweichung: $\sigma = +\sqrt{\sigma^2}$

Beispiel

Gegeben ist die Variable $X$ mit der folgenden Wahrscheinlichkeitsdichtefunktion:

\[ f(x) = \left\{ \begin{array}{ll} 0 & \text{bei } x < 0 \\ e^{-x} & \text{bei } x \geq 0 \end{array} \right. \]

Der Mittelwert beträgt:

\[ \begin{aligned} \mu &= \int_{-\infty}^\infty xf(x)\;dx = \int_{-\infty}^0 xf(x)\;dx +\int_0^\infty xf(x)\;dx = \int_{-\infty}^0 0\;dx +\int_0^\infty xe^{-x}\;dx =\\ &= \left[-e^{-x}(1+x)\right]_0^{\infty} = 1. \end{aligned} \]

Die Varianz beträgt:

\[ \begin{aligned} \sigma^2 &= \int_{-\infty}^\infty x^2f(x)\;dx -\mu^2 = \int_{-\infty}^0 x^2f(x)\;dx +\int_0^\infty x^2f(x)\;dx -\mu^2 = \\ &= \int_{-\infty}^0 0\;dx +\int_0^\infty x^2e^{-x}\;dx -\mu^2= \left[-e^{-x}(x^2+2x+2)\right]_0^{\infty} - 1^2= 2e^0-1 = 1. \end{aligned} \]

Die wichtigsten kontinuierlichen Wahrscheinlichkeitsverteilungsmodelle sind:

Gleichverteilung
Normalverteilung
Student’s t-Verteilung
Chi-Quadrat-Verteilung

7.2 stetige Gleichverteilung

Wenn alle Werte einer Zufallsvariablen $X$ dieselbe Wahrscheinlichkeit haben, dann ist die Wahrscheinlichkeitsverteilung von $X$ gleichverteilt.

Definition “Kontinuierliche gleichverteilte Verteilung” $U(a,b)$)

Eine kontinuierliche Zufallsvariable $X$ folgt dem Wahrscheinlichkeitsverteilungsmodell der Gleichverteilung mit den Parametern $a$ und $b$, notiert als $X\sim U(a,b)$, wenn ihr Bereich $\mbox{Ran}(X) = [a,b]$ ist und ihre Dichtefunktion

\[ f(x)= \frac{1}{b-a}\quad \forall x\in [a,b] \]

ist.

Dabei sind $a$ und $b$ der minimale bzw. maximale Wert des Bereichs, und die Dichtefunktion ist konstant.

Der Erwartungswert und die Varianz sind:

\[ \mu = \frac{a+b}{2}\qquad \sigma^2=\frac{(b-a)^2}{12}. \]

Beispiel

Die Generierung einer Zufallszahl zwischen 0 und 1 folgt der kontinuierlichen gleichverteilten Verteilung $U(0, 1)$.

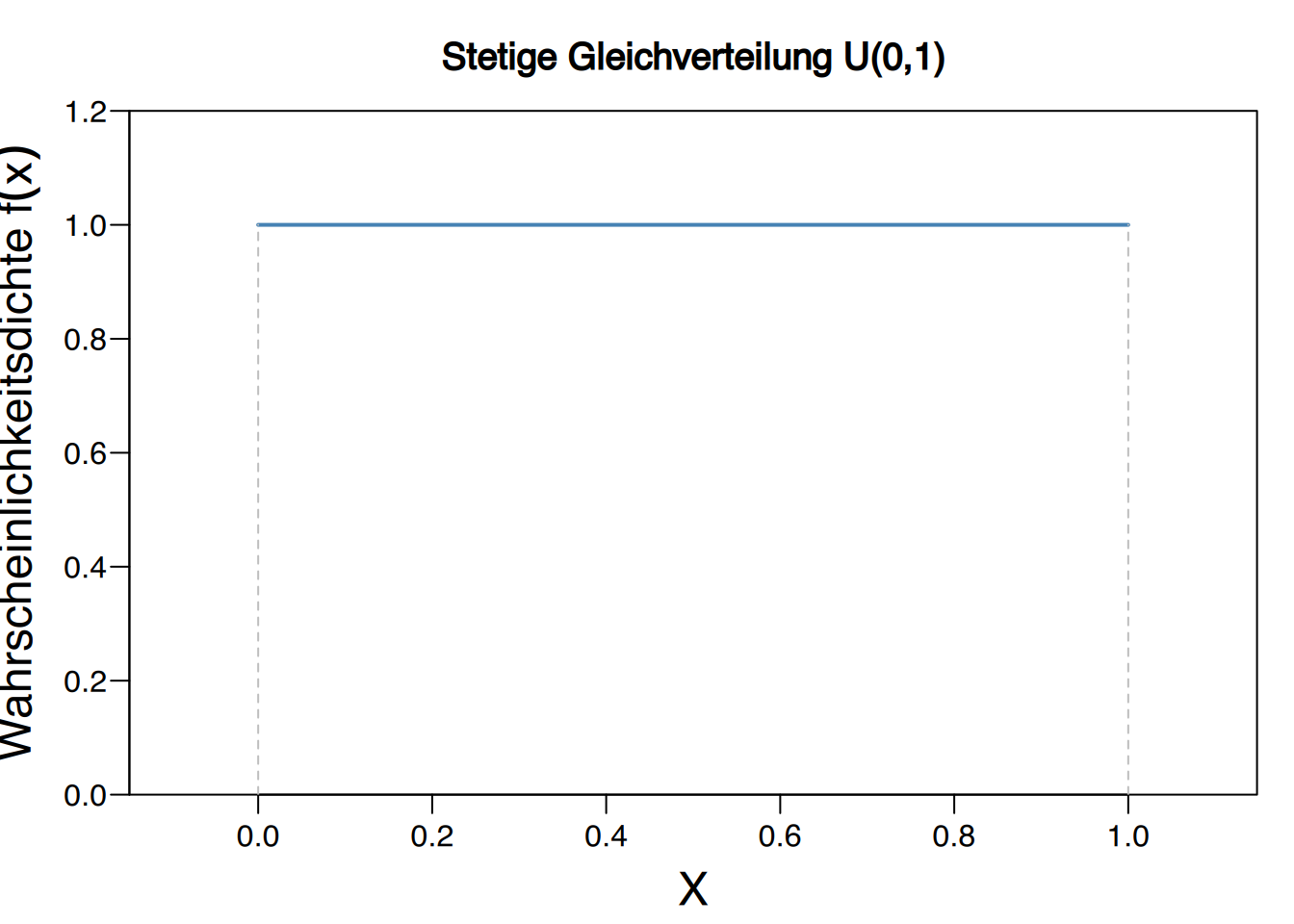
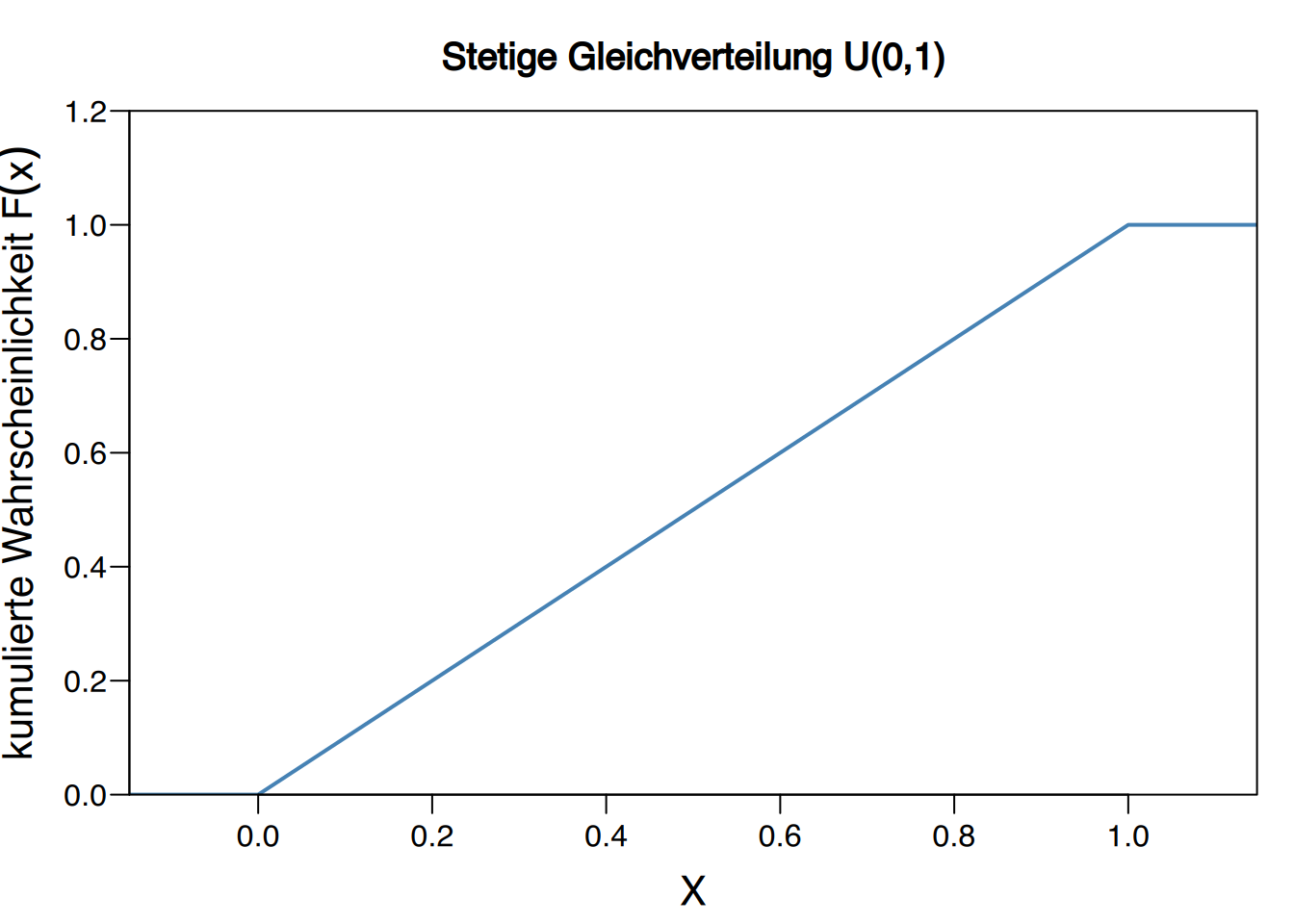
Da die Dichtefunktion konstant ist, wächst die Verteilungsfunktion linear.

Beispiel: Wartezeit für einen Bus

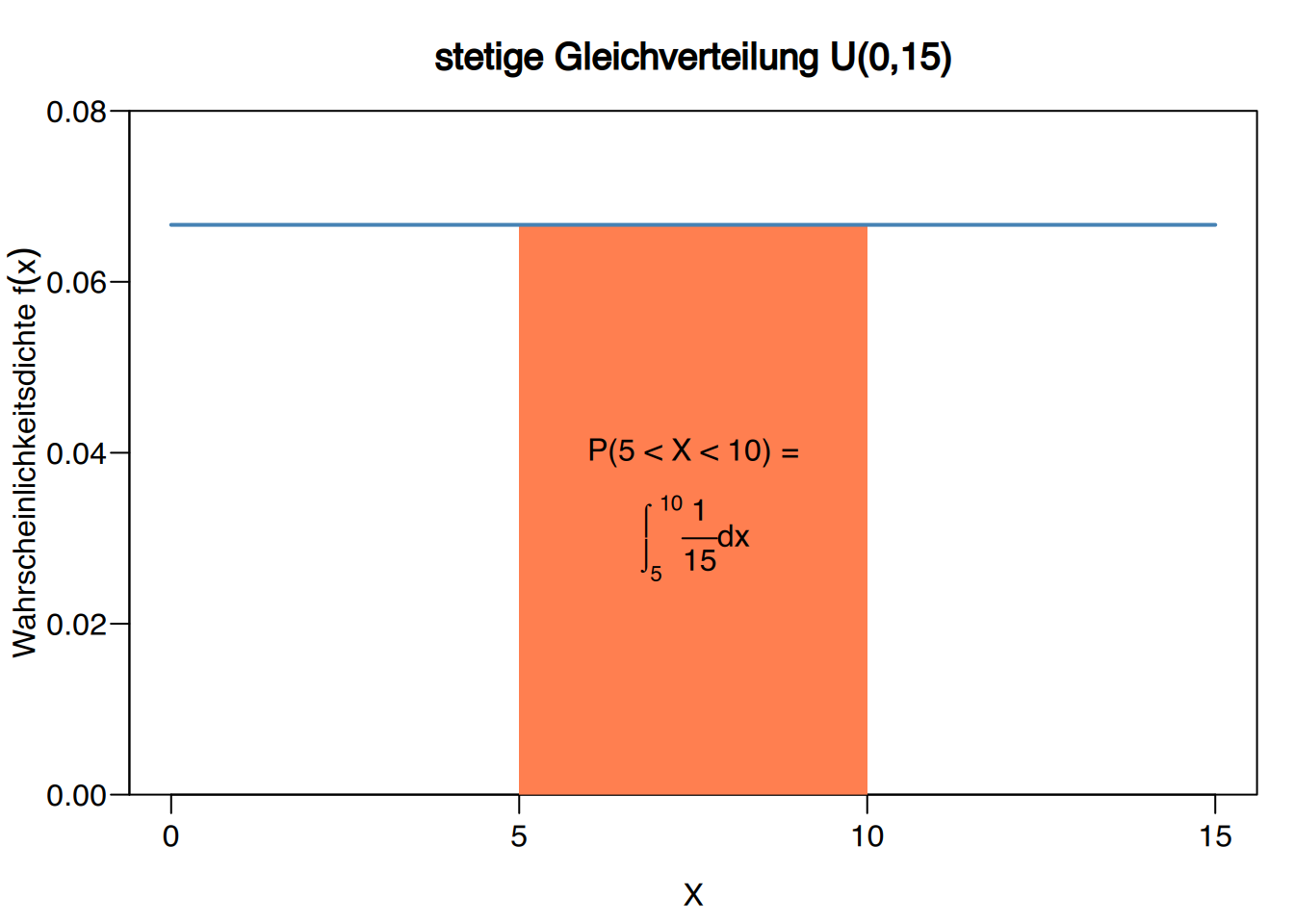
Ein Bus hat eine Frequenz von 15 Minuten. Angenommen, eine Person kann zu jeder Zeit an der Bushaltestelle ankommen. Wie groß ist die Wahrscheinlichkeit, dass man auf den Bus zwischen 5 und 10 Minuten wartet?

In diesem Fall folgt die Variable $X$, welche die Wartezeit misst, einer kontinuierlichen gleichverteilten Verteilung $U(0, 15)$, da jede Wartezeit zwischen $0$ und $15$ gleich wahrscheinlich ist.

Die Wahrscheinlichkeit, zwischen $5$ und $10$ Minuten auf den Bus zu warten, beträgt:

\[ \begin{aligned} P(5\leq X\leq 10) &= \int_{5}^{10} \frac{1}{15}\;dx = \left[\frac{x}{15}\right]_5^{10} = \\ &= \frac{10}{15}-\frac{5}{15} =\frac{1}{3}. \end{aligned} \]

Die erwarete (durchschnittliche) Wartezeit ist $\mu=\frac{0+15}{2}=7.5$ Minuten.

7.3 Normalverteilung

Das Normalverteilungsmodell ist ohne Zweifel das wichtigste Modell für kontinuierliche Verteilungen und das häufigste in der Natur.

Definition “Normalverteilung” $N(\mu, \sigma)$

Eine stetige Zufallsvariable $X$ folgt dem Normalverteilungsmodell $N(\mu, \sigma)$, wenn ihr Wertebereich $\mbox{Ran}(X) = (-\infty,\infty)$ ist und ihre Dichtefunktion

\[ f(x)= \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}. \]

Die beiden Parameter $\mu$ und $\sigma$ sind der Mittelwert (Erwartungswert) bzw. die Standardabweichung der Population.

7.3.1 Dichtefunktion der Normalverteilung

Der Graph der Wahrscheinlichkeitsdichtefunktion einer Normalverteilung $N(\mu, \sigma)$ ist glockenförmig und wird auch als Gauß-Glocke bezeichnet.

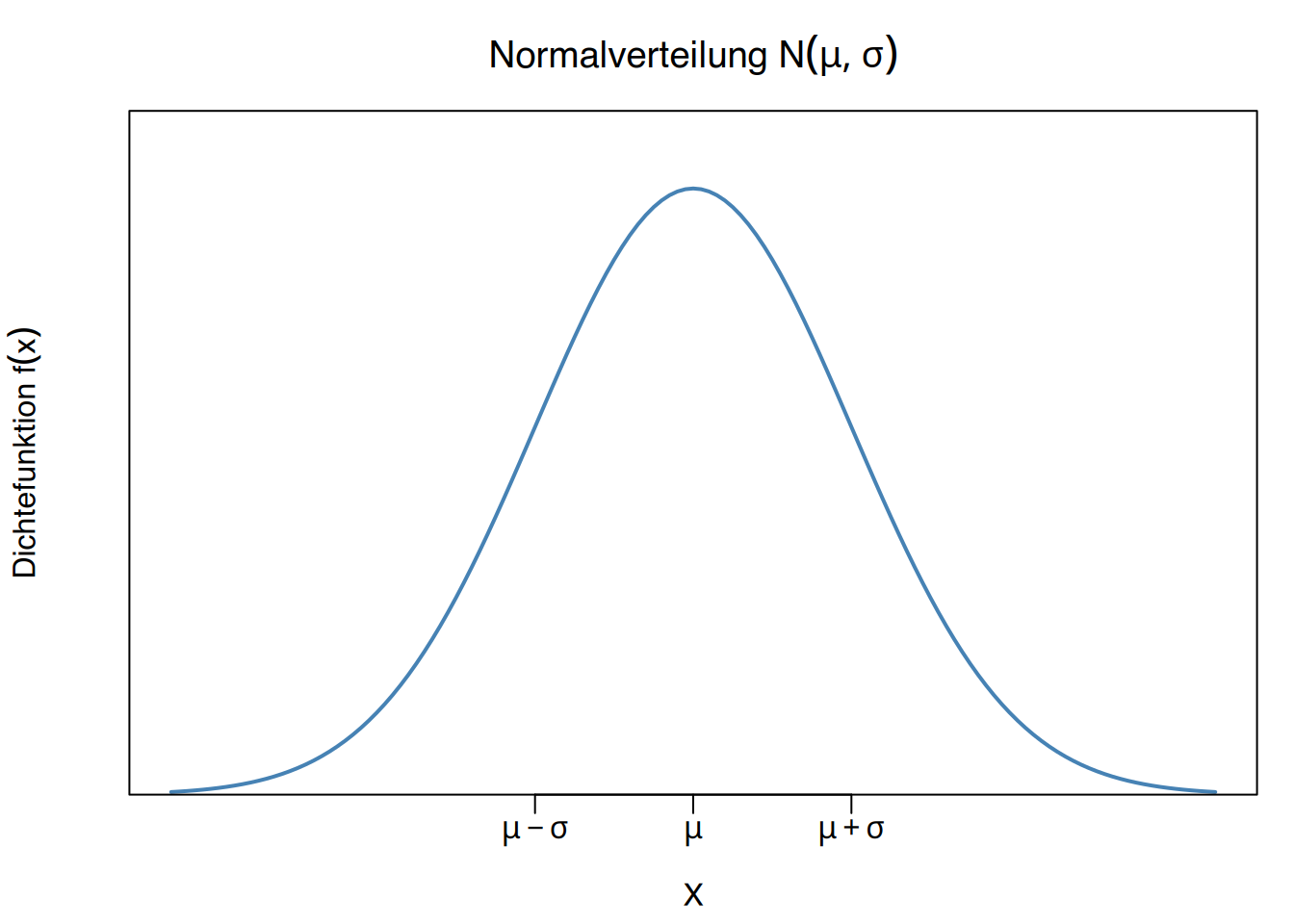
Die Glockenform hängt vom Mittelwert $\mu$ und der Standardabweichung $\sigma$ ab.

Der Mittelwert $\mu$ legt die Mitte der Glocke fest.
Die Standardabweichung $\sigma$ legt die Breite der Glocke fest.

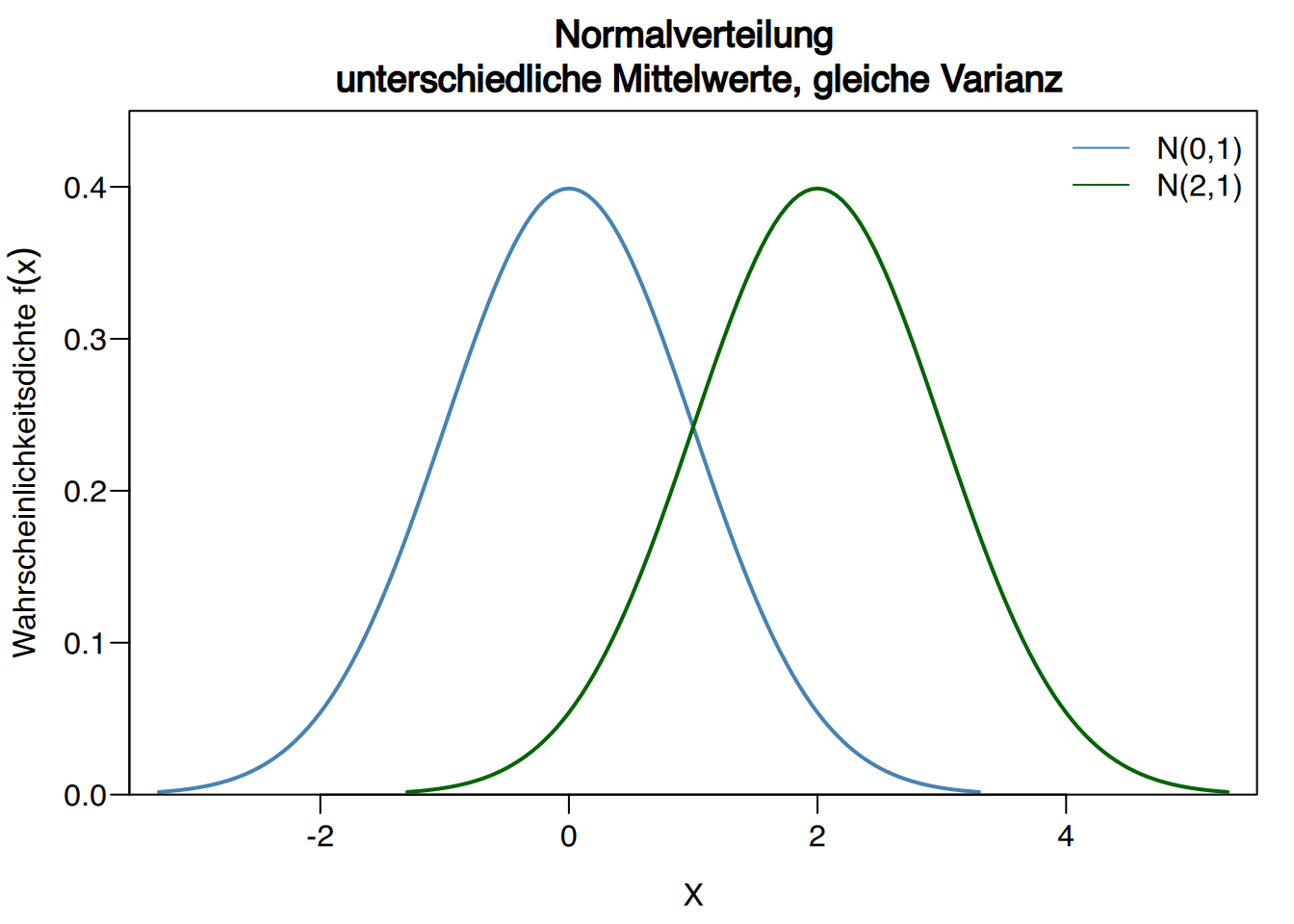
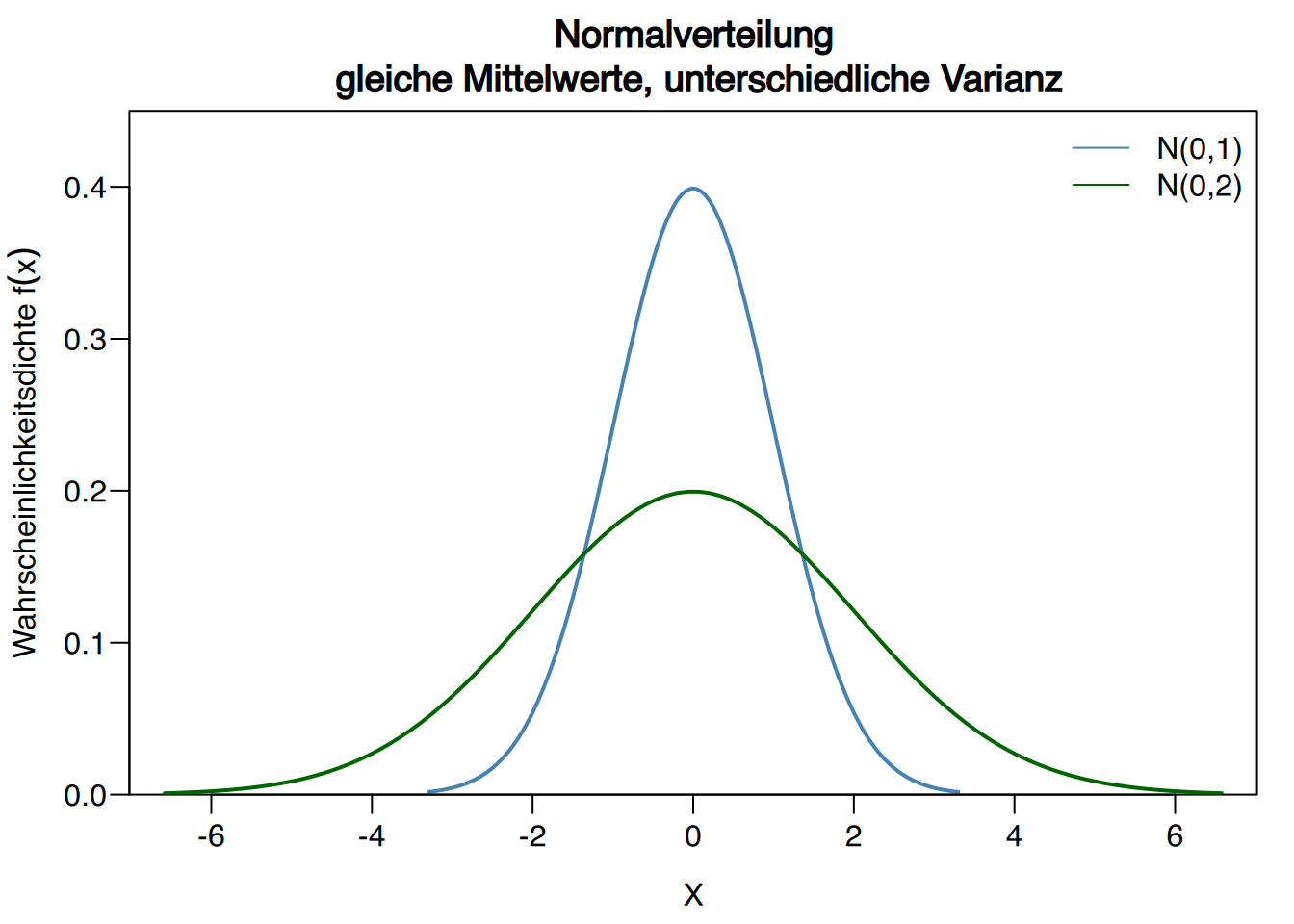
7.3.2 Verteilungsfunktion

Die Verteilungsfunktion der Normalverteilung ist S-förmig

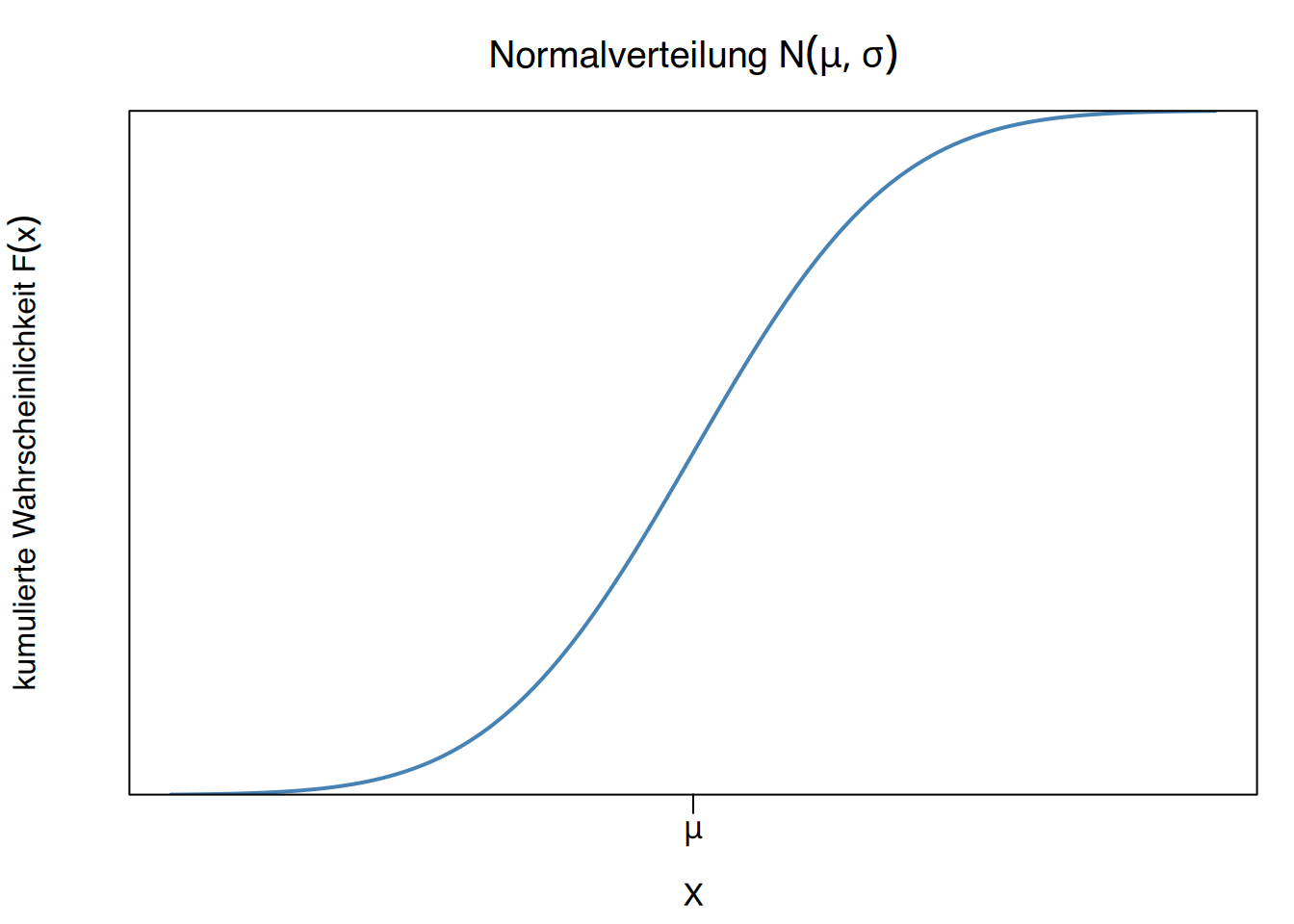
7.3.3 Eigenschaften der Normalverteilung

Sie ist symmetrisch bezüglich der Mitte, sodass Schiefe null ist: $g_1=0$.
Sie ist mesokurtisch, da die Dichtefunktion glockenförmig ist und der Kurtosiskoeffizient daher null beträgt: $g_2=0$.
Mittelwert, Median und Modalwert sind gleich: $\mu = Me = Mo$.
Sie nähert sich asymptotisch Null an, wenn $x$ gegen $\pm \infty$ geht.

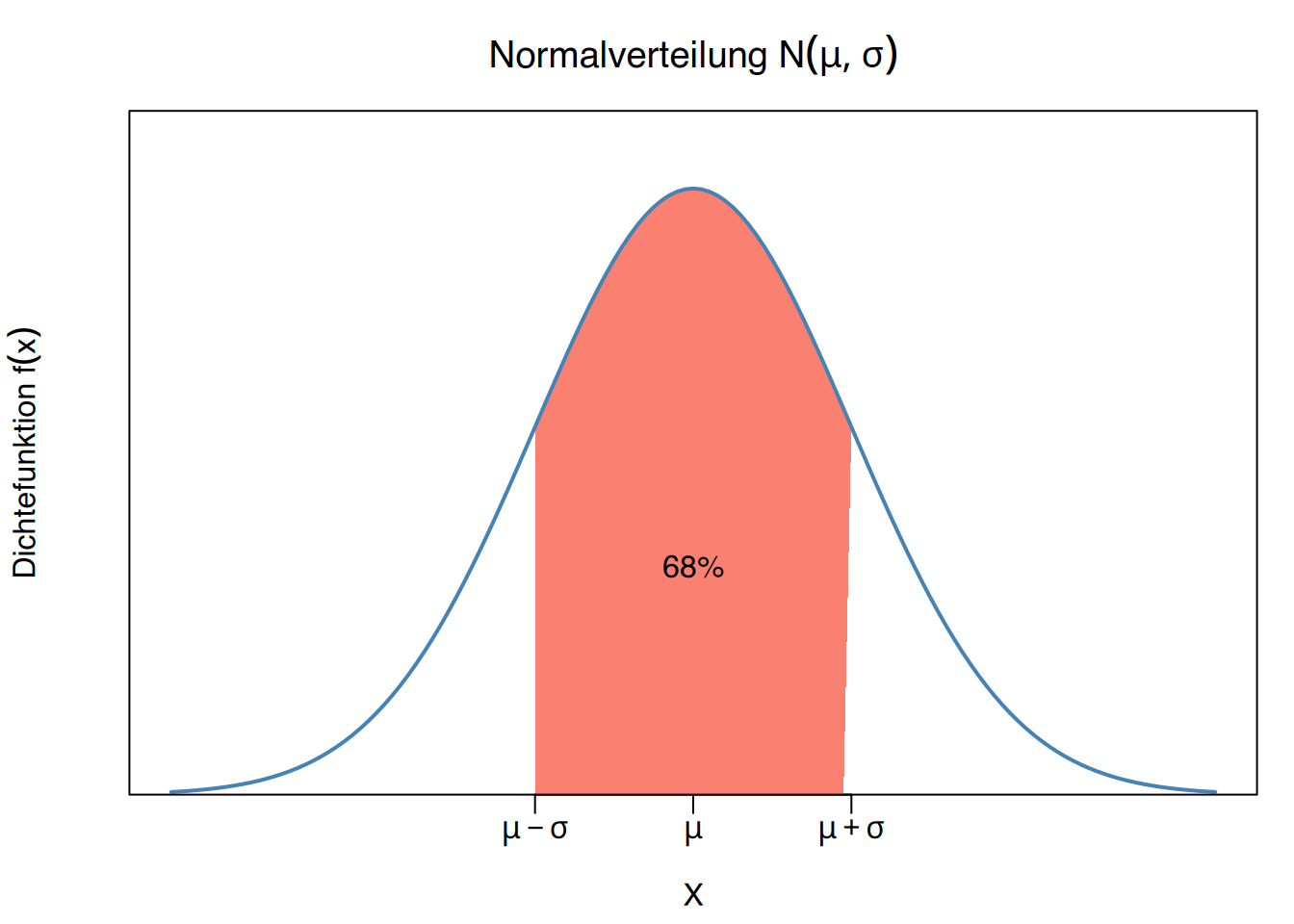
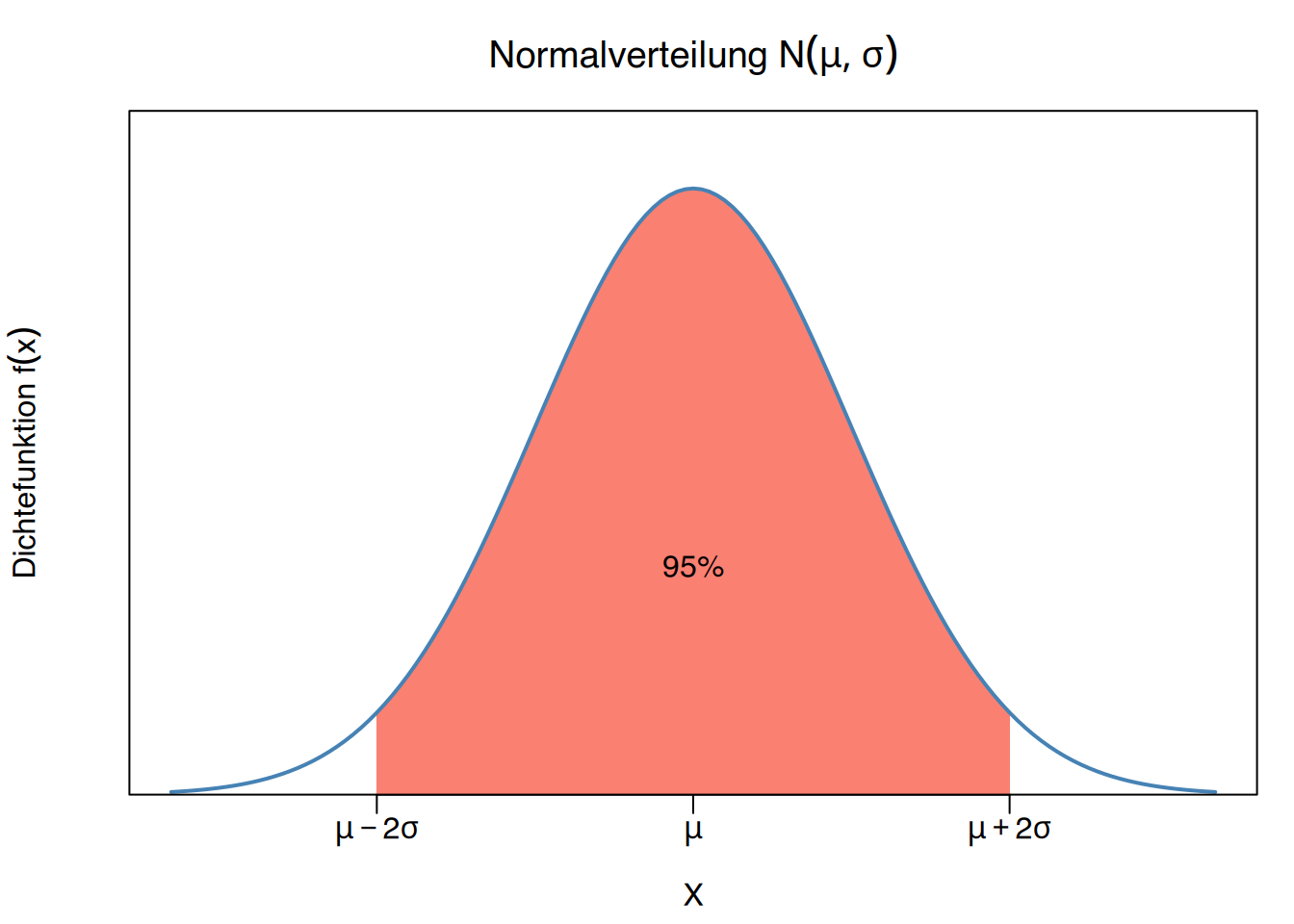
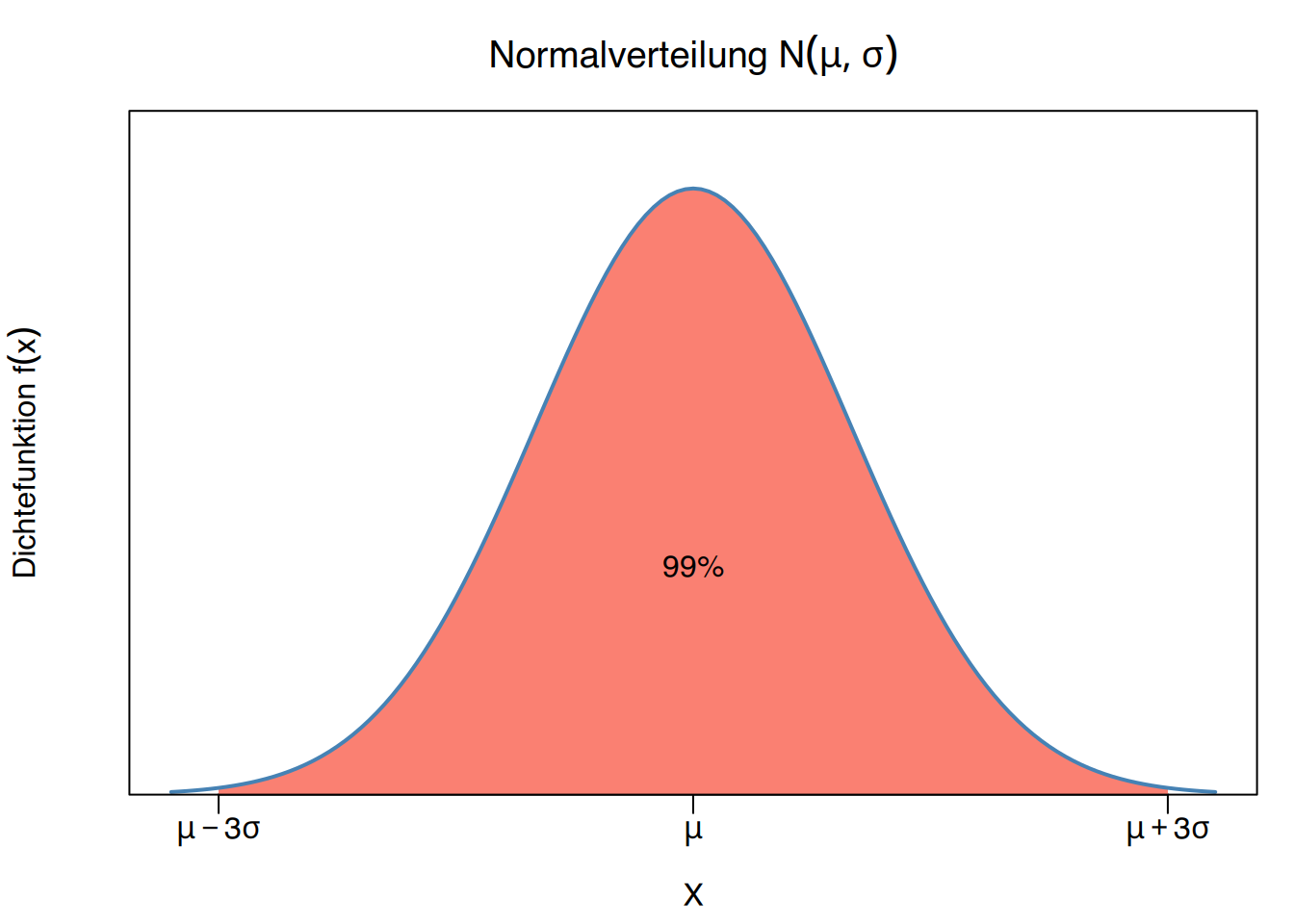
\[ \begin{aligned} P(\mu-\sigma \leq X \leq \mu+\sigma) = 0.68\\ P(\mu-2\sigma \leq X \leq \mu+2\sigma) = 0.95\\ P(\mu-3\sigma \leq X \leq \mu+3\sigma) = 0.99 \end{aligned} \]

Beispiel Cholesterin

Es ist bekannt, dass die Cholesterinwerte von Frauen im Alter zwischen 40 und 50 Jahren einer Normalverteilung mit $\mu=210$mg/dl und $\sigma=20$mg/dl folgen.

Durch die Eigenschaften der Glockenkurve wissen wir, dass

68% der Frauen einen Cholesterinwert von $210\pm 20$ mg/dl aufweisen, also Werte zwischen 190 und 230 mg/dl.
95% der Frauen einen Cholesterinwert von $210\pm 2\cdot20$ mg/dl aufweisen, also Werte zwischen 170 und 250 mg/dl.
99% der Frauen einen Cholesterinwert von $210\pm 3\cdot20$ mg/dl aufweisen, also Werte zwischen 150 und 270 mg/dl.

Beispiel Blutanalyse

Bei der Blutanalyse wird häufig das Intervall $verwendet, um mögliche Pathologien zu erkennen. Im Fall des Cholesterins liegt dieses Intervall bei $[170\text{ mg/dl}, 250\text{ mg/dl}]$.

Somit wird eine Frau im Alter zwischen 40 und 50 Jahren mit einem Cholesteringehalt außerhalb dieses Intervalls häufig auf eine mögliche Erkrankung untersucht. Allerdings könnte diese Person gesund sein, obwohl die Wahrscheinlichkeit dafür nur 5 % beträgt.

7.3.4 Der Zentrale Grenzwertsatz

Dieses Verhalten ist bei vielen physikalischen und biologischen Variablen in der Natur zu beobachten.

Wenn man zum Beispiel an die Verteilung der Körpergröße denkt, kann man feststellen, dass die meisten Menschen in der Bevölkerung eine Körpergröße um den Mittelwert haben. Allerdings gibt es immer weniger Menschen mit Körpergrößen, je weiter sie vom Mittelwert entfernt sind - sowohl darunter als auch darüber. Die Erklärung für dieses Verhalten ist der Zentrale Grenzwertsatz, auf den wir im nächsten Kapitel zurückkommen werden. Er besagt, dass eine stetige Zufallsvariable, deren Werte von einer großen Anzahl unabhängiger Faktoren abhängen, die ihre Effekte addieren, immer einer Normalverteilung folgt.

7.3.5 Standardnormalverteilung

Die wichtigste Normalverteilung hat einen Mittelwert $\mu=0$ und eine Standardabweichung $\sigma=1$.

Sie wird als Standardnormalverteilung bezeichnet und üblicherweise mit $Z\sim N(0,1)$ dargestellt.

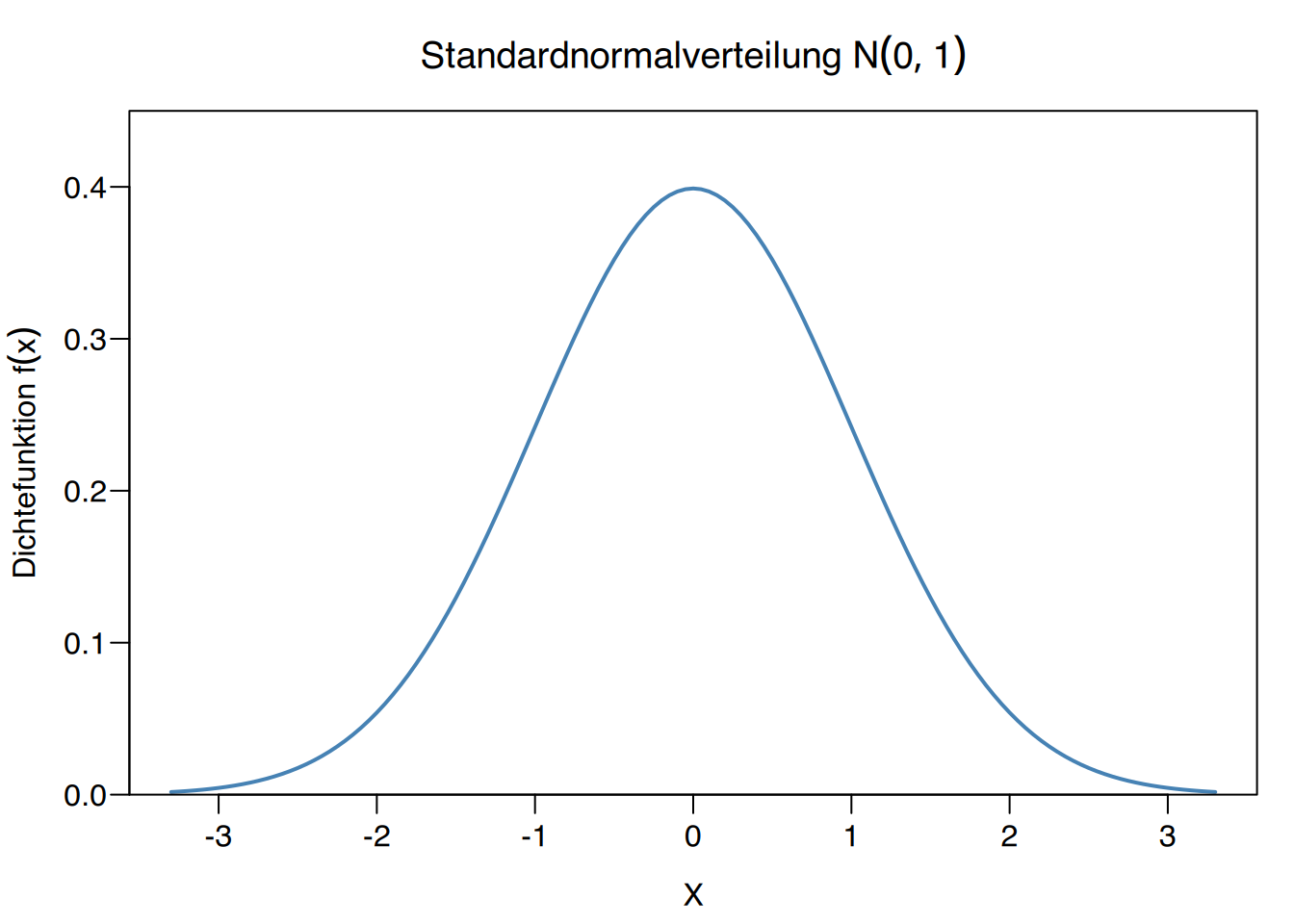
7.3.6 Berechnung von Wahrscheinlichkeiten

Um die Integration der normalen Dichtefunktion zu vermeiden, ist es üblich, die Verteilungsfunktion zu verwenden, die in Tabellenform wie unten angegeben ist.

Beispiel: Werte aus Tabellen ablesen

Bestimmung von $P(Z\leq 0.52)$

$\rightarrow$ Reihe $0.5$ + Spalte $0.02$ $\rightarrow$ 0,6985 ist der gesuchte Wert.

\[ \begin{array}{|r||r|r|r|r|} \hline \mathbf{z} & \mathbf{0.00} & \mathbf{0.01} & \color{red}{\mathbf{0.02}} & \mathbf{\cdots} \\ \hline\hline \mathbf{0.0} & 0.5000 & 0.5040 & 0.5080 & \cdots \\ \hline \mathbf{0.1} & 0.5398 & 0.5438 & 0.5478 & \cdots \\ \hline \mathbf{0.2} & 0.5793 & 0.5832 & 0.5871 & \cdots \\ \hline \mathbf{0.3} & 0.6179 & 0.6217 & 0.6255 & \cdots \\ \hline \mathbf{0.4} & 0.6554 & 0.6591 & 0.6628 & \cdots \\ \hline \color{red}{\mathbf{0.5}} & 0.6915 & 0.6950 & \color{blue}{\color{red}{\mathbf{0.6985}}} & \cdots \\ \hline \mathbf{\vdots} & \vdots & \vdots & \vdots & \ddots \\ \hline \end{array} \]

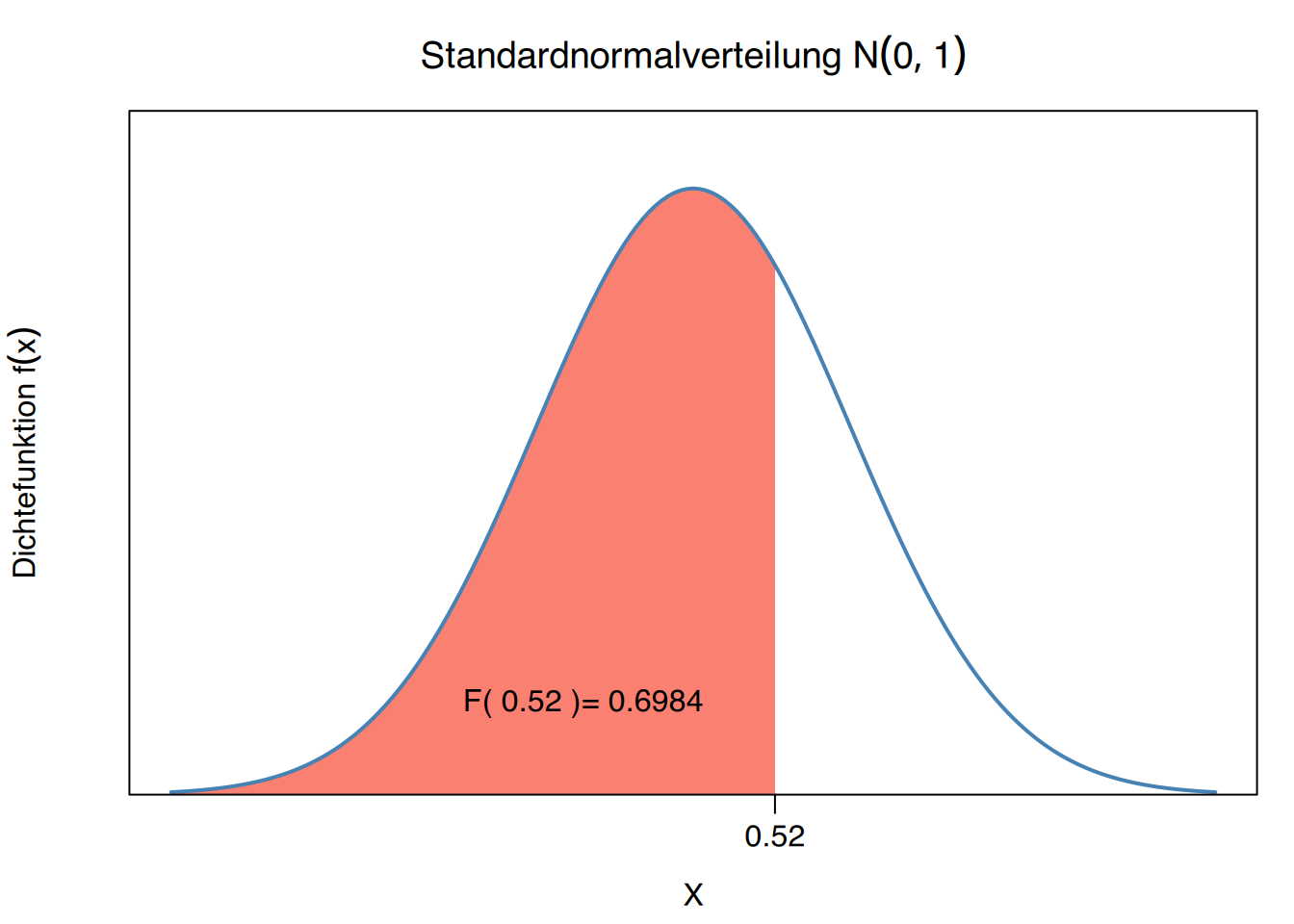
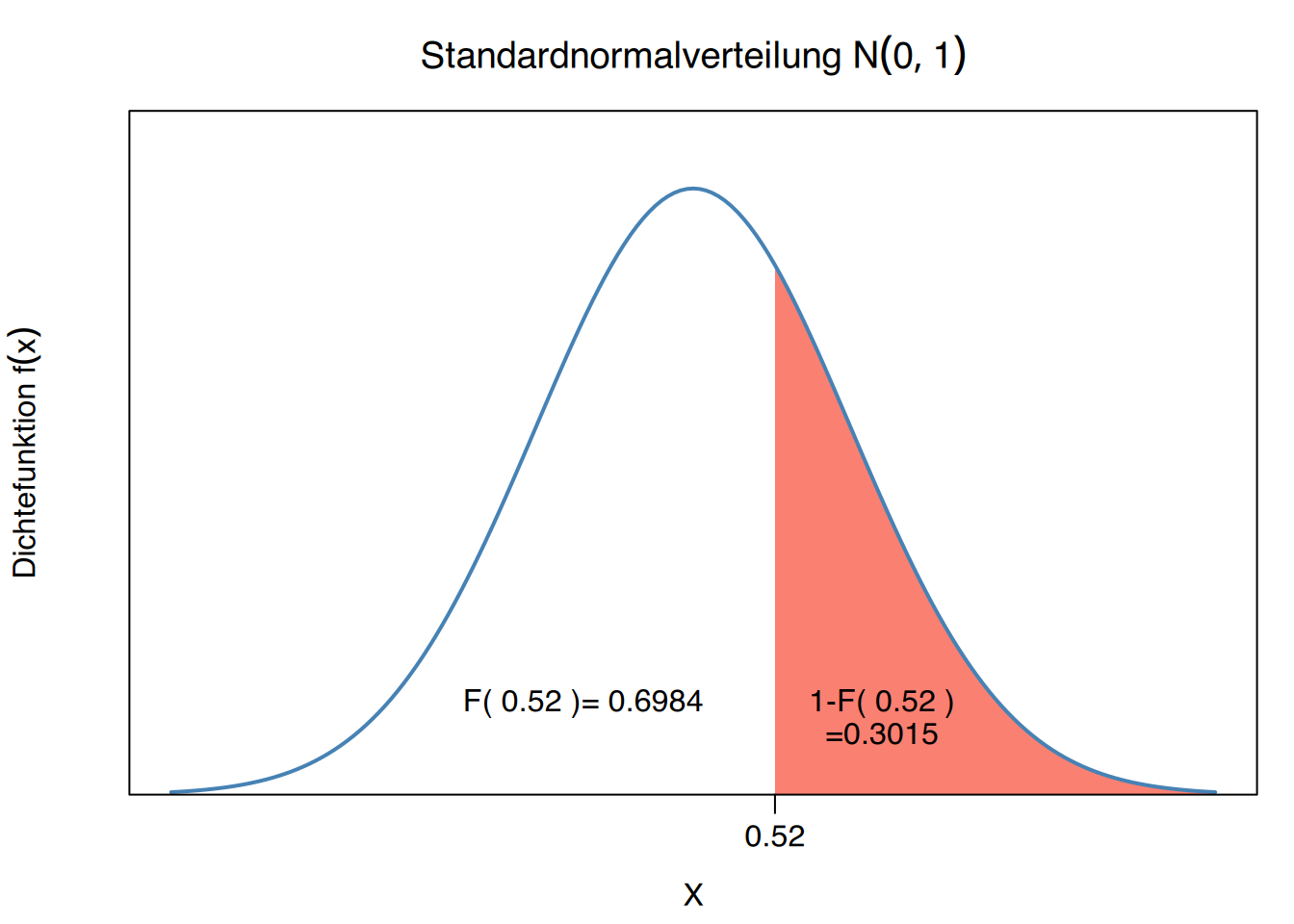
Um kumulative Wahrscheinlichkeiten für Werte rechts von einem Wert zu berechnen, kann die Regel für komplementäre Ereignisse angewendet werden, beispielsweise:

\[ P(Z>0.52) =1-P(Z\leq 0.52) = 1-F(0.52) = 1 - 0.6985 = 0.3015. \]

7.3.7 Standardisierung

Wir haben gelernt, wie wir die Tabelle der Standardnormalverteilungsfunktion verwenden können, um Wahrscheinlichkeiten zu berechnen. Aber was tun wir, wenn es sich nicht um die Standardnormalverteilung handelt?

In diesem Fall können wir Standardisierung anwenden, um jede Normalverteilung in eine Standardnormalverteilung umzuwandeln.

Definition “Standardisierung”

Wenn $X$ eine stetige Zufallsvariable ist, die einer Normalverteilungsfunktion mit Mittelwert $\mu$ und Standardabweichung $\sigma$ folgt, $X\sim N(\mu,\sigma)$, dann folgt die Variable, die durch Subtrahieren von $\mu$ und Dividieren durch $\sigma$ erhalten wird, einer Standardnormalverteilung:

\[ X\sim N(\mu,\sigma) \Rightarrow Z=\frac{X-\mu}{\sigma}\sim N(0,1). \]

Um daher Wahrscheinlichkeiten mit einer nicht-standardmäßigen Normalverteilung zu berechnen, müssen wir die Variable zuerst standardisieren, bevor wir die Tabelle der Standardnormalverteilungsfunktion verwenden.

Beispiel

Angenommen, die Note $X$ eines Examens folgt einer normalen Wahrscheinlichkeitsverteilungsfunktion $N(\mu=6,\sigma=1.5)$. Welcher Prozentsatz der Schüler hat das Examen nicht bestanden?

Da $X$ einer nicht-standardmäßigen Normalverteilung folgt, müssen wir zuerst standardisieren,

\[ Z=\displaystyle \frac{X-\mu}{\sigma} = \frac{X-6}{1.5} \]

\[ P(X<5) = P\left(\frac{X-6}{1.5}<\frac{5-6}{1.5}\right) = P(Z<-0.67). \] Jetzt können wir die Tabelle der Standardnormalverteilungsfunktion verwenden:

\[ P(Z<-0.67) = F(-0.67) = 0.2514. \]

Demnach haben 25,14% der Schüler das Examen nicht bestanden.

7.4 Chi-Quadrat-Verteilung

Definition “Chi-Quadrat-Verteilung $\Chi^2(n)$

Gegeben $n$ unabhängige Zufallsvariablen $Z_1,\ldots,Z_n$, die alle einer Standardnormalverteilung folgen, folgt die Variable

\[ \chi^2(n) = Z_1^2+\cdots +Z_n^2, \]

einer Chi-Quadrat-Verteilung mit $n$ Freiheitsgraden. Ihr Bereich ist $\mathbb{R}^+$, und ihr Mittelwert und ihre Varianz sind:

\[ \mu = n, \qquad \sigma^2 = 2n. \]

Die Chi-Quadrat-Verteilung spielt eine wichtige Rolle bei der Schätzung der Populationsvarianz und beim Studium von Beziehungen zwischen qualitativen Variablen.

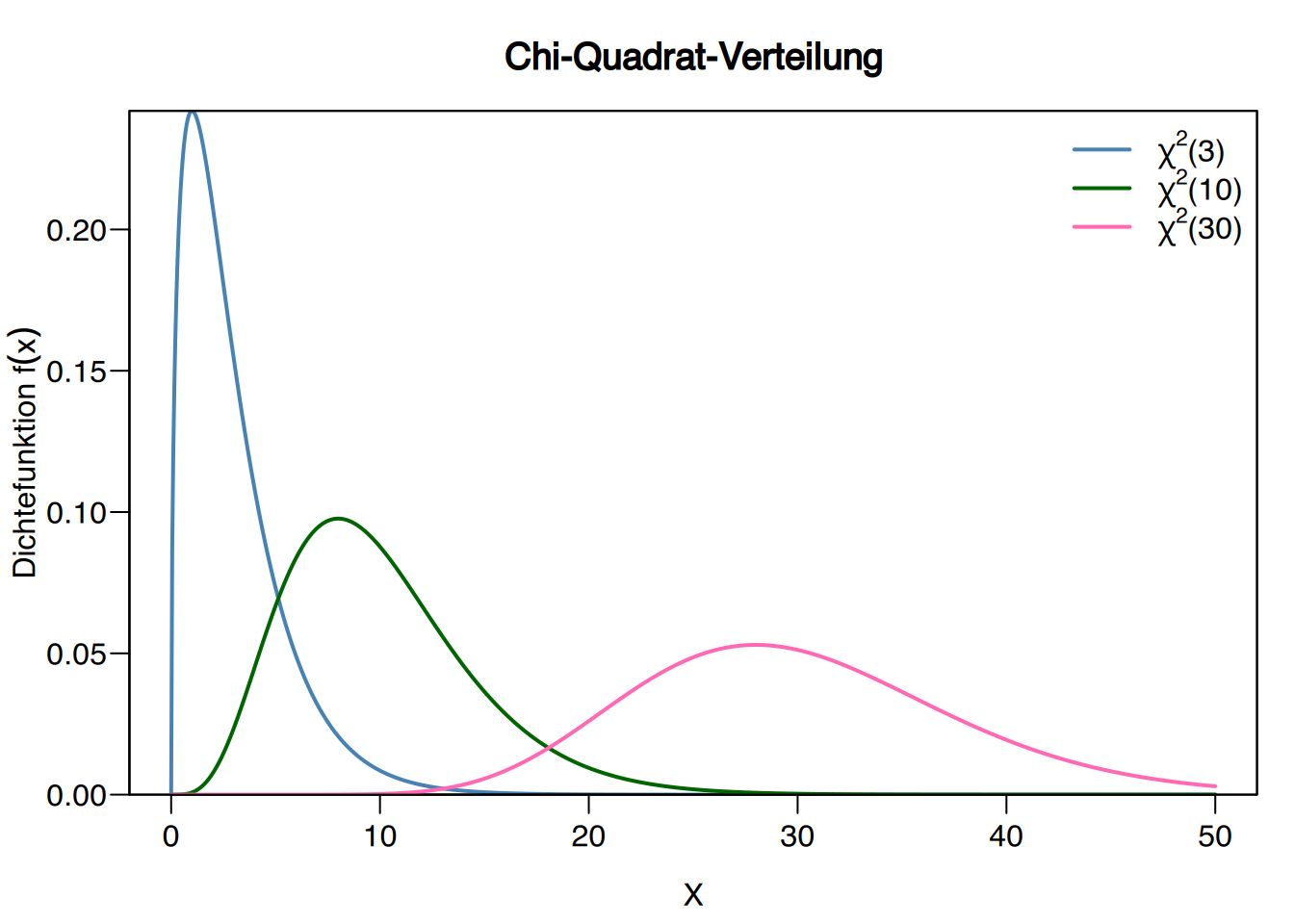
Eigenschaften der Chi-Quadrat-Verteilung

Die Spannweite ist nicht-negativ.
Wenn $X\sim \chi^2(n)$ and $Y\sim \chi^2(m)$, dann gilt $X+Y \sim \chi^2(n+m)$.
Sie nähert sich asymptotisch einer normalen Verteilung an, wenn die Anzahl an Freiheitsgraden zunimmt.

7.5 Student’s t-Verteilung

Definition “Student’s t-Verteilung” $T(n)$

Gegeben eine Variable $Z$, die einer Standardnormalverteilung folgt, $Z\sim N(0,1)$, und eine Variable $X$, die einer Chi-Quadrat-Verteilung mit $n$ Freiheitsgraden folgt, \[X\sim \chi^2(n)\], dann folgt die Variable

\[ T = \frac{Z}{\sqrt{X/n}}, \]

einer Student’s t-Verteilung mit $n$ Freiheitsgraden. Ihr Bereich ist $\mathbb{R}$ , und ihr Mittelwert und ihre Varianz sind:

\[ \mu = 0, \qquad \sigma^2 = \frac{n}{n-2}\ \mbox{ wenn } n>2. \]

Die t-Verteilung spielt eine wichtige Rolle bei der Schätzung des Populationsmittelwerts.

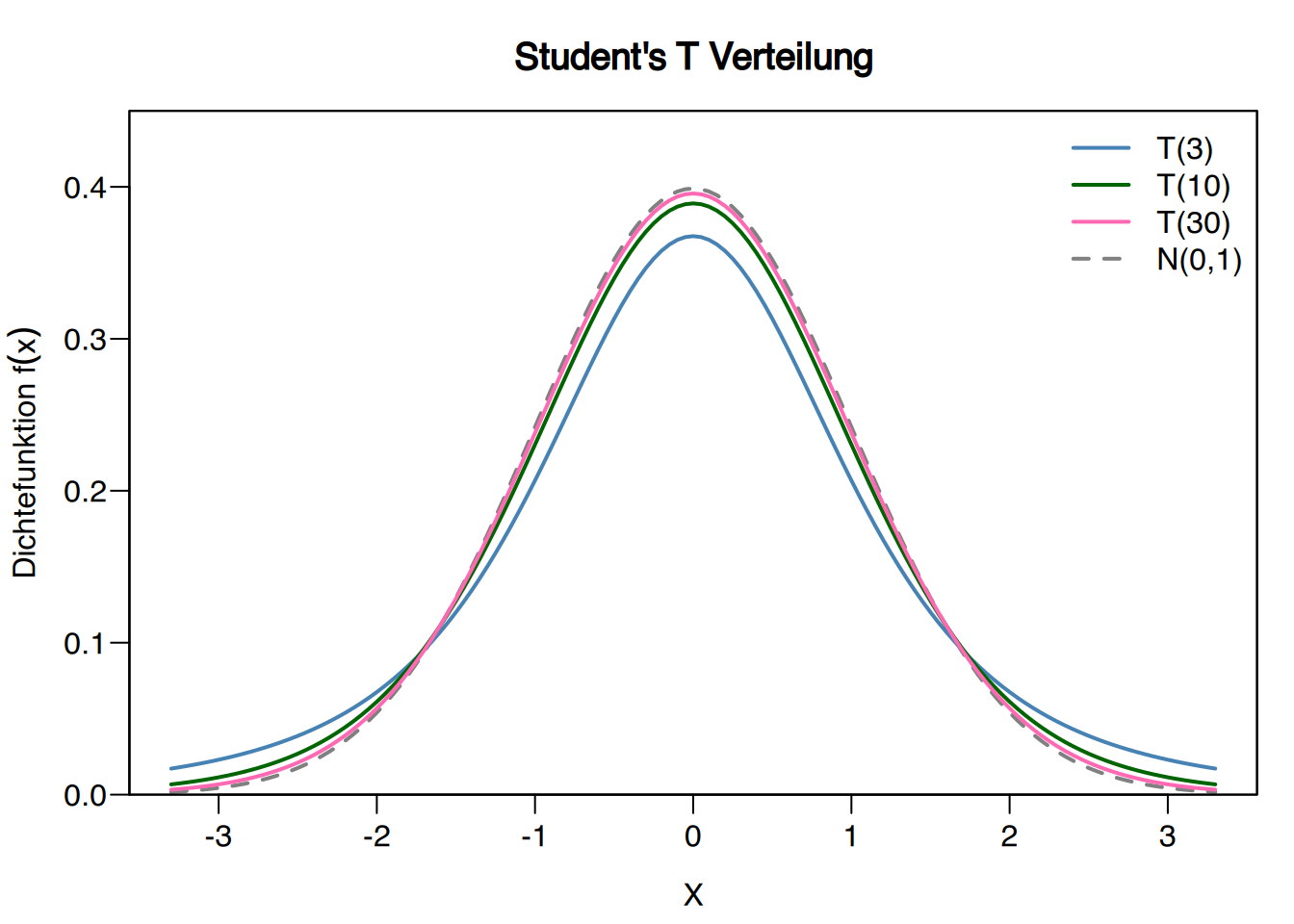
Eigenschaften der Student’s t-Verteilung:

Der Mittelwert, der Median und der Modus sind gleich, $\mu=Me=Mo$.
Sie ist symmetrisch, $g_1=0$.
Sie nähert sich asymptotisch einer Standardnormalverteilung an, wenn die Anzahl der Freiheitsgrade abnimmt. In der Praxis gilt für n ≥ 30, dass beide Verteilungen annähernd gleich sind.

\[ T(n)\stackrel{n\rightarrow \infty}{\approx}N(0,1). \]

7.6 Fisher-Snedecor-Verteilung

Definition “Fisher-Snedecor-Verteilung” $F(m,n)$

Gegeben zwei unabhängige Variablen $X$ und $Y$, die jeweils einer Chi-Quadrat-Verteilung mit $m$ bzw. $n$ Freiheitsgraden folgen, $X\sim \chi^2(m)$ and $Y\sim \chi^2(n)$, folgt die Variable

\[ F = \frac{X/m}{Y/n}, \]

einer Fisher-Snedecor-Verteilung mit $m$ und $n$ Freiheitsgraden. Ihr Bereich ist $\mathbb{R}^+$, und ihr Mittelwert und ihre Varianz sind:

\[ \mu = \frac{n}{n-2}, \qquad \sigma^2 =\frac{2n^2(m+n−2)}{m(n-2)^2(n-4)}\ \mbox{ wenn } n>4. \]

Die Fisher-Snedecor-Verteilung spielt eine wichtige Rolle beim Vergleich von Populationsvarianzen und bei der ANOVA-Analyse (Analysis of Variance).

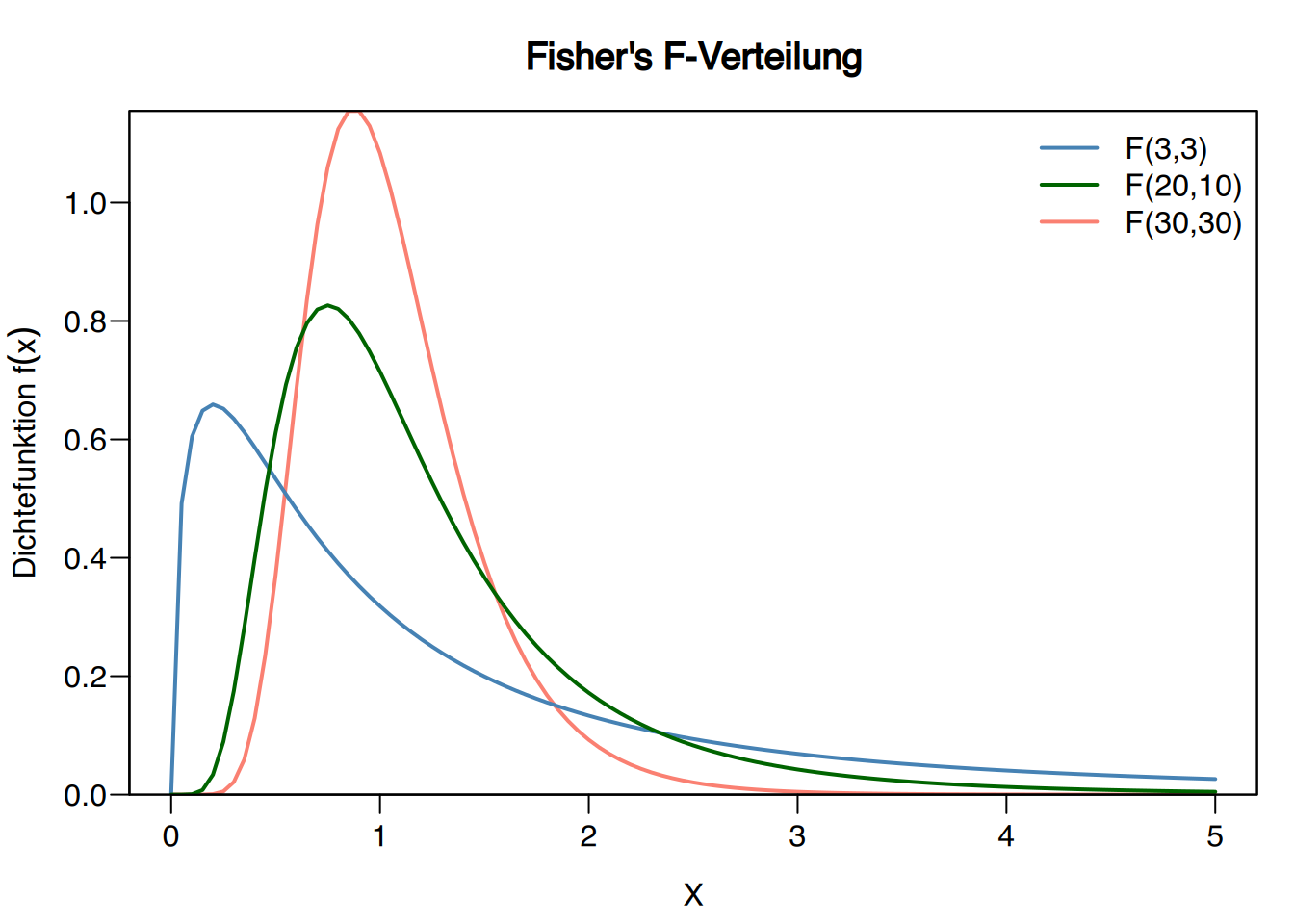
Eigenschaften der Fisher-Snedecor-Verteilung:

Der Bereich ist nicht-negativ.
Sie erfüllt die Beziehung \[ F(m,n) =\frac{1}{F(n,m)}. \]

Dies bedeutet, dass wenn wir den Wert $f(m,n)_p$ definieren als den Wert, der die Gleichung $P(F(m,n)\leq f(m,n)_p)=p$ erfüllt, dann gilt:

\[ f(m,n)_p =\frac{1}{f(n,m)_{1-p}} \]

Dies ist hilfreich beim Berechnen von Wahrscheinlichkeiten mithilfe der Verteilungsfunktionstabelle.