8  Schätzen der Populationsparameter

Die Wahrscheinlichkeitsverteilungsmodelle, die im vorherigen Abschnitt behandelt wurden, erklären das Verhalten von Zufallsvariablen. Hierfür muss bekannt sein, welchem Verteilungsmodell eine bestimmte Variable folgt. Dies ist der erste Schritt der inferenziellen Statistik.

Um das Verteilungsmodell einer Variable genau zu bestimmen, müssen die charakteristischen Merkmale aller Individuen in der Population bekannt sein, was in den meisten Fällen nicht möglich ist (wirtschaftliche, körperliche, zeitliche Unmöglichkeit usw.).

Um diese Nachteile zu vermeiden, wird auf die Untersuchung einer Stichprobe zurückgegriffen, mit dem Ziel, das Verteilungsmodell der Variable in der Population ungefähr zu bestimmen.

Die Untersuchung einer kleineren Anzahl von Individuen aus einer Stichprobe statt der gesamten Population (Vollerhebung) hat eindeutige Vorteile:

Es hat jedoch auch einige Nachteile:

Im Idealfall können diese Nachteile überwunden werden:

8.1 Stichprobenverteilungen

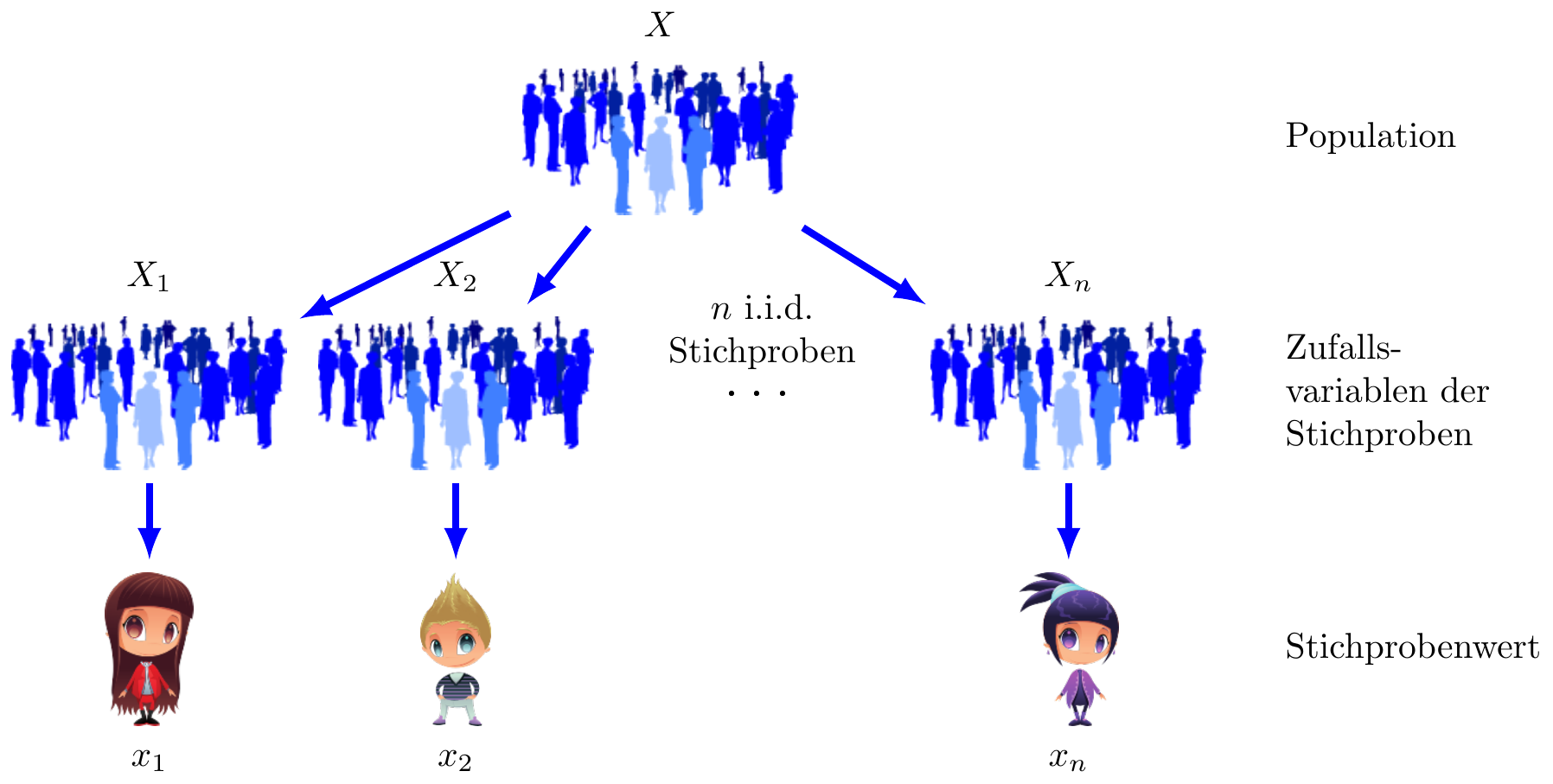
Eine Stichprobe der Größe \(n\) aus einer Zufallsvariable \(X\) kann als Realisation einer \(n\)-dimensionalen Zufallsvariablen \(X=(X_1, \dots, X_n)\) aufgefasst werden.

Definition “Stichprobe unabhängiger identisch verteilter Zufallsvariablen” (i.i.d.)

Eine Stichprobe unabhängiger identisch verteilter Zufallsvariablen (abgekürzt i.i.d., von independent and identically distributed) einer Zufallsvariable \(X\), die in einer Population untersucht wird, ist eine Sammlung von \(n\) Zufallsvariablen \(X_1,\ldots,X_n\), die folgende Eigenschaften erfüllen:

  • Jede der Zufallsvariablen \(X_i\) folgt derselben Wahrscheinlichkeitsverteilung wie die Variable \(X\) in der Population.
  • Alle Zufallsvariablen \(X_i\) sind voneinander unabhängig.

Die möglichen Werte dieser \(n\)-dimensionalen Zufallsvariablen entsprechen allen denkbaren Stichproben der Größe \(n\), die aus der Population gezogen werden können.

Die drei grundlegenden Merkmale der Stichproben-Zufallsvariable sind:

  1. Homogenität: Die Variablen, die die Stichproben-Zufallsvariable bilden, folgen der gleichen Verteilung.
  2. Unabhängigkeit: Die Variablen sind voneinander unabhängig.
  3. Verteilungsmodell: Das Verteilungsmodell, dem die \(n\) Variablen folgen.

Die ersten beiden Punkte können gelöst werden, wenn eine einfache Zufallsstichprobe zur Erhebung der Daten verwendet wird. Beim dritten Punkt müssen wiederum zwei Fragen beantwortet werden:

  1. Welches Verteilungsmodell passt am besten zu unserem Datensatz? Dies wird teilweise durch den Einsatz nichtparametrischer Methoden geklärt.
  2. Sobald das passendste Verteilungsmodell ausgewählt wurde: Welcher Parameter des Modells ist von Interesse, und wie kann sein Wert bestimmt werden? Damit befasst sich der Teil der statistischen Inferenz, der als Parameterschätzung bekannt ist.

In diesem Abschnitt wird die zweite Frage behandelt, d. h., unter der Annahme, dass das Verteilungsmodell einer Grundgesamtheit bekannt ist, werden die wichtigsten Parameter geschätzt, die es beschreiben. Zum Beispiel sind die zentralen Parameter, die die im vorherigen Thema behandelten Verteilungen definieren:

Verteilung Parameter
Binomial \(n,p\)
Poisson \(\lambda\)
Uniform \(a,b\)
Normal \(\mu,\sigma\)
Chi-Quadrat \(n\)
T-Student \(n\)
F-Fisher \(m,n\)

Die Wahrscheinlichkeitsverteilung der Werte der Stichprobenvariablen hängt eindeutig von der Wahrscheinlichkeitsverteilung der Werte in der Grundgesamtheit ab.

Beispiel: Kinder in Familien

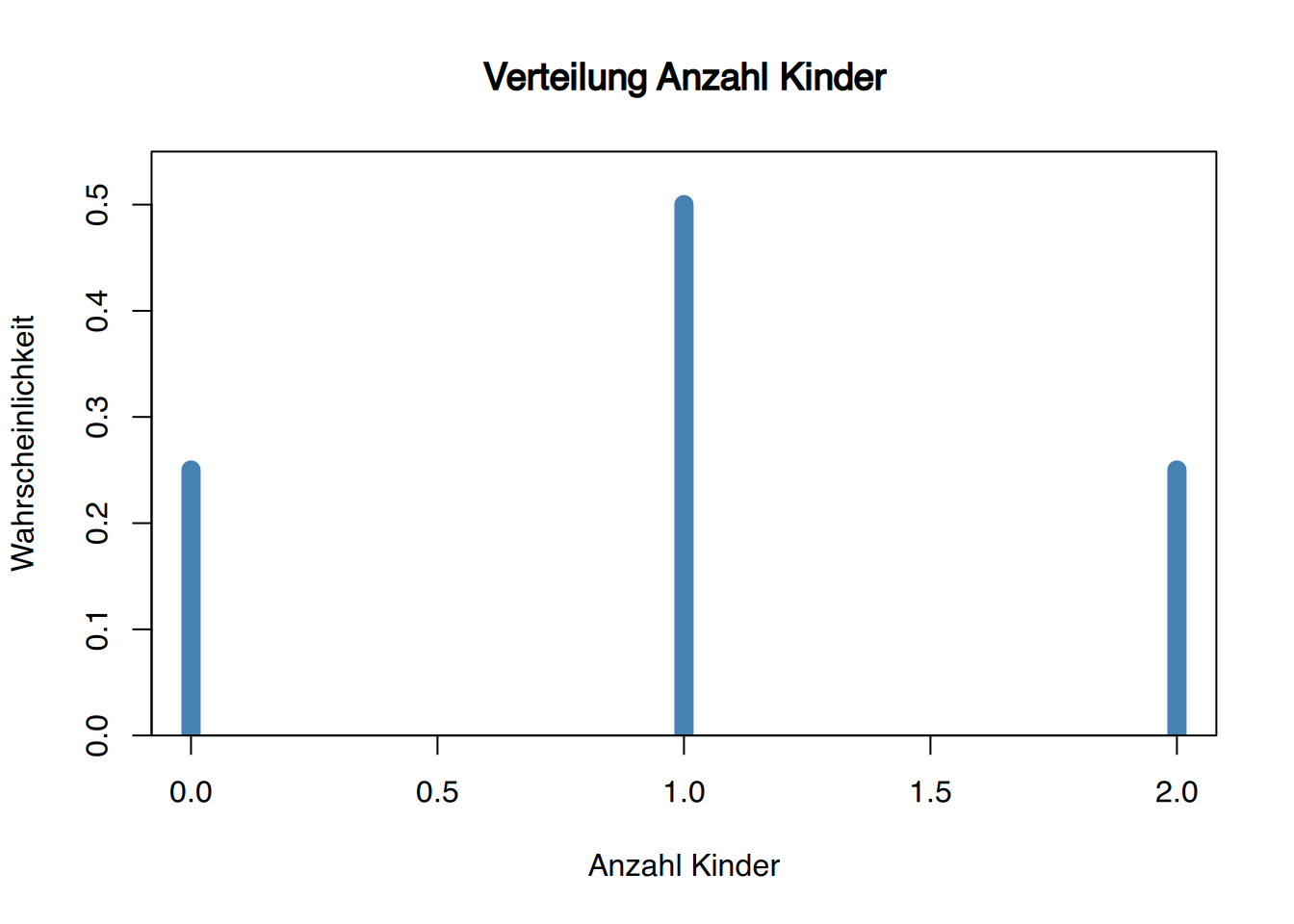
Betrachten wir eine Grundgesamtheit, in der ein Viertel der Familien keine Kinder hat, die Hälfte der Familien ein Kind besitzt und der Rest zwei Kinder hat.

\[ \begin{array}{ccc} \text{Verteilung in der Population} & & \text{Verteilung in den Stichproben} \\ \begin{array}{|c|c|}\hline X & P(x) \\\hline 0 & 0,25 \\\hline 1 & 0,50 \\\hline 2 & 0,25 \\\hline \end{array} & \xrightarrow{\text{Stichproben vom Umfang 2}} & \begin{array}{|c|c|}\hline (X_1, X_2) & P(x_1, x_2) \\\hline (0,0) & 0,0625 \\\hline (0,1) & 0,1250 \\\hline (0,2) & 0,0625 \\\hline (1,0) & 0,1250 \\\hline (1,1) & 0,2500 \\\hline (1,2) & 0,1250 \\\hline (2,0) & 0,0625 \\\hline (2,1) & 0,1250 \\\hline (2,2) & 0,0625 \\\hline \end{array} \end{array} \]

Da ein Statistikergebnis eine Funktion einer Zufallsvariable ist, stellt es selbst ebenfalls eine Zufallsvariable dar. Somit hängt seine Wahrscheinlichkeitsverteilung ebenfalls von der Verteilung der Grundgesamtheit und den sie bestimmenden Parametern ab (\(\mu\), \(\sigma\), \(p\), …).

Beispiel: Mittelwert

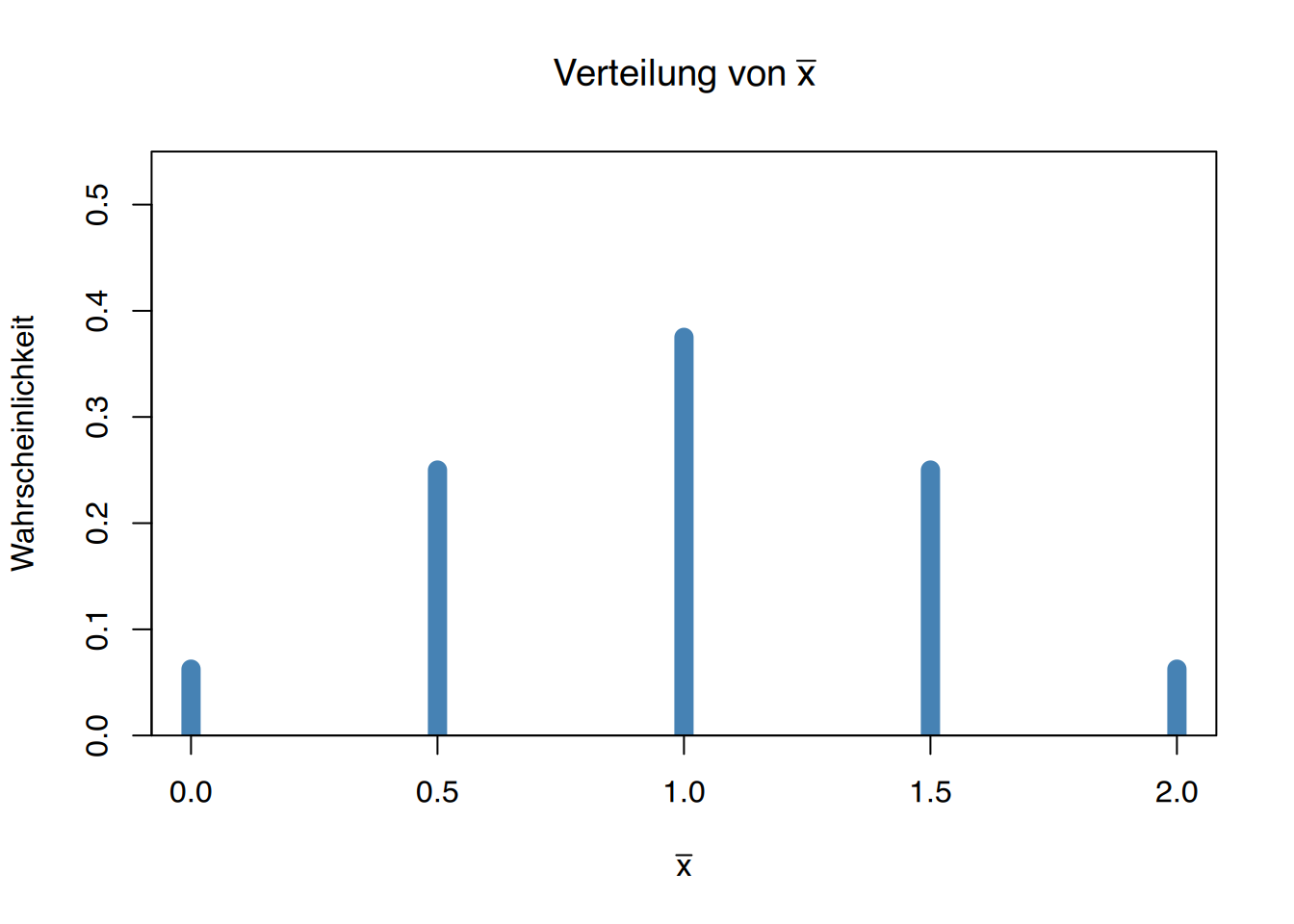
Wird der Stichprobenmittelwert \(\bar X\) aus Stichproben der Größe 2 (gemäß vorherigem Beispiel) berechnet, ergibt sich folgende Wahrscheinlichkeitsverteilung:

\[ \begin{array}{ccc} \text{Verteilung in den Stichproben} & & \text{Verteilung von}\ \overline x \\ \begin{array}{|c|c|}\hline (X_1, X_2) & P(x_1, x_2) \\\hline (0,0) & 0,0625 \\\hline (0,1) & 0,1250 \\\hline (0,2) & 0,0625 \\\hline (1,0) & 0,1225 \\\hline (1,1) & 0,2500 \\\hline (1,2) & 0,1225 \\\hline (2,0) & 0,0625 \\\hline (2,1) & 0,1250 \\\hline (2,2) & 0,0625 \\\hline \end{array} & \Large\xrightarrow{\overline x = \frac{X_1+X_2}{2}} & \begin{array}{|c|c|}\hline \overline{X} & P(x) \\\hline 0 & 0,0625 \\\hline 0,5 & 0,2500 \\\hline 1 & 0,3750 \\\hline 1,5 & 0,2500 \\\hline 2 & 0,0625 \\\hline \end{array} \end{array} \]

Wie hoch ist die Wahrscheinlichkeit, einen Stichprobenmittelwert zu erhalten, der den wahren Populationsmittelwert mit einem maximalen Fehler von 0,5 approximiert?

Wie wir gesehen haben, ist für die Bestimmung der Verteilung einer Stichprobenkennfunktion die Kenntnis der Populationsverteilung erforderlich, was jedoch nicht immer möglich ist. Glücklicherweise lässt sich für große Stichproben die Verteilung bestimmter Kennfunktionen wie des Mittelwerts näherungsweise bestimmen, dank des folgenden Theorems:

Zentraler Grenzwertsatz

Wenn \(X_1,\ldots, X_n\) unabhängige Zufallsvariablen (\(n\geq 30\)) mit Erwartungswerten \(\mu_i=E(X_i)\) und Varianzen \(\sigma^2_i=Var(X_i)\) (für \(i=1,\ldots,n\)) sind, dann folgt die Zufallsvariable \(X=X_1+\cdots+X_n\) annähernd einer Normalverteilung.

\[ X=X_1+\cdots+X_n\stackrel{n\geq 30} \sim N\left(\sum_{i=1}^n \mu_i, \sqrt{\sum_{i=1}^n \sigma^2_i}\right) \]

Der zentrale Grenzwertsatz erklärt auch, warum die meisten biologischen Variablen einer Normalverteilung folgen: Sie entstehen typischerweise durch das Zusammenspiel zahlreicher Faktoren, deren Effekte sich unabhängig voneinander addieren.

8.1.1 Verteilung des Stichprobenmittels für große Stichproben (\(n\geq 30\))

Das Stichprobenmittel einer Zufallsstichprobe vom Umfang \(n\) ist die Summe von \(n\) unabhängigen, identisch verteilten Zufallsvariablen:

\[ \bar X = \frac{X_1+\cdots+X_n}{n} = \frac{X_1}{n}+\cdots+\frac{X_n}{n} \]

Gemäß den Eigenschaften linearer Transformationen sind Erwartungswert und Varianz jeder dieser Variablen:

\[ E\left(\frac{X_i}{n}\right) =\frac{\mu}{n} \quad \mbox{und} \quad Var\left(\frac{X_i}{n}\right) = \frac{\sigma^2}{n^2} \]

wobei \(\mu\) und \(\sigma^2\) den Erwartungswert und die Varianz der zugrundeliegenden Population darstellen.

Somit folgt für große Stichprobenumfänge (\(n\geq 30\)) nach dem zentralen Grenzwertsatz, dass die Verteilung des Stichprobenmittels normal ist:

\[ \bar X \sim N\left(\sum_{i=1}^n \frac{\mu}{n},\sqrt{\sum_{i=1}^n \frac{\sigma^2}{n^2}} \right) = N\left(\mu,\frac{\sigma}{\sqrt{n}} \right). \]

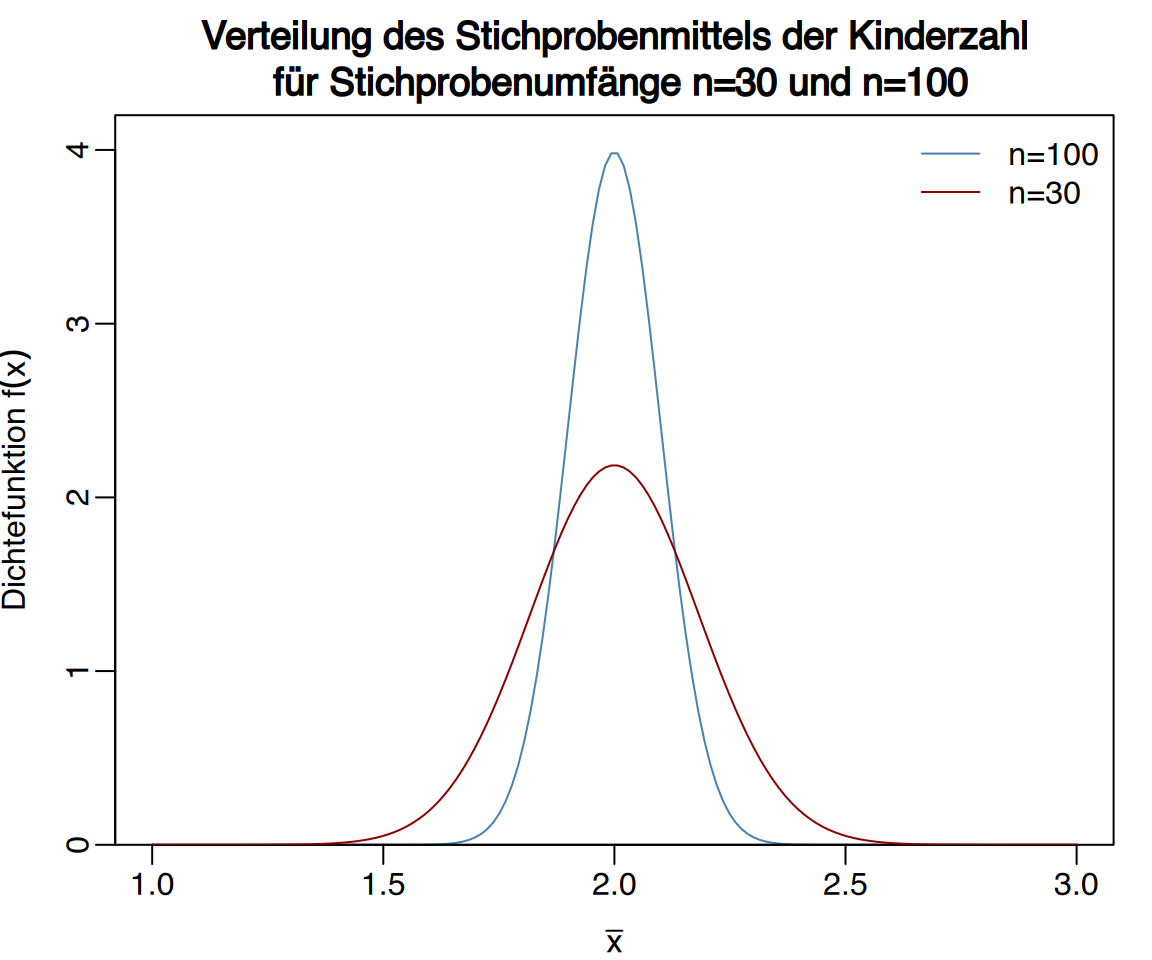
Beispiel für große Stichproben (n ≥ 30)

Angenommen, man möchte die durchschnittliche Kinderzahl in einer Population schätzen, wobei der wahre Mittelwert \(\mu=2\) Kinder und die Standardabweichung \(\sigma=1\) Kind beträgt.

Wie hoch ist die Wahrscheinlichkeit, \(\mu\) mittels \(\bar x\)̅ mit einem Fehler von weniger als 0,2 zu schätzen?

Gemäß dem zentralen Grenzwertsatz gilt:

  1. Für \(n=30\) ist \(\bar x\sim N(2,1/\sqrt{30})\) und

\[ P(1.8<\bar x<2.2) = 0.7267. \]

  1. Für \(n=100\) ist \(\bar x\sim N(2,1/\sqrt{100})\) und

\[ P(1.8<\bar x<2.2) = 0.9545. \]

8.1.2 Verteilung einer Stichprobenproportion für große Stichproben (n ≥ 30)

Eine Populationsproportion \(p\) kann als Mittelwert einer dichotomen \((0,1)\)-Variable berechnet werden. Diese Variable wird als Bernoulli-Variable \(B(p)\) bezeichnet, ein Spezialfall der Binomialverteilung für \(n=1\).

Für eine Zufallsstichprobe vom Umfang \(n\) lässt sich die Stichprobenproportion \(\hat p\) somit als Summe von \(n\) unabhängigen, identisch verteilten Zufallsvariablen darstellen:

\[ \hat p = \bar X = \frac{X_1+\cdots+X_n}{n} = \frac{X_1}{n}+\cdots+\frac{X_n}{n}, \mbox{ mit } X_i\sim B(p) \]

mit Erwartungswert und Varianz

\[ E\left(\frac{X_i}{n}\right) =\frac{p}{n} \quad \mbox{und} \quad Var\left(\frac{X_i}{n}\right) = \frac{p(1-p)}{n^2} \]

Für große Stichprobenumfänge (\(n\geq 30\)) folgt nach dem zentralen Grenzwertsatz, dass die Verteilung der Stichprobenproportion ebenfalls normalverteilt ist:

\[ \hat p \sim N\left(\sum_{i=1}^n \frac{p}{n},\sqrt{\sum_{i=1}^n \frac{p(1-p)}{n^2}} \right) = N\left(p,\sqrt{\frac{p(1-p)}{n}} \right). \]

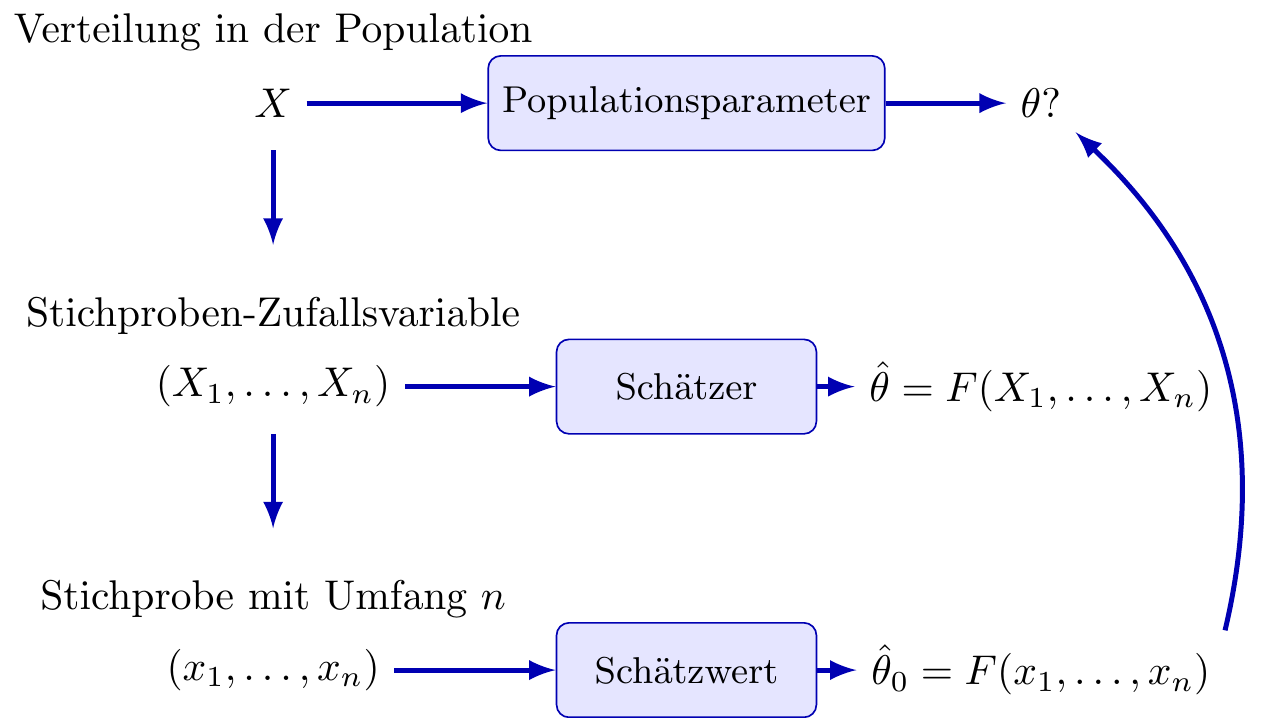
8.2 Schätzer

Stichprobenstatistiken können zur Approximation von Populationsparametern verwendet werden. Wenn ein Kennwert zu diesem Zweck eingesetzt wird, bezeichnet man ihn als Schätzer für den Parameter.

Definition “Schätzer und Schätzwert”

Ein Schätzer ist eine Funktion der Stichproben-Zufallsvariablen:

\[ \hat \theta = F(X_1,\ldots,X_n). \]

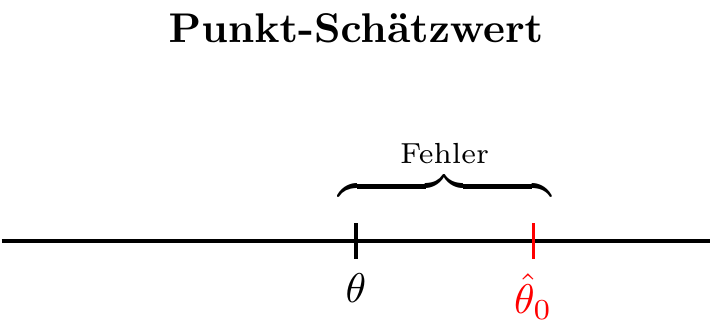
Für eine konkrete Stichprobe \((x_1,\ldots,x_n)\) wird der Wert des Schätzers, angewendet auf diese Stichprobe, als Schätzwert bezeichnet:

\[ \hat \theta_0 = F(x_1,\ldots,x_n). \]

Da es sich um eine Funktion der Stichproben-Zufallsvariablen handelt, ist ein Schätzer selbst wieder eine Zufallsvariable, deren Verteilung von der zugrundeliegenden Population abhängt.

Während der Schätzer als Funktion eindeutig ist, ist der Schätzwert nicht eindeutig, sondern hängt von der gezogenen Stichprobe ab.

Beispiel Raucher

Angenommen, man möchte den Anteil \(p\) der Raucher in einer Stadt ermitteln. In diesem Fall folgt die dichotome Variable, die misst, ob eine Person raucht \((1)\) oder nicht \((0)\), einer Bernoulli-Verteilung \(B(p)\).

Wenn eine Zufallsstichprobe vom Umfang 5, \((X_1,X_2,X_3,X_4,X_5)\), aus dieser Grundgesamtheit gezogen wird, kann der Anteil der Raucher in der Stichprobe als Schätzer für den Anteil der Raucher in der Grundgesamtheit verwendet werden:

\[ \hat p = \frac{\sum_{i=1}^5 X_i}{5} \]

Dieser Schätzer ist eine Zufallsvariable, die folgendermaßen verteilt ist:

\[ \hat p\sim \frac{1}{n}B\left(p,\sqrt{\frac{p(1-p)}{n}}\right). \]

Wenn verschiedene Stichproben gezogen werden, erhält man unterschiedliche Schätzwerte:

\[ \begin{array}{|c|c|} \hline \mbox{Stichprobe} & \mbox{Schätzwert}\\ \hline\hline (1, 0, 0, 1, 1) & 3/5\\ \hline (1, 0, 0, 0, 0) & 1/5\\ \hline (0, 1, 0, 0, 1) & 2/5\\ \hline \cdots & \cdots\\ \hline \end{array} \]

Die Parameterschätzung kann auf zwei Arten durchgeführt werden:

  1. Punktschätzung: Es wird ein einzelner Schätzer verwendet, der einen Wert oder eine Näherung für den Parameter liefert. Der Hauptnachteil dieser Schätzmethode besteht darin, dass die Genauigkeit der Schätzung nicht angegeben wird.
  2. Intervallschätzung: Hier werden zwei Schätzer verwendet, die die Grenzen eines Intervalls liefern, in dem der wahre Wert des Parameters mit einer bestimmten Sicherheit vermutet wird. Diese Schätzmethode ermöglicht es, den Schätzfehler zu kontrollieren.

8.3 Punktschätzung

Die Punktschätzung verwendet einen einzelnen Schätzer, um den Wert eines unbekannten Parameters der Grundgesamtheit zu schätzen.

Theoretisch können verschiedene Schätzer für denselben Parameter verwendet werden. Zum Beispiel hätte man zur Schätzung des Raucheranteils in einer Stadt neben dem Stichprobenanteil auch andere mögliche Schätzer verwenden können, wie:

\[ \begin{aligned} \hat \theta_1 &= \sqrt[5]{X_1X_2X_3X_4X_5} \ \hat \theta_2 &= \frac{X_1 + X_5}{2} \ \hat \theta_3 &= X_1 \cdots \end{aligned} \]

Welcher Schätzer ist der beste?

Die Antwort hängt von den Eigenschaften der einzelnen Schätzer ab.

Obwohl die Punktschätzung keine direkte Aussage über die Genauigkeit der Schätzung liefert, gibt es verschiedene Eigenschaften, die diese Qualität sicherstellen.

Die wünschenswertesten Eigenschaften eines Schätzers sind:

  • Erwartungstreue (Unverzerrtheit)
  • Effizienz
  • Konsistenz
  • Asymptotische Normalverteilung
  • Vollständigkeit
Definition “Erwartungstreuer Schätzer” (unverzerrter Schätzer)

Ein Schätzer \(\hat \theta\) heißt erwartungstreu (oder unverzerrt) für einen Parameter \(\theta\), wenn sein Erwartungswert genau \(\theta\) entspricht, d. h.,

\[ E(\hat \theta)=\theta. \]

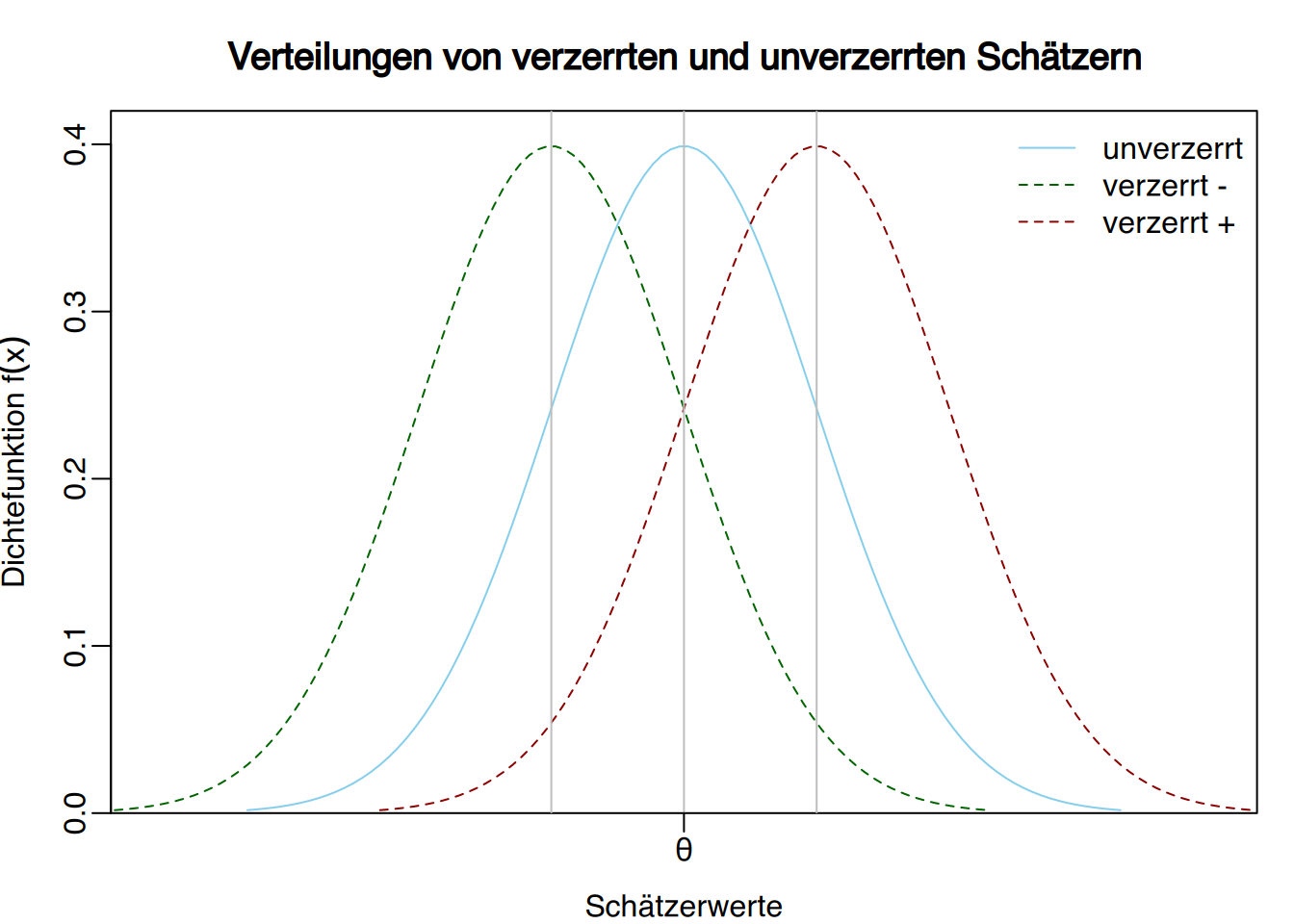
Wenn ein Schätzer nicht erwartungstreu ist, wird die Differenz zwischen seinem Erwartungswert und dem wahren Parameterwert \(\theta\) als Verzerrung (Bias) bezeichnet:

\[ \text{Bias}(\hat \theta) = E(\hat \theta)-\theta. \]

Je kleiner die Verzerrung eines Schätzers ist, desto näher liegen seine Schätzwerte am tatsächlichen Parameterwert.

Definition “Konsistenter Schätzer”

Ein Schätzer \(\hat \theta_n\) für Stichproben des Umfangs \(n\) heißt konsistent für einen Parameter \(\theta\), wenn für jedes beliebige \(\epsilon > 0\) gilt:

\[ \lim_{n\rightarrow \infty} P(|\hat \theta_n-\theta|<\epsilon)=1. \]

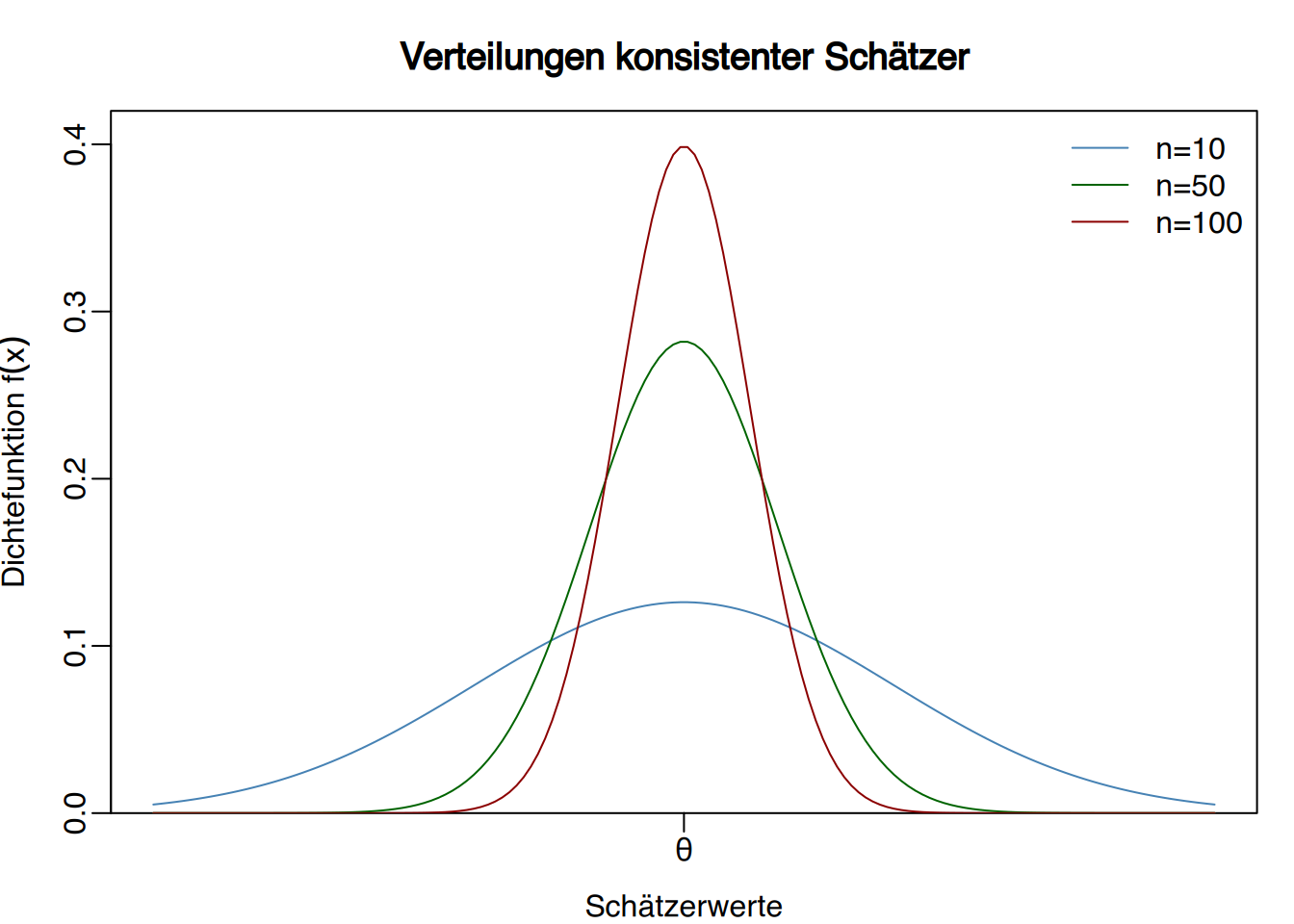
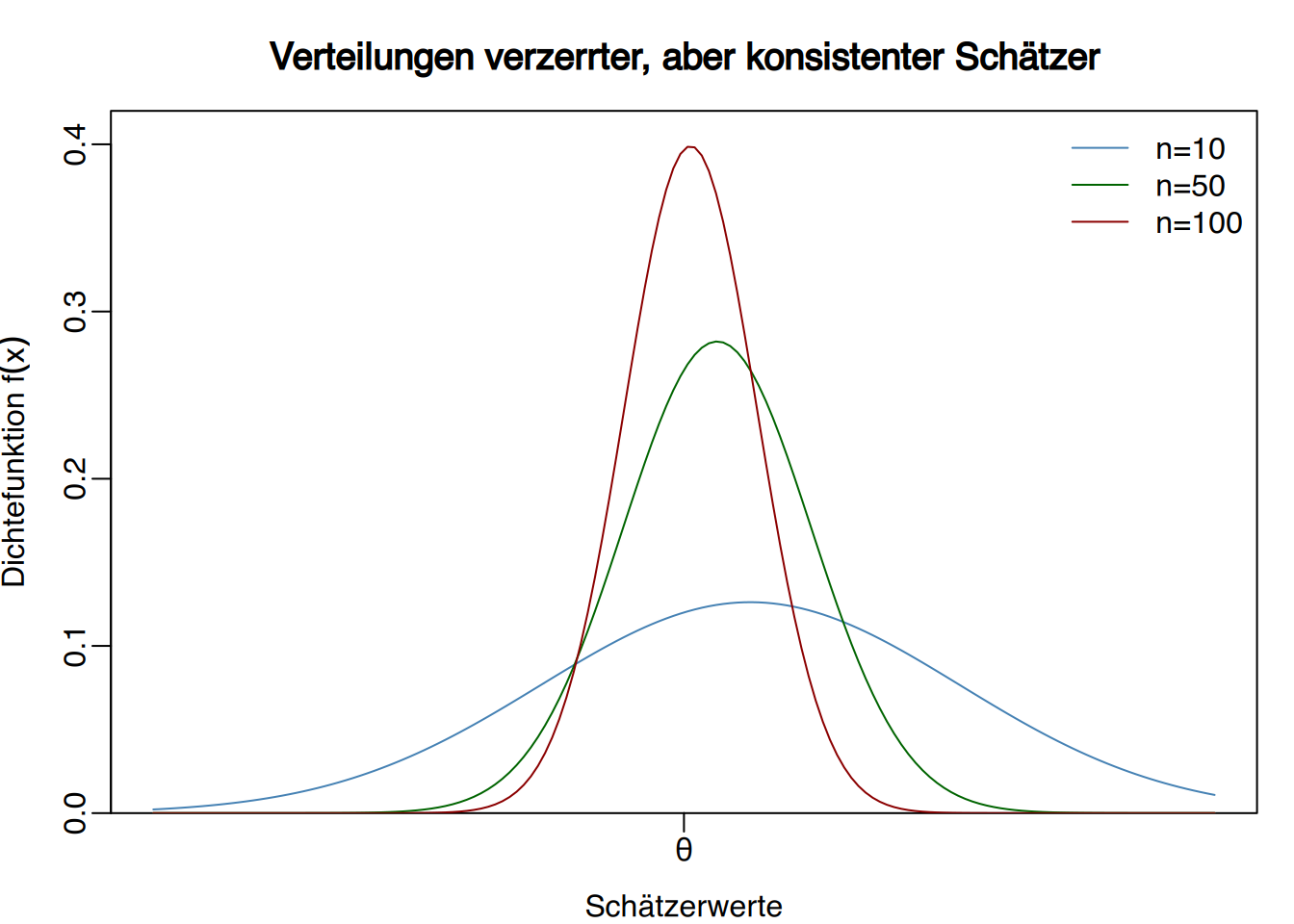
Ein Schätzer ist konsistent, wenn folgende Bedingungen erfüllt sind:

  • \(\text{Bias}(\hat \theta_n) = 0\) oder \(\lim_{n\rightarrow \infty}\text{Bias}(\hat \theta_n) = 0\)
  • \(\lim_{n\rightarrow \infty}\text{Var}(\hat \theta_n) = 0\)

Wenn also sowohl die Varianz als auch die Verzerrung mit wachsendem Stichprobenumfang abnehmen, ist der Schätzer konsistent.

Definition “Effizienter Schätzer”

Ein Schätzer \(\hat \theta\) für einen Parameter \(\theta\) heißt effizient, wenn er den mittleren quadratischen Fehler (MSE) minimiert:

\[ \text{MSE}(\hat \theta) = \text{Bias}(\hat \theta)^2+Var(\theta). \]

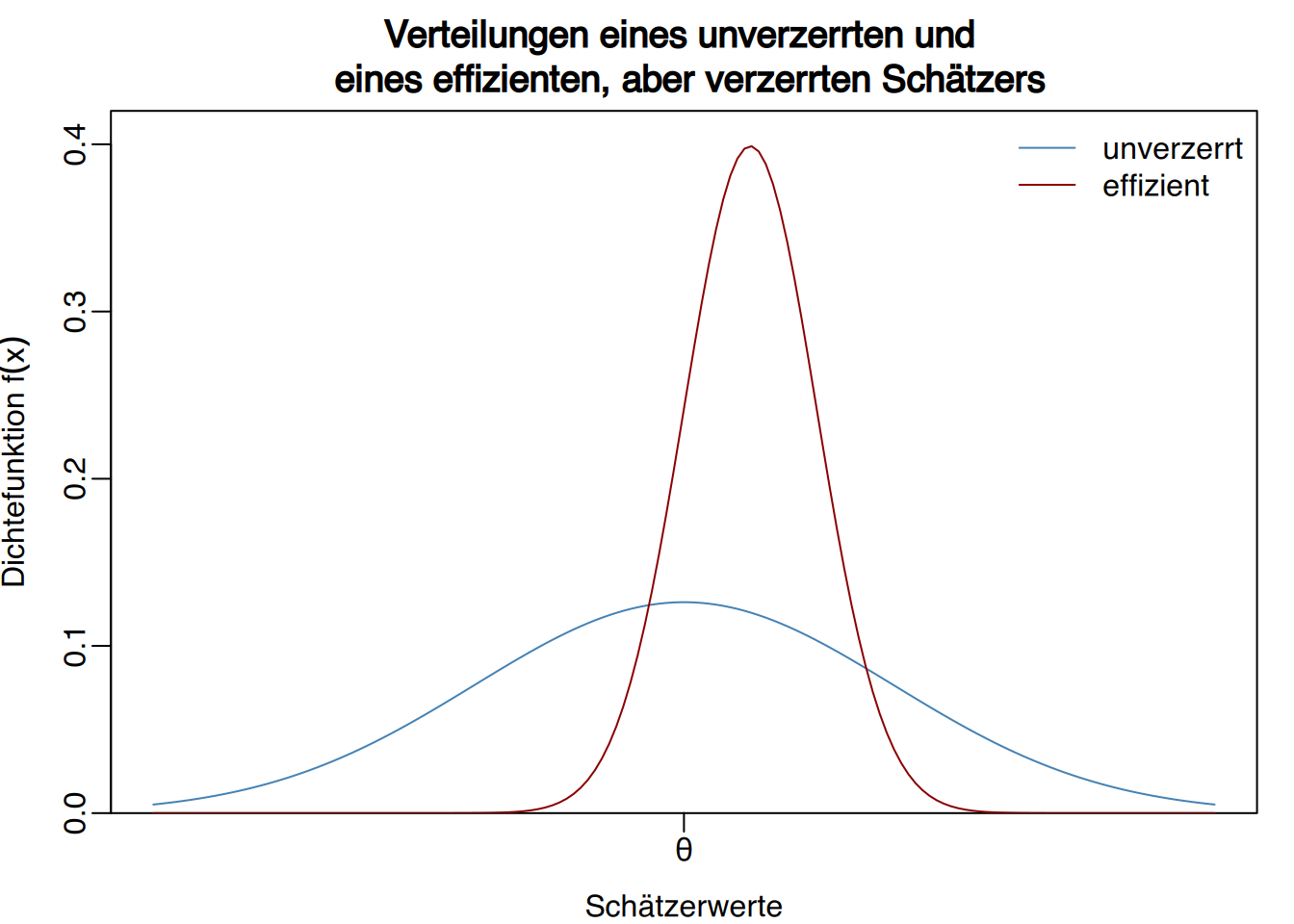
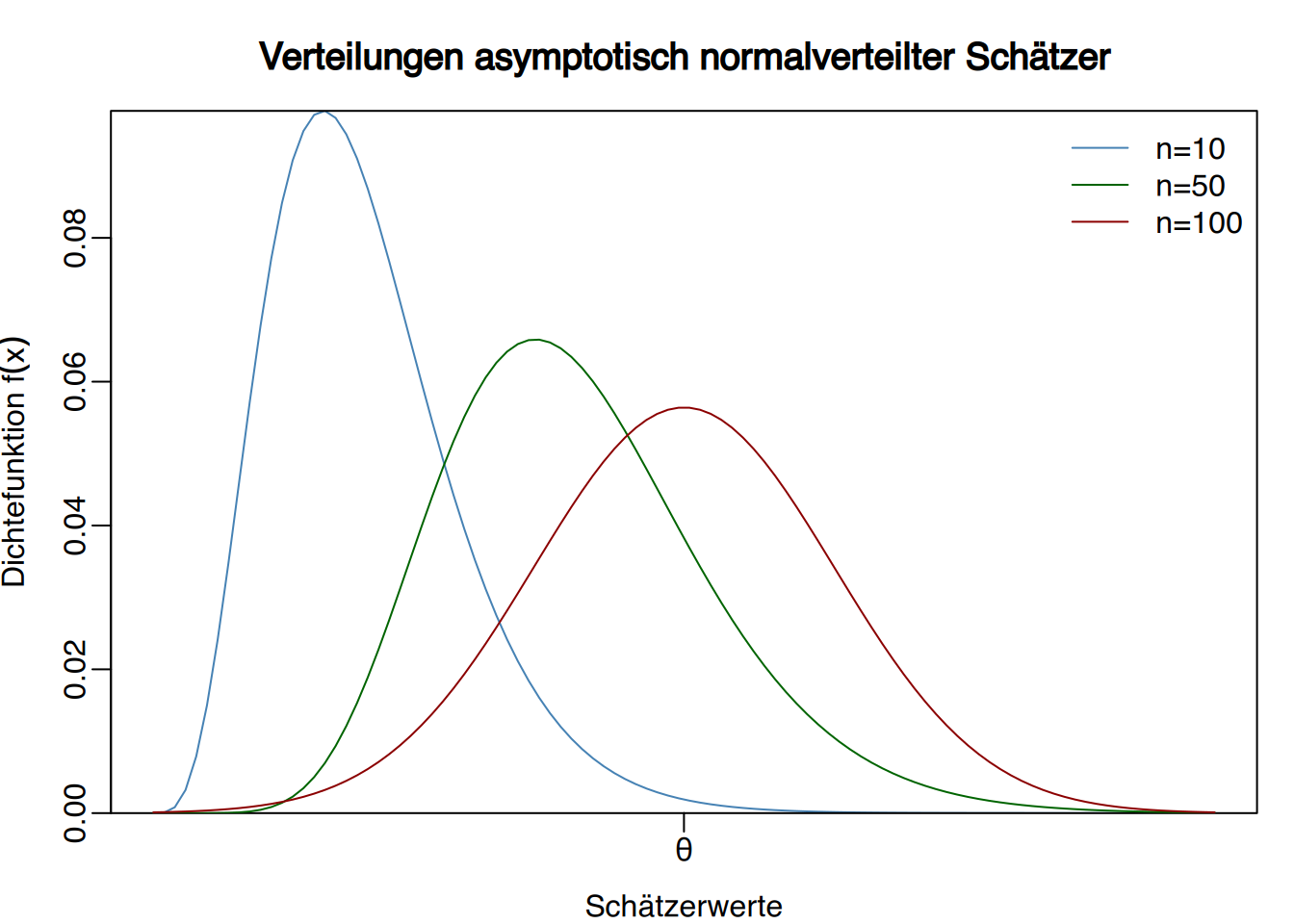
Definition “Asymptotisch normalverteilter Schätzer”

Ein Schätzer \(\hat \theta\) heißt asymptotisch normalverteilt, wenn – unabhängig von der Verteilung der Zufallsvariablen in der Stichprobe – seine Verteilung bei hinreichend großem Stichprobenumfang einer Normalverteilung folgt.

Wie wir später sehen werden, ist diese Eigenschaft besonders wichtig für die Parameterschätzung mittels Konfidenzintervallen.

Definition “Suffizienter Schätzer”

Ein Schätzer \(\hat \theta\) heißt suffizient (erschöpfend) für einen Parameter \(\theta\), wenn die bedingte Verteilung der Stichprobenvariablen gegeben den Schätzwert \(\hat \theta = \hat \theta_0\) nicht mehr von \(\theta\) abhängt.

Dies bedeutet, dass nach Erhalt der Schätzung alle weiteren Informationen über die Stichprobe für \(\theta\) irrelevant werden.

Der übliche Schätzer für den Erwartungswert ist das Stichprobenmittel:

Für Stichproben vom Umfang \(n\) ergibt sich die Zufallsvariable:

\[ \bar X = \frac{X_1+\cdots+X_n}{n} \] Wenn die Grundgesamtheit den Mittelwert \(\mu\) und Varianz \(\sigma^2\) besitzt, gilt:

\[ E(\bar X) = \mu \quad \mbox{und} \quad Var(\bar X)=\frac{\sigma^2}{n} \]

Somit ist das Stichprobenmittel:

  • ein erwartungstreuer Schätzer
  • konsistent (da die Varianz mit wachsendem \(n\) gegen \(0\) geht)
  • effizient

Die Stichprobenvarianz:

\[ S^2 = \frac{\sum_{i=1}^n (X_i-\bar X)^2}{n} \]

ist jedoch ein verzerrter Schätzer für die Populationsvarianz, denn:

\[ E(S^2)= \frac{n-1}{n}\sigma^2. \]

Diese Verzerrung lässt sich leicht korrigieren, um einen erwartungstreuen Schätzer zu erhalten.

Definition “Stichproben-Quasivarianz”

Für eine Stichprobe vom Umfang \(n\) einer Zufallsvariablen \(X\) wird die Stichproben-Quasivarianz definiert als:

\[ \hat{S}^2 = \frac{\sum_{i=1}^n (X_i-\bar X)^2}{n-1} = \frac{n}{n-1}S^2. \]

8.4 Intervallschätzer

Das Hauptproblem der Punktschätzung besteht darin, dass nach Auswahl der Stichprobe und Berechnung der Schätzung der tatsächliche Fehler unbekannt bleibt.

Um den Schätzfehler kontrollieren zu können, ist die Intervallschätzung die bessere Methode.

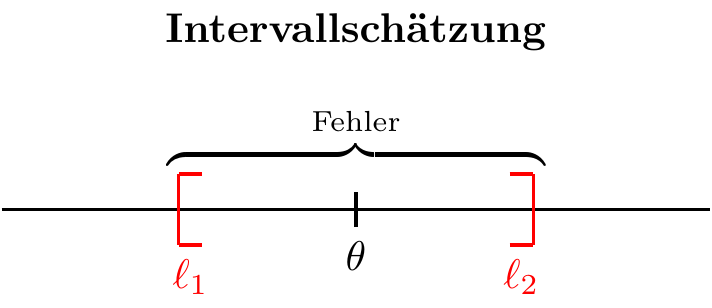
Bei der Intervallschätzung wird versucht, ausgehend von der Stichprobe ein Intervall zu konstruieren, in dem der zu schätzende Parameter mit einer bestimmten Konfidenzwahrscheinlichkeit vermutet wird. Hierzu werden zwei Schätzer verwendet - einer für die untere und einer für die obere Intervallgrenze.

Definition “Konfidenzintervall”

Gegeben zwei Schätzer \(\hat l_i(X_1,\ldots,X_n)\) und \(\hat l_s(X_1,\ldots,X_n)\) sowie deren jeweilige Schätzwerte \(l_1\) und \(l_2\) für eine konkrete Stichprobe, heißt das Intervall \(I=[l_1,l_2]\) Konfidenzintervall für einen Populationsparameter \(\theta\) zum Konfidenzniveau \(1-\alpha\) (oder Signifikanzniveau \(\alpha\)), wenn gilt:

\[ P(\hat l_i(X_1,\ldots,X_n)\leq \theta \leq \hat l_s(X_1,\ldots,X_n))= 1-\alpha. \]

Wichtige Anmerkungen zu Konfidenzintervallen:

  • Ein Konfidenzintervall garantiert niemals mit absoluter Sicherheit, dass der Parameter darin enthalten ist.
  • Man kann nicht sagen, die Wahrscheinlichkeit, dass der Parameter im Intervall liegt, betrage \(1-\alpha\) - denn nach Berechnung des Intervalls haben die Zufallsvariablen feste Werte angenommen.
  • Die korrekte Interpretation ist: \((1-\alpha)%\) aller möglichen Stichprobenintervalle enthalten den wahren Parameter.
  • Daher spricht man von Konfidenz (Vertrauen), nicht von Wahrscheinlichkeit.

Typische Konfidenzniveaus in der Praxis:

\[ \begin{aligned} 1-\alpha &= 0.90 \quad (\alpha=0.10) \\ 1-\alpha &= 0.95 \quad (\alpha=0.05) \quad \text{(am häufigsten verwendet)} \\ 1-\alpha &= 0.99 \quad (\alpha=0.01) \quad \text{(für kritische Anwendungen)} \end{aligned} \]

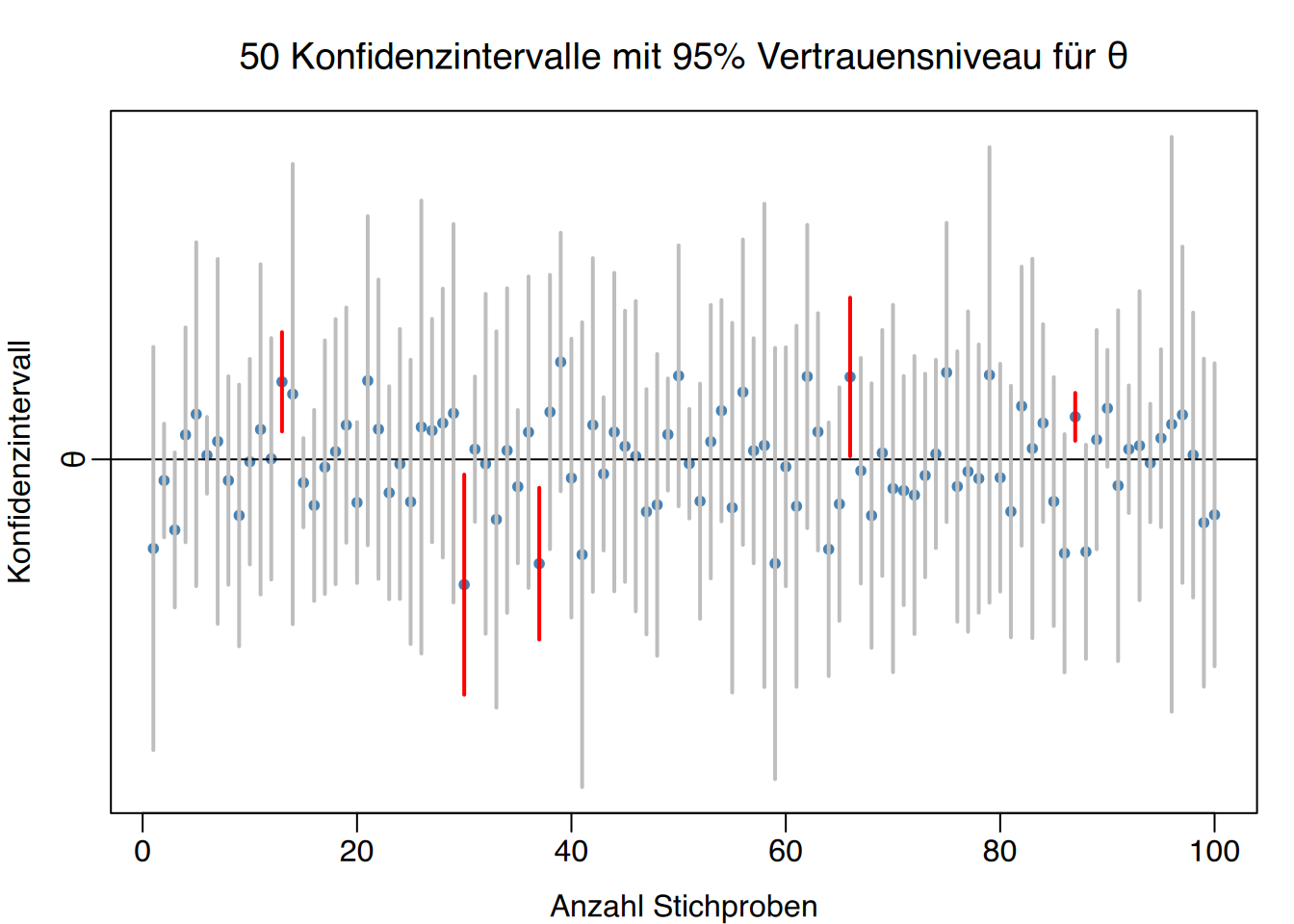
Theoretisch enthalten bei einem Konfidenzniveau von \(1-\alpha = 0,95\ \) etwa 95 von 100 berechneten Intervallen den wahren Parameter \(\theta\), während etwa 5 Intervalle ihn nicht enthalten.

8.4.1 Schätzfehler

Ein weiterer zentraler Aspekt von Konfidenzintervallen ist ihre Fehlerspanne.

Definition “Fehlerspanne”

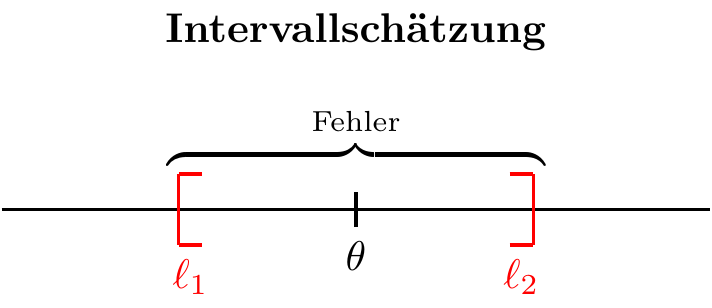
Die Fehlerspanne oder Ungenauigkeit eines Konfidenzintervalls \([l_i,l_s]\) wird durch seine Breite bestimmt:

\[ A=l_s-l_i. \]

Damit ein Intervall praktisch nutzbar ist, darf diese Ungenauigkeit nicht zu groß sein.

Grundsätzlich hängt die Präzision eines Intervalls von drei Faktoren ab:

  1. Streuung der Grundgesamtheit: Je größer die Streuung, desto ungenauer das Intervall.
  2. Konfidenzniveau: Höhere Konfidenzniveaus führen zu weniger präzisen Intervallen.
  3. Stichprobenumfang: Größere Stichproben erhöhen die Präzision.

Wenn Konfidenz und Präzision im Konflikt stehen - wie kann man dann Präzision gewinnen ohne Konfidenz zu verlieren?

In der Praxis geht man typischerweise wie folgt vor:

  • Man beginnt mit einem Punktschätzer, dessen Stichprobenverteilung bekannt ist.
  • Auf Basis dieser Verteilung bestimmt man die Intervallgrenzen so, dass sie eine Wahrscheinlichkeit von \(1-\alpha\) einschließen.
  • Üblicherweise wählt man die Grenzen symmetrisch:
    • Die untere Grenze schließt \(\alpha/2\) der Wahrscheinlichkeit aus
    • Die obere Grenze schließt ebenfalls \(\alpha/2\) aus

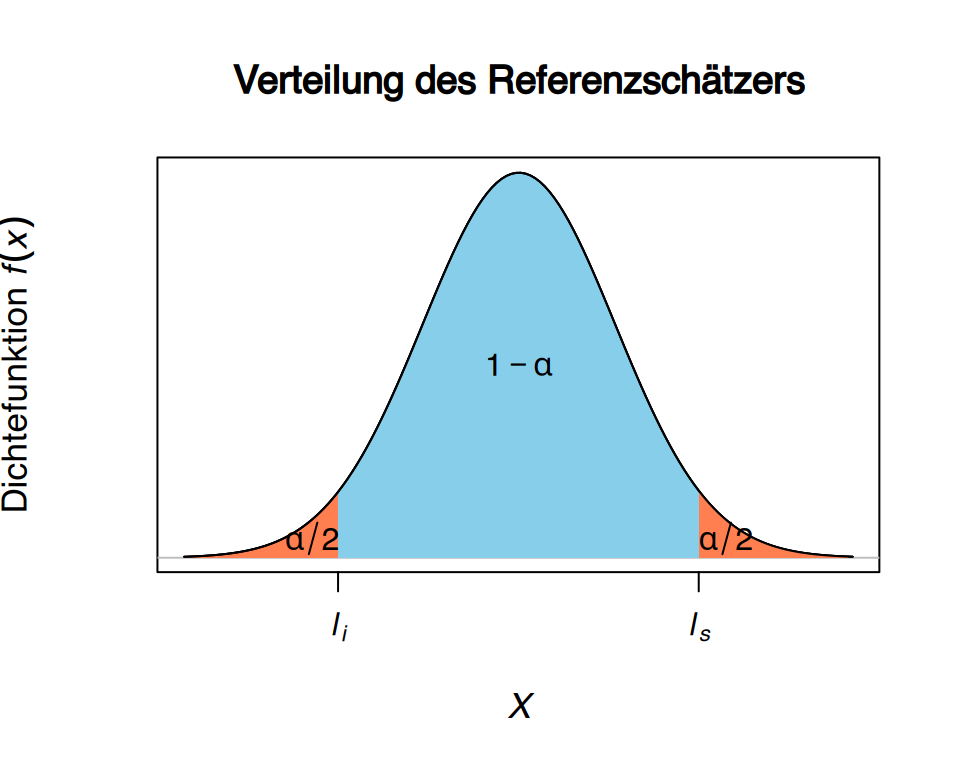
8.5 Konfidenzintervalle für eine Grundgesamtheit

Im Folgenden werden Konfidenzintervalle zur Schätzung von Parametern einer Grundgesamtheit dargestellt:

  • Konfidenzintervall für den Mittelwert einer normalverteilten Grundgesamtheit mit bekannter Varianz
  • Konfidenzintervall für den Mittelwert einer normalverteilten Grundgesamtheit mit unbekannter Varianz
  • Konfidenzintervall für den Mittelwert einer Grundgesamtheit mit unbekannter Varianz bei großen Stichproben
  • Konfidenzintervall für die Varianz einer normalverteilten Grundgesamtheit
  • Konfidenzintervall für einen Anteilswert einer Grundgesamtheit

8.5.1 Konfidenzintervall für den Mittelwert einer normalverteilten Grundgesamtheit mit bekannter Varianz

Sei \(X\) eine Zufallsvariable, die folgende Annahmen erfüllt:

  • Sie ist normalverteilt: \(X\sim N(\mu,\sigma)\)
  • Der Mittelwert \(\mu\) ist unbekannt, aber die Varianz \(\sigma^2\) ist bekannt

Unter diesen Annahmen folgt der Stichprobenmittelwert für Stichproben des Umfangs \(n\) ebenfalls einer Normalverteilung:

\[ \bar X \sim N\left(\mu,\frac{\sigma}{\sqrt n}\right) \]

Durch Standardisierung der Variable erhält man:

\[ Z=\frac{\bar X-\mu}{\sigma/\sqrt n} \sim N(0,1) \]

Auf dieser Verteilung lassen sich einfach die Werte \(z_i\) und \(z_s\) berechnen, so dass gilt:

\[ P(z_i\leq Z \leq z_s) = 1-\alpha. \]

Da die Standardnormalverteilung symmetrisch um \(0\) ist, wählt man am besten entgegengesetzte Werte \(-z_{\alpha/2}\) und \(z_{\alpha/2}\) , die jeweils \(\alpha/2\) der Wahrscheinlichkeit in den Rändern lassen.

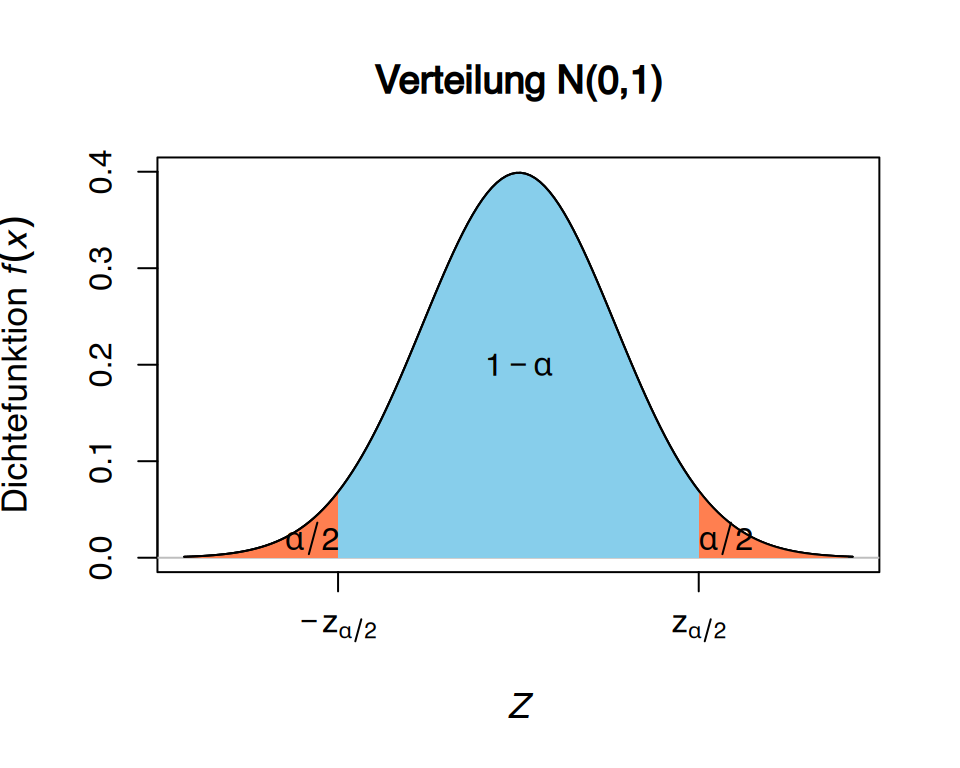
Ausgehend von der Standardisierung lässt sich durch Umformung einfach zu den Schätzern für die Grenzen des Konfidenzintervalls gelangen:

\[ \begin{aligned} 1-\alpha &= P(-z_{\alpha/2}\leq Z \leq z_{\alpha/2}) = P\left(-z_{\alpha/2}\leq \frac{\bar X -\mu}{\sigma/\sqrt{n}} \leq z_{\alpha/2}\right) =\\ &= P\left(-z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\leq \bar X -\mu \leq z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\right)=\\ &= P\left(-\bar{X}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\leq -\mu \leq -\bar{X}+z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\right)= \\ &= P\left(\bar{X}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\leq \mu \leq \bar{X}+z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\right). \end{aligned} \]

Konfidenzintervall für den Mittelwert einer Normalverteilung mit bekannter Varianz

Falls \(X\sim N(\mu, \sigma)\) mit bekannter Standardabweichung \(\sigma\), dann lautet das Konfidenzintervall für den Mittelwert \(\mu\) zum Konfidenzniveau \(1-\alpha\):

\[ \left[\bar{X}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{X}+z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\right] \]

alternativ geschrieben als:

\[ \bar{X}\pm z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \]

Aus der Intervallformel

\[ \bar{X}\pm z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \]

ergeben sich folgende Charakteristika:

  1. Das Intervall ist zentriert um den Stichprobenmittelwert \(\bar X\), den besten Schätzer für den Populationsmittelwert.
  2. Die Breite (Ungenauigkeit) des Intervalls beträgt: \[ A= 2 z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \]

Diese hängt ab von:

  • \(\sigma:\quad\) Je größer die Populationsvarianz, desto ungenauer das Intervall
  • \(z_{\alpha/2 :\quad}\) Abhängig vom Konfidenzniveau - höhere Konfidenzniveaus (\(1-\alpha\)) führen zu größeren Intervallen
  • \(n:\quad\) Größere Stichproben verringern die Ungenauigkeit

Die einzige Möglichkeit, die Intervallgenauigkeit bei gleichbleibendem Konfidenzniveau zu verbessern, besteht folglich in der Erhöhung des Stichprobenumfangs.

8.5.1.1 Berechnung des Stichprobenumfangs zur Schätzung des Mittelwerts einer Normalverteilung mit bekannter Varianz

Unter Berücksichtigung der Breite (Ungenauigkeit) des Konfidenzintervalls für den Mittelwert einer Normalverteilung mit bekannter Varianz:

\[ A= 2 z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \]

kann der erforderliche Stichprobenumfang zur Erzielung einer Intervallbreite \(A\) mit Konfidenzniveau \(1-\alpha\) leicht berechnet werden:

\[ A= 2 z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \Leftrightarrow \sqrt{n}= 2 z_{\alpha/2}\frac{\sigma}{A}, \]

woraus folgt:

\[ {n = 4 z_{\alpha/2}^2\frac{\sigma^2}{A^2}} \]

Beispiel

Betrachten wir eine Studentenpopulation, deren Prüfungsergebnisse einer Normalverteilung \(X\sim N(\mu,\sigma=1.5)\) folgen.

Zur Schätzung der Durchschnittsnote \(\mu\) wird eine Stichprobe von 10 Studenten gezogen:

\[ 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \]

Daraus berechnen wir das 95%-Konfidenzintervall (\(\alpha=0.05\)) für \(\mu\):

  • \(\bar X = \frac{4+\cdots+3}{10}= \frac{53}{10} = 5.3\) Punkte

  • \(z_{\alpha/2}=z_{0.025} \approx 1.96\) (Standardnormalverteilung)

Einsetzen in die Intervallformel ergibt:

\[ \bar{X}\pm z_{\alpha/2}\frac{\sigma}{\sqrt{n}} = 5.3\pm 1.96\frac{1.5}{\sqrt{10}} = 5.3\pm 0.93 = \left[4.37,\,6.23\right]. \]

Mit 95%iger Sicherheit liegt \(\mu\) somit zwischen 4.37 und 6.23 Punkten.

Beispiel

Die Ungenauigkeit dieses Intervalls beträgt \(\pm 0.93\) Punkte.

Für eine höhere Präzision von \(\pm 0.5\) Punkten berechnet sich der erforderliche Stichprobenumfang zu:

\[ n = 4 z_{\alpha/2}^2\frac{\sigma^2}{A^2} = 4\cdot 1.96^2\frac{1.5^2}{(2\cdot 0.5)^2} = 34.57. \]

Es wird daher eine Stichprobe von mindestens 35 Studenten benötigt, um ein 95%-Konfidenzintervall mit \(\pm 0,5\) Punkten Genauigkeit zu erhalten.

8.5.2 Konfidenzintervall für den Mittelwert einer Normalverteilung mit unbekannter Varianz

Gegeben sei eine Zufallsvariable \(X\), die folgende Annahmen erfüllt:

  • Normalverteilung:\(X\sim N(\mu,\sigma)\)
  • Sowohl der Mittelwert \(\mu\) als auch die Varianz \(\sigma^2\) sind unbekannt

Wenn die Populationsvarianz unbekannt ist, wird sie typischerweise durch die korrigierte Stichprobenvarianz \(\hat{S}^2\) geschätzt. Dadurch folgt der Referenzschätzer nicht mehr einer Normalverteilung (wie bei bekannter Varianz), sondern einer \(t\)-Verteilung mit \(n-1\) Freiheitsgraden:

\[ \left. \begin{array}{l} \bar X \sim N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)\\ \displaystyle\frac{(n-1)\hat{S}^2}{\sigma^2}\sim \chi^2(n-1) \end{array} \right\} \Rightarrow \frac{\bar X -\mu}{\hat{S}/\sqrt{n}}\sim T(n-1), \]

Da die t-Verteilung (wie die Normalverteilung) symmetrisch um \(0\) ist, können zwei entgegengesetzte Werte \(-t^{n-1}_{\alpha/2}\) und \(t^{n-1}_{\alpha/2}\) gewählt werden, sodass gilt:

\[ \begin{aligned} 1-\alpha &= P\left(-t^{n-1}_{\alpha/2}\leq \frac{\bar X -\mu}{\hat{S}/\sqrt{n}} \leq t^{n-1}_{\alpha/2}\right)\\ &= P\left(-t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}}\leq \bar X -\mu \leq t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}}\right)\\ &= P\left(\bar X-t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}}\leq \mu \leq \bar X t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}}\right) \end{aligned} \]

Konfidenzintervall für den Mittelwert einer Normalverteilung mit unbekannter Varianz

Falls \(X\sim N(\mu, \sigma)\) mit unbekannter Standardabweichung \(\sigma\), dann lautet das Konfidenzintervall für den Mittelwert \(\mu\) zum Konfidenzniveau \(1-\alpha\):

\[ \left[\bar{X}-t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}},\bar{X}+t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}}\right] \]

alternativ geschrieben als:

\[ \bar{X}\pm t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}} \]

8.5.2.1 Berechnung des Stichprobenumfangs zur Schätzung des Mittelwerts einer Normalverteilung mit unbekannter Varianz

Analog zum vorherigen Fall ergibt sich die Breite (Ungenauigkeit) des Konfidenzintervalls für den Mittelwert bei unbekannter Varianz zu:

\[ A= 2 t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}} \]

Daraus lässt sich der benötigte Stichprobenumfang für eine gewünschte Intervallbreite \(A\) mit Konfidenzniveau \(1-\alpha\) ableiten:

\[ A= 2 t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}} \Leftrightarrow \sqrt{n}= 2 t^{n-1}_{\alpha/2}\frac{\hat{S}}{A}, \]

was zu folgender Formel führt:

\[ {n = 4 (t^{n-1}_{\alpha/2})^2\frac{\hat{S}^2}{A^2}} \]

Der entscheidende Unterschied zum Fall mit bekannter Varianz besteht darin, dass \(\hat{S}\) bekannt sein muss. Daher wird typischerweise wie folgt vorgegangen:

  • Eine kleine Vorstichprobe wird gezogen, um \(\hat{S}\) zu schätzen
  • Der \(t\)-Wert kann für größere Stichproben durch den \(z\)-Wert der Normalverteilung approximiert werden: \(t^{n-1}_{\alpha/2}\approx z_{\alpha/2}\)
Beispiel

Angenommen, im vorherigen Beispiel sei die Populationsvarianz der Prüfungsergebnisse unbekannt.

Mit derselben Stichprobe von 10 Studenten:

\[ 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \]

ergibt sich das 95%-Konfidenzintervall (\(\alpha=0.05\)) für \(\mu\) wie folgt:

  • \(\bar X = \frac{53}{10} = 5.3\) Punkte
  • \(\hat{S}^2= \frac{\sum(x_i-\bar x)^2}{9} = 3.5667\) und \(\hat{S}=1.8886\) Punkte
  • \(t^{n-1}_{\alpha/2}=t^9_{0.025} = 2.2622\) (\(t\)-Verteilung mit 9 Freiheitsgraden)

Das Konfidenzintervall berechnet sich zu:

\[ \bar{X}\pm t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}} = 5.3\pm 2.2622\frac{1.8886}{\sqrt{10}} = 5.3\pm 1.351 = \left[3.949,\,6.651\right]. \]

Beispiel

Die Ungenauigkeit des Intervalls (\(\pm 1,8886\) Punkte) ist deutlich größer als bei bekannter Varianz - dies erklärt sich durch die zusätzliche Unsicherheit bei der Schätzung der Populationsvarianz.

Der benötigte Stichprobenumfang für eine Genauigkeit von \(\pm 0,5\) Punkten beträgt:

\[ n = 4 (z_{\alpha/2})^2\frac{\hat{S}^2}{A^2} = 4\cdot 1.96^2\frac{3.5667}{(2\cdot 0.5)^2} = 54.81. \]

Somit sind mindestens 55 Studenten nötig, um bei unbekannter Varianz ein 95%-Konfidenzintervall mit \(\pm 0,5\) Punkten Genauigkeit zu erhalten.

8.5.3 Konfidenzintervall für den Mittelwert einer nicht-normalverteilten Grundgesamtheit

Gegeben sei eine Zufallsvariable \(X\) mit folgenden Eigenschaften:

  • Ihre Verteilung ist nicht normal
  • Sowohl der Mittelwert \(\mu\) als auch die Varianz \(\sigma^2\) sind unbekannt

Bei nicht-normalverteilten Grundgesamtheiten ändern sich die Verteilungen der Referenzschätzer, sodass die bisherigen Intervalle nicht anwendbar sind.

Für große Stichproben (\(n\geq 30\)) gilt jedoch nach dem zentralen Grenzwertsatz, dass sich die Verteilung des Stichprobenmittelwerts einer Normalverteilung annähert:

\[ \bar X \sim N\left(\mu,\frac{\sigma}{\sqrt{n}}\right) \]

Somit bleibt das zuvor beschriebene Intervall gültig.

Konfidenzintervall für den Mittelwert einer nicht-normalverteilten Grundgesamtheit bei großen Stichproben

Für eine nicht-normalverteilte Variable \(X\) mit \(n\geq 30\) lautet das (\(1-\alpha\))-Konfidenzintervall für \(\mu\):

\[ \bar{X}\pm t^{n-1}_{\alpha/2}\frac{\hat{S}}{\sqrt{n}} \]

8.5.4 Konfidenzintervall für die Varianz einer normalverteilten Grundgesamtheit

Voraussetzungen:

  • \(X\) ist normalverteilt: \(X\sim N(\mu,\sigma)\)
  • Sowohl \(\mu\) als auch \(\sigma^2\) sind unbekannt

Als Ausgangspunkt dient der Referenzschätzer:

\[ \frac{nS^2}{\sigma^2} = \frac{(n-1)\hat{S}^2}{\sigma^2}\sim \chi^2(n-1), \]

der einer Chi-Quadrat-Verteilung mit \(n-1\) Freiheitsgraden folgt.

Es müssen die Werte \(\chi_i\) und \(\chi_s\) bestimmt werden, für die gilt:

\[ P(\chi_i\leq \chi^2(n-1) \leq \chi_s) = 1-\alpha. \]

Da die Chi-Quadrat-Verteilung nicht symmetrisch ist, werden die Quantile \(\chi^{n-1}_{\alpha/2}\) und \(\chi^{n-1}_{1-\alpha/2}\) verwendet.

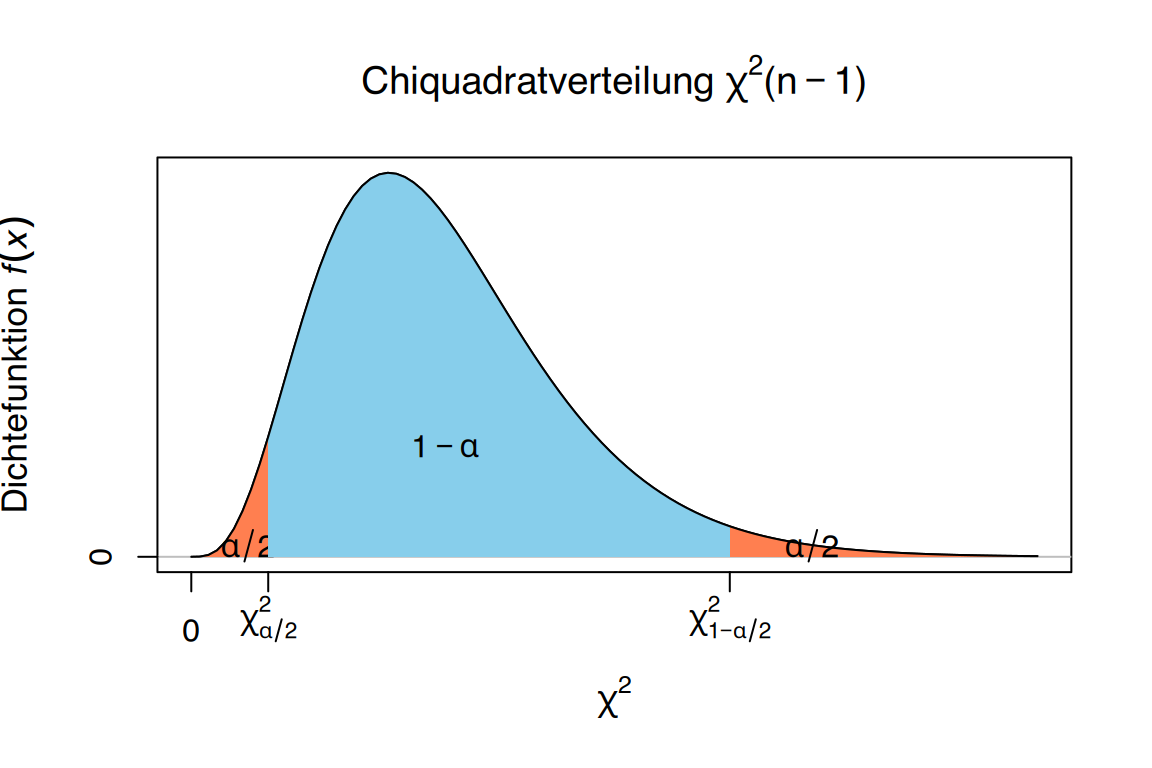
Somit ergibt sich

\[ \begin{aligned} 1-\alpha &= P\left(\chi^{n-1}_{\alpha/2}\leq \frac{nS^2}{\sigma^2} \leq \chi^{n-1}_{1-\alpha/2}\right) = P\left(\frac{1}{\chi^{n-1}_{\alpha/2}}\geq \frac{\sigma^2}{nS^2} \geq \frac{1}{\chi^{n-1}_{1-\alpha/2}}\right)=\\ &= P\left(\frac{1}{\chi^{n-1}_{1-\alpha/2}}\leq \frac{\sigma^2}{nS^2} \leq \frac{1}{\chi^{n-1}_{\alpha/2}}\right) = P\left(\frac{nS^2}{\chi^{n-1}_{1-\alpha/2}}\leq \sigma^2 \leq \frac{nS^2}{\chi^{n-1}_{\alpha/2}}\right). \end{aligned} \]

Daher lautet das Konfidenzintervall für die Varianz einer normalverteilten Population:

Konfidenzintervall für die Varianz einer normalverteilten Grundgesamtheit

Für \(X\sim N(\mu, \sigma)\) lautet das (\(1-\alpha\))-Konfidenzintervall für \(\sigma\) :

\[ \left[\frac{nS^2}{\chi^{n-1}_{1-\alpha/2}},\frac{nS^2}{\chi^{n-1}_{\alpha/2}}\right] \]

Beispiel

Fortsetzung des Prüfungsbeispiels mit der Stichprobe:

\[ 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \]

Das Konfidenzintervall für \(\sigma^2\) bei einem Vertrauensniveau von 95% (\(\alpha=0,05\)) lautet:

  • \(S^2= \frac{(4-5.3)^2+\cdots+(3-5.3)^2}{10} = 3.21\) Punkte\(^2\).
  • \(\chi^{n-1}_{\alpha/2}=\chi^9_{0.025}\) ist der Wert der Chi-Quadrat-Verteilung mit \(9\) Freiheitsgraden, der eine kumulative Wahrscheinlichkeit von \(0,025\) unterschreitet, und beträgt \(2,7\).
  • \(\chi^{n-1}_{1-\alpha/2}=\chi^9_{0.975}\) ist der Wert der Chi-Quadrat-Verteilung mit \(9\) Freiheitsgraden, der eine kumulative Wahrscheinlichkeit von \(0,975\) unterschreitet, und beträgt \(19\).

Das Intervall berechnet sich zu:

\[ \left[\frac{nS^2}{\chi^{n-1}_{1-\alpha/2}},\frac{nS^2}{\chi^{n-1}_{\alpha/2}}\right] = \left[\frac{10\cdot 3.21}{19},\frac{10\cdot 3.21}{2.7}\right] = [1.69,\,11.89] \text{ Punkte}^2. \]

8.5.5 Konfidenzintervall für einen Anteilswert

Zur Schätzung des Anteils p einer Grundgesamtheit mit einer bestimmten Eigenschaft geht man von der Zufallsvariablen X aus, die die Anzahl der Individuen mit dieser Eigenschaft in einer Stichprobe vom Umfang n zählt. Diese Variable folgt einer Binomialverteilung:

\[ X\sim B(n,p) \]

Für ausreichend große Stichproben (genauer: wenn \(np\geq 5\) und \(n(1-p)\geq 5\)) gilt) besagt der zentrale Grenzwertsatz, dass \(X\) approximativ normalverteilt ist:

\[ X\sim N(np,\sqrt{np(1-p)}). \]

Folglich ist auch der Stichprobenanteil \(\hat{p}=X/n\) approximativ normalverteilt:

\[ \hat{p}=\frac{X}{n} \sim N\left(p,\sqrt{\frac{p(1-p)}{n}}\right), \]

Dies dient als Referenzschätzer. Durch Standardisierung erhält man:

\[ \hat p\sim N\left(p,\sqrt{\frac{p(1-p)}{n}}\right) \]

Nach der Standardisierung lassen sich – genauso wie zuvor – leicht die Werte \(-z_{\alpha/2}\) und \(z_{\alpha/2}\) finden, die erfüllen:

\[ P\left(-z_{\alpha/2}\leq \frac{\hat p-p}{\sqrt{p(1-p)/n}}\leq z_{\alpha/2} \right) = 1-\alpha. \]

Somit erhält man, indem man die Standardisierung rückgängig macht und analog zum vorherigen Vorgehen argumentiert:

\[ \begin{aligned} 1-\alpha &= P\left(-z_{\alpha/2}\leq \frac{\hat p-p}{\sqrt{p(1-p)/n}}\leq z_{\alpha/2} \right) \\ &= P\left(-z_{\alpha/2}\frac{\sqrt{p(1-p)}}{n}\leq \hat p-p\leq z_{\alpha/2}\frac{\sqrt{p(1-p)}}{n} \right) \\ &= P\left(\hat{p}-z_{\alpha/2}\frac{\sqrt{p(1-p)}}{n}\leq p\leq \hat{p}+z_{\alpha/2}\frac{\sqrt{p(1-p)}}{n} \right) \end{aligned} \]

Durch Umformung ergibt sich das Konfidenzintervall:

Konfidenzintervall für einen Anteilswert

Für \(X\sim B(n,p)\) mit \(np\geq 5\) und \(n(1-p)\geq 5\) lautet das (\(1-\alpha\))-Konfidenzintervall für \(p\):

\[ \left[\hat{p}-z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}},\hat{p}+z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right] \]

oder alternativ:

\[ \hat{p}\pm z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]

8.5.5.1 Berechnung des Stichprobenumfangs zur Schätzung eines Anteils

Die Breite oder Ungenauigkeit des Konfidenzintervalls für einen Anteil in einer Population beträgt

\[ A= 2 z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]

Daher lässt sich der erforderliche Stichprobenumfang leicht berechnen, um ein Intervall mit der Breite \(A\) und einem Konfidenzniveau von \(1-\alpha\) zu erhalten:

\[ A= 2 z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \Leftrightarrow A^2= 4 z_{\alpha/2}^2\frac{\hat{p}(1-\hat{p})}{n}, \]

woraus sich ableiten lässt:

\[ {n= 4 z_{\alpha/2}^2\frac{\hat{p}(1-\hat{p})}{A^2}} \]

Für die Berechnung wird eine Schätzung des Anteils \(\hat{p}\) benötigt. Daher wird üblicherweise eine kleine Vorstichprobe gezogen, um diesen Wert zu ermitteln. Im schlimmsten Fall, wenn keine Vorstichprobe verfügbar ist, kann \(\hat{p}=0.5\) angenommen werden.

Beispiel

Angenommen, es soll der Anteil der Raucher in einer bestimmten Population geschätzt werden. Dazu wird eine Stichprobe von 20 Personen gezogen, und es wird erfasst, ob sie rauchen \((1)\) oder nicht \((0)\):

\[ 0 - 1 - 1 - 0 - 0 - 0 - 1 - 0 - 0 - 1 - 0 - 0 - 0 - 1 - 1- 0 - 1 - 1 - 0 - 0 \]

Daraus ergibt sich:

  • \(\hat p=\frac{8}{20}=0.4\). Somit gilt \(np=20\cdot 0.4 = 8\geq 5\) und \(n(1-p)=20\cdot 0.6= 12\geq 5\).
  • \(z_{\alpha/2}=z_{0.025}\) ist der Wert der Standardnormalverteilung, der eine obere kumulative Wahrscheinlichkeit von \(0.025\) aufweist und ungefähr \(1.96\) beträgt.

Durch Einsetzen dieser Werte in die Formel für das Konfidenzintervall ergibt sich:

\[ \hat{p}\pm z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = 0.4\pm 1.96\sqrt{\frac{0.4\cdot 0.6}{10}} = 0.4\pm 0.3 = \left[0.1,\,0.7\right]. \]

Das bedeutet, mit einer 95%igen Konfidenz liegt der wahre Anteil \(p\) zwischen \(0.1\) und \(0.7\).

Beispiel

Wie zu erkennen ist, beträgt die Ungenauigkeit des obigen Intervalls \(\pm 0.215\), was angesichts eines Anteils sehr groß ist.

Um präzise Konfidenzintervalle für Anteilsschätzungen zu erhalten, sind relativ große Stichprobenumfänge erforderlich. Wenn beispielsweise eine Genauigkeit von \(\pm 0,05\) gewünscht wird, wäre der erforderliche Stichprobenumfang:

\[ n= 4 z_{\alpha/2}^2\frac{\hat{p}(1-\hat{p})}{A^2}=4\cdot 1.96^2\frac{0.4\cdot 0.6}{(2\cdot0.05)^2}= 368.79. \] Das heißt, es wären mindestens 369 Personen notwendig, um ein 95%-Konfidenzintervall für den Anteil mit einer Genauigkeit von \(\pm 0,05\) zu erhalten.

8.6 Konfidenzintervalle für den Vergleich zweier Populationen

In vielen Studien besteht das eigentliche Ziel nicht darin, den Wert eines Parameters zu ermitteln, sondern ihn mit dem einer anderen Population zu vergleichen.

Beispielsweise könnte man untersuchen, ob ein bestimmter Parameter in der männlichen und der weiblichen Population denselben Wert aufweist.

In solchen Fällen geht es nicht primär um die separate Schätzung der beiden Parameter, sondern um eine Schätzung, die ihren Vergleich ermöglicht.

Es werden drei Fälle betrachtet:

  • Vergleich von Mittelwerten: Schätzung der Differenz der Mittelwerte \(\mu_1-\mu_2\).
  • Vergleich von Varianzen: Schätzung des Verhältnisses der Varianzen \(\displaystyle \frac{\sigma^2_1}{\sigma^2_2}\).
  • Vergleich von Anteilen: Schätzung der Differenz der Anteile \(\hat p_1-\hat p_2\).

Im Folgenden werden die folgenden Konfidenzintervalle für den Vergleich zweier Populationen vorgestellt:

  • Intervall für die Differenz der Mittelwerte zweier normalverteilter Populationen mit bekannten Varianzen.
  • Intervall für die Differenz der Mittelwerte zweier normalverteilter Populationen mit unbekannten, aber gleichen Varianzen.
  • Intervall für die Differenz der Mittelwerte zweier normalverteilter Populationen mit unbekannten und ungleichen Varianzen.
  • Intervall für das Verhältnis der Varianzen zweier normalverteilter Populationen.
  • Intervall für die Differenz der Anteile zweier Populationen.

8.6.1 Konfidenzintervall für die Differenz der Mittelwerte normalverteilter Populationen mit bekannten Varianzen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen, die folgende Annahmen erfüllen:

  • Sie sind normalverteilt: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\).
  • Ihre Mittelwerte \(\mu_1\) und \(\mu_2\) sind unbekannt, aber ihre Varianzen \(\sigma^2_1\) und \(\sigma^2_2\) sind bekannt.

Unter diesen Annahmen folgt die Differenz der Stichprobenmittelwerte aus zwei unabhängigen Stichproben der Größen \(n_1\) bzw. \(n_2\) einer Normalverteilung:

\[ \left. \begin{array}{l} \bar{X}_1\sim N\left(\mu_1,\frac{\sigma_1}{\sqrt{n_1}} \right)\\ \bar{X}_2\sim N\left(\mu_2,\frac{\sigma_2}{\sqrt{n_2}} \right) \end{array} \right\} \Rightarrow \bar{X}_1-\bar{X}_2 \sim N\left(\mu_1-\mu_2,\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\right). \]

Durch Standardisierung ergeben sich die Werte der Standardnormalverteilung \(-z_{\alpha/2}\) und \(z_{\alpha/2}\), die folgende Bedingung erfüllen:

\[ P\left(-z_{\alpha/2}\leq \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}} \leq z_{\alpha/2}\right) = 1-\alpha. \]

Durch Rückgängigmachen der Standardisierung erhält man:

\[ \begin{aligned} 1-\alpha &= P\left(-z_{\alpha/2}\leq \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}} \leq z_{\alpha/2}\right) \\ &= P\left(-z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\leq (\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)\leq z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\right) \\ &= P\left(\bar{X}_1-\bar{X}_2 - z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\leq \mu_1-\mu_2\leq \bar{X}_1-\bar{X}_2 + z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\right) \end{aligned} \]

Somit lautet das Konfidenzintervall für die Differenz der Mittelwerte:

Konfidenzintervall für die Differenz der Mittelwerte normalverteilter Populationen mit bekannten Varianzen

Falls \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\) mit bekannten \(\sigma_1\) und \(\sigma_2\), dann ist das Konfidenzintervall für die Differenz der Mittelwerte \(\mu_1-\mu_2\) zum Konfidenzniveau \(1-\alpha\) gegeben durch:

\[ \left[\bar{X}_1-\bar{X}_2-z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}},\bar{X}_1-\bar{X}_2+z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}\right] \]

oder alternativ:

\[ \bar{X}_1-\bar{X}_2\pm z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}} \]

8.6.2 Konfidenzintervall für die Differenz der Mittelwerte zweier normalverteilter Populationen mit unbekannten, aber gleichen Varianzen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen, die folgende Annahmen erfüllen:

  • Sie sind normalverteilt: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\)
  • Ihre Mittelwerte \(\mu_1\) und \(\mu_2\) sind unbekannt und ihre Varianzen ebenfalls, aber sie sind gleich: \(\sigma^2_1=\sigma^2_2=\sigma^2\)

Wenn die Populationsvarianz unbekannt ist, kann sie aus Stichproben der Größen \(n_1\) und \(n_2\) beider Populationen mittels der gewichteten Stichprobenvarianz (gepoolte Varianz) geschätzt werden:

\[ \hat{S}^2_p = \frac{n_1S^2_1+n_2S^2_2}{n_1+n_2-2}. \]

Die Teststatistik folgt in diesem Fall einer t-Verteilung:

\[ \left. \begin{array}{l} \bar{X}_1-\bar{X}_2\sim N\left(\mu_1-\mu_2,\sigma\sqrt{\frac{n_1+n_2}{n_1n_2}} \right)\\ \displaystyle \frac{n_1S_1^2+n_2S_2^2}{\sigma^2} \sim \chi^2(n_1+n_2-2) \end{array} \right\} \Rightarrow \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}} \sim T(n_1+n_2-2). \]

Daraus lassen sich die kritischen Werte \(-t^{n_1+n_2-2}{\alpha/2}\) und \(t^{n_1+n_2-2}{\alpha/2}\) der t-Verteilung bestimmen, die folgende Bedingung erfüllen:

\[ P\left(-t^{n_1+n_2-2}_{\alpha/2}\leq \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}} \leq t^{n_1+n_2-2}_{\alpha/2}\right) = 1-\alpha. \]

Und durch Rücktransformation ergibt sich

\[ \begin{aligned} 1-\alpha &= P\left(-t^{n_1+n_2-2}_{\alpha/2}\leq \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}} \leq t^{n_1+n_2-2}_{\alpha/2}\right) \\ &= P\left(-t^{n_1+n_2-2}_{\alpha/2}\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}\leq (\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2) \leq t^{n_1+n_2-2}_{\alpha/2}\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}\right) \\ &= P\left(\bar{X}_1-\bar{X}_2 - t^{n_1+n_2-2}_{\alpha/2}\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}\leq \mu_1-\mu_2 \leq \bar{X}_1-\bar{X}_2 + t^{n_1+n_2-2}_{\alpha/2}\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}\right). \end{aligned} \]

Durch weitere Umformung erhält man das Konfidenzintervall:

Konfidenzintervall für die Differenz der Mittelwerte normalverteilter Populationen mit unbekannten, aber gleichen Varianzen

Wenn \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\) mit unbekannten, aber gleichen Varianzen \(\sigma_1 = \sigma_2\), dann ist das Konfidenzintervall für die Mittelwertdifferenz \(\mu_1-\mu_2\) zum Konfidenzniveau \(1-\alpha\) gegeben durch:

\[ \left[\bar{X}_1-\bar{X}_2-t^{n_1+n_2-2}_{\alpha/2}\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}},\bar{X}_1-\bar{X}_2+t^{n_1+n_2-2}_{\alpha/2}\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}}\right] \]

oder alternativ:

\[ \bar{X}_1-\bar{X}_2\pm t^{n_1+n_2-2}_{\alpha/2}\hat{S}_p\sqrt{\frac{n_1+n_2}{n_1n_2}} \]

Wenn \([l_i,l_s]\) ein Konfidenzintervall mit dem Niveau \(1-\alpha\) für die Differenz der Mittelwerte \(\mu_1-\mu_2\) ist, dann gilt

\[ \mu_1-\mu_2 \in [l_i,l_s] \]

Interpretation des Konfidenzintervalls \([l_i,l_s]\) für \(\mu_1-\mu_2\):

  • Wenn das Intervall vollständig negativ ist (\(l_s < 0\)), dann gilt mit \((1-\alpha)%\) Konfidenz, dass \(\mu_1 < \mu_2\)
  • Wenn das Intervall vollständig positiv ist (\(l_i > 0\)), dann gilt mit \((1-\alpha)%\) Konfidenz, dass \(\mu_1 > \mu_2\)
  • Wenn das Intervall die Null enthält, gibt es keinen statistisch signifikanten Unterschied zwischen den Mittelwerten

In den ersten beiden Fällen spricht man von statistisch signifikanten Unterschieden zwischen den Mittelwerten.

Beispiel

Vergleich der akademischen Leistungen zweier Schülergruppen (10 bzw. 12 Schüler) mit unterschiedlichen Lehrmethoden:

\[ \begin{aligned} X_1 &: 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \\ X_2 &: 8 - 9 - 5 - 3 - 8 - 7 - 8 - 6 - 8 - 7 - 5 - 7 \end{aligned} \] Unter der Annahme, dass beide Variablen dieselbe Varianz besitzen, ergibt sich

  • \(\bar{X}_1 = \frac{4+\cdots +3}{10}=5.3\) und \(\bar{X}_2=\frac{8+\cdots +7}{12}=6.75\) Punkte.
  • \(S_1^2= \frac{4^2+\cdots + 3^2}{10}-5.3^2=3.21\) und \(S_2^2= \frac{8^2+\cdots +3^2}{12}-6.75^2=2.6875\) Punkte\(^2\).
  • \(\hat{S}_p^2 = \frac{10\cdot 3.21+12\cdot 2.6875}{10+12-2}= 3.2175\) Punkte\(^2\), und \(\hat S_p=1.7937\).
  • \(t^{n_1+n_2-2}_{\alpha/2}=t^{20}_{0.025}\) ist der Wert der Student-t-Verteilung mit 20 Freiheitsgraden, der eine obere kumulierte Wahrscheinlichkeit von \(0,025\) abbildet, und beträgt ungefähr \(2,09\).

Das 95%-Konfidenzintervall für die Leistungsdifferenz beträgt:

\[ 5.3-6.75 \pm 2.086\cdot 1.7937\sqrt{\frac{10+12}{10\cdot 12}} = -1.45\pm 1.6021 = [-3.0521,\,0.1521] \text{ Punkte}. \]

Das heißt, die Differenz der durchschnittlichen Werte \(\mu_1-\mu_2\) liegt mit einer Konfidenz von 95% zwischen \(-3.0521\) und \(0.1521\) Punkten.

Angesichts dieses Intervalls kann man folgern, dass, da das Intervall sowohl positive als auch negative Werte enthält und somit auch die \(0\) einschließt, nicht festgestellt werden kann, dass eine der Mittelwerte größer ist als die andere. Daher wird angenommen, dass sie gleich sind, und es kann nicht gesagt werden, dass es signifikante Unterschiede zwischen den Gruppen gibt.

8.6.3 Konfidenzintervall für die Differenz der Mittelwerte zweier normalverteilter Populationen mit unbekannten und ungleichen Varianzen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen, die folgende Annahmen erfüllen:

  • Ihre Verteilung ist normal: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\).
  • Ihre Mittelwerte \(\mu_1\), \(\mu_2\) und Varianzen \(\sigma_1^2\), \(\sigma_2^2\) sind unbekannt, aber es gilt \(\sigma^2_1\neq \sigma^2_2\).

In diesem Fall folgt die Teststatistik einer t-Verteilung:

\[ \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}} \sim T(g), \]

wobei die Anzahl der Freiheitsgrade \(g=n_1+n_2-2-\Delta\) beträgt, mit

\[ \Delta = \frac{(\frac{n_2-1}{n_1}\hat{S}_1^2-\frac{n_1-1}{n_2}\hat{S}_2^2)^2}{\frac{n_2-1}{n_1^2}\hat{S}_1^4+\frac{n_1-1}{n_2^2}\hat{S}_2^4}. \]

Daraus lassen sich die kritischen Werte der t-Verteilung \(-t^{g}{\alpha/2}\) und \(t^{g}{\alpha/2}\) bestimmen, die folgende Bedingung erfüllen:

\[ P\left(-t^{g}_{\alpha/2}\leq \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}} \leq t^{g}_{\alpha/2}\right) = 1-\alpha. \]

Durch Umstellung erhält man:

\[ \begin{aligned} 1-\alpha &= P\left(-t^{g}_{\alpha/2}\leq \frac{(\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}} \leq t^{g}_{\alpha/2}\right) \\ &= P\left(-t^{g}_{\alpha/2}\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}\leq (\bar{X}_1-\bar{X}_2)-(\mu_1-\mu_2) \leq t^{g}_{\alpha/2}\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}\right) \\ &= P\left(\bar{X}_1-\bar{X}_2 - t^{g}_{\alpha/2}\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}\leq\mu_1-\mu_2 \leq \bar{X}_1-\bar{X}_2 + t^{g}_{\alpha/2}\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}\right) \\ \end{aligned} \]

Somit ergibt sich das Konfidenzintervall für die Differenz der Mittelwerte:

Konfidenzintervall für die Differenz der Mittelwerte normalverteilter Populationen mit unbekannten und ungleichen Varianzen

Wenn \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\) mit unbekannten und ungleichen Varianzen \(\sigma_1 \neq \sigma_2\), dann ist das Konfidenzintervall für die Mittelwertdifferenz \(\mu_1-\mu_2\) zum Konfidenzniveau \(1-\alpha\) gegeben durch:

\[ \left[\bar{X}_1-\bar{X}_2-t^{g}_{\alpha/2}\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}},\bar{X}_1-\bar{X}_2-t^{g}_{\alpha/2}\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}}\right] \]

oder alternativ:

\[ \bar{X}_1-\bar{X}_2\pm t^{g}_{\alpha/2}\sqrt{\frac{\hat{S}^2_1}{n_1}+\frac{\hat{S}^2_2}{n_2}} \]

Wie wir gesehen haben, gibt es zwei mögliche Konfidenzintervalle zur Schätzung der Mittelwertdifferenz: eines für den Fall gleicher Populationsvarianzen und eines für ungleiche Varianzen.

Doch wenn die Populationsvarianzen unbekannt sind,

wie lässt sich entscheiden, welches Intervall verwendet werden soll?

Die Antwort liefert das nächste Konfidenzintervall, das wir betrachten werden. Es ermöglicht die Schätzung des Varianzverhältnisses \(\frac{\sigma_2^2}{\sigma_1^2}\) und somit deren Vergleich.

Daher ist es notwendig, bevor man das Konfidenzintervall für den Mittelwertvergleich berechnet (wenn die Populationsvarianzen unbekannt sind), zuerst das Konfidenzintervall für das Varianzverhältnis zu bestimmen. Auf Grundlage dieses Intervalls kann dann die geeignete Methode für den Mittelwertvergleich ausgewählt werden.

8.6.4 Konfidenzintervall für das Verhältnis von Varianzen

Seien \(X_1\) und \(X_2\) zwei Zufallsvariablen, die folgende Annahmen erfüllen:

  • Ihre Verteilung ist normal: \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\).
  • Ihre Mittelwerte \(\mu_1\), \(\mu_2\) und Varianzen \(\sigma_1^2\), \(\sigma_2^2\) sind unbekannt.

In diesem Fall folgt die Teststatistik für Stichproben der Größen \(n_1\) und \(n_2\) einer F-Verteilung nach Fisher-Snedecor:

\[ \left. \begin{array}{l} \displaystyle \frac{(n_1-1)\hat{S}_1^2}{\sigma_1^2}\sim \chi^2(n_1-1) \\ \displaystyle \frac{(n_2-1)\hat{S}_2^2}{\sigma_2^2}\sim \chi^2(n_2-1) \end{array} \right\} \Rightarrow \frac{\frac{\frac{(n_2-1)\hat{S}_2^2}{\sigma_2^2}}{n_2-1}}{\frac{\frac{(n_1-1)\hat{S}_1^2}{\sigma_1^2}}{n_1-1}} = \frac{\sigma_1^2}{\sigma_2^2}\frac{\hat{S}_2^2}{\hat{S}_1^2}\sim F(n_2-1,n_1-1). \]

Da die F-Verteilung nicht symmetrisch ist, werden zwei kritische Werte \(f^{n_2-1,n_1-1}{\alpha/2}\) und \(f^{n_2-1,n_1-1}{1-\alpha/2}\) verwendet, die jeweils untere Wahrscheinlichkeiten von \(\alpha/2\) und \(1-\alpha/2\) begrenzen.

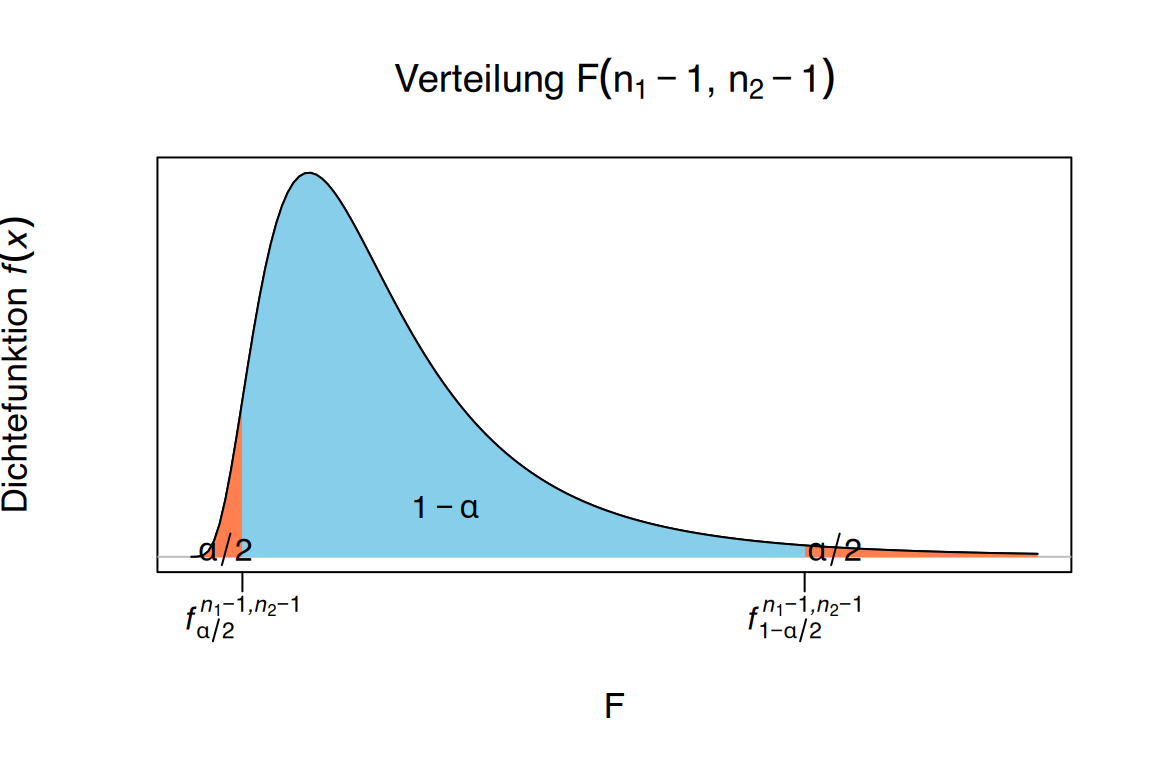
Somit ergibt sich:

\[ \begin{aligned} 1-\alpha &= P\left(f^{n_2-1,n_1-1}_{\alpha/2}\leq \frac{\sigma_1^2}{\sigma_2^2}\frac{\hat{S}_2^2}{\hat{S}_1^2} \leq f^{n_2-1,n_1-1}_{1-\alpha/2}\right) = \\ &= P\left(f^{n_2-1,n_1-1}_{\alpha/2}\frac{\hat{S}_1^2}{\hat{S}_2^2} \leq \frac{\sigma_1^2}{\sigma_2^2} \leq f^{n_2-1,n_1-1}_{1-\alpha/2}\frac{\hat{S}_1^2}{\hat{S}_2^2}\right) \end{aligned} \]

Daher lautet das Konfidenzintervall für den Vergleich von Varianzen zweier normalverteilter Populationen:

Konfidenzintervall für das Verhältnis von Varianzen normalverteilter Populationen

Wenn \(X_1\sim N(\mu_1,\sigma_1)\) und \(X_2\sim N(\mu_2,\sigma_2)\), dann ist das Konfidenzintervall für das Varianzverhältnis \(\sigma_1/\sigma_2\) zum Konfidenzniveau \(1-\alpha\) gegeben durch:

\[ \left[f^{n_2-1,n_1-1}_{\alpha/2}\frac{\hat{S}_1^2}{\hat{S}_2^2},f^{n_2-1,n_1-1}_{1-\alpha/2}\frac{\hat{S}_1^2}{\hat{S}_2^2}\right] \]

Das Verhältnis der Varianzen \(\frac{\sigma_1^2}{\sigma_2^2}\) liegt mit einer Konfidenz von \(1-\alpha\) im Intervall \([l_i,l_s]\).

\[ \frac{\sigma_1^2}{\sigma_2^2} \in [l_i,l_s] \]

Interpretation des Konfidenzintervalls \([l_i,l_s]\) für \(\frac{\sigma_1^2}{\sigma_2^2}\):

  • Wenn alle Werte des Intervalls kleiner als 1 sind \((l_s<1)\), kann geschlossen werden, dass \(\sigma_1^2<\sigma_2^2\)
  • Wenn alle Werte des Intervalls größer als 1 sind \((l_i>1)\), kann geschlossen werden, dass \(\sigma_1^2>\sigma_2^2\)
  • Wenn das Intervall sowohl Werte unter als auch über \(1\) enthält (also \(1\) im Intervall liegt), kann keine Aussage über die Größenverhältnisse der Varianzen gemacht werden. In diesem Fall wird normalerweise die Hypothese gleicher Varianzen \(\sigma_1^2=\sigma_2^2\) angenommen.
Beispiel

Fortsetzung des Beispiels mit den Punktzahlen zweier Gruppen:

\[ \begin{aligned} X_1 &: 4 - 6 - 8 - 7 - 7 - 6 - 5 - 2 - 5 - 3 \\ X_2 &: 8 - 9 - 5 - 3 - 8 - 7 - 8 - 6 - 8 - 7 - 5 - 7 \end{aligned} \]

Zur Berechnung des Konfidenzintervalls für das Varianzverhältnis bei einem Konfidenzniveau von 95% gilt:

  • \(\bar{X}_1 = 5.3\) Punkte und \(\bar{X}_2=6.75\) Punkte
  • \(\hat{S}_1^2= 3.5667\) Punkte\(^2\) und \(\hat{S}_2^2= 2.9318\) Punkte\(^2\)
  • \(f^{11,9}_{0.025} \approx 0.2787\) (unterer kritischer F-Wert)
  • \(f^{11,9}_{0.975} \approx 3.9121\) (oberer kritischer F-Wert)

Einsetzen in die Formel ergibt das Intervall:

\[ \left[0.2787\frac{3.5667}{2.9318},\, 3.9121\frac{3.5667}{2.9318}\right] = [0.3391,\, 4.7591] \text{ Punkte}^2. \]

Das bedeutet, das Varianzverhältnis \(\frac{\sigma_1^2}{\sigma_2^2}\) liegt mit 95% Konfidenz zwischen \(0,3391\) und \(4,7591\).

Da das Intervall sowohl Werte unter als auch über \(1\) enthält, kann keine signifikante Unterschiedlichkeit der Varianzen angenommen werden. Für den Mittelwertvergleich wäre daher das Verfahren mit der Annahme gleicher Varianzen zu verwenden - genau die Methode, die wir bereits zuvor angewendet haben.

8.6.5 Konfidenzintervall für die Differenz von Proportionen

Um die Proportionen \(p_1\) und \(p_2\) von Individuen, die eine bestimmte Eigenschaft in zwei unabhängigen Populationen aufweisen, zu vergleichen, wird ihre Differenz \(p_1-p_2\) geschätzt.

Wenn aus jeder Population eine Stichprobe mit den Umfängen \(n_1\) und \(n_2\) gezogen wird, folgen die Variablen, die die Anzahl der Individuen mit der Eigenschaft in jeder Stichprobe messen, den Verteilungen

\[ X_1\sim B(n_1,p_1)\quad \mbox{y}\quad X_2\sim B(n_2,p_2) \]

Wenn die Stichprobenumfänge groß sind (tatsächlich reicht es aus, dass \(n_1p_1\geq 5\), \(n_1(1-p_1)\geq 5\), \(n_2p_2\geq 5\) und \(n_2(1-p_2)\geq 5\) erfüllt sind), sichert der zentrale Grenzwertsatz, dass \(X_1\) und \(X_2\) Normalverteilungen folgen

\[ X_1\sim N(n_1p_1,\sqrt{n_1p_1(1-p_1)}) \quad \mbox{und}\quad X_2\sim N(n_2p_2,\sqrt{n_2p_2(1-p_2)}), \]

und die Stichprobenproportionen

\[ \hat{p}_1=\frac{X_1}{n_1} \sim N\left(p_1,\sqrt{\frac{p_1(1-p_1)}{n_1}}\right) \quad \mbox{und}\quad \hat{p}_2=\frac{X_2}{n_2} \sim N\left(p_2,\sqrt{\frac{p_2(1-p_2)}{n_2}}\right) \]

Aus den Stichprobenproportionen wird der Referenzschätzer konstruiert

\[ \hat{p}_1-\hat{p}_2\sim N\left(p_1-p_2,\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\right). \]

Durch Standardisierung werden Werte \(-z_{\alpha/2}\) und \(z_{\alpha/2}\) gesucht, die erfüllen

\[ P\left(-z_{\alpha/2}\leq \frac{(\hat{p}_1-\hat{p_2})-(p_1-p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}\leq z_{\alpha/2} \right) = 1-\alpha. \]

Und durch Rückgängigmachen der Standardisierung ergibt sich

\[ \begin{aligned} 1-\alpha &= P\left(-z_{\alpha/2}\leq \frac{(\hat{p}_1-\hat{p_2})-(p_1-p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}\leq z_{\alpha/2} \right) \\ &= P\left(-z_{\alpha/2}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\leq (\hat{p}_1-\hat{p_2})-(p_1-p_2)\leq z_{\alpha/2}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}} \right) \\ &= P\left(\hat{p}_1-\hat{p_2} -z_{\alpha/2}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\leq \hat{p}_1-\hat{p_2} + p_1-p_2\leq z_{\alpha/2}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}} \right) \end{aligned} \]

Somit ist das Konfidenzintervall für die Differenz der Proportionen

Konfidenzintervall für die Differenz von Proportionen

Wenn \(X_1\sim B(n_1,p_1)\) und \(X_2\sim B(n_2,p_2)\), mit \(n_1p_1\geq 5\), \(n_1(1-p_1)\geq 5\), \(n_2p_2\geq 5\) und \(n_2(1-p_2)\geq 5\), dann ist das Konfidenzintervall für die Differenz der Proportionen \(p_1-p_2\) mit dem Konfidenzniveau \(1-\alpha\)

\[ \hat{p}_1-\hat{p}_2\pm z_{\alpha/2}\sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}} \]

Beispiel

Angenommen, es sollen die Proportionen oder Prozentsätze der bestandenen Prüfungen in zwei Gruppen verglichen werden, die unterschiedliche Methoden verfolgt haben. In der ersten Gruppe haben 24 von 40 Schülern bestanden, während in der zweiten Gruppe 48 von 60 Schülern bestanden haben.

Um das Konfidenzintervall für die Differenz der Proportionen mit einem Konfidenzniveau von 95% zu berechnen, gilt:

  • \(\hat{p}_1=24/40= 0.6\ \) und
  • \(\hat{p}_2=48/60=0.8\), sodass die Hypothesen
    • \(n_1\hat{p}_1=40\cdot 0.6=24\geq 5\),
    • \(n_1(1-\hat{p}_1)=40(1-0.6)=26\geq 5\),
    • \(n_2\hat{p}_2=60\cdot 0.8 =48\geq 5\) und
    • \(n_2(1-\hat{p}_2)=60(1-0.8)=12\geq 5\) erfüllt sind.
  • \(z_{\alpha/2}=z_{0.025}= 1.96\).

Durch Einsetzen in die Formel des Intervalls ergibt sich

\[ 0.6-0.8\pm 1.96 \sqrt{\frac{0.6(1-0.6)}{40}+\frac{0.8(1-0.8)}{60}} = -0.2\pm 0.17 = [-0.37,\, -0.03]. \]

Da das Intervall negativ ist, gilt \(p_1-p_2<0\Rightarrow p_1<p_2\), und es kann geschlossen werden, dass es signifikante Unterschiede in den Bestehensquoten gibt.