Kugeln im Kelch
Der Durchmesser jeder betrachteten Kugel im Kelch ergibt sich durch Multiplikation des Durchmessers der jeweils direkt über ihr liegenden größeren Kugel mit einem konstanten Faktor $q$. Mit dieser Eigenschaft lässt sich die Abfolge der Kugeldurchmesser als unendliche geometrische Reihe beschreiben. Für eine bestimmte Anzahl $n$ der obersten Kugeln im Kelch erhält man danach die Durchmessersumme \begin{align} S_{d,n} = d_{1}\cdot(1+q^1+q^2+\cdots +q^{n-1}) = \sum\limits_{k=0}^{n-1} d_{1}\cdot q^k = d_{1}\cdot\frac{1-q^n}{1-q} \end{align}
und für die gegebene, unendlich große Kugelanzahl die Durchmessersumme \begin{align} S_{d} = \lim\limits_{n\rightarrow\infty}\left(d_{1}\cdot\frac{1-q^n}{1-q} \right) =\frac{d_{1}}{1-q} \end{align}
Die zuletzt genannte entspricht logischerweise der lichten Höhe $h$ des kegelförmigen Innenraums des Kelchs, so dass aus Gleichung 2 folgt: \begin{align} q = 1- \frac{d_{1}}{h} \end{align}
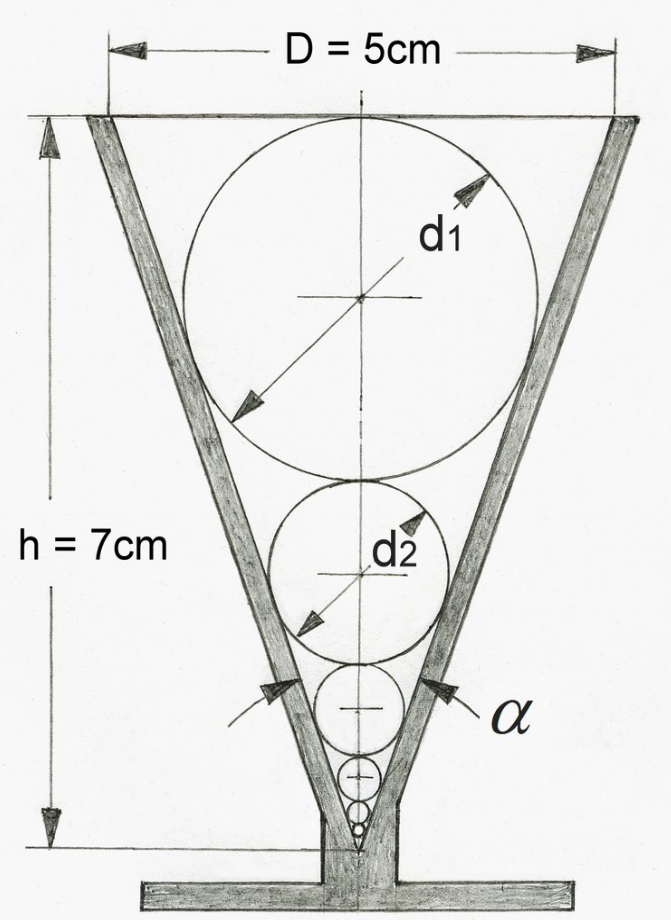
Abb.1
Den Durchmesser der im Kelch zuoberst liegenden größten Kugel erhält man unter Beachtung von Abbildung 1 aus dem Ansatz: \begin{align} tan(\frac{\alpha}{2}) = \frac{D}{2\cdot h}= \frac{\frac{d_{1}}{2}}{\sqrt{(h-\frac{d_{1}}{2})^-(\frac{d_{1}}{2})^2}} = \frac{d}{2\cdot\sqrt{h\cdot(h-d_{1})}} \end{align}
zu \begin{align} d_{1} = \frac{2\cdot h}{1+\sqrt{1+4\cdot(\frac{h}{D})^2}} \end{align}
Für das Volumen der ersten (obersten) $n$ Kugeln im Kelch gilt: \begin{align} V_{Ku,n} &= \frac{\pi\cdot d_{1}^3}{6}\cdot\left(1+(q^1)^3+(q^2)^3+\cdots +(q^{n-1})^3 \right)\newline &= \sum\limits_{k=0}^{n-1}\frac{\pi\cdot d_{1}^3}{6}\cdot q^{3k}\newline &= \frac{\pi\cdot d_{1}^3}{6}\cdot\frac{1-q^{3n}}{1-q^3} \end{align}
und für das Volumen aller Kugeln zusammengenommen:
\begin{align} V_{Ku} = \lim\limits_{n\rightarrow\infty}\left(\frac{\pi\cdot d_{1}^3}{6}\cdot\frac{1-q^{3n}}{1-q^3} \right) =\frac{\pi}{6}\cdot\frac{d_{1}^3}{1-q^3} \end{align}
Mit $q$ nach Gleichung 3 und $d_{1}$ nach Gleichung 5 kann Gleichung 9 umgeformt werden in den Ausdruck
\begin{align} V_{Ku} = \frac{\pi}{6}\cdot\frac{h^3}{1+3\cdot(\frac{h}{D})^2} = \frac{\pi}{6}\cdot \frac{D^2\cdot h}{(\frac{D}{h})^2+3} \end{align}
womit sich das Kugelvolumen in direkter Abhängigkeit von den Innenabmessungen $h$ und $D$ des Kelchs berechnen lässt. Berücksichtigt man das Füllvolumen von letzterem mit \begin{align} V_{Ke} = \frac{\pi}{12}\cdot D^2\cdot h \end{align}
so ergibt sich für das Verhältnis $\lambda =V_{Ku}/V_{Ke}$, das den Füllungsgrad des Kelchs definiert, die Formel:
\begin{align} \lambda \frac{V_{Ku}}{V_{Ke}} = \frac{2\cdot(\frac{h}{D})^2}{1+3\cdot(\frac{h}{D})^2} =\frac{2}{(\frac{D}{h})^2 +3} \end{align}
Für die in Abbildung 1 vorgegebenen Kelchmaße, $h=7cm$ und $D=5cm$, liefert Gleichung 12 den Füllungsgrad $\lambda=\mathbf{0,569767}$.
Die Kugeln nehmen also $56,9767\%$ des Innenraums (Füllvolumens) ein.
Der Graph in Abbildung 2 zeigt, wie sich $\lambda$ in Abhängigkeit vom Verhältnis $h/D$ ändert.
Abb.2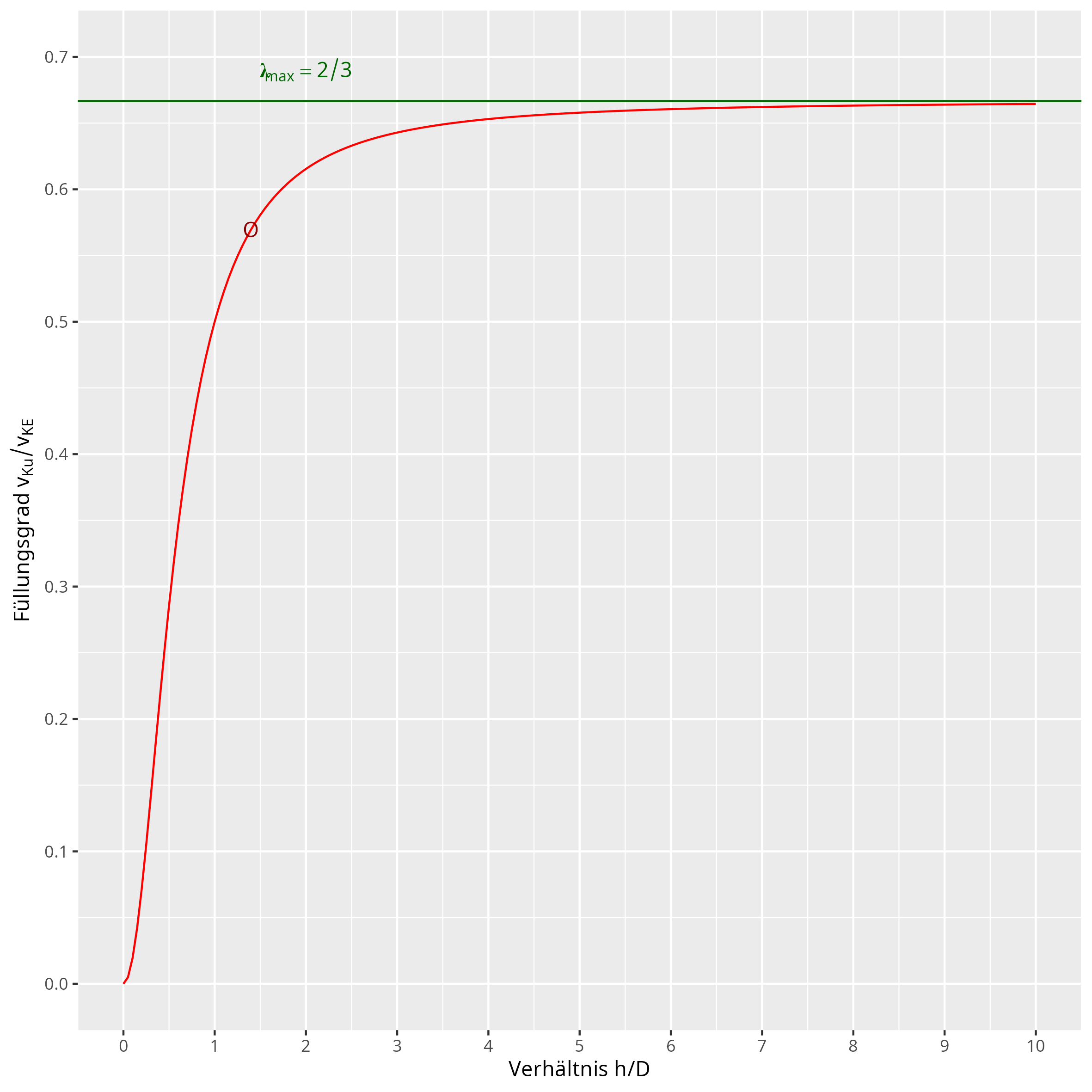
So ist erkennbar, dass die Kugeln niemals mehr als $\frac{2}{3}$ des Innenraums einnehmen können.
 Opa Jupp
Opa Jupp