Angeleinte Ziege grast um kreisrunden Zaun
Wie schon im ersten Ziegenrätsel stehen uns auch hier zwei Lösungswege zur Verfügung:
- Lösung durch Flächenintegration in kartesischen Koordinaten
- Lösung durch Flächenintegration in Polarkoordinaten
Lösung durch Flächenintegration in kartesischen Koordinaten
Die nachstehende Abbildung 1 zeigt den aus einem Halbkreis und zwei gleichen Kreisevolventen zusammengesetzten Verlauf des äußeren Randes der gesuchten Fläche. Die Ziege erreicht diesen Rand mit ihrem Maul, wenn sie den Zaun an der gespannten Leine umrundet.
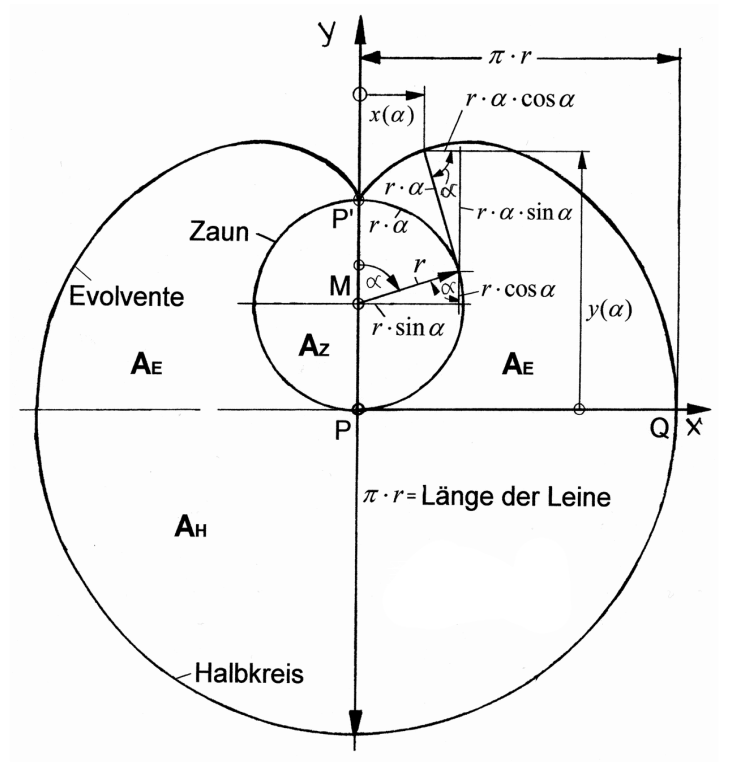
Abb. 1
Mit $A_{H}$ als dem Flächeninhalt des Halbkreises mit dem Radius $\pi\cdot r$, $A_{E}$ als dem Inhalt von einer der beiden gleich großen Flächen, die von der x-Achse und einer Evolvente eingeschlossen werden sowie $A_{Z}$ als dem Flächeninhalt des Zaunkreises mit dem Radius $r$, ergibt sich die Gesamtfäche, auf der die Ziege grasen kann zu $$ \begin{align} A= 2\cdot A_{E} + A_{H} - A_{Z} \end{align} $$
Für die Berechnung der Fläche $A_{E}$ wird angenommen, dass die Halteleine der Ziege den halben Brunnenzaun bereits vollständig umschlungen hat und das Tier sie nun in gespanntem Zustand wieder abwickelt. Der Endpunkt der Leine - identisch mit dem Ziegenmaul - bewegt sich dabei entlang einer der beiden Evolventen. Jedem in Betracht kommenden Wert des Winkels $\alpha$, der den Zaunkreissektor definiert, von dem die Leine abgewickelt sein möge, ist so ein bestimmter Punkt der Evolvente zugeordnet. Bezogen auf das in Abbildung 1 festgelegte kartesische Koordinatensystem gilt:
$$ \begin{align} x(\alpha) &= r\cdot sin \alpha - r\cdot \alpha\cdot cos \alpha = r\cdot (sin \alpha - \alpha\cdot cos \alpha)\newline y(\alpha) &= r + r\cdot cos \alpha + r\cdot \alpha\cdot sin \alpha = r\cdot (1 + cos \alpha + \alpha\cdot sin \alpha) \end{align} $$
Da $y$ nicht in direkter Abhängigkeit von $x$ darstellbar ist, muss auch der Flächeninhalt, den jede der beiden Evolventen im Intervall von $x=0$ bis $x=\pi\cdot r$ mit der x-Achse einschließt, als Funktion des Parameters $\alpha$ ermittelt werden. Mit der ersten Ableitung von $x(\alpha)$:
$$ \begin{align} x’(\alpha) = \frac{dx}{d\alpha} = r\cdot\alpha\cdot sin \alpha \end{align} $$
ergibt sich: $$ \begin{align} A_{E} &= \int\limits_{\alpha=0}^{\pi} y(\alpha)\cdot x’(\alpha)\cdot d \alpha \newline &= \int\limits_{\alpha=0}^{\pi}\left[1+cos \alpha + \alpha\cdot sin \alpha\right]\cdot\alpha\cdot sin \alpha\cdot d \alpha \end{align} $$
Die analytische Berechnung dieses Integrals ist verhältnismäßig aufwändig und wird hier nicht dargestellt. Als Lösung erhält man
$$ \begin{align} A_{E} = \frac{\pi}{2}\cdot (1+\frac{\pi^2}{3}) \cdot r^2 \end{align} $$
Zusammen mit den Flächeninhalten
$$ \begin{align} A_{H} = \frac{\pi}{2}\cdot (\pi\cdot r)^2 = \frac{\pi^3}{2}\cdot r^2 \end{align} $$
für den Halbkreis mit dem Radius $\pi\cdot r$ und
$$ \begin{align} A_{z} = \pi\cdot r^2 \end{align} $$
für den Zaunkreis mit dem Radius $r$, gilt nach Gleichung 1 für die Gesamtfäche, auf der die Ziege grasen kann:
$$ \begin{align} A &= 2\cdot \frac{\pi}{2}\cdot (1+\frac{\pi^2}{3}) \cdot r^2 + \frac{\pi^3}{2}\cdot r^2 - \pi\cdot r^2\newline &= \frac{5}{6}\pi^3 \cdot r^2 \end{align} $$
Mit $r=4m$ erhält man $A=\mathbf{413,42m^2}$
Lösung durch Flächenintegration in Polarkoordinaten
Wie schon in Abbildung 1 wird auch in Abbildung 2 davon ausgegangen, dass die Ziege ihren Umlauf um den Sicherungszaun des Brunnens im Punkt $P‘$ beginnt.
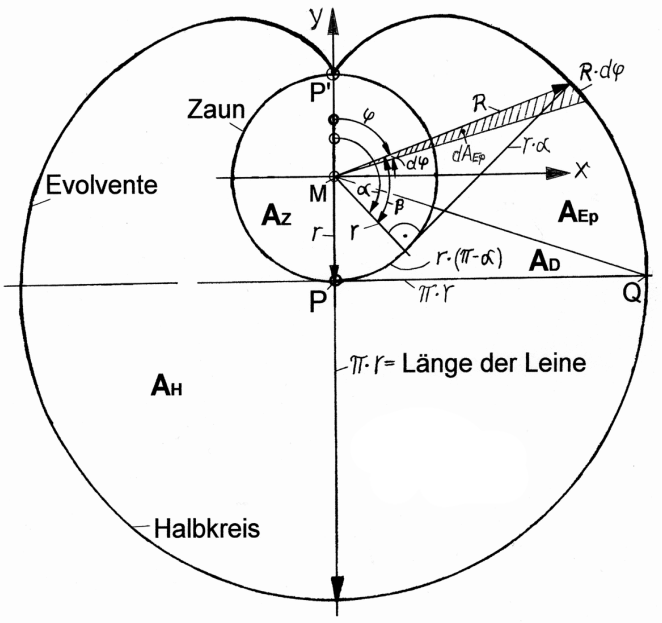
Abb. 2
Ihre Halteleine umspannt also bereits den halben Umfang des Zauns und wird nun von $P‘$ aus wieder abgewickelt. Als Pol für das Polarkoordinatensystem und Ursprung für das zugehörige kartesische x-y-Koordinatensystem wurde der Mittelpunkt $M$ des Zaunkreises festgelegt.
Die y-Achse bildet die Polachse. Von dort aus läuft im Uhrzeigersinn die Winkelkoordinate $\varphi$ um, in Abhängigkeit derer die Radialkoordinate $R$ definiert ist. Letztere überstreicht entlang der Evolventenkurve die Fläche $A_{Ep}$ mit den Eckpunkten $M, Q, P‘$.
Des Weiteren bezeichnen in Abbilung 2 $A_{D}$ die Fläche des rechtwinkligen Dreiecks mit den Eckpunkten $M, P, Q, A_{H}$ die bereits aus Abbildung 1 bekannte Fläche des Halbkreises mit dem Radius $\pi\cdot r$ und $A_{Z}$ die gleichfalls aus Abbildung 1 bekannte Fläche des Zaunkreises mit dem Radius $r$ .
Für die Gesamtfäche $A$ , auf der die Ziege grasen kann, gilt damit:
$$ \begin{align} A= 2\cdot (A_{Ep}+A_{D})+A_{H}-A_{Z} \end{align} $$
Berechnung von $A_{Ep}$
Einem Bogenelement $R\cdot d\varphi$ der Evolvente lässt sich, wie in der Abbildung 2 dargestellt, das Flächenelement
$$ \begin{align} dA_{Ep}(\varphi) = \frac{1}{2}\cdot R^2 (\varphi)\cdot d\varphi \end{align} $$
zuordnen. In dieser Ausgangsgleichung wird der Winkel $\varphi$ durch den Winkel $\alpha$ ersetzt, der den Zaunkreissektor definiert, von dem die Halteleine der Ziege bereits abgewickelt wurde.
Die Länge des abgewickelten Leinenstücks ist $r\cdot\alpha$.
Nach Abbildung 2 gilt: $$ \begin{align} \varphi(\alpha) &= \alpha - \beta = \alpha - arctan\frac{r\cdot\alpha}{r}\newline &= \alpha - arctan \alpha\ \end{align} $$ und $$ \begin{align} R(\alpha) &= \sqrt{r^2 + (r\cdot\alpha)^2} = r\cdot\sqrt{1+\alpha^2} \end{align} $$
Aus der Ableitung von $\varphi(\alpha)$, das heißt aus $$ \begin{align} \varphi’(\alpha) = \frac{d\varphi}{d\alpha} = 1-\frac{1}{1+\alpha^2} = \frac{\alpha^2}{1+\alpha^2} \end{align} $$
ergibt sich noch $$ \begin{align} d\varphi=\varphi’(\alpha)\cdot d\alpha = \frac{\alpha^2}{1+\alpha^2}\cdot d\alpha \end{align} $$
Hiermit und mit $R(\alpha)$ nach Gleichung 16 geht Gleichung 13 über in die Formel $$ \begin{align} dA_{Ep}(\varphi) &= \frac{1}{2}\cdot R^2 (\alpha)\cdot d\alpha \newline &= \frac{1}{2}\cdot r^2 \cdot (1+\alpha^2)\cdot\frac{\alpha^2}{1+\alpha^2}\cdot d\alpha \newline &= \frac{1}{2}\cdot r^2 \cdot \alpha^2 \cdot d\alpha \end{align} $$
woraus folgt $$ \begin{align} A_{Ep} &= \frac{r^2}{2}\cdot \int\limits_{\alpha=0}^{\pi} \alpha^2 \cdot d\alpha\newline &= \frac{\pi^3}{6}\cdot r^2 \end{align} $$
Der Flächeninhalt des rechtwinkligen Dreiecks $M, P, Q$ in Abbildung 2 entspricht mit $$ \begin{align} A_{D}=\frac{\pi}{2}\cdot r^2 \end{align} $$ dem halben Flächeninhalt des Zaunkreises, und zusammengenommen sind $A_{D}$ und $A_{Ep}$ genauso groß wie die Fläche $A_{E}$ in Abbildung 1.
Berücksichtigt man nun in Gleichung 12 neben $A_{Ep}$ nach Gleichung 23 und $A_{D}$ nach Gleichung 24 noch $A_{H}$ nach Gleichung 8 sowie $A_{Z}$ nach Gleichung 9, dann ergibt sich wieder:
$$ \begin{align} A &= 2\cdot (\frac{\pi^3}{6}\cdot r^2 + \frac{\pi}{2}\cdot r^2) + \frac{\pi^3}{2}\cdot r^2 - \pi\cdot r^2\newline &= \frac{5}{6}\cdot\pi^3 \cdot r^2\newline &= \mathbf{413,42m^2} \end{align} $$
Übrigens,
auch Wikipedia hat seit 2016 einen Eintrag zum Ziegenrätsel, siehe https://de.m.wikipedia.org/wiki/Ziegenproblem_(Geometrie)
 Opa Jupp
Opa Jupp