5  Lösungswege zu den Aufgaben für geübte Anwender:innen

Autor:in
Zugehörigkeit

Prof. Dr. Jörg große Schlarmann

Hochschule Niederrhein

Wenn Ihr R-Code eleganter ist als die hier präsentierten Lösungswege, dann freuen Sie sich! Wenn Sie meinen, Ihr Code sei zu klobig und umständlich, dann Kopf hoch: wenn er tut, was er soll, dann ist er genau richtig.

5.1 Lösungen zu Objekten in R

5.1.1 Lösung zur Aufgabe 2.1.1 Hogwarts-Kurse

a) Benutzen Sie die tribble()-Funktion, um die Daten in die Objekte tab1 und tab2 zu überführen. 
library(tibble)
tab1 <- tribble(
    ~Hufflepuff,                  ~Slytherin,
  "Kräuterkunde",               "Zaubertränke", 
  "Pflege magischer Geschöpfe", "Zauberkunst",
  "Geschichte der Zauberei",    "Dunkle Künste", 
  "Alte Runen",                 "Legilimentik"
)

tab2 <- tribble(
  ~Gryffindor,                             ~Ravenclaw,
  "Verteidigung gegen die dunklen Künste", "Arithmantik", 
  "Zauberkunst",                           "Astronomie",
  "Verwandlung",                           "Verwandlung",
  "Besenflugunterricht", "Verteidigung gegen die dunklen Künste"
)
# anzeigen
tab1
# A tibble: 4 × 2
  Hufflepuff                 Slytherin    
  <chr>                      <chr>        
1 Kräuterkunde               Zaubertränke 
2 Pflege magischer Geschöpfe Zauberkunst  
3 Geschichte der Zauberei    Dunkle Künste
4 Alte Runen                 Legilimentik 
tab2
# A tibble: 4 × 2
  Gryffindor                            Ravenclaw                            
  <chr>                                 <chr>                                
1 Verteidigung gegen die dunklen Künste Arithmantik                          
2 Zauberkunst                           Astronomie                           
3 Verwandlung                           Verwandlung                          
4 Besenflugunterricht                   Verteidigung gegen die dunklen Künste
b) Fügen Sie tab1 und tab2 zu einem Objekt Hogwarts zusammen. 
Hogwarts <- cbind(tab1, tab2)

# anzeigen
str(Hogwarts)
'data.frame':   4 obs. of  4 variables:
 $ Hufflepuff: chr  "Kräuterkunde" "Pflege magischer Geschöpfe" "Geschichte der Zauberei" "Alte Runen"
 $ Slytherin : chr  "Zaubertränke" "Zauberkunst" "Dunkle Künste" "Legilimentik"
 $ Gryffindor: chr  "Verteidigung gegen die dunklen Künste" "Zauberkunst" "Verwandlung" "Besenflugunterricht"
 $ Ravenclaw : chr  "Arithmantik" "Astronomie" "Verwandlung" "Verteidigung gegen die dunklen Künste"
c) Nutzen Sie die mutate()-Funktion, um die Datenklassen der Variablen anzupassen (Skalenniveau). 
library(dplyr)
Hogwarts <- Hogwarts %>% 
              mutate_if(is.character, as.factor)

# anzeigen
str(Hogwarts)
'data.frame':   4 obs. of  4 variables:
 $ Hufflepuff: Factor w/ 4 levels "Alte Runen","Geschichte der Zauberei",..: 3 4 2 1
 $ Slytherin : Factor w/ 4 levels "Dunkle Künste",..: 4 3 1 2
 $ Gryffindor: Factor w/ 4 levels "Besenflugunterricht",..: 2 4 3 1
 $ Ravenclaw : Factor w/ 4 levels "Arithmantik",..: 1 2 4 3
d) Ändern Sie anschließend mit der mutate()-Funktion den Kurs “Geschichte der Zauberei” in “Geisterkunde” um. 
library(dplyr)
library(forcats)
Hogwarts <- Hogwarts %>% 
    mutate(Hufflepuff = fct_recode(Hufflepuff, 
                                   "Geisterkunde" = "Geschichte der Zauberei"))

# anzeigen
Hogwarts
                  Hufflepuff     Slytherin
1               Kräuterkunde  Zaubertränke
2 Pflege magischer Geschöpfe   Zauberkunst
3               Geisterkunde Dunkle Künste
4                 Alte Runen  Legilimentik
                             Gryffindor                             Ravenclaw
1 Verteidigung gegen die dunklen Künste                           Arithmantik
2                           Zauberkunst                            Astronomie
3                           Verwandlung                           Verwandlung
4                   Besenflugunterricht Verteidigung gegen die dunklen Künste
e) Die Daten liegen nicht im Tidy-Data-Format vor. Erzeugen Sie ein neues Objekt Kurse mit den Variablen Haus und Kurs. 
library(tidyr)
Kurse <- Hogwarts %>% 
          pivot_longer(Hufflepuff:Ravenclaw,
                       names_to = "Haus",
                       values_to = "Kurs")
# anzeigen
Kurse
# A tibble: 16 × 2
   Haus       Kurs                                 
   <chr>      <fct>                                
 1 Hufflepuff Kräuterkunde                         
 2 Slytherin  Zaubertränke                         
 3 Gryffindor Verteidigung gegen die dunklen Künste
 4 Ravenclaw  Arithmantik                          
 5 Hufflepuff Pflege magischer Geschöpfe           
 6 Slytherin  Zauberkunst                          
 7 Gryffindor Zauberkunst                          
 8 Ravenclaw  Astronomie                           
 9 Hufflepuff Geisterkunde                         
10 Slytherin  Dunkle Künste                        
11 Gryffindor Verwandlung                          
12 Ravenclaw  Verwandlung                          
13 Hufflepuff Alte Runen                           
14 Slytherin  Legilimentik                         
15 Gryffindor Besenflugunterricht                  
16 Ravenclaw  Verteidigung gegen die dunklen Künste
Überführen Sie die Objekte tab1 und tab2 aus a) jeweils in eine data.table. Wiederholen Sie nun die Aufgaben c) bis e), indem Sie ausschließlich Funktionen des data.table-Paketes nutzen. 
library(data.table)

# überführe in data.table Objekte
dt1 <- as.data.table(tab1)
dt2 <- as.data.table(tab2)

# verschmelze dt2 in dt1
dt1[, names(dt2) := dt2 ]

# passe Skalenniveau an
dt1[, let(Slytherin = factor(Slytherin),
          Gryffindor = factor(Gryffindor),
          Hufflepuff = factor(Hufflepuff),
          Ravenclaw = factor(Ravenclaw))]

# “Geschichte der Zauberei” => “Geisterkunde” 
dt1[Hufflepuff == "Geschichte der Zauberei", Hufflepuff := "Geisterkunde"]

# Tidy-Objekt "Kurse"
Kurse <- melt(dt1, variable.name = "Haus", value.name = "Kurs",
              value.factor = TRUE,
              measure.vars = c("Hufflepuff", "Slytherin", 
                               "Ravenclaw", "Gryffindor"))

# anschauen
Kurse
          Haus                                  Kurs
        <fctr>                                <fctr>
 1: Hufflepuff                          Kräuterkunde
 2: Hufflepuff            Pflege magischer Geschöpfe
 3: Hufflepuff                          Geisterkunde
 4: Hufflepuff                            Alte Runen
 5:  Slytherin                          Zaubertränke
 6:  Slytherin                           Zauberkunst
 7:  Slytherin                         Dunkle Künste
 8:  Slytherin                          Legilimentik
 9:  Ravenclaw                           Arithmantik
10:  Ravenclaw                            Astronomie
11:  Ravenclaw                           Verwandlung
12:  Ravenclaw Verteidigung gegen die dunklen Künste
13: Gryffindor Verteidigung gegen die dunklen Künste
14: Gryffindor                           Zauberkunst
15: Gryffindor                           Verwandlung
16: Gryffindor                   Besenflugunterricht

5.1.2 Lösung zur Aufgabe 2.1.2 Aufnahme und Entlassung

a) Laden Sie den Datensatz Krankenhaus.RData in Ihre R-Session. 
# Lese Daten ein
load("https://www.produnis.de/trainingslager/data/Krankenhaus.RData")
# anschauen
str(St.Gott.Hospital)
tibble [6,383 × 4] (S3: tbl_df/tbl/data.frame)
 $ Geschlecht: chr [1:6383] "m" "w" "m" "m" ...
 $ ALter     : num [1:6383] 65 75 76 82 71 71 57 82 61 84 ...
 $ Aufnahme  : chr [1:6383] "201509000000" "201510000000" "201606050000" "201606051914" ...
 $ Entlassung: chr [1:6383] "201509000000" "201510000000" "201606052359" "201606061300" ...
b) Ein Variablenname enthält einen Tippfehler. Reparieren Sie auch die Datenklassen der Variablen. Entfernen Sie alle Einträge mit ungültigen Zeitstempeln. 
# Variable ALter korrigieren
library(dplyr)
kh <- St.Gott.Hospital %>% 
  select(Geschlecht, Alter = ALter, Aufnahme, Entlassung)
                 
# Datenklassen anpassen
# Geschlecht als Faktor
kh$Geschlecht <- factor(kh$Geschlecht)

# Erzeuge POSIX Zeitobjekte
# CET = Europäische Zeit
library(lubridate)
kh$Aufnahme <- ymd_hm(kh$Aufnahme, tz="CET")
kh$Entlassung <- ymd_hm(kh$Entlassung, tz="CET")

# anzeigen
str(kh)
tibble [6,383 × 4] (S3: tbl_df/tbl/data.frame)
 $ Geschlecht: Factor w/ 2 levels "m","w": 1 2 1 1 2 2 1 2 2 2 ...
 $ Alter     : num [1:6383] 65 75 76 82 71 71 57 82 61 84 ...
 $ Aufnahme  : POSIXct[1:6383], format: NA NA ...
 $ Entlassung: POSIXct[1:6383], format: NA NA ...

Durch die Umwandlung der Aufnahme- und Entlassungsdaten sind die Datenreihen mit fehlerhaften oder unvollständigen Zeitstempeln in NAs umgewandelt worden.

kh <- kh %>% 
  drop_na(Aufnahme, Entlassung)

# anschauen
glimpse(kh)
Rows: 6,251
Columns: 4
$ Geschlecht <fct> m, m, w, w, m, w, w, w, m, w, w, w, w, m, w, m, m, w, m, m,…
$ Alter      <dbl> 76, 82, 71, 71, 57, 82, 61, 84, 88, 74, 92, 73, 88, 86, 76,…
$ Aufnahme   <dttm> 2016-06-05 00:00:00, 2016-06-05 19:14:00, 2016-06-06 13:39…
$ Entlassung <dttm> 2016-06-05 23:59:00, 2016-06-06 13:00:00, 2016-06-14 13:30…
c) Erstellen Sie die neue Variable Liegedauer, welche die Aufenthaltsdauer in Tagen beinhaltet. 
# Liegedauer berechnen
# entweder...
kh$Liegedauer <- as_date(kh$Entlassung) - as_date(kh$Aufnahme)

# ...oder
kh$Liegedauer <- ceiling(difftime(kh$Entlassung, kh$Aufnahme, units="days"))

# anzeigen
head(kh$Liegedauer)
Time differences in days
[1]  1  1  8 14 14 22
str(kh)
tibble [6,251 × 5] (S3: tbl_df/tbl/data.frame)
 $ Geschlecht: Factor w/ 2 levels "m","w": 1 1 2 2 1 2 2 2 1 2 ...
 $ Alter     : num [1:6251] 76 82 71 71 57 82 61 84 88 74 ...
 $ Aufnahme  : POSIXct[1:6251], format: "2016-06-05 00:00:00" "2016-06-05 19:14:00" ...
 $ Entlassung: POSIXct[1:6251], format: "2016-06-05 23:59:00" "2016-06-06 13:00:00" ...
 $ Liegedauer: 'difftime' num [1:6251] 1 1 8 14 ...
  ..- attr(*, "units")= chr "days"
d) Über welchen Zeitraum wurden die Daten erhoben? 
erste <- min(kh$Aufnahme, na.rm=TRUE)
letzte <- max(kh$Entlassung, na.rm=TRUE)

# Zeitspanne in Tagen
as_date(letzte) - as_date(erste)
Time difference of 2284 days
# Zeitspanne in Wochen
difftime(letzte, erste, units="weeks")
Time difference of 326.3253 weeks
# Zeitspanne in Jahren
as.numeric(as_date(letzte) - as_date(erste)) / 365
[1] 6.257534
e) Klassieren Sie die Daten der Aufnahme in einer neuen Variable Kalenderjahr. 
# cut ausprobieren
a <- cut.POSIXt(kh$Aufnahme, breaks="years")
head(a)
[1] 2016-01-01 2016-01-01 2016-01-01 2016-01-01 2016-01-01 2016-01-01
7 Levels: 2015-01-01 2016-01-01 2017-01-01 2018-01-01 ... 2021-01-01
# lubridate::year() ist einfacher
a <- year(kh$Aufnahme)
head(a)
[1] 2016 2016 2016 2016 2016 2016
# in neue Variable schreiben
kh$Kalenderjahr <- year(kh$Aufnahme)

# anschauen
glimpse(kh)
Rows: 6,251
Columns: 6
$ Geschlecht   <fct> m, m, w, w, m, w, w, w, m, w, w, w, w, m, w, m, m, w, m, …
$ Alter        <dbl> 76, 82, 71, 71, 57, 82, 61, 84, 88, 74, 92, 73, 88, 86, 7…
$ Aufnahme     <dttm> 2016-06-05 00:00:00, 2016-06-05 19:14:00, 2016-06-06 13:…
$ Entlassung   <dttm> 2016-06-05 23:59:00, 2016-06-06 13:00:00, 2016-06-14 13:…
$ Liegedauer   <drtn> 1 days, 1 days, 8 days, 14 days, 14 days, 22 days, 3 day…
$ Kalenderjahr <dbl> 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 201…
f) Klassieren Sie die Daten der Entlassung je mit einer neuen Variable Wochentag und Monat. 
# Wochentag
kh$Wochentag <- wday(kh$Entlassung, label=TRUE)

# Monat
kh$Monat <- month(kh$Entlassung, label=TRUE)

# anschauen
glimpse(kh)
Rows: 6,251
Columns: 8
$ Geschlecht   <fct> m, m, w, w, m, w, w, w, m, w, w, w, w, m, w, m, m, w, m, …
$ Alter        <dbl> 76, 82, 71, 71, 57, 82, 61, 84, 88, 74, 92, 73, 88, 86, 7…
$ Aufnahme     <dttm> 2016-06-05 00:00:00, 2016-06-05 19:14:00, 2016-06-06 13:…
$ Entlassung   <dttm> 2016-06-05 23:59:00, 2016-06-06 13:00:00, 2016-06-14 13:…
$ Liegedauer   <drtn> 1 days, 1 days, 8 days, 14 days, 14 days, 22 days, 3 day…
$ Kalenderjahr <dbl> 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 201…
$ Wochentag    <ord> So, Mo, Di, Di, Mo, Di, Do, Mi, Mi, Mi, Fr, Fr, Mo, Do, D…
$ Monat        <ord> Jun, Jun, Jun, Jul, Jun, Jun, Jun, Jun, Aug, Jul, Jun, Ju…

5.1.3 Lösung zur Aufgabe 2.1.3 SPSS Datensatz

a) alteDaten.sav

Dateien mit Endung .sav stammen von SPSS.

# Lese Daten ein
c <- haven::read_sav("https://www.produnis.de/trainingslager/data/alteDaten-kurz.sav")
b) Passen Sie die Datenklassen der Variablen entsprechend des Skalenniveaus an, indem Sie nur Funktionen aus der R Standardinstallation verwenden. Dabei sollen die Variablennamen als Labels erhalten bleiben. 
# Datenklassen anschauen
str(c)
tibble [1,000 × 4] (S3: tbl_df/tbl/data.frame)
 $ Frage_1: dbl+lbl [1:1000] 4, 4, 4, 4, 3, 2, 2, 2, 4, 3, 2, 5, 2, 2, 4, 5, 5, 0,...
   ..@ label        : chr "Statistik ist mein Lieblingsfach?"
   ..@ format.spss  : chr "F1.0"
   ..@ display_width: int 12
   ..@ labels       : Named num [1:6] 0 1 2 3 4 5
   .. ..- attr(*, "names")= chr [1:6] "nicht vorhanden" "stimme gar nicht zu" "stimme nicht zu" "weiß nicht" ...
 $ Frage_2: dbl+lbl [1:1000] 4, 4, 4, 3, 3, 3, 1, 5, 4, 3, 2, 2, 2, 2, 4, 5, 1, 2,...
   ..@ label        : chr "Das Statistikprogramm R gefällt mir besser als SPSS?"
   ..@ format.spss  : chr "F1.0"
   ..@ display_width: int 12
   ..@ labels       : Named num [1:6] 0 1 2 3 4 5
   .. ..- attr(*, "names")= chr [1:6] "nicht vorhanden" "stimme gar nicht zu" "stimme nicht zu" "weiß nicht" ...
 $ Frage_3: dbl+lbl [1:1000] 4, 4, 4, 3, 2, 3, 3, 3, 4, 3, 2, 2, 2, 3, 4, 2, 3, 3,...
   ..@ label        : chr "Ich hätte gerne mehr Übungen in Statistik?"
   ..@ format.spss  : chr "F1.0"
   ..@ display_width: int 12
   ..@ labels       : Named num [1:6] 0 1 2 3 4 5
   .. ..- attr(*, "names")= chr [1:6] "nicht vorhanden" "stimme gar nicht zu" "stimme nicht zu" "weiß nicht" ...
 $ Frage_4: dbl+lbl [1:1000] 0, 0, 0, 4, 2, 2, 2, 3, 5, 4, 2, 4, 4, 2, 0, 4, 4, 2,...
   ..@ label        : chr "Schalke ist mein Lieblingsverein?"
   ..@ format.spss  : chr "F1.0"
   ..@ display_width: int 12
   ..@ labels       : Named num [1:6] 0 1 2 3 4 5
   .. ..- attr(*, "names")= chr [1:6] "nicht vorhanden" "stimme gar nicht zu" "stimme nicht zu" "weiß nicht" ...
# Variable
head(c$Frage_1)
<labelled<double>[6]>: Statistik ist mein Lieblingsfach?
[1] 4 4 4 4 3 2

Labels:
 value               label
     0     nicht vorhanden
     1 stimme gar nicht zu
     2     stimme nicht zu
     3          weiß nicht
     4           stimme zu
     5      stimme voll zu

Die Daten sind gelabelt und scheinen ordinalskaliert zu sein.

# Antwortlabels von Hand aufschreiben
c.labels <- c("nicht vorhanden", "stimme gar nicht zu", "stimme nicht zu", 
              "weiß nicht", "stimme zu", "stimme voll zu")  
# oder einfach
c.labels <- names(attr(c$Frage_1, "labels"))

# Variablenbezeichnung speichern
c.vars <- c(attr(c$Frage_1, "label"), attr(c$Frage_2, "label") ,
            attr(c$Frage_3, "label"), attr(c$Frage_4, "label"))

# Variablen in ordinale Faktoren umwandeln
c$Frage_1 <- factor(c$Frage_1, ordered=TRUE, levels=c(0:5))
c$Frage_2 <- factor(c$Frage_2, ordered=TRUE, levels=c(0:5))
c$Frage_3 <- factor(c$Frage_3, ordered=TRUE, levels=c(0:5))
c$Frage_4 <- factor(c$Frage_4, ordered=TRUE, levels=c(0:5))

# Levelnamen ändern
levels(c$Frage_1) <- c.labels
levels(c$Frage_2) <- c.labels
levels(c$Frage_3) <- c.labels
levels(c$Frage_4) <- c.labels

# Variabeln wieder labeln
attr(c$Frage_1, "label") <- c.vars[1]
attr(c$Frage_2, "label") <- c.vars[2]
attr(c$Frage_3, "label") <- c.vars[3]
attr(c$Frage_4, "label") <- c.vars[4]

# anschauen
str(c)
tibble [1,000 × 4] (S3: tbl_df/tbl/data.frame)
 $ Frage_1: Ord.factor w/ 6 levels "nicht vorhanden"<..: 5 5 5 5 4 3 3 3 5 4 ...
  ..- attr(*, "label")= chr "Statistik ist mein Lieblingsfach?"
 $ Frage_2: Ord.factor w/ 6 levels "nicht vorhanden"<..: 5 5 5 4 4 4 2 6 5 4 ...
  ..- attr(*, "label")= chr "Das Statistikprogramm R gefällt mir besser als SPSS?"
 $ Frage_3: Ord.factor w/ 6 levels "nicht vorhanden"<..: 5 5 5 4 3 4 4 4 5 4 ...
  ..- attr(*, "label")= chr "Ich hätte gerne mehr Übungen in Statistik?"
 $ Frage_4: Ord.factor w/ 6 levels "nicht vorhanden"<..: 1 1 1 5 3 3 3 4 6 5 ...
  ..- attr(*, "label")= chr "Schalke ist mein Lieblingsverein?"
c) Wiederholen Sie den Vorgang und verwenden dabei Funktionen aus dem tidyverse. 
# Lese Daten ein
c <- haven::read_sav("https://www.produnis.de/trainingslager/data/alteDaten-kurz.sav")
library(tidyverse)
# wandle die Antwortlabels in Factoren um
c <- c %>% 
  mutate(haven::as_factor(., ordered=TRUE))

# anzeigen
str(c)
tibble [1,000 × 4] (S3: tbl_df/tbl/data.frame)
 $ Frage_1: Ord.factor w/ 6 levels "nicht vorhanden"<..: 5 5 5 5 4 3 3 3 5 4 ...
  ..- attr(*, "label")= chr "Statistik ist mein Lieblingsfach?"
 $ Frage_2: Ord.factor w/ 6 levels "nicht vorhanden"<..: 5 5 5 4 4 4 2 6 5 4 ...
  ..- attr(*, "label")= chr "Das Statistikprogramm R gefällt mir besser als SPSS?"
 $ Frage_3: Ord.factor w/ 6 levels "nicht vorhanden"<..: 5 5 5 4 3 4 4 4 5 4 ...
  ..- attr(*, "label")= chr "Ich hätte gerne mehr Übungen in Statistik?"
 $ Frage_4: Ord.factor w/ 6 levels "nicht vorhanden"<..: 1 1 1 5 3 3 3 4 6 5 ...
  ..- attr(*, "label")= chr "Schalke ist mein Lieblingsverein?"

5.2 Lösungen zu den Datensatzauswertungen

5.2.1 Lösung zur Aufgabe 2.2.1 Aufnahme und Entlassung

a) Laden Sie den Datensatz Krankenhaus.RData in Ihre R-Session, korrigieren Sie den Tippfehler der Variable ALter, reparieren Sie die Datenklassen der Variablen und entfernen Sie alle Einträge mit ungültigen Zeitstempeln. 
# Lese Daten ein
load("https://www.produnis.de/trainingslager/data/Krankenhaus.RData")
library(dplyr)
library(lubridate)
# repariere Typo und Datenklassen und
# entferne NAs
kh <- St.Gott.Hospital %>% 
  select(Geschlecht, Alter = ALter, Aufnahme, Entlassung) %>% 
  mutate(Geschlecht = factor(Geschlecht),
         Aufnahme = ymd_hm(Aufnahme, tz="CET"),
         Entlassung = ymd_hm(Entlassung, tz="CET")
         ) %>% 
  drop_na(Aufnahme, Entlassung)

# anzeigen
glimpse(kh)
Rows: 6,251
Columns: 4
$ Geschlecht <fct> m, m, w, w, m, w, w, w, m, w, w, w, w, m, w, m, m, w, m, m,…
$ Alter      <dbl> 76, 82, 71, 71, 57, 82, 61, 84, 88, 74, 92, 73, 88, 86, 76,…
$ Aufnahme   <dttm> 2016-06-05 00:00:00, 2016-06-05 19:14:00, 2016-06-06 13:39…
$ Entlassung <dttm> 2016-06-05 23:59:00, 2016-06-06 13:00:00, 2016-06-14 13:30…
b) Plotten Sie die absoluten Häufigkeiten der Aufnahmen und Entlassungen pro Kalendertag. Was fällt Ihnen auf? 
library(ggplot2)
# Hilfsdatenframe mit Anzahl Aufnahmen pro Tag
Aufnahmen <- kh %>%
  group_by(as_date(Aufnahme)) %>%
  summarise(freq = n()) %>% 
  # Spalten umbenennen
  select(Datum = `as_date(Aufnahme)`, freq) %>% 
  # Variable "Typ" hinzufügen
  mutate(Typ="Aufnahme")

# Hilfsdatenframe mit Anzahl Entlassungen pro Tag
Entlassungen <- kh %>%
  group_by(as_date(Entlassung)) %>%
  summarise(freq = n()) %>% 
  select(Datum = `as_date(Entlassung)`, freq) %>% 
  mutate(Typ="Entlassung")

# Zusammenführen
df <- rbind(Aufnahmen, Entlassungen)

# Plotten
ggplot(df, aes(x=Datum, y=freq)) +
  geom_line(aes(color=Typ)) +
  labs(title = "Absolute Häufigkeit der Datumswerte",
       x = "Datum",
       y = "Absolute Häufigkeit") +
  theme_minimal()

Es fällt auf, dass für das Jahr 2019 keine Daten zur Verfügung stehen.

c) Plotten Sie die durchschnittlichen (arithmetisches Mittel) absoluten Häufigkeiten an täglichen Aufnahmen und Entlassungen pro Wochentag. Was fällt Ihnen auf? 
# nochmal Hilfsdatenframe mit Anzahl Aufnahmen pro Tag
Aufnahmen <- kh %>%
  group_by(as_date(Aufnahme)) %>%
  summarise(freq = n()) %>% 
  # Spalten umbenennen
  select(Datum = `as_date(Aufnahme)`, freq) %>% 
  # Variable "Typ" hinzufügen
  mutate(Typ = "Aufnahme",
         # Wochentag hinzufügen
         Tag= wday(Datum, label=TRUE))


# Hilfsdatenframe mit Anzahl Entlassungen pro Tag
Entlassungen <- kh %>%
  group_by(as_date(Entlassung)) %>%
  summarise(freq = n()) %>% 
  select(Datum = `as_date(Entlassung)`, freq) %>% 
  mutate(Typ = "Entlassung",
         # Wochentag hinzufügen
         Tag = wday(Datum, label=TRUE))

# zusammenführen
Wochentage <- rbind(Aufnahmen, Entlassungen)

# absolute Häufigkeiten anzeigen
table(Wochentage$Typ, Wochentage$Tag)
            
              So  Mo  Di  Mi  Do  Fr  Sa
  Aufnahme   165 195 205 192 169 137 130
  Entlassung 107 213 219 220 222 222 174
# durchschnittliche Häufigkeiten
Wochentage  %>% 
  group_by(Typ, Tag) %>% 
  summarise(Mean = mean(freq))
# A tibble: 14 × 3
# Groups:   Typ [2]
   Typ        Tag    Mean
   <chr>      <ord> <dbl>
 1 Aufnahme   So     3.98
 2 Aufnahme   Mo     7.02
 3 Aufnahme   Di     5.87
 4 Aufnahme   Mi     6.04
 5 Aufnahme   Do     5.25
 6 Aufnahme   Fr     4.66
 7 Aufnahme   Sa     2.6 
 8 Entlassung So     1.57
 9 Entlassung Mo     4.35
10 Entlassung Di     5.10
11 Entlassung Mi     5.21
12 Entlassung Do     4.81
13 Entlassung Fr     5.77
14 Entlassung Sa     3.13
# durchschnittliche (arith.) Häufigkeiten
ggplot(Wochentage, aes(x=Tag, y=freq, fill=Typ)) +
  stat_summary(fun=mean, geom="bar", position="dodge")

An Sonn- und Montag gibt es deutlich mehr Aufnahmen als Entlassungen.

d) Plotten Sie die durchschnittlichen absoluten Häufigkeiten an täglichen Aufnahmen und Entlassungen pro Monat sowie die absoluten Häufigkeiten pro Tagesstunde. 
# nochmal Hilfsdatenframe mit Anzahl Aufnahmen pro Monat
Aufnahmen <- kh %>%
  group_by(as_date(Aufnahme)) %>%
  summarise(freq = n()) %>% 
  # Spalten umbenennen
  select(Datum = `as_date(Aufnahme)`, freq) %>% 
  # Variable "Typ" hinzufügen
  mutate(Typ = "Aufnahme",
         # Monat hinzufügen
         Monat= month(Datum, label=TRUE))


# Hilfsdatenframe mit Anzahl Entlassungen pro Tag
Entlassungen <- kh %>%
  group_by(as_date(Entlassung)) %>%
  summarise(freq = n()) %>% 
  select(Datum = `as_date(Entlassung)`, freq) %>% 
  mutate(Typ = "Entlassung",
         # Monate hinzufügen
         Monat= month(Datum, label=TRUE))

# zusammenführen
Monate <- rbind(Aufnahmen, Entlassungen)

# absolute Häufigkeiten anzeigen
table(Monate$Typ, Monate$Monat)
            
             Jan Feb Mär Apr Mai Jun Jul Aug Sep Okt Nov Dez
  Aufnahme    82  73  86  95  93  87 121 108 124 141 103  80
  Entlassung  77  84 121 108 108  97 125 128 132 163 128 106
# durchschnittliche Häufigkeiten
 Monate %>% 
  group_by(Typ,Monat) %>% 
  summarise(Median = median(freq))
# A tibble: 24 × 3
# Groups:   Typ [2]
   Typ      Monat Median
   <chr>    <ord>  <dbl>
 1 Aufnahme Jan        5
 2 Aufnahme Feb        5
 3 Aufnahme Mär        6
 4 Aufnahme Apr        3
 5 Aufnahme Mai        4
 6 Aufnahme Jun        5
 7 Aufnahme Jul        5
 8 Aufnahme Aug        4
 9 Aufnahme Sep        4
10 Aufnahme Okt        5
# ℹ 14 more rows
# durchschnittliche (Median) Häufigkeiten
ggplot(Monate, aes(x=Monat, y=freq, fill=Typ)) +
  stat_summary(fun=median, geom="bar", position="dodge")

Wiederholen wir nun den Vorgang für die Häufigkeiten pro Tagesstunde.

# nochmal Hilfsdatenframe mit Anzahl Aufnahmen pro Tagesstunde
kh$Aufnahmestunde <- hour(kh$Aufnahme)
kh$Entlassungstunde <- hour(kh$Entlassung)

Aufnahmen <- kh %>%
  group_by(Aufnahmestunde) %>%
  summarise(freq = n()) %>% 
  # Variable "Typ" hinzufügen
  mutate(Typ = "Aufnahme") %>% 
  select(Stunde = Aufnahmestunde, freq, Typ)


# Hilfsdatenframe mit Anzahl Entlassungen pro Tagesstunde
Entlassungen <- kh %>%
  group_by(Entlassungstunde) %>%
  summarise(freq = n()) %>% 
  # Variable "Typ" hinzufügen
  mutate(Typ = "Entlassungen") %>% 
  select(Stunde = Entlassungstunde, freq, Typ)

# zusammenführen
Stunden <- rbind(Aufnahmen, Entlassungen)

# absolute Häufigkeiten pro Tagesstunde
ggplot(Stunden, aes(x=Stunde, y=freq, fill=Typ)) +
  geom_col(position="dodge")

e) Erstellen Sie ein Poissionregressionsmodell für die Anzahl der täglichen Aufnahmen erklärt durch den Wochentag. Ist das Modell überdispersioniert? Wieviele Aufnahmen sind an einem Dienstag und an einem Sonntag zu erwarten? 
# nur Aufnahmen
dfA <- subset(Wochentage, Typ=="Aufnahme")

# "Tag" für Poisson vorbereiten
# ordered entfernen
dfA$Tag <- factor(dfA$Tag, ordered=FALSE)
# Montag als Basiswert
dfA$Tag <- relevel(dfA$Tag, "Mo")

# Poisson-Modell erstellen
fit <- glm(freq ~ Tag, data=dfA, family = poisson)

# Zusammenfassung des Modells
summary(fit)

Call:
glm(formula = freq ~ Tag, family = poisson, data = dfA)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  1.94884    0.02703  72.107  < 2e-16 ***
TagSo       -0.56710    0.04746 -11.949  < 2e-16 ***
TagDi       -0.17927    0.03952  -4.536 5.72e-06 ***
TagMi       -0.15102    0.03992  -3.783 0.000155 ***
TagDo       -0.29089    0.04310  -6.749 1.49e-11 ***
TagFr       -0.41048    0.04794  -8.563  < 2e-16 ***
TagSa       -0.99332    0.06074 -16.354  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 2994.4  on 1192  degrees of freedom
Residual deviance: 2574.6  on 1186  degrees of freedom
AIC: 6501.8

Number of Fisher Scoring iterations: 5
# alternative Zusammenfassung
sjPlot::tab_model(fit)
  freq
Predictors Incidence Rate Ratios CI p
(Intercept) 7.02 6.66 – 7.40 <0.001
Tag [So] 0.57 0.52 – 0.62 <0.001
Tag [Di] 0.84 0.77 – 0.90 <0.001
Tag [Mi] 0.86 0.80 – 0.93 <0.001
Tag [Do] 0.75 0.69 – 0.81 <0.001
Tag [Fr] 0.66 0.60 – 0.73 <0.001
Tag [Sa] 0.37 0.33 – 0.42 <0.001
Observations 1193
R2 Nagelkerke 0.323

Testen wir, ob das Modell überdispersioniert ist.

AER::dispersiontest(fit, trafo=1)

    Overdispersion test

data:  fit
z = 10.82, p-value < 2.2e-16
alternative hypothesis: true alpha is greater than 0
sample estimates:
   alpha 
1.273968

Der Test ist signifikant, d.h. das Modell ist überdispersioniert. Wir müssen das Modell daher anpassen:

fit <- glm(freq ~ Tag, data=dfA, family = quasipoisson)
summary(fit)

Call:
glm(formula = freq ~ Tag, family = quasipoisson, data = dfA)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.94884    0.04088  47.677  < 2e-16 ***
TagSo       -0.56710    0.07178  -7.900 6.30e-15 ***
TagDi       -0.17927    0.05977  -2.999  0.00276 ** 
TagMi       -0.15102    0.06037  -2.502  0.01250 *  
TagDo       -0.29089    0.06519  -4.462 8.88e-06 ***
TagFr       -0.41048    0.07250  -5.662 1.88e-08 ***
TagSa       -0.99332    0.09186 -10.813  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for quasipoisson family taken to be 2.28739)

    Null deviance: 2994.4  on 1192  degrees of freedom
Residual deviance: 2574.6  on 1186  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 5

 

Mit dem neuen Modell können nun die Vorhersagen erfolgen.

# Vorhersage Dienstag
predict(fit, list(Tag="Di"), type = "response")
       1 
5.868293 
# Vorhersage Sonntag
predict(fit, list(Tag="So"), type = "response")
       1 
3.981818
f) Fügen Sie den Monat als weiteren Prädiktor hinzu. Wird das Modell dadurch besser? Wieviele Aufnahmen sind an einem Donnerstag im Mai zu erwarten, und wieviele im September? 
dfA$Monat <- month(dfA$Datum, label=TRUE)
dfA$Monat <- factor(dfA$Monat, ordered=FALSE)
dfA$Monat <- relevel(dfA$Monat, "Jan")

fit <- glm(freq ~ Tag + Monat, data=dfA, family="poisson")
summary(fit)

Call:
glm(formula = freq ~ Tag + Monat, family = "poisson", data = dfA)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.13203    0.05032  42.368  < 2e-16 ***
TagSo       -0.56984    0.04749 -11.998  < 2e-16 ***
TagDi       -0.17175    0.03955  -4.342 1.41e-05 ***
TagMi       -0.14825    0.03995  -3.711 0.000207 ***
TagDo       -0.28742    0.04316  -6.660 2.74e-11 ***
TagFr       -0.41400    0.04798  -8.629  < 2e-16 ***
TagSa       -0.98855    0.06079 -16.263  < 2e-16 ***
MonatFeb     0.02741    0.06389   0.429 0.667963    
MonatMär    -0.01210    0.06150  -0.197 0.844042    
MonatApr    -0.29136    0.06485  -4.492 7.04e-06 ***
MonatMai    -0.32501    0.06576  -4.942 7.72e-07 ***
MonatJun    -0.26052    0.06548  -3.979 6.93e-05 ***
MonatJul    -0.14788    0.05923  -2.497 0.012536 *  
MonatAug    -0.19857    0.06124  -3.243 0.001184 ** 
MonatSep    -0.29288    0.06052  -4.839 1.30e-06 ***
MonatOkt    -0.21975    0.05802  -3.788 0.000152 ***
MonatNov    -0.18356    0.06151  -2.984 0.002842 ** 
MonatDez    -0.29117    0.06761  -4.307 1.66e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 2994.4  on 1192  degrees of freedom
Residual deviance: 2493.2  on 1175  degrees of freedom
AIC: 6442.3

Number of Fisher Scoring iterations: 5

Das Modell hat einen größeren AIC-Wert als das alte.

Testen wir, ob das Modell überdispersioniert ist.

AER::dispersiontest(fit, trafo=1)

    Overdispersion test

data:  fit
z = 10.534, p-value < 2.2e-16
alternative hypothesis: true alpha is greater than 0
sample estimates:
   alpha 
1.185659

Der Test ist signifikant, d.h. das Modell ist überdispersioniert. Wir müssen das Modell anpassen.

fit <- glm(freq ~ Tag + Monat, data=dfA, family = quasipoisson)
summary(fit)

Call:
glm(formula = freq ~ Tag + Monat, family = quasipoisson, data = dfA)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.13203    0.07498  28.436  < 2e-16 ***
TagSo       -0.56984    0.07076  -8.053 1.97e-15 ***
TagDi       -0.17175    0.05893  -2.915 0.003630 ** 
TagMi       -0.14825    0.05952  -2.491 0.012892 *  
TagDo       -0.28742    0.06430  -4.470 8.59e-06 ***
TagFr       -0.41400    0.07148  -5.791 8.95e-09 ***
TagSa       -0.98855    0.09057 -10.915  < 2e-16 ***
MonatFeb     0.02741    0.09519   0.288 0.773478    
MonatMär    -0.01210    0.09163  -0.132 0.894978    
MonatApr    -0.29136    0.09663  -3.015 0.002623 ** 
MonatMai    -0.32501    0.09798  -3.317 0.000937 ***
MonatJun    -0.26052    0.09756  -2.670 0.007681 ** 
MonatJul    -0.14788    0.08825  -1.676 0.094064 .  
MonatAug    -0.19857    0.09124  -2.176 0.029728 *  
MonatSep    -0.29288    0.09017  -3.248 0.001195 ** 
MonatOkt    -0.21975    0.08645  -2.542 0.011147 *  
MonatNov    -0.18356    0.09164  -2.003 0.045410 *  
MonatDez    -0.29117    0.10073  -2.891 0.003916 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for quasipoisson family taken to be 2.219922)

    Null deviance: 2994.4  on 1192  degrees of freedom
Residual deviance: 2493.2  on 1175  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 5

 

Mit dem neuen Modell können wir nun die Vorhersagen treffen.

# Vorhersagen
predict(fit, list(Tag="Do", Monat="Mai"), type = "response")
       1 
4.570387 
predict(fit, list(Tag="Do", Monat="Sep"), type = "response")
       1 
4.719636
g) Wie groß ist die Wahrscheinlichkeit, dass an einem Mittwoch im Mai 10 Patienten aufgenommen werden? 
# Schätzen der mittleren Häufigkeit
mu <- predict(fit, list(Tag="Mi", Monat="Mai"), type = "response")

# Wahrscheinlichkeit für 10 Aufnahmen berechnen
dpois(10, lambda = mu)
[1] 0.02306207

Die Wahrscheinlichkeit liegt bei 2,3%.

h) Wie groß ist die Wahrscheinlichkeit, dass an einem Mittwoch im Mai zwischen 4 und 7 Patienten aufgenommen werden? 
# Schätzen der mittleren Häufigkeit
mu <- predict(fit, list(Tag="Mi", Monat="Mai"), type = "response")

# Wahrscheinlichkeit für 4 bis 7 Aufnahmen berechnen
# entweder
ppois(7, lambda=mu) - ppois(3, lambda=mu)
[1] 0.607611
# oder
sum(dpois(4:7, lambda=mu))
[1] 0.607611

Die Wahrscheinlichkeit liegt bei 60,76%.

i) Wie groß ist die Wahrscheinlichkeit, dass an einem Montag im Januar maximal 2 Patienten aufgenommen werden? 
# Schätzen der mittleren Häufigkeit
mu <- predict(fit, list(Tag="Mo", Monat="Jan"), type = "response")

# Wahrscheinlichkeit für maximal 2 Aufnahmen berechnen
ppois(2, lambda = mu)
[1] 0.009796846

Die Wahrscheinlichkeit liegt bei 0,98%.

j) Erzeugen Sie ein Histogramm des Alters der Probanden. Was fällt Ihnen auf? Korrigieren Sie wenn nötig die Daten. Ist das Alter der Probanden normalverteilt? 
# Histogramm mit Rbase
hist(kh$Alter)

# Wahrscheinlichkeit für maximal 2 Aufnahmen berechnen
ppois(2, lambda = mu)
[1] 0.009796846

Es fällt auf, dass es viele Probanden mit Alter=0 gibt. Dabei handelt es sich wahrscheinlich um Geburten. Da die Geburtsstation gesondert betrachtet werden muss, wandeln wir diese Datenreihen in NA um. So gehen sie nicht verloren und stören dennoch nicht bei der Auswertung.

kh$Alter[kh$Alter==0] <- NA

# Histogram wiederholen
hist(kh$Alter)

# Teste, ob Alter normalverteilt ist
ks.test(kh$Alter, "pnorm")
Warning in ks.test.default(kh$Alter, "pnorm"): ties should not be present for
the one-sample Kolmogorov-Smirnov test

    Asymptotic one-sample Kolmogorov-Smirnov test

data:  kh$Alter
D = 1, p-value < 2.2e-16
alternative hypothesis: two-sided

Der Test ist signifikant, das heisst, es liegt keine Normalverteilung vor.

k) Stellen Sie das Alter der Männern und Frauen tabellarisch und graphisch dar. Unterscheidet sich das Alter der Probanden zwischen Männern und Frauen? 
# Tabellarisch
kh %>%
  group_by(Geschlecht) %>%
  drop_na(Alter) %>%
  summarise(Min = min(Alter),
            Q1 = quantile(Alter, probs=0.25, type=6),
            Median = median(Alter),
            Mittel = mean(Alter),
            Q3 = quantile(Alter, probs=0.75, type=6),
            Max = max(Alter))
# A tibble: 2 × 7
  Geschlecht   Min    Q1 Median Mittel    Q3   Max
  <fct>      <dbl> <dbl>  <dbl>  <dbl> <dbl> <dbl>
1 m             18    61     73   69.4    81   105
2 w             18    58     74   68.5    81    99
# graphisch
boxplot(Alter ~ Geschlecht, data=kh)

Männer und Frauen unterscheiden sich nicht hinsichtlich des Alters.

l) Ist der Unterschied signifikant? 
# subsets vorbereiten
m <- subset(kh, Geschlecht=="m")
w <- subset(kh, Geschlecht=="w")

# keine Normalverteilung = kein t.Test
wilcox.test(m$Alter, w$Alter)

    Wilcoxon rank sum test with continuity correction

data:  m$Alter and w$Alter
W = 3621860, p-value = 0.74
alternative hypothesis: true location shift is not equal to 0

Der Test ist nicht signifikant, es liegt kein Unterschied vor.

m) Ab welchem Alter sind 10% der Männer älter als dieser Wert? 
# nur Männer
m <- subset(kh, Geschlecht=="m")
# beim 90. Perzentil liegen 10% der Werte darüber
quantile(m$Alter, 0.9, na.rm=TRUE, type=6)
90% 
 86

Es sind 10% der Männer älter als 86 Jahre.

n) Ab welchem Alter sind 80% der Frauen jünger als dieser Wert? 
# nur Frauen
w <- subset(kh, Geschlecht=="w")
# beim 90. Perzentil liegen 10% der Werte darüber
quantile(w$Alter, 0.8, na.rm=TRUE, type=6)
80% 
 83

Es sind 80% der Frauen jünger als 83 Jahre.

o) Wie groß ist die mittlere Liegedauer in Tagen? Stellen Sie die Liegedauer mittels Kennwerten sowie graphisch dar. Was fällt Ihnen auf? 
# Liegedauer berechnen
kh$Liegedauer <- as_date(kh$Entlassung) - as_date(kh$Aufnahme)
# mittlere Liegedauer, Median
mean(kh$Liegedauer)
Time difference of 8.582627 days
# mittlere Liegedauer, Median
median(kh$Liegedauer)
Time difference of 6 days
# Tabellarische Darstellung
summary(as.numeric(kh$Liegedauer))
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.000   3.000   6.000   8.583  10.000 260.000 
# graphische Darstellung
boxplot(kh$Liegedauer)

hist(as.numeric(kh$Liegedauer))

Es fällt auf, dass sehr viele Ausreißer enthalten sind.

p) Wie viel Prozent der Patienten haben eine Liegedauer von mehr als 7 Tagen? 
sum(kh$Liegedauer > 7) / length(kh$Liegedauer)
[1] 0.3722604

Im Datensatz haben 37,23 % der Patienten eine Liegedauer von mehr als 7 Tagen.

q) Unterscheiden sich Männer und Frauen hinsichtlich der Liegedauer? Stellen Sie den Unterschied ebenfalls tabellarisch und graphisch dar. 
# Tabellarische Darstellung
kh %>%
  group_by(Geschlecht) %>%
  summarise(Min = min(Liegedauer),
            Q1 = quantile(Liegedauer, probs=0.25, type=6),
            Median = median(Liegedauer),
            Mittel = mean(Liegedauer),
            Q3 = quantile(Liegedauer, probs=0.75, type=6),
            Max = max(Liegedauer))
# A tibble: 2 × 7
  Geschlecht Min    Q1     Median Mittel        Q3      Max     
  <fct>      <drtn> <drtn> <drtn> <drtn>        <drtn>  <drtn>  
1 m          0 days 3 days 6 days 8.684497 days 10 days 203 days
2 w          0 days 3 days 5 days 8.480984 days 10 days 260 days
# graphische Darstellung
boxplot(Liegedauer ~ Geschlecht, data=kh)

Es ist kein Unterschied erkennbar.

r) Ist der Unterschied der Liegedauer zwischen Männern und Frauen signifikant? 
# Teste auf Normalverteilung
ks.test(kh$Liegedauer, "pnorm")

    Asymptotic one-sample Kolmogorov-Smirnov test

data:  kh$Liegedauer
D = 0.84543 days, p-value < 2.2e-16
alternative hypothesis: two-sided

Der Test ist signifikant, d.h. es liegt keine Normalverteilung vor. Als Signifikanztest ist daher der Mann-Whitney-U-Test durchzuführen

# Vorbereitung
kh$Liegedauer <- as.numeric(kh$Liegedauer)
m <- subset(kh, Geschlecht=="m")
w <- subset(kh, Geschlecht=="w")

# Mann-Whitney-U-Test
wilcox.test(w$Liegedauer, m$Liegedauer)

    Wilcoxon rank sum test with continuity correction

data:  w$Liegedauer and m$Liegedauer
W = 4624670, p-value = 0.0002638
alternative hypothesis: true location shift is not equal to 0

Das Ergebnis ist signifikant. Es scheint doch einen Unterschied zwischen Männern und Frauen zu geben.

5.2.2 Lösung zur Aufgabe 2.2.2 Lungenkapazität

a) Laden Sie den Datensatz lungcap in Ihre R-Session. 
# aktiviere den Datensatz
library(GLMsData)
data("lungcap")

# anschauen
str(lungcap)
'data.frame':   654 obs. of  5 variables:
 $ Age   : int  3 4 4 4 4 4 4 5 5 5 ...
 $ FEV   : num  1.072 0.839 1.102 1.389 1.577 ...
 $ Ht    : num  46 48 48 48 49 49 50 46.5 49 49 ...
 $ Gender: Factor w/ 2 levels "F","M": 1 1 1 1 1 1 1 1 1 1 ...
 $ Smoke : int  0 0 0 0 0 0 0 0 0 0 ...
b) Erzeugen Sie eine neue Variable, welche die Körpergröße in Zentimetern enthält (1 Zoll = 2,54cm) 
lungcap$Körpergröße <- lungcap$Ht*2.54

# anschauen
str(lungcap)
'data.frame':   654 obs. of  6 variables:
 $ Age        : int  3 4 4 4 4 4 4 5 5 5 ...
 $ FEV        : num  1.072 0.839 1.102 1.389 1.577 ...
 $ Ht         : num  46 48 48 48 49 49 50 46.5 49 49 ...
 $ Gender     : Factor w/ 2 levels "F","M": 1 1 1 1 1 1 1 1 1 1 ...
 $ Smoke      : int  0 0 0 0 0 0 0 0 0 0 ...
 $ Körpergröße: num  117 122 122 122 124 ...
c) Plotten Sie nebeneinander die Boxplots der Lungenkapazität nichtrauchenden und rauchenden Kindern. Legt das Diagramm einen Zusammenhang nahe? 
boxplot(lungcap$FEV ~ lungcap$Smoke,
        col=c("darkgreen", "orchid"))

Es scheint, als ob rauchende Kinder eine größere Lungenkapazität hätten.

d) Führen Sie einen Signifikanztest durch, um zu überprüfen, ob sich die Lungenkapazitäten in Abhängigkeit zu Smoke unterscheidet. 
# Prüfe auf Normalverteilung
shapiro.test(lungcap$FEV)

    Shapiro-Wilk normality test

data:  lungcap$FEV
W = 0.97052, p-value = 3.391e-10

Der Test ist signifikant, d.h. FEV ist nicht normalverteilt. Wir müssen daher den Mann-Whitney-U-Test verwenden.

raucher <- subset(lungcap, Smoke==1)
nraucher <- subset(lungcap, Smoke==0)
wilcox.test(raucher$FEV, nraucher$FEV, alternative = "greater")

    Wilcoxon rank sum test with continuity correction

data:  raucher$FEV and nraucher$FEV
W = 28686, p-value = 2.035e-11
alternative hypothesis: true location shift is greater than 0

Der Test ist signifikant. Die Raucher haben eine größere Lungenkapazität als Nichtraucher.

e) Erzeugen Sie eine Punktwole des Lungenvolumens und des Alters. Legt das Diagramm einen Zusammenhang nahe? 
scatter.smooth(lungcap$Age, lungcap$FEV, col="skyblue2")

Es scheint einen linearen Zusammenhang zwischen dem Alter und der Lungenkapazität zu geben.

f) Erzeugen Sie eine Punktwole des Lungenvolumens und der Körpergröße. Legt das Diagramm einen Zusammenhang nahe? 
scatter.smooth(lungcap$Körpergröße, lungcap$FEV, col="thistle")

Es scheint einen linearen Zusammenhang zwischen der Körpergröße und der Lungenkapazität zu geben.

g) Welches Regressionsmodell ist am besten geeignet, um FEV erklärt durch Alter zu bestimmen? 
jgsbook::compare.lm(lungcap$FEV, lungcap$Age)
Registered S3 method overwritten by 'statip':
  method         from      
  predict.kmeans parameters
         Modell  R.square
7        potenz 0.6308534
4  exponentiell 0.5957878
3       kubisch 0.5925193
6     sigmoidal 0.5902058
2   quadratisch 0.5840171
1        linear 0.5722302
5 logarithmisch 0.5701891

Am besten geeignet ist ein Potenzmodell.

h) Welches Regressionsmodell ist am besten geeignet, um FEV erklärt durch Körpergröße zu bestimmen? 
jgsbook::compare.lm(lungcap$FEV, lungcap$Körpergröße)
         Modell  R.square
4  exponentiell 0.7956073
7        potenz 0.7944652
6     sigmoidal 0.7879391
3       kubisch 0.7741673
2   quadratisch 0.7740993
1        linear 0.7536584
5 logarithmisch 0.7370097

Am besten geeignet ist ein exponentielles Modell. Dabei ist R2 mit 0,79 größer als beim Potenzmodell des Alters (0,63). Die Lungenkapazität wird am besten durch die Körpergröße erklärt.

i) Berechnen Sie das Modell, welches FEV am besten erklärt. 
# exponentielles Modell erstellen
fit <- lm(log(FEV) ~ Körpergröße, data=lungcap)
summary(fit)

Call:
lm(formula = log(FEV) ~ Körpergröße, data = lungcap)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.70208 -0.08986  0.01190  0.09337  0.43174 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -2.2713118  0.0635310  -35.75   <2e-16 ***
Körpergröße  0.0205193  0.0004073   50.38   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1508 on 652 degrees of freedom
Multiple R-squared:  0.7956,    Adjusted R-squared:  0.7953 
F-statistic:  2538 on 1 and 652 DF,  p-value: < 2.2e-16
j) Plotten Sie eine Punktwolke, mit FEV auf der Y-Achse, und dem besten Prädiktor auf der X-Achse. Färben Sie die Daten mittels der Variable Smoke. Fügen Sie anschließend Ihre Modelllinie dem Plot hinzu. 
# Subsets
raucher <- subset(lungcap, Smoke==1)
nraucher <- subset(lungcap, Smoke==0)

#-- Hilfswert für Modellinie
helper <- jgsbook::compare.lm(lungcap$FEV, lungcap$Körpergröße, predict=TRUE)

# plot()
plot(nraucher$Körpergröße, nraucher$FEV, col="darkgreen", 
     xlab="Körpergröße", ylab="Lungenkapazität")
points(raucher$Körpergröße, raucher$FEV, col="orchid", pch=19)
lines(helper$pred.x, helper$expo, col="blue", lwd=4)
#--------
# ggplot()
#---------
ggplot(lungcap, aes(x=Körpergröße, y=FEV)) +
  geom_point(aes(color=factor(Smoke))) +
  scale_color_manual(values=c("darkgreen", "orchid")) +
  geom_line(data=helper, aes(x=pred.x, y=expo), color="blue")

k) Fügen Sie Smoke, Age und Gender als weitere Prädiktor dem Modell hinzu. Hat Rauchen einen Einfluss auf FEV? 
# exponentielles Modell um "Smoke", "Age" und "Gender" erweitern
fit  <- lm(log(FEV) ~ Körpergröße + Age + Gender + Smoke, data=lungcap)
summary(fit)

Call:
lm(formula = log(FEV) ~ Körpergröße + Age + Gender + Smoke, 
    data = lungcap)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.63278 -0.08657  0.01146  0.09540  0.40701 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.943998   0.078639 -24.721  < 2e-16 ***
Körpergröße  0.016849   0.000661  25.489  < 2e-16 ***
Age          0.023387   0.003348   6.984  7.1e-12 ***
GenderM      0.029319   0.011719   2.502   0.0126 *  
Smoke       -0.046067   0.020910  -2.203   0.0279 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1455 on 649 degrees of freedom
Multiple R-squared:  0.8106,    Adjusted R-squared:  0.8095 
F-statistic: 694.6 on 4 and 649 DF,  p-value: < 2.2e-16

Alle Prädiktoren sind signifikant. Der Beitrag von Smoke ist negativ. Dies spricht dafür, dass Rauchen die Lungenkapazität verschlechtert.

# Modelle vergleichen
fit0 <- lm(log(FEV) ~ Körpergröße, data=lungcap)
# R^2 vergleichen
summary(fit0)$r.squared - summary(fit)$r.squared 
[1] -0.01503201

Durch Hinzunahme der Prädiktoren verbessert sich R2, aber nur minimal.

5.2.3 Lösung zur Aufgabe 2.2.3 Brustkrebs

a) Importieren Sie den Datensatz in Ihre R-Session und machen Sie sich mit dem Datensatz vertraut. 
# lade den Datensatz
breast <- haven::read_sav("https://www.produnis.de/trainingslager/data/breast.sav")
# anschauen
head(breast)
# A tibble: 6 × 9
     id   age pathsize lnpos histgrad    er            pr          status   time
  <dbl> <dbl>    <dbl> <dbl> <dbl+lbl>   <dbl+lbl>     <dbl+lbl>   <dbl+l> <dbl>
1     1    60       NA     0 3           0 [Negativ]   0 [Negativ] 0 [Zen…  9.47
2     2    79       NA     0 4 [Unknown] 2 [Unbekannt] 2 [Unbekan… 0 [Zen…  8.6 
3     3    82       NA     0 2           2 [Unbekannt] 2 [Unbekan… 0 [Zen… 19.3 
4     4    66       NA     0 2           1 [Positiv]   1 [Positiv] 0 [Zen… 16.3 
5     5    52       NA     0 3           2 [Unbekannt] 2 [Unbekan… 0 [Zen…  8.5 
6     6    58       NA     0 4 [Unknown] 2 [Unbekannt] 2 [Unbekan… 0 [Zen…  9.4 
str(breast)
tibble [1,207 × 9] (S3: tbl_df/tbl/data.frame)
 $ id      : num [1:1207] 1 2 3 4 5 6 7 8 9 10 ...
  ..- attr(*, "label")= chr "ID"
  ..- attr(*, "format.spss")= chr "F8.0"
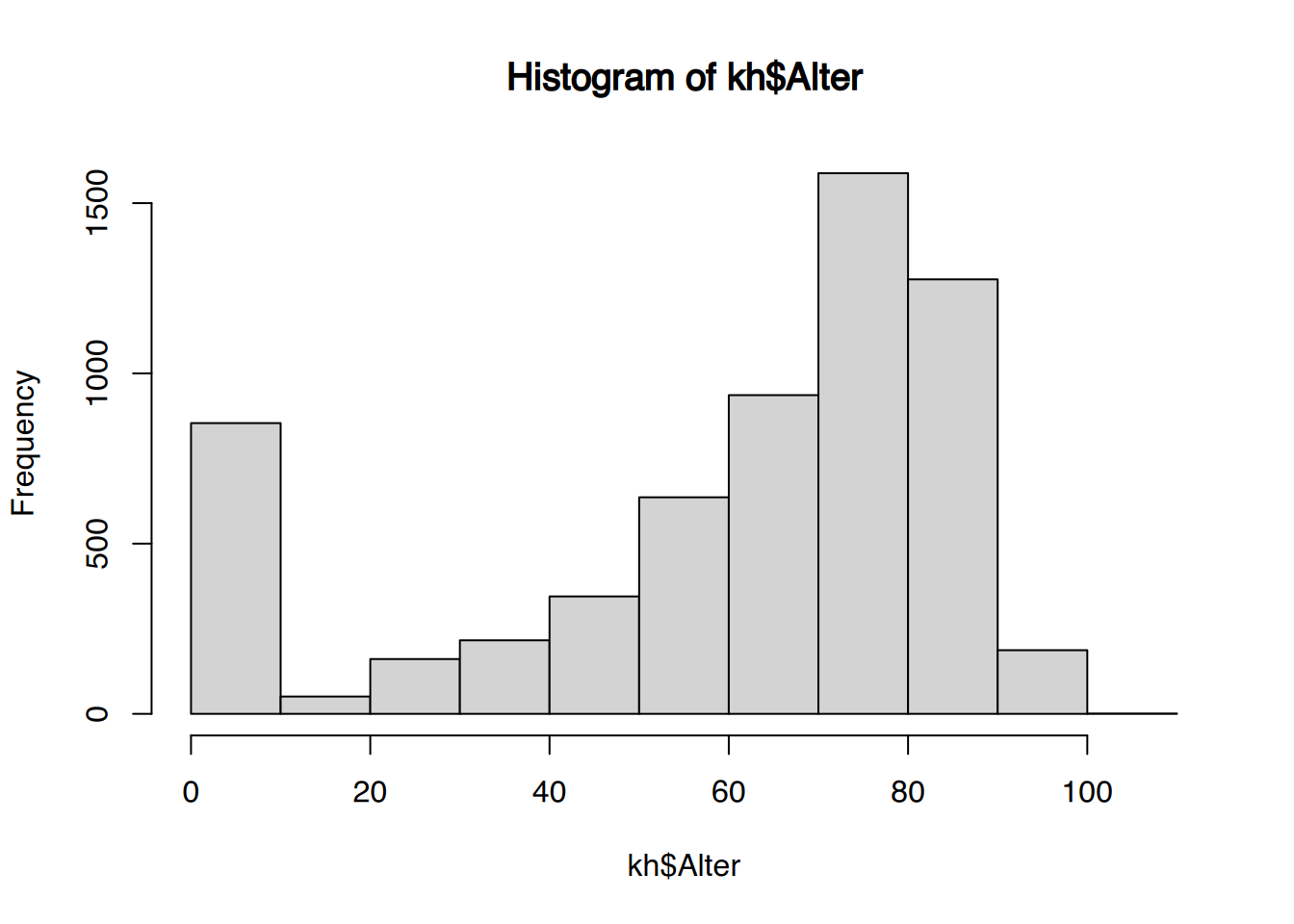
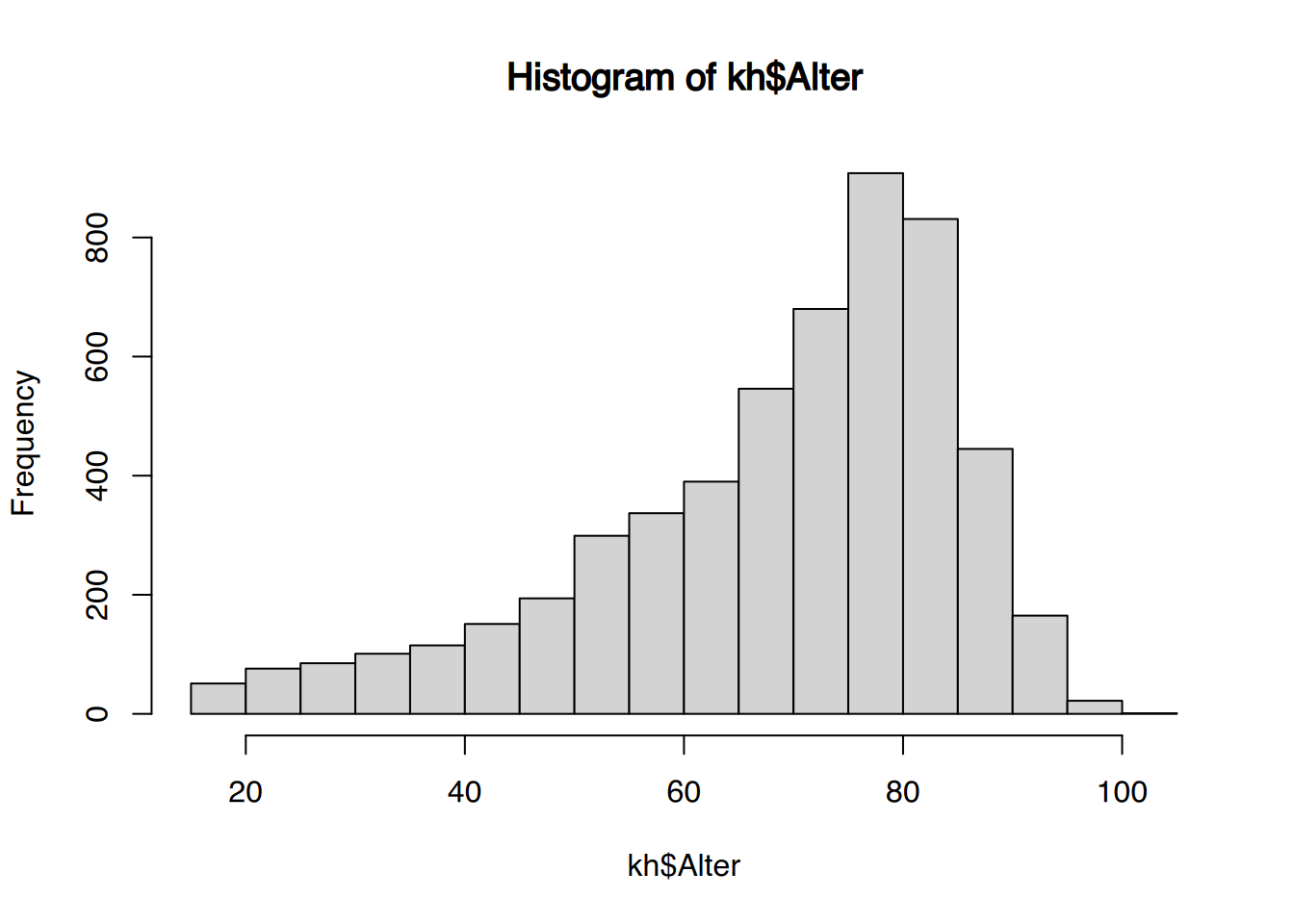
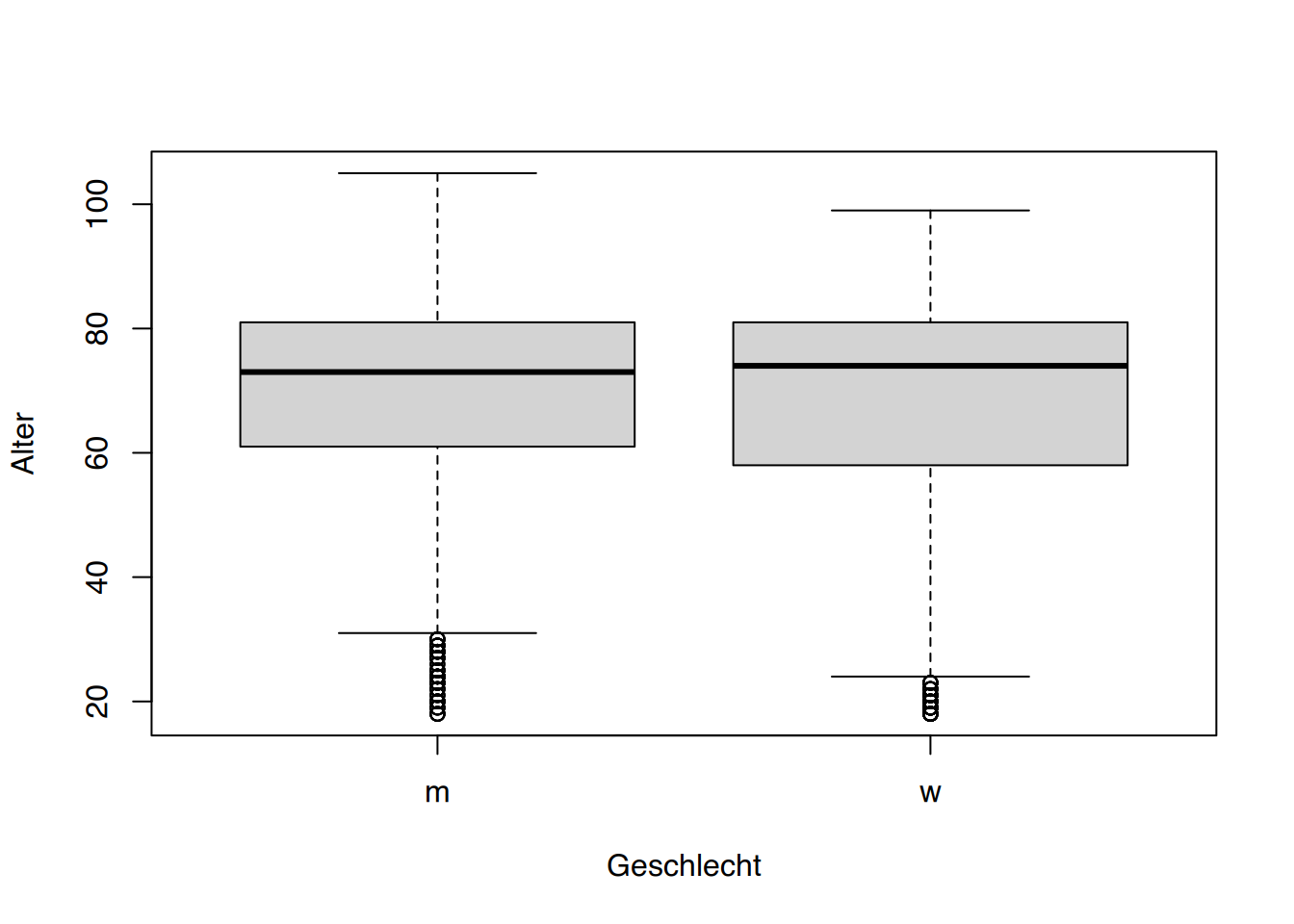
 $ age     : num [1:1207] 60 79 82 66 52 58 50 83 46 54 ...
  ..- attr(*, "label")= chr "Alter [Jahre]"
  ..- attr(*, "format.spss")= chr "F8.0"
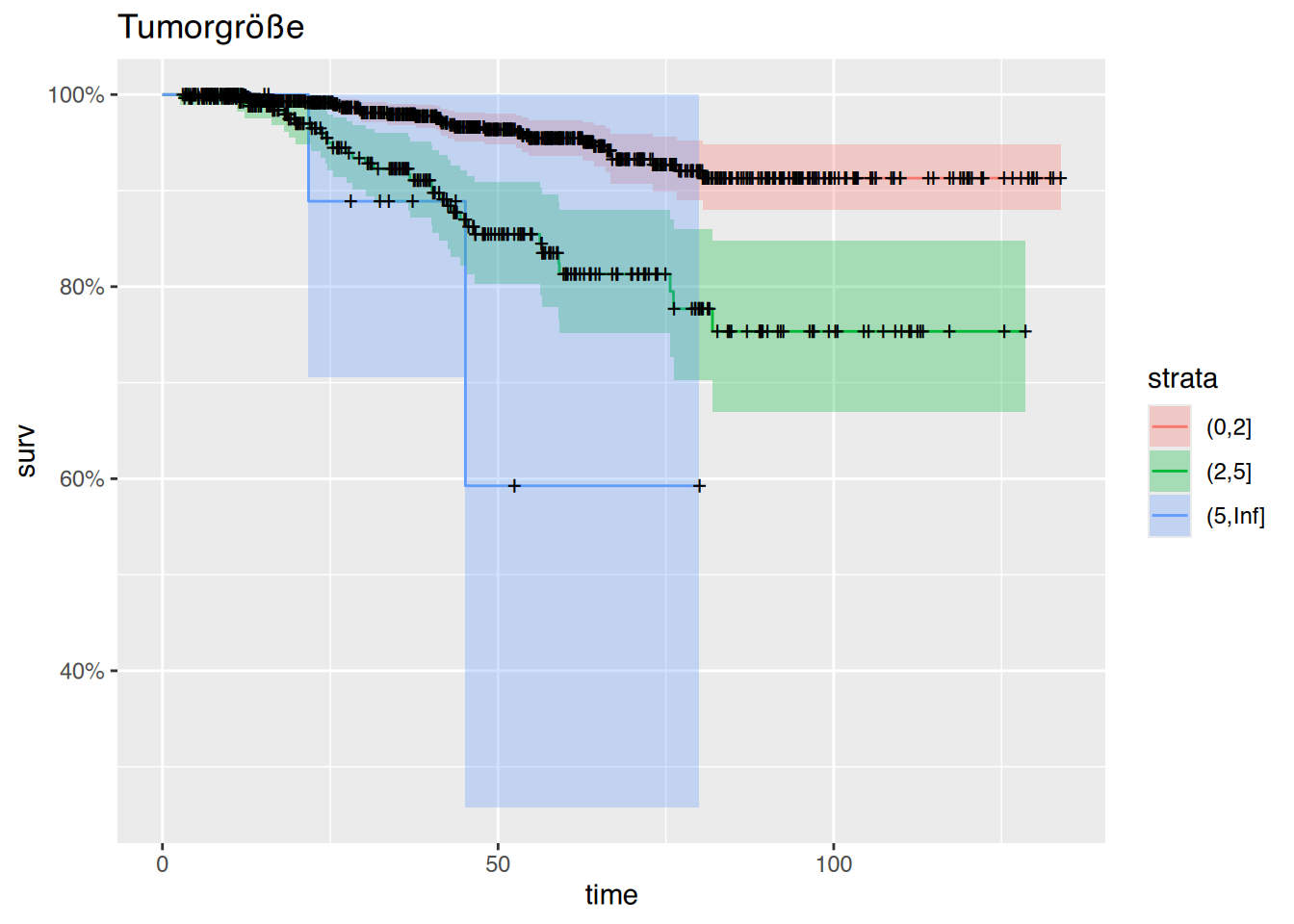
 $ pathsize: num [1:1207] NA NA NA NA NA NA NA NA NA NA ...
  ..- attr(*, "label")= chr "Göße des pathologischen Tumors [cm]"
  ..- attr(*, "format.spss")= chr "F8.2"
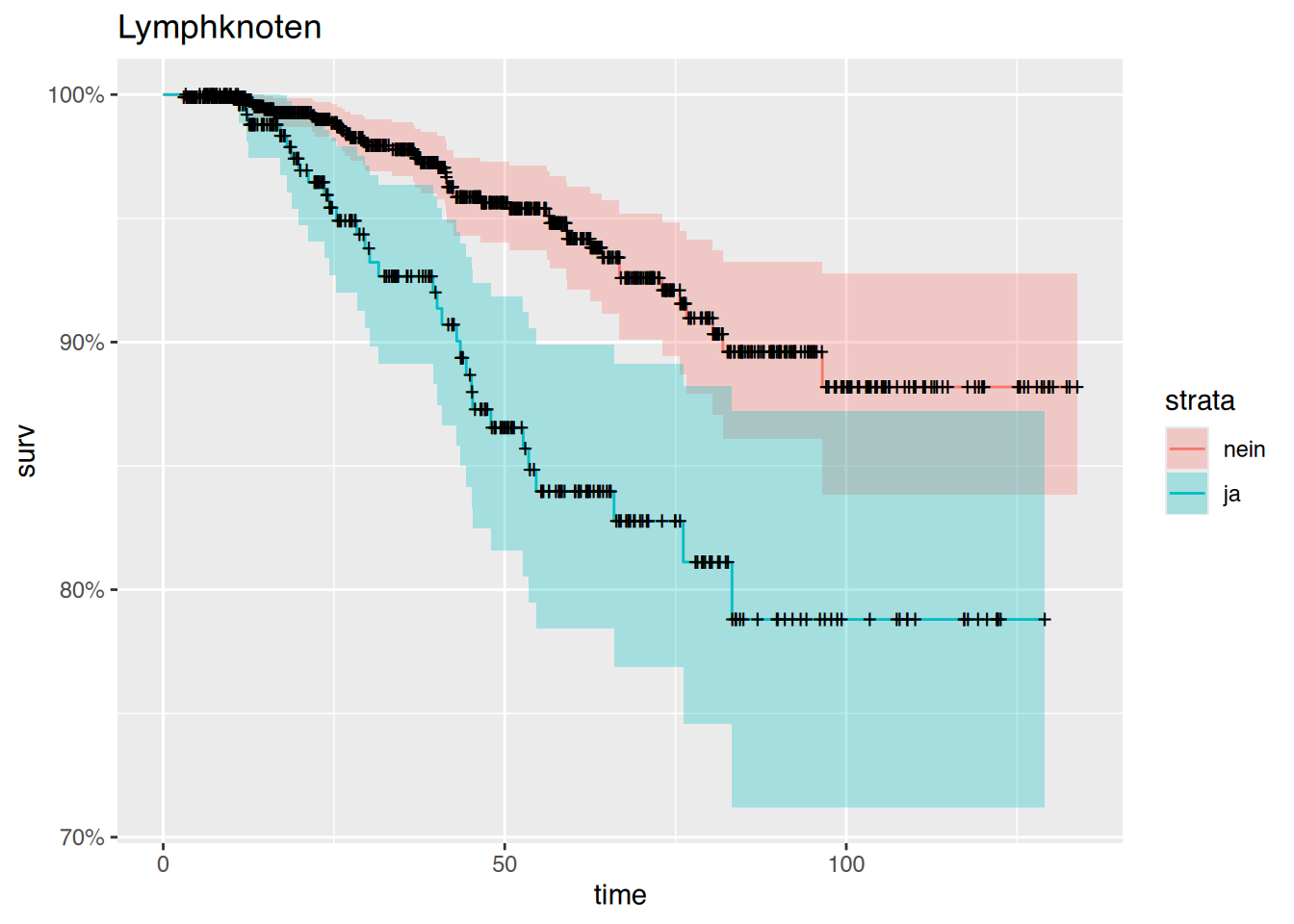
 $ lnpos   : num [1:1207] 0 0 0 0 0 0 0 0 17 6 ...
  ..- attr(*, "label")= chr "Positive Lymphknoten [Anzahl]"
  ..- attr(*, "format.spss")= chr "F8.0"
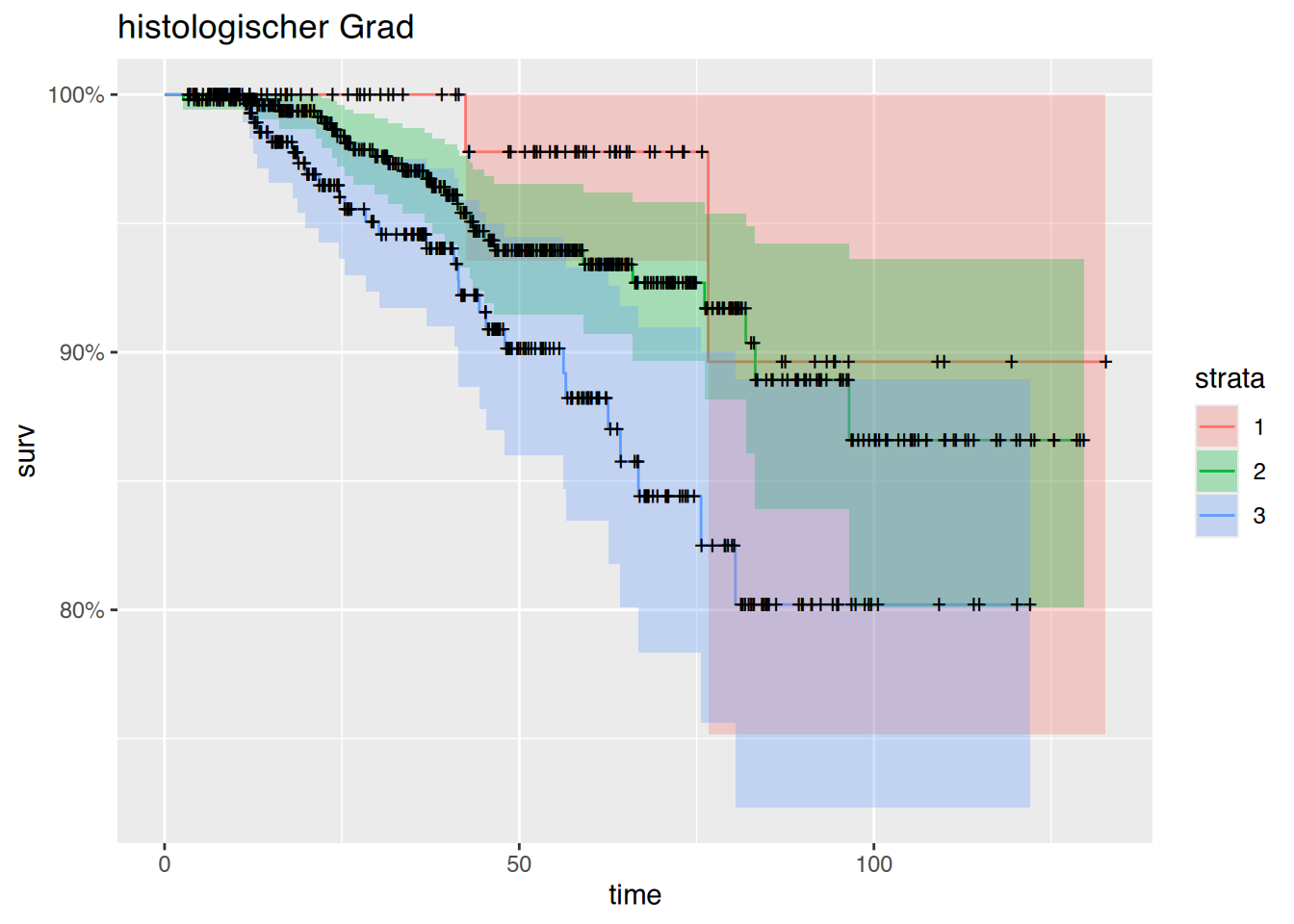
 $ histgrad: dbl+lbl [1:1207] 3, 4, 2, 2, 3, 4, 2, 3, 4, 2, 4, 3, 4, 4, 1, 1, 1, 2,...
   ..@ label      : chr "Histologischer Grad"
   ..@ format.spss: chr "F8.0"
   ..@ labels     : Named num 4
   .. ..- attr(*, "names")= chr "Unknown"
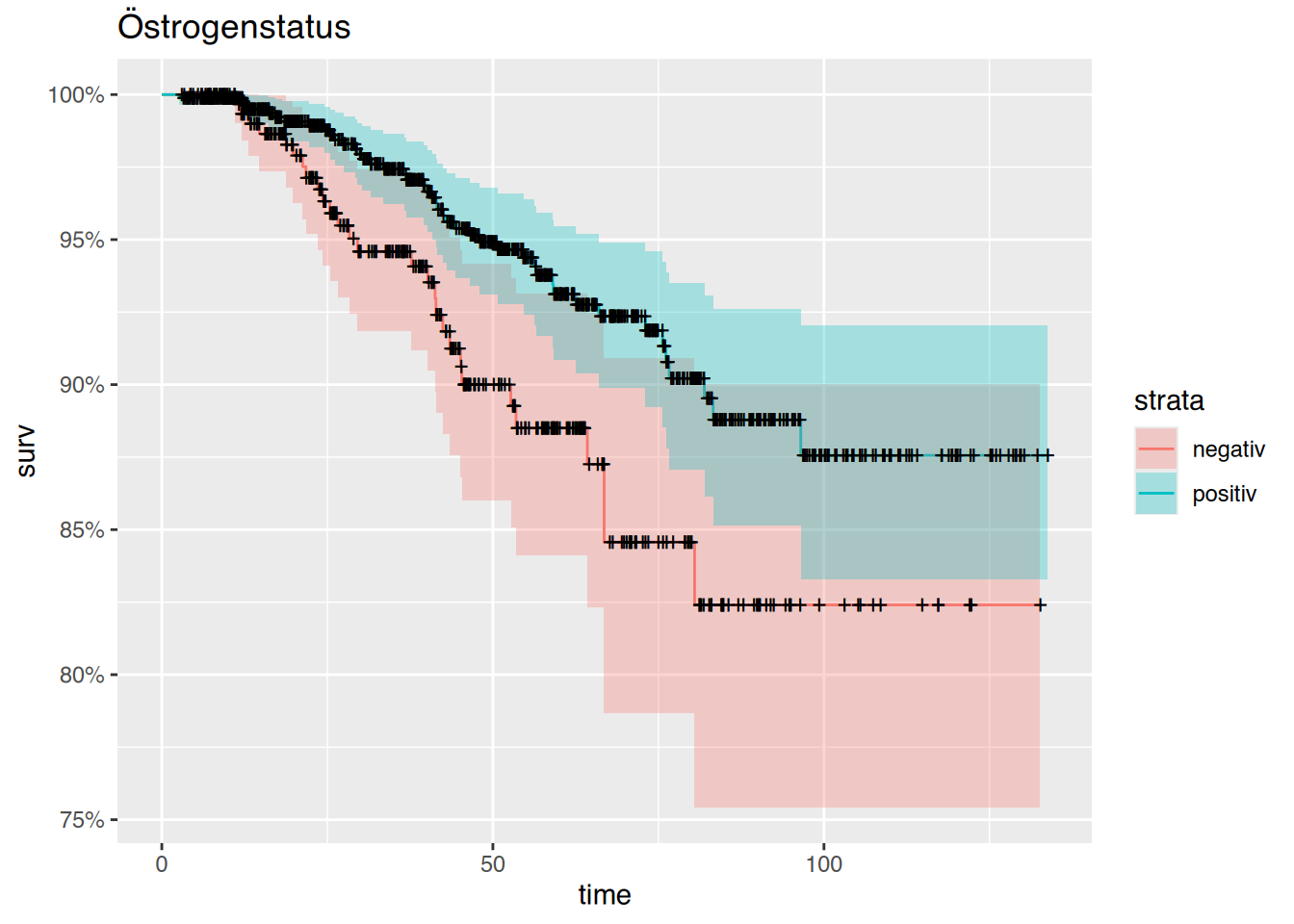
 $ er      : dbl+lbl [1:1207] 0, 2, 2, 1, 2, 2, 1, 0, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2,...
   ..@ label      : chr "Östrogen-Rezeptor-Status"
   ..@ format.spss: chr "F6.0"
   ..@ labels     : Named num [1:3] 0 1 2
   .. ..- attr(*, "names")= chr [1:3] "Negativ" "Positiv" "Unbekannt"
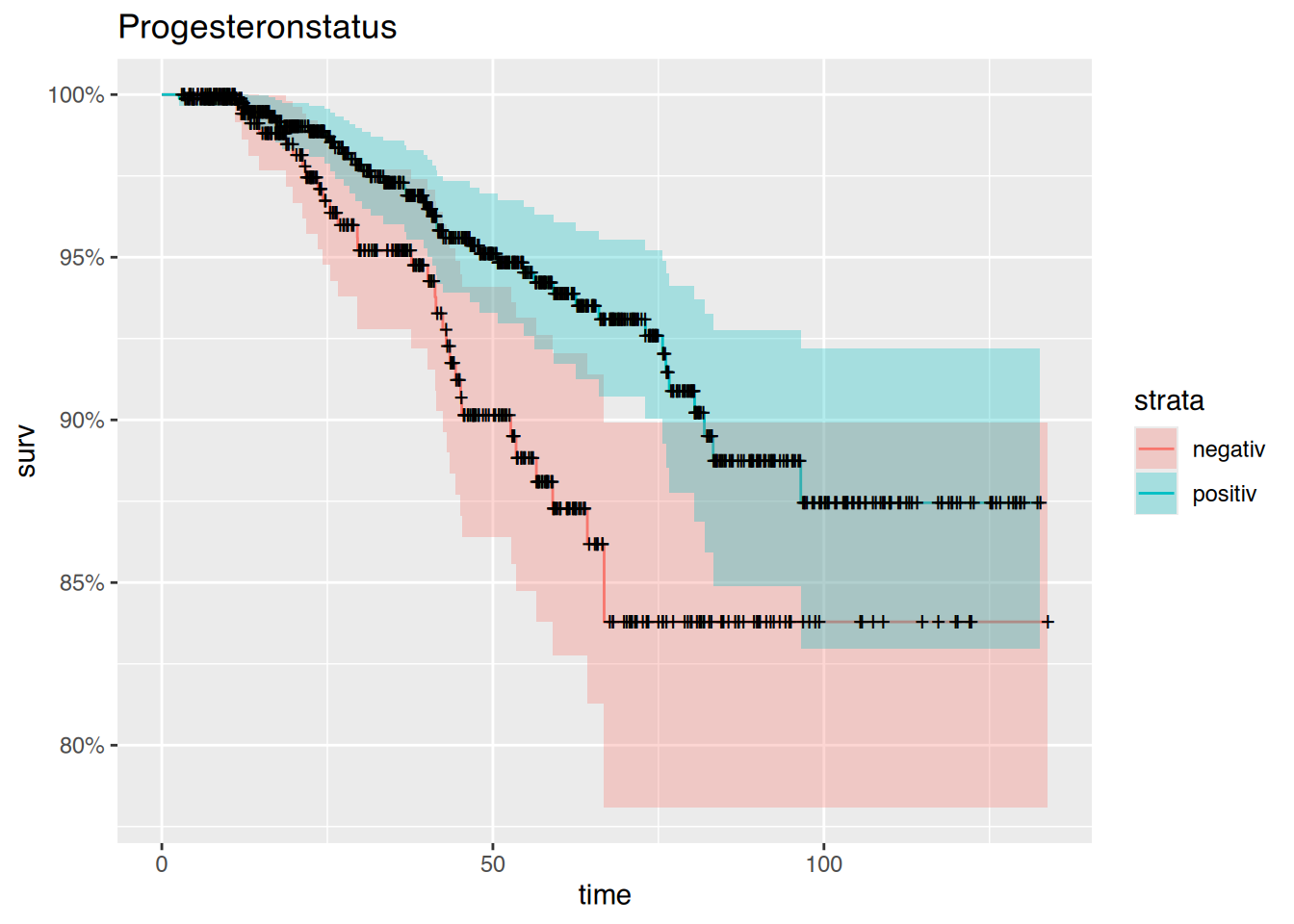
 $ pr      : dbl+lbl [1:1207] 0, 2, 2, 1, 2, 2, 0, 0, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2,...
   ..@ label      : chr "Progesteron-Rezeptor-Status"
   ..@ format.spss: chr "F6.0"
   ..@ labels     : Named num [1:3] 0 1 2
   .. ..- attr(*, "names")= chr [1:3] "Negativ" "Positiv" "Unbekannt"
 $ status  : dbl+lbl [1:1207] 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,...
   ..@ label      : chr "Status"
   ..@ format.spss: chr "F8.0"
   ..@ labels     : Named num [1:2] 0 1
   .. ..- attr(*, "names")= chr [1:2] "Zensiert" "Verstorben"
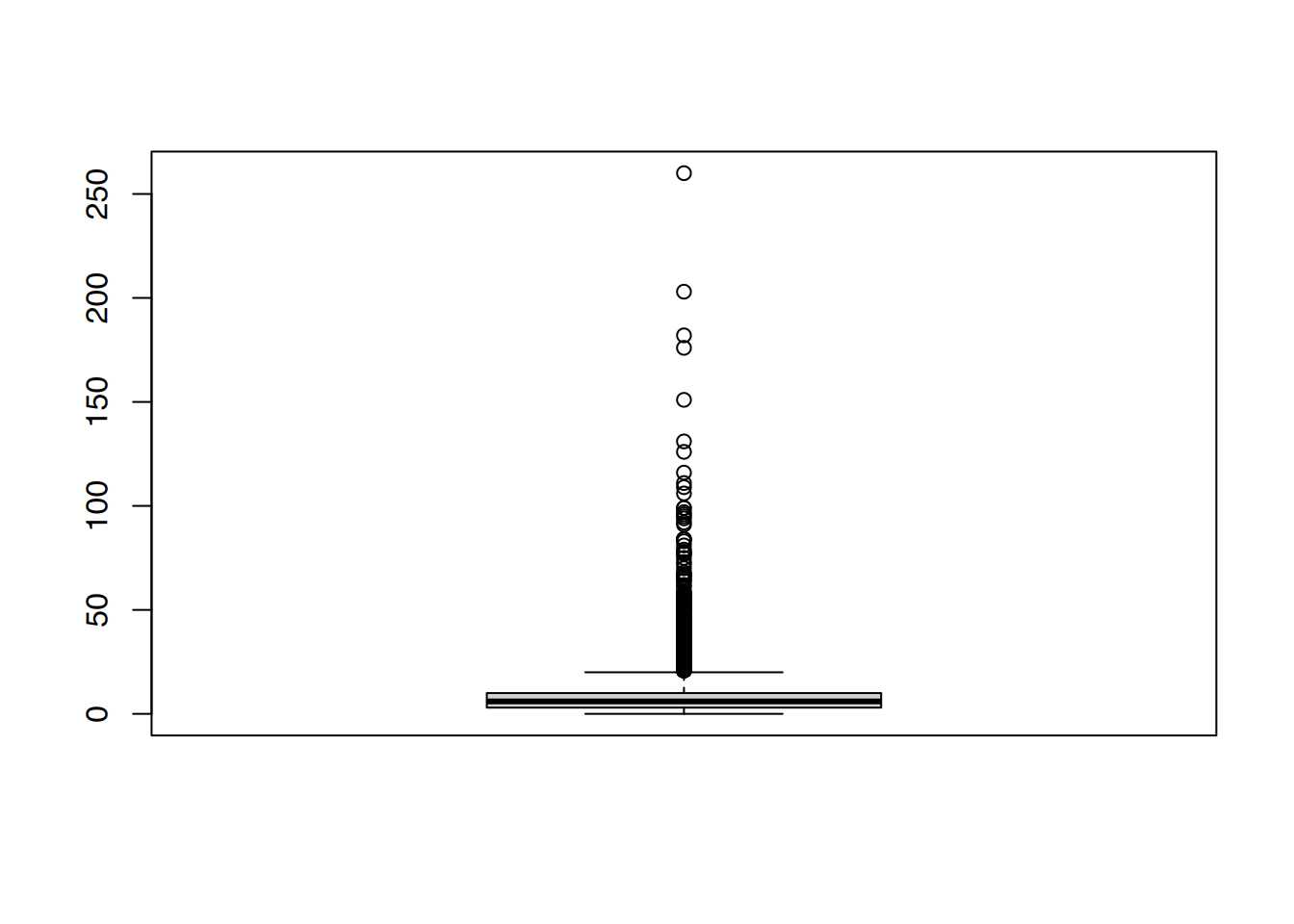
 $ time    : num [1:1207] 9.47 8.6 19.33 16.33 8.5 ...
  ..- attr(*, "label")= chr "Zeit [Monate]"
  ..- attr(*, "format.spss")= chr "F8.2"
b) Klassieren Sie die Variablen? 
# klassieren
library(dplyr)
df <- breast %>%
  mutate(tumorK = cut(pathsize, breaks= c(0,2,5,Inf)),
         lymphK = cut(lnpos, breaks=c(0, 1, Inf), right=FALSE, 
                      labels=c("nein", "ja")),
         oestroK = cut(er, breaks=c(0, 1, Inf), right=FALSE, 
                      labels=c("negativ", "positiv")),
         progesK = cut(pr, breaks=c(0, 1, Inf), right=FALSE, 
                      labels=c("negativ", "positiv"))
         )
c) Kodieren Sie die Variable histgrad um, so dass korrekte NAs enthalten sind. 
# klassieren
head(df$histgrad)
<labelled<double>[6]>: Histologischer Grad
[1] 3 4 2 2 3 4

Labels:
 value   label
     4 Unknown

Alle Werte “4” entsprechen NAs.

# klassieren
df <- df %>%
  mutate(histgrad = replace(histgrad, histgrad == 4,NA),
         histgrad = factor(histgrad))
d) Erstellen Sie ein Überlebenszeitmodell status erklärt durch time und geben Sie die Überlebenstafel sowie die Kaplan-Meier-Plots der kumulierten Überlebenswahrscheinlichkeiten aus. 
# Das Gesamtmodell lässt sich nun so darstellen:
library(survival)
survival <- Surv(df$time, df$status)
km_fit   <- survfit(survival ~ 1, data=df)
summary(km_fit)
Call: survfit(formula = survival ~ 1, data = df)

  time n.risk n.event survival  std.err lower 95% CI upper 95% CI
  2.63   1207       1    0.999 0.000828        0.998        1.000
 11.03   1089       1    0.998 0.001235        0.996        1.000
 12.00   1076       1    0.997 0.001544        0.994        1.000
 12.20   1071       1    0.996 0.001801        0.993        1.000
 12.43   1066       1    0.995 0.002028        0.991        0.999
 13.03   1053       1    0.995 0.002235        0.990        0.999
 13.10   1049       1    0.994 0.002426        0.989        0.998
 14.73   1028       1    0.993 0.002609        0.988        0.998
 16.20   1004       1    0.992 0.002787        0.986        0.997
 17.13    990       1    0.991 0.002959        0.985        0.996
 18.10    969       1    0.990 0.003128        0.983        0.996
 18.77    956       1    0.989 0.003291        0.982        0.995
 19.83    942       1    0.988 0.003451        0.981        0.994
 21.27    923       1    0.986 0.003609        0.979        0.994
 21.77    919       1    0.985 0.003762        0.978        0.993
 22.20    914       1    0.984 0.003909        0.977        0.992
 23.57    884       1    0.983 0.004060        0.975        0.991
 24.33    871       1    0.982 0.004209        0.974        0.990
 24.63    867       1    0.981 0.004354        0.972        0.989
 25.37    859       1    0.980 0.004496        0.971        0.989
 25.43    856       1    0.979 0.004634        0.970        0.988
 26.13    841       1    0.977 0.004773        0.968        0.987
 26.60    836       1    0.976 0.004908        0.967        0.986
 27.40    828       1    0.975 0.005042        0.965        0.985
 28.33    809       1    0.974 0.005178        0.964        0.984
 29.27    801       1    0.973 0.005312        0.962        0.983
 29.53    796       1    0.971 0.005444        0.961        0.982
 29.57    795       1    0.970 0.005573        0.959        0.981
 30.23    785       1    0.969 0.005701        0.958        0.980
 31.53    771       1    0.968 0.005831        0.956        0.979
 33.47    753       1    0.966 0.005963        0.955        0.978
 36.63    707       1    0.965 0.006109        0.953        0.977
 36.87    704       1    0.964 0.006252        0.952        0.976
 37.70    688       1    0.962 0.006398        0.950        0.975
 39.50    661       1    0.961 0.006552        0.948        0.974
 40.10    656       1    0.959 0.006704        0.946        0.973
 40.17    653       1    0.958 0.006853        0.945        0.971
 40.80    640       1    0.956 0.007004        0.943        0.970
 41.27    631       1    0.955 0.007155        0.941        0.969
 41.40    628       1    0.953 0.007303        0.939        0.968
 41.47    626       1    0.952 0.007448        0.937        0.967
 41.53    625       1    0.950 0.007591        0.936        0.965
 42.43    609       2    0.947 0.007880        0.932        0.963
 42.97    604       1    0.946 0.008021        0.930        0.962
 43.50    598       1    0.944 0.008162        0.928        0.960
 44.37    584       1    0.942 0.008307        0.926        0.959
 45.13    577       1    0.941 0.008452        0.924        0.958
 45.30    574       1    0.939 0.008594        0.923        0.956
 46.47    559       1    0.938 0.008742        0.921        0.955
 47.97    532       1    0.936 0.008901        0.918        0.953
 50.67    498       1    0.934 0.009079        0.916        0.952
 52.70    466       1    0.932 0.009278        0.914        0.950
 53.50    453       1    0.930 0.009483        0.911        0.949
 54.60    438       1    0.928 0.009696        0.909        0.947
 56.23    421       1    0.925 0.009921        0.906        0.945
 56.57    417       1    0.923 0.010142        0.904        0.943
 59.03    384       1    0.921 0.010397        0.901        0.941
 59.13    382       1    0.918 0.010645        0.898        0.940
 62.53    338       1    0.916 0.010955        0.895        0.937
 64.27    314       1    0.913 0.011302        0.891        0.935
 66.00    300       1    0.910 0.011666        0.887        0.933
 66.80    292       2    0.904 0.012391        0.880        0.928
 73.03    241       1    0.900 0.012894        0.875        0.925
 75.63    219       1    0.896 0.013474        0.870        0.922
 76.13    214       1    0.892 0.014046        0.864        0.919
 76.63    207       1    0.887 0.014623        0.859        0.916
 80.47    181       1    0.882 0.015342        0.853        0.913
 81.93    164       1    0.877 0.016164        0.846        0.909
 83.27    152       1    0.871 0.017057        0.838        0.905
 96.50     84       1    0.861 0.019756        0.823        0.900

Die Plots können klassisch mit plot(fit) erzeugt werden, oder mittels autoplot() und ggsurvplot().

library(ggplot2)
library(ggfortify) # für autoplot
autoplot(km_fit)
survminer::ggsurvplot(km_fit, pval=T)

e) Gruppieren Sie Ihr Modell mit dem zuvor klassierten Variablen und plotten Sie jeweils die Kaplan-Meier-Kurven. 
# Tumorgröße
km_fit <- survfit(survival ~ tumorK, data=df)
autoplot(km_fit, main="Tumorgröße")
# Lymphknoten
km_fit <- survfit(survival ~ lymphK, data=df)
autoplot(km_fit, main="Lymphknoten")
# Östrogenstatus
km_fit <- survfit(survival ~ oestroK, data=df)
autoplot(km_fit, main="Östrogenstatus")
# Progesteronstatus
km_fit <- survfit(survival ~ progesK, data=df)
autoplot(km_fit, main="Progesteronstatus")
# histologischer Grad
km_fit <- survfit(survival ~ histgrad, data=df)
autoplot(km_fit, main="histologischer Grad")
# Gesamtmodell
km_fit <- survfit(survival ~ 1, data=df)
autoplot(km_fit, main="Gesamtmodell")

f) Führen Sie eine Cox-Regression auf das Überleben durch, wobei die klassierten Werte der Tumorgröße, des Lymphknotenbefalls, des Östrogen- und Progesteronstatus sowie des histologischen Grades als Prädiktoren verwendet werden. Stellen Sie Ihre Ergebnisse als Forste-Plot dar. 
## Cox-Regression
cox <- survival::coxph(survival ~ tumorK + lymphK + histgrad + oestroK + progesK, data=df)
# Modell ausgeben
cox
Call:
survival::coxph(formula = survival ~ tumorK + lymphK + histgrad + 
    oestroK + progesK, data = df)

                   coef exp(coef) se(coef)      z        p
tumorK(2,5]     1.10749   3.02676  0.29071  3.810 0.000139
tumorK(5,Inf]   1.65322   5.22378  0.76058  2.174 0.029732
lymphKja        0.66144   1.93759  0.28892  2.289 0.022056
histgrad2       0.25885   1.29544  0.74524  0.347 0.728336
histgrad3       0.66025   1.93528  0.75989  0.869 0.384909
oestroKpositiv  0.05618   1.05778  0.39540  0.142 0.887021
progesKpositiv -0.49618   0.60885  0.38198 -1.299 0.193956

Likelihood ratio test=33.35  on 7 df, p=2.274e-05
n= 874, number of events= 52 
   (333 Beobachtungen als fehlend gelöscht)

Die Spalte exp(coef) entspricht der Hazard-Ratio, mit welcher Richtung und Stärke des jeweiligen Einflusses interpretiert werden kann.

# Forest-Plot
forestmodel::forest_model(cox)

5.2.4 Lösung zur Aufgabe 2.2.4 data.table Rolling Stone

a) Importieren Sie den Datensatz als data.table in Ihre R-Session und machen Sie sich mit dem Datensatz vertraut. 
# aktiviere data.table
library(data.table)

# lade den Datensatz
rs <- fread("https://www.produnis.de/trainingslager/data/rolling_stone.csv")

# anzeigen
str(rs)
Classes 'data.table' and 'data.frame':  691 obs. of  21 variables:
 $ sort_name               : chr  "Sinatra, Frank" "Diddley, Bo" "Presley, Elvis" "Sinatra, Frank" ...
 $ clean_name              : chr  "Frank Sinatra" "Bo Diddley" "Elvis Presley" "Frank Sinatra" ...
 $ album                   : chr  "In the Wee Small Hours" "Bo Diddley / Go Bo Diddley" "Elvis Presley" "Songs for Swingin' Lovers!" ...
 $ rank_2003               : int  100 214 55 306 50 NA NA 421 NA 12 ...
 $ rank_2012               : int  101 216 56 308 50 NA 451 420 NA 12 ...
 $ rank_2020               : int  282 455 332 NA 227 32 33 NA 68 31 ...
 $ differential            : int  -182 -241 -277 -195 -177 469 468 -80 433 -19 ...
 $ release_year            : int  1955 1955 1956 1956 1957 2016 2006 1957 1985 1959 ...
 $ genre                   : chr  "Big Band/Jazz" "Rock n' Roll/Rhythm & Blues" "Rock n' Roll/Rhythm & Blues" "Big Band/Jazz" ...
 $ type                    : chr  "Studio" "Studio" "Studio" "Studio" ...
 $ weeks_on_billboard      : int  14 NA 100 NA 5 87 173 NA 27 NA ...
 $ peak_billboard_position : int  2 201 1 2 13 1 2 201 30 201 ...
 $ spotify_popularity      : int  48 50 58 62 64 73 67 47 75 52 ...
 $ spotify_url             : chr  "spotify:album:3GmwKB1tgPZgXeRJZSm9WX" "spotify:album:1cbtDEwxCjMhglb49OgNBR" "spotify:album:7GXP5OhYyPVLmcVfO9Iqin" "spotify:album:4kca7vXd1Wo5GE2DMafvMc" ...
 $ artist_member_count     : int  1 1 1 1 1 1 1 4 1 1 ...
 $ artist_gender           : chr  "Male" "Male" "Male" "Male" ...
 $ artist_birth_year_sum   : int  1915 1928 1935 1915 1932 1981 1983 7752 1958 1926 ...
 $ debut_album_release_year: int  1946 1955 1956 1946 1957 2003 2003 1957 1978 1951 ...
 $ ave_age_at_top_500      : num  40 27 21 41 25 35 23 19 27 33 ...
 $ years_between           : int  9 0 0 10 0 13 3 0 7 8 ...
 $ album_id                : chr  "3GmwKB1tgPZgXeRJZSm9WX" "1cbtDEwxCjMhglb49OgNBR" "7GXP5OhYyPVLmcVfO9Iqin" "4kca7vXd1Wo5GE2DMafvMc" ...
 - attr(*, ".internal.selfref")=<externalptr>