1  Aufgaben für Einsteiger:innen

Autor:in
Zugehörigkeit

Prof. Dr. Jörg große Schlarmann

Hochschule Niederrhein

Schön, dass Sie Ihre R-Fähigkeiten überprüfen möchten. Bleiben Sie am Ball, Sie schaffen das!

1.1 Objekte in R

In diesem Abschnitt üben Sie den Umgang mit R-Objekten wie Vektoren, Faktoren und Datenframes.

1.1.1 Aufgabe 1.1.1 Taschenrechner

Nutzen Sie R als Taschenrechner und lösen Sie folgende Aufgaben:

  1. \((15,4 + 0,2) ⋅ (7 − 10,2) ∶ 9\)

  2. \(\frac{5}{10} + \frac{11}{7} - \frac{8}{3}\)

  3. \((13 + 2)^3 \cdot (17 − 8)^2 ∶ 9\)

  4. \(\sqrt{\frac{(1+3)\cdot25}{(5\cdot5 -15)^2}}\)

Lösung siehe Abschnitt 4.1.1

1.1.2 Aufgabe 1.1.2 Vektoren

  1. Erzeugen Sie mit möglichst wenig Aufwand einen Datenvektor aus den Zahlen 1 bis 100.

  2. Erzeugen Sie einen Datenvektor, der aus den Wörtern “Apfel”, “Birne” und “Postauto” besteht.

  3. Erzeugen Sie einen weiteren Datenvektor, in welchem die Wörter “Apfel”, “Birne” und “Postauto” 30 mal wiederholt werden.

Schauen Sie sich die Hilfeseite zur Funktion rep() an, um Aufgabe c) besser lösen zu können

?rep()
# oder
help(rep)

Lösung siehe Abschnitt 4.1.2

1.1.3 Aufgabe 1.1.3 Zufallsvektoren

  1. Erzeugen Sie einen Datenvektor aus 200 zufälligen Zahlen zwischen 1 und 500, ohne dass eine Zahl doppelt vorkommt (sog. “ohne zurücklegen”).

  2. Erzeugen Sie einen weiteren Datenvektor mit ebenfalls 200 zufälligen Zahlen zwischen 1 und 500, wobei Zahlen nun doppelt vorkommen dürfen (sog. “mit zurücklegen”).

Schauen Sie sich die Hilfeseite zur Funktion sample() an, um die Aufgaben leichter lösen zu können.

?sample
# oder
help(sample)

Lösung siehe Abschnitt 4.1.3

1.1.4 Aufgabe 1.1.4 Krankenhausaufenthalte

Hundert zufällig ausgewählte Personen wurden befragt, wie oft sie im letzten Jahr im Krankenhaus stationär behandelt wurden. Die Antworten wurden wie folgt notiert:

          1,0,0,3,1,5,1,2,2,0,1,0,5,2,1,0,1,0,0,4,0,1,1,3,0,
          1,1,1,3,1,0,1,4,2,0,3,1,1,7,2,0,2,1,3,0,0,0,0,6,1,
          1,2,1,0,1,0,3,0,1,3,0,5,2,1,0,2,4,0,1,1,3,0,1,2,1,
          1,1,1,2,2,0,3,0,1,0,1,0,0,0,5,0,4,1,2,2,7,1,3,1,5
  1. Überführen Sie die Daten in ein R-Objekt mit dem Namen KHAufenthalte.
  2. Entfernen Sie den ersten und den dritten Eintrag aus Ihrem R-Objekt.
  3. Fügen Sie die Werte \(7\) und \(2\) dem Objekt hinzu.
  4. Benennen Sie das Objekt in hospital.stays um.
  5. Unterteilen Sie die Kranenhausaufenthalte mit der cut()-Funktion in die Klassen
    • 0,
    • 1-2 und
    • mehr als 2 Aufenthalte.

Lösung siehe Abschnitt 4.1.4

1.1.5 Aufgabe 1.1.5 Größe und Gewicht

Von 10 Personen wurden folgende Körpergrößen in Meter gemessen:

          1,68   1,87   1,95   1,74   1,80
          1,75   1,59   1,77   1,82   1,74

… sowie folgende Gewichte in Gramm:

          78500  110100  97500   69200   82500
          71500   81500  87200   75500   65500
  1. Überführen Sie die Daten in R-Objekte mit den Namen Groesse und Gewicht.
  2. Rechnen Sie das Gewicht um in Kilogramm, und speichern Sie Ihr Ergebnis in der Variable Kilogramm.
  3. Berechnen Sie den BMI (kg/m2) der Probanden und speichern Ihr Ergebnis in das Objekt BMI (Dabei könnten Ihnen die zuvor erstellten Variablen von Nutzen sein!).
  4. Fügen Sie die Objekte Groesse, Gewicht (aber in Kilogramm) und BMI zu einem Datenframe zusammen.
  5. Lassen Sie die Daten von Proband 4, 7 und 9 ausgeben.
  6. Lassen Sie die Daten der Probanden ausgeben, deren Gewicht größer ist als 80kg.

Lösung siehe Abschnitt 4.1.5

1.1.6 Aufgabe 1.1.6 ordinale Faktoren

  1. Erstellen Sie die ordinale Variable Monate, in welcher die 12 ausgeschriebenen Monatsnamen in korrekter Levelreihenfolge enthalten sind.

  2. Erstellen Sie die ordinale Variable Schulnoten, in welcher die 6 ausgeschriebenen Schulnoten in korrekter Levelreihenfolge enthalten sind.

  3. Erzeugen Sie einen ordinalen Factor woche, welcher die Wochentagen von Montag bis Sonntag mit korrekter Levelreihenfolge enthält.

  4. Ändern Sie die Levelnamen so um, dass nun die Wochentage in englischer Sprache (Monday to Sunday) enthalten sind.

  5. Erzeugen Sie aus den folgenden Daten einen ordinalen Faktor mit korrekter Levelreihenfolge.

vielleicht, glaube nicht, nein, glaube nicht, ja, glaube schon, vielleicht, nein, glaube nicht, ja, ja, glaube schon, ja, ja, nein, glaube nicht, glaube schon, vielleicht, vielleicht, glaube nicht, vielleicht, glaube nicht, nein, glaube nicht, ja, glaube schon, vielleicht, nein, glaube nicht, ja, ja, glaube schon, ja, ja, nein, glaube nicht, glaube schon, vielleicht, vielleicht, glaube nicht

  1. Ändern Sie die Levelnamen in -2, -1, 0, 1, 2.

Lösung siehe Abschnitt 4.1.6

1.1.7 Aufgabe 1.1.7 kleines Datenframe

  1. Erstellen Sie ein Dataframe mit den Spalten “Name”, “Alter” und “Geschlecht” und fügen Sie drei Beispielzeilen mit Daten hinzu.

  2. Fügen Sie eine neue Spalte “Hobbys” hinzu und füllen Sie diese mit drei Beispielwerten.

  3. Ändern Sie den Namen der zweiten Person auf “Kunigunde”.

Lösung siehe Abschnitt 4.1.7

1.1.8 Aufgabe 1.1.8 Studiengänge

An den Fachbereichen 06 und 10 der HSNR wurden 2022 folgende Studiengänge angeboten:

Fachbereich 06
  • BA Soziale Arbeit
  • BA Kulturpädagogik
  • BA Kindheitspädagogik

und

  • MA Soziale Arbeit
  • MA Kulturpädagogik & Kulturmanagement
  • MA Sozialmanagement
Fachbereich 10
  • BA Health Care Management
  • BA Medizinische Informatik
  • BA Angewandte Therapiewissenschaften
  • BA Pflege
  • BA Angewandte Hebammenwissenschaft

und

  • MA Health Care
  1. Erstellen Sie das Datenframe Studiengaenge mit den Variablen “Fachbereich”, “Studiengang” und “Niveau” (Bachelor/Master), und überführen Sie die oben stehenden Daten in das Datenframe. Achten Sie dabei darauf, dass alle Daten das korrekte Skalenniveau aufweisen.

Lösung siehe Abschnitt 4.1.8

1.1.9 Aufgabe 1.1.9 Hogwarts-Kurse

In Hogwarts wurden jeweils die vier beliebtesten Kurse der Schüler pro Haus ermittelt.

Haus Kurs
Gryffindor Verteidigung gegen die dunklen Künste
Gryffindor Zauberkunst
Gryffindor Verwandlung
Gryffindor Besenflugunterricht
Hufflepuff Kräuterkunde
Hufflepuff Pflege magischer Geschöpfe
Hufflepuff Geschichte der Zauberei
Hufflepuff Alte Runen
Ravenclaw Arithmantik
Ravenclaw Astronomie
Ravenclaw Verwandlung
Ravenclaw Verteidigung gegen die dunklen Künste
Slytherin Zaubertränke
Slytherin Zauberkunst
Slytherin Dunkle Künste
Slytherin Legilimentik
  1. Erstellen Sie das Datenframe Kurse, in welchem die Daten aus den Tabellenspalten Haus und Kurs enthalten sind.
  2. Wieviele Kurse haben es in die Auswahlliste geschafft?
  3. Erstellen Sie per subset() für jedes Haus ein eigenes Datenframe
  4. Wandeln Sie in jedem Haus-Datenframe die Variablen in Faktoren um.
  5. Fügen Sie die Haus-Datenframes zu einem einzigen Datenframe Hogwarts zusammen, in der Reihenfolge Ravenclaw, Gryffindor, Syltherin und Hufflepuff. Ändern Sie anschließend den Kurs “Geschichte der Zauberei” in “Geisterkunde” um.
  6. Sortieren Sie den Datensatz, so dass die Kurse in alphabetischer Reihenfolge angezeigt werden.
  7. Speichern Sie den so sortierten Datensatz in das Objekt sorted, und reparieren Sie die Zeilennummerierung von sorted.

Lösung siehe Abschnitt 4.1.9

1.1.10 Aufgabe 1.1.10 Datentabelle

Von 6 Probanden wurde der Cholesterolspiegel in mg/dl gemessen.

Name Geschlecht Gewicht Größe Cholesterol
Anna Tomie W 85 179 182
Bud Zillus M 115 173 232
Dieter Mietenplage M 79 181 191
Hella Scheinwerfer W 60 170 200
Inge Danken W 57 158 148
Jason Zufall M 96 174 249
  1. Übertragen Sie die Daten in das Datenframe chol.
  2. Erstellen Sie eine neue Variable Alter, die zwischen Name und Geschlecht liegt und folgende Daten beinhaltet:
Name Alter
Anna Tomie 18
Bud Zillus 32
Dieter Mietenplage 24
Hella Scheinwerfer 35
Inge Danken 46
Jason Zufall 68
  1. Fügen Sie einen weiteren Fall mit folgenden Daten dem Datenframe hinzu
Name Alter Geschlecht Gewicht Größe Cholesterol
Mitch Mackes 44 M 92 178 220
  1. Erzeugen Sie eine neue Variable BMI (\(\text{BMI}=\frac{kg}{m^2}\)).
  2. Fügen Sie die Variable Adipositas hinzu, in welcher Sie die BMI-Werte wie folgt klassieren:
    • weniger als 18,5 \(\rightarrow\ \) Untergewicht
    • zwischen 18,5 und 24.5 \(\rightarrow\ \) Normalgewicht
    • zwischen 24,5 und 30 \(\rightarrow\ \) Übergewicht
    • größer als 30 \(\rightarrow\ \) Adipositas
  3. Filtern Sie Ihren Datensatz, so dass Sie einen neuen Datensatz male erhalten, welcher nur die Daten der Männer beinhaltet.

Lösung siehe Abschnitt 4.1.10

1.1.11 Aufgabe 1.1.11 Zusatzpaket

Das Zusatzpaket jgsbook enthält Funktionen und Datensätze aus dem freien Buch von große Schlarmann (2025).

  1. Installieren Sie das Zusatzpaket jgsbook mit allen Abhängigkeiten.
  2. Welche Datensätze sind in dem Paket enthalten?
  3. Speichern Sie den Datensatz pf8 aus dem jgsbook in das Objekt df. Welche Variablen sind im Datensatz enthalten?
  4. Rufen Sie Dokumentation für das jgsbook-Paket auf.
  5. Wenden Sie die Funktion freqTable() aus dem Paket jgsbook auf die Variable df$Kinder an, ohne das Paket vorher per library() zu aktivieren.

Lösung siehe Abschnitt 4.1.11

1.1.12 Aufgabe 1.1.12 Daten laden

Laden Sie die folgenden Datensätz jeweils in ein R-Objekt und passen Sie die Datenklassen der Variablen entsprechend des Skalenniveaus an.

  1. https://www.produnis.de/trainingslager/data/Datentabelle.txt
  2. https://www.produnis.de/trainingslager/data/anwesenheitnoten.csv
  3. https://www.produnis.de/trainingslager/data/Testdatumdaten.xlsx

Lösung siehe Abschnitt 4.1.12

1.2 Deskriptive Statistik

In diesem Abschnitt üben Sie typische Funktionen und Arbeitsfolgen zur deskriptiven Auswertung der Daten.

1.2.1 Aufgabe 1.2.1 Median Mittelwert

  1. erzeugen Sie einen Datenvektor mit Werten von \(1\) bis \(10\)
  2. berechnen Sie den Median und das arithmetische Mittel
  3. fügen Sie den Wert \(45881\) dem Datenvektor hinzu
  4. berechnen Sie erneut den Median und das arithmetische Mittel. Was fällt Ihnen auf?

Lösung siehe Abschnitt 4.2.1

1.2.2 Aufgabe 1.2.2 Punktwolke und Balkendiagramm

Gegeben sind folgende Werte

x: 1 2 3 4 5 6 7 8 9 10
y: 4 7 8 11 12 9 9 6 4 2
  1. Überführen Sie die Daten in ein Datenframe.
  2. Stellen Sie die Werte als Punktwolke dar.
  3. Stellen Sie die Werte als Balkendiagramm (nicht Säulendiagramm) dar.

Lösung siehe Abschnitt 4.2.2

1.2.3 Aufgabe 1.2.3 Taylor Swift

Im Datensatz taylor_swift_spotify2024.csv1 sind Daten von Taylor Swift bei Spotify enthalten (Stand 2024).

  1. Laden Sie den Datensatz taylor_swift_spotify2024.csv in Ihre R-Session. Nennen Sie Ihr Datenframe dabei ts.
  2. Verschaffen Sie sich mittels str() und summary() einen Überblick über die enthaltenen Daten.
  3. Wenn nötig, korrigiern Sie das Skalenniveau (nominal, ordinal, metrisch) der Variablen innerhalb des Datensatzes.
  4. Wie lang dauern die Songs im Durchschnitt? Bei welcher Songlänge liegt der Median? Bitte geben Sie die Ergebnisse in Sekunden (nicht Millisekunden) an.
  5. Erstellen Sie ein ausreichend beschriftetes Histogramm der Songlängen in Sekunden.
  6. Welcher Song ist laut Datensatz der populärste, welcher der längste, und welcher der langsamste?
  7. Welches Album hat die meisten Songs, und welches hat die wenigsten Songs?
  8. Plotten Sie die Anzahl der Tracks pro Album als Punkt-Liniendiagramm, wobei das Datum auf der X-Achse, und die Trackanzahl auf der Y-Achse dargestellt werden.

Lösung siehe Abschnitt 4.2.3

1.2.4 Aufgabe 1.2.4 Serumcholesterin

Ein Internist misst bei 20 seiner Patienten folgende Serumcholesterinspiegel in mmol/l

4,5  4,9  7,3  5,2  5,8  6,2  5,0  5,6  6,4  7,6
5,4  4,4  6,6  5,3  5,7  4,7  8,2  6,7  4,8  5,9

  1. Überführen Sie die Daten in ein Datenframe mit der Variable chol.

  2. Klassieren Sie die Serumcholesterinwerte nach folgendem Schema:

    • 4,0 bis 4,9;
    • 5,0 bis 5,9;
    • …..mmol/l

  3. Erstellen Sie eine ausreichend beschriftete Häufigkeitstabelle mit nicht kumulierten und kumulierten absoluten und relativen Häufigkeiten für die Häufigkeiten in den zuvor erstellten Serumcholesterinklassen.

  4. Bestimmen Sie bitte folgende Kenngrößen:

    • Median arithmetisches Mittel Spannweite
    • Varianz und Standardabweichung
    • Minimum 10. Perzentil 1. Quartil 3. Quartil 90. Perzentil Maximum
    • Interquartilsabstand

  5. In R gibt es keine generische Funktion zur Berechnung der Summe der quadrierten Abnweichungen \(\ \sum(x_{i}-\bar{x})^2\)

    Bitte berechnen Sie diesen Wert dennoch.

  6. Erstellen Sie einen Boxplot der Werte.

  7. Stellen Sie die in a) aufgelisteten absoluten nicht kumulierten Häufigkeiten als Histogramm dar.

  8. Welche Form hat die Verteilung?

Lösung siehe Abschnitt 4.2.4

1.2.5 Aufgabe 1.2.5 Gewichtsreduktion

Zu einer Gruppe von 20 Teilnehmern an einem Kurs zur Gewichtsreduktion liegen Ihnen die Angaben zu Alter [Jahren] und Geschlecht [1: männlich; 2: weiblich] vor.

Alter:       4  7  8  9  11 12 13 14 15 16 16 20 20 22 25 26 26 28 29 34
Geschlecht:  1  2  2  2   1 1   2  2  2  1  1  2  2  2  1  0  2  1  2  0
  1. Übertragen Sie die Daten in ein R-Datenframe.
  2. Geben Sie der Variable “Geschlecht” die Werte
                 'männlich' (statt 1)
                 'weiblich' (statt 2)
                 'divers'   (statt 0)
  1. Klassieren Sie das Alter der Probanden nach folgendem Schema:
                 0-5     6-10   
                11-15   16-20   
                21-25   26-30   
                31-35
  1. Bestimmen Sie folgende Stichprobenkennzahlen für das Merkmal ‘Alter’:
    • Minimum 5. Perzentil 1. Quartil Median Mittelwert
      1. Quartil 95. Perzentil Maximum Interquartilsabstand
  2. Zeichnen Sie ein Histogramm und ein Balkendiagramm für die nicht kumulierten absoluten Häufigkeiten zur Anzahl der Studienteilnehmer in den zuvor gebildeten Altersklassen.
  3. Erstellen Sie eine Kontingenztafel zur gleichzeitigen Darstellung der beiden Merkmale Altersgruppe und Geschlecht.
  4. Stellen Sie die Häufigkeitsverteilung der beiden Merkmale Altersgruppe und Geschlecht in einer geeigneten Graphik dar.

Lösung siehe Abschnitt 4.2.5

1.2.6 Aufgabe 1.2.6 Anscombe-Quartett

Das Anscombe-Quartett ist ein bekannter Datensatz in der Statistik, der von Francis Anscombe (1973) erdacht wurde. Lesen Sie sich zunächst den Wikipedia-Artikel durch, siehe https://de.wikipedia.org/wiki/Anscombe-Quartett.

Der dazugehörige Datensatz ist in der R-Standardinstallation bereits implementiert und heisst anscombe.

  1. Laden Sie den Datensatz anscombe in Ihre R-Session.
  2. Schreiben Sie die 4 Anscombe-Datensätze (x1 bis x4 und y1 bis y4) in 4 neue Datenframes mit den Namen Anscombe1 bis Anscombe4. Die enthaltenen Spalten sollten jeweils x und y heissen.
  3. Führen Sie für jedes Datenframe die Berechnungen von Anscombe durch (Mittelwert, Varianz, Korrelation und lineare Regression), wobei Sie Ihre Ergebnisse auf 2 Stellen runden sollen.
  4. Erzeugen Sie die 4 Anscombe-Diagramme (Punktwolke und Regressionsgerade) mit der plot()-Funktion, und hübschen Sie die Plots mit etwas Farbe auf.
  5. Erzeugen Sie die 4 Anscombe-Diagramme mittels ggplot(), wobei alle 4 Diagramme mit einem Plotaufruf erzeugt werden sollen. Dies geht am einfachsten, wenn der Datensatz im Tidy-Data-Format (long table) vorliegt.

Lösung siehe Abschnitt 4.2.6

1.2.7 Aufgabe 1.2.7 Kinder und Wohnräume

Man befragt 5 Ehepaare, bei denen beide Partner zwischen 20 und 40 Jahre alt sind, nach der Anzahl der im Haushalt lebenden Kinder (X) und nach der Anzahl der Wohnräume der Wohnung (Y). Die Antworten lauten:

Ehepaar                        1  2  3  4  5
Anzahl Kinder im Haushalt (X)  0  2  3  0  1
Anzahl der Wohnräume (Y)       1  4  3  2  3
  1. Berechnen Sie den Korrelationskoeffizienten r
  2. Berechnen Sie die Regressionsgerade und erstellen Sie die Graphik dazu!

Lösung siehe Abschnitt 4.2.7

1.2.8 Aufgabe 1.2.8 Kinder und Geschwister

Man befragt 5 verheiratete Personen im Alter von mindestens 50 Jahren nach der Anzahl ihrer eigenen Kinder (X) und nach der Anzahl ihrer Geschwister (Y). Die Antworten lauten:

Person                          1  2  3  4  5
Anzahl eigener Kinder (X)       1  0  3  2  1
Anzahl eigener Geschwister (Y)  0  1  4  1  2
  1. Berechnen Sie den Korrelationskoeffizienten r
  2. Berechnen Sie die Gleichung der Regressionsgeraden und erstellen Sie die Graphik dazu!
  3. Was geschieht mit r und mit der Regressionsgeraden, falls Sie die Angaben der 3. Person streichen und dann die Auswertung wiederholen?

Lösung siehe Abschnitt 4.2.8

1.2.9 Aufgabe 1.2.9 Tribble Tibble

Sie erzeugen mit der Funktion tribble() ein Tibble mit folgenden Daten:

Vorname Geschlecht Alter Wohnort Groesse Gewicht Rauchen
Hannah weiblich 25 Berlin 1,75 65 FALSE
Max maennlich 30 Hamburg 1,85 75 TRUE
Sophia weiblich 20 Muenchen 1,65 55 FALSE
Lukas maennlich 35 Frankfurt 1,95 85 TRUE
Emma weiblich 18 Stuttgart 1,70 60 FALSE
Jonas maennlich 40 Duesseldorf 1,80 70 TRUE
Lea weiblich 22 Hannover 1,60 50 FALSE
Jan divers 28 Nuernberg 1,90 80 TRUE
Mia weiblich 24 Bremen 1,73 63 FALSE
Luca maennlich 33 Gelsenkirchen 1,88 78 TRUE
  1. Wandeln Sie mittels mutate() die Variablen Geschlecht und Wohnort in Faktoren um.
  2. Verwenden Sie filter(), um nur die Fälle anzuzeigen, die Raucher sind.
  3. Verwenden Sie group_by() und summarise(), um Mittelwert, Standardabweichung und Median der Variable Alter für jedes Geschlecht zu berechnen.
  4. Verwenden Sie arrange(), um den Datensatz nach Wohnort in alphabetischer Reihenfolge zu sortieren.

Lösung siehe Abschnitt 4.2.9

1.2.10 Aufgabe 1.2.10 Abschlussnoten

Gegeben sind folgende Abschlussnoten von \(82\) Studierenden:

2, 2, 4+, 2, 2-, durchgefallen, 2, 2-, 2+, 2+, 4, 2, 2, 3-, 2, 2, 1-, 2, 2, 4, 3+, 2-, 2-, 2+, 1+, 1, 2, 2+, 3+, 2-, 3-, 1-, 3, 1-, 4, 4+, 2, 3+, 3, 2-, 2, 1-, 3+, 1+, 3, 2, durchgefallen, 2-, 1-, 2+, 3, 3+, 2-, 2+, 2+, durchgefallen, 2-, 2+, 2+, 2+, 1, 1-, 2, 4, 1-, 1+, 3, 2+, 2-, 2+, 2-, 2-, 2-, 4, 3+, 1, 2-, durchgefallen, 1, 2+, 2-, 2

  1. Überführen Sie die Daten in R und
  2. erstellen Sie eine vollständige Häufigkeitstabelle, ohne dabei die Funktion jgsbook::freqTable() zu verwenden.

Kopieren Sie die Werte in eine leere Scriptdatei und verwenden Sie “Find” und “Replace” (Tasten [STRG] + [F]), um die Werte in Anführungszeichen zu hüllen.

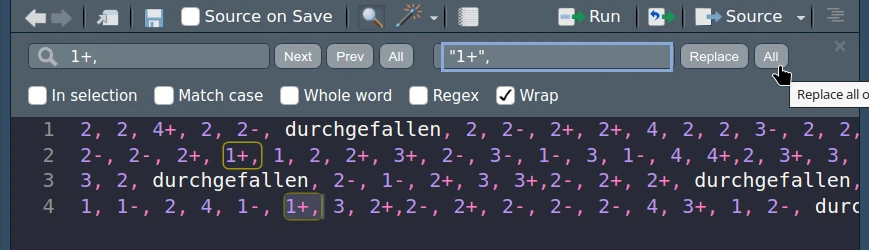
  1. Stellen Sie die relativen Häufigkeiten als ausreichend beschriftetes Säulendiagramm dar.

Lösung siehe Abschnitt 4.2.10

1.2.11 Aufgabe 1.2.11 Modulnoten

In einem Modul haben \(76\) Studierende folgende Noten erzielt:

Note 1+ 1 1- 2+ 2 2- 3+ 3 3- 4+ 4 nb
n 1 3 2 7 12 15 13 6 5 4 4 4
  1. Übertragen Sie die Daten mittels der rep()-Funktion in R und
  2. erstellen Sie eine vollständige Häufigkeitstabelle, ohne dabei die Funktion jgsbook::freqTable() zu verwenden.
  3. Stellen Sie die relativen Häufigkeiten als ausreichend beschriftetes Balkendiagramm (nicht Säulendiagramm) dar.

Lösung siehe Abschnitt 4.2.11

1.2.12 Aufgabe 1.2.12 Statistikklausur

Nachfolgend sind die erreichten Punkte von Studierenden in der Statistikklausur aufgeführt.

0, 0, 1, 85, 95, 63, 89, 98, 88, 75, 90, 41, 89, 99, 97, 68, 49, 59, 96, 57, 65, 94, 48, 71, 96, 72, 98, 88, 66, 58, 43, 66, 76, 98, 44, 74, 99, 86, 87, 97, 99, 86, 61, 41, 77, 73, 71, 40, 63, 71, 78, 72, 58, 52, 68, 81, 75, 80, 70, 65, 86, 63, 97, 45, 58, 96, 48, 64, 67, 100, 49, 90, 63, 69, 93, 90, 85, 78, 62, 84, 100, 67, 88, 71, 42, 72, 44, 89, 73, 42, 71, 88, 74, 60, 81, 58, 56, 94, 90, 69, 44, 42, 69, 100, 100

Insgesamt konnten 100 Punkte erreicht werden. Zur Bestimmung der Note wurde folgender Notenschlüssel verwendet:

Prozent Punkte Note
95.00 95.0 1.0
90.00 90.0 1.3
85.00 85.0 1.7
80.00 80.0 2.0
75.00 75.0 2.3
70.00 70.0 2.7
65.00 65.0 3.0
60.00 60.0 3.3
55.00 55.0 3.7
50.00 50.0 4.0
49.99 49.9 5.0

 

Wie Sie sehen sind Studierende, die weniger als 50 Punkte erreichten, durchgefallen.

  1. Überführen Sie die Ergebnisse der Studierende in ein Datenframe.
  2. Erzeugen Sie eine neue Spalte Note, indem Sie die erreichten Punkte mit Hilfe der cut()-Funktion in “echte” Noten umwandeln.
ACHTUNG

Die Aufgabe enthällt einen Fallstrick! Schauen Sie sich Ihre Klassifikationsergebnisse genau an und achten Sie dabei auf die Ränder (\(0\) Punkte und \(100\) Punkte).

  1. Erzeugen Sie mit wenig Aufwand eine vollständige Häufigkeitstabelle der Noten.

  2. Erzeugen Sie ein farbiges Histogramm, welches die Klassengrenzen nachahmt. Denken Sie daran, dass hist() die “Originaldaten” erwartet und die Klassierung selbst (nach Ihren Angaben) vornimmt. Geben Sie dem Plot eine Überschrift und beschriften Sie die Achsen.

Lösung siehe Abschnitt 4.2.12

1.2.13 Aufgabe 1.2.13 Klausurergebnisse

Die erreichten Punkte in der Statistikklausur sind normalverteilt mit \(\bar{x} = 80\) Punkten und \(sd = 8\) Punkten.

  1. Berechnen Sie die Punktzahl, die dem 77. Perzentil entspricht, d.h. bei welcher Punktzahl 77% der Studierenden schlechter abgeschnitten haben.
  2. Wie viele Punkte muss eine Studentin mindestens erreichen, um zu den besten 5% der Klausur zu gehören?
  3. Bei welchem Punktwert liegt der Median?
  4. Ein Student behauptet, dass er zu den besten 25% des Kurses gehöre. Berechnen Sie, wie viele Punkte er mindestens erreicht haben müsste.
  5. Plotten Sie die Glockenkurve der Verteilung.

Lösung siehe Abschnitt 4.2.13

1.2.14 Aufgabe 1.2.14 Ampullen aufziehen

Die Studierenden im Pflegestudiengang benötigen im Schnitt 110 Sekunden für das Aufziehen einer Ampulle bei einer Standardabweichung von 17 Sekunden. Die Zeiten sind normalverteilt.

Unsere Kollegin Tina benötigt für das Aufziehen der Ampulle 105 Sekunden.

  1. Wie lautet der z-transformierte Wert von Tina?
  2. Wieviel Prozent der Kolleginnen sind schneller als Tina?
  3. Wieviele sind langsamer als Tina?
  4. Plotten Sie die Glockenkurve der Verteilung.

Lösung siehe Abschnitt 4.2.14

1.2.15 Aufgabe 1.2.15 Partys und Prüfungen

Zu Beginn des neuen Semesters führen Sie eine Befragung an 10 Studierenden zur Zahl der während der Klausurvorbereitung besuchten Partys und der Zahl der bestandenen Klausuren durch. Die Daten der Befragung liegen als Texttabelle vor:

Proband Partys bestanden
1 2 3
2 3 3
3 6 1
4 4 0
5 0 5
6 1 3
7 4 0
8 0 4
9 8 1
10 4 2
  1. Übertragen Sie die Daten in R und passen Sie wo notwendig das Skalenniveau an.
  2. Gibt es einen Zusammenhang zwischen der Anzahl an Partys und der Anzahl an bestandenen Prüfungen? Prüfen Sie mittels geeigneter Korrelationverfahren.
  3. Führen Sie eine Regression bestanden erklärt durch Partys durch. Wie stark ist der Zusammenhang?
  4. Plotten Sie die Werte als Punktwolke, fügen Sie die Regressionsgerade hinzu und beschriften Sie Ihr Diagramm ausreichend.
  5. Ein weiterer Student gibt an, er habe keine Party besucht aber leider auch keine Prüfung bestanden. Fügen Sie diese Daten Ihrem Datenframe hinzu.
  6. Wie ändern sich dadurch der Korrelationskoeffizient, das Bestimmtheitsmaß R^2 und die Regressionsgerade?

Lösung siehe Abschnitt 4.2.15

  1. siehe https://www.produnis.de/trainingslager/data/taylor_swift_spotify2024.csv↩︎