Überlappende Kreise
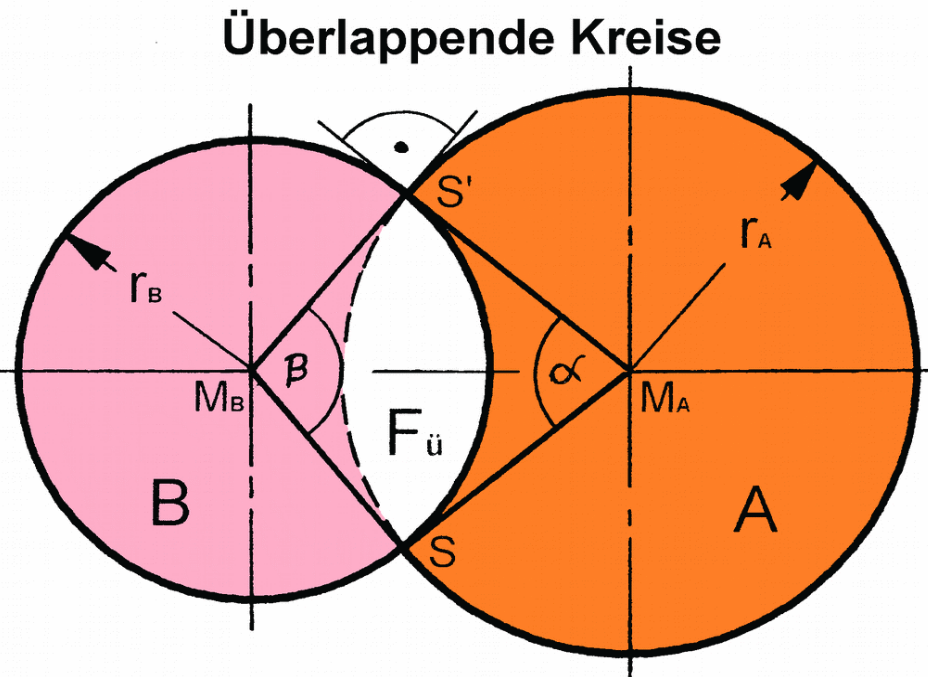
Für eine allgemeine Lösung werden neben den oben bereits definierten Variablen noch folgende weitere verwendet: $F_{S\alpha}$ und $F_{S\beta}$ bezeichnen die Flächen der Kreissektoren die den Überlappungsanteil $F_{ü}$ beinhalten.
Die Winkel $\alpha$ und $\beta$ sind die Mittelpunktswinkel und $b_{\alpha}$ sowie $b_{\beta}$ die Bogenlängen dieser Sektoren.
$F_{D}$ bezeichnet zudem den Flächeninhalt des Drachenvierecks mit den Eckpunkten $M_{B}$, $S$, $M_{A}$, $S´$ ,das in der Abbildung von den Radien $r_{A}$ und $r_{B}$ gebildet wird.
Für die Berechnung von $r_{A}$ und $r_{B}$ werden zunächst die Flächeninhalte $F_{A}$ und $F_{B}$ ausgehend von den Beziehungen
\begin{align} \Delta F_{nü} = F_{A} - F_{ü} - (F_{B}-F_{ü}) = F_{A}- F_{B} \end{align}
und
\begin{align} F_{A+B} = F_{A} + F_{B} \end{align}
zu
\begin{align} F_{A} &= \frac{1}{2}\cdot (F_{A+B} + \Delta F_{nü}) \newline &= \frac{1}{2}\cdot (\pi\cdot 41cm^2 + \pi\cdot 9cm^2)\newline &= (25\cdot\pi)cm^2 \end{align}
und
\begin{align} F_{B} &= F_{A+B} - F_{A} = \pi \cdot 41cm^2 - \pi\cdot 25cm^2 \newline &= (16\cdot\pi)cm^2 \end{align}
Es folgt daraus
\begin{align} r_{A} &= \sqrt{\frac{F_{A}}{\pi}} = \sqrt{\frac{\pi\cdot 25cm^2}{\pi}} = \mathbf{5cm} \end{align}
und
\begin{align} r_{B} &= \sqrt{\frac{F_{B}}{\pi}} = \sqrt{\frac{\pi\cdot 16cm^2}{\pi}} = \mathbf{4cm} \end{align}
Die gesuchte Überlappungsfläche $F_{ü}$ stellt sich als Summe der Sektorenflächen $F_{S\alpha}$ und $F_{S\beta}$, abzüglich der Fläche $F_{D}$ des Drachenvierecks $M_{B}$, $S$, $M_{A}$, $S´$ dar, das heisst, es gilt die Formel:
\begin{align} F_{ü} &= F_{S\alpha} + F_{S\beta} - F_{D} \end{align}
Diese geht unter Berücksichtigung von \begin{align} F_{S\alpha} &= \frac{r_{A}\cdot b_{\alpha}}{2} = r_{A}^2 \cdot tan^{-1}(\frac{r_{B}}{r_{A}})\newline F_{S\beta} &= \frac{r_{B}\cdot b_{\beta}}{2} = r_{B}^2 \cdot tan^{-1}(\frac{r_{A}}{r_{B}}) \end{align}
und $F_{D} = r_{A}\cdot r_{B}$ über in
\begin{align} F_{ü} &= r_{A}^2 \cdot tan^{-1}(\frac{r_{B}}{r_{A}})+r_{B}^2 \cdot tan^{-1}(\frac{r_{A}}{r_{B}}) - r_{A} \cdot r_{B} \end{align}
und liefert als Ergebnis:
\begin{align} F_{ü} &= (5cm)^2 \cdot tan^{-1}(\frac{4}{5})+(4cm)^2 \cdot tan^{-1}(\frac{5}{4}) - 5\cdot 4cm^2\newline &= \mathbf{11,20541cm^2} \end{align}
 Opa Jupp
Opa Jupp