Die unterstützte Leiter
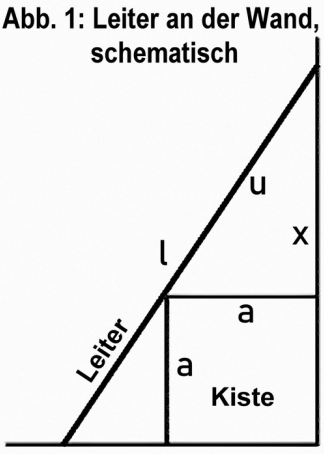
Abbildung 1
Mit den in Abb. 1 verwendeten Maßzahlen $l$ und $u$ für die Gesamtlänge und obere Teillänge der Leiter, der Maßzahl $a$ für die Kantenlänge der Kiste sowie der Maßzahl $x$ für den gesuchten Abstand des Leiter-Wand-Kontaktpunktes von der Kistenoberseite, gilt nach dem Strahlensatz:
\begin{align} \frac{u}{x} = \frac{l}{a+x} \end{align}
und nach Pythagoras
\begin{align} x^2 +a^2 = u^2 \end{align}
oder
\begin{align} 1+\left(\frac{a}{x}\right)^2 = \left(\frac{u}{x}\right)^2 \end{align}
Tauscht man in Gleichung (3) den Quotienten $u/x$ gegen die rechte Seite von Gleichung (1) aus, so lässt sich die erstgenannte wie folgt umformen:
\begin{align} 1+\left(\frac{a}{x}\right)^2 = \left(\frac{l}{x+a}\right)^2\newline (x+a)^2 \cdot \left(1+ \left(\frac{a}{x} \right)^2 \right) &= l^2\newline (x^2 +2\cdot a\cdot x + a^2) \cdot \frac{x^2 + a^2}{x^2} &= l^2\newline \frac{x^2 +a^2 +2\cdot a \cdot x}{x} \cdot \frac{x^2 +a^2}{x} &= l^2\newline \left( \frac{x^2 + a^2}{x} +2\cdot a \right) \cdot \frac{x^2 +a^2}{x} &= l^2 \end{align}
Ersetzt man nun in der letzten Formel den Term $\frac{x^2 +a^2}{x}$ durch die Hilfsvariable $z$, so gelangt man zu der quadratischen Gleichung
\begin{align} (z+2\cdot a)\cdot z = z^2 +2\cdot a\cdot z \newline = (z+a)^2 - a^2 = l \end{align}
mit den Lösungen
\begin{align} z_{1} &= -a+\sqrt{a^2 +l^2} \newline &= 1m +\sqrt{(1m)^2 + (3,6m)^2}\newline &= 2,73631m \end{align}
und
\begin{align} z_{2} &= -a-\sqrt{a^2 +l^2} \newline &= 1m -\sqrt{(1m)^2 + (3,6m)^2}\newline &= -4,73631m \end{align}
Für die Berechnung der in diesen $z$-Werten enthaltenen $x$-Werte muss wieder auf das Substitut
\begin{align} \frac{x^2 +a^2}{x} = z \end{align}
zurückgegriffen werden. Nach dessen beidseitiger Multiplikation mit $x$ erhält man abermals eine quadratische Gleichung, nämlich
\begin{align} x^2 -z\cdot x + a^2 = 0 \end{align}
bzw.
\begin{align} \left(\frac{x-z}{2} \right)^2 - \left(\frac{z}{2} \right)^2 +a^2 = 0 \end{align}
mit den Lösungen
\begin{align} x_{1} = \frac{z}{2} + \sqrt{\left( \frac{z}{2} \right)^2 - a^2} \end{align}
und
\begin{align} x_{2} = \frac{z}{2} - \sqrt{\left( \frac{z}{2} \right)^2 - a^2} \end{align}
Da in jede dieser beiden Lösungsformeln einmal $z_{1}$ und einmal $z_{2}$ einzusetzen ist, ergeben sich für $x$ die folgenden vier Werte:
\begin{align} x_{1,1} &= \frac{z_1}{2} + \sqrt{\left( \frac{z_1}{2} \right)^2 - a^2} \newline &= \frac{2,73631m}{2} + \sqrt{ \left(\frac{2,73631m}{2}\right)^2 - (1m)^2 }\newline &= 2,3019m \end{align}
\begin{align} x_{1,2} &= \frac{z_2}{2} + \sqrt{\left( \frac{z_2}{2} \right)^2 - a^2} \newline &= \frac{4,73631m}{2} + \sqrt{ \left(\frac{4,73631m}{2}\right)^2 - (1m)^2 }\newline &= -0,22149m \end{align}
\begin{align} x_{2,1} &= \frac{z_1}{2} - \sqrt{\left( \frac{z_1}{2} \right)^2 - a^2} \newline &= \frac{2,73631m}{2} - \sqrt{ \left(\frac{2,73631m}{2}\right)^2 - (1m)^2 }\newline &= 0,43443m \end{align}
\begin{align} x_{2,2} &= \frac{z_2}{2} - \sqrt{\left( \frac{z_2}{2} \right)^2 - a^2} \newline &= \frac{4,73631m}{2} - \sqrt{ \left(\frac{4,73631m}{2}\right)^2 - (1m)^2 }\newline &= -4,5148m \end{align}
Relevant sind davon nur die beiden positiven Ergebnisse:
- $x_{1,1}=2,3019m$ und
- $x_{2,1}=0,43443m$.
Im ersten Fall steht die Leiter mit einem Steigungswinkel von $arctan(\frac{x_{1,1}}{a})=66,52°$ an der Wand und im zweiten Fall mit einem Steigungswinkel von $arctan(\frac{x_{2,1}}{a})=23,48°$.
Abbildung 2 zeigt den Graphen der aus Gleichung (5) mit $a=1m$ und $l=3,6m$ herleitbaren Funktion
\begin{align} f(x) = (x+1)^2 \cdot \left(1+ \frac{1}{x^2} \right) - 3,6^2 \end{align}
Erwartungsgemäß schneidet dieser die $x$-Achse an den zuvor berechneten Stellen.
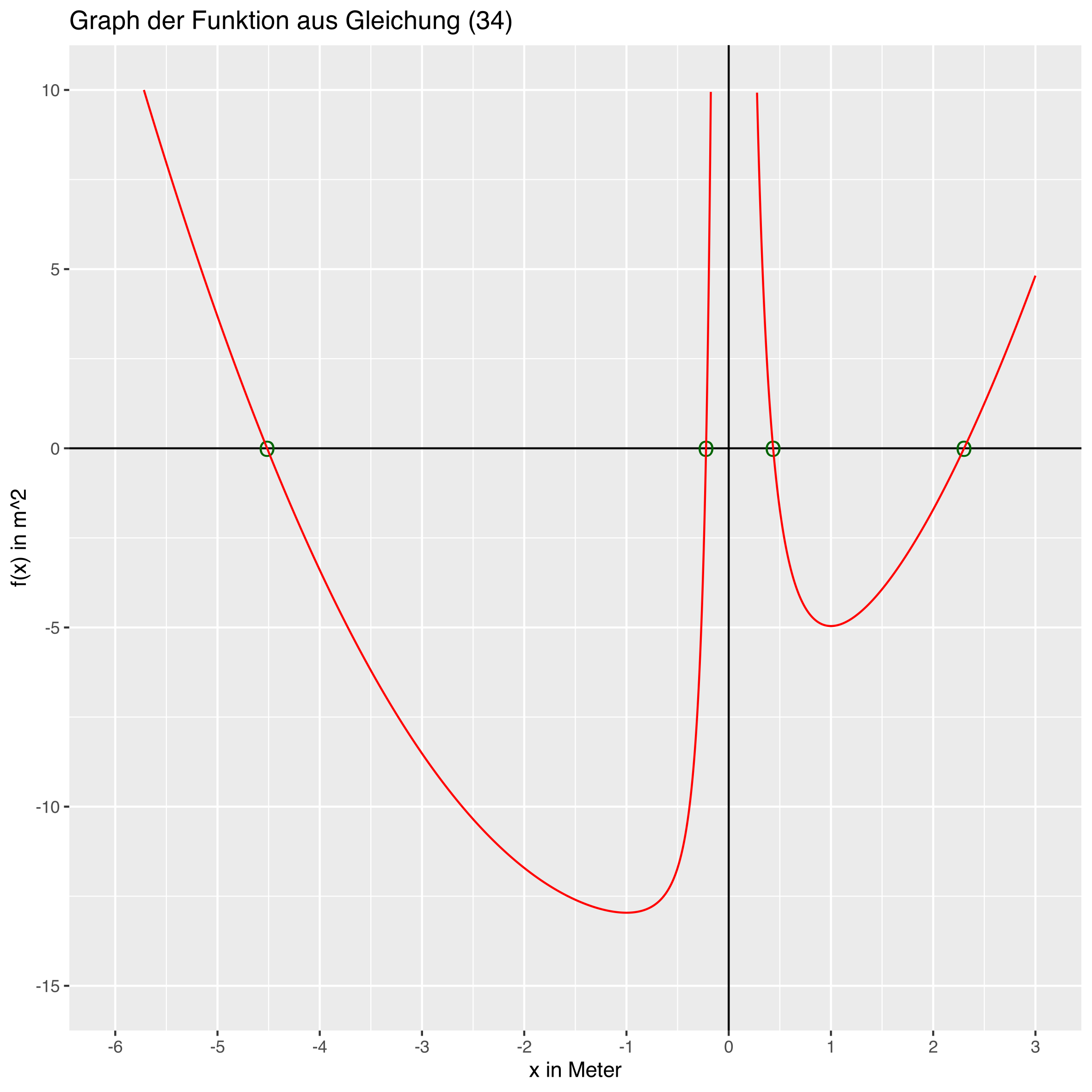
Abbildung 2
 Opa Jupp
Opa Jupp