Angeleinte Ziege grast auf kreisrunder Wiese
Im gespannten Zustand der Halteleine grast die Ziege entlang eines Kreisbogens mit dem Radius $R$, dessen Größe mit der Leinenlänge identisch ist.
In den folgenden Berechnungen wird für das Radienverhältnis $\frac{R}{r}$ das Kurzzeichen $\lambda$ verwendet.
Es stehen zwei Lösungswege zur Verfügung.
- Lösung mit Flächenberechnung durch Integrale
- Lösung ohne Verwendung von Integralen
Lösung mit Flächenberechnung durch Integrale
Verdeutlichen wir uns die Gegebenheiten mit Hilfe einer Zeichnung.
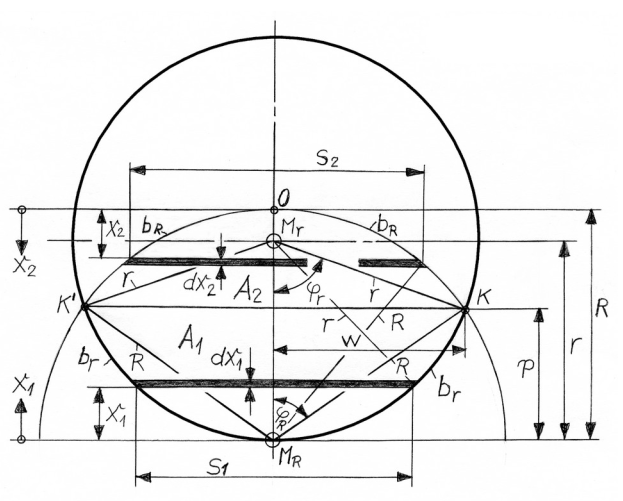
Abbildung 1
Berechnung der die Schnittpunkte der beiden Kreise definierenden Größen $p$ und $w$
Aus der Beziehung $w^2 = R^2 - p^2 = r^2 - (r-p)^2$ ergeben sich:
\begin{align} p &= \frac{R^2}{2\cdot r} = R \cdot \frac{\lambda}{2} = r \cdot \frac{\lambda^2}{2} \newline w &= R\cdot \sqrt{1 - (\frac{R}{2\cdot r})^2} = r\cdot \lambda\cdot \sqrt{1 - \frac{\lambda^2}{4}} \end{align}
Berechnung der Kreisabschnittsfläche $A_{1}$
Mit den Bezeichnungen in Abbildung 1 gilt:
$$ \begin{align} A_{1} &= \int\limits_{x_{1}=0}^{x_{1}=p} s_{1}(x_{1})\cdot dx_{1} \newline \ \newline &= 2 \cdot \int\limits_{x_{1}=0}^{x_{1}=p} \sqrt{r^2 - (r - x_{1})^2}\cdot dx_{1} \newline &= 2\cdot r\cdot \int\limits_{x_{1}=0}^{x_{1}=p} \sqrt{1 - (1 - \frac{x_{1}}{r})^2}\cdot dx_{1} \end{align} $$
Nach Einführen von
$$ \begin{align} z_{1} &= 1 - \frac{x_{1}}{r}\newline \ \newline dx_{1} &= -r \cdot dz_{1}\newline \ \newline z_{1}(x_{1}=0) &= 1 \newline \ \newline z_{1}(x_{1}=p) &= 1 - \frac{\lambda^2}{2} \end{align} $$
erhält man als Lösung des Integrals:
$$ \begin{align} A_{1} &= r^2 \cdot \left[ z_{1} \cdot\sqrt{1 - z_{1}^2} + \alpha sin(z_{1}) \right]_{z1=\frac{\lambda^2}{2}-1}^{z1=1}\newline &= \frac{r^2}{2} \cdot \left[\pi + \lambda \cdot (2-\lambda^2) \cdot \sqrt{1-\frac{\lambda^2}{4}} - 2\cdot \alpha sin(1-\frac{\lambda^2}{2})\right] \end{align} $$
Berechnung der Kreisabschnittsflche $A_{2}$
Hier gilt:
$$ \begin{align} A_{2} &= \int\limits_{x_{2}=0}^{x_{2}=R-p} s_{2}(x_{2})\cdot dx_{2} \newline &= 2\cdot\int\limits_{x_{2}=0}^{x_{2}=R-p} \sqrt{R^2 - (R-x_{2})^2}\cdot dx_{2}\newline &= 2\cdot R \cdot\int\limits_{x_{2}=0}^{x_{2}=R-p} \sqrt{1 - (1-\frac{x_{2}}{R})^2}\cdot dx_{2} \end{align} $$
und nach Einführen von $$ \begin{align} z_{2} &= 1 - \frac{x_{2}}{R} \newline dx_{2} &= -R\cdot dz_{2}\newline z_{2}(x_{2}=0) &=1\newline z_{2}(x_{2}=R-p) &=\frac{\lambda}{2} \end{align} $$
erhält man als Lösung des Integrals:
$$ \begin{align} A_{2} &= R^2 \left[ z_{2}\cdot \sqrt{1-z_{2}^2} - \alpha sin(z_{2})\right]_{z2=\frac{\lambda}{2}}^{z2=1}\newline &= \frac{r^2}{2} \cdot \lambda^2 \cdot \left[\pi \cdot \lambda \cdot \sqrt{1-\frac{\lambda^2}{4}} - 2 \cdot \alpha sin(\frac{\lambda}{2})\right] \end{align} $$
Zusammenfassung:
Aus der Bedingung: \begin{equation} A_{1}+A{2} = \frac{\pi}{2}\cdot r^2 \end{equation}
lässt sich nunmehr für die Bestimmung von $\lambda$ die Gleichung
\begin{equation} \lambda^2 \cdot \left[\frac{\pi}{2} - \alpha sin(\frac{\lambda}{2}) \right] - \alpha sin \left( 1-\frac{\lambda^2}{2} \right) - \lambda\cdot\sqrt{1-\frac{\lambda^2}{4}}=0 \end{equation}
entwickeln, die mit analytischen Methoden nicht lösbar ist. Alternative numerische Lösungsmöglichkeiten hierfür gibt es dagegen viele. In der Regel werden fertige, anpassungsfähige Computerprogramme verwendet, die mit unterschiedlichen Iterationsalgorithmen arbeiten. Im vorliegenden Fall bietet sich ein Verfahren an, das ohne Programmierkenntnisse auf einfachen Schul-Taschenrechnern anwendbar ist und gewöhnlich als “sukzessive Approximation” bezeichnet wird.
Für diese Methode gilt es aus Gleichung (26) ein einzelnes $\lambda$ zu isolieren, um eine für Iterationen geeignete Formel der Form
\begin{equation} x = g(x) \end{equation}
zu erhalten.
Dabei ist es gleichgültig, ob und an welcher Stelle im rechten Teil dieser Formel, d. h. in $g(x)$, noch weitere $\lambda$ verbleiben.
Von verschiedenen Möglichkeiten, die keineswegs alle zielführend sind, weil sie eventuell nicht das erforderliche Konvergenzverhalten zeigen, wird hier die Umformung von Gleichung (26) in die Iterationsformel
\begin{equation} \lambda=\sqrt{\frac{\lambda\cdot\sqrt{1-\frac{\lambda^2}{4}} + \alpha sin(1-\frac{\lambda^2}{2}) }{\frac{\pi}{2}-\alpha sin(\frac{\lambda}{2})}} \end{equation}
favorisiert. Mit jedem Wert von $\lambda$, den diese Formel in einem betrachteten Iterationsschritt
abhängig vom unmittelbar zuvor berechneten $\lambda$-Wert als Zwischenergebnis liefert, berechnet man im nachfolgenden Iterationsschritt einen noch genaueren Wert für diese Zielgröße.
Gestartet wird die Iteration mit einem Schätzwert für $\lambda$. Ihr Ende, der sogenannte Fixpunkt ist erreicht, wenn sich trotz weiterer Iterationsschritte an den Berechnungs- ergebnissen nichts Wesentliches mehr ändert. Startet man die Iteration nach Gleichung (28) mit dem Schätzwert $\lambda=1$, so ergibt sich der Fixpunktwert dieser Variablen nach nur drei Iterationsschritten ausreichend genau zu \begin{equation} \lambda = 1,158728473 \end{equation}
Damit erhält man den Kreisradius $R$, der vom Halteseil der Ziege gebildet wird, zu
\begin{equation} R=\lambda\cdot r = 1,158728473\cdot 20m = \mathbf{23,1745695m} \end{equation}
Lösung ohne Verwendung von Integralen
In diesem Fall wird die Summe der Kreisabschnittsflächen $A_{1}$ und $A_{2}$ als Flächensumme der Kreissektoren mit den Mittelpunkts-Halbwinkeln $\varphi_{R}$ und $\varphi_{r}$ , abzüglich der Fläche des Drachenvierecks mit den Eckpunkten $M_{R}, K, M_{r}, K’$ berechnet.
Es gilt also:
$$ \begin{align} A_{1}+A_{2} &=& \frac{R}{2}\cdot b_{R} + \frac{r}{2}\cdot b_{r} - r\cdot w \newline &=& \frac{r}{2}\cdot b_{R} \cdot \lambda + \frac{r}{2}\cdot b_{r} -r \cdot w \end{align} $$
Setzt man darin ein:
$$ \begin{align} b_{R} &= 2\cdot R\cdot \varphi_{R} = 2\cdot R \cdot \alpha cos(\frac{p}{R}) \newline &= 2\cdot R \cdot \alpha cos(\frac{\lambda}{2})= 2\cdot r \cdot\lambda\cdot \alpha cos(\frac{\lambda}{2})\newline b_{r} &= 2\cdot r \cdot \varphi_{r} = 2\cdot r\cdot\alpha cos(\frac{r-p}{r}) \newline &= 2\cdot r\cdot\alpha cos(1-\frac{\lambda^2}{2})\newline r\cdot w &= r^2\cdot\lambda\cdot\sqrt{1-\frac{\lambda^2}{4}} \end{align} $$
dann ergibt sich \begin{equation} A_{1}+A_{2} = r^2 \cdot \left[\lambda^2 \cdot\alpha cos(\frac{\lambda}{2}) + \alpha cos(1-\frac{\lambda^2}{2}) - \lambda\cdot\sqrt{1-\frac{\lambda^2}{4}}\right] \end{equation}
und aus der Bedingung \begin{equation} A_{1}+A_{2} = \frac{\pi}{2}\cdot r^2 \end{equation}
folgt für die Bestimmung von $\lambda$ die Gleichung
\begin{equation} \lambda^2 \cdot \alpha cos(\frac{\lambda}{2}) + \alpha cos(1-\frac{\lambda^2}{2}) - \lambda\cdot\sqrt{1-\frac{\lambda^2}{4}}-\frac{\pi}{2}=0 \end{equation}
Für deren numerische Lösung nach der Methode der “sukzessiven Approximation” eignet sich die Iterationsformel
\begin{equation} \lambda = \sqrt{\frac{\frac{\pi}{2}+\lambda\cdot\sqrt{1-\frac{\lambda^2}{4}}-\alpha cos(1-\frac{\lambda^2}{2})}{\alpha cos(\frac{\lambda}{2})}} \end{equation}
Diese liefert mit $\lambda=1$ als Startwert nach drei Iterationsschritten den schon bekannten Fixpunktwert
\begin{equation} \lambda = \frac{R}{r} = 1,158728473 \end{equation}
Damit erhält man den Kreisradius $R$, der vom Halteseil der Ziege gebildet wird, zu
\begin{equation} R=\lambda\cdot r = 1,158728473\cdot 20m = \mathbf{23,1745695m} \end{equation}
Übrigens,
auch Wikipedia hat seit 2016 einen Eintrag zum Ziegenrätsel, siehe https://de.m.wikipedia.org/wiki/Ziegenproblem_(Geometrie) und seit 2004 gibt es bei khloebnel diese etwas ungenauere Lösung.
 Opa Jupp
Opa Jupp