GNU R: Logistische Regression mit R

Als Beispiel dienen Daten der Challenger-Katastrophe [Am 28. Januar 1986 explodierte die Raumfähre Challenger 73 Sekunden nach dem Start. Der Ausfall eines oder mehrerer Dichtungsringe in einer der seitlichen Feststoffrakten wurde als Grund der Katastrophe ermittelt.]

Probleme mit den Dichtungsringen sind auch vorher am Boden aufgetreten. So liegen Erhebungsdaten vor, die den Defekt eines Rings in Zusammenhang mit der Außentemperatur darstellen können: Je kälter es draußen ist, desto höher die Ausfallwahrscheinlichkeit eines Rings. Bedauerlicher Weise wurden diese Daten erst rückwirkend ausgewertet.

Diese Daten übertragen wir wie folgt in R:

Temp = c(66,67,68,70,72,75,76,79,53,58,70,75,67,67,69,70,73,76,78,81,57,63,70)
Ausfall = factor(c(0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1))
shuttle = data.frame(Temp, Ausfall)
colnames(shuttle) = c("Temp", "Ausfall")

Die Kodierung des factor Ausfall lautet: 0=kein Ausfall | 1=Ausfall Die Einheit für Temp lautet Fahrenheit.

Der Aufruf zur logistischen Regression [Ausfall erklärt durch Temperatur] lautet:

fit = glm(Ausfall~Temp,data=shuttle, family=binomial); fit

Call:  glm(formula = Ausfall ~ Temp, family = binomial, data = shuttle)

Coefficients:
(Intercept)         Temp  
    15.0429      -0.2322  

Degrees of Freedom: 22 Total (i.e. Null);  21 Residual
Null Deviance:      28.27 
Residual Deviance: 20.32    AIC: 24.32

Die Odds Ratio (OR) errechnet sich wie folgt:

exp(-0.2322)

[1] 0.7927875

Dies liefert das Ergebnis OR = 0.7927875. Die Interpretation lautet: Mit jedem höhren Grad an Temparatur ändert sich die Chance auf einem Ausfall um den Faktor 0.7927. Das bedeutet, dass die Chancen eines Ausfalls niedriger werden, je höher die Außentemperatur steigt. In der Nacht vor dem Challengerstart konnte eine Temperatur von 37°Fahrenheit gemessen werden. Auf Grundlage der logistischen Regression lässt sich nun die Ausfallwahrscheinlichkeit bei 37° Außentemperatur berechnen

# zuerst eine Hilfsfunktion zum umrechnen
y = function(x){
     blup = exp(15.0429 + (x*(-0.2322)))
     bla = blup/(1+blup)
     return(bla)}

# jetzt setzen wir 37 ein:
y(37)

[1] 0.9984243

Das Modell sagt bei einer Außentemperatur von 37° eine Ausfallwahrscheinlichkeit von 99,84% voraus.

Die Funktion hätten wir uns auch sparen können, da der Befehl predict diese Arbeit übernimmt.

predict(fit, data.frame(Temp=37),type="response")

        1 
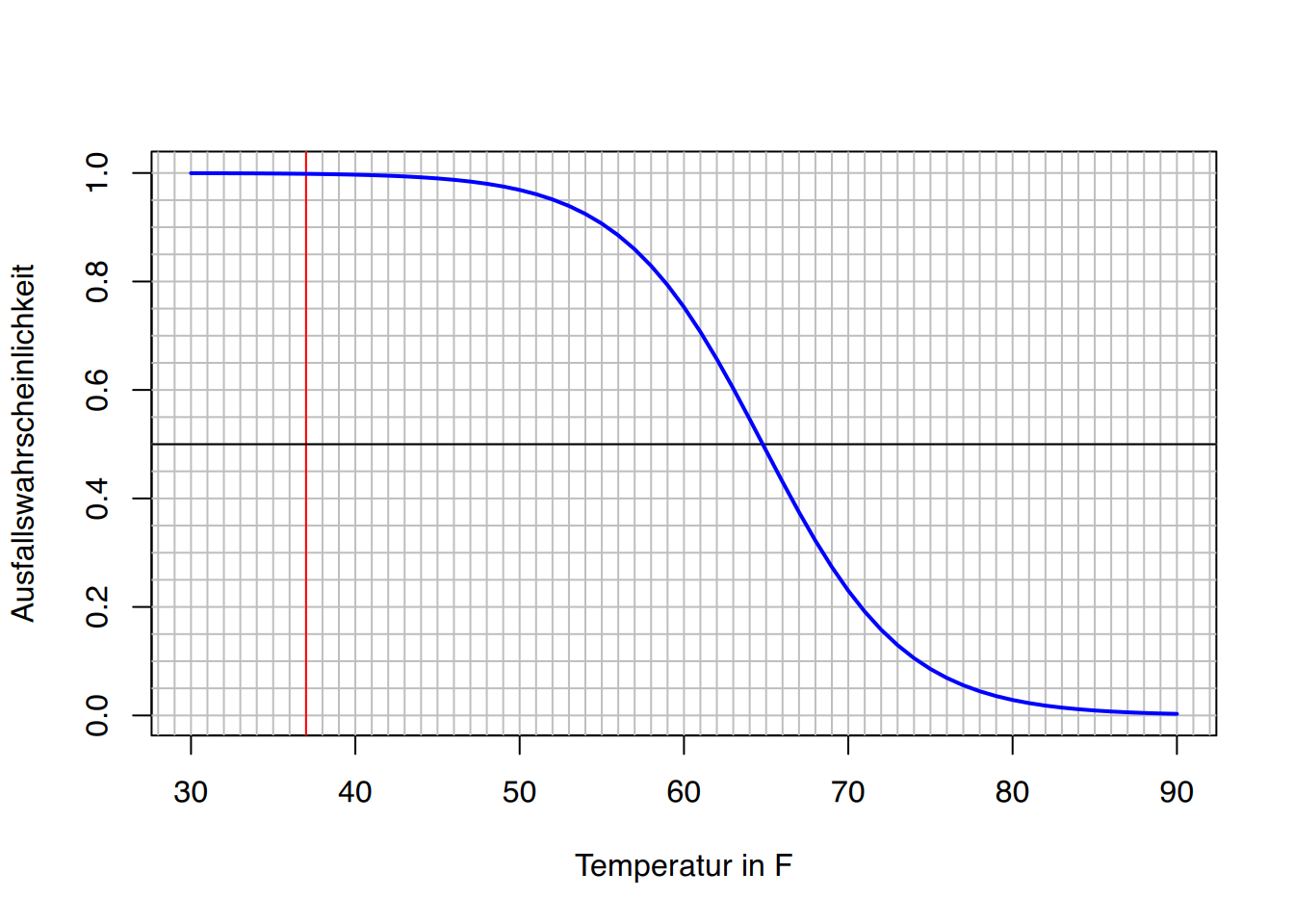
0.9984265 

Jetzt kann man dies für jede mögliche Temperatur durchmachen, und schon erhält man dieses schöne Plot.

y = predict(fit, data.frame(Temp=30:90),type="response")
plot(30:90, y, type="l", ylab="Ausfallswahrscheinlichkeit", xlab="Temperatur in F")
abline(v=seq(20,100,1),h=seq(-0.2,1.2,0.05),col="gray") #Mathegitter
abline(v=37,col="red") # 37-Grad
abline(h=0.5,col="black") # Mittellinie
points(30:90, y, type="l",lwd=2,col="blue") # Schätzwerte in "blau"