# einlesen
df <- read.table(url("http://www.produnis.de/nagut/anwesenheitnoten.csv"),
sep=";",
header=TRUE)Wer selbst als Dozent:in tätig ist, kennt diese Hypothese vermutlich: Studierende, die im Seminar anwesend sind, schneiden bei den Modulabschlussprüfungen besser ab. Es wäre doch echt schön, wenn sich diese Bauch-Hypothese irgendwie mit Evidenzstückchen stützen lassen würde…
Datensatz
An einem Seminar meiner Hochschule nahmen 27 Studierende teil. Auf unserer Lehrplattform Moodle wurden für das Seminar über die Aktivität “Anwesenheit” die Anwesenheiten der Studierenden erfasst. Moodle berechnet aus den eingetragenen Daten die prozentuale Gesamt-Anwesenheit für alle Teilnehmer:innen (100% = war immer da, 0% = war nie da). Zusätzlich wurden über die Aktivität “Abgabe” die Hausarbeiten der Studierenden (Modulabschlussprüfung) verarbeitet.
Wenn man nun die Moodle-Kursdaten extrahiert, kann man die Anwesenheiten sowie die Abschlussnoten in einer Tabelle “übereinanderlegen”. In eine CSV-Datei übertragen sieht das dann so aus:
Daten in R importieren
Mittels read.table() in Kombination mit url() lesen wir die CSV-Datei in unsere R-Session.
# anzeigen
df Anwesenheit Note
1 90,9 1,7
2 40,9 5
3 100 1
4 81,8
5 0 5
6 100 2
7 27,3 3,7
8 27,3 5
9 54,5 3,3
10 54,5
11 45,5 4
12 100 1,3
13 50 3,3
14 27,3 4
15 68,2 2,3
16 100
17 100 1
18 50 2
19 63,6 2,7
20 16,7
21 31,8 4
22 72,7 3,3
23 27,3 4
24 31,8 3
25 18,2 4
26 80 1,7
27 90,9 1,3# Datentyp
str(df)'data.frame': 27 obs. of 2 variables:
$ Anwesenheit: chr "90,9" "40,9" "100" "81,8" ...
$ Note : chr "1,7" "5" "1" "" ...Die Daten sind als char eingelesen worden. Um sie per as.numeric() umzuwandlen, müssen zuvor mittels gsub() alle Kommata in Punkte umgewandelt werden. Andernfalls werden die Dezimalstellen nicht erkannt, und R meldet für jeden Eintrag nur ein NA zurück.
df$Anwesenheit <- as.numeric(gsub(",", ".", df$Anwesenheit))
df$Note <- as.numeric(gsub(",", ".", df$Note))
#anzeigen
df Anwesenheit Note
1 90.9 1.7
2 40.9 5.0
3 100.0 1.0
4 81.8 NA
5 0.0 5.0
6 100.0 2.0
7 27.3 3.7
8 27.3 5.0
9 54.5 3.3
10 54.5 NA
11 45.5 4.0
12 100.0 1.3
13 50.0 3.3
14 27.3 4.0
15 68.2 2.3
16 100.0 NA
17 100.0 1.0
18 50.0 2.0
19 63.6 2.7
20 16.7 NA
21 31.8 4.0
22 72.7 3.3
23 27.3 4.0
24 31.8 3.0
25 18.2 4.0
26 80.0 1.7
27 90.9 1.3# Datentyp
str(df)'data.frame': 27 obs. of 2 variables:
$ Anwesenheit: num 90.9 40.9 100 81.8 0 100 27.3 27.3 54.5 54.5 ...
$ Note : num 1.7 5 1 NA 5 2 3.7 5 3.3 NA ...Jetzt ist alles richtig eingelesen.
Auswertung
Da die Noten unserer Hochschule Equidistanz aufweisen (die Abstände zwischen den einzelnen Noten sind gleich breit), werden metrische Verfahren angewendet.
Punktwolke
Zunächst werden die Daten in einer Punktwolke dargestellt.
# Punktewolke
plot(df$Note, df$Anwesenheit,
ylab="Anwesenheit in %", xlab="Abschlussnote",
main="Anwesenheit und Noten")
# Regressionsgerade
abline(lm( Anwesenheit ~ Note, data=df), col="red")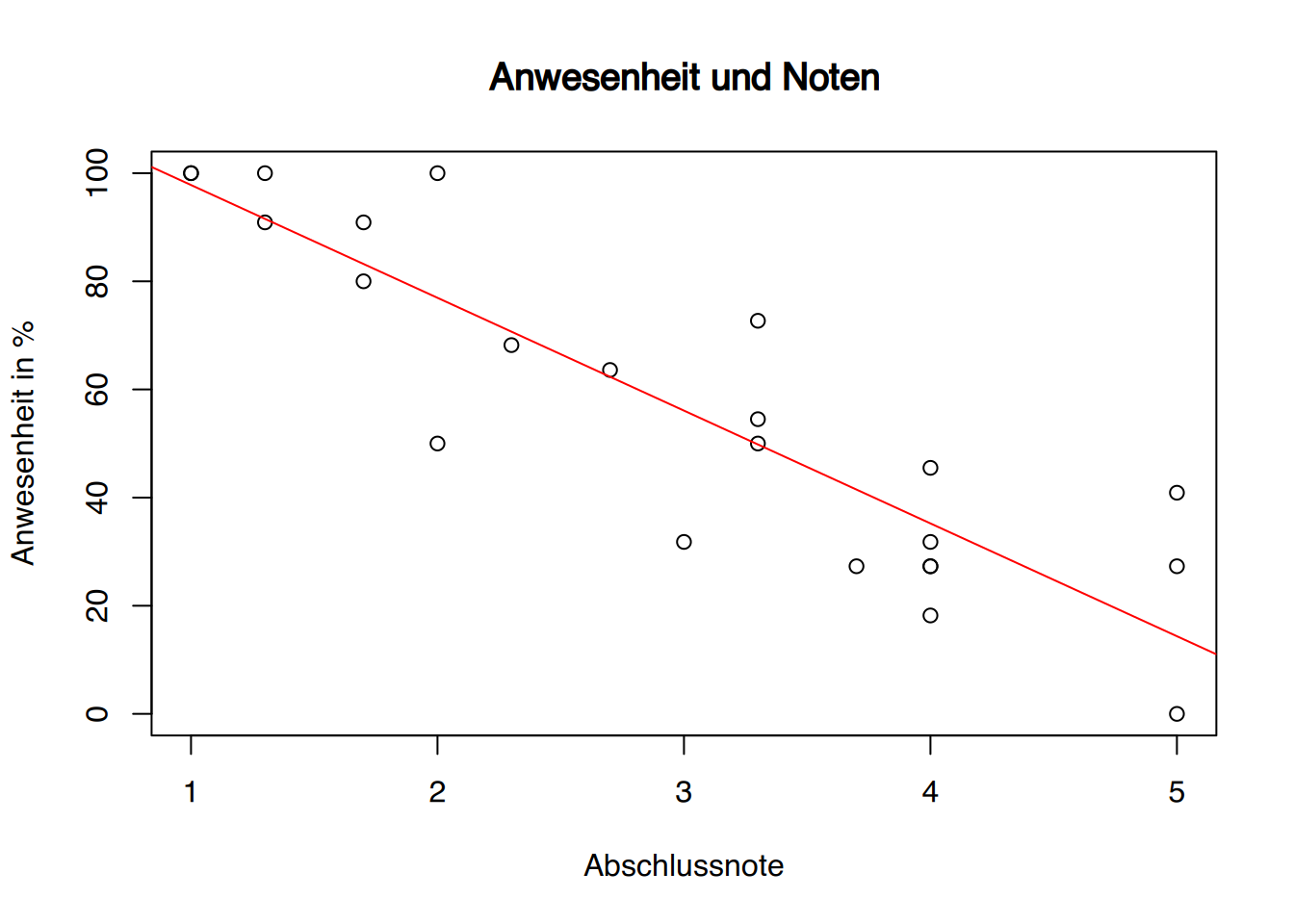
An dem Diagramm ist bereits ein Zusammenhang ablesbar. Auch die rote Regressionslinie sieht passend aus.
Korreltation
Berechnen wir nun den Maßkorrelationskoeffizienten nach Pearson:
cor.test(df$Note, df$Anwesenheit)
Pearson's product-moment correlation
data: df$Note and df$Anwesenheit
t = -8.8624, df = 21, p-value = 1.536e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9519299 -0.7510824
sample estimates:
cor
-0.8882762 Der Koeffizient ist mit -0,888 nahe an -1.
Es existiert ein starker negativer Zusammenhang zwischen Anwesenheit und Abschlussnote.
Da eine “bessere” Note mit einer “kleineren” Zahl einhergeht, ist der Einfluss negativ (je geringer die Anwesenheit, desto größer die Zahl der Note).
lineare Regression
Um die Stärke des Einflusses zu berechnen, erstellen wir zudem ein lineares Regressionsmodell nach der Struktur “Note erklärt durch Anwesenheit”.
fit <- lm(Note ~ Anwesenheit, data=df)
summary(fit)
Call:
lm(formula = Note ~ Anwesenheit, data = df)
Residuals:
Min 1Q Median 3Q Max
-1.22631 -0.35731 -0.08487 0.16461 1.42951
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.117412 0.272765 18.761 1.34e-14 ***
Anwesenheit -0.037822 0.004268 -8.862 1.54e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6137 on 21 degrees of freedom
(4 Beobachtungen als fehlend gelöscht)
Multiple R-squared: 0.789, Adjusted R-squared: 0.779
F-statistic: 78.54 on 1 and 21 DF, p-value: 1.536e-08Das Modell ist signifikant und erklärt ca. 78% des Rauschens. Die Anwesenheit hat einen Einfluss auf die Abschlussnote. Je weniger Anwesenheit, desto schlechter die Note. Da eine “bessere” Note mit einer “kleineren” Zahl einhergeht, ist der Einfluss negativ (je geringer die Anwesenheit, desto größer die Zahl der Note).
Mit jedem Prozentpunkt Anwesenheit verändert sich die Note um 0,04 Notenpunkte.
Diskussion
Korrelationen sind keine Kausalzusammenhänge! Die Daten zeigen “lediglich”, dass sich die Anwesenheiten und Notenergebnisse nach einem bestimmten Muster “gemeinsam verändern”. Dass dies so ist, kann viele Gründe haben. Es ist nicht zwingend notwendig, dass Anwesenheit die Note kausal beeinflusst.
In dem untersuchten Seminar geht es jedoch um die Anwendung spezifischen Wissens auf konkrete praktische Situationen. Im Seminar wird diese Anwendung erprobt und gefestigt. Es ist schwierig (und erfordert Überwindung des “inneren Schweinehundes”), diese Anwendungen privat, alleine und ohne “Korrekturinstanz” einzuüben. Somit ist nicht verwunderlich, dass Studierende, die wenig anwesend waren, schlechtere Ergebnisse erzielten.
Dies ist vermutlich von Fach zu Fach unterschiedlich. Es lässt sich wahrscheinlich viel leichter für eine Mathe- oder Statistikklausur lernen, wobei Übungsaufgaben bearbeitet und mit Lösungsblättern verglichen werden können. In medizinisch-pflegerischen Fächern wie “Kommunikation”, “Ethik” oder “Diagnostik” gibt es meist nicht “den einen” Lösungsweg, und das untersuchte Seminar zählt zu einem der drei genannten.
Fazit
So lange die Untersuchung nicht mit unterschiedlichen Kohorten in unterschiedlichen Seminaren wiederholt wird, gelten die Ergebnisse nur für den untersuchten Kurs. Eine verallgemeinernde Aussage ist nicht zulässig.
